1 Introduction

Adaptive filtering algorithms are widely used for signal processing in practical systems [1, 8, 9, 16]. Recently, diffusion adaptive filtering algorithms over distributed network have been widely studied [4, 5, 12, 19, 20]. These algorithms for distributed network are useful in many applications such as wireless sensor networks, distributed cooperative sensing and so on [6, 11].

In the adaptive filtering algorithms, the step size governs the convergence rate and the steady-state error. To meet the conflicting requirements of fast convergence rate and small steady-state error, the step size needs to be controlled. In the literatures, various schemes for controlling the step size have been proposed [2, 17], and they are expanded to diffusion adaptive filtering algorithm recently [7, 10, 14, 15].

In the diffusion adaptive filtering algorithms, a set of nodes in the network cooperates to estimate an unknown system. That is, each node of the network can share and fuse information at its neighbors through a combination method. The combination method determines weights connecting each node to its neighbor nodes. Therefore, the performance of the diffusion algorithms depends a lot on the design of the combination method. From this point of view, many algorithms mainly focused on designing the combination method by utilizing the network topology and/or statistics such as the signal-to-noise ratio (SNR) conditions. General combination methods are shown in Table 1. Among them, the uniform [4] and the metropolis [20] methods are based solely on topology of the distributed network. Therefore, they are sensitive to the network characteristics such as SNR conditions. To determine the weights by considering the network characteristics, the relative degree-variance method [5] is proposed. In this method, the estimate of every neighbor is weighted proportionally according to its inverse of noise variance. Thus, combination weights for the nodes that has the larger measurement noise will be smaller than other nodes.

Table 1 Combination methods
Full size table

This paper proposes a variable step size scheme and a combination method by analyzing the mean-square deviation (MSD) for the diffusion normalized least-mean-square (D-NLMS) algorithm. The MSD analysis is carried out based on [3, 13, 18]. For the adaptation step, the upper bound of the MSD is derived by analyzing the behavior of the MSD propagation instead of the exact MSD value because it cannot be obtained directly. The variable step size is obtained by minimizing the upper bound of the MSD at next iteration. The step size could be optimally controlled from the variable step size, and it yields improved performance in terms of the convergence rate and the steady-state error. The upper bound of the MSD and the optimal step size are reciprocally updated from each others at every iteration. For the diffusion step, a new combination method based on the MSD is proposed to overcome drawbacks of existing combination methods. The MSD at each node is used as its own reliability indicator because it represents preciseness of estimation and contains information that how much the estimate at each node is reliable. In the proposed MSD-based combination method, the combination weights can be determined adaptively because the MSD at each node is iteratively updated by using the recursion of the upper bound of the MSD that is derived in the adaptation step. Therefore, it provides more intuitive and effective weights than existing methods. The proposed variable step size and the MSD-based combination method provide performance improvement of the algorithm. The performance of the proposed algorithm is verified by simulations.

Fig. 1
figure 1

A distributed network with N nodes. At every \(i\), node \(k\) takes a measurement \(\{d_{k,i},\mathbf {u}_{k,i}\}\) and generates an estimate \(\mathbf {w}_{k,i}\) in cooperation with its neighbor set \(\mathcal {N}_k\)

Full size image

2 Diffusion Least-Mean-Square Algorithms

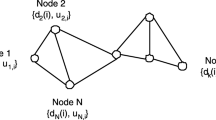
Consider a distributed network with \(N\) nodes (Fig. 1). The global system has an FIR vector \(\mathbf {w}^o \in \mathcal R^{M \times 1}\). At every node \(k\) and time instant \(i\), the desired signal \(d_{k,i}\) is represented as

$$\begin{aligned} d_{k,i}= \mathbf {u}_{k,i}^T \mathbf {w}^o + v_{k,i}, \end{aligned}$$
(1)

where \(\mathbf {u}_{k,i} \) denotes the white Gaussian input vector; \(v_{k,i}\) is the measurement noise that is assumed to be identically distributed and statistically independent of the input vector. It is assumed that \(v_{k,i}\) has a zero-mean white Gaussian distribution with variance \(\sigma _{v,k}^2\).

The adapt-then-combine (ATC) scheme [5] has been introduced in the literature for the diffusion least-mean-square (D-LMS) algorithm. By assuming that only intermediate estimates at each node are exchanged without their measurement data, the D-LMS algorithm is given as following two steps : the adaptation and the diffusion steps.

In the adaptation step, each node updates an intermediate estimate as

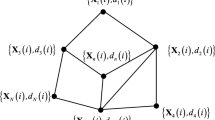
$$\begin{aligned} \varvec{\psi }_{k,i}&= \mathbf {w}_{k,i-1}+\mu _{k,i}\mathbf {u}_{k,i} \left( d_{k,i}-\mathbf {u}_{k,i}^T\mathbf {w}_{k,i-1}\right) , \end{aligned}$$
(2)

where \(\mathbf {w}_{k,i}\) is an individual estimate of \(\mathbf {w}^o\), \(\varvec{\psi }_{k,i}\) is an intermediate estimate, and \(\mu _{k,i}\) is a local step size at node \(k\). In the diffusion step, each node computes an individual estimate from weighted sum of intermediate estimates of its neighbor nodes as

$$\begin{aligned} \mathbf {w}_{k,i}&= \sum _{l=1}^N a_{l,k} \varvec{\psi }_{l,i}. \end{aligned}$$
(3)

The \(a_{l,k}\) is the weight connecting node \(k\) to its neighbor node \(l \in \mathcal {N}_k\), where \(\mathcal {N}_k\) is set of neighbor nodes for node \(k\) including itself and \(n_k\) is the degree at node \(k\) (the number of neighbor nodes for node \(k\)). The weight \(a_{l,k}\) can be formed using several combination methods in Table 1.

3 Variable Step Size Diffusion Normalized Least-Mean-Square Algorithm with MSD-Based Combination Method

The D-NLMS algorithm can be easily formulated as an extension of the D-LMS algorithm which solves its sensitivity to the input data. Based on the conventional normalized least-mean-square (NLMS) algorithm [8] with consideration about the distributed network, the D-NLMS algorithm is given by

$$\begin{aligned}&\text {(Adaptation Step)} \nonumber \\&~~\varvec{\psi }_{k,i} = \mathbf {w}_{k,i-1} +\mu _{k,i}\frac{\mathbf {u}_{k,i}\left( d_{k,i}-\mathbf {u}_{k,i}^T\mathbf {w}_{k,i-1}\right) }{\mathbf {u}_{k,i}^T\mathbf {u}_{k,i}}, \end{aligned}$$
(4)
$$\begin{aligned}&\text {(Diffusion Step)} \nonumber \\&~~\mathbf {w}_{k,i}= \sum _{l=1}^N a_{l,k} \varvec{\psi }_{l,i}. \end{aligned}$$
(5)

In this section, the variable step size is derived for the adaptation step to establish the fast convergence rate and small steady-state estimation errors. Furthermore, for the diffusion step, a new combination method interprets the MSD as a reliability indicator and adopts it to determine the weights for the intermediate estimates.

3.1 The Adaptation Step : MSD Analysis and Variable Step Size

In the adaptation step, the step size \(\mu _{k,i} \) is adjusted by minimizing the MSD which is defined as

$$\begin{aligned} \widehat{p}_{k,i}&\triangleq E\left( \varvec{\widetilde{\psi }}_{k,i}^T\varvec{\widetilde{\psi }}_{k,i}|\mathcal {U}_{k,i}\right) =\text {Tr}(\mathbf {\widehat{P}}_{k,i}) ,\end{aligned}$$
(6)
$$\begin{aligned} p_{k,i}&\triangleq E\left( \mathbf {\widetilde{w}}_{k,i}^T\mathbf {\widetilde{w}}_{k,i}|\mathcal {U}_{k,i}\right) =\text {Tr}(\mathbf {P}_{k,i}), \end{aligned}$$
(7)

where \(\varvec{\widetilde{\psi }}_{k,i} = \mathbf {w}^o - \varvec{\psi }_{k,i}\) and \(\mathbf {\widetilde{w}}_{k,i} = \mathbf {w}^o - \mathbf {w}_{k,i}\) are the intermediate and the individual weight error vectors, \(\mathbf {P}_{k,i}=E\left( \mathbf {\widetilde{w}}_{k,i}\mathbf {\widetilde{w}}_{k,i}^T|\mathcal {U}_{k,i}\right) \), \(\mathbf {\widehat{P}}_{k,i}=E\left( \varvec{\widetilde{\psi }}_{k,i}\varvec{\widetilde{\psi }}_{k,i}^T|\mathcal {U}_{k,i}\right) \), \(\mathcal {U}_{k,i} = \{\mathbf {u}_{k,j} |0 \le j < i\}\), and \(\text {Tr}(\cdot )\) is the trace of the matrix. The update Eq. (4) can be described in terms of \(\varvec{\widetilde{\psi }}_{k,i}\) and \(\mathbf {\widetilde{w}}_{k,i}\) as

$$\begin{aligned} \varvec{\widetilde{\psi }}_{k,i} = \mathbf {F}_{k,i}\mathbf {\widetilde{w}}_{k,i-1} - \mu _{k,i} v_{k,i}\mathbf {u}_{k,i}\left( \mathbf {u}_{k,i}^T\mathbf {u}_{k,i}\right) ^{-1}, \end{aligned}$$
(8)

where

$$\begin{aligned} \mathbf {F}_{k,i}=\left( \mathbf {I}-\mu _{k,i}\mathbf {u}_{k,i}\left( \mathbf {u}_{k,i}^T\mathbf {u}_{k,i}\right) ^{-1}\mathbf {u}_{k,i}^T\right) . \end{aligned}$$
(9)

To describe the transient behavior of the MSD, the input vector \(\mathbf {u}_{k,i}\) is considered as a given quantity because \(\mathbf {P}_{k,i}\) is a conditional expectation associated with \(\mathbf {u}_{k,i}\). If the dependencies of \(\varvec{\widetilde{\psi }}_{k,i-1}\) and \(v_{k,i}\) are neglected, \(\mathbf {\widehat{P}}_{k,i}\) is obtained as follows:

$$\begin{aligned} \mathbf {\widehat{P}}_{k,i}=\mathbf {F}_{k,i}\mathbf {P}_{k,i-1}\mathbf {F}_{k,i}^T + \mu _{k,i}^2\sigma _{v,k}^2\mathbf {u}_{k,i}(\mathbf {u}_{k,i}^T\mathbf {u}_{k,i})^{-2}\mathbf {u}_{k,i}^T. \end{aligned}$$
(10)

Then, recursion of the MSD is derived by taking the trace of both sides of Eq. (10) as follows:

$$\begin{aligned} \text {Tr}\left( \mathbf {\widehat{P}}_{k,i}\right) = \text {Tr}\left( \mathbf {F}_{k,i}^T\mathbf {F}_{k,i}\mathbf {P}_{k,i-1}\right) + \mu _{k,i}^2\sigma _{v,k}^2\left( \mathbf {u}_{k,i}^T\mathbf {u}_{k,i}\right) ^{-1}. \end{aligned}$$
(11)

In this recursion, \(\text {Tr}\left( \mathbf {F}_{k,i}^T\mathbf {F}_{k,i}\mathbf {P}_{k,i-1}\right) \) satisfies the relation according [13] as

$$\begin{aligned}&(-2\mu _{k,i} + \mu _{k,i}^2)\lambda _1(\mathbf {P}_{k,i-1}) + \text {Tr}(\mathbf {P}_{k,i-1}), \nonumber \\&\qquad \le \text {Tr}\left( \mathbf {F}_{k,i}^T\mathbf {F}_{k,i}\mathbf {P}_{k,i-1}\right) \nonumber \\&\qquad \le (-2\mu _{k,i} + \mu _{k,i}^2)\lambda _M(\mathbf {P}_{k,i-1}) + \text {Tr}(\mathbf {P}_{k,i-1}), \end{aligned}$$
(12)

where \(\lambda _j(\mathbf {P}_{k,i-1})\) is the \(j\)th largest eigenvalue of the \(\mathbf {P}_{k,i-1}\). Since \(\lambda _M(\mathbf {P}_{k,i-1}) \le \text {Tr}(\mathbf {P}_{k,i-1})/M\), there exists a positive constant \(\beta \ge 1\) such that

$$\begin{aligned} \lambda _M(\mathbf {P}_{k,i-1}) \simeq \frac{\text {Tr}(\mathbf {P}_{k,i-1})}{\beta M}. \end{aligned}$$
(13)

For white Gaussian input case, all diagonal elements of \(\mathbf {P}_{k,i-1}\) have the same value because the elements in the input vector are independent to each other. Therefore, \(\mathbf {P}_{k,i-1}\) can be simplified with only one element \(p_{k,i-1}/M\) such as \(p_{k,i-1}/M\times \mathbf {I}\). Then, above equation can be simply rewritten as

$$\begin{aligned} \lambda _M(\mathbf {P}_{k,i-1}) = \frac{p_{k,i-1}}{M}. \end{aligned}$$
(14)

That is, the value of \(\beta \) can be set to \(1\) for the white Gaussian input case. On the other hand, when the input vector is correlated, the condition number of matrix \(\mathbf {P}_{k,i-1}\) will be worse. So, differences have arisen between the eigenvalues. In this case, \(\beta \) should be properly selected to compensate the effects of the bad condition number of \(\mathbf {P}_{k,i-1}\). From above discussion and inequality in (12), Eq. (11) can be written as

$$\begin{aligned} \widehat{p}_{k,i} \le \left( 1-\frac{2\mu _{k,i} - \mu _{k,i}^2}{\beta M}\right) p_{k,i-1} + \frac{\mu _{k,i}^2\sigma _{v,k}^2}{\mathbf {u}_{k,i}^T\mathbf {u}_{k,i}}. \end{aligned}$$
(15)

From Eq. (15), the upper bound of the intermediate MSD is recursively determined by using the individual MSD at previous iteration. By minimizing the upper bound of \(\widehat{p}_{k,i}\) in (15) with respect to \(\mu _{k,i}\), the variable step size that most largely decreases the MSD of the intermediate estimate can be chosen. According to

$$\begin{aligned} \frac{\partial \widehat{p}_{k,i} }{\partial \mu _{k,i}} = \frac{2\mu _{k,i}-2}{\beta M}p_{k,i-1} + \frac{2\mu _{k,i}\sigma _{v,k}^2}{\mathbf {u}_{k,i}^T\mathbf {u}_{k,i}}, \end{aligned}$$
(16)

the variable step size for the best performance at node \(k\) and time instant \(i\) is obtained as follows:

$$\begin{aligned} \mu _{k,i} = \frac{p_{k,i-1}\mathbf {u}_{k,i}^T\mathbf {u}_{k,i}}{p_{k,i-1}\mathbf {u}_{k,i}^T\mathbf {u}_{k,i}+ \beta M \sigma _{v,k}^2}. \end{aligned}$$
(17)

The proposed step size contains regularization effects because of \(\beta M \sigma _{v,k}^2\) term in the denominator. Therefore, the proposed algorithm can maintain its performance even for badly excited input signals. Furthermore, the step size can reduce the computational complexity because it is obtained by minimizing the scalar recursive Eq. (15) for the MSD instead of the matrix recursion. By using the proposed variable step size, the proposed algorithm can achieve fast convergence and small steady-state estimation error.

3.2 The Diffusion Step : MSD-Based Combination Method

In the diffusion step, the individual estimate at the node \(k\) is determined by fusing the intermediate estimates from neighbors of node \(k\) with combination methods. As mentioned in Sect. 1, however, general combination methods do not reflect the network characteristics or are too complicated to implement in real-time process. In this section, therefore, a new combination method based on the MSD at each node is proposed to improve preciseness of the individual estimate.

The intermediate MSD denotes how close the intermediate estimates are to the unknown system, so the inverse of \(\hat{p}_{l,i}\) can be used as the weight for \(\varvec{\psi }_{l,i}\). To satisfy \(\sum _{l=1}^N a_{l,k} = 1\) as a convex parameter, the weights are defined as

$$\begin{aligned} a_{l,k} \triangleq \left\{ \begin{array}{ll} \left( \sum _{m \in \mathcal {N}_k}\widehat{p}_{m,i}^{-1}\right) ^{-1}\widehat{p}_{l,i}^{-1}, &{} \quad \text {if}~ l \in \mathcal {N}_k \\ 0, &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$
(18)

In this proposed MSD-based combination method, the node \(k\) uses \(\widehat{p}_{l,i}^{-1}\) as the reliability indicator for the node \(l\). The key advantage of working with the inverse of MSD instead of conventional combination methods is that it directly provides information that node has good characteristics and how much the intermediate estimate at each node is reliable. This strategy allows each node to cooperate with only reliable information. For example, if node \(l\) has large MSD because of the large noise of the node \(l\), then \(\widehat{p}_{l,i}^{-1}\) becomes small. Thus, the weight for \(\varvec{\psi }_{l,i}\) will be smaller than those of the other neighbor nodes. Consequently, the MSD-based combination method can effectively determine which node is reliable to estimate the unknown system and will show more improved performance than existing combination methods. By fusing \(\varvec{\psi }_{l,i}\) for \(l \in \mathcal {N}_k\) through the MSD-based combination method in (18), \(\mathbf {w}_{k,i}\) is determined as follows:

$$\begin{aligned} \mathbf {w}_{k,i}&= \sum _{l=1}^N a_{l,k} \varvec{\psi }_{l,i} \nonumber \\&= \sum _{l \in \mathcal {N}_k} \left( \sum _{m \in \mathcal {N}_k}\widehat{p}_{m,i}^{-1}\right) ^{-1}\widehat{p}_{l,i}^{-1} \varvec{\psi }_{l,i}. \end{aligned}$$
(19)

To extract the relationship between the individual and the intermediate MSDs at current iteration, (5) is developed in terms of \(\widetilde{\mathbf {w}}_{k,i}\) and \(\widetilde{\varvec{\psi }}_{k,i}\) by subtracting \(\mathbf {w}^o\) from both sides as

$$\begin{aligned} \widetilde{\mathbf {w}}_{k,i}= \sum _{l \in \mathcal {N}_k}a_{l,k}\widetilde{\varvec{\psi }}_{l,i}. \end{aligned}$$
(20)

Multiplying \({\mathbf {w}^o}^T\) to both sides of (20) and taking expectation lead to the following equation:

$$\begin{aligned} E\left( \widetilde{\mathbf {w}}_{k,i}{\mathbf {w}^o}^T\right) = E\left( \sum _{l \in \mathcal {N}_k}a_{l,k}\widetilde{\varvec{\psi }}_{l,i}{\mathbf {w}^o}^T\right) . \end{aligned}$$
(21)

Assume that the intermediate and the individual weight error vectors, \(\widetilde{\varvec{\psi }}_{k,i}\) and \(\widetilde{\mathbf {w}}_{k,i}\), are orthogonal to \(\varvec{\psi }_{k,i}\) and \(\mathbf {w}_{k,i}\), respectively, then the following relation is established:

$$\begin{aligned} -E\left( \widetilde{\mathbf {w}}_{k,i}\widetilde{\mathbf {w}}_{k,i}^T\right) = -E\left( \sum _{l \in \mathcal {N}_k}a_{l,k}\widetilde{\varvec{\psi }}_{l,i}\widetilde{\varvec{\psi }}_{l,i}^T\right) , \end{aligned}$$
(22)

which is represented as

$$\begin{aligned} \mathbf {P}_{k,i} = \sum _{l \in \mathcal {N}_k}a_{l,k} \mathbf {\widehat{P}}_{l ,i}. \end{aligned}$$
(23)

Taking trace to both sides of (23) leads to

$$\begin{aligned} p_{k,i}&= \sum _{l \in \mathcal {N}_k}a_{l,k}\widehat{p}_{l,i},\nonumber \\&=\sum _{l \in \mathcal {N}_k}\left( \sum _{m \in \mathcal {N}_k}\widehat{p}_{m,i}^{-1}\right) ^{-1}\widehat{p}_{l,i}^{-1}\widehat{p}_{l,i}\nonumber \\&= \frac{n_k}{\sum _{m \in \mathcal {N}_k}\widehat{p}_{m,i}^{-1}}, \end{aligned}$$
(24)

which is described with the harmonic sum of the intermediate MSD values. According to (24), \(p_{k,i}\) is recursively updated by using \(\widehat{p}_{l,i}\) where \(l \in \mathcal {N}_k\). Subsequently, the reliability indicator at next iteration (\(\widehat{p}_{k,i+1}^{-1}\)) is recursively updated according to (15) by using the \(p_{k,i}\) at the present iteration which is updated in (24). The proposed algorithm is summarized in Table 2.

Table 2 The proposed algorithm
Full size table

4 Simulation Results

The computer simulations are used to confirm that the proposed algorithm provides more precise estimates of \(\mathbf {w}^o\) than other algorithms. An unknown system is randomly generated with 16 taps (\(M = 16\)). The SNR for the measurement at node \(k\) is defined as follows:

$$\begin{aligned} \text {SNR}_k \triangleq 10 \log _{10} \frac{E(y_{k,i}^2)}{E(v_{k,i}^2)}, \end{aligned}$$
(25)

where \(y_{k,i} = \mathbf {u}_{k,i}^T\mathbf {w}^o\). The noise variance at the node \(k\), \(\sigma _{v,k}^2\), is considered as known value because it can be easily estimated during silences in practice. The MSD and the normalized mean squared deviation (NMSD) at node \(k\) can be computed as follows:

$$\begin{aligned}&\displaystyle \text {MSD}_k \triangleq E\left( \Vert \mathbf {w}^o - \mathbf {w}_{k,i} \Vert ^2 \right) , \end{aligned}$$
(26)
$$\begin{aligned}&\displaystyle \text {NMSD}_k \triangleq E\left( \Vert \mathbf {w}^o-\mathbf {w}_{k,i} \Vert ^2 / \Vert \mathbf {w}^o \Vert ^2 \right) . \end{aligned}$$
(27)

The network NMSD is chosen as a performance indicator that is defined as follows:

$$\begin{aligned} \text {Network NMSD }\triangleq \frac{1}{N}\sum _{k=1}^{N}\text {NMSD}_k. \end{aligned}$$
(28)

All simulation results are obtained by ensemble averaging over 100 trials. For fair comparison, the best tuning parameter values of the existing algorithms are determined after many trials. The relative degree-variance method is used in the diffusion step for the competing algorithms because it yields the best performance. Three distributed network topologies with the SNR values at each node are considered for simulations in Figs. 3, 5, and 7.

Fig. 2
figure 2

Simulated MSD learning curve (dashed gray line) and its prediction (solid black line) based on the proposed analysis for distributed network with one node (SNR = 30 dB)

Full size image
Fig. 3
figure 3

A general distributed network with 13 nodes and the their SNR values

Full size image

A Monte Carlo simulation is carried out in Fig. 2 to discuss regarding the accuracy of the proposed theoretical analysis to predict the MSD. Figure 2 demonstrates how the proposed analysis predicts the MSD learning behavior of the D-NLMS. It shows that the proposed approach excellently predicts the learning behavior of the practice MSD. Therefore, proposed theoretical analysis of the MSD has enough accuracy to derive the optimal step size and the MSD-based combination method.

Fig. 4
figure 4

NMSD learning curves of seven diffusion algorithms for the general distributed network in Fig. 3. \(\alpha =0.9\) [10], \(\delta =10^{-4}\) [10], \(\alpha =0.999\) [14], \(\gamma =0.01\) [14], \(\alpha =5\times 10^{-4}\) [15], \(\gamma =300\) [15], \(\epsilon =10^{-6}\) [7], \(\lambda =0.8\) [7], and \(\beta =1\) for the proposed algorithm

Full size image
Fig. 5
figure 5

A tree structure distributed network with 13 nodes and the their SNR values. In this topology, there exist no cycle path

Full size image

Figures 4 and 6 represent the network NMSD learning curves of the conventional D-LMS [5], the VSS-D-LMS [10], the VSS-D-LMS [14], the NC-D-LMS [15], the OSS-D-LMS [7], and the proposed algorithms with respect to the topologies in Figs. 3 and 5, respectively. The proposed algorithm achieves the smallest steady-state error and the fastest convergence rate among the competing algorithms, which means that the step size derived in this paper is very close to the optimal value in the concern of the fast convergence rate on every iteration.

Fig. 6
figure 6

NMSD learning curves of seven diffusion algorithms for the tree structure distributed network in Fig. 5. \(\alpha =0.95\) [10], \(\delta =10^{-5}\) [10], \(\alpha =0.999\) [14], \(\gamma =0.01\) [14], \(\alpha =5\times 10^{-4}\) [15], \(\gamma =300\) [15], \(\epsilon =10^{-5}\) [7], \(\lambda =0.7\) [7], and \(\beta =1\) for the proposed algorithm

Full size image
Fig. 7
figure 7

An extremely bad distributed network with 30 nodes. At every node, \(k\) takes small measurement except node \(15\). As an interference, \(0\) dB measurement noise is added at the node \(15\)

Full size image
Fig. 8
figure 8

NMSD learning curves of seven diffusion algorithms for the extremely bad distributed network in Fig. 7. \(\alpha =0.95\) [10], \(\delta =10^{-3}\) [10], \(\alpha =0.999\) [14], \(\gamma =10^{-3}\) [14], \(\alpha =7\times 10^{-4}\) [15], \(\gamma =300\) [15], \(\epsilon =10^{-6}\) [7], \(\lambda =0.55\) [7], and \(\beta =1\) for the proposed algorithm

Full size image
Fig. 9
figure 9

NMSD learning curves of the D-LMS algorithm with different combination methods for the extremely distributed network in Fig. 7. \(\mu = 0.2\) for the D-LMS, \(\beta = 1\) for the proposed algorithm

Full size image

Figure 8 shows the network NMSD learning curves of the competing algorithms and the proposed algorithm with respect to the topology in Fig. 7. The network topology is ring structure, and all nodes are contaminated by white Gaussian noise with SNR = 30 dB except node 15. The node 15 contains extremely bad information with SNR = 0 dB, which may affect other nodes in the diffusion step. As can be seen, the proposed algorithm establishes the fastest convergence rate and the smallest steady-state error, where the performances of the other algorithms are degraded due to bad information at node 15.

To confirm the effect of the proposed MSD-based combination method more clearly, an additional simulation result is represented in Fig. 9. It represents the NMSD learning curves of the conventional D-LMS algorithm with two different combination methods (metropolis and relative degree-variance) and the proposed algorithms. The D-LMS algorithm with the metropolis method is directly affected by bad information at node 15 because the combination is based only on the network topology. The D-LMS algorithm with the relative degree-variance method shows rather flat-shaped NMSD learning curves because it reflects the noise variance at each node as well as network topology when determining the combination coefficients to assign the smaller weight to the lower-SNR node. The NMSD learning curves of the proposed algorithm are clearly flat in spite of the bad information, and it can be said that the proposed variable step size scheme and the MSD-based combination method effectively suppress the effect of bad information.

5 Conclusion

In this paper, the variable step size and the MSD-based combination method were proposed for distributed networks. The variable step size derived by minimizing the upper bound of the MSD provided improvement of the filter performance in the aspects of the convergence rate and the steady-state estimation error. Furthermore, the MSD-based combination method can provide effective weights between the individual estimate and intermediate estimates by using the inverse of the MSD as a reliability indicator. The D-NLMS algorithm with the MSD-based combination method improved the performance against various network characteristics. Simulations showed that the proposed algorithm outperforms the existing diffusion algorithms.