1 Introduction

When implementing a state feedback controller, it is essential to measure all state variables, which increases the implementation cost due to expensive sensors. Thus, estimating state variables from some measurements has become an important issue [1,2,3]. Among many types of estimating methods, an \({H}_{\infty }\) filter has some interesting properties; it does not need statistical assumptions, and its noise signals only require arbitrary signals with boundary energy. Moreover, the \({H}_{\infty }\) filter is insensitive to the uncertainties regarding system dynamics. Hence, many researchers have studied the \({H}_{\infty }\) filter and applied it to various systems [4,5,6]. However, designing the filter for nonlinear systems is still challenging because of its complex dynamics.

The Takagi–Sugeno (T-S) fuzzy model approach is used to efficiently analyze nonlinear systems and has attracted great attention from researchers [7,8,9]. In the T-S fuzzy model approach, the nonlinear system is represented as the convex summation of multiple linear subsystems based on IF–THEN rules. This feature allows to application of existing linear control theories to nonlinear systems represented as a T-S fuzzy model [10,11,12,13]. In addition, a control system's stability is normally determined by solving linear matrix inequalities (LMIs), which are efficiently solved by contemporary numerical solvers. For these reasons, a variety of T-S fuzzy model-based controller and filter design methods are increasingly growing. In [14], the imperfect premise matching problem of the decentralized \({H}_{\infty }\) fuzzy filter was studied. In [15], the robust \({H}_{\infty }\) filtering problem for the in-vehicle networked system was dealt with considering the quantization and data dropouts.

Recently, a sampled-data system, which is a system handling continuous- and discrete-time signals simultaneously, has been in the limelight as a promising research topic due to the rapid development of computer technology. Most of the researchers employed the input-delay approach [16,17,18,19,20] when designing sampled-data \({H}_{\infty }\) filter systems. In this approach, the stability of a sampled-data system is analyzed in the continuous-time domain, by converting the discretized measurements and state variables into the continuous-time time-delayed signals. Also, the input-delay approach can be applied to systems with variable sampling periods by using the time-dependent Lyapunov–Krasovskii functional (LKF).

The issue of conservativeness in stability conditions for sampled-data systems remains unresolved. To relax the conservativeness, researchers have been focusing on developing a new LKF or introducing a novel matrix inequality condition. In [21], a sampled-data fuzzy observer design method was proposed for a nonlinear system with a nonlinear output equation, incorporating a two-sided LKF that fully considers available information about actual sampling patterns. In [22], a controller for a sampled-data system was designed using exponential time-varying gains, improving the maximum allowable sampling period than previous studies. Despite the advantages of utilizing the exponential time-varying gains, to the best of the authors' knowledge, there is an absence of studies focusing on employing time-varying gains to the filter design problem.

Meanwhile, the unpredictable occurrence of faults in actuators or sensors presents a significant threat. Once they occur, it leads to performance degradation or even system instability. Consequently, addressing fault detection and making controllers and filters robust to fault has become crucial in enhancing system reliability. In [23], the fault detection problem was addressed through the design of an interval type-2 fuzzy semi-Markov mode-dependent filter. Additionally, in [24] and [25], actuator faults were modeled as uncertain time-varying matrices. Under this actuator fault model, a robust controller for a T-S fuzzy system was developed, contributing to increased system reliability.

Motivated by the preceding analysis, this paper introduces a fault-tolerant sampled-data fuzzy filter design method for a T-S fuzzy system. The main contributions can be summarized as follows:

  1. 1)

    The proposed fault-tolerant \({H}_{\infty }\) sampled-data fuzzy filter design method incorporates an exponential time-varying gain concept, showcasing innovation and flexibility in filter design.

  2. 2)

    The utilization of exponential time-varying gains not only achieves a substantial reduction in convergence time but also relaxes design conditions, enlarging the efficiency and adaptability of the designed filter.

  3. 3)

    Through the integration of a robust control technique, the proposed filter is equipped with enhanced fault-tolerant capabilities, ensuring robust performance in the presence of sensor faults.

  4. 4)

    The derivation of the sufficient condition ensuring \({H}_{\infty }\) performance in terms of LMIs based on the LKF provides a systematic filter design framework.

Notations: For a symmetric matrix \(X\), \(X\succ 0\) (resp. \(X\prec 0\)) means that it is a positive (resp. negative) definite matrix. For any matrix \(X\), \({\text{He}}\{X\}=X+{X}^{T}\). For an invertible matrix \(X\), \({X}^{-T}\) denotes the inverse of \({X}^{T}\). For a square matrix \(X\), \({\lambda }_{{\text{min}}}(X)\) means the minimum eigenvalue of \(X\). \({\mathbb{Z}}_{\ge 0}\) denotes a set of all integers greater than or equal to 0. For positive integers \(a\) and \(b\), \({I}_{a\times b}\) is an identity matrix whose dimension is \(a\times b\).

2 Preliminaries

In this paper, the following T-S fuzzy system is considered:

$$\begin{array}{c}\dot{x}\left(t\right)=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left(t\right)\right)\left\{{A}_{i}x\left(t\right)+{B}_{i}\omega \left(t\right)\right\}\\ s\left(t\right)=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left(t\right)\right){C}_{1i}x(t)\\ y\left(t\right)=y\left({t}_{k}\right)=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left({t}_{k}\right)\right){C}_{2i}x\left({t}_{k}\right), t\in [{t}_{k},{t}_{k+1})\end{array}$$
(1)

where \({A}_{i}\in {\mathbb{R}}^{n\times n}\), \({B}_{i}\in {\mathbb{R}}^{n\times z}\), \({C}_{1i}\in {\mathbb{R}}^{{m}_{1}\times n}\), and \({C}_{2i}\in {\mathbb{R}}^{{m}_{2}\times n}\) are system matrices; \(x\left(t\right)\in {\mathbb{R}}^{n}\), \(\omega \left(t\right)\in {\mathbb{L}}_{2}^{z}\), and \(s\left(t\right)\in {\mathbb{R}}^{{m}_{1}}\) are the state vector, disturbance, and output vector to be estimated, respectively; \(y\left(t\right)\in {\mathbb{R}}^{{m}_{2}}\) is the measurement output vector, which holds its value at the sampling time \({t}_{k}>0\) for \(t\in \left[{t}_{k},{t}_{k+1}\right]\) and \(k\in {\mathbb{Z}}_{\ge 0}\). \(z(t)\) is the premise variables, \({w}_{i}\left(z\left(t\right)\right)\in \left[\mathrm{0,1}\right]\) is the membership function which holds \({\sum }_{i=1}^{r}{w}_{i}\left(z\left(t\right)\right)=1\). Also, the sampling period satisfies the following relationship:

$${t}_{k+1}- {t}_{k}:={h}_{k} \le h,$$

where \({h}_{k}\) is the sampling period for \(k\) th sampling time, and \(h\) is the maximum allowable sampling period.

Now, we propose the following fuzzy filter composed of exponential time-varying gains to estimate the state variables of (1):

$$\begin{array}{c}\dot{\widehat{x}}\left(t\right)=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{r}{w}_{i}\left(z\left(t\right)\right){w}_{j}\left(z\left({t}_{k}\right)\right)\left\{{\widehat{A}}_{i}\widehat{x}\left(t\right)\right.\\ \left.+{e}^{-\eta \left(t-{t}_{k}\right)}\left\{{\widehat{G}}_{ij}\widehat{x}\left({t}_{k}\right)+{\widehat{B}}_{i}{y}_{F}\left({t}_{k}\right)\right\}\right\}\\ \widehat{s}\left(t\right)=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left(t\right)\right){\widehat{C}}_{i}\widehat{x}(t)\end{array}$$
(2)

where \(\widehat{x}\left(t\right)\in {\mathbb{R}}^{n}\) and \(\widehat{s}\left(t\right)\in {\mathbb{R}}^{{m}_{1}}\) are the state and output vectors of the filter; \({\widehat{A}}_{i}\in {\mathbb{R}}^{n\times n}\), \({\widehat{G}}_{ij}\in {\mathbb{R}}^{n\times n}\), \({\widehat{B}}_{i}\in {\mathbb{R}}^{n\times {m}_{2}}\), and \({\widehat{C}}_{i}\in {\mathbb{R}}^{{m}_{1}\times n}\) are the filter gain matrices to be determined by the proposed design condition; \(\eta \in {\mathbb{R}}_{>0}\) is a given positive scalar; \({y}_{F\left({t}_{k}\right)}\in {\mathbb{R}}^{{m}_{2}}\) is the output of the system with the unknown fault.

Assumption 1

All premise variables can be measured for all time.

Remark 1

The output vector \(y(t)\) is measurable only when \(t={t}_{k}\). Also, some elements of the state vector \(x(t)\) are not measurable at all times. Thus, if we cannot exactly measure premise variables at time instances between \({t}_{k}\) and \({t}_{k+1}\), the system synthesis process becomes too complicated. To avoid this problem, we define Assumption 1.

Remark 2

The composition of the filter considered in this paper contains the exponential time-varying gain as shown in (2). It was studied in [22] and [26] that \(\eta\) is related to both the conservativeness of the stability condition and the convergence time of the state variables. Despite this fruitful feature, there has been limited research on the design of a sampled-data fuzzy filter composed of the exponential time-varying gain. Hence, we think that the proposed method, concentrating on the design of a sampled-data filter with exponential time-varying gain, makes a considerable contribution.

Motivated on [24] and [25], we assume that the faulty output, \({y}_{F({t}_{k})}\), is represented as the product of the unknown time-varying matrix and the sampled output of the system:

$${y}_{F\left({t}_{k}\right)}=F\left({t}_{k}\right)y\left({t}_{k}\right),$$

where \(F\left({t}_{k}\right)\in {\mathbb{R}}^{{m}_{2}\times {m}_{2}}\) is an unknown time-varying matrix representing unknown fault. Also, the fault matrix \(F\left({t}_{k}\right)\) is assumed to be decomposed as follows:

$$\begin{array}{c}F\left({t}_{k}\right)={\text{diag}}\left\{{f}_{1}\left({t}_{k}\right),{f}_{2}\left({t}_{k}\right),\cdots ,{f}_{m}\left({t}_{k}\right)\right\}\\ ={F}_{0}\left(I+{F}_{1}\left({t}_{k}\right)\right),{f}_{a}\left({t}_{k}\right)\in \left[{\underline{f}}_{a}, {\overline{f} }_{a}\right], a\in {I}_{m},\\ \begin{array}{c}{F}_{0}={\text{diag}}\left\{{f}_{01},{f}_{02},\cdots ,{f}_{0m}\right\},{f}_{0a}=\frac{{\underline{f}}_{a}+{\overline{f} }_{a}}{2},\\ {F}_{1}\left({t}_{k}\right)={\text{diag}}\left\{{f}_{11},{f}_{12},\cdots ,{f}_{1m}\right\},{f}_{1a}=\frac{{f}_{a}\left({t}_{k}\right)-{f}_{0a}}{{f}_{0a}},\\ {F}_{2}={\text{diag}}\left\{{f}_{21},{f}_{22},\cdots ,{f}_{2m}\right\},{f}_{2a}=\frac{{\overline{f} }_{a}-{\underline{f}}_{a}}{{\underline{f}}_{a}+{\overline{f} }_{a}},\end{array}\end{array}$$
(3)

where \({F}_{1}\left({t}_{k}\right)\) and \({F}_{2}\) hold \({F}_{1}^{T}\left({t}_{k}\right){F}_{1}\left({t}_{k}\right)\le {F}_{2}^{T} {F}_{2}\le I\); \(\overline{{f }_{a}}\) and \({\underline{f}}_{a}\) are the known upper and lower bounds of the element in the fault matrix, respectively.

Before proceeding further, we introduce the following shorthand notations for any matrix \({\mathcal{M}}_{i}\) for simplicity:

$$\begin{array}{c}\mathcal{M}\left(t\right):=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left(t\right)\right){\mathcal{M}}_{i},\mathcal{M}\left({t}_{k}\right):=\sum\limits_{i=1}^{r}{w}_{i}\left(z\left({t}_{k}\right)\right){\mathcal{M}}_{i},\\ \mathcal{M}\left(t,{t}_{k}\right):=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{r}{w}_{i}\left(z\left(t\right)\right){w}_{j}\left(z\left({t}_{k}\right)\right){\mathcal{M}}_{ij}.\end{array}$$

Applying the above shorthand notation, we can obtain the following estimation error system from (1) and (2):

$$\begin{array}{c}\dot{\overline{x} }\left(t\right)=\widetilde{A}\left(t\right)\overline{x }\left(t\right)+{e}^{-\eta \left(t-{t}_{k}\right)}\overline{G }\left(t,{t}_{k}\right)\overline{x }\left({t}_{k}\right)+\overline{B }\left(t\right)\omega \left(t\right),\\ \overline{e }(t)=\overline{C }\left(t\right)\overline{x }(t),\end{array}$$
(4)

where \(\overline{x }\left(t\right)={\text{col}}\left\{x\left(t\right),x\left(t\right)-\widehat{x}\left(t\right)\right\}\); \(\overline{e }(t)=s(t)-\widehat{s}(t)\)

$$\widetilde{A}\left(t\right)=\left[\begin{array}{cc}A\left(t\right)& 0\\ A\left(t\right)-\widehat{A}\left(t\right)& \widehat{A}\left(t\right)\end{array}\right]$$
$$\overline{G }\left(t,{t}_{k}\right)=\left[\begin{array}{cc}0& 0\\ -\widehat{G}\left(t,{t}_{k}\right)-\widehat{B}\left(t\right)F\left({t}_{k}\right){C}_{2}\left({t}_{k}\right)& \widehat{G}\left(t,{t}_{k}\right)\end{array}\right]$$
$$\overline{B }\left(t\right)=\left[\begin{array}{c}B\left(t\right)\\ B\left(t\right)\end{array}\right]; \overline{C }(t)=\left[\begin{array}{cc}{C}_{1}\left(t\right)-\widehat{C}\left(t\right)& \widehat{C}(t)\end{array}\right]$$
$$\widehat{B}\left(t\right)F\left({t}_{k}\right){C}_{2}\left({t}_{k}\right)=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{r}{w}_{i}\left(z\left(t\right)\right){w}_{j}\left({t}_{k}\right){\widehat{B}}_{i}F\left({t}_{k}\right){C}_{2i}$$

By denoting the filter error \(\varepsilon \left(t\right):={e}^{\eta t}\overline{x }\left(t\right)\) and the estimation error \({\overline{e} }_{\eta }\left(t\right):={e}^{\eta t}\overline{e }\left(t\right)\), (4) can be rewritten as follows:

$$\begin{array}{c}\dot{\varepsilon }\left(t\right)=\eta {e}^{\eta t}\overline{x }\left(t\right)+{e}^{\eta t}\dot{\overline{x} }\left(t\right)\\ =\overline{A }\left(t\right)\varepsilon \left(t\right)+\overline{G }\left(t,{t}_{k}\right)\varepsilon \left({t}_{k}\right)+\overline{B }\left(t\right){\omega }_{\eta }\left(t\right),\\ {\overline{e} }_{\eta }\left(t\right)=\overline{C }\left(t\right)\varepsilon \left(t\right)\end{array}$$
(5)

where

$$\overline{A }\left(t\right)=\widetilde{A}\left(t\right)+\left[\begin{array}{cc}\eta I& 0\\ 0& \eta I\end{array}\right]; {\omega }_{\eta }\left(t\right)={e}^{\eta t}\omega \left(t\right)$$

Before closing this section, we introduce the following lemmas:

Lemma 1

[27] For a given matrix \(X\succ 0\), the following inequality holds for all continuously differentiable function \(u\left(t\right)\) in \(\left[a,b\right]\to {\mathbb{R}}^{n}\):

$$-{\int }_{a}^{b}{\dot{u}}^{T}\left(\tau \right)X\dot{u}\left(\tau \right)d\tau \le -\frac{1}{b-a}\left({\Sigma }^{T}X\Sigma +3{\Upsilon}^{T}X\Upsilon\right),$$

where \(\Sigma =u\left(b\right)-u\left(a\right)\) and \(\Upsilon =u\left(b\right)+u\left(a\right)-\frac{2}{b-a}{\int }_{a}^{b}u\left(\tau \right)d\tau\)

Lemma 2

[28] The following statements are equivalent for any matrices \({\mathcal{Z}}_{1}\), \({\mathcal{Z}}_{2}\), and \({\mathcal{Z}}_{3}\) with appropriate dimensions and \(\tau \left(t\right)\in \left({\tau }_{1},{\tau }_{2}\right]\):

  1. 1)

    \({\mathcal{Z}}_{1}+\left({\tau }_{2}-\tau \left(t\right)\right){\mathcal{Z}}_{2}+\left(\tau \left(t\right)-{\tau }_{1}\right){\mathcal{Z}}_{3}\prec 0.\)

  2. 2)

    \(\left\{\begin{array}{c}{\mathcal{Z}}_{1}+\left({\tau }_{2}-{\tau }_{1}\right){\mathcal{Z}}_{2}\prec 0,\\ {\mathcal{Z}}_{1}+\left({\tau }_{2}-{\tau }_{1}\right){\mathcal{Z}}_{3}\prec 0.\end{array}\right.\)

3 Main results

In this section, the sufficient condition solving the following problem is derived in terms of LMIs:

Problem 1

Find the filter gain matrices \({\widehat{A}}_{i}\), \({\widehat{B}}_{i}\), \({\widehat{G}}_{ij}\), \({\widehat{C}}_{i}\) such that the following criteria hold for given scalars \(\eta >0\), \(\alpha \in \left(-\eta ,0\right]\), and \(h\ge {t}_{k+1}-{t}_{k}\):

  1. 1)

    The equilibrium point of (4) is exponentially stable with decay rate of \(\eta +\alpha\) when \(\omega \left(t\right)=0\).where \({t}_{f}\in {\mathbb{R}}_{>0}\) is the terminate time and \(\upgamma\) is a given positive scalar.

  2. 2)

    The following \({H}_{\infty }\) criterion is satisfied under the zero initial condition.where \({t}_{f}\in {\mathbb{R}}_{>0}\) is the terminate time and \(\upgamma\) is a given positive scalar.

    $${\int }_{0}^{{t}_{f}}{\overline{e} }_{\eta }^{T}\left(\tau \right){\overline{e} }_{\eta }\left(\tau \right)\hspace{0.17em}d\tau \le {\gamma }^{2}{\int }_{0}^{{t}_{f}}{\omega }_{\eta }^{T}\left(\tau \right){\omega }_{\eta }\left(\tau \right)\hspace{0.17em}d\tau$$
    (6)

The solution to the above problem is summarized in the following theorem:

Theorem 1

The estimation error system (4) satisfies the conditions given in Problem 1 if there exist positive definite matrices \({P}_{1}\in {\mathbb{R}}^{2n\times 2n}\), \({P}_{3}\in {\mathbb{R}}^{2n\times 2n}\), \(Q\in {\mathbb{R}}^{2n\times 2n}\), full rank matrices \({P}_{2}\in {\mathbb{R}}^{2n\times 2n}\), \({M}_{1}\in {\mathbb{R}}^{n\times n}\), \({M}_{2}\in {\mathbb{R}}^{n\times n}\), \({U}_{1}\in {\mathbb{R}}^{2n\times 2n}\), \({U}_{2}\in {\mathbb{R}}^{2n\times 2n}\), \({R}_{i}\in {\mathbb{R}}^{n\times n}\), \({S}_{i}\in {\mathbb{R}}^{n\times {m}_{2}}\),

\({\widehat C}_i\in\mathbb{R}^{m_1\times n},\;T_{ij}\in\mathbb{R}^{n\times n},\;Y_1\in\mathbb{R}^{2n\times\left(8n+z\right)},\;\mathrm{and}\;Y_2\in\mathbb{R}^{2n\times\left(8n+z\right)}\), and such that the following LMIs hold for given scalars \(\mu_1>0\mu_2>0{\underline f}_a>0{\overline f}_a>0\gamma>0\sigma>0h>0\eta>0\alpha\in\left(-\eta,0\right]\):

$$P=\left[\begin{array}{cc}{P}_{1}& *\\ {P}_{2}& {P}_{3}\end{array}\right]\succ 0$$
(7)
$${\Pi }_{1ij}=\left[\begin{array}{ccc}{\Gamma }_{1ij} + h{\Gamma }_{2}& *& \begin{array}{cc}*& *\end{array}\\ \begin{array}{c}{\overline{C} }_{i}{I}_{1}^{T}\\ \left[\begin{array}{cc}0& {F}_{0}^{T}{S}_{i}^{T}\end{array}\right]{\Omega }^{T}\\ \left[\begin{array}{cc}{C}_{2j}& 0\end{array}\right]{I}_{2}^{T}\end{array}& \begin{array}{c}-I\\ 0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}*\\ -{\left(\sigma {F}_{2}\right)}^{-1}I\\ 0\end{array}& \begin{array}{c}*\\ *\\ -\sigma {F}_{2}^{-1}I\end{array}\end{array}\end{array}\right]\prec 0$$
(8)
$${\Pi }_{2ij}=\left[\begin{array}{ccc}{\Gamma }_{1ij} + h{\Gamma }_{3}& *& \begin{array}{cc}*& \begin{array}{ccc}*& *& *\end{array}\end{array}\\ {\overline{C} }_{i}{I}_{1}^{T}& -I& \begin{array}{cc}*& \begin{array}{ccc}*& *& *\end{array}\end{array}\\ \begin{array}{c}\left[\begin{array}{cc}0& {F}_{0}^{T}{S}_{i}^{T}\end{array}\right]{\Omega }^{T}\\ \left[\begin{array}{cc}{C}_{2j}& 0\end{array}\right]{I}_{2}^{T}\\ \begin{array}{c}h{Y}_{1}\\ 3h{Y}_{2}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}-{\left(\sigma {F}_{2}\right)}^{-1}I& \begin{array}{ccc}*& *& *\end{array}\end{array}\\ \begin{array}{cc}0& \begin{array}{ccc}-\sigma {F}_{2}^{-1}I& *& *\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}0& \begin{array}{ccc}0& -hQ& *\end{array}\end{array}\\ \begin{array}{cc}0& \begin{array}{ccc}0& 0& -3hQ\end{array}\end{array}\end{array}\end{array}\end{array}\right]\prec 0$$
(9)

where

$$\begin{array}{c}{\Gamma }_{1ij}=2\mathrm{\alpha }{I}_{1}{P}_{1}{I}_{1}^{T}-\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}-{\upgamma }^{2}{I}_{5}{I}_{5}^{T}\\ +{\text{He}}\{{I}_{1}{P}_{2}{I}_{1}^{T}+{I}_{1}{P}_{1}{I}_{3}^{T}-{W}_{1}^{T}{Y}_{1}-3{W}_{2}^{T}{Y}_{2}+\Omega {\Phi }_{0ij}\};\\ \begin{array}{c}{\Gamma }_{2}=2\mathrm{\alpha }\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}+{I}_{3}Q{I}_{3}^{T}\\ +{\text{He}}\{{I}_{3}\left(\frac{{U}_{1}+{U}_{1}^{T}}{2}\right){I}_{1}^{T}+ {I}_{3}\left(-{U}_{1}+{U}_{2}\right){I}_{2}^{T}\};\\ \begin{array}{c}{\Gamma }_{3}=2\mathrm{\alpha }h{I}_{4}{P}_{3}{I}_{4}^{T}+{\text{He}}\{{I}_{4}\left(2\mathrm{\alpha }{P}_{2}+{P}_{3}\right){I}_{1}^{T}+{I}_{4}{P}_{2}{I}_{3}^{T}\};\\ {\Phi }_{0{\text{ij}}}=\left[\begin{array}{cc}{M}_{1}^{T}{A}_{i}+\eta {M}_{1}^{T}& 0\\ {M}_{2}^{T}{A}_{i}-{R}_{i}& {R}_{i}+\eta {M}_{2}^{T}\end{array}\right]{I}_{1}^{T}\\ \begin{array}{c}+\left[\begin{array}{cc}0& 0\\ -{T}_{ij}-{S}_{i}{F}_{0}{C}_{2j}& {T}_{ij}\end{array}\right]{I}_{2}^{T}-{M}^{T}{I}_{3}^{T}+{M}^{T}{\overline{B} }_{i}{I}_{5}^{T};\\ U=\left[\begin{array}{cc}\frac{{U}_{1}+{U}_{1}^{T}}{2}& *\\ {\left(-{U}_{1}+{U}_{2}\right)}^{T}& -{U}_{2}-{U}_{2}^{T}\frac{{U}_{1}+{U}_{1}^{T}}{2}\end{array}\right];\\ \begin{array}{c}M=\left[\begin{array}{cc}{M}_{1}& *\\ 0& {M}_{2}\end{array}\right]; {W}_{1}={\left({I}_{1}-{I}_{2}\right)}^{T};\\ {W}_{2}={\left({I}_{1}+{I}_{2}-2{I}_{4}\right)}^{T};\Omega ={I}_{1}+{\mu }_{1}{I}_{2}+{\mu }_{2}{I}_{3};\\ \begin{array}{c}{I}_{q}={\left[\begin{array}{cccc}{0}_{2n\times \left(q-1\right)2n}& {I}_{2n\times 2n}& {0}_{2n\times \left(4-q\right)2n}& {0}_{2n\times z}\end{array}\right]}^{T}\\ q\in {I}_{4}, {I}_{5}={\left[\begin{array}{cc}{0}_{z\times 8n}& {I}_{z\times z}\end{array}\right]}^{T}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}$$

Then, the filter gain matrices are obtained by \({\widehat{A}}_{i}={M}_{2}^{-T}{R}_{i}\), \({\widehat{B}}_{i}={M}_{2}^{-T}{S}_{i}\), \({\widehat{G}}_{ij}={M}_{2}^{-T}{T}_{ij}\).

Proof

Consider the following LKF:

$$V\left(t\right)={V}_{1}\left(t\right)+{V}_{2}\left(t\right)+{V}_{3}\left(t\right)$$

where

$$\begin{array}{c}{V}_{1}\left(t\right)={{e}^{2\alpha t}\left[\begin{array}{c}\varepsilon \left(t\right)\\ {\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \end{array}\right]}^{T}P\left[\begin{array}{c}\varepsilon \left(t\right)\\ {\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \end{array}\right]\\ {V}_{2}\left(t\right)=\left({t}_{k+1}-t\right){e}^{2\alpha t}{\left[\begin{array}{c}\varepsilon \left(t\right)\\ \varepsilon \left({t}_{k}\right)\end{array}\right]}^{T}U\left[\begin{array}{c}\varepsilon \left(t\right)\\ \varepsilon \left({t}_{k}\right)\end{array}\right]\\ {V}_{3}\left(t\right)=\left({t}_{k+1}-t\right){\int }_{{t}_{k}}^{t}{e}^{2\alpha \tau }{\dot{\varepsilon }}^{T}\left(\tau \right)Q\dot{\varepsilon }(t)d\tau .\end{array}$$

With the conditions of \({P}_{3}\succ 0\) and \(h\ge t-{t}_{k}\), the time derivative of \({V}_{1}\left(t\right)\) can be obtained as follows:

$$\begin{array}{c}{\dot{V}}_{1}\left(t\right)={e}^{2\alpha t}[2{\varepsilon }^{T}\left(t\right)\left(\alpha {P}_{1}+{P}_{2}^{T}\right)\varepsilon \left(t\right)+2{\varepsilon }^{T}\left(t\right){P}_{1}\dot{\varepsilon }(t)\\ +\left(t-{t}_{k}\right)\{2{\left(\frac{1}{t-{t}_{k}}{\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \right)}^{T}\\ \begin{array}{c}\times (2\alpha {P}_{2}+{P}_{3})\varepsilon (t)\\ +2\alpha \left(t-{t}_{k}\right){\left(\frac{1}{t-{t}_{k}}{\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \right)}^{T}{P}_{3}\\ \begin{array}{c}\times \left(\frac{1}{t-{t}_{k}}{\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \right)\\ +2{\left(\frac{1}{t-{t}_{k}}{\int }_{{t}_{k}}^{t}\varepsilon \left(\tau \right)d\tau \right)}^{T}{P}_{2}\dot{\varepsilon }(t)\}]\\ \begin{array}{c}\le {e}^{2\alpha t}{\upzeta }^{T}(t)[2\alpha {I}_{1}{P}_{1}{I}_{1}^{T}+{\text{He}}\{{I}_{1}{P}_{2}{I}_{1}^{T}+{I}_{1}{P}_{1}{I}_{3}^{T}\}\\ +\left(t-{t}_{k}\right)\{2\alpha h{I}_{4}{P}_{3}{I}_{4}^{T}+{\text{He}}\{{I}_{4}\left(2\alpha {P}_{2}+{P}_{3}\right){I}_{1}^{T}\\ +{I}_{4}{P}_{2}{I}_{3}^{T}\} \}]\zeta (t),\end{array}\end{array}\end{array}\end{array}$$
(10)

where

$$\upzeta \left(t\right)={\text{col}}\left\{\upvarepsilon \left(t\right),\upvarepsilon \left({t}_{k}\right),\dot{\upvarepsilon }\left(t\right),\frac{1}{t-{t}_{k}}{\int }_{{t}_{k}}^{t}\upvarepsilon \left(\uptau \right)\hspace{0.17em}d\uptau ,{\upomega }_{\upeta }\left(t\right)\right\}.$$

Next, the time derivative of \({V}_{2}\left(t\right)\) is given as follows:

$$\begin{array}{c}{V}_{2}\left(t\right)={e}^{2\alpha t}{\zeta }^{T}\left(t\right)[-\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}\\ +\left({t}_{k+1}-t\right)\{2\alpha \left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}\\ \begin{array}{c}+{\text{He}}\{{I}_{3}\left(\frac{{U}_{1}+{U}_{1}^{T}}{2}\right){I}_{1}^{T}\\ + {I}_{3}\left(-{U}_{1}+{U}_{2}\right){I}_{2}^{T}\}\}]\zeta \left(t\right)\end{array}\end{array}$$
(11)

The time derivative of \({{\text{V}}}_{3}\left({\text{t}}\right)\) becomes:

$$\begin{array}{c}\dot{{V}_{3}}\left(t\right)=-{\int }_{{t}_{k}}^{t}{e}^{2\alpha \tau }{\dot{\varepsilon }}^{T}\left(\tau \right)Q\dot{\varepsilon }\left(\tau \right)\hspace{0.17em}d\tau \\ +\left({t}_{k+1}-t\right){e}^{2\alpha t}{\dot{\varepsilon }}^{T}\left(t\right)Q\dot{\varepsilon }\left(t\right)\\ \begin{array}{c}\le -{e}^{2\alpha t}{\int }_{{t}_{k}}^{t}{\dot{\varepsilon }}^{T}\left(\tau \right)Q\dot{\varepsilon }\left(\tau \right)d\tau \\ +\left({t}_{k+1}-t\right){e}^{2\alpha t}{\dot{\varepsilon }}^{T}\left(t\right)Q\dot{\varepsilon }\left(t\right)\end{array}\end{array}$$
(12)

Applying Lemma 1 to the first term in (12), we have:

$$\begin{array}{c}{\dot{V}}_{3}\left(t\right)\le {e}^{2\alpha t}{\zeta }^{T}\left(t\right)\{-\frac{1}{t-{t}_{k}}({W}_{1}Q{W}_{1}^{T}+3{W}_{2}Q{W}_{2}^{T})\\ +\left({t}_{k+1}-t\right){I}_{3}Q{I}_{3}^{T} \}\zeta (t),\end{array}$$
(13)

where \(\Delta \left({\text{t}}\right)=\upvarepsilon \left({\text{t}}\right)+\upvarepsilon \left({{\text{t}}}_{{\text{k}}}\right)-\frac{2}{{\text{t}}-{{\text{t}}}_{{\text{k}}}}{\int }_{{{\text{t}}}_{{\text{k}}}}^{{\text{t}}}\varepsilon \left(\tau \right){\text{d}}\tau\), and \({W}_{1}\) and \({W}_{2}\) are defined in Theorem 1.

Next, because of the positive definiteness of \(Q\), the following inequalities always hold for any matrices \({Y}_{1}\) and \({Y}_{2}\) and the integer set \(i\in \{\mathrm{1,2}\}\):

$$\frac{1}{t-{t}_{k}}({W}_{i}Q-\left(t-{t}_{k}\right){Y}_{i}^{T}) {Q}^{-1}{\left({W}_{i}Q-\left(t-{t}_{k}\right){Y}_{i}^{T}\right)}^{T}\succ 0.$$

Summing the above for all \(i\in \left\{\mathrm{1,2}\right\}\), we obtain:

$$\begin{array}{c}-\frac{1}{t-{t}_{k}}\left({W}_{1}Q{W}_{1}^{T}+3{W}_{2}Q{W}_{2}^{T}\right)\\ \prec -{\text{He}}\left\{{W}_{1}{Y}_{1}+3{W}_{2}{Y}_{2}\right\}\\ +(t-{t}_{k})({Y}_{1}^{T}{Q}^{-1}{Y}_{1}+3{Y}_{2}^{T}{Q}^{-1}{Y}_{2})\end{array}$$

Applying the above result to (13), we can rewrite it as follows:

$$\begin{array}{c}{\dot{V}}_{3}\left(t\right)\le {e}^{2\alpha t}{\zeta }^{T}\left(t\right)\{-{\text{He}}\left\{{W}_{1}{Y}_{1}+3{W}_{2}{Y}_{2}\right\}\\ +\left(t-{t}_{k}\right)\left({Y}_{1}^{T}{Q}^{-1}{Y}_{1}+3{Y}_{2}^{T}{Q}^{-1}{Y}_{2}\right)\\ +\left({t}_{k+1}-t\right){I}_{3}Q{I}_{3}^{T}\}\zeta (t)\end{array}$$
(14)

Given positive scalars \({\upmu }_{1}\) and \({\upmu }_{2}\) and full-rank matrices \({M}_{1}\) and \({M}_{2}\) whose dimension is \(2n\times 2n\), we can derive the following null term from (5):

$$\begin{array}{c}0=2{e}^{2\alpha t}{\left\{M\varepsilon \left(t\right)+{\mu }_{1}M\varepsilon \left({t}_{k}\right)+{\mu }_{2}M\dot{\varepsilon }\left(t\right)\right\}}^{T}\\ \times \{-\dot{\varepsilon }(t)+\overline{A }\left(t\right)\varepsilon (t)+\overline{G }\left(t,{t}_{k}\right)\varepsilon ({t}_{k})+\overline{B }\left(t\right){\omega }_{\eta }(t)\}\\ \begin{array}{c}={e}^{2\alpha t}{\zeta }^{T}(t){\text{He}}\{\Omega {M}^{T}\{\overline{A }\left(t\right){I}_{1}^{T}+\overline{G }\left(t,{t}_{k}\right){I}_{2}^{T}-{I}_{3}^{T}\\ +\overline{B }\left(t\right){I}_{5}^{T}\}\}\zeta (t)\end{array}\end{array}$$
(15)

where \(M={\text{diag}}\{{M}_{1}, {M}_{2}\}\) \(\Omega ={I}_{1}+{\upmu }_{1}{I}_{2}+{\upmu }_{2}{I}_{3}\). On the other hand, using (3) and (5), we can reformulate the fault matrix \(F\left({t}_{k}\right)\) in (15) as follows:

$$\begin{array}{c}{\text{He}}\left\{\Omega {M}^{T}\left\{\overline{A }\left(t\right){I}_{1}^{T}+\overline{G }\left(t,{t}_{k}\right){I}_{2}^{T}-{I}_{3}^{T}+\overline{B }\left(t\right){I}_{5}^{T}\right\}\right\}\\ ={\text{He}}\{\Omega {M}^{T}\{\overline{A }\left(t\right){I}_{1}^{T}-{I}_{3}^{T}+\overline{B }\left(t\right){I}_{5}^{T}\\ \begin{array}{c}+\left(\left[\begin{array}{cc}0& 0\\ -\widehat{G}\left(t,{t}_{k}\right)-\widehat{B}\left(t\right){F}_{0}{C}_{2}\left({t}_{k}\right)& \widehat{G}\left(t,{t}_{k}\right)\end{array}\right]\right.\\ +\left.\left[\begin{array}{cc}0& 0\\ -\widehat{B}\left(t\right){F}_{0}{F}_{1}({t}_{k}){C}_{2}({t}_{k})& 0\end{array}\right]\right){I}_{2}^{T}\}\}\\ \begin{array}{c}={\text{He}}\{\Omega {\Phi }_{0}\left(t,{t}_{k}\right)\\ +\Omega {M}^{T}\left[\begin{array}{cc}0& 0\\ -\widehat{B}\left(t\right){F}_{0}{F}_{1}({t}_{k}){C}_{2}({t}_{k})& 0\end{array}\right]{I}_{2}^{T}\end{array}\end{array}\end{array}$$
(16)

where

$$\begin{array}{c}{\Phi }_{0}\left(t,{t}_{k}\right)=\left[\begin{array}{cc}{M}_{1}^{T}A\left(t\right)+\eta {M}_{1}^{T}& 0\\ {M}_{2}^{T}A\left(t\right)-R\left(t\right)& R\left(t\right)+\eta {M}_{2}^{T}\end{array}\right]{I}_{1}^{T}\\ +\left[\begin{array}{cc}0& 0\\ -T\left(t,{t}_{k}\right)-S\left(t\right){F}_{0}{C}_{2}\left({t}_{k}\right)& T\left(t,{t}_{k}\right)\end{array}\right]{I}_{2}^{T}\\ \begin{array}{c}-\left[\begin{array}{cc}{M}_{1}^{T}& 0\\ 0& {M}_{2}^{T}\end{array}\right]{I}_{3}^{T}+\left[\begin{array}{c}{M}_{1}^{T}B\left(t\right)\\ {M}_{2}^{T}B\left(t\right)\end{array}\right]{I}_{5}^{T},\\ R\left(t\right)={M}_{2}^{T}\widehat{A}\left(t\right), S\left(t\right)={M}_{2}^{T}\widehat{B}\left(t\right),\\ T\left(t,{t}_{k}\right)={M}_{2}^{T}\widehat{G}\left(t,{t}_{k}\right)\end{array}\end{array}$$

In addition, the last term of (16) can be further reformulated as follows:

$$\begin{array}{c}-{\text{He}}\left\{\Omega {M}^{T}\left[\begin{array}{cc}0& 0\\ \widehat{B}\left(t\right){F}_{0}{F}_{1}\left({t}_{k}\right){C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\right\}\\ =-{\text{He}}\left\{\Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{1}\left({t}_{k}\right)\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\right\}\\ \begin{array}{c}\le \sigma \Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{2}{\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]}^{T}M{\Omega }^{T}\\ +{\sigma }^{-1}{I}_{2}{\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]}^{T}{F}_{2}\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\end{array}\end{array}$$
(17)

Here, we applied the well-known matrix inequality \({X}^{T}Y+{Y}^{T}X\le \rho {X}^{T}X+{\rho }^{-1}{Y}^{T}Y\), where \(X\) and \(Y\) are any matrices and \(\rho\) is a scalar.

Now, summing (10), (11), (14), (15) with (16) and (17), the following inequality is obtained:

$$\begin{array}{c}\dot{V}\left(t\right)+{e}^{2\alpha t}\left\{{\overline{e} }_{\eta }^{T}\left(t\right){\overline{e} }_{\eta }\left(t\right)-{\gamma }^{2}{\omega }_{\eta }^{T}\left(t\right){\omega }_{\eta }\left(t\right)\right\}\\ \le {e}^{2\alpha t}{\zeta }^{T}\left(t\right)\left[{\Gamma }_{1}\right.\left(t,{t}_{k}\right)+{I}_{1}{\overline{C} }^{T}\left(t\right)\overline{C }\left(t\right){I}_{1}^{T}\\ \begin{array}{c}+\sigma \Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{2}{\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]}^{T}M{\Omega }^{T}\\ +{\sigma }^{-1}{I}_{2}{\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]}^{T}{F}_{1}\left({t}_{k}\right)\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\\ \begin{array}{c} +\left({t}_{k+1}-t\right){\Gamma }_{2}+\left(t-{t}_{k}\right)\left\{{\Gamma }_{3}+{Y}_{1}^{T}{Q}^{-1}{Y}_{1}\right.\\ +\left.\left.3{Y}_{2}^{T}{Q}^{-1}{Y}_{2}\right\}\right]\zeta \left(t\right),\end{array}\end{array}\end{array}$$
(18)

where

$$\begin{array}{c}{\Gamma }_{1}\left(t,{t}_{k}\right)=2\alpha {I}_{1}{P}_{1}{I}_{1}^{T}-\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}-{\gamma }^{2}{I}_{5}{I}_{5}^{T}\\ +{\text{He}}\{{I}_{1}{P}_{2}{I}_{1}^{T}+{I}_{1}{P}_{1}{I}_{3}^{T}-{W}_{1}^{T}{Y}_{1}\\ \begin{array}{c}\left.-3{W}_{2}^{T}{Y}_{2}+\Omega {\Phi }_{0}\left(t,{t}_{k}\right)\right\}\\ {\Gamma }_{2}=2\alpha \left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]U{\left[\begin{array}{cc}{I}_{1}& {I}_{2}\end{array}\right]}^{T}+{I}_{3}Q{I}_{3}^{T}\\ \begin{array}{c}+{\text{He}}\left\{{I}_{3}\left(\frac{{U}_{1}+{U}_{1}^{T}}{2}\right){I}_{1}^{T}+{I}_{3}\left(-{U}_{1}+{U}_{2}\right){I}_{2}^{T}\right\},\\ {\Gamma }_{3}=\mathrm{ He}\left\{{I}_{4}\left(2\alpha {P}_{2}+{P}_{3}\right){I}_{1}^{T}+{I}_{4}{P}_{2}{I}_{3}^{T}\right\}+2\alpha h{I}_{4}{P}_{3}{I}_{4}^{T}\end{array}\end{array}\end{array}$$

We know that \(\dot{V}\left(t\right)+{e}^{2\alpha t}\left\{{\overline{e} }_{\eta }^{T}\left(t\right){\overline{e} }_{\eta }\left(t\right)-{\gamma }^{2}{\omega }_{\eta }^{T}\left(t\right){\omega }_{\eta }\left(t\right)\right\}\)

\(\le 0\) if the following matrix inequality holds:

$$\begin{array}{c}{\Gamma }_{1}\left(t,{t}_{k}\right)+{I}_{1}{\overline{C} }^{T}\left(t\right)\overline{C }\left(t\right){I}_{1}^{T}\\ +\sigma \Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{2}{\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]}^{T}M{\Omega }^{T}\\ \begin{array}{c}+{\sigma }^{-1}{I}_{2}{\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]}^{T}{F}_{2}\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\\ \begin{array}{c}+\left(t-{t}_{k}\right)\left\{{\Gamma }_{3}+{Y}_{1}^{T}{Q}^{-1}{Y}_{1}+3{Y}_{2}^{T}{Q}^{-1}{Y}_{2}\right\}\\ +\left({t}_{k+1}-t\right){\Gamma }_{2}\prec 0.\end{array}\end{array}\end{array}$$
(19)

From Lemma 2, we know that (19) holds if the following two matrix inequalities are satisfied simultaneously:

$$\begin{array}{c}{\Gamma }_{1}\left(t,{t}_{k}\right)+{I}_{1}{\overline{C} }^{T}\left(t\right)\overline{C }\left(t\right){I}_{1}^{T}\\ +\sigma \Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{2}{\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]}^{T}M{\Omega }^{T}\\ +{\sigma }^{-1}{I}_{2}{\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]}^{T}{F}_{2}\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}+h{\Gamma }_{2}\prec 0\end{array}$$
(20)
$$\begin{array}{c}{\Gamma }_{1}\left(t,{t}_{k}\right)+{I}_{1}{\overline{C} }^{T}\left(t\right)\overline{C }\left(t\right){I}_{1}^{T}\\ +\sigma \Omega {M}^{T}\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]{F}_{2}{\left[\begin{array}{c}0\\ \widehat{B}\left(t\right){F}_{0}\end{array}\right]}^{T}M{\Omega }^{T}\\ \begin{array}{c}+{\sigma }^{-1}{I}_{2}{\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]}^{T}{F}_{2}\left[\begin{array}{cc}{C}_{2}\left({t}_{k}\right)& 0\end{array}\right]{I}_{2}^{T}\\ +h\left({\Gamma }_{3}+{Y}_{1}^{T}{Q}^{-1}{Y}_{1}+3{Y}_{2}^{T}{Q}^{-1}{Y}_{2}\right)\prec 0\end{array}\end{array}$$
(21)

Applying the Schur complement to (20) and (21), we can obtain LMIs (8) and (9), ensuring the following:

$$\dot{V}\left(t\right)+{e}^{2\alpha t}\left\{{\overline{e} }_{\eta }^{T}\left(t\right){\overline{e} }_{\eta }\left(t\right)-{\gamma }^{2}{\omega }_{\eta }^{T}\left(t\right){\omega }_{\eta }\left(t\right)\right\}\le 0.$$
(22)

If we assume that \({\omega }_{\eta }\left(t\right)=0\), then we obtain:

$$0\ge \dot{V}\left(t\right)+{e}^{2\alpha t}{\varepsilon }^{T}\left(t\right)\varepsilon \left(t\right)\ge \dot{V}\left(t\right).$$
(23)

Therefore, Lemma 1 in [29] validates that:

$$\begin{array}{c}{\Vert \varepsilon \left(t\right)\Vert }^{2}\le \beta {\Vert \varepsilon \left({t}_{k}\right)\Vert }^{2}\\ =\frac{\beta }{{\lambda }_{min}\left({P}_{1}\right)}{\lambda }_{min}\left({P}_{1}\right){e}^{-2\alpha t}{e}^{2\alpha t}{\Vert \varepsilon \left(t\right)\Vert }^{2}\\ =\frac{\beta }{{\lambda }_{min}\left({P}_{1}\right)}{e}^{-2\alpha t}V\left(0\right)\end{array}$$

where \(\beta\) is a positive scalar that satisfies Lemma 1 in [29]. Consequently, we can get the following inequality:

$$\Vert \varepsilon \left(t\right)\Vert \le \sqrt{\frac{\beta V\left(0\right)}{{\lambda }_{min}\left({P}_{1}\right)}}{e}^{-\alpha t}$$

Which implies that:

$$\Vert \overline{x }\left(t\right)\Vert \le \sqrt{\frac{\beta V\left(0\right)}{{\lambda }_{min}\left({P}_{1}\right)}}{e}^{-\left(\eta +\alpha \right)t}$$

Thus, we can say that the first condition of Problem 1 is achieved.

Next, by integrating (22) for \(t\in \left[0,{t}_{f}\right]\), we have:

$$V\left({t}_{f}\right)-V\left(0\right)+{\int }_{0}^{{t}_{f}}{e}^{2\alpha \tau }\left\{{\overline{e} }_{\eta }^{T}\left(\tau \right){\overline{e} }_{\eta }\left(\tau \right)-{\gamma }^{2}{\omega }_{\eta }^{T}\left(\tau \right){\omega }_{\eta }\left(\tau \right)\right\}d\tau \le 0.$$
(24)

Therefore, letting \(\alpha =0\), it is easy to prove that the second condition of Problem 1 is also satisfied because \(V\left(t\right)\ge 0.\)

Summarizing the above, we can conclude that if there exists a solution to LMIs given in (7)-(9), the designed sampled-data fuzzy filter meets the conditions given in Problem 1. This concludes the proof.

Remark 3

In this paper, we let the unknown time-varying matrix \(F\left({t}_{k}\right)\) represent the sensor fault. When included in its current form within the stabilization condition, existing numerical solvers are impossible to solve the condition. Therefore, we imposed upper and lower bounds on the norm of \(F\left({t}_{k}\right)\) as specified in (3). By doing so, the stability condition can be reformulated as LMIs, making it solvable using contemporary numerical optimization tools.

4 Simulation Example

In this section, we provide two examples to validate the effectiveness of the proposed method. Example 1 shows the state estimation performances of the proposed method when the fault occurs on the sensor. In Example 2, we compare the maximum allowable sampling period with conventional methods without considering the sensor fault.

4.1 Example 1

Let us consider the numerical T-S fuzzy system (1), whose parameters are given as follows:

$$\begin{array}{c}{A}_{1}=\left[\begin{array}{cc}-3& 0.6\\ 0.2& -2\end{array}\right], {A}_{2}=\left[\begin{array}{cc}-3& 0.6\\ 0.2& -2\end{array}\right]\\ {B}_{1}=\left[\begin{array}{c}1\\ 0.3\end{array}\right], {B}_{2}=\left[\begin{array}{c}1\\ 0.2\end{array}\right]\\ \begin{array}{c}{C}_{11}=\left[\begin{array}{cc}0.1& 0.08\end{array}\right], {C}_{12}=\left[\begin{array}{cc}0.2& 0.05\end{array}\right]\\ {C}_{21}={C}_{22}=\left[\begin{array}{cc}1& 0\end{array}\right]\\ \begin{array}{c}x\left(t\right)={\left[\begin{array}{cc}{x}_{1}^{T}\left(t\right)& {x}_{2}^{T}\left(t\right)\end{array}\right]}^{T}, z\left(t\right)={x}_{1}\left(t\right)\\ {w}_{1}\left(z\left(t\right)\right)=\left(1-\frac{1}{1+{e}^{-7z\left(t\right)-\frac{\pi }{6}}}\right)\left(1-\frac{1}{1+{e}^{-10z\left(t\right)+\frac{\pi }{6}}}\right)\\ {w}_{2}\left(z\left(t\right)\right)=1-{w}_{1}\left(z\left(t\right)\right), \omega \left(t\right)={e}^{-0.2t}{\text{sin}}\left(3t\right)\end{array}\end{array}\end{array}$$

To determine the filter gains, we set the hyperparameters in the LMIs (7)-(9) as follows: \(\upeta =1\), \(\mathrm{\alpha }=-0.9\), \(\upsigma =1\), \({\upmu }_{1}=1\), \({\upmu }_{2}=0.1\), \(\upgamma =0.0775\), and \(h=0.01\). Moreover, the sensor fault in this example is assumed to be described by:

$$F\left({t}_{k}\right)=\left(\overline{{f }_{a}}-{\underline{f}}_{a}\right)\left({\text{sin}}\left(3{t}_{k}\right)+1\right)/2+{\underline{f}}_{a}$$

where \(\overline{{f }_{a}}=0.5\) and \({\underline{f}}_{a}=0.1\). Also, \({F}_{0}\) and \({F}_{2}\) can be given through (3). Now, by solving the LMIs (7)-(9), we obtained the following filter gains:

$$\begin{array}{c}{\widehat{A}}_{1}=\left[\begin{array}{cc}-0.5963& -3.1898\\ 0.5645& -2.5887\end{array}\right], {\widehat{A}}_{2}=\left[\begin{array}{cc}-0.3592& -1.2350\\ 0.1223& -1.8284\end{array}\right]\\ {\widehat{B}}_{1}=\left[\begin{array}{c}37.5403\\ 10.0878\end{array}\right], {\widehat{B}}_{2}=\left[\begin{array}{c}42.0335\\ 9.4825\end{array}\right]\\ \begin{array}{c}{\widehat{G}}_{11}=\left[\begin{array}{cc}-10.4941& -0.3732\\ -2.9144& 0.4496\end{array}\right]\\ {\widehat{G}}_{12}=\left[\begin{array}{cc}-10.4941& -0.3732\\ -2.9144& 0.4496\end{array}\right]\\ \begin{array}{c}{\widehat{G}}_{21}=\left[\begin{array}{cc}-11.5934& 1.1317\\ -2.9144& 0.4496\end{array}\right]\\ {\widehat{G}}_{22}=\left[\begin{array}{cc}-11.5934& 1.1317\\ -2.9144& 0.4496\end{array}\right]\\ {\widehat{C}}_{1}=\left[\begin{array}{cc}0.0727& 0.0434\end{array}\right], {\widehat{C}}_{2}=\left[\begin{array}{cc}0.1447& 0.0364\end{array}\right]\end{array}\end{array}\end{array}$$

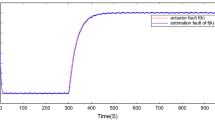
Under the initial conditions \(x\left(0\right)=\widehat{x}(0)={\left[\begin{array}{cc}0& 0\end{array}\right]}^{T}\), we carried out the simulation and obtained the state trajectories of \(s\left(t\right)\) and \(\widehat{s}\left(t\right)\) as shown in Fig. 1. Also, in this example, we assumed that the output of the system was measured by the sensor which suffers from its fault. As depicted in Fig. 2, the measured output, \({y}_{F}\left(t\right)\), deviates from the actual output, \(y\left(t\right)\). Therefore, we can say that Figs. 1 and 2 clearly demonstrate that the filter designed by the proposed method effectively estimates the output of the system output, even in the presence of an insufficient input caused by the sensor fault.

Fig. 1
figure 1

The time responses of the estimated output of the system \({\varvec{s}}\left({\varvec{t}}\right)\) (solid) and the filter \(\widehat{{\varvec{s}}}\left({\varvec{t}}\right)\) (dashed).

Full size image
Fig. 2
figure 2

The time responses of the input of the filter: the actual output (solid) and the measured output by the faulty sensor (dashed)

Full size image

4.2 Example 2

In this example, we aim to compare the maximum sampling period that allows for solving the LMI-based design conditions given in existing works. To achieve this, we utilized the tunnel diode circuit system [30] which is modeled by the T-S fuzzy system (1), with parameters given as:

$$\begin{array}{c}{A}_{1}=\left[\begin{array}{cc}-0.1& 50\\ -1& -10\end{array}\right], {A}_{2}=\left[\begin{array}{cc}-4.6& 50\\ -1& -10\end{array}\right]\\ {B}_{1}={B}_{2}=\left[\begin{array}{c}0\\ 1\end{array}\right], {C}_{11}={C}_{12}\left[\begin{array}{cc}1& 0\end{array}\right]\\ \begin{array}{c}{C}_{21}={C}_{22}=\left[\begin{array}{cc}0& 1\end{array}\right], x\left(t\right)={\left[\begin{array}{cc}{x}_{1}^{T}\left(t\right)& {x}_{2}^{T}\left(t\right)\end{array}\right]}^{T}\\ z\left(t\right)={x}_{1}\left(t\right), {w}_{1}\left(z\left(t\right)\right)=1-{z}^{2}(t)/9\\ {w}_{2}\left(z\left(t\right)\right)=1-{w}_{1}\left(z\left(t\right)\right), \omega \left(t\right)={0.5e}^{-0.5t}{\text{cos}}\left(5t\right)\end{array}\end{array}$$

For some selected \(\upgamma\), the maximum allowable sampling periods in which an LMI condition of each method is feasible are summarized in Table 1. As can be seen in Table 1, the method proposed in [31] is infeasible for all sampling periods if \(\gamma =0.7416\) or \(\upgamma =0.8660\). In addition, compared to existing approaches [31, 32], the proposed method shows a larger maximum sampling period.

Table 1 Comparisons of the Maximum Sampling Period
Full size table

Also, Fig. 3 depicts the time response of \(\overline{e }\left(t\right)\), the difference between the output vector of the system, \(s\left(t\right)\), and the filter, \(\widehat{s}\left(t\right)\) under \(h=0.202\). As seen from the figure, the sampled-data fuzzy filter designed by the proposed method can successfully estimate the system's output.

Fig. 3
figure 3

The time responses of \(\overline{{\varvec{e}} }\left({\varvec{t}}\right)={\varvec{s}}\left({\varvec{t}}\right)-\widehat{{\varvec{s}}}\left({\varvec{t}}\right)\)

Full size image

5 Conclusion

This paper addressed an LMI-based design methodology for a fault-tolerant \({H}_{\infty }\) sampled-data fuzzy filter with gains were applied to reduce convergence time and relax design conditions. Additionally, the proposed design process employs a robust control technique to enhance the filter's fault-tolerant capabilities. Furthermore, the sufficient condition ensuring \({H}_{\infty }\)-based state estimation performance was formulated in terms of LMIs using the LKF. The effectiveness and superiority of the proposed method were demonstrated through simulation examples.