Existence, stability and numerical results for a Timoshenko beam with thermodiffusion effects

Abstract

In this paper, we consider a new Timoshenko beam model with thermal and mass diffusion effects. Heat and mass exchange with the environment during thermodiffusion in Timoshenko beam. Firstly, by the ${C}_{0}$-semigroup theory, we prove the well posedness of the considered problem with Dirichlet or Neumann boundary conditions. Then we show, without assuming the well-known equal wave speeds condition, the lack of exponential stability for the Neumann problem, meanwhile one linear frictional damping is strong enough to guarantee the exponential stability for the Dirichlet problem. Then, we introduce a finite element approximation and we prove that the associated discrete energy decays. Finally, we obtain some a priori error estimates assuming additional regularity on the solution and we present some numerical results which demonstrate the accuracy of the approximation and the behaviour of the solution.

1 Introduction

During the past decades, an increasing interest has been developed to study the asymptotic behaviour of solutions to several Timoshenko problems, in seek of a thorough description on the thermomechanical interactions in elastic materials. The Timoshenko system is written as,

$$\begin{aligned} \rho _{1}\varphi _{tt}(x,t)=S_{x}(x,t),\quad \rho _{2}\psi _{tt}(x,t)=M_{x}(x,t)-S(x,t), \end{aligned}$$

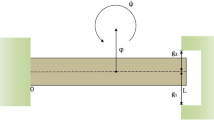
where $(x,t)\in (0,L)\times (0,\infty )$, t is the time, x is the distance along the centre line of the beam structure, L is the length of the beam, $\varphi$ is the transverse displacement and $\psi$ is the rotation of the neutral axis due to bending. Here, $\rho _{1}=\rho A$ and $\rho _{2}=\rho I$, where $\rho >0$ is the density, A is the cross-sectional area and I is the second moment of the cross-sectional area. By S, we denote the shear force and M is the bending moment.

Assuming that the constitutive laws are given by (see [1])

$$\begin{aligned} S(x,t)=k (\varphi _{x}(x,t)+\psi (x,t)), \quad M(x,t)=b\psi _{x}(x,t) \,\, \hbox {for}\,\, (x,t)\in (0,L)\times (0,\infty ), \end{aligned}$$

then the Timoshenko equations are given by

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k (\varphi _{x}+\psi )_{x}=0,\\ \rho _{2}\psi _{tt}-b\psi _{xx}+k (\varphi _{x}+\psi )=0. \end{array}\right. \end{aligned}$$

(1.1)

Here, b and k stands for $b=EI$ and $k=k_{1}GA$ where E, G and $k_1$ represent the Young’s modulus, the modulus of rigidity and the transverse shear factor, respectively.

However, the stability of system (1.1) depends on the difference of velocities of propagation. Then, it is uniformly stable for weak solutions if

$$\begin{aligned} \chi =\frac{k}{\rho _1}-\frac{b}{\rho _2}=0. \end{aligned}$$

(1.2)

Therefore, $\chi$ plays an important role in the asymptotic behaviour of system (1.1). This has been showed in different papers (see, for instance, [2,3,4]).

Many authors studied the Timoshenko system with thermoelastic dissipation, effective in the bending moment equation, when the evolution equations become

$$\begin{aligned} \rho _{1}\varphi _{tt}=S_{x},\qquad \rho _{2}\psi _{tt}=M_{x}-S,\qquad \Psi _{t}=-q_{x} \end{aligned}$$

(1.3)

in $(0,L)\times (0,\infty )$, where $\Psi$ is the entropy and q is the heat flux. The constitutive laws with temperature following the Fourier’s law are given by

$$\begin{aligned} S=k(\varphi _{x}+\psi ),\qquad M=b\psi _{x}+\gamma \theta , \qquad \Psi =-\gamma \psi _{x}+\rho _3\theta , \qquad q=-\kappa \theta _x \end{aligned}$$

(1.4)

in $(0,L)\times (0,\infty )$. Substituting (1.4) into (1.3), we get the governing equations of Timoshenko beam equations with temperature following the Fourier’s law:

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k(\varphi _{x}+\psi )_{x}=0\\ \rho _{2}\psi _{tt}-b\psi _{xx}+k(\varphi _{x}+\psi )-\gamma \theta _{x}=0\\ \rho _{3}\theta _{t}-\kappa \theta _{xx}-\gamma \psi _{tx}=0 \end{array}\right\} \quad \text {in}\quad (0,L)\times (0,\infty ). \end{aligned}$$

(1.5)

The constants $\rho _{3},\ \kappa ,\ \gamma > 0$ respect the physical parameters from thermoelasticity theory.

Rivera and Racke [5] studied the exponential stability of system (1.5), under certain boundary conditions, proving that it is exponentially stable if and only if (1.2) holds. Aouadi and Soufyane [6] showed that the dissipation produced by the memory effect working on the boundary is sufficiently strong to prove a general decay result obtained without imposing condition (1.2). Bernardi and Copetti [7] studied a contact problem for a nonlinear thermoviscoelastic Timoshenko beam, proving the well posedness of the problem, analysing a finite element approximation and performing some numerical experiments.

Júnior et al. [8] considered the Timoshenko system, when the constitutive laws are given by

$$\begin{aligned} S=k(\varphi _{x}+\psi )-\sigma \theta , \quad M=b\psi _{x}, \quad \Psi =\sigma (\varphi _x+\psi )+\rho _3\theta , \quad q=-\kappa \theta _x, \end{aligned}$$

that is

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k(\varphi _{x}+\psi )_{x}+\sigma \theta _{x}=0\\ \rho _{2}\psi _{tt}-b\psi _{xx}+k(\varphi _{x}+\psi )-\sigma \theta =0\\ \rho _{3}\theta _{t}-\kappa \theta _{xx}+\sigma (\varphi _{x}+\psi )_{t}=0 \end{array} \right\} \quad \text {in }(0,L)\times (0,\infty ). \end{aligned}$$

(1.6)

They showed in [8] that system (1.6) with Dirichlet boundary conditions is exponentially stable if and only if condition (1.2) holds. However, system (1.6) loses its exponential stability with Neumann conditions if condition (1.2) fails.

We may think that the dissipation phenomenon cannot only be described by thermal conduction in Timoshenko beams. However, the research conducted in the development of high technologies after the second world war confirmed that the field of diffusion in solids cannot be ignored. So, the obvious question is: what happens when the diffusion effect is considered with the thermal effect in Timoshenko beams. Hence, diffusion can be defined as the random walk of a set of particles from regions of high concentration to regions of lower concentration. Thermodiffusion in an elastic solid is due to the coupling of the fields of strain, temperature and mass diffusion. The processes of heat and mass diffusion play an important role in many engineering applications, such as satellites problems, returning space vehicles and aircraft landing on water or land. There is now a great deal of interest in the process of diffusion in the manufacturing of integrated circuits, integrated resistors, semiconductor substrates and MOS transistors. Oil companies are also interested to this phenomenon in order to improve the conditions of oil extractions.

If the mass diffusion is taken into account in the Timoshenko equations, the evolution equations become

$$\begin{aligned} \rho _{1}\varphi _{tt}=S_{x},\quad \rho _{2}\psi _{tt}=M_{x}-S,\quad \Psi _{t}=-q_{x},\quad C_{t}=-\eta _{x} \end{aligned}$$

(1.7)

in $(0,L)\times (0,\infty )$, where C is the concentration of the diffusive material in the elastic body and $\eta$ is the mass diffusion flux. In this case, the constitutive laws with temperature and diffusion following the Fourier’s law and the Fick’s law, respectively, are given by

$$\begin{aligned} \left. \begin{array}{l} S=k (\varphi _{x}+\psi ),\quad M=b\psi _{x}+\gamma \theta +\beta C,\quad \Psi =-\gamma \psi _{x}+\rho _3\theta +\varpi C\\ q=-\kappa \theta _x,\qquad \eta =-\hbar P_{x},\quad P=\beta \psi _{x}+\varrho C-\varpi \theta \end{array}\right\} \end{aligned}$$

(1.8)

in $(0,L)\times (0,\infty )$, where P is the chemical potential, $\hbar >0$ is the diffusion coefficient, $\varpi$ is a measure of the thermodiffusion effect and $\varrho$ is a measure of the diffusive effect. Substituting (1.8) into (1.7), we get

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k(\varphi _{x}+\psi )_{x}=0\\ \rho _{2}\psi _{tt}-b\psi _{xx}+k(\varphi _{x}+\psi )-\gamma \theta _{x}-\beta C_{x}=0 \\ \rho _3\theta _{t}+\varpi C_{t}-\kappa \theta _{xx}-\gamma \psi _{tx}=0\\ C_{t}-\hbar (\beta \psi _{x}+\varrho C-\varpi \theta )_{xx}=0 \end{array}\right\} \hbox { in } (0,L)\times (0,\infty ). \end{aligned}$$

(1.9)

We shall now formulate a different alternative form that will be useful in the next sections. In this new formulation, we will use the chemical potential as a state variable instead of the concentration. The alternative form can be written by substituting the last equation of (1.8), namely

$$\begin{aligned} C=\frac{1}{\varrho }(P-\beta \psi _{x}+\varpi \theta ) \end{aligned}$$

into (1.9)$_{2,3,4}$, and we obtain the governing equations of the Timoshenko beam problem with temperature and chemical potential in the classical form:

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k(\varphi _{x}+\psi )_{x}=0\\ \rho _{2}\psi _{tt}-\alpha \psi _{xx}+k(\varphi _{x}+\psi )-\gamma _1 \theta _{x}-\gamma _2 P_{x}=0\\ c\theta _{t}+d P_{t}-\kappa \theta _{xx}-\gamma _1 \psi _{tx}=0\\ d\theta _{t}+r P_{t}-\hbar P_{xx}-\gamma _2 \psi _{tx}=0 \end{array}\right\} \hbox { in } (0,L)\times (0,\infty ), \end{aligned}$$

(1.10)

where

$$\begin{aligned} \alpha =b-\frac{\beta ^2}{\varrho },\ \ \ \gamma _1=\gamma +\frac{\beta \varpi }{\varrho },\ \ \ \gamma _2=\frac{\beta }{\varrho }, \ \ \ c=\rho _3+\frac{\varpi ^{2}}{\varrho },\ \ d=\frac{\varpi }{\varrho },\ \ \ r=\frac{1}{\varrho } \end{aligned}$$

are physical positive constants.

In this paper, we study some qualitative properties of system (1.10) subject to the following initial conditions

$$\begin{aligned} \left. \begin{array}{l} \varphi (x,0)=\varphi ^{0}(x),\quad \psi (x,0)=\psi ^{0}(x),\quad \theta (x,0)=\theta ^{0}(x) \hbox { for } x\in (0,L), \\ P(x,0)=P^{0}(x),\quad \varphi _{t}(x,0)=\varphi ^{1}(x),\ \psi _{t}(x,0)=\psi ^{1}(x)\hbox { for } x\in (0,L), \end{array} \right\} \end{aligned}$$

(1.11)

with either Dirichlet boundary conditions:

$$\begin{aligned} \begin{array}{l} \varphi (0,t)=\psi (0,t)=\theta (0,t)=P(0,t)=0 \quad \hbox {for}\quad t>0,\\ \varphi (L,t)=\psi (L,t)=\theta (L,t)=P(L,t)=0,\quad \hbox {for}\quad t>0,\end{array} \end{aligned}$$

(1.12)

or either Neumann boundary conditions:

$$\begin{aligned} \begin{array}{l} \varphi (0,t)=\psi _{x}(0,t)=\theta (0,t)=P(0,t)=0,\\ \varphi (L,t)=\psi _x(L,t)=\theta (L,t)=P(L,t)=0,\ t>0. \end{array} \end{aligned}$$

(1.13)

It should be noted that system (1.10) has never been studied before and there is neither mathematical nor numerical results for this system in the literature.

We assume that the symmetric matrix $\Lambda = \left( \begin{array}{cc} c &{}\quad d \\ d &{}\quad r \\ \end{array} \right)$ is positive definite, i.e.

$$\begin{aligned} \delta =cr-d^{2}>0. \end{aligned}$$

(1.14)

Note that (1.14) implies that for $\theta ,\,P\ne 0$,

$$\begin{aligned} c\theta ^{2}+2d\theta P+rP^{2}>0. \end{aligned}$$

(1.15)

We remark that condition (1.14) is needed to stabilize the system when diffusion effects are added to thermal effects.

We think that the concept of mass diffusion introduced into Timoshenko’s equations could have very significant physical effects other than body deformations. For example, recent studies have focused on the effect of mass diffusion on the damping ratio in micro-beam resonators (see, e.g. [9]). Moreover, mass diffusion introduces a new critical thickness in addition to the conventional critical thickness of thermoelastic damping.

The explanations above indicate that mass diffusion will play an important role in the clarification of the thermomechanical behaviour of Timoshenko’s model. To the best of the authors’ knowledge, however, no theoretical or numerical simulation has been available to study mass diffusion effects on the thermal vibration of a Timoshenko beam. Therefore, the goal of this work is to examine the effect of mass diffusion alongside the effect of temperature on the behaviour of a Timoshenko beam.

The sections of this paper are organized as follows. In Sect. 2, we shall prove that problem (1.10)–(1.11) under boundary conditions (1.12) or (1.13) is well posed. In Sect. 3, under the condition of nonequal wave speeds, we prove the lack of exponential stability of problem (1.10)–(1.11) with boundary conditions (1.13). In Sect. 4, under the same condition, we prove the exponential stability of problem (1.10)–(1.11) but with boundary conditions (1.12) by adding a frictional damping term. Then, in Sect. 5, we introduce the numerical approximation of the variational form of problem (1.10)–(1.12) by using the finite element method to approximate the spatial variable and the implicit Euler scheme to discretize the time derivatives. The decay of the discrete energy is proved, from which we conclude a discrete stability property. Some a priori error estimates are provided in Sect. 6, which lead to the linear convergence of the algorithm under suitable additional regularity conditions. Finally, some numerical simulations are presented in Sect. 7 to demonstrate the accuracy of the approximation and the behaviour of the solution.

2 Well posedness of the problem

In this section, we shall study the well posedness of system (1.10)–(1.11) under boundary conditions (1.12) or (1.13). To give an accurate formulation of this problem, we introduce the following Hilbert spaces:

$$\begin{aligned} {\mathscr {H}}_1:=H^1_0(0,L)\times L^{2} (0,L)\times H^1_0(0,L)\times L^{2} (0,L)\times L^{2} (0,L)\times L^{2} (0,L), \end{aligned}$$

and

$$\begin{aligned} {\mathscr {H}}_2:=H^1_0(0,L)\times L^{2} (0,L)\times H^1_*(0,L)\times L_*^{2} (0,L)\times L^{2} (0,L)\times L^{2} (0,L), \end{aligned}$$

endowed with an inner product, for $U_{j}=(\varphi _{j},v_{j},\psi _{j},\phi _{j},\theta _{j},P_{j})\in {\mathscr {H}}_i$ and $j=1,2,$

$$\begin{aligned} \Big (U_{1},U_{2}\Big )_{{\mathscr {H}}_i}= & {} \int _{0}^{L}\Big [ \rho _{1}v_{1}\overline{v_{2}}+\rho _{2}\phi _{1} \overline{\phi _{2}}+\alpha \psi _{1,x}\overline{\psi _{2,x}} +k\Big (\varphi _{1,x} +\psi _{1}\Big )\overline{\Big (\varphi _{2,x}+\psi _{2}\Big )}\\&+\Lambda \left( \begin{array}{c} \theta _1\\ P_1\\ \end{array} \right) \cdot \left( \begin{array}{c} \overline{\theta _2} \\ \overline{P_2} \\ \end{array} \right) \Big ]\hbox {d}x,\\ \end{aligned}$$

where

$$\begin{aligned} L^{2}_*(0,L):= & {} \Big \{ u\in L^{2}(0,L)\ |\ \int _0^Lu(x)\hbox {d}x=0\Big \},\\H^1_*(0,L):= & {} H^1_0(0,L)\cap L_*^{2} (0,L). \end{aligned}$$

It is easy to check that $({\mathscr {H}}_i, \parallel .\parallel _{{\mathscr {H}}_i})\$ is a Hilbert space. Then, we define the operator ${\mathscr {A}}_i:{\mathscr {D}}({\mathscr {A}}_i)\subset {\mathscr {H}}_i\rightarrow {\mathscr {H}}_i$

$$\begin{aligned} {\mathscr {A}}_i\left[ \begin{array}{c} \varphi \\ v \\ \psi \\ \phi \\ \theta \\ P \end{array} \right] =\left( \begin{array}{c} v \\ \rho _{1}^{-1}k(\varphi _{xx}+\psi _x) \\ \phi \\ \rho _{2}^{-1}\Big (\alpha \psi _{xx}-k(\varphi _{x}+\psi ) +\gamma _1\theta _{x}+\gamma _2 P_{x}\Big ) \\ -\delta ^{-1}\Big ( (d \gamma _2-r \gamma _1)\phi _x- r\kappa \theta _{xx} + d \hbar P_{xx}\Big )\\ -\delta ^{-1}\Big ( (d \gamma _1-c \gamma _2)\phi _x+ d\kappa \theta _{xx} - {c\hbar }P_{xx}\Big )\\ \end{array}\right) ,\\ \end{aligned}$$

with domain

$$\begin{aligned} {\mathscr {D}}({\mathscr {A}}_1):=\left\{ U\in {\mathscr {H}}_1\ |\ \varphi ,\ \psi \in H^1_0(0,L)\cap H^{2} (0,L),\quad v,\ \phi ,\ \theta ,\ P \in H^1_0(0,L)\right\} , \end{aligned}$$

and

$$\begin{aligned}&{\mathscr {D}}({\mathscr {A}}_2):=\big \{U\in {\mathscr {H}}_2\ |\ \varphi \in H^1_0(0,L)\cap H^{2} (0,L),\\&\qquad \qquad \psi \in H^1_*(0,L)\cap H^{2} (0,L),\quad v,\ \theta ,\ P\in H^1_0(0,L),\ \phi \in H^1_*(0,L)\big \}. \end{aligned}$$

We note that ${\mathscr {D}}({\mathscr {A}}_i)$ is dense in ${\mathscr {H}}_i$. When we omit subindex i, with $i = 1, 2$, we refer to both boundary conditions. Hence, system (1.10)–(1.11) under boundary conditions (1.12) or (1.13) can be rewritten as an evolutionary equation as follows,

$$\begin{aligned} \left. \begin{array}{ll} \frac{\hbox {d} U(t)}{\hbox {d}t}={\mathscr {A}}U(t),\ t>0, &{} \\ U(0)=U^{0}, \end{array} \right\} \end{aligned}$$

(2.1)

where $U(t)=\Big (\varphi (t),v(t),\psi (t),\phi (t),\theta (t),P(t) \Big )$, and

$$\begin{aligned} U(0)=\Big (\varphi ^{0}(x),\varphi ^{1}(x),\psi ^{0}(x), \psi ^{1}(x),\theta ^{0}(x),P^{0}(x)\Big )\in {\mathscr {H}} \end{aligned}$$

is given. The following property of ${\mathscr {A}}$ holds.

Lemma 2.1

Let ${\mathscr {A}}$ and ${\mathscr {H}}$ be defined as before. Then, ${\mathscr {A}}$ is dissipative in ${\mathscr {H}}$.

Proof

(i) Firstly, for any $U=(\varphi ,v,\psi ,\phi ,\theta ,P)\in {\mathscr {D}}({\mathscr {A}}),\$ a direct calculation yields

$$\begin{aligned} \Big ({\mathscr {A}}U,U \Big )_{{\mathscr {H}}}= & {} k\int _{0}^{L}(\varphi _{x}+\psi )_{x}{\overline{v}}\hbox {d}x +\int _{0}^{L}(\alpha \psi _{x}+\gamma _1\theta +\gamma _2 P)_{x}{\overline{\phi }}\hbox {d}x \\&-k\int _{0}^{L}(\varphi _{x}+\psi ){\overline{\phi }}\hbox {d}x+ \alpha \int _{0}^{L}\phi _{x}\overline{\psi _{x}}\hbox {d}x+k\int _{0}^{L}(v_{x}+\phi ) \overline{(\varphi _{x}+\psi )}\hbox {d}x\\&+\int _{0}^{L}\Lambda \left( \begin{array}{c} \Theta \\ \Phi \\ \end{array} \right) \cdot \left( \begin{array}{c} {\overline{\theta }} \\ {\overline{P}} \\ \end{array} \right) \hbox {d}x, \end{aligned}$$

where

$$\begin{aligned} \Theta =-\delta ^{-1}\Big ( (d \gamma _2-r \gamma _1)\phi _x- r\kappa \theta _{xx} + d \hbar P_{xx}\Big ),\quad \Phi =-\delta ^{-1}\Big ( (d \gamma _1-c \gamma _2)\phi _x+ d\kappa \theta _{xx} - {c\hbar }P_{xx}\Big ), \end{aligned}$$

and

$$\begin{aligned} \Big (U,{\mathscr {A}}U \Big )_{{\mathscr {H}}}= & {} k\int _{0}^{L}v \overline{(\varphi _{x}+\psi )}_{x}\hbox {d}x +\int _{0}^{L}{\phi }\overline{(\alpha \psi _{x}+\gamma _1\theta +\gamma _2 P)}_{x}\hbox {d}x\\&-k\int _{0}^{L}{\phi }\overline{(\varphi _{x}+\psi )}\hbox {d}x+\alpha \int _{0}^{L}{\psi _{x}}\overline{\phi _{x}}\hbox {d}x +k\int _{0}^{L}{(\varphi _{x}+\psi )}\overline{(v_{x}+\phi )}\hbox {d}x\\&+\int _{0}^{L}\Lambda \left( \begin{array}{c} \theta \\ P \\ \end{array} \right) \cdot \left( \begin{array}{c} {\overline{\Theta }} \\ {\overline{\Phi }} \\ \end{array} \right) \hbox {d}x. \end{aligned}$$

Therefore,

$$\begin{aligned} 2\mathfrak {R}\Big ({\mathscr {A}}U,U \Big )= & {} \Big ({\mathscr {A}}U,U \Big ) +\Big (U,{\mathscr {A}}U \Big ) =-2k\int _{0}^{L}\mid \theta _x\mid ^{2} \hbox {d}x\nonumber \\&-2\hbar \int _{0}^{L}\mid P_x\mid ^{2}\hbox {d}x<0, \end{aligned}$$

(2.2)

where $k>0$ and $\hbar >0$. This implies that ${\mathscr {A}}$ is dissipative in ${\mathscr {H}}$. $\square$

We prove now a property for operator $I -{\mathscr {A}}$.

Lemma 2.2

Let ${\mathscr {A}}$ defined in (2.1). Then, it follows that operator $I -{\mathscr {A}}$ is onto.

Proof

For any $F = (f_1, f_2, f_3, f_4, f_5, f_6)^T \in {\mathscr {H}}$, we want to find $U=(\varphi ,v,\psi ,\phi ,\theta ,P)\in {\mathscr {D}}({\mathscr {A}})$ satisfying the equation $(I -{\mathscr {A}})U=F,\$ i.e.

$$\begin{aligned} \left. \begin{array}{ll} \varphi -v=f_{1},\quad \psi -\phi =f_{3}, &{} \\ \rho _{1}v-k(\varphi _{x}+\psi )_{x}=\rho _1f_{2}, \\ \rho _{2}\phi -\alpha \psi _{xx}+k(\varphi _{x}+\psi ) -\gamma _1\theta _{x}-\gamma _2 P_{x}=\rho _2f_{4}, \\ \delta \theta +(d \gamma _2-r \gamma _1)\phi _x-rk\theta _{xx} + d \hbar P_{xx}=\delta f_{5},\\ \delta P+(d \gamma _1-c \gamma _2)\phi _x + d\kappa \theta _{xx} - {c\hbar }P_{xx}=\delta f_{6}. \end{array} \right\} \end{aligned}$$

(2.3)

Substituting (2.3)$_1$ into (2.3)$_{2,3}$, we get

$$\begin{aligned} \left. \begin{array}{ll} \rho _{1}\varphi -k(\varphi _{x}+\psi )_{x}=\rho _1(f_{1}+f_{2}), \\ \rho _{2}\psi -\alpha \psi _{xx}+k(\varphi _{x}+\psi )-\gamma _1\theta _{x}-\gamma _2 P_{x}=\rho _2(f_{3}+f_{4}), \\ \delta \theta +(d \gamma _2-r \gamma _1)\psi _x- r\kappa \theta _{xx} + d \hbar P_{xx}=\delta f_{5}+(d \gamma _2-r \gamma _1)f_{3,x},\\ \delta P+(d \gamma _1-c \gamma _2)\psi _x+d\kappa \theta _{xx} -{c\hbar }P_{xx}=\delta f_{6}+(d \gamma _1-c \gamma _2)f_{3,x}. \end{array} \right\} \end{aligned}$$

(2.4)

Now, we will prove the existence of a weak solution by using the Lax–Milgram’s theorem. To do this, let us define the following bilinear form over ${\mathscr {H}}\times {\mathscr {H}}$:

$$\begin{aligned}&{\mathscr {B}}\Big ((\varphi ,\psi ,\theta ,P),(\varphi ',\psi ',\theta ',P') \Big )=\rho _1\int _{0}^{L} \varphi \overline{\varphi '}\hbox {d}x+k\int _{0}^{L}(\varphi _{x} +\psi )(\overline{\varphi '_{x} +\psi '})\hbox {d}x\\&\quad +\rho _2\int _{0}^{L}\psi \overline{\psi '}\hbox {d}x +\alpha \int _{0}^{L}\psi _x\overline{\psi '}_x\hbox {d}x -\int _{0}^{L}(\gamma _1\theta _{x}-\gamma _2 P_{x})\overline{\psi '}\hbox {d}x\\&\quad +\int _{0}^{L}\Big (\delta \theta +(d \gamma _2-r \gamma _1)\psi _x- r\kappa \theta _{xx} + d \hbar P_{xx}\Big )\overline{\theta '} \hbox {d}x \\&\quad +\int _{0}^{L}\Big ( \delta P+(d \gamma _1-c \gamma _2)\psi _x+d\kappa \theta _{xx} -{c\hbar }P_{xx}\Big )\overline{P'} \hbox {d}x. \end{aligned}$$

It is easy to see that ${\mathscr {B}}(\cdot ,\cdot )$ is continuous and coercive over ${\mathscr {H}}\times {\mathscr {H}}$. We also define the following continuous linear form ${\mathscr {L}}(\cdot )$ over ${\mathscr {H}}$ by

$$\begin{aligned} {\mathscr {L}}(\varphi ',\psi ',\theta ',P')= & {} \int _{0}^{L}\Big [ \rho _1(f_{1}+f_{2})\overline{\varphi '}+\rho _2(f_{3}+f_{4})\overline{\psi '}\\&+\Big (\delta f_{5}+(d \gamma _2-r \gamma _1)f_{3,x}\Big )\overline{\theta '} +\Big (\delta f_{6}+(d \gamma _1-c \gamma _2)f_{3,x}\Big )\overline{P'} \Big ]\hbox {d}x. \end{aligned}$$

From Lax-Milgram’s theorem (see [10]), we conclude that there exists only one solution satisfying

$$\begin{aligned} {\mathscr {B}}\Big ((\varphi ,\psi ,\theta ,P),(\varphi ,\psi ,\theta ,P)\Big ) ={\mathscr {L}}(\varphi ',\psi ',\theta ',P') \quad \forall (\varphi ',\psi ',\theta ',P')\in {\mathscr {H}} \end{aligned}$$

such that

$$\begin{aligned} \varphi ,\ \psi ,\ \theta ,\ P \in H^1_0 (0, L)\qquad \text {or}\quad \varphi ,\ \theta ,\ P \in H^1_0 (0, L),\ \psi \in H^1_* (0, L). \end{aligned}$$

Now, from (2.3)$_1$, we have

$$\begin{aligned} v,\ \phi \in H^1_0 (0, L)\qquad \text {or}\quad v \in H^1_0 (0, L),\ \phi \in H^1_* (0, L). \end{aligned}$$

On the other hand, from (2.4)$_{1,2}$, it follows that $\varphi ,\ \psi \in H^2(0, L)$. Thus, we have obtained that $U\in {\mathscr {D}}({\mathscr {A}})$ such that $I-{\mathscr {A}}$ is onto. The proof is complete. $\square$

Since ${\mathscr {D}}({\mathscr {A}})$ is dense in ${\mathscr {H}}$ ($\overline{{\mathscr {D}}({\mathscr {A}})}={\mathscr {H}}$), ${\mathscr {A}}$ is a dissipative operator and $I-{\mathscr {A}}$ is onto, then the following theorem follows using the well-known Lumer–Phillips theorem (see [11]).

Proposition 2.3

Under the above conditions, we find that the operator ${\mathscr {A}}$ is the infinitesimal generator of a $C_0$-semigroup $T(t)=\hbox {e}^{t{\mathscr {A}}}$ of contractions over the space ${\mathscr {H}}$.

Now, an application of the theory of semigroups (see [11]) gives the following.

Theorem 2.4

Let ${\mathscr {A}}\$ and ${\mathscr {H}}\$ be defined as before. Hence, problem (2.1) is well posed, i.e. for any $U_{0}\in {\mathscr {H}},\$ problem (2.1) has a unique weak solution $U(t)=\hbox {e}^{t{\mathscr {A}}}U_{0}\in C([0,\infty );{\mathscr {H}}).\$ Furthermore, if $U_{0}\in {\mathscr {D}}({\mathscr {A}}),\$ $U(t)\in C^1([0,\infty );{\mathscr {H}})\cap C^0([0,\infty );{\mathscr {D}}({\mathscr {A}}))$ becomes the classic solution to problem (2.1).

3 The lack of exponential stability for Neumann boundary conditions

In this section, we show the lack of exponential stability of system (1.10)–(1.11) subject to boundary conditions (1.13) under the condition of different wave speeds of propagation:

$$\begin{aligned} \frac{k}{\rho _1}\not =\frac{\alpha }{\rho _2}. \end{aligned}$$

(3.1)

The proposed method is based on the Gearhart–Herbst–Prüss–Huang theorem (see, e.g. [12, 13]).

Theorem 3.1

Let $S(t) =\hbox {e}^{t{\mathscr {A}}}$ be a $C_0$-semigroup of contractions on a Hilbert space ${\mathscr {H}}$ with infinitesimal generator ${\mathscr {A}}$ with resolvent set $\rho ({\mathscr {A}})$. Then, S(t) is exponentially stable if and only if, for all $\lambda \in {\mathbb {R}}$,

$$\begin{aligned} \rho ({\mathscr {A}})\supseteq \{i\lambda ;\ \lambda \in {\mathbb {R}}\}\equiv i{\mathbb {R}},\quad \text {and}\quad \limsup _{|\lambda | \rightarrow \infty }\Vert (i\lambda I -{\mathscr {A}})^{-1}\Vert _{{\mathscr {L}}({\mathscr {H}})}<\infty . \end{aligned}$$

The expression $\Vert \cdot \Vert _{{\mathscr {L}}({\mathscr {H}})}$ denotes the norm in the space of continuous linear functions in ${\mathscr {H}}$.

Following the arguments employed in [5], we have the next result which states the lack of exponential stability.

Theorem 3.2

Under condition (3.1), the semigroup associated with system (1.10)–(1.11) with boundary conditions (1.13) is not exponentially stable.

Proof

We will show that for all $n\in {\mathbb {N}}$, given $F=F_{n} =(0,0,0,f_4,0,0),$ there exists $\lambda _{n}$ such that the sequence $\lambda =\lambda _{n}\$is in ${\mathbb {R}}$, and $U_{n}=U=(\varphi ,v,\psi ,\phi ,\theta ,P)=(i\lambda -{\mathscr {A}}_2)^{-1}F\in {\mathscr {D}}({\mathscr {A}}_2)$ such that

$$\begin{aligned} \underset{\lambda _{n}\rightarrow \infty }{\lim }\left\| U_{n}\right\| _{{\mathscr {H}}_2}=\infty . \end{aligned}$$

We use the same approach as in [5] and references therein. We find that $F_{n}$ is bounded in ${\mathscr {H}}_2$ and the solution $U_{n}=U=(\varphi ,v,\psi ,\phi ,\theta ,P)=(i\lambda -{\mathscr {A}}_2)^{-1}F$ must satisfy

$$\begin{aligned} \left. \begin{array}{l} i\lambda \varphi -v\ \ =0, \\ i\rho _1\lambda v-k(\varphi _x+\psi )_x\ =0, \\ i\lambda \psi -\phi \ \ =0, \\ i\rho _2\lambda \phi -\alpha \psi _{xx}+k(\varphi _{x}+\psi )-\gamma _1 \theta _{x}-\gamma _2 P_{x} =f_4,\ \\ i\lambda c\theta +i\lambda d P-\kappa \theta _{xx}-\gamma _1 \phi _{x}=0,\\ i\lambda d\theta +i\lambda r P-\hbar P_{xx}-\gamma _2 \phi _{x}=0. \end{array} \right\} \end{aligned}$$

(3.2)

Because of boundary conditions (1.13), we can take the following solution:

$$\begin{aligned} \left. \begin{array}{l} \varphi =A_{n}\sin \left( \frac{n\pi }{L}{x}\right) ,\ \psi =B_{n}\cos \left( \frac{n\pi }{L}{x}\right) ,\ \theta =C_{n}\sin \left( \frac{n\pi }{L}{x}\right) ,\\ P=D_{n}\sin \left( \frac{n\pi }{L}{x}\right) , \ f_4=\cos \left( \frac{n\pi x}{L}\right) . \end{array}\right\} \end{aligned}$$

(3.3)

Substituting (3.3) into (3.2), we find that $A_{n},\ B_{n}$ and $C_{n}$ satisfy

$$\begin{aligned} \left. \begin{array}{l} \left( -\lambda ^{2}\rho _1+\left( \frac{n\pi }{L}\right) ^{2}k\right) A_{n}+\left( \frac{n\pi }{L}\right) k B_{n}=0, \\ \left( \frac{n\pi }{L}\right) \lambda kA_{n}+\left( {-\lambda ^{2}\rho _2+ \left( \frac{n\pi }{L}\right) ^{2}}\alpha +k\right) B_n-\gamma _1\left( \frac{n\pi }{L}\right) C_{n}-\gamma _2 \left( \frac{n\pi }{L}\right) D_{n}=1, \\ \left( \frac{n\pi }{L}\right) i\lambda \gamma _1 B_{n}+ \left( i\lambda c+\left( \frac{n\pi }{L}\right) ^{2}\kappa \right) C_n+i\lambda dD_{n} =0, \\ \left( \frac{n\pi }{L}\right) i\lambda \gamma _2B_{n}+ i\lambda dC_{n}+\left( i\lambda r+\left( \frac{n\pi }{L}\right) ^{2}\hbar \right) D_n =0. \\ \end{array} \right\} \end{aligned}$$

(3.4)

We choose $-\lambda ^{2}\rho _2+(\frac{n\pi }{L})^{2}\alpha =0$, which gives $\lambda \equiv \lambda _n:=\pm {\varpi }\frac{n\pi }{L}$, where $\varpi =\sqrt{\frac{\alpha }{\rho _2}}$. Taking $\lambda ={\varpi }\frac{n\pi }{L}$, system (3.4) becomes

$$\begin{aligned} \left[ \begin{array}{cccc}(k-\rho _1\varpi ^2)\frac{n\pi }{L}&{}k&{}0&{}0\\ k\frac{n\pi }{L}&{} k &{} -\gamma _{1}\frac{n\pi }{L}&{} -\gamma _{2}\frac{n\pi }{L} \\ 0&{}\left( \frac{n\pi }{L}\right) i\gamma _1 \varpi &{}ic\varpi +\left( \frac{n\pi }{L}\right) \kappa &{} id\varpi \\ 0&{}\left( \frac{n\pi }{L}\right) i\gamma _2 \varpi &{} id\varpi &{} ir\varpi +\left( \frac{n\pi }{L}\right) \hbar \end{array} \right] \left[ \begin{array}{c} A_{n} \\ B_{n} \\ C_{n} \\ D_{n} \end{array} \right] =\left[ \begin{array}{c} 0\\ 1 \\ 0 \\ 0 \end{array} \right] . \end{aligned}$$

The resolution of the last two equations gives

$$\begin{aligned} C_n=Q_1(\lambda )B_n,\qquad D_n=Q_2(\lambda )B_n, \end{aligned}$$

(3.5)

where

$$\begin{aligned} Q_1(\lambda )= & {} -i\varpi \left( \frac{n\pi }{L}\right) \frac{ i\varpi (\gamma _1r-d\gamma _2)+\left( \frac{n\pi }{L}\right) \gamma _1\hbar }{-\varpi ^2(cr-d^2)+\left( \frac{n\pi }{L}\right) ^{2}\kappa \hbar +i\varpi \left( \frac{n\pi }{L}\right) (\kappa r+c \hbar )},\\ Q_2(\lambda )= & {} -i\varpi \left( \frac{n\pi }{L}\right) \frac{ i\varpi (c\gamma _2+d\gamma _1)+\left( \frac{n\pi }{L}\right) \gamma _2\kappa }{-\varpi ^2(cr-d^2)+\left( \frac{n\pi }{L}\right) ^{2}\kappa \hbar +i\varpi \left( \frac{n\pi }{L}\right) (\kappa r+c \hbar )}, \end{aligned}$$

satisfy

$$\begin{aligned} \lim _{n\rightarrow \infty }Q_1(\lambda )=-i\frac{\gamma _1\varpi }{\kappa },\qquad \lim _{n\rightarrow \infty }Q_2(\lambda )=-i\frac{\gamma _2\varpi }{\hbar }. \end{aligned}$$

Combining the first and second equations of (3.4) with (3.5), we obtain

$$\begin{aligned} \rho _1\varpi ^2A_n=({\gamma _1}Q_1+{\gamma _2}Q_2)B_n+\frac{L}{n\pi }. \end{aligned}$$

Substituting this equation into the first one of (3.4) again, we get

$$\begin{aligned} B_n=\frac{-1}{\frac{\rho _1\varpi ^2k}{k-\rho _1\varpi ^2}+(\gamma _1Q_1+\gamma _2Q_2) \frac{n\pi }{L}}. \end{aligned}$$

Since $\frac{k}{\rho _1}\not =\frac{\alpha }{\rho _2}=\varpi ^2$, then $A_n$ and $B_n$ satisfy

$$\begin{aligned} \lim _{n\rightarrow \infty }B_n=\frac{i}{\varpi \left( \frac{\gamma _1^2}{\kappa } +\frac{\gamma _2^2}{\hbar }\right) \left( \frac{n\pi }{L}\right) },\qquad \lim _{n\rightarrow \infty }A_n=\frac{2}{\rho _1\varpi ^2\left( \frac{n\pi }{L}\right) }. \end{aligned}$$

(3.6)

On the other hand, we have

$$\begin{aligned} \left\| U_{n}\right\| _{{\mathscr {H}}_2}^{2}\ge \rho _2 \left\| \phi _{n}\right\| ^{2}= & {} \rho _2\lambda ^2|B_n|^2 \int _0^{L}|\cos (\lambda {x})|^2\hbox {d}x\sim \frac{L\rho _2}{2\left( \frac{\gamma _1^2}{\kappa } +\frac{\gamma _2^2}{\hbar }\right) ^2}\qquad \text {as }n\rightarrow \infty ,\\ \left\| U_{n}\right\| _{{\mathscr {H}}_2}^{2}\ge \rho _1 \left\| v_{n}\right\| ^{2}= & {} \rho _1\lambda ^2|A_n|^2 \int _0^{L}|\sin (\lambda {x})|^2\hbox {d}x\sim \frac{2L}{\rho _1\varpi ^2}\qquad \text {as }n\rightarrow \infty . \end{aligned}$$

This proves the uniform boundedness of the norm $\Vert U_{n}\Vert _{{\mathscr {H}}_2}$. Now, we will show that if we assume that $\Vert U_{n}\Vert _{{\mathscr {H}}_2}$ remains bounded as $n\rightarrow \infty$, then it leads to a contradiction.

Multiplying Eq. (3.2)$_4$ by $\varphi _x + \psi$ and integrating, we obtain

$$\begin{aligned}&i\lambda \rho _2\int _0^L \phi (\varphi _x + \psi )\hbox {d}x +\alpha \int _0^L \psi _{x}(\varphi _x + \psi )_x\hbox {d}x+k\int _0^L(\varphi _{x}+\psi )^2\hbox {d}x\nonumber \\&\qquad -\int _0^L(\gamma _1 \theta _{x}+\gamma _2 P_{x})(\varphi _x + \psi )\hbox {d}x\nonumber \\&\quad =\int _0^L\cos \left( \frac{n\pi x}{L}\right) (\varphi _x + \psi )\hbox {d}x. \end{aligned}$$

(3.7)

Let

$$\begin{aligned} {\mathfrak {I}}= & {} i\lambda \rho _2\int _0^L \phi \varphi _x \hbox {d}x +\alpha \int _0^L \psi _{x}(\varphi _x + \psi )_x\hbox {d}x\qquad (\text {use}\ (3.2)_2)\\= & {} i\lambda \rho _2\int _0^L \phi \varphi _x \hbox {d}x +i\lambda \alpha \frac{\rho _1}{k}\int _0^L \psi _{x}v\hbox {d}x\qquad (\text {use}\, ({3.2})_1\ \text {and}\ (3.2)_3)\\= & {} i\lambda \left( 1-\frac{\alpha \rho _1}{k\rho _2}\right) \int _0^L \psi _x v \hbox {d}x. \end{aligned}$$

As (3.1) holds, from (3.7) we have

$$\begin{aligned} {\mathfrak {I}}= & {} -k\int _0^L (\varphi _x + \psi )^2\hbox {d}x-i\lambda \rho _2\int _0^L \phi \psi \hbox {d}x\nonumber \\&+\int _0^L (\gamma _1\theta _x+\gamma _2P_x)(\varphi _x + \psi )\hbox {d}x+\int _0^L\cos \left( \frac{n\pi x}{L}\right) (\varphi _x + \psi )\hbox {d}x. \end{aligned}$$

(3.8)

If $\Vert U_{n}\Vert _{{\mathscr {H}}}$ remains bounded, using (3.1), from (3.8) we conclude that $\displaystyle \Big |\lambda \int _0^L \psi _x v \hbox {d}x\Big |$ remains bounded as $\lambda \rightarrow \infty$.

On the other hand, using (3.2)$_1$, we have

$$\begin{aligned} i\lambda \int _0^L \psi _xv \hbox {d}x= & {} \lambda ^2\left( \frac{n\pi }{L}\right) A_nB_n \int _0^{L}\sin ^2 \left( \frac{n\pi }{L}{x}\right) \hbox {d}x\qquad (\text {use}\ (3.6))\nonumber \\\sim & {} \frac{in\pi }{\rho _1\varpi \left( \frac{\gamma _1^2}{\kappa } +\frac{\gamma _2^2}{\hbar }\right) }\rightarrow \infty \quad \text {as}\ n\rightarrow \infty , \end{aligned}$$

(3.9)

which contradicts the uniform boundedness of the norm $\Vert U_{n}\Vert _{{\mathscr {H}}_2}$. This completes the proof of the theorem. $\square$

4 Exponential stability

In this section, we show the exponential stability of system (1.10)–(1.11) subject to the boundary conditions (1.12) under the condition of nonequal wave speeds of propagation (3.1). For this, we add to the first equation of (1.10) the damping term $\mu \varphi _t$:

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}\varphi _{tt}-k(\varphi _{x}+\psi )_{x}+\mu \varphi _t=0\\ \rho _{2}\psi _{tt}-\alpha \psi _{xx}+k(\varphi _{x}+\psi )-\gamma _1 \theta _{x}-\gamma _2 P_{x}=0\\ c\theta _{t}+d P_{t}-\kappa \theta _{xx}-\gamma _1 \psi _{tx}=0\\ d\theta _{t}+r P_{t}-\hbar P_{xx}-\gamma _2 \psi _{tx}=0 \end{array}\right\} \text { in }(0,L)\times (0,\infty ). \end{aligned}$$

(4.1)

The energy of system (4.1) subject to the boundary conditions (1.12) is defined by

$$\begin{aligned} \begin{aligned} E(t)&= \frac{1}{2}\int _0^{L}\Big [\rho _1\varphi _{t}^2+\rho _2\psi _{t}^2 + \alpha \psi _{x}^2+\kappa (\varphi _{x}+\psi )^2 +c\theta ^2\\&\quad +2d \theta P+rP^2\Big ]\,\hbox {d}x. \end{aligned} \end{aligned}$$

(4.2)

Our approach is based on the construction of a Lyapunov functional ${\mathscr {L}}$ satisfying

$$\begin{aligned}\beta _1E(t) \le {\mathscr {L}}(t) \le \beta _2E(t)\end{aligned}$$

for $t \ge 0$ and positive constants $\beta _1,\ \beta _2$, and

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} {\mathscr {L}}(t) \le -\alpha {\mathscr {L}}(t) \end{aligned}$$

for some $\alpha >0$. A careful choice of multipliers and the sequence of estimates in the energy method will give the desired result. Multiplying (4.1)$_1$ by $\varphi _t$, (4.1)$_2$ by $\psi _t$, (4.1)$_3$ by $\theta$ and (4.1)$_4$ by P, one easily concludes

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t} E(t)=-{\kappa }\int _0^{L}\theta _x^{2}\hbox {d}x-{\hbar }\int _0^{L}P_x^{2}\hbox {d}x -{\mu }\int _0^{L}\varphi _t^{2}\hbox {d}x. \end{aligned}$$

Lemma 4.1

Let us assume that conditions (1.15) and (3.1) hold and $(\varphi , \varphi _t, \psi , \psi _t, \theta , P)$ be the solution to problem (4.1), (1.11), (1.12). Then, the functional $\mathcal {F}$ defined by

$$\begin{aligned} \mathcal {F}(t) = \int _0^{L}(\rho _1\varphi _t\varphi +\rho _2\psi _t \psi )\hbox {d}x+\frac{\mu }{2}\int _0^{L}\varphi ^2\mathrm{d}x, \end{aligned}$$

(4.3)

satisfies

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\mathcal {F}(t)\le & {} \rho _1\int _0^{L}\varphi _t^2\hbox {d}x+\rho _2\int _0^{L}\psi _t^2\mathrm{d}x -k\int _0^{L} (\varphi _x+\psi )^2\hbox {d}x-\frac{\alpha }{2} \int _0^{L} \psi _x^2\mathrm{d}x\nonumber \\&+C_1\int _0^{L}\theta _{x}^{2}\hbox {d}x+C_2\int _0^{L}P_{x}^{2}\mathrm{d}x. \end{aligned}$$

(4.4)

Proof

Taking the derivative of $\mathcal {F}(t)$, we can obtain that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\mathcal {F}(t)=\rho _1\int _0^{L}(\varphi _t^2 +\varphi \varphi _{tt})\hbox {d}x+\rho _2\int _0^{L}(\psi _t^2+\psi \psi _{tt})\hbox {d}x +\mu \int _0^{L}\varphi \varphi _t\hbox {d}x. \end{aligned}$$

It follows from (4.1)$_1$ and (4.1)$_2$ that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\int _0^{^L}\rho _1\varphi _t\varphi \hbox {d}x=\rho _1\int _0^{L}\varphi _t^2\hbox {d}x-k\int _0^{L}(\varphi _x+\psi )\varphi _x \hbox {d}x-\mu \int _0^{L}\varphi \varphi _t\hbox {d}x, \end{aligned}$$

(4.5)

and

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\int _0^{L}\rho _2\psi _t\psi \hbox {d}x= & {} \rho _2\int _0^{L}\psi _t^2\hbox {d}x+\int _0^{L}(\alpha \psi _{xx} -k(\varphi _x+\psi )+\gamma _1\theta _x +\gamma _2 P_x)\psi \hbox {d}x\nonumber \\= & {} \rho _2\int _0^{L}\psi _t^2\hbox {d}x-k\int _0^{L} (\varphi _x+\psi )\psi \hbox {d}x-\alpha \int _0^{L} \psi _x^2\hbox {d}x\nonumber \\&-\int _0^{L}(\gamma _1\theta +\gamma _2 P)\psi _x \hbox {d}x. \end{aligned}$$

(4.6)

Adding (4.5) and (4.6), we get

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\mathcal {F}(t)&=\rho _1\int _0^{L}\varphi _t^2\hbox {d}x+ \rho _2\int _0^{L}\psi _t^2\hbox {d}x -k\int _0^{L}(\varphi _x+\psi )^2-\alpha \int _0^{L} \psi _x^2\hbox {d}x\\&\quad -\int _0^{L}(\gamma _1\theta +\gamma _2 P)\psi _x \hbox {d}x. \end{aligned} \end{aligned}$$

Using the Young’s and Poincaré’s inequalities, we arrive at (4.4). $\square$

Now, we define the functional ${\mathscr {S}} (t)$

$$\begin{aligned} {\mathscr {S}} (t) =\rho _2\int _0^L \psi _t\omega \hbox {d}x, \end{aligned}$$

(4.7)

where $-\gamma _1\omega _x = c\theta +dP$ with $\omega (0) = \omega (L) = 0$.

Lemma 4.2

Let the assumptions of Lemma 4.1 hold, then the functional ${\mathscr {S}}$ defined by (4.7) satisfies

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}{\mathscr {S}}}{{d}t}(t)&\le -\frac{\rho _2}{2}\int _0^{L}\psi _t^{2}{d}x+\frac{\alpha }{16} \int _0^{L}\psi _x^2{d}x +\frac{k}{8}\int _0^{L}(\varphi _x+\psi )^2 {d}x\\&\quad +C_1\int _0^{L}\theta _{x}^{2}{d}x +C_2\int _0^{L}P_{x}^{2}{d}x. \end{aligned} \end{aligned}$$

(4.8)

Proof

Taking the derivation of (4.7), we can get

$$\begin{aligned} \frac{\hbox {d}{\mathscr {S}}}{\hbox {d}t}(t) = \int _0^L \rho _2\psi _t\omega _t \hbox {d}x +\int _0^L \rho _2\psi _{tt}\omega \hbox {d}x:={\mathscr {S}}_1(t)+ {\mathscr {S}}_2(t). \end{aligned}$$

(4.9)

By using (4.9)$_1$ and Young’s inequality, we shall see that

$$\begin{aligned} \begin{aligned} {\mathscr {S}}_1(t)&:=\int _0^L \rho _2\psi _t\omega _t \hbox {d}x\\&= -\frac{\rho _2}{\gamma _1}\int _0^{L}\psi _t\partial _x^{-1} \Big (\kappa \theta _{xx}+\gamma _1\psi _{xt}\Big )\hbox {d}x\\&=-\rho _2\int _0^{L}\psi _t^{2}\hbox {d}x-\frac{\rho _2\kappa }{\gamma _1} \int _0^{L}\psi _t\theta _{x}\hbox {d}x\\&\le -\frac{\rho _2}{2}\int _0^{L}\psi _t^{2}\hbox {d}x+C_1\int _0^{L} \theta _{x}^{2}\hbox {d}x. \end{aligned} \end{aligned}$$

It follows from (4.9)$_2$ that

$$\begin{aligned} \begin{aligned} {\mathscr {S}}_2(t)&:=\int _0^L \rho _2\psi _{tt}\omega \hbox {d}x\\&= \int _0^{L}\Big (\alpha \psi _{xx}-k(\varphi _x+\psi )+\gamma _1 \theta _{x}+\gamma _2 P_{x}\Big )\omega \,\hbox {d}x\\&=-\alpha \int _0^{L}\omega _x\psi _x\hbox {d}x-k\int _0^{L}(\varphi _x+\psi )\omega \hbox {d}x\\&\quad +\int _0^{L}\omega (\gamma _1\theta _{x}+\gamma _2 P_{x})\hbox {d}x. \end{aligned} \end{aligned}$$

By using Young’s and Poincaré’s inequalities, we arrive at

$$\begin{aligned} \begin{aligned}&-\alpha \int _0^{L}\omega _x\psi _x\hbox {d}x \le \frac{\alpha }{16}\int _0^{L} \psi _x^2\hbox {d}x+C_1\int _0^{L}\theta _{x}^{2}\hbox {d}x+C_2\int _0^{L}P_{x}^{2}\hbox {d}x,\\&\quad -k\int _0^{L}(\varphi _x+\psi )\omega \hbox {d}x\le \frac{k}{8}\int _0^{L} (\varphi _x+\psi )^2 \hbox {d}x+C_1\int _0^{L}\theta _{x}^{2}\hbox {d}x+C_2\int _0^{L}P_{x}^{2}\hbox {d}x,\\&\quad \int _0^{L}\omega (\gamma _1\theta _{x}+\gamma _2 P_{x}) \hbox {d}x\le C_1\int _0^{L}\theta _{x}^{2}\hbox {d}x+C_2\int _0^{L}P_{x}^{2}\hbox {d}x. \end{aligned} \end{aligned}$$

Then, estimate (4.8) follows from the previous estimates. $\square$

Next, we define a Lyapunov functional $\aleph$ and we show that it is equivalent to the energy functional E.

Lemma 4.3

Under the assumptions of Theorem 4.1, there exists a constant $\beta _0> 0$ such that

$$\begin{aligned} (N-\beta _0) {{E}}(t)\le \aleph (t) \le (N+\beta _0) {{E}}(t),\qquad \forall t \ge 0, \end{aligned}$$

(4.10)

where $\aleph (t)$ is a Lyapunov functional defined by

$$\begin{aligned} \aleph (t) =N {{E}}(t) + \mathcal {F}(t) + 4 {\mathscr {S}}(t), \end{aligned}$$

(4.11)

and $N>\beta _0$ is a sufficiently large constant.

Proof

It follows from Young’s, Poincaré, Cauchy–Schwarz inequalities that

$$\begin{aligned} |\mathcal {F}(t)|\le & {} \frac{\rho _1}{2}\int _0^{L}\varphi _{t}^{2}\hbox {d}x+ \frac{\rho _2}{2}\int _0^{L}\psi _{t}^{2}\hbox {d}x+\frac{\rho _1L^2}{2}\int _0^{L}\psi _{x}^{2}\hbox {d}x+\frac{\mu }{2}\int _0^{L}\varphi ^{2}\hbox {d}x,\\ |{\mathscr {S}}(t)|\le & {} \frac{\rho _2}{2}\int _0^{L}\psi _{t}^{2} \hbox {d}x+c_1\int _0^{L}\theta ^{2}\hbox {d}x+c_2\int _0^{L}P^{2}\hbox {d}x. \end{aligned}$$

Thus, there exists a constant $\beta _0 > 0$ such that

$$\begin{aligned} |\aleph (t) -N {{E}}(t)| =| \mathcal {F}(t) + 4{\mathscr {S}}(t)|\le \beta _0 {{E}}(t), \end{aligned}$$

and therefore estimate (4.10) holds. $\square$

Theorem 4.4

Let the assumptions of Lemma 4.1 hold. Then, there exist positive constants $c_0$, $c_1$ such that the energy functional satisfies

$$\begin{aligned} {E}(t)\le c_1 {E}(0)\hbox {e}^{-c_0t},\qquad \forall t \ge 0. \end{aligned}$$

(4.12)

Proof

It follows from (4.3), (4.8) and (4.11) that for any $t > 0$,

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\aleph (t)\le & {} -({\kappa }N-C_1)\int _0^{L}\theta _x^{2} \hbox {d}x-({\hbar }N-C_2)\int _0^{L}P_x^{2}\hbox {d}x -({\mu }N-\rho _1)\int _0^{L} \varphi _t^{2}\hbox {d}x\nonumber \\&-\rho _2\int _0^{L}\psi _t^2\hbox {d}x -\frac{k}{2}\int _0^{L} (\varphi _x+\psi )^2\hbox {d}x -\frac{\alpha }{4}\int _0^{L} \psi _x^2\hbox {d}x. \end{aligned}$$

(4.13)

We choose N large enough such that

$$\begin{aligned} N>\sup \left\{ \frac{C_1}{\kappa },\frac{C_2}{\hbar }, \frac{\rho _1}{\mu }\right\} . \end{aligned}$$

Thus, there exists a positive constant $\varsigma$ such that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\aleph (t)\le \varsigma E(t) \end{aligned}$$

which yields, by using (4.10),

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\aleph (t)\le C \aleph (t) \end{aligned}$$

for some positive constant C. Then, estimate (4.12) follows by using (4.10) again, which completes the proof. $\square$

5 Numerical approximation

In this section, we propose a finite element approximation to system (1.10) with initial conditions (1.11) and boundary conditions (1.12). We note that it is straightforward to extend the results shown in this section, and in the following one, to the combined Neumann conditions (1.13). Moreover, we prove that the discrete energy decays, from which we derive a discrete stability property.

Multiplying (1.10) by test functions $\chi , \eta , \varsigma , z \in H^1_{0}(0,L)$, we obtain the following weak form:

$$\begin{aligned} \left. \begin{array}{l} \rho _{1}(v_{t},\chi )+k(\varphi _{x}+\psi , \chi _{x})=0,\\ \rho _{2}(w_{t}, \eta )+\alpha (\psi _{x},\eta _x)+k(\varphi _{x}+\psi ,\eta )+\gamma _1 (\theta , \eta _{x})+\gamma _2 (P, \eta _{x})=0,\\ c(\theta _{t}, \varsigma )+d (P_{t}, \varsigma )+\kappa (\theta _{x}, \varsigma _x)-\gamma _1 (w_{x},\varsigma )=0,\\ d(\theta _{t},z)+r(P_{t},z)+\hbar (P_{x},z_x)-\gamma _2 (w_{x},z)=0, \end{array}\right\} \end{aligned}$$

(5.1)

where we used the notations $v=\varphi _t$ and $w=\psi _t$.

Let us partition the interval (0, L) into subintervals $I_j=(x_{j-1},x_j)$ of length $h=1/s$ with $0=x_0<x_1< \ldots < x_s=L$ and define

$$\begin{aligned} S^h_0= \{ u \in H^1_0(0,L) \ | \ u \in C([0,L]), \ u|_{I_j} \mathrm{\ is \ a \ linear \ polynomial }\}. \end{aligned}$$

For a given final time T and a positive integer N,  let $\Delta t =T/N$ be the time step and $t_n=n\Delta t,$ $n=0, \ldots , N$. The finite element method for (5.1) with Dirichlet homogeneous boundary conditions is to find $v^n_h, w^n_h, \theta ^n_h, P^n_h$ $\in S^h_0,$ $n=1, \ldots , N,$ such that, for all $\chi _h, \eta _h, \varsigma _h, z_h$ $\in S^h_0,$

$$\begin{aligned} \left. \begin{array}{l} \displaystyle \frac{\rho _{1}}{\Delta t}(v^{n}_{h}- v^{n-1}_h,\chi _h)+k(\varphi ^n_{hx}+\psi ^n_h, \chi _{hx})=0,\\ \displaystyle \frac{\rho _{2}}{\Delta t}(w^{n}_{h}- w^{n-1}_h, \eta _h)+\alpha (\psi ^n_{hx},\eta _{hx}) +k(\varphi ^n_{hx}+\psi ^n_h,\eta _h)\\ \qquad +\gamma _1 (\theta ^n_h, \eta _{hx})+\gamma _2 (P^n_h, \eta _{hx})=0,\\ \displaystyle \frac{c}{\Delta t}(\theta ^{n}_h- \theta ^{n-1}_h, \varsigma _h)+\frac{\hbox {d}}{\Delta t} (P^{n}_h-P^{n-1}_h, \varsigma _h)+\kappa (\theta ^n_{hx}, \varsigma _{hx})\\ \qquad -\gamma _1 (w^n_{hx},\varsigma _h)=0,\\ \displaystyle \frac{\hbox {d}}{\Delta t}(\theta ^{n}_h-\theta ^{n-1}_h ,z_h)+\frac{r}{\Delta t}(P^{n}_h-P^{n-1}_h,z_h)+\hbar (P^n_{hx},z_{hx})\\ \qquad -\gamma _2 (w^n_{hx},z_h)=0, \end{array}\right\} \end{aligned}$$

(5.2)

with $\varphi ^n_h= \varphi ^{n-1}_h + \Delta t v^n_h$ and $\psi ^n_h= \psi ^{n-1}_h + \Delta t w^n_h$. Here, $\varphi ^0_h,$ $v^0_h,$ $\psi ^0_h,$ $w^0_h,$ $\theta ^0_h,$ $P^0_h$ are adequate approximations to $\varphi ^0,$ $\varphi ^1,$ $\psi ^0,$ $\psi ^1,$ $\theta ^0$ and $P^0,$ respectively.

Let us introduce the discrete energy given by

$$\begin{aligned} E^n_h= & {} \frac{1}{2} \Big ( \rho _{1} \Vert v^n_h \Vert ^2 +\rho _{2} \Vert w^{n}_h\Vert ^2+ k \Vert \varphi ^n_{hx}+\psi ^n_h\Vert ^2 + \alpha \Vert \psi ^n_{hx}\Vert ^2\\&+c \Vert \theta ^{n}_h\Vert ^2 + r \Vert P^{n}_h\Vert ^2 + 2d(P^{n}_h,\theta _h^n )\Big ), \end{aligned}$$

where $\Vert \cdot \Vert$ represents the norm in the space $L^2(0,\ell )$.

Thus, the following decay result, similarly to the continuous case, holds.

Theorem 5.1

Let the assumptions of Theorem 2.4 hold. Then, the discrete energy decays to zero, that is,

$$\begin{aligned} \frac{E^n_h - E^{n-1}_h}{\Delta t} \le 0, \ \ \ n=1, \ldots ,N. \end{aligned}$$

Proof

Choosing $\chi _h =v^n_h,$ $\eta _h=w^n_h,$ $\varsigma _h=\theta _h^n$ and $z_h=P^n_h$ in (5.2), we obtain

$$\begin{aligned}&\frac{\rho _{1}}{2\Delta t}\left( \Vert v^{n}_{h}- v^{n-1}_h\Vert ^2 + \Vert v^n_h \Vert ^2 - \Vert v^{n-1}_h\Vert ^2\right) +k(\varphi ^n_{hx}+\psi ^n_h, v^n_{hx})=0,\\&\frac{\rho _{2}}{2\Delta t}\left( \Vert w^{n}_{h}- w^{n-1}_h\Vert ^2 + \Vert w^{n}_h\Vert ^2 - \Vert w^{n-1}_h \Vert ^2 \right) +\alpha (\psi ^n_{hx},w^n_{hx})+k(\varphi ^n_{hx}+\psi ^n_h,w^n_h)\\&\quad +\gamma _1 (\theta ^n_h, w^n_{hx})+\gamma _2 (P^n_h,w^n_{hx} )=0,\\&\frac{c}{2\Delta t}\left( \Vert \theta ^{n}_h- \theta ^{n-1}_h\Vert ^2 +\Vert \theta ^{n}_h\Vert ^2 - \Vert \theta ^{n-1}_h\Vert ^2 \right) +\frac{\hbox {d}}{\Delta t} (P^{n}_h-P^{n-1}_h,\theta _h^n )\\&\quad +\kappa \Vert \theta ^n_{hx}\Vert ^2-\gamma _1 (w^n_{hx},\theta _h^n)=0,\\&\frac{\hbox {d}}{\Delta t}(\theta ^{n}_h-\theta ^{n-1}_h ,P^n_h)+\frac{r}{2\Delta t}\left( \Vert P^{n}_h-P^{n-1}_h\Vert ^2 +\Vert P^{n}_h\Vert ^2-\Vert P^{n-1}_h\Vert ^2 \right) \\&\quad +\hbar \Vert P^n_{hx}\Vert ^2-\gamma _2 (w^n_{hx},P^n_h)=0, \end{aligned}$$

and adding the latter equations we find that

$$\begin{aligned}&\frac{\rho _{1}}{2\Delta t}\left( \Vert v^{n}_{h}- v^{n-1}_h\Vert ^2 + \Vert v^n_h \Vert ^2 - \Vert v^{n-1}_h\Vert ^2\right) + \frac{\rho _{2}}{2\Delta t}\left( \Vert w^{n}_{h}- w^{n-1}_h\Vert ^2 + \Vert w^{n}_h\Vert ^2 - \Vert w^{n-1}_h \Vert ^2 \right) \\&\quad + k(\varphi ^n_{hx}+\psi ^n_h, v^n_{hx} + w^n_h) + \alpha (\psi ^n_{hx},w^n_{hx})+ \frac{c}{2\Delta t}\left( \Vert \theta ^{n}_h- \theta ^{n-1}_h\Vert ^2 +\Vert \theta ^{n}_h\Vert ^2 - \Vert \theta ^{n-1}_h\Vert ^2 \right) \\&\quad + \frac{r}{2\Delta t}\left( \Vert P^{n}_h-P^{n-1}_h\Vert ^2 +\Vert P^{n}_h\Vert ^2-\Vert P^{n-1}_h\Vert ^2 \right) +\frac{\hbox {d}}{\Delta t} (P^{n}_h-P^{n-1}_h,\theta _h^n )\\&\quad +\frac{\hbox {d}}{\Delta t}(\theta ^{n}_h-\theta ^{n-1}_h ,P^n_h)+\kappa \Vert \theta ^n_{hx}\Vert ^2 +\hbar \Vert P^n_{hx}\Vert ^2 =0. \end{aligned}$$

Now, we note that

$$\begin{aligned}&k(\varphi ^n_{hx}+\psi ^n_h, v^n_{hx} + w^n_h)= \frac{k}{\Delta t} (\varphi ^n_{hx}+\psi ^n_h,\varphi ^ n_{hx} + \psi ^n_h - (\varphi ^ {n-1}_{hx}+ \psi ^ {n-1}_h))\\&\quad \ge \frac{k}{2\Delta t} \left( \Vert \varphi ^n_{hx}+\psi ^n_h\Vert ^2 - \Vert \varphi ^ {n-1}_{hx}+ \psi ^ {n-1}_h\Vert ^2 \right) ,\\&\alpha (\psi ^n_{hx},w^n_{hx})= \frac{\alpha }{\Delta t}(\psi ^n_{hx},\psi ^n_{hx}-\psi ^{n-1}_n)\ge \frac{\alpha }{2\Delta t}\left( \Vert \psi ^n_{hx}\Vert ^2 -\Vert \psi ^{n-1}_n\Vert ^2\right) ,\\&(P^{n}_h-P^{n-1}_h,\theta _h^n )+(\theta ^{n}_h-\theta ^{n-1}_h ,P^n_h)\\&\quad = (P^{n}_h,\theta _h^n ) -(P^{n-1}_h,\theta _h^{n-1} )+ (\theta ^{n}_h-\theta ^{n-1}_h ,P^n_h-P^{n-1}_h). \end{aligned}$$

These results, together with (1.15), yield

$$\begin{aligned}&\frac{\rho _{1}}{2\Delta t}\left( \Vert v^n_h \Vert ^2 - \Vert v^{n-1}_h\Vert ^2\right) + \frac{\rho _{2}}{2\Delta t}\left( \Vert w^{n}_h\Vert ^2 - \Vert w^{n-1}_h \Vert ^2 \right) \nonumber \\&\quad + \frac{k}{2\Delta t} \left( \Vert \varphi ^n_{hx}+\psi ^n_h\Vert ^2 - \Vert \varphi ^ {n-1}_{hx}+ \psi ^ {n-1}_h\Vert ^2 \right) +\frac{\alpha }{2\Delta t}\left( \Vert \psi ^n_{hx}\Vert ^2 -\Vert \psi ^{n-1}_n\Vert ^2\right) \nonumber \\&\quad + \frac{c}{2\Delta t}\left( \Vert \theta ^{n}_h\Vert ^2 - \Vert \theta ^{n-1}_h\Vert ^2 \right) + \frac{r}{2\Delta t}\left( \Vert P^{n}_h\Vert ^2-\Vert P^{n-1}_h\Vert ^2 \right) \nonumber \\&\quad + \frac{\hbox {d}}{\Delta t} \left( (P^{n}_h,\theta _h^n ) -(P^{n-1}_h,\theta _h^{n-1} )\right) +\kappa \Vert \theta ^n_{hx}\Vert ^2 +\hbar \Vert P^n_{hx}\Vert ^2 \le 0, \end{aligned}$$

(5.3)

and the theorem is proved using the definition of the discrete energy. $\square$

As a consequence, the following stability estimates are derived.

Corollary 5.2

Under the assumptions of Theorem 2.4, the discrete solution $\{ v^n_h, w^n_h, \varphi ^n_h, \psi ^n_h, \theta ^n_h, P^n_h \}$, generated by discrete problem (5.2) , satisfies

$$\begin{aligned} \Vert v^n_h \Vert ^2 + \Vert w^{n}_h\Vert ^2 + \Vert \varphi ^n_{hx}+\psi ^n_h\Vert ^2 +\Vert \psi ^n_{hx}\Vert ^2 +\Delta t\sum _{i=1}^n \Vert \theta ^i_{hx}\Vert ^2 + \Delta t\sum _{i=1}^n \Vert P^i_{hx}\Vert ^2 \le C. \end{aligned}$$

Proof

Summing (5.3) over n and recalling (1.15), the result follows. $\square$

6 Error analysis: a priori error estimates

In this section, we will obtain some a priori error estimates on the numerical approximation, from which we derive the linear convergence of the algorithm under suitable additional regularity conditions.

Theorem 6.1

Let the assumptions of Theorem 2.4 hold. If we denote by $(v,w,\varphi ,\psi ,\theta ,P)$, the solution to problem (5.1), and by $\{v_h^n,w_h^n,\varphi _h^n,\psi _h^n,\theta _h^n,P_h^n\}_{n=0}^N$, the solution to problem (5.2), then we have the following a priori error estimates for all $\{\chi _h^n\}_{n=0}^N,\, \{\eta _h^n\}_{n=0}^N,\,\{\varsigma _h^n\}_{n=0}^N,\,\{z_h^n\}_{n=0}^N\subset S_0^h,$

$$\begin{aligned}&\max _{0\le n\le N}\Big \{ \Vert v^n- v^n_h\Vert ^2 + \Vert w^n- w^n_h\Vert ^2 + \Vert \varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h)\Vert ^2 \nonumber \\&\qquad + \Vert \psi ^n_x-\psi ^n_{hx}\Vert ^2 + \Vert P^n- P^n_h \Vert ^2 + \Vert \theta ^n- \theta ^n_h \Vert ^2 \Big \} \nonumber \\&\quad \le C \Delta t \sum _{i=1}^n\Big ( \Vert v_t^i-\delta v^i \Vert ^2 + \Vert w^i_t - \delta w^i\Vert ^2 + \Vert \psi ^i_{xt}-\delta \psi ^i_{x}\Vert ^2 + \Vert \theta ^i_t-\delta \theta ^i\Vert ^2 \nonumber \\&\qquad + \Vert P^i_t- \delta P^i\Vert ^2 + \Vert \varphi _{xt}^i +\psi ^i_t- (\delta \varphi ^i_x+ \delta \psi ^i) \Vert ^2 + \Vert v^i-\chi ^i_h\Vert ^2\nonumber \\&\qquad + \Vert v^i_x-\chi ^i_{hx}\Vert ^2 + \Vert w^i-\eta ^i_h\Vert ^2 + \Vert w^i_x-\eta ^i_{hx}\Vert ^2 + \Vert \theta ^i_x-\varsigma ^i_{hx}\Vert ^2 \nonumber \\&\qquad + \Vert P^i_x - z^i_{hx}\Vert ^2\Big )+\frac{C}{\Delta t}\sum _{i=1}^{N-1}\Vert v^i-\chi ^i_h-(v^{i+1}-\chi ^{i+1}_h)\Vert ^2\nonumber \\&\qquad +\frac{C}{\Delta t}\sum _{i=1}^{N-1}\Vert w^i-\eta ^i_h-(w^{i+1}-\eta ^{i+1}_h)\Vert ^2+\frac{C}{\Delta t}\sum _{i=1}^{N-1}\Vert \theta ^i-\varsigma ^i_h-(\theta ^{i+1} -\varsigma ^{i+1}_h)\Vert ^2\nonumber \\&\qquad +\frac{C}{\Delta t}\sum _{i=1}^{N-1}\Vert P^i-z^i_h-(P^{i+1}-z^{i+1}_h)\Vert ^2+C\max _{0\le n\le N}\Big (\Vert v^n-\chi _h^n\Vert ^2\nonumber \\&\qquad +\Vert w^n-\eta _h^n\Vert ^2+\Vert \theta ^n-\varsigma _h^n\Vert ^2+\Vert P^n-z_h^n\Vert ^2 \Big )\nonumber \\&\qquad +C \Big ( \Vert \varphi ^1- v^0_h\Vert ^2 + \Vert \psi ^1- w^0_h\Vert ^2 + \Vert \varphi ^0_x+ \psi ^0-(\varphi ^0_{hx}+\psi ^0_h)\Vert ^2\nonumber \\&\qquad + \Vert \psi ^0_x-\psi ^0_{hx}\Vert ^2 + \Vert \theta ^0- \theta ^0_h \Vert ^2+ \Vert P^0- P^0_h \Vert ^2 \Big ), \end{aligned}$$

(6.1)

where C is a positive constant assumed to be independent of the discretization parameters h and $\Delta t$.

Proof

Let us recall that $v=\varphi _t$ and $w=\psi _t$. For a continuous function f(t),  let $f^n=f(t_n)$ and, for a sequence $\{ f^n\}_{n=1}^N,$ let $\delta f^n= (f^n-f^{n-1})/\Delta t$.

Subtracting equation (5.1)$_1$ at time $t=t_n$ for $\chi =\chi _h \in S^h _0$ and (5.2)$_1$, we have

$$\begin{aligned} \rho _{1}(v_t^n-\delta v^{n}_{h},\chi _h)+k(\varphi _x^n+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), \chi _{hx})=0. \end{aligned}$$

Thus, for all $\chi \in S^h_0,$ we obtain

$$\begin{aligned}&\rho _{1}(v_t^n-\delta v^{n}_{h},v^n- v^n_h) + k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v_x^n- v^n_{hx}) \nonumber \\&\quad = \rho _{1}(v^n_{t}-\delta v^{n}_{h},v^n-\chi _h)+k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v^n_x-\chi _{hx}). \end{aligned}$$

(6.2)

Similarly, from equations (5.1)$_2$ - (5.1)$_4$ and (5.2)$_2$ - (5.2)$_4$ we deduce, for all $\eta _h, \varsigma _h, z_h$ $\in S^h_0,$

$$\begin{aligned}&\rho _{2}( w^n_t - \delta w^{n}_{h}, w^n-w^n_h) +\alpha (\psi ^n_x-\psi ^n_{hx},w^n_x-w^n_{hx}) \\&\qquad +\gamma _1 (\theta ^n-\theta ^n_h, w^n_x-w^n_{hx})+\gamma _2 (P^n-P^n_h, w^n_x-w^n_{hx}) \\&\qquad +k(\varphi ^n_{x}+\psi ^n-(\varphi ^n_{hx}+\psi ^n_h),w^n-w^n_h)\\&\quad = \rho _{2}( w^n_t - \delta w^{n}_{h}, w^n- \eta _h)+\alpha (\psi ^n_x-\psi ^n_{hx},w^n_x-\eta _{hx}) \\&\qquad +\gamma _1 (\theta ^n-\theta ^n_h, w^n_x-\eta _{hx})+\gamma _2 (P^n-P^n_h, w^n_x-\eta _{hx}),\\&\qquad +k(\varphi ^n_{x}+\psi ^n-(\varphi ^n_{hx}+\psi ^n_h),w^n-\eta _h),\\&c (\theta ^{n}_t-\delta \theta ^{n}_h, \theta ^{n}-\theta ^n_h)+d( P^n_t-\delta P^{n}_h, \theta ^{n}-\theta ^n_h) +\kappa (\theta ^{n}_x-\theta ^n_{hx}, \theta ^{n}_x-\theta ^n_{hx})\\&\qquad -\gamma _1 (w^n_x-w^n_{hx},\theta ^{n}-\theta ^n_h) \\&\quad = c (\theta ^{n}_t-\delta \theta ^{n}_h, \theta ^{n}-\varsigma _h)+d( P^n_t-\delta P^{n}_h, \theta ^{n}-\varsigma _h)+\kappa (\theta ^{n}_x-\theta ^n_{hx}, \theta ^{n}_x-\varsigma _{hx})\\&\qquad -\gamma _1 (w^n_x-w^n_{hx},\theta ^{n}-\varsigma _h),\\&d( \theta ^n_t-\delta \theta ^{n}_h , P^n-P^n_h)+r (P^n_t- \delta P^{n}_h,P^n- P^n_h)+\hbar (P^n_x-P^n_{hx}, P^n_x- P^n_{hx})\\&\qquad -\gamma _2 (w^n_x-w^n_{hx},P^n-P^n_h) \\&\quad = d( \theta ^n_t-\delta \theta ^{n}_h , P ^n-z_h)+r (P^n_t- \delta P^{n}_h,P^n- z_h)+\hbar (P^n_x-P^n_{hx}, P^n_x- z_{hx})\\&\qquad -\gamma _2 (w^n_x-w^n_{hx},P^n-z_h). \end{aligned}$$

Using that $(a-b)a = 0.5\Big ( (a-b)^2+ a^2-b^2 \Big )$, we obtain

$$\begin{aligned}&(v_t^n-\delta v^{n}_{h},v^n- v^n_h)= (v_t^n-\delta v^n ,v^n- v^n_h)+ (\delta v^n - \delta v^{n}_{h},v^n- v^n_h)\nonumber \\&\quad \ge (v_t^n-\delta v^n ,v^n- v^n_h) + \frac{1}{2\Delta t} \left( \Vert v^n- v^n_h\Vert ^2 - \Vert v^{n-1}- v^{n-1}_h\Vert ^2 \right) . \end{aligned}$$

(6.3)

In the same way, we find

$$\begin{aligned}&(w^n_t - \delta w^{n}_{h}, w^n-w^n_h)\ge ( w^n_t - \delta w^{n}, w^n-w^n_h) \\&\qquad + \frac{1}{2\Delta t} \left( \Vert w^n- w^n_h\Vert ^2 - \Vert w^{n-1}- w^{n-1}_h\Vert ^2 \right) ,\\&(\psi ^n_x-\psi ^n_{hx},w^n_x-w^n_{hx}) = (\psi ^n_x-\psi ^n_{hx},\psi ^n_{xt}-\delta \psi ^n_{hx}) \\&\quad \ge (\psi ^n_x-\psi ^n_{hx},\psi ^n_{xt}-\delta \psi ^n_{x}) + \frac{1}{2\Delta t} \left( \Vert \psi ^n_x-\psi ^n_{hx}\Vert ^2 - \Vert \psi ^{n-1}_x-\psi ^{n-1}_{hx}\Vert ^2 \right) ,\\&(\theta ^{n}_t-\delta \theta ^{n}_h, \theta ^{n}-\theta ^n_h)= (\theta ^{n}_t-\delta \theta ^{n}, \theta ^{n}-\theta ^n_h)\\&\qquad + \frac{1}{2\Delta t} \left( \Vert \theta ^n- \theta ^n_h - ( \theta ^{n-1} - \theta ^{n-1}_h)\Vert ^2 + \Vert \theta ^n- \theta ^n_h \Vert ^2 - \Vert \theta ^{n-1} - \theta ^{n-1}_h\Vert ^2 \right) ,\\&(P^n_t- \delta P^{n}_h,P^n- P^n_h)= (P^n_t- \delta P^{n},P^n- P^n_h) \\&\qquad + \frac{1}{2\Delta t} \Big ( \Vert P^n- P^n_h - ( P^{n-1} - P^{n-1}_h)\Vert ^2 + \Vert P^n- P^n_h \Vert ^2 - \Vert P^{n-1} - P^{n-1}_h\Vert ^2 \Big ). \end{aligned}$$

From the previous estimates it follows that

$$\begin{aligned}&\frac{\rho _1}{2\Delta t} \left( \Vert v^n- v^n_h\Vert ^2 - \Vert v^{n-1}- v^{n-1}_h\Vert ^2 \right) + \frac{\rho _2}{2\Delta t} \left( \Vert w^n- w^n_h\Vert ^2 - \Vert w^{n-1}- w^{n-1}_h\Vert ^2 \right) \\&\qquad + k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v_x^n- v^n_{hx}+ w^n-w^n_h)) +\kappa \Vert \theta ^{n}_x-\theta ^n_{hx} \Vert ^2\\&\qquad + \frac{c}{2\Delta t} \left( \Vert \theta ^n- \theta ^n_h - ( \theta ^{n-1} - \theta ^{n-1}_h)\Vert ^2 + \Vert \theta ^n- \theta ^n_h \Vert ^2 - \Vert \theta ^{n-1} - \theta ^{n-1}_h\Vert ^2 \right) \\&\qquad + d( P^n_t-\delta P^{n}_h, \theta ^{n}-\theta ^n_h) + d( \theta ^n_t-\delta \theta ^{n}_h , P^n-P^n_h) + \hbar \Vert P^n_x-P^n_{hx}\Vert ^2 \\&\qquad + \frac{r}{2\Delta t} \left( \Vert P^n- P^n_h - ( P^{n-1} - P^{n-1}_h)\Vert ^2 + \Vert P^n- P^n_h \Vert ^2 - \Vert P^{n-1} - P^{n-1}_h\Vert ^2 \right) \\&\qquad + \frac{\alpha }{2\Delta t} \left( \Vert \psi ^n_x-\psi ^n_{hx}\Vert ^2 - \Vert \psi ^{n-1}_x-\psi ^{n-1}_{hx}\Vert ^2 \right) \\&\quad = -\rho _{1}(v_t^n-\delta v^n ,v^n- v^n_h) - \rho _2 (w^n_t - \delta w^{n}, w^n-w^n_h) - \alpha (\psi ^n_x-\psi ^n_{hx},\psi ^n_{xt}-\delta \psi ^n_{x}) \\&\qquad - c(\theta ^{n}_t-\delta \theta ^{n}, \theta ^{n}-\theta ^n_h) - r(P^n_t- \delta P^{n},P^n- P^n_h) + \rho _{1}(v^n_{t}-\delta v^{n}_{h},v^n-\chi _h) \\&\qquad + k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v^n_x-\chi _{hx}) + \rho _{2}( w^n_t - \delta w^{n}_{h}, w^n- \eta _h) \\&\qquad +k(\varphi ^n_{x}+\psi ^n-(\varphi ^n_{hx}+\psi ^n_h),w^n-\eta _h) +\gamma _1 (\theta ^n-\theta ^n_h, w^n_x-\eta _{hx}) \\&\qquad + c (\theta ^{n}_t-\delta \theta ^{n}_h, \theta ^{n}-\varsigma _h)+d( P^n_t-\delta P^{n}_h, \theta ^{n}-\varsigma _h)+\kappa (\theta ^{n}_x-\theta ^n_{hx}, \theta ^{n}_x-\varsigma _{hx}) \\&\qquad -\gamma _1 (w^n_x-w^n_{hx},\theta ^{n}-\varsigma _h) + d( \theta ^n_t-\delta \theta ^{n}_h , P ^n-z_h)+r (P^n_t- \delta P^{n}_h,P^n- z_h) \\&\qquad +\hbar (P^n_x-P^n_{hx}, P^n_x- z_{hx}) -\gamma _2 (w^n_x-w^n_{hx},P^n-z_h) +\alpha (\psi ^n_x-\psi ^n_{hx},w^n_x-\eta _{hx}) \\&\qquad +\gamma _2 (P^n-P^n_h, w^n_x-\eta _{hx}) . \end{aligned}$$

Now, keeping in mind that

$$\begin{aligned}&k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v_x^n- v^n_{hx}+ w^n-w^n_h))\\&\quad = k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), \varphi _{xt}^n- \delta \varphi ^n_{hx}+ \psi ^n_t-\delta \psi ^n_h))\\&\quad \ge k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), \varphi _{xt}^n + \psi ^n_t- (\delta \varphi ^n_x+ \delta \psi ^n))\\&\qquad + \frac{k}{2\Delta t}\Vert \varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h)\Vert ^2- \frac{k}{2\Delta t}\Vert \varphi ^{n-1}_x+ \psi ^{n-1}-(\varphi ^{n-1}_{hx}+\psi ^{n-1}_h)\Vert ^2, \\&d( P^n_t -\delta P^{n}_h, \theta ^{n}-\theta ^n_h) + d( \theta ^n_t-\delta \theta ^{n}_h , P^n-P^n_h)\\&\quad = d( P^n_t - \delta P^{n}+ \delta P^{n}-\delta P^{n}_h, \theta ^{n}-\theta ^n_h) + d( \theta ^n_t-\delta \theta ^{n}+ \delta \theta ^{n}- \delta \theta ^{n}_h , P^n-P^n_h) \\&\quad = d( P^n_t - \delta P^{n}, \theta ^{n}-\theta ^n_h) + d( \theta ^n_t-\delta \theta ^{n} , P^n-P^n_h) + \frac{\hbox {d}}{\Delta t}( \theta ^n-\theta ^n_h, P^n-P^n_h) \\&\qquad + \frac{\hbox {d}}{\Delta t}( \theta ^n - \theta ^{n-1} - (\theta ^n_h - \theta ^{n-1}_h), P^n - P^{n-1} - (P^n_h - P^{n-1}_h)\\&\qquad - \frac{\hbox {d}}{\Delta t} ( \theta ^{n-1}-\theta ^{n-1}_h, P^{n-1}-P^{n-1}_h), \end{aligned}$$

recalling (1.15), we deduce from the previous estimate that

$$\begin{aligned}&\frac{\rho _1}{2\Delta t} \left( \Vert v^n- v^n_h\Vert ^2 - \Vert v^{n-1}- v^{n-1}_h\Vert ^2 \right) + \frac{\rho _2}{2\Delta t} \left( \Vert w^n- w^n_h\Vert ^2 - \Vert w^{n-1}- w^{n-1}_h\Vert ^2 \right) \\&\qquad + \frac{k}{2\Delta t}\Vert \varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h)\Vert ^2 - \frac{k}{2\Delta t}\Vert \varphi ^{n-1}_x + \psi ^{n-1}-(\varphi ^{n-1}_{hx}+\psi ^{n-1}_h)\Vert ^2 \\&\qquad + \frac{\alpha }{2\Delta t} \left( \Vert \psi ^n_x-\psi ^n_{hx}\Vert ^2 - \Vert \psi ^{n-1}_x-\psi ^{n-1}_{hx}\Vert ^2 \right) \\&\qquad + \frac{c}{2\Delta t} \left( \Vert \theta ^n- \theta ^n_h \Vert ^2 - \Vert \theta ^{n-1} - \theta ^{n-1}_h\Vert ^2 \right) \\&\qquad + \frac{\hbox {d}}{\Delta t}( \theta ^n-\theta ^n_h, P^n-P^n_h) - \frac{\hbox {d}}{\Delta t} ( \theta ^{n-1}-\theta ^{n-1}_h, P^{n-1}-P^{n-1}_h) +\kappa \Vert \theta ^{n}_x-\theta ^n_{hx} \Vert ^2\\&\qquad + \hbar \Vert P^n_x-P^n_{hx}\Vert ^2 + \frac{r}{2\Delta t} \left( \Vert P^n- P^n_h \Vert ^2 - \Vert P^{n-1} - P^{n-1}_h\Vert ^2 \right) \\&\quad \le -\rho _{1}(v_t^n-\delta v^n ,v^n- v^n_h) - \rho _2 (w^n_t - \delta w^{n}, w^n-w^n_h) - \alpha (\psi ^n_x-\psi ^n_{hx},\psi ^n_{xt}-\delta \psi ^n_{x}) \\&\qquad - c(\theta ^{n}_t-\delta \theta ^{n}, \theta ^{n}-\theta ^n_h) - r(P^n_t- \delta P^{n},P^n- P^n_h) + \rho _{1}(v^n_{t}-\delta v^{n}_{h},v^n-\chi _h) \\&\qquad + k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), v^n_x-\chi _{hx}) + \rho _{2}( w^n_t - \delta w^{n}_{h}, w^n- \eta _h)\\&\qquad +k(\varphi ^n_{x}+\psi ^n-(\varphi ^n_{hx}+\psi ^n_h),w^n-\eta _h) +\gamma _1 (\theta ^n-\theta ^n_h, w^n_x-\eta _{hx}) \\&\qquad + c (\theta ^{n}_t-\delta \theta ^{n}_h, \theta ^{n}-\varsigma _h)+d( P^n_t-\delta P^{n}_h, \theta ^{n}-\varsigma _h) +\kappa (\theta ^{n}_x-\theta ^n_{hx}, \theta ^{n}_x-\varsigma _{hx})\\&\qquad -\gamma _1 (w^n_x-w^n_{hx},\theta ^{n}-\varsigma _h) + d( \theta ^n_t-\delta \theta ^{n}_h , P ^n-z_h) +r (P^n_t- \delta P^{n}_h,P^n- z_h) \\&\qquad +\hbar (P^n_x-P^n_{hx}, P^n_x- z_{hx}) -\gamma _2 (w^n_x-w^n_{hx},P^n-z_h) \\&\qquad -k(\varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h), \varphi _{xt}^n + \psi ^n_t- (\delta \varphi ^n_x+ \delta \psi ^n))\\&\qquad -d( P^n_t - \delta P^{n}, \theta ^{n}-\theta ^n_h) - d( \theta ^n_t-\delta \theta ^{n} , P^n-P^n_h)\\&\qquad +\alpha (\psi ^n_x-\psi ^n_{hx},w^n_x-\eta _{hx}) +\gamma _2 (P^n-P^n_h, w^n_x-\eta _{hx}). \end{aligned}$$

From conditions (1.14), we conclude that $d/c < r/d$. Thus, let $\epsilon$ be such that $d/c< \epsilon < r/d$. As a consequence of the Cauchy–Schwarz inequality and the Young’s inequality, we obtain

$$\begin{aligned} 2d ( \theta ^n-\theta ^n_h, P^n-P^n_h) \le \frac{\hbox {d}}{\epsilon } \Vert \theta ^n-\theta ^n_h\Vert ^2 + d\epsilon \Vert P^n-P^n_h\Vert ^2 . \end{aligned}$$

Hence, summing (6.4) over n yields, for all $\chi ^i_h, \eta ^i_n, \varsigma ^i_h, z^i_n \in S^h_0,$

$$\begin{aligned}&\rho _1 \Vert v^n- v^n_h\Vert ^2 + \rho _2\Vert w^n- w^n_h\Vert ^2 + k\Vert \varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h)\Vert ^2 + \alpha \Vert \psi ^n_x-\psi ^n_{hx}\Vert ^2 \\&\qquad + (r-d\epsilon ) \Vert P^n- P^n_h \Vert ^2 + (c -d/\epsilon ) \Vert \theta ^n- \theta ^n_h \Vert ^2 \\&\quad \le C \Delta t \sum _{i=1}^n\Big ( \Vert v^i- v^i_h\Vert ^2 + \Vert w^i-w^i_h\Vert ^2 + \Vert \psi ^i_x-\psi ^i_{hx}\Vert ^2 + \Vert \theta ^i-\theta ^i_h\Vert ^2 \nonumber \\&\qquad + \Vert P^i- P^i_h\Vert ^2 + \Vert \varphi ^i_x+ \psi ^i-(\varphi ^i_{hx}+\psi ^i_h)\Vert ^2 +\Vert v_t^i-\delta v^i \Vert ^2 + \Vert w^i_t - \delta w^i\Vert ^2 \\&\qquad + \Vert \psi ^i_{xt}-\delta \psi ^i_{x}\Vert ^2 + \Vert \theta ^i_t-\delta \theta ^i\Vert ^2 + \Vert P^i_t- \delta P^i\Vert ^2 + \Vert \varphi _{xt}^i +\psi ^i_t- (\delta \varphi ^i_x+ \delta \psi ^i) \Vert ^2 \\&\qquad + \Vert v^i-\chi ^i_h\Vert ^2 + \Vert v^i_x-\chi ^i_{hx}\Vert ^2 + \Vert w^i-\eta ^i_h\Vert ^2 + \Vert w^i_x-\eta ^i_{hx}\Vert ^2 \nonumber \\&\qquad + (\delta \theta ^i-\delta \theta ^i_h, \theta ^i-\varsigma ^i_h) + (\delta P^i-\delta P^i_h, \theta ^i-\varsigma ^i_h) + \Vert \theta ^i_x-\varsigma ^i_{hx}\Vert ^2 \\&\qquad + (\delta \theta ^i-\delta \theta ^i_h , P^i-z_h^i) + (\delta P^i- \delta P^i_h,P^i- z^i_h)+ \Vert P^i_x - z^i_{hx}\Vert ^2\\&\qquad +(\delta v^i-\delta v_h^i,v^i-\chi _h^i)+(\delta w^i-\delta w_h^i,w^i-\eta _h^i)\Big )\\&\qquad +C \Big ( \Vert v^0- v^0_h\Vert ^2 + \Vert w^0- w^0_h\Vert ^2 + \Vert \varphi ^0_x+ \psi ^0-(\varphi ^0_{hx}+\psi ^0_h)\Vert ^2 + \Vert \psi ^0_x-\psi ^0_{hx}\Vert ^2\\&\qquad + \Vert \theta ^0- \theta ^0_h \Vert ^2+ \Vert P^0- P^0_h \Vert ^2 \Big ). \end{aligned}$$

Finally, taking into account that (see [15])

$$\begin{aligned}&\Delta t \sum _{i=1}^n (\delta v^i- \delta v^i_{h},v^i-\chi ^i_h) =(v^n-v^n_{h},v^n-\chi ^n_h)+(v^0_h-\varphi ^1,v^1-\chi ^1_h)\\&\qquad + \sum _{i=1}^{n-1} (v^j-v^j_{h},v^j-\chi ^j_h-(v^{j+1}-\chi ^{j+1}_h)),\\&\Delta t \sum _{i=1}^n (\delta w^i- \delta w^i_{h},w^i-\eta ^i_h) =(w^n-w^n_{h},w^n-\eta ^n_h)+(w^0_h-\psi ^1,w^1-\eta ^1_h)\\&\qquad + \sum _{i=1}^{n-1} (w^j-w^j_{h},w^j-\eta ^j_h-(w^{j+1}-\eta ^{j+1}_h)),\\&\Delta t \sum _{i=1}^n (\delta \theta ^i- \delta \theta ^i_{h},\theta ^i-\varsigma ^i_h) =(\theta ^n-\theta ^n_{h},\theta ^n-\varsigma ^n_h)+ (\theta ^0_h-\theta ^0,\theta ^1-\varsigma ^1_h)\\&\qquad + \sum _{i=1}^{n-1} (\theta ^j-\theta ^j_{h},\theta ^j-\varsigma ^j_h-(\theta ^{j+1} -\varsigma ^{j+1}_h)),\\&\Delta t \sum _{i=1}^n (\delta P^i- \delta P^i_{h},P^i-z^i_h) =(P^n-P^n_{h},P^n-z^n_h)+(P^0_h-P^0,P^1-z^1_h)\\&\qquad + \sum _{i=1}^{n-1} (P^j-P^j_{h},P^j-z^j_h-(P^{j+1}-z^{j+1}_h)),\\&\Delta t \sum _{i=1}^n (\delta \theta ^i- \delta \theta ^i_{h},P^i-z^i_h) =(\theta ^n-\theta ^n_{h}, P^n-z^n_h)+(\theta ^0_h-\theta ^0,P^1-z^1_h)\\&\qquad + \sum _{i=1}^{n-1} (\theta ^j-\theta ^j_{h},P^j-z^j_h-(P^{j+1}-z^{j+1}_h)),\\&\Delta t \sum _{i=1}^n (\delta P^i- \delta P^i_{h},\theta ^i-\varsigma ^i_h) =(P^n-P^n_{h},\theta ^n-\varsigma ^n_h)+(P^0_h-P^0,\theta ^1-\varsigma ^1_h)\\&\qquad + \sum _{i=1}^{n-1} (P^j-P^j_{h},\theta ^j-\varsigma ^j_h-(\theta ^{j+1}-\varsigma ^{j+1}_h)), \end{aligned}$$

from the above estimates, using a discrete version of Gronwall’s inequality (see, for instance, [16]), we conclude the proof. $\square$

We note that error estimates (6.1) are the basis to get the convergence order of the approximations given by problem (5.2). Therefore, as an example, if we assume the following additional regularity:

$$\begin{aligned}&\varphi ,\psi \in H^3(0,T;L^2(0,L))\cap H^2(0,T;H^1(0,L))\cap C^1([0,T];H^2(0,L)),\nonumber \\&\theta ,P\in H^2(0,T;L^2(0,L))\cap H^1(0,T;H^1(0,L))\cap C([0,T];H^2(0,L)), \end{aligned}$$

(6.4)

and we define the discrete initial conditions as

$$\begin{aligned}&v_h^0=P_h\varphi ^1,\quad w_h^0=P_h\psi ^1,\quad \varphi _h^0=P_h\varphi ^0,\quad \psi _h^0=P_h\psi ^0,\nonumber \\&\theta _h^0=P_h\theta ^0,\quad P_h^0=P_hP^0, \end{aligned}$$

(6.5)

where $P_h$ is the classical interpolation operator defined over the finite element space $S_0^h$; using the classical results on the approximation by finite elements (see, for instance, [14]), we obtain the following.

Corollary 6.2

Let the assumptions of Theorem 2.4 hold. Under the additional regularity (6.4), if the discrete initial conditions are given by (6.5), then it follows that the approximations obtained by problem (5.2) are linearly convergent, that is, there exists a positive constant C, independent of the discretization parameters h and $\Delta t$, such that

$$\begin{aligned}&\max _{0\le n\le N}\Big \{ \Vert v^n- v^n_h\Vert + \Vert w^n- w^n_h\Vert + \Vert \varphi ^n_x+ \psi ^n-(\varphi ^n_{hx}+\psi ^n_h)\Vert + \Vert \psi ^n_x-\psi ^n_{hx}\Vert \\&\qquad \quad + \Vert P^n- P^n_h \Vert + \Vert \theta ^n- \theta ^n_h \Vert \Big \} \le C(h+\Delta t). \end{aligned}$$

7 Numerical results

In order to verify the behaviour of the numerical method analysed in the previous section, some numerical experiments have been performed.

7.1 Numerical scheme

Given the solution $\varphi ^{n-1}_{h}, v^{n-1}_{h}, \psi ^{n-1}_{h}, w^{n-1}_{h}, \theta ^{n-1}_{h}$ and $P^{n-1}_{h}$ at time $t_{n-1},$ the transverse velocity field is obtained from the discrete linear variational equation:

$$\begin{aligned}&\rho _1(v^n_{h},\chi _h)+\Delta t^2 k((v^n_{h})_{x},(\chi _h)_{x}) =\rho _1(v^{n-1}_{h},\chi _h) -\Delta t k((\varphi ^{n-1}_{h})_x,(\chi ^h)_x)\\&\quad +\Delta t k((\psi ^n_{h})_x,\chi ^h). \end{aligned}$$

Later, we get the rotation velocity from the variational equation:

$$\begin{aligned}&\rho _2(w^n_{h},\eta _h)+\Delta t^2\alpha ((w^n_{h})_{x},(\eta _h)_{x}) + \Delta t^2 k(w^n_{h},\eta _h)=\rho _2(w^{n-1}_{h},\eta _h) \\&\quad -\Delta t \alpha ((\psi ^{n-1}_{h})_x,(\eta _h)_x)-\Delta t k(\psi ^{n-1}_{h},\eta _h)-\Delta t k((\varphi ^n_{h})_x,\eta _h)\\&\quad +\Delta t\gamma _1((\theta ^n_{h})_x,\eta _h)+\Delta t \gamma _2((P^n_{h})_x,\eta _h). \end{aligned}$$

Finally, the calculations for the temperature $\theta$ and the chemical potential P can be expressed in terms of a product variable ${\varvec{y}}^n=(\theta ^n_{h},P^n_{h})$ to solve the equations:

$$\begin{aligned}&(c\theta ^n_{h}+dP^n_{h}, \varsigma _h) +\Delta t\kappa ((\theta ^n_{h})_x,(\varsigma _h)_x) =(c\theta ^{n-1}_{h}+dP^{n-1}_{h}, \varsigma _h)\\&\qquad +\Delta t \gamma _1((w^n_{h})_x,\varsigma _h),\\&(d\theta ^n_{h}+rP^n_{h}, z_h) +\Delta t \hbar ((P^n_{h})_x,(z_h)_x) =(d\theta ^{n-1}_{h}+rP^{n-1}_{h}, z_h)\\&\qquad +\Delta t \gamma _2((w^n_{h})_x,z_h). \end{aligned}$$

Finally, the transverse displacement and the rotation are obtained from the equations:

$$\begin{aligned} \varphi ^n_{h}=\Delta t\sum _{i=1}^n v^i_{h}+\varphi ^0_h, \quad \psi ^n_{h}=\Delta t\sum _{i=1}^n w^i_{h}+\psi ^0_h. \end{aligned}$$

We note that with this strategy, the numerical problem consists of four coupled symmetric linear equations, and so a fixed-point algorithm was applied for their solution with Cholesky’s method for matrix factorization.

The numerical scheme was implemented using MATLAB on a Intel Core $i5-3337U$ @ 1.80 GHz and a typical run ($10^{4}$ step times and $10^{4}$ nodes) took about 200 s of CPU time.

Table 1 Example 1: Numerical errors $(\times 10^2)$ for some discretization parameters

7.2 A first example: numerical convergence

Our aim with this first example is to verify the numerical convergence of the numerical scheme. In this sense, the following problem is considered.

Problem $\hbox {P}^{ex}$. Find the velocity field $v:[0,1]\times [0,1]\mapsto {\mathbb {R}}$ and $w:[0,1]\times [0,1]\mapsto {\mathbb {R}},$ the temperature field $\theta :[0,1]\times [0,1]\mapsto {\mathbb {R}}$ and the chemical potential $P:[0,1]\times [0,1]\mapsto {\mathbb {R}}$ such that

$$\begin{aligned}&\varphi _{tt}-(\varphi _x+\psi )=f_1 \quad \text {in}\quad (0,1)\times (0,1), \\&\psi _{tt}-\psi _{xx}+(\varphi _x+\psi )- \theta _x-P_x=f_2 \quad \text {in}\quad (0,1)\times (0,1), \\&2\theta _t+P_t-\theta _{xx}-\psi _{tx}=f_3 \quad \text {in}\quad (0,1)\times (0,1),\\&\theta _t+P_t-P_{xx}-\psi _{tx}=f_4 \quad \text {in}\quad (0,1)\times (0,1),\\&\varphi (0,t)=\varphi (1,t)=0\quad \text {for a.e.}\;\; t\in (0,1),\\&\psi (0,t)=\psi (1,t)=0\quad \text {for a.e.}\;\; t\in (0,1), \\&\theta (0,t)=\theta (1,t)=P(0,t)=P(1,t)=0, \quad \text {for a.e.}\;\; t\in (0,1), \\&\varphi (x,0)=\varphi _t(x,0)=4x(1-x)\quad \text {for a.e.}\;\; x\in (0,1),\\&\psi (x,0)=\psi _t(x,0)=4x(1-x)\quad \text {for a.e.}\;\; x\in (0,1),\\&\theta (x,0)=4x(1-x), \quad P(x,0)=4x(1-x) \quad \text {for a.e.}\;\; x\in (0,1), \end{aligned}$$

being the artificial forces $f_i$, $i=1,2,3,4,$ involved:

$$\begin{aligned} f_1(x,t)= & {} 4{\mathrm {e}}^t(-x^2+3x+1),\\ f_2(x,t)= & {} 4{\mathrm {e}}^t(-2x^2+4x+1),\\ f_3(x,t)= & {} 4{\mathrm {e}}^t(-3x^2+5x+1) ,\\ f_4(x,t)= & {} 4{\mathrm {e}}^t(-2x^2+4x+1) , \end{aligned}$$

which corresponds to problem (1.10)–(1.12) with the following data:

$$\begin{aligned}&\rho _1=\rho _2=1,\quad k=1, \quad T=1,\quad \alpha =1, \quad \gamma _1=\gamma _2=1,\\&c=2, \quad d=1, \quad \kappa =1, \quad r=1, \quad \hbar =1, \\&\varphi ^0(x)=\varphi ^1(x)=4x(1-x), \quad \psi ^0(x)=\psi ^1(x)=4x(1-x) \quad \text {for all }\;\; x\in (0,1),\\&\theta ^0(x)=4x(1-x), \quad P^0(x)=4x(1-x) \quad \text {for all }\;\; x\in (0,1). \end{aligned}$$

The exact solution to Problem $\hbox {P}^{ex}$ is the following:

$$\begin{aligned}&\varphi (x,t)=4\mathrm {e}^tx(1-x), \quad \psi (x,t)=4\mathrm {e}^tx(1-x) \quad \text {for all}\; (x,t)\in [0,1]\times [0,1], \\&\theta (x)=4\mathrm {e}^tx(1-x), \quad P(x)=4\mathrm {e}^tx(1-x) \quad \text {for all}\; (x,t)\in [0,1]\times [0,1], \end{aligned}$$

which is consistent with boundary conditions (1.12).

The errors obtained for different discretization parameters $n_{el}$ and $\Delta t$ are depicted in Table 1 (being $n_{el}$ the number of finite elements of the discretization and $h=\frac{1}{n_{el}}$ the spatial discretization parameter). Moreover, the evolution of the error depending on $h+\Delta t$ is plotted in Fig. 1. We observe that the linear convergence stated in Corollary 6.2 is achieved.

Fig. 1

Example 1: Asymptotic behaviour of the numerical scheme

7.3 Example 2: numerical stability

In order to study the energy evolution, the modified problem (4.1) is solved for different values of the damping parameter $\mu$, and also using both Dirichlet (1.12) or Neumann (1.13) boundary conditions. We note that their numerical analyses can be performed in a similar form. A different set of thermomechanical parameters has been considered:

$$\begin{aligned}&\rho _1=\rho _2=10^{-4},\quad k=0.2, \quad \alpha =1, \quad \gamma _1=0.01931, \quad \gamma _2=r=0.0004635,\\&c=1.0136, \quad d=0.00251, \quad \kappa =365, \quad \hbar =0.03058. \end{aligned}$$

If we assume that there are no forces and we observe the system until final time $T=1,$ using the same initial conditions than in the previous case and discretization parameters $\Delta t=h=10^{-3}$, the evolution in time of the discrete energy is plotted in Fig. 2 corresponding to boundary conditions (1.12). We observe that an exponential energy decay has been achieved, confirming the theoretical results, even for the undamped case $\mu =0$, which has been included for comparison.

Using now the initial condition $\psi _0=4x^2(1-x)^2$ and the discretization parameters $h=10^{-3}$ and $\Delta t=0.5\times 10^{-3}$, the evolution in time of the discrete energy, considering Neumann boundary conditions (1.13), is shown in Fig. 3. As it was predicted by the theory (lack of exponential stability), the decay presents some oscillations and this is non-exponential, again even in the undamped case.

Fig. 2

Example 2: Energy evolution in normal and semi-log scales (Dirichlet conditions)

Fig. 3

Example 2: Energy evolution in normal and semi-log scales (Neumann conditions)

7.4 Example 3: influence of the chemical potential

The aim of this third example is try to observe the influence of diffusion of the chemical potential in the model. Therefore, null initial conditions have been considered in all the variables but the one for the chemical potential, where $P(x,0)=4x(1-x)$ has been taken. The same material constants than in the previous example have been used and, again, no external forces nor temperature sources act on the body. Moreover, the discretization parameters $\Delta t=h=10^{-3}$ have been employed.

In Fig. 4, the evolution in time of both the temperature and the chemical potential at central point is presented. Moreover, in Fig. 5 both the temperature field (left-hand side) and the chemical potential field (right-hand side) are shown at several time instants. As expected, the temperature is generated initially but it converges to zero, with some oscillations due to the influence of the chemical potential. Similarly, the chemical potential has a quadratic behaviour and, again, it converges to zero.

Fig. 4

Example 3: Evolution in time of temperature (left) and chemical potential (right) at central point

Fig. 5

Example 3: Temperature (left) and chemical potential (right) at different time instants

Finally, we analyse the effect of using different initial conditions for the chemical potential, remaining the rest of the data the same than in Example 2. Therefore, taking again discretization parameters $\Delta t=h=10^{-3}$ in Fig. 6 we plot the evolution in time of the vertical displacement (left) and rotation (right). As expected, both are generated due to the diffusion and they increase as the diffusion increases, although typical oscillations are found.

Fig. 6

Example 3: Evolution in time of the vertical displacement (left) and rotation (right) at central point