Uniform stability of a thermodiffusion Timoshenko beam

Abstract

The main object of the present work is the study of a new Timoshenko beam model with thermal and mass diffusion effects where the coupling is acting on the shear force. We prove the well-posedness of the system using the semigroup theory. Furthermore, we establish that the system is exponentially stable if and only if the wave speeds of the system are equal. When the speeds of the mechanical waves are different, we show a lack of exponential stability. Additionally, in the case of different wave speeds, we show that the solution decays polynomially.

1 Introduction

In 1921, Timoshenko [32] introduced the so-called Timoshenko model describing the transverse vibrations of a beam, it is given by the following system of coupled hyperbolic equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} - k \left( \varphi _{x} + \psi \right) _{x} = 0, &{}\quad \text {in} \, (0, L) \times (0, \infty ),\\ \rho _{2} \psi _{tt} - b \psi _{xx} + k \left( \varphi _{x} + \psi \right) = 0, &{}\quad \text {in} \, (0, L) \times (0, \infty ), \end{array}\right. } \end{aligned}$$

(1)

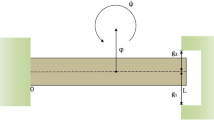
where $\varphi$ denotes the transverse displacement of the beam and $\psi$ is the rotation angle of the filament of the beam. $\rho _{1}, \rho _{2}, k$ and b stands for $\rho _{1} = \rho A$, $\rho _{2} = \rho I$, $k = k^{'} A G$ and $b = E I$ such that $\rho$ is the density, A is the cross-sectional area, I is the second moment of area of the cross-sectional area, $k^{'}$ is the shear coefficient, G is the modulus of rigidity and E is the Young’s modulus of elasticity. t is the time variable and x is the space variable along the beam of length L.

Soufyane [30] studied system (1) with a single weak damping in the second equation and demonstrated exponential stability result provided the mechanical wave velocities are equal. i.e,

$$\begin{aligned} \frac{\rho _{1}}{k} = \frac{\rho _{2}}{b}. \end{aligned}$$

(2)

A vital aspect of research concerning system (1) is to search for a minimal dissipation by which solutions to the system decay exponentially. In this regards, various types of damping mechanisms, such as internal or boundary feedback, finite or infinite memory and Kelvin Voigt dissipation have been used to stabilize the system, see for example [4, 20, 21, 24, 26, 31].

Muñoz Rivera et al. [25] analyzed the following thermoelastic Timoshenko system

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} = k \left( \varphi _{x} + \psi \right) _{x}, &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{2} \psi _{tt} = b \psi _{xx} - k \left( \varphi _{x} + \psi \right) - \gamma \theta _{x}, &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{3} \theta _{t} = \kappa \theta _{xx} - \gamma \psi _{tx}, &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}, \end{array}\right. } \end{aligned}$$

(3)

where $\theta$ represents the temperature difference, the coefficients $\rho _{3}, \kappa$ and $\gamma$ denote the physical parameters from thermoelasticity theory which are positive. The dissipation in the system is through thermal damping on the bending moment equation. The authors established an exponential stability result for (3) provided assumption (2) holds. Recently, in [1], Almeida Júnior et al. proposed a new coupling to thermoelastic Timoshenko beam where the thermoelastic coupling acts on shear force

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} = k \left( \varphi _{x} + \psi \right) _{x} - \gamma \theta _{x}, &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{2} \psi _{tt} = b \psi _{xx} - k \left( \varphi _{x} + \psi \right) + \gamma \theta , &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{3} \theta _{t} = \kappa \theta _{xx} - \gamma \left( \varphi _{x} + \psi \right) _{t}, &{}\quad \text {in} \ (0, L) \times {\mathbb {R}}_{+}. \end{array}\right. } \end{aligned}$$

(4)

The authors proved that the system is exponentially stable if and only if the wave speeds are equal. For more results on Timoshenko systems with thermal effects affecting on shear force, we refer the reader to [3, 9, 13, 14]. We should mention that the coupling of Timoshenko beam with thermal effects on both the shear force and the bending moment leads to an exponential stability irrespective of any relationship among the coefficients. This has been independently established by Alves et al. [2] and Djellali et al. [11].

Lately, Aouadi et al. [7] introduced a new Timoshenko beam model with thermal and mass diffusion effects given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} - k {\big (} \varphi _{x} + \psi {\big )}_{x} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+},\\ \rho _{2} \psi _{tt} - \alpha \psi _{xx} - k {\big (} \varphi _{x} + \psi {\big )} \, - \gamma _{1} \theta _{x} - \gamma _{2} P_{x} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+},\\ c \theta _{t} + d P_{t} - \kappa \theta _{xx} - \gamma _{1} \psi _{tx} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+},\\ d \theta _{t} + r P_{t} - h P_{xx} - \gamma _{2} \psi _{tx} = 0,&{} \quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \end{array}\right. } \end{aligned}$$

(5)

and proved an exponential decay result for system (5) with Dirichlet boundary conditions after adding a frictional damping term to the first equation. However, Feng [17] considered system (5) and proved the exponential stability provided $\frac{\rho _{1}}{k} = \frac{\rho _{2}}{\alpha }$. We cite [5, 6, 8, 10, 15, 18, 29] for some other related results.

Motivated by the above results, we intend to study a Timoshenko system where the mass diffusion is taken into account, the evolution equations are given by

$$\begin{aligned} \begin{aligned} \rho _{1} \varphi _{tt} - S_{x} = 0, \quad \rho _{2} \psi _{tt} - M_{x} + S = 0, \quad \Psi _{t} + q_{x} = 0, \quad C_{t} + \eta _{x} = 0, \end{aligned} \end{aligned}$$

(6)

here, S denotes the shear force, M is the bending moment, $\Psi$ is the entropy, q is the heat flux, $\eta$ is the mass diffusion flux and C is the concentration of the diffusive material in the elastic body. The constitutive equations with temperature and mass diffusion following the Fourier’s law and the Fick’s law respectively, are given by

$$\begin{aligned} \begin{aligned}&M = b \psi _{x}, \qquad \qquad \, S = k \left( \varphi _{x} + \psi \right) + \gamma \theta + \beta C, \\&q = - \kappa \theta _{x}, \qquad \qquad \Psi = - \gamma \left( \varphi _{x} + \psi \right) + \rho _{3} \theta + \varpi C,\\&\eta = - h P_{x}, \qquad \quad \ \ P = \beta \left( \varphi _{x} + \psi \right) + \varrho C - \varpi \theta , \end{aligned} \end{aligned}$$

(7)

where P is the chemical potential, $\varpi$ is a measure of the thermodiffusion effect, $h > 0$ is the diffusion coefficient and $\varrho$ is a measure of the diffusive effect. By inserting (7) into (6), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} - k \left( \varphi _{x} + \psi \right) _{x} - \gamma \theta _{x} - \beta C_{x} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{2} \psi _{tt} - b \psi _{xx} + k \left( \varphi _{x} + \psi \right) + \gamma \theta + \beta C = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{3} \theta _{t} + \varpi C_{t} - \kappa \theta _{xx} - \gamma \left( \varphi _{x} + \psi \right) _{t} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ C_{t} - h \left[ \beta \left( \varphi _{x} + \psi \right) + \varrho C - \varpi \theta \right] _{xx} = 0,&{} \quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}. \end{array}\right. } \end{aligned}$$

(8)

As in [7], we shall formulate a different alternative form where the chemical potential P is considered as a state variable instead of the concentration C. This alternative form can be written by inserting the last equation of (7), i.e.

$$\begin{aligned} C = \frac{1}{\varrho } \left[ P - \beta \left( \varphi _{x} + \psi \right) + \varpi \theta \right] , \end{aligned}$$

into (8). So, we get the following Timoshenko system with temperature and chemical potential in the classical form

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{1} \varphi _{tt} - k_{1} \left( \varphi _{x} + \psi \right) _{x} - \gamma _{1} \theta _{x} - \gamma _{2} P_{x} = 0,&{} \quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ \rho _{2} \psi _{tt} - b \psi _{xx} + k_{1} \left( \varphi _{x} + \psi \right) + \gamma _{1} \theta + \gamma _{2} P = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ c \theta _{t} + d P_{t} - \kappa \theta _{xx} - \gamma _{1} \left( \varphi _{x} + \psi \right) _{t} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \\ d \theta _{t} + r P_{t} - h P_{xx} - \gamma _{2} \left( \varphi _{x} + \psi \right) _{t} = 0, &{}\quad \text {in} \, (0, L) \times {\mathbb {R}}_{+}, \end{array}\right. } \end{aligned}$$

(9)

where

$$\begin{aligned} k_{1} = k - \dfrac{\beta ^{2}}{\varrho }, \quad c = \rho _{3} + \frac{\varpi ^{2}}{\varrho }, \quad d = \frac{\varpi }{\varrho }, \quad r = \frac{1}{\varrho }, \quad \gamma _{1} = \gamma + \frac{\beta \varpi }{\varrho }, \quad \gamma _{2} = \frac{\beta }{\varrho }, \end{aligned}$$

are physical positive constants. We study system (9) with the following initial conditions

$$\begin{aligned} \begin{aligned} \varphi (x, 0) = \varphi _{0}(x), \quad \varphi _{t}(x, 0) = \varphi _{1}(x), \quad \psi (x, 0) = \psi _{0}(x), \quad x \in (0, L),\\ \psi _{t}(x, 0) = \psi _{1}(x), \quad \theta (x, 0) = \theta _{0}(x), \quad P(x, 0) = P_{0}(x), \ \quad x \in (0, L), \end{aligned} \end{aligned}$$

(10)

and boundary conditions

$$\begin{aligned} \begin{aligned} \varphi _{x}(0, t) = \psi (0, t) = \theta (0, t) = P(0, t) = 0, \qquad t> 0, \\ \varphi _{x}(L, t) = \psi (L, t) = \theta (L, t) = P(L, t) = 0, \qquad t > 0. \end{aligned} \end{aligned}$$

(11)

To stabilize the system when diffusion effects are added to thermal effects, we assume that the physical constants c, r and d satisfy

$$\begin{aligned} c \, r \, > \, d^{2}. \end{aligned}$$

(12)

Our aim in this work, is to prove that system (9)–(11) is exponentially stable provided

$$\begin{aligned} \frac{\rho _{1}}{k_{1}} = \frac{\rho _{2}}{b}. \end{aligned}$$

(13)

In order to be able to use Poincaré’s inequality for $\varphi$, using (9)$_{1}$ and boundary conditions, we have

$$\begin{aligned} \frac{d^{2}}{dt^{2}} \int _{0}^{L} \varphi (x,t) dx = 0, \qquad \forall t \ge 0, \end{aligned}$$

(14)

using initial data of $\varphi$ and solving (14), we get

$$\begin{aligned} \int _{0}^{L} \varphi (x,t) dx = t \int _{0}^{L} \varphi _{1}(x) dx + \int _{0}^{L} \varphi _{0}(x) dx, \qquad \forall t \ge 0. \end{aligned}$$

Consequently, if we set

$$\begin{aligned} \overline{\varphi }(x,t) = \varphi (x,t) - \frac{t}{L} \int _{0}^{L} \varphi _{1}(x) dx - \frac{1}{L} \int _{0}^{L} \varphi _{0}(x) dx, \end{aligned}$$

we obtain

$$\begin{aligned} \int _{0}^{L} \overline{\varphi }(x,t) \, dx \, = \, 0, \qquad \forall t \ge 0. \end{aligned}$$

Clearly, the use of Poincaré’s inequality for $\overline{\varphi }$ is justified. In addition $\left( \overline{\varphi }, \psi , \theta , P \right)$ satisfies system (9)–(11). Henceforth, we work with $\overline{\varphi }$ instead of $\varphi$ but we write $\varphi$ for simplicity of notations.

The rest of the paper is organized as follows. In the next Section, we prove the well-posedness of system (9)–(11). In Sect. 3, we show the lack of exponential stability under the condition of different wave speeds. The exponential stability for (9)–(11) in case of equal wave speeds condition will be established in Sect. 4. Section 5 is dedicated to the optimal polynomial stability result. Finally, some general remarks and open problem are highlighted in Sect. 6.

2 Well posedness

In this section, we discuss the well-posedness of the problem (9)–(11) using the semigroup theory. So, if we denote $U = \left( \varphi , u, \psi , v, \theta , P \right) ^{T}$, where $u = \varphi _{t}$, and $v = \psi _{t}$. Then, system (9)–(11) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} U_{t}(t) = {\mathcal {A}} U(t), \qquad t > 0\\ U (0) = U_{0} = \left( \varphi _{0}, \varphi _{1}, \psi _{0}, \psi _{1}, \theta _{0}, P_{0} \right) ^{T}, \end{array}\right. } \end{aligned}$$

(15)

where the operator ${\mathcal {A}}$ is defined by

$$\begin{aligned} {\mathcal {A}} U(t) = \left( \begin{matrix} u \\ \frac{1}{\rho _{1}} {\Big (} k_{1} \left( \varphi _{x} + \psi \right) _{x} + \gamma _{1} \theta _{x} + \gamma _{2} P_{x} {\Big )} \\ v \\ \frac{1}{\rho _{2}} {\Big (} b \psi _{xx} - k_{1} \left( \varphi _{x} + \psi \right) - \gamma _{1} \theta - \gamma _{2} P {\Big )} \\ \frac{1}{c r - d^{2}} {\Big [} r \kappa \theta _{xx} - h d P_{xx} + \left( r \gamma _{1} - d \gamma _{2} \right) \left( u_{x} + v \right) {\Big ]} \\ \frac{1}{c r - d^{2}} {\Big [} h c P_{xx} - \kappa d \theta _{xx} + \left( c \gamma _{2} - d \gamma _{1} \right) \left( u_{x} + v \right) {\Big ]} \end{matrix} \right) . \end{aligned}$$

We consider the following spaces

$$\begin{aligned}&L^{2}_{*}(0,L) = \left\{ \phi \in L^{2}(0,L) : \, \int _{0}^{L} \, \phi (x) \, dx = 0 \right\} , \\&H^{1}_{*}(0,L) = H^{1}(0,L) \cap L^{2}_{*}(0,L), \\&H^{2}_{*}(0,L) = \left\{ \phi \in H^{2}(0,L) : \, \phi _{x}(0) = \phi _{x}(L) = 0 \right\} , \end{aligned}$$

and let the space

$$\begin{aligned} {\mathcal {H}} = H^{1}_{*}(0,L) \times L^{2}_{*}(0,L) \times H^{1}_{0}(0,L) \times L^{2}(0,L) \times L^{2}(0,L) \times L^{2}(0,L), \end{aligned}$$

endowed with the inner product

$$\begin{aligned} \begin{aligned} \left( U, {\tilde{U}} \right) _{{\mathcal {H}}}&= \rho _{1} \int _{0}^{L} u {\tilde{u}} dx + b \int _{0}^{L} \psi _{x} \tilde{\psi }_{x} dx + \rho _{2} \int _{0}^{L} v {\tilde{v}} dx \\&\quad + k_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) \left( \tilde{\varphi }_{x} + \tilde{\psi } \right) dx + c \int _{0}^{L} \theta \tilde{\theta } dx \\&\quad + r \int _{0}^{L} P {\tilde{P}} dx + d \int _{0}^{L} \left( \theta {\tilde{P}} + P \tilde{\theta } \right) dx, \end{aligned} \end{aligned}$$

(16)

for any $U = {\Big (} \varphi , u, \psi , v, \theta , P {\Big )}^{T} \in {\mathcal {H}}$ and ${\tilde{U}} = \left( \tilde{\varphi }, {\tilde{u}}, \tilde{\psi }, {\tilde{v}}, \tilde{\theta }, {\tilde{P}} \right) ^{T} \in {\mathcal {H}}$.

The domain of the operator ${\mathcal {A}}$ is given by

$$\begin{aligned} \mathcal {D(A)} = {\Bigg \lbrace } \begin{matrix} U \in {\mathcal {H}} \, {\Big \vert } \ \varphi \in H^{2}_{*}(0,L) \cap H^{1}_{*}(0,L); \quad \psi \in H^{2}(0,L) \cap H^{1}_{0}(0,L); \\ \qquad u \in H^{1}_{*}(0,L); \ v \in H^{1}_{0}(0,L); \ \theta , P \in H^{2}(0,L) \cap H^{1}_{0}(0,L) \end{matrix} {\Bigg \rbrace }. \end{aligned}$$

Clearly $\mathcal {D(A)}$ is dense in ${\mathcal {H}}$. Hence, from the inner product (16), we have

$$\begin{aligned} \left( {\mathcal {A}} U, U \right) _{{\mathcal {H}}}&= \int _{0}^{L} {\Big [} k_{1} \left( \varphi _{x} + \psi \right) _{x} + \gamma _{1} \theta _{x} + \gamma _{2} P_{x} {\Big ]} u dx + b \int _{0}^{L} \psi _{x} v_{x} dx \\&\quad + \int _{0}^{L} {\Big [} b \psi _{xx} - k_{1} \left( \varphi _{x} + \psi \right) - \gamma _{1} \theta - \gamma _{2} P {\Big ]} v dx \\&\quad + k_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) \left( u_{x} + v \right) dx \\&\quad + c \int _{0}^{L} \frac{1}{c r - d^{2}} {\Big [} r \kappa \theta _{xx} - h d P_{xx} + \left( r \gamma _{1} - d \gamma _{2} \right) \left( u_{x} + v \right) {\Big ]} \theta dx \\&\quad + r \int _{0}^{L} \frac{1}{c r - d^{2}} {\Big [} h c P_{xx} - \kappa d \theta _{xx} + \left( c \gamma _{2} - d \gamma _{1} \right) \left( u_{x} + v \right) {\Big ]} P dx \\&\quad + d \int _{0}^{L} \frac{1}{c r - d^{2}} {\Big [} r \kappa \theta _{xx} - h d P_{xx} + \left( r \gamma _{1} - d \gamma _{2} \right) \left( u_{x} + v \right) {\Big ]} P dx \\&\quad + d \int _{0}^{L} \frac{1}{c r - d^{2}} {\Big [} h c P_{xx} - \kappa d \theta _{xx} + \left( c \gamma _{2} - d \gamma _{1} \right) \left( u_{x} + v \right) {\Big ]} \theta dx. \end{aligned}$$

Integrating by parts, and after several simplifications we obtain

$$\begin{aligned} \left( {\mathcal {A}} U, U \right) _{{\mathcal {H}}}&= - \frac{\kappa \left( c r - d^{2} \right) }{c r - d^{2}} \int _{0}^{L} \theta _{x}^{2} dx - \frac{h \left( c r - d^{2} \right) }{c r - d^{2}} \int _{0}^{L} P_{x}^{2} dx \\&= - \kappa \int _{0}^{L} \theta _{x}^{2} dx - h \int _{0}^{L} P_{x}^{2} dx \le 0, \end{aligned}$$

which implies that ${\mathcal {A}}$ is dissipative in ${\mathcal {H}}$. Now, by using Lax–Milgram lemma and classical regularity arguments, it can easily be shown that the operator $( I - {\mathcal {A}} )$ is surjective. So, by using Lumer phillips theorem (see [23, 27]), we deduce that ${\mathcal {A}}$ is an infinitesimal generator of a linear $C_{0}$-semigroup on ${\mathcal {H}}$. Therefore, we have the following well-posedness result for the problem (9)–(11).

Theorem 2.1

Let $U_{0} \in {\mathcal {H}}$. Then problem (9)–(11) has a unique weak solution $U \in C({\mathbb {R}}^{+}, {\mathcal {H}})$. Moreover, if $U_{0} \in \mathcal {D(A)}$, then the solution U is classical solution satisfies $U \in C({\mathbb {R}}^{+}, \mathcal {D(A)}) \cap C^{1} ({\mathbb {R}}^{+}, {\mathcal {H}})$.

3 Lack of exponential stability

In this section, we prove the lack of exponential stability of system (9)–(11). The method we use here is based on the following Gearhart–Herbst–Prüss–Huang theorem to dissipative systems (see [19, 22, 28]).

Theorem 3.1

Let $S(t) = e^{{\mathcal {A}}t}$ be a $C_{0}-$semigroup of contractions on Hilbert space ${\mathcal {H}}$. Then, S(t) is exponentially stable if and only if

$$\begin{aligned} \varrho ({\mathcal {A}}) \supset \left\{ i \lambda : \lambda \in {\mathbb {R}} \right\} \equiv i {\mathbb {R}}, \quad \text {and} \quad \underset{ \vert \lambda \vert \rightarrow \infty }{\overline{\lim }} {\big \Vert } (i \lambda I - {\mathcal {A}})^{-1} {\big \Vert }_{{\mathscr {L}}({\mathcal {H}})} < \infty , \end{aligned}$$

(17)

where $\varrho ({\mathcal {A}})$ is the resolvent set of the differential operator ${\mathcal {A}}$, and ${\big \Vert } \cdot {\big \Vert }_{{\mathscr {L}}({\mathcal {H}})}$ denotes the norm in the space of continuous linear functions in ${\mathcal {H}}$.

Next, we state the main result of this section, as follows

Theorem 3.2

Let us suppose that

$$\begin{aligned} \frac{\rho _{1}}{k_{1}} \ne \frac{\rho _{2}}{b}, \end{aligned}$$

then the semigroup associated with system (9)–(11) is not exponentially stable.

Proof

We need to show that there exists a sequence of real number $\lambda _{\mu }$ and functions $G_{\mu } \in {\mathcal {H}}$, with $\Vert G_{\mu } \Vert _{{\mathcal {H}}} \le 1$ such that

$$\begin{aligned} {\big \Vert } (i \lambda _{\mu } I - {\mathcal {A}})^{-1} G_{\mu } {\big \Vert }_{{\mathscr {L}}({\mathcal {H}})} \longrightarrow \infty , \end{aligned}$$

where

$$\begin{aligned} i \lambda _{\mu } U_{\mu } - {\mathcal {A}} U_{\mu } = G_{\mu }, \end{aligned}$$

(18)

with $U_{\mu } = \left( \varphi , u, \psi , v, \theta , P \right) ^{T}$ not bounded.

By taking $G_{\mu } = \left( 0, 0, 0, \frac{1}{\rho _{2}} \sin \left( \frac{\mu \pi }{L} x \right) ,0, 0 \right)$ and rewriting the spectral equation (18) in terms of its components, we obtain

$$\begin{aligned} \begin{aligned}&i \lambda \varphi - u = 0, \\&i \lambda \rho _{1} u - k_{1} \left( \varphi _{x} + \psi \right) _{x} - \gamma _{1} \theta _{x} - \gamma _{2} P_{x} = 0, \\&i \lambda \psi - v = 0, \\&i \lambda \rho _{2} v - b \psi _{xx} + k_{1} \left( \varphi _{x} + \psi \right) + \gamma _{1} \theta + \gamma _{2} P = \sin \left( \frac{\mu \pi }{L} x \right) , \\&i \lambda c \theta + i \lambda d P - \kappa \theta _{xx} - \gamma _{1} u_{x} - \gamma _{1} v = 0, \\&i \lambda r P + i \lambda d \theta - h P_{xx} - \gamma _{2} u_{x} - \gamma _{2} v = 0. \end{aligned} \end{aligned}$$

(19)

Inserting u and v from the first and the third equations of (19) in the other equations, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} - \rho _{1} \lambda ^{2} \varphi - k_{1} \left( \varphi _{x} + \psi \right) _{x} - \gamma _{1} \theta _{x} - \gamma _{2} P_{x} = 0, \\ - \rho _{2} \lambda ^{2} \psi - b \psi _{xx} + k_{1} \left( \varphi _{x} + \psi \right) + \gamma _{1} \theta + \gamma _{2} P = \sin \left( \frac{\mu \pi }{L} x \right) , \\ i \lambda c \theta + i \lambda d P - \kappa \theta _{xx} - i \lambda \gamma _{1} \varphi _{x} - i \lambda \gamma _{1} \psi = 0, \\ i \lambda r P + i \lambda d \theta - h P_{xx} - i \lambda \gamma _{2} \varphi _{x} - i \lambda \gamma _{2} \psi = 0. \end{array}\right. } \end{aligned}$$

(20)

Looking for solutions (compatible with the boundary conditions) of the form

$$\begin{aligned} \begin{aligned}&\varphi = A_{\mu } \cos \left( \frac{\mu \pi }{L} x \right) , \qquad \psi = B_{\mu } \sin \left( \frac{\mu \pi }{L} x \right) , \\&\theta = C_{\mu } \sin \left( \frac{\mu \pi }{L} x \right) , \qquad P = D_{\mu } \sin \left( \frac{\mu \pi }{L} x \right) . \end{aligned} \end{aligned}$$

Consequently, we arrive at

$$\begin{aligned} {\left\{ \begin{array}{ll} \left[ - \rho _{1} \lambda ^{2} + k_{1} \left( \frac{\mu \pi }{L} \right) ^{2} \right] A_{\mu } - k_{1} \left( \frac{\mu \pi }{L} \right) B_{\mu } - \gamma _{1} \left( \frac{\mu \pi }{L} \right) C_{\mu } - \gamma _{2} \left( \frac{\mu \pi }{L} \right) D_{\mu } = 0, \\ - k_{1} \left( \frac{\mu \pi }{L} \right) A_{\mu } + \left[ - \rho _{2} \lambda ^{2} + b \left( \frac{\mu \pi }{L} \right) ^{2} + k_{1} \right] B_{\mu } + \gamma _{1} C_{\mu } + \gamma _{2} D_{\mu } = 1, \\ i \lambda \gamma _{1} \left( \frac{\mu \pi }{L} \right) A_{\mu } - i \lambda \gamma _{1} B_{\mu } + \left[ i \lambda c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right] C_{\mu } + i \lambda d D_{\mu } = 0, \\ i \lambda \gamma _{2} \left( \frac{\mu \pi }{L} \right) A_{\mu } - i \lambda \gamma _{2} B_{\mu } + i \lambda d C_{\mu } + \left[ i \lambda r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right] D_{\mu } = 0. \end{array}\right. } \end{aligned}$$

(21)

Now, taking $\lambda \equiv \lambda _{\mu }$ such that

$$\begin{aligned} \lambda = \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \ \Longrightarrow \ \rho _{2} \lambda ^{2} - b \left( \frac{\mu \pi }{L} \right) ^{2} = 0, \end{aligned}$$

then, system (21) is equivalent to

$$\begin{aligned} \underbrace{ \left( \begin{matrix} Q_{1}(\mu ) &{}\quad - k_{1} \left( \frac{\mu \pi }{L} \right) &{}\quad - \gamma _{1} \left( \frac{\mu \pi }{L} \right) &{}\quad - \gamma _{2} \left( \frac{\mu \pi }{L} \right) \\ - k_{1} \left( \frac{\mu \pi }{L} \right) &{}\quad k_{1} &{}\quad \gamma _{1} &{}\quad \gamma _{2} \\ i \lambda \gamma _{1} \left( \frac{\mu \pi }{L} \right) &{}\quad - i \lambda \gamma _{1} &{}\quad Q_{3}(\mu ) &{}\quad i \lambda d \\ i \lambda \gamma _{2} \left( \frac{\mu \pi }{L} \right) &{}\quad - i \lambda \gamma _{2} &{}\quad i \lambda d &{}\quad Q_{4}(\mu ) \end{matrix} \right) }_{K} \left( \begin{matrix} A_{\mu } \\ B_{\mu } \\ C_{\mu } \\ D_{\mu } \end{matrix} \right) = \left( \begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix} \right) , \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned}&Q_{1}(\mu ) = \left( k_{1} - \frac{\rho _{1} b}{\rho _{2}} \right) \left( \frac{\mu \pi }{L} \right) ^{2}, \\&Q_{3}(\mu ) = i \lambda c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2}, \\&Q_{4}(\mu ) = i \lambda r + h \left( \frac{\mu \pi }{L} \right) ^{2}. \end{aligned} \end{aligned}$$

Solving (22), we have

$$\begin{aligned} \begin{aligned} \det K&= \left( Q_{1} - k_{1} \left( \frac{\mu \pi }{L} \right) ^{2} \right) {\Big [} k_{1} Q_{3} Q_{4} + i \lambda \gamma _{2}^{2} Q_{3} + i \lambda \gamma _{1}^{2} Q_{4} + 2 \lambda ^{2} \gamma _{1} \gamma _{2} d + \lambda ^{2} d^{2} k_{1} {\Big ]} \\&= - \frac{\rho _{1} b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} {\Big [} k_{1} Q_{3} Q_{4} + i \lambda \gamma _{2}^{2} Q_{3} + i \lambda \gamma _{1}^{2} Q_{4} + 2 \lambda ^{2} \gamma _{1} \gamma _{2} d + \lambda ^{2} d^{2} k_{1} {\Big ]}. \end{aligned} \end{aligned}$$

So,

$$\begin{aligned} \begin{aligned} A_{\mu } = \frac{{\tilde{A}}_{\mu }}{\det K}, \end{aligned} \end{aligned}$$

with ${\tilde{A}}_{\mu }$ defined as

$$\begin{aligned} \begin{aligned} {\tilde{A}}_{\mu }&= \det \left( \begin{matrix} 0 &{}\quad - k_{1} \left( \frac{\mu \pi }{L} \right) &{}\quad - \gamma _{1} \left( \frac{\mu \pi }{L} \right) &{}\quad - \gamma _{2} \left( \frac{\mu \pi }{L} \right) \\ 1 &{}\quad k_{1} &{}\quad \gamma _{1} &{}\quad \gamma _{2} \\ 0 &{}\quad - i \lambda \gamma _{1} &{}\quad Q_{3}(\mu ) &{}\quad i \lambda d \\ 0 &{}\quad - i \lambda \gamma _{2} &{}\quad i \lambda d &{}\quad Q_{4}(\mu ) \end{matrix} \right) \\&= \left( \frac{\mu \pi }{L} \right) {\Big [} k_{1} Q_{3} Q_{4} + i \lambda \gamma _{2}^{2} Q_{3} + i \lambda \gamma _{1}^{2} Q_{4} + 2 \lambda ^{2} \gamma _{1} \gamma _{2} d + \lambda ^{2} d^{2} k_{1} {\Big ]}, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} A_{\mu } = - \frac{\rho _{2}}{\rho _{1} b \left( \frac{\mu \pi }{L} \right) }. \end{aligned} \end{aligned}$$

Similarly, we get

$$\begin{aligned} B_{\mu } = \frac{{\tilde{B}}_{\mu }}{- \frac{\rho _{1} b}{\rho _{2}} \Lambda _{\mu }}, \quad C_{\mu } = \frac{{\tilde{C}}_{\mu }}{\Lambda _{\mu }}, \quad D_{\mu } = \frac{{\tilde{D}}_{\mu }}{\Lambda _{\mu }}, \end{aligned}$$

where

$$\begin{aligned} \Lambda _{\mu }&= k_{1} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right) \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{2}^{2} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{1}^{2} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + 2 \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} \gamma _{1} \gamma _{2} d + \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} d^{2} k_{1}, \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\tilde{B}}_{\mu }&= \left( k_{1} - \frac{\rho _{1} b}{\rho _{2}} \right) \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right) \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{2}^{2} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{1}^{2} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right) \\&\quad + 2 \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} \gamma _{1} \gamma _{2} d + \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} d^{2} \left( k_{1} - \frac{\rho _{1} b}{\rho _{2}} \right) , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\tilde{C}}_{\mu } = i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{1} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) r + h \left( \frac{\mu \pi }{L} \right) ^{2} \right) + \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} \gamma _{2} d , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\tilde{D}}_{\mu }&= i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) \gamma _{2} \left( i \sqrt{\frac{b}{\rho _{2}}} \left( \frac{\mu \pi }{L} \right) c + \kappa \left( \frac{\mu \pi }{L} \right) ^{2} \right) + \frac{b}{\rho _{2}} \left( \frac{\mu \pi }{L} \right) ^{2} \gamma _{1} d . \end{aligned} \end{aligned}$$

Therefore, as $\mu \longrightarrow \infty$, one gets the convergences

$$\begin{aligned} \begin{aligned}&A_{\mu } \longrightarrow 0, \qquad B_{\mu } \approx {\mathcal {O}} (\mu ) \longrightarrow \infty , \\&C_{\mu } \longrightarrow 0, \qquad D_{\mu } \longrightarrow 0. \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned} \Vert U \Vert _{{\mathcal {H}}}^{2}&\ge b \int _{0}^{L} \vert \psi _{x} \vert ^{2} dx = b \int _{0}^{L} {\bigg \vert } \left( \frac{\mu \pi }{L} \right) B_{\mu } \cos \left( \frac{\mu \pi }{L} x \right) {\bigg \vert }^{2} dx \\&\ge b {\bigg \vert } \frac{\mu \pi }{L} B_{\mu } {\bigg \vert }^{2} \frac{L}{2} \ \longrightarrow \ \infty , \quad \text {as} \ \mu \longrightarrow \infty . \end{aligned} \end{aligned}$$

(23)

So we have no exponential stability. $\square$

4 Exponential stability

In this section, we use the energy method to prove that system (9)–(11) is exponentially stable. For this purpose, we need to state and prove some technical lemmas.

Lemma 4.1

Let $\left( \varphi , \psi , \theta , P \right)$ be a solution of (9)–(11), then the energy functional defined by

$$\begin{aligned} \begin{aligned} E(t) = \frac{1}{2} \int _{0}^{L} {\bigg [} \rho _{1} \varphi _{t}^{2} + k_{1} \left( \varphi _{x} + \psi \right) ^{2} + \rho _{2} \psi _{t}^{2} + b \psi _{x}^{2} + c \theta ^{2} + r P^{2} + 2 d \theta P {\bigg ]} dx, \end{aligned} \end{aligned}$$

(24)

satisfies

$$\begin{aligned} E^{'}(t) = - \kappa \int _{0}^{L} \theta _{x}^{2} dx - h \int _{0}^{L} P_{x}^{2} dx \le 0. \end{aligned}$$

(25)

Proof

Multiplying the equations of system (9) by $\varphi _{t}, \, \psi _{t},\, \theta$ and P respectively, integrating over (0, L) , using integration by parts and boundary conditions (11), we establish (25). $\square$

Remark 1

The energy E(t) defined by (24) is non-negative. In fact, we can easily show that

$$\begin{aligned} c \theta ^{2} + r P^{2} + 2 d \theta P&= \frac{1}{2} {\bigg [} c \left( \theta + \frac{d}{c} P \right) ^{2} + r \left( P + \frac{d}{r} \theta \right) ^{2} \\&\quad + \left( c - \frac{d^{2}}{r} \right) \theta ^{2} + \left( r - \frac{d^{2}}{c} \right) P^{2} {\bigg ]}. \end{aligned}$$

So, by using (12), we arrive at

$$\begin{aligned} c \theta ^{2} + r P^{2} + 2 d \theta P> c_{1} \theta ^{2} + r_{1} P^{2} > 0, \end{aligned}$$

where $c_{1} = \frac{1}{2} {\Big (} c - \frac{d^{2}}{r} {\Big )}$ and $r_{1} = \frac{1}{2} {\Big (} r - \frac{d^{2}}{c} {\Big )}$.

Consequently,

$$\begin{aligned} \begin{aligned} E(t) > \frac{1}{2} \int _{0}^{L}&{\bigg [} \rho _{1} \varphi _{t}^{2} + k_{1} \left( \varphi _{x} + \psi \right) ^{2} + \rho _{2} \psi _{t}^{2} + b \psi _{x}^{2} + c_{1} \theta ^{2} + r_{1} P^{2} {\bigg ]} dx. \end{aligned} \end{aligned}$$

(26)

Therefore, E(t) is non-negative.

Lemma 4.2

Let $\left( \varphi , \psi , \theta , P \right)$ be the solution of (9)–(11), then the functional

$$\begin{aligned} I_{1}(t) = \rho _{2} \int _{0}^{L} \psi _{t} \psi dx - \rho _{1} \int _{0}^{L} \varphi _{t} \left( \int _{0}^{x} \psi (y,t) dy \right) dx, \end{aligned}$$

(27)

satisfies, for any $\varepsilon _{1} > 0$, the estimate

$$\begin{aligned} \frac{d}{dt} I_{1}(t) \le - b \int _{0}^{L} \psi _{x}^{2} dx + \varepsilon _{1} \int _{0}^{L} \varphi _{t}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{1}} \right) \int _{0}^{L} \psi _{t}^{2} dx. \end{aligned}$$

(28)

Proof

Differentiating $I_{1}(t)$, we obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{1}(t)&= \rho _{2} \int _{0}^{L} \psi _{tt} \psi dx + \rho _{2} \int _{0}^{L} \psi _{t}^{2} dx - \rho _{1} \int _{0}^{L} \varphi _{t} \left( \int _{0}^{x} \psi _{t}(y,t) dy \right) dx \\&\quad - \rho _{1} \int _{0}^{L} \varphi _{tt} \left( \int _{0}^{x} \psi (y,t) dy \right) dx, \end{aligned} \end{aligned}$$

using the first two equations in (9), we find

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{1}(t)&= \int _{0}^{L} {\bigg [} b \psi _{xx} - k_{1} \left( \varphi _{x} + \psi \right) - \gamma _{1} \theta - \gamma _{2} P {\bigg ]} \psi dx + \rho _{2} \int _{0}^{L} \psi _{t}^{2} dx \\&\quad - \rho _{1} \int _{0}^{L} \varphi _{t} \left( \int _{0}^{x} \psi _{t}(y,t) dy \right) dx \\&\quad + \int _{0}^{L} {\bigg [} - k_{1} \left( \varphi _{x} + \psi \right) _{x} - \gamma _{1} \theta _{x} - \gamma _{2} P_{x} {\bigg ]} \left( \int _{0}^{x} \psi (y,t) dy \right) dx. \end{aligned} \end{aligned}$$

Integrating by parts and boundary conditions (11), we arrive at

$$\begin{aligned} \frac{d}{dt} I_{1}(t) = - b \int _{0}^{L} \psi _{x}^{2} dx + \rho _{2} \int _{0}^{L} \psi _{t}^{2} dx - \rho _{1} \int _{0}^{L} \varphi _{t} \left( \int _{0}^{x} \psi _{t}(y,t) dy \right) dx. \end{aligned}$$

(29)

By virtue of Young’s and Cauchy–Schwarz’s inequalities, we find for $\varepsilon _{1} > 0$

$$\begin{aligned} - \rho _{1} \int _{0}^{L} \varphi _{t} \left( \int _{0}^{x} \psi _{t}(y,t) dy \right) dx&\le \varepsilon _{1} \int _{0}^{L} \varphi _{t}^{2} dx + \frac{C_{1}}{\varepsilon _{1}} \int _{0}^{L} \left( \int _{0}^{x} \psi _{t}(y,t) dy \right) ^{2} dx \nonumber \\&\le \varepsilon _{1} \int _{0}^{L} \varphi _{t}^{2} dx + \frac{C_{1}}{\varepsilon _{1}} \left( \int _{0}^{L} \psi _{t}(x,t) dx \right) ^{2} \nonumber \\&\le \varepsilon _{1} \int _{0}^{L} \varphi _{t}^{2} dx + \frac{C_{1}}{\varepsilon _{1}} \int _{0}^{L} \psi _{t}^{2} dx. \end{aligned}$$

(30)

The substitution of (30) into (29) completes the proof. $\square$

Lemma 4.3

Let $\left( \varphi , \psi , \theta , P \right)$ be the solution of (9)–(11), then the functional

$$\begin{aligned} I_{2}(t) = - \, \rho _{1} \int _{0}^{L} \varphi _{t} \varphi dx, \end{aligned}$$

(31)

satisfies, for $\varepsilon _{2} > 0$, the following estimate

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{2}(t)&\le - \rho _{1} \int _{0}^{L} \varphi _{t}^{2} dx + \varepsilon _{2} \int _{0}^{L} \psi _{x}^{2} dx + \left( \varepsilon _{2} + \frac{C_{1}}{\varepsilon _{2}} \right) \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} \theta _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} P_{x}^{2} dx. \end{aligned} \end{aligned}$$

(32)

Proof

Direct computation, using equation (9)$_{1}$ and then integrating by parts, we get

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{2}(t)&= - \rho _{1} \int _{0}^{L} \varphi _{t}^{2} dx - \rho _{1} \int _{0}^{L} \varphi _{tt} \varphi dx \\&= - \rho _{1} \int _{0}^{L} \varphi _{t}^{2} dx + k_{1} \int _{0}^{L} \varphi _{x} \left( \varphi _{x} + \psi \right) dx + \gamma _{1} \int _{0}^{L} \varphi _{x} \theta dx + \gamma _{2} \int _{0}^{L} \varphi _{x} P dx. \end{aligned} \end{aligned}$$

Thanks to Young’s and Poincaré’s inequalities, we have

$$\begin{aligned} k_{1} \int _{0}^{L} \varphi _{x} \left( \varphi _{x} + \psi \right) dx \le \frac{\varepsilon _{2}}{4} \int _{0}^{L} \varphi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx, \end{aligned}$$

$$\begin{aligned} \gamma _{1} \int _{0}^{L} \varphi _{x} \theta dx \le \frac{\varepsilon _{2}}{8} \int _{0}^{L} \varphi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} \theta _{x}^{2} dx, \end{aligned}$$

$$\begin{aligned} \gamma _{2} \int _{0}^{L} \varphi _{x} P dx \le \frac{\varepsilon _{2}}{8} \int _{0}^{L} \varphi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} P_{x}^{2} dx. \end{aligned}$$

So, we arrive at

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{2}(t)&\le - \rho _{1} \int _{0}^{L} \varphi _{t}^{2} dx + \frac{\varepsilon _{2}}{2} \int _{0}^{L} \varphi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} \theta _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{2}} \int _{0}^{L} P_{x}^{2} dx, \end{aligned} \end{aligned}$$

(33)

and by substituting the following relation

$$\begin{aligned} \frac{\varepsilon _{2}}{2} \int _{0}^{L} \varphi _{x}^{2} dx = \frac{\varepsilon _{2}}{2} \int _{0}^{L} \left( \varphi _{x} + \psi - \psi \right) ^{2} dx \le \varepsilon _{2} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + \varepsilon _{2} \int _{0}^{L} \psi ^{2} dx \\ \le \varepsilon _{2} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + \varepsilon _{2} \int _{0}^{L} \psi _{x}^{2} dx, \end{aligned}$$

into (33), then the desired result follows. $\square$

Lemma 4.4

Let $\left( \varphi , \psi , \theta , P \right)$ be the solution of (9)–(11), define the functional

$$\begin{aligned} I_{3}(t) = - \frac{\rho _{1}}{k_{1}} \int _{0}^{L} \varphi _{t} \psi _{x} dx - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t} \left( \varphi _{x} + \psi \right) dx, \end{aligned}$$

(34)

then, the functional $I_{3}$ satisfies, for $\varepsilon _{3} > 0$

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{3}(t)&\le - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t}^{2} dx + \varepsilon _{3} \int _{0}^{L} \psi _{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} P_{x}^{2} dx \\&\quad + \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} \varphi _{tx} \psi _{t} dx. \end{aligned} \end{aligned}$$

(35)

Proof

Differentiating $I_{3}(t)$, using equations (9)$_{1}$ and (9)$_{2}$, we get

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{3}(t)&= - \frac{\rho _{1}}{k_{1}} \int _{0}^{L} \varphi _{tt} \psi _{x} dx - \frac{\rho _{1}}{k_{1}} \int _{0}^{L} \varphi _{t} \psi _{tx} dx \\&\quad - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t} \left( \varphi _{x} + \psi \right) _{t} dx - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{tt} \, \left( \varphi _{x} + \psi \right) dx \\&= - \frac{1}{k_{1}} \int _{0}^{L} {\bigg [} k_{1} \left( \varphi _{x} + \psi \right) _{x} + \gamma _{1} \theta _{x} + \gamma _{2} P_{x} {\bigg ]} \psi _{x} dx \\&\quad - \frac{\rho _{1}}{k_{1}} \int _{0}^{L} \varphi _{t} \psi _{tx} dx - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t} \varphi _{tx} dx - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t}^{2} dx \\&\quad + \frac{1}{b} \int _{0}^{L} {\bigg [} - b \psi _{xx} + k_{1} \left( \varphi _{x} + \psi \right) + \gamma _{1} \theta + \gamma _{2} P {\bigg ]} \left( \varphi _{x} + \psi \right) dx. \end{aligned} \end{aligned}$$

Integrating by parts, we obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{3}(t)&= - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t}^{2} dx + \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} \varphi _{tx} \psi _{t} dx \\&\quad + \frac{k_{1}}{b} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx - \frac{\gamma _{1}}{k_{1}} \int _{0}^{L} \theta _{x} \psi _{x} dx - \frac{\gamma _{2}}{k_{1}} \int _{0}^{L} P_{x} \psi _{x} dx \\&\quad + \frac{\gamma _{1}}{b} \int _{0}^{L} \theta \left( \varphi _{x} + \psi \right) dx + \frac{\gamma _{2}}{b} \int _{0}^{L} P \left( \varphi _{x} + \psi \right) dx. \end{aligned} \end{aligned}$$

(36)

Using Young’s and Poincaré’s inequalities for any $\varepsilon _{3} > 0$, we have

$$\begin{aligned} - \frac{\gamma _{1}}{k_{1}} \int _{0}^{L} \theta _{x} \psi _{x} dx&\le \frac{\varepsilon _{3}}{2} \int _{0}^{L} \psi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{3}} \int _{0}^{L} \theta _{x}^{2} dx, \end{aligned}$$

(37)

$$\begin{aligned} - \frac{\gamma _{2}}{k_{1}} \int _{0}^{L} P_{x} \psi _{x} dx&\le \frac{\varepsilon _{3}}{2} \int _{0}^{L} \psi _{x}^{2} dx + \frac{C_{1}}{\varepsilon _{3}} \int _{0}^{L} P_{x}^{2} dx, \end{aligned}$$

(38)

$$\begin{aligned} \frac{\gamma _{1}}{b} \int _{0}^{L} \theta \left( \varphi _{x} + \psi \right) dx&\le C_{1} \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx, \end{aligned}$$

(39)

$$\begin{aligned} \frac{\gamma _{2}}{b} \int _{0}^{L} P \left( \varphi _{x} + \psi \right) dx&\le C_{1} \int _{0}^{L} P_{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx, \end{aligned}$$

(40)

which yields the desired result (35), by substituting (37)–(40) into (36). $\square$

Lemma 4.5

Let $\left( \varphi , \psi , \theta , P \right)$ be the solution of (9)–(11), then the functional

$$\begin{aligned} I_{4}(t) = \frac{\rho _{1}}{\gamma _{1}} \int _{0}^{L} {\bigg [} c \theta + d P - \gamma _{1} \left( \varphi _{x} + \psi \right) {\bigg ]} \left( \int _{0}^{x} \varphi _{t}(y,t) dy \right) dx, \end{aligned}$$

(41)

satisfies, for any $\varepsilon _{4} > 0$, the following estimate

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{4}(t)&\le - \frac{k_{1}}{2} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + \varepsilon _{4} \int _{0}^{L} \varphi _{t}^{2} dx \\&\quad + C_{1} \left( 1 + \frac{1}{\varepsilon _{4}} \right) \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \int _{0}^{L} P_{x}^{2} dx. \end{aligned} \end{aligned}$$

(42)

Proof

Differentiating $I_{4}(t)$, we have

$$\begin{aligned} \frac{d}{dt}I_{4}(t)&= \frac{\rho _{1}}{\gamma _{1}} \int _{0}^{L} {\bigg [} c \theta + d P - \gamma _{1} \left( \varphi _{x} + \psi \right) {\bigg ]} \left( \int _{0}^{x} \varphi _{tt}(y,t) dy \right) dx \\&\quad + \frac{\rho _{1}}{\gamma _{1}} \int _{0}^{L} {\bigg [} c \theta _{t} + d P_{t} - \gamma _{1} \left( \varphi _{x} + \psi \right) _{t} {\bigg ]} \left( \int _{0}^{x} \varphi _{t}(y,t) dy \right) dx. \end{aligned}$$

By using the first and third equations of (9), integrating by parts, boundary conditions (11) and using the fact that $\int _{0}^{L} \varphi (x) \, dx = 0$, we find

$$\begin{aligned} \frac{d}{dt}I_{4}(t)&= \frac{1}{\gamma _{1}} \int _{0}^{L} {\bigg [} c \theta + d P - \gamma _{1} \left( \varphi _{x} + \psi \right) {\bigg ]} {\bigg [} k_{1} \left( \varphi _{x} + \psi \right) + \gamma _{1} \theta + \gamma _{2} P {\bigg ]} dx \nonumber \\&\quad + \frac{\rho _{1}}{\gamma _{1}} \int _{0}^{L} \kappa \theta _{xx} \left( \int _{0}^{x} \varphi _{t}(y,t) dy \right) dx \nonumber \\&= - k_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + c \int _{0}^{L} \theta ^{2} dx + \frac{\gamma _{2} d}{\gamma _{1}} \int _{0}^{L} P^{2} dx \nonumber \\&\quad - \frac{\kappa \rho _{1}}{\gamma _{1}} \int _{0}^{L} \theta _{x} \varphi _{t} dx + \left( \frac{c k_{1}}{\gamma _{1}} - \gamma _{1} \right) \int _{0}^{L} \theta \left( \varphi _{x} + \psi \right) dx \nonumber \\&\quad + \left( \frac{d k_{1}}{\gamma _{1}} - \gamma _{2} \right) \int _{0}^{L} P \left( \varphi _{x} + \psi \right) dx + \left( \frac{c \gamma _{2}}{\gamma _{1}} + d \right) \int _{0}^{L} \theta P dx. \end{aligned}$$

(43)

The last four terms at the right hand side of (43) are estimated as follows

$$\begin{aligned} - \frac{\kappa \rho _{1}}{\gamma _{1}} \int _{0}^{L} \theta _{x} \varphi _{t} dx \le \varepsilon _{4} \int _{0}^{L} \varphi _{t}^{2} dx + \frac{C_{1}}{\varepsilon _{4}} \int _{0}^{L} \theta _{x}^{2} dx, \end{aligned}$$

(44)

$$\begin{aligned} \left( \frac{c k_{1}}{\gamma _{1}} - \gamma _{1} \right) \int _{0}^{L} \theta \left( \varphi _{x} + \psi \right) dx \le \frac{k_{1}}{4} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + C_{1} \int _{0}^{L} \theta _{x}^{2} dx, \end{aligned}$$

(45)

$$\begin{aligned} \left( \frac{d k_{1}}{\gamma _{1}} - \gamma _{2} \right) \int _{0}^{L} P \left( \varphi _{x} + \psi \right) dx \le \frac{k_{1}}{4} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx + C_{1} \int _{0}^{L} P_{x}^{2} dx, \end{aligned}$$

(46)

$$\begin{aligned} \left( \frac{c \gamma _{2}}{\gamma _{1}} + d \right) \int _{0}^{L} \theta P dx \le C_{1} \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \int _{0}^{L} P_{x}^{2} dx. \end{aligned}$$

(47)

Consequently, we establish (42) by inserting (44)–(47) into (43). $\square$

In the following, we assume that (13) holds and define the Lyapunov functional ${\mathcal {L}}(t)$ by

$$\begin{aligned} {\mathcal {L}}(t) = N E(t) + I_{1}(t) + I_{2}(t) + N_{1} I_{3}(t) + N_{2} I_{4}(t), \end{aligned}$$

(48)

where $N, N_{1}$ and $N_{2}$ are positive constants to be chosen appropriately later.

Lemma 4.6

Let $( \varphi , \psi , \theta , P )$ be the solution of (9)–(11). Then, there exist two positive constants $\alpha _{1}, \alpha _{2}$ such that

$$\begin{aligned} \alpha _{1} E(t) \le {\mathcal {L}}(t) \le \alpha _{2} E(t), \qquad \forall t \ge 0, \end{aligned}$$

(49)

and

$$\begin{aligned} {\mathcal {L}}^{'}(t) \le - \lambda _{1} E(t), \qquad \lambda _{1} > 0. \end{aligned}$$

(50)

Proof

It follows that

$$\begin{aligned} {\Big \vert } {\mathcal {L}}(t) - N E(t) {\Big \vert }&\le \rho _{2} \int _{0}^{L} {\Big \vert } \psi _{t} \psi {\Big \vert } dx + \rho _{1} \int _{0}^{L} {\Bigg \vert } \varphi _{t} \int _{0}^{x} \psi (y,t) dy {\Bigg \vert } dx + \rho _{1} \int _{0}^{L} {\Big \vert } \varphi _{t} \varphi {\Big \vert } dx \\&\quad + \frac{\rho _{1}}{k_{1}} N_{1} \int _{0}^{L} {\Big \vert } \varphi _{t} \psi _{x} {\Big \vert } dx + \frac{\rho _{2}}{b} N_{1} \int _{0}^{L} {\Big \vert } \psi _{t} \left( \varphi _{x} + \psi \right) {\Big \vert } dx \\&\quad + \frac{d \rho _{1}}{\gamma _{1}} N_{2} \int _{0}^{L} {\Bigg \vert } P \int _{0}^{x} \varphi _{t}(y,t) dy {\Bigg \vert } dx + \frac{c \rho _{1}}{\gamma _{1}} N_{2} \int _{0}^{L} {\Bigg \vert } \theta \int _{0}^{x} \varphi _{t}(y,t) dy {\Bigg \vert } dx \\&\quad + \rho _{1} N_{2} \int _{0}^{L} {\Bigg \vert } \left( \varphi _{x} + \psi \right) \int _{0}^{x} \varphi _{t}(y,t) dy {\Bigg \vert } dx. \end{aligned}$$

By using Young’s, Poincaré’s and Cauchy–Schwarz’s inequalities, we obtain

$$\begin{aligned} {\Big \vert } {\mathcal {L}}(t) - N E(t) {\Big \vert } \le C_{2} \int _{0}^{L} {\bigg [} \varphi _{t}^{2} + \left( \varphi _{x} + \psi \right) ^{2} + \psi _{t}^{2} + \psi _{x}^{2} + \theta ^{2} + P^{2} {\bigg ]} dx, \quad C_{2} > 0. \end{aligned}$$

Consequently, from (26), we have

$$\begin{aligned} {\Big \vert } {\mathcal {L}}(t) - N E(t) {\Big \vert } \le C_{3} E(t), \quad C_{3} > 0, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \left( N - C_{3} \right) E(t) \le {\mathcal {L}}(t) \le \left( N + C_{3} \right) E(t). \end{aligned}$$

Therefore, (49) is established by choosing N (depending on $N_{1}$ and $N_{2}$) large enough.

Now, differentiating (48), recalling (25), (28), (32), (35) and (42), we find

$$\begin{aligned} {\mathcal {L}}^{'}(t)&\le - {\Big [} b - \varepsilon _{2} - \varepsilon _{3} N_{1} {\Big ]} \int _{0}^{L} \psi _{x}^{2} dx - {\Big [} \rho _{1} - \varepsilon _{1} - \varepsilon _{4} N_{2} {\Big ]} \int _{0}^{L} \varphi _{t}^{2} dx \\&\quad - \left[ \frac{\rho _{2}}{b} N_{1} - C_{1} \left( 1 + \frac{1}{\varepsilon _{1}} \right) \right] \int _{0}^{L} \psi _{t}^{2} dx \\&\quad - \left[ \frac{k_{1}}{2} N_{2} - C_{1} N_{1} - \left( \varepsilon _{2} + \frac{C_{1}}{\varepsilon _{2}} \right) \right] \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad - \left[ \kappa N - C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) N_{1} - C_{1} \left( 1 + \frac{1}{\varepsilon _{4}} \right) N_{2} - \frac{C_{1}}{\varepsilon _{2}} \right] \int _{0}^{L} \theta _{x}^{2} dx \\&\quad - \left[ h N - C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) N_{1} - C_{1} N_{2} - \frac{C_{1}}{\varepsilon _{2}} \right] \int _{0}^{L} P_{x}^{2} dx, \end{aligned}$$

and by letting

$$\begin{aligned} \varepsilon _{1} = \frac{\rho _{1}}{4} , \qquad \varepsilon _{2} = \frac{b}{4}, \qquad \varepsilon _{3} = \frac{b}{4 N_{1}}, \qquad \varepsilon _{4} = \frac{\rho _{1}}{4 N_{2}}, \end{aligned}$$

we arrive at

$$\begin{aligned} {\mathcal {L}}^{'}(t)&\le - \frac{b}{2} \int _{0}^{L} \psi _{x}^{2} dx - \frac{\rho _{1}}{2} \int _{0}^{L} \varphi _{t}^{2} dx - {\Big [} \frac{\rho _{2}}{b} N_{1} - C_{1} {\Big ]} \int _{0}^{L} \psi _{t}^{2} dx \\&\quad - \left[ \frac{k_{1}}{2} N_{2} - C_{1} N_{1} - C_{1} \right] \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad - {\Big [} \kappa N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} \left( 1 + N_{2} \right) N_{2} - C_{1} {\Big ]} \int _{0}^{L} \theta _{x}^{2} dx \\&\quad - {\Big [} h N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} N_{2} - C_{1} {\Big ]} \int _{0}^{L} P_{x}^{2} dx. \end{aligned}$$

Now, we select our parameters appropriately, we start by choosing $N_{1}$ large enough such that

$$\begin{aligned} \frac{\rho _{2}}{b} N_{1} - C_{1} > 0. \end{aligned}$$

Next, we choose $N_{2}$ large enough so that

$$\begin{aligned} \frac{k_{1}}{2} N_{2} - C_{1} N_{1} - C_{1} > 0. \end{aligned}$$

Finally, we select N very large enough such that

$$\begin{aligned} \kappa N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} \left( 1 + N_{2} \right) N_{2} - C_{1} > 0, \end{aligned}$$

and

$$\begin{aligned} h N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} N_{2} - C_{1} > 0. \end{aligned}$$

All these choices leads to

$$\begin{aligned} {\mathcal {L}}^{'}(t)&\le - \lambda _{2} \int _{0}^{L} {\bigg [} \varphi _{t}^{2} + \left( \varphi _{x} + \psi \right) ^{2} + \psi _{t}^{2} + \psi _{x}^{2} + \theta _{x}^{2} + P_{x}^{2} {\bigg ]} dx, \ \lambda _{2} > 0. \end{aligned}$$

(51)

On the other hand, from (24), using Poincaré’s and Young’s inequalities, we arrive at

$$\begin{aligned} E(t)&\le \frac{1}{2} \int _{0}^{L} {\bigg [} \rho _{1} \varphi _{t}^{2} + k_{1} \left( \varphi _{x} + \psi \right) ^{2} + \rho _{2} \psi _{t}^{2} + b \psi _{x}^{2} + \left( c + d \right) \theta ^{2} + \left( r + d \right) P^{2} {\bigg ]} dx \\&\le \lambda _{3} \int _{0}^{L} {\bigg [} \varphi _{t}^{2} + \left( \varphi _{x} + \psi \right) ^{2} + \psi _{t}^{2} + \psi _{x}^{2} + \theta _{x}^{2} + P_{x}^{2} {\bigg ]} dx, \qquad \lambda _{3} > 0. \end{aligned}$$

That is,

$$\begin{aligned} - \int _{0}^{L} {\bigg [} \varphi _{t}^{2} + \left( \varphi _{x} + \psi \right) ^{2} + \psi _{t}^{2} + \psi _{x}^{2} + \theta _{x}^{2} + P_{x}^{2} {\bigg ]} dx \le - \lambda _{4} E(t), \quad \lambda _{4} > 0. \end{aligned}$$

(52)

Therefore, we obtain the desired result (50) by combining (51) and (52). $\square$

Now, we are ready to prove the following stability result.

Theorem 4.1

Assume that (13) holds and let $( \varphi , \psi , \theta , P )$ be the solution of (9)–(11). Then for any $U_{0} \in \mathcal {D(A)}$, there exist two positive constants $\alpha _{3}, \alpha _{4}$ such that the energy functional defined by (24) satisfies

$$\begin{aligned} E(t) \le \alpha _{3} e^{- \alpha _{4} t}, \qquad \forall t > 0. \end{aligned}$$

(53)

Proof

From the equivalence of E(t) and ${\mathcal {L}}(t)$ (relation (49)) and estimation (50), we have

$$\begin{aligned} {\mathcal {L}}^{'}(t) \le - \alpha _{4} {\mathcal {L}}(t), \qquad t \ge 0, \end{aligned}$$

(54)

where $\alpha _{4} = \frac{\lambda _{1}}{\alpha _{2}}$. A simple integration of (54) gives

$$\begin{aligned} {\mathcal {L}}(t) \le {\mathcal {L}}(0) e^{- \alpha _{4} t}, \qquad t \ge 0, \end{aligned}$$

which yields the desired result (53) by using the other side of the equivalence relation again. $\square$

5 Polynomial stability and optimality

In this section, we consider the polynomial stability for system (9)–(11) in case of different wave speeds ($\frac{\rho _{1}}{k_{1}} \ne \frac{\rho _{2}}{b}$). For this purpose, we use the second-order energy method. The second-order energy is defined by

$$\begin{aligned} {\mathcal {E}}(t) = \frac{1}{2} \int _{0}^{L} {\bigg [} \rho _{1} \varphi _{tt}^{2} + k_{1} \left( \varphi _{x} + \psi \right) _{t}^{2} + \rho _{2} \psi _{tt}^{2} + b \psi _{tx}^{2} + c \theta _{t}^{2} + r P_{t}^{2} + 2 d \theta _{t} P_{t} {\bigg ]} dx. \end{aligned}$$

(55)

As in Lemma 4.1, it follows that ${\mathcal {E}}(t)$ satisfies

$$\begin{aligned} {\mathcal {E}}^{'}(t) = - \kappa \int _{0}^{L} \theta _{tx}^{2} dx - h \int _{0}^{L} P_{tx}^{2} dx \le 0, \quad \forall t > 0. \end{aligned}$$

(56)

Lemma 5.1

Let $\left( \varphi , \psi , \theta , P \right)$ be the solution of (9)–(11), then the functional

$$\begin{aligned} F_{3}(t) = I_{3} (t) - \frac{h}{\gamma _{2}}\left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} P_{x} \psi _{x} dx, \end{aligned}$$

(57)

satisfies, for any $\varepsilon _{3} > 0$, the estimate

$$\begin{aligned} \begin{aligned} \frac{d}{dt} F_{3}(t)&\le - \frac{\rho _{1}}{2 k_{1}} \int _{0}^{L} \psi _{t}^{2} dx + 2 \varepsilon _{3} \int _{0}^{L} \psi _{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} P_{x}^{2} dx \\&\quad + C_{1} \int _{0}^{L} \theta _{tx}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} P_{tx}^{2} dx . \end{aligned} \end{aligned}$$

(58)

Proof

We showed that the derivative of $I_{3}(t)$ (Lemma 4.4) satisfies

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I_{3}(t)&\le - \frac{\rho _{2}}{b} \int _{0}^{L} \psi _{t}^{2} dx + \varepsilon _{3} \int _{0}^{L} \psi _{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} P_{x}^{2} dx \\&\quad + \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} \varphi _{tx} \psi _{t} dx. \end{aligned} \end{aligned}$$

(59)

Now, from the fourth equation in (9), we have

$$\begin{aligned} \int _{0}^{L} \varphi _{tx} \psi _{t} dx&= \frac{d}{\gamma _{2}} \int _{0}^{L} \theta _{t} \psi _{t} dx + \frac{r}{\gamma _{2}} \int _{0}^{L} P_{t} \psi _{t} dx \\&\quad + \frac{h}{\gamma _{2}} \int _{0}^{L} P_{x} \psi _{tx} dx - \int _{0}^{L} \psi _{t}^{2} dx. \end{aligned}$$

Consequently, we get

$$\begin{aligned} \begin{aligned} \int _{0}^{L} \varphi _{tx} \psi _{t} dx&= \frac{d}{\gamma _{2}} \int _{0}^{L} \theta _{t} \psi _{t} dx + \frac{r}{\gamma _{2}} \int _{0}^{L} P_{t} \psi _{t} dx + \frac{d}{dt} \left[ \frac{h}{\gamma _{2}} \int _{0}^{L} P_{x} \psi _{x} dx \right] \\&\quad - \frac{h}{\gamma _{2}} \int _{0}^{L} P_{tx} \psi _{x} dx - \int _{0}^{L} \psi _{t}^{2} dx. \end{aligned} \end{aligned}$$

(60)

So, by inserting (60) into (59), we arrive at

$$\begin{aligned} \frac{d}{dt} F_{3}(t)&\le - \frac{\rho _{1}}{k_{1}} \int _{0}^{L} \psi _{t}^{2} dx + \varepsilon _{3} \int _{0}^{L} \psi _{x}^{2} dx + C_{1} \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} \theta _{x}^{2} dx + C_{1} \left( 1 + \frac{1}{\varepsilon _{3}} \right) \int _{0}^{L} P_{x}^{2} dx \\&\quad + \frac{d}{\gamma _{2}} \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} \theta _{t} \psi _{t} dx + \frac{r}{\gamma _{2}} \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} P_{t} \psi _{t} dx \\&\quad - \frac{h}{\gamma _{2}} \left( \frac{\rho _{1}}{k_{1}} - \frac{\rho _{2}}{b} \right) \int _{0}^{L} P_{tx} \psi _{x} dx. \end{aligned}$$

Then, the desired result follows by using Young’s and Poincaré’s inequalities. $\square$

The main result of this section is given by the following theorem.

Theorem 5.1

Let $( \varphi , \psi , \theta , P )$ be the solution of (9)–(11) and assume that $\frac{\rho _{1}}{k_{1}} \ne \frac{\rho _{2}}{b}$. Then, there exists a positive constant $\alpha _{5}$ such that the energy functional E(t) satisfies

$$\begin{aligned} E(t) \le \frac{\alpha _{5}}{t}, \qquad \forall t > 0. \end{aligned}$$

(61)

Proof

We define a Lyapunov functional ${\mathcal {K}}$ as

$$\begin{aligned} {\mathcal {K}}(t) = N \left( E(t) + {\mathcal {E}}(t) \right) + I_{1}(t) + I_{2}(t) + N_{1} F_{3}(t) + N_{2} I_{4}(t). \end{aligned}$$

(62)

Next, by differentiating ${\mathcal {K}}(t)$, recalling (25), (28), (32), (42), (56) and (58) with the same choice of $\varepsilon _{1}, \varepsilon _{2}, \varepsilon _{4}$, except for $\varepsilon _{3}$, we choose $\varepsilon _{3} = \frac{b}{8 N_{1}}$, we arrive at

$$\begin{aligned} {\mathcal {K}}^{'}(t)&\le - \frac{b}{2} \int _{0}^{L} \psi _{x}^{2} dx - \frac{\rho _{1}}{2} \int _{0}^{L} \varphi _{t}^{2} dx - {\Big [} \frac{\rho _{1}}{2 k_{1}} N_{1} - C_{1} {\Big ]} \int _{0}^{L} \psi _{t}^{2} dx \\&\quad - \left[ \frac{k_{1}}{2} N_{2} - C_{1} N_{1} - C_{1} \right] \int _{0}^{L} \left( \varphi _{x} + \psi \right) ^{2} dx \\&\quad - {\Big [} \kappa N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} \left( 1 + N_{2} \right) N_{2} - C_{1} {\Big ]} \int _{0}^{L} \theta _{x}^{2} dx \\&\quad - {\Big [} h N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} N_{2} - C_{1} {\Big ]} \int _{0}^{L} P_{x}^{2} dx \\&\quad - {\Big [} \kappa N - C_{1} N_{1} {\Big ]} \int _{0}^{L} \theta _{tx}^{2} dx - {\Big [} h N - C_{1} \left( 1 + N_{1} \right) N_{1} {\Big ]} \int _{0}^{L} P_{tx}^{2} dx. \end{aligned}$$

Similarly to what we did with ${\mathcal {L}}^{'}(t)$, we choose $N_{1}$ large enough so that

$$\begin{aligned} \frac{\rho _{1}}{2 k_{1}} N_{1} - C_{1} > 0. \end{aligned}$$

Then, we select $N_{2}$ large enough such that

$$\begin{aligned} \frac{k_{1}}{2} N_{2} - C_{1} N_{1} - C_{1} > 0. \end{aligned}$$

Finally, we choose N very large enough such that

$$\begin{aligned} \kappa N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} \left( 1 + N_{2} \right) N_{2} - C_{1}> 0, \qquad \kappa N - C_{1} N_{1}> 0, \\ h N - C_{1} \left( 1 + N_{1} \right) N_{1} - C_{1} N_{2} - C_{1}> 0, \qquad h N - C_{1} \left( 1 + N_{1} \right) N_{1} > 0. \end{aligned}$$

Consequently, by exploiting (24), we find

$$\begin{aligned} {\mathcal {K}}^{'}(t) \le - \alpha _{6} E(t), \qquad \alpha _{6}> 0, \quad \forall t > 0. \end{aligned}$$

(63)

A simple integration of (63) over (0, t) , recalling that E(t) is non-increasing and positive, yields

$$\begin{aligned} t E(t) \le \int _{0}^{t} E(s) ds \le \frac{{\mathcal {K}}(0) - {\mathcal {K}}(t)}{\alpha _{6}} \le \frac{{\mathcal {K}}(0)}{\alpha _{6}}, \quad \forall t > 0. \end{aligned}$$

(64)

That is, for $\alpha _{5} = \frac{{\mathcal {K}}(0)}{\alpha _{6}} = \frac{E(0) + {\mathcal {E}}(0)}{\alpha _{6}}$, we have

$$\begin{aligned} E(t) \le \frac{\alpha _{5}}{t}, \qquad \forall t > 0, \end{aligned}$$

(65)

which completes the proof. $\square$

Next, we show that the polynomial decay rate is optimal. To achieve this optimality result, we prove by contradiction. It should be noted that the polynomial result given by (61) is equivalent to

$$\begin{aligned} \Vert U \Vert _{{\mathcal {H}}} \le \alpha _{5}t^{-\frac{1}{2}},\qquad \forall t>0. \end{aligned}$$

(66)

Assume the result can be improved from $t^{-\frac{1}{2}}$ to $t^{-\frac{1}{2-\varepsilon }}$, for some $0<\varepsilon <2$. Then $\dfrac{1}{\mu ^{2-\varepsilon }}\Vert U \Vert _{{\mathcal {H}}}$ must be bounded. In other words,

$$\begin{aligned} \dfrac{1}{\mu ^{4-2\varepsilon }}\Vert U \Vert _{{\mathcal {H}}} \end{aligned}$$

must be bounded. Unfortunately, from (23) we have $\Vert U \Vert ^2_{{\mathcal {H}}}\ge c\mu ^4,$ for large $\mu$. Consequently, the decay rate cannot be improved. Thus, the polynomial stability result obtained for the different wave speeds is optimal.

6 General remark and open problem

A one-dimensional Timoshenko system coupled with thermal and mass diffusion effects is considered. The stability results (exponential and polynomial) obtained depend on the behavior of the wave speeds. In other words, the system is exponentially stable if the wave speeds on the first two equations of the system are equal; otherwise, a polynomial result was demonstrated. Even though we have investigated the system for Neumann–Dirichlet–Dirichlet–Dirichlet conditions, the results are also true for some other boundary conditions. One of interesting open problems is to consider system (9) free of the second spectrum. This is achieved by replacing $\psi _{tt}$ in the second equation of (9) with $\varphi _{ttx}$. We believe that the resulting system will be exponentially stable, irrespective of the wave propagation velocities of the system.