Introduction

Soil slope stability is a major concern nowadays as it plays a major role in the construction of various structure with use of soil e.g. earth dams, embankments and stability of various open pits. Soil is a natural occurring material found on earth, having high variability in its properties due to process of formation. Therefore, it’s very hard to determine the properties of soil with certainty. In spite of various methods e.g. Strength Reduction Method and Limit Equilibrium Method are available to solve or find the solution for stability of soil slope, failure of slopes are occurring in high percentage, as these methods follows the deterministic approach which is highly conservative. And also due to the various errors like the testing error or sampling error there are testing data variability as shown by Phoon (2002). To overcome these limitation of deterministic approach nowadays approach is shifting towards the probabilistic way and to implement the probabilistic approach reliability analysis is used for the slope stability analysis of soil slope. In the reliability analysis various models are being worked out using the soil parameters on which stability of slope depends as input and output of the models are analyzed to find their adaptability to the problem.

In past many researchers have used probabilistic approach in their research work. Researchers have used field and laboratory data values to perform probabilistic analysis to show the uncertainty in soil properties of an embankment (Christian et al. 1994). El-Ramly et al. (2002) showed the probabilistic analysis on the design of slope by using spreadsheet approach based on MCS and also applied the approach using the James Bay hydroelectric project as an example. Wang et al. (2019) showed the probabilistic analysis of post-failure of soil slope using RSPH (random smoothed particle hydrodynamics) and incorporated the slope failure analysis. Liang et al. (1999) performed the reliability analysis on the multi-layer embankment and showed the incorporation of variability in the soil properties. Cheng (2003) showed how to locate the critical failure surface with higher level of precision in short time using annealing method. Babu and Srivastava (2010) conducted the reliability analysis using response surface methodology (RSM) on selected earth dam section. By the use of multi-modal optimisation method (Reale et al. 2015), multiple failure modes were located using various probabilistic models. Earth dams were being analyzed by using ANN model in various conditions e.g. static and dynamic and the model showed good capability of predicting factor of safety of slope (Zeroual et al. 2009). Kumar et al. (2017) used various models like MARS, ANFIS for the reliability analysis of infinite slope and the results showed that the models are reliable for the condition. Gao et al. (2018) developed GPR model for the forecasting of rock fragmentation in mines and also GPR model along with MPMR model were being developed by Samui et al. (2019) to determine the uplift capacity of suction caisson. After reviewing many critical literature, authors found out that in conventional methods of analysis variability in the soil properties parameters are not incorporated. Therefore, the main purpose of present study is to perform reliability analysis of soil slope stability using MARS, GPR and FN soft computing models. In addition, all these models are also tested for reliability analysis of soil slope stability.

Theoretical background of models

Multivariate adaptive regression spline

MARS was developed with an idea that in different sample spaces, all the variables have different level of impact on the response surface. The adaptive in the MARS is basically defines the same i.e. MARS ability to find the dominant variables in each and every sample space region. In MARS there is simple approach to use piecewise polynomials (Splines) is adopted. In order to develop MARS model, it uses basis function. The inputs and output values x and y, respectively, are related using the following equation i.e. Eq. (1):

$$ y = a_{o} + \mathop \sum \limits_{m = 1}^{M} a_{m} B_{m} \left( x \right), $$
(1)

where \(B_{m} \left( x \right)\), basis function; M, no. of functions; \(a_{o}\) and \(a_{m}\) are the constant and coefficient of the mth function.

Knots used to connect data points, MARS characterizes data using regressions or by finding it globally (Friedman 1991; Abraham and Steinberg 2001). For getting continues output, the basis function in the adjacent domain intersect at the knot. MARS uses bended regression in place of conventional regressions, to connect x properly between subgroups and between spline. The no. of knots should be 3–4 times the no. of \(B_{m} \left( x \right)\) of MARS model (Sharda et al. 2008). To avoid over-fitting adequate data in subgroup is ensured by the model using shortest distance between the knots (Sephton 2001; Adamowski et al. 2012).

Two segmented truncated power functions separated by a knot location used for the formation of spline basis functions for MARS. The expression for the truncated function to the left and right are as follows:

$$ \left[ { - \left( {x - t} \right)} \right]_{ + }^{q} = \left\{ {\begin{array}{*{20}l} {\left( {t - x} \right)^{q} ,} \hfill & {{\text{if}} x < t} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right., $$
(2)
$$ \left[ { + \left( {x - t} \right)} \right]_{ + }^{q} = \left\{ {\begin{array}{*{20}l} {\left( {t - x} \right)^{q} ,} \hfill & { {\text{if}} x < t} \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.. $$
(3)

Here q is power to which spline is raised and t is knot location.

For developing MARS model two steps are followed.

Forward step: In this step, \(B_{m} \left( x \right)\) functions are defined with the help of Eq. (1). But, due to large no. of basis functions there is over fitting problem.

Backward step: \(B_{m} \left( x \right)\) basis functions are selected based on the generalized cross-validation (GCV) statistic which was calculated using the Craven and Wahba method (Craven and Wahba 1978):

$$ {\text{GVC}} = \frac{{\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left[ {y_{i} - f\left( {x_{i} } \right)} \right]^{2} }}{{\left[ {1 - \frac{C\left( B \right)}{N}} \right]^{2} }}, $$
(4)

where N is the no. of data objects, C(B) is factor of penalty:

$$ C\left( B \right)\, = \,\left( {B\, + \,{1}} \right)\, + \,{\text{d}}B, $$
(5)

where d is the penalty each function defined in the model.

Gaussian process regression (GPR)

A Gaussian process (GP) is a nonparametric model used for probabilistic analysis, in which observations are defined within a domain of continuous range (Grbić et al. 2013). This model is applicable to both types of problems i.e. regression having non-linear behavior (Williams 1997) and classification (Williams and Barber 1998). GPR is defined using its mean and covariance. The mean function is generally taken equal to zero, as it encodes central tendency of the function (Zhang et al. 2016). The covariance function is having the information of structure of the function which is needed for our defined problem. In this study, ϒ, ϕ and c are taken as input variables and FOS as output of GPR. So, x = [ϒ, ϕ, c] and y = [FOS].

GPR uses the following connecting equation between the inputs and the output:

$$ y_{i} = f\left( {x_{i} } \right) + \varepsilon . $$
(6)

It is assumed that Gaussian noise (\(\varepsilon\)) is independent and having a distribution with mean = 0 and variance = \(\sigma_{n}^{2}\).

Expression for evaluating output for the new input is:

$$ \left( {\begin{array}{*{20}c} y \\ {y_{N + 1} } \\ \end{array} } \right)\sim {\mathcal{N}}\left( {0,K_{N + 1} } \right), $$
(7)

where \(y_{N + 1}\) is target variable and \(x_{N + 1}\) is new input.

The KN+1 and other parameters are related by the Eq. (8) and yN+1 follows the Gaussian distribution:

$$ K_{N + 1} = \left[ {\begin{array}{*{20}c} {\left[ K \right]} & {\left[ {k\left( {x_{N + 1} } \right)} \right]} \\ {\left[ {k\left( {x_{N + 1} } \right)^{T} } \right]} & {\left[ {k_{1} \left( {x_{N + 1} } \right)} \right]} \\ \end{array} } \right]. $$
(8)

Covariance between the training inputs and test input is given by k(xN+1) and test input auto-covariance is expressed as k1(xN+1). The covariance (kernel) function is a critical component in a Gaussian process regression. In this study radial basis function is adopted as covariance function to develop the GPR model.

Functional network (FN)

Artificial neural networks are inspired by the working of brain i.e. to learn from the behavior and then reproduce a system accordingly as per the field. Artificial neural networks works by using the neurons (Armaghani et al. 2020) to form a neural network which gives output as per the inputs provided.

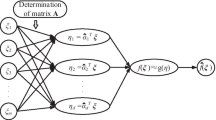
Functional network (FN) (Castillo et al. 1999) is a recently developed useful extension of artificial neural networks, FN in order to develop structure of the network for its working uses the domain background knowledge and also the knowledge of data provided. In FN various arbitrary neural functions were used and also used in the form of multiple argument (Fig. 1).

Fig. 1
figure 1

The basis functions and knot location in the MARS model

Full size image

In Functional network system of functional equations are formed by the help of the arrangement of the neurons in the neural network, which provides outputs in various formats. The most important step in functional network is the procedure of learning (Castillo et al. 2000) using the domain background knowledge and also the knowledge of data provided. There are generally two types of learning:

  1. i.

    Structural learning—In this initial knowledge of system background and the properties of the system are used for the design.

  2. ii.

    Parametric learning—In this neurons are linked in the network with the parameters with the help of the data available.

Layers included in the formation of functional network model:

  1. 1.

    Storing units

    1. (i)

      Input layer—layer which takes input data x1, x2, x3 etc. as an input for the model.

    2. (ii)

      Middle layers—layers which evaluate the input from previous layer and provide output for the next layer, f4, f5.

    3. (iii)

      Output storing units’ layer—output data f6 are stored in this layer.

  2. 2.

    Layers consists of neuron—A neuron being a computing unit uses the input from the previous layer to provide an output set for the next layer. Layer consisting computing units, f1, f2, f3.

  3. 3.

    Direction links—These are used to connect layer from each other in a right form to get a functional network. These directed links are used to show the direction of flow of information. The intermediate functions work based on the structure of the network. Example x7 = f4 (x4, x5, x6) as in Fig. 2.

Fig. 2
figure 2

Network diagram of functional network

Full size image

Model development

In this study, a 15 m high c–ϕ soil slope with side slope 1:1 described as an example by Cho (2010) used for our reliability analysis of soil slope stability using MARS, GPR and FN soft computing models. Details of c–ϕ soil slope is shown in Fig. 3. In the probabilistic analysis, the variation in parameter is considered for cohesion (c), angle of shear resistance (ϕo) and unit weight (γ). The coefficient of variation for cohesion, angle of shear resistance and unit weight is taken as 0.3, 0.2 and 0.03, respectively, and mean value as 10, 30 and 20, respectively.

Fig. 3
figure 3

Cross section of typical c–ϕ soil slope

Full size image

For determining the factor of safety (FOS) of c–ϕ soil slope using Morgenstern-Price method is used using the GeoStudio 2016 software. The factor of safety (FOS) of c–ϕ soil slope depends on the parameters γ (unit weight), c (cohesion of soil) and ϕ (angle of shear resistance), which are taken as input variables and factor of safety (FOS) of slope as result. The permissible range of γ, c and ϕ are used to get 100 data set and corresponding 100 data set of factor of safety (FOS) using GeoStudio 2016 software. For using these data set in MATLAB for the MARS, GPR and FN models need to be normalized as given by Eq. (9):

$$ X_{{{\text{nor}}}} = \frac{{X - X_{{{\text{min}}{.}}} }}{{X_{{{\text{max}}{.}}} - X_{{{\text{min}}{.}}} }}, $$
(9)

where \(X_{{{\text{nor}}}} = {\text{ normalised value}}\), \(X = {\text{ value of parameter}}\), \(X_{{{\text{min}}{.}}} = {\text{ min}}.{\text{ value}}\), \(X_{{{\text{max}}{.}}} = {\text{ max}}.{\text{ value}}\).

The data set are used as input to the models in the normalized form and corresponding predicted output of models are obtained. The actual observed FOS and predicted FOS values which are obtained using models are tested using various fitness parameters to compare and find the best models on their prediction capability.

Performance parameters

Models performance are assessed using the following parameters:

Nash–Sutcliffe efficiency (NS) (Jain and Sudheer 2008) shows the prediction capability of the model which is maximum if its value comes equal to 1:

$$ {\text{NS}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} (d_{i} - y_{i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {d_{i} - d_{{{\text{mean}}}} } \right)^{2} }}. $$
(10)

Root mean square error (RMSE) (Kisi et al. 2013) calculate the prediction error for the shows the error in prediction of the target value:

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{n} \left( {d_{i} - y_{i} } \right)^{2} } . $$
(11)

Variance account factor (VAF) (Grima and Babuška 1999; Gokceoglu 2002; Yılmaz and Yuksek 2008) value used to exhibit the performance of each and the ideal value for VAF equal to 100 for the best performance:

$$ {\text{VAF}} = \left( {1 - \frac{{{\text{var}} (d_{i} - y_{i} )}}{{{\text{var}} (d_{i} )}}} \right) \times 100. $$
(12)

R2 (Coefficient of determination) (Babu and Srivastava 2007) is a parameter which shows that how much the model have incorporated the variability in the soil properties, along with Adj. R2 (adjusted Coefficient of determination) value and the values of both parameter need to close to 1 and to each other also:

$$ R^{2} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} (d_{i} - d_{{{\text{mean}}}} )^{2} - \mathop \sum \nolimits_{i = 1}^{n} (d_{i} - y_{i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (d_{i} - d_{{{\text{mean}}}} )^{2} }}, $$
(13)
$$ {\text{Adj}}R^{2} = 1 - \frac{{\left( {n - 1} \right)}}{{\left( {n - p - 1} \right)}}\left( {1 - R^{2} } \right). $$
(14)

Performance index (PI) (Kung et al. 2007) shows how well each model is performing while predicting the target values:

$$ {\text{PI}} = {\text{adj}}{.}R^{2} + 0.01\;{\text{VAF}} - {\text{RMSE}}{.} $$
(15)

Bias factor (Prasomphan and Machine 2013) value indicates whether the model’s estimation is over or under as per the factor value is greater or less than 1, respectively:

$$ {\text{Bias factor = }}\frac{1}{N}\mathop \sum \limits_{i = 1}^{n} \frac{{y_{i} }}{{d_{i} }}. $$
(16)

RSR (Moriasi et al. 2007) shows the accuracy in prediction and if RSR is closer to 0 prediction is good:

$$ {\text{RSR}} = \frac{{{\text{RMSE}}}}{{\sqrt {\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{n} \left( {d_{i} - d_{{{\text{mean}}}} } \right)^{2} } }}. $$
(17)

Normalized mean bias error (NMBE) (Srinivasulu and Jain 2006) value gives the percentage of biasness of predicted value from the mean in normalized format:

$$ {\text{NMBE}} \left( \% \right) = \frac{{\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - d_{i} } \right)}}{{\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{n} d_{i} }} \times 100. $$
(18)

MAPE (mean absolute percentage error) (Armstrong and Collopy 1992) parameter value indicate the good amount of accuracy in prediction if it comes in closer to zero:

$$ {\text{MAPE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{d_{i} - y_{i} }}{{d_{i} }}} \right|. $$
(19)

Relative percentage difference (RPD) (Ray et al. 2020) value indicates the how the model is performing based on the values and corresponding performances given in Table1:

$$ {\text{RPD = }}\frac{{{\text{SD}}}}{{{\text{RMSE}}}}. $$
(20)
Table 1 RPD for the performance of models
Full size table

Willmott’s Index for agreement (WI). (Willmott 1981, 1982, 1984) value varies between 0 and 1 and the index value indicates the error in prediction of targeted values:

$$ {\text{WI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {d_{i} - y_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {\left| {y_{i} - d_{{{\text{mean}}}} \left| + \right|d_{i} - d_{{{\text{mean}}}} } \right|} \right)^{2} }}} \right]\quad . $$
(21)

Mean bias error (MBE) and mean absolute error (MAE). Raventos-Duran et al. (2010) both the values are error calculator, and values closer to 0 indicates good model with lesser error:

$$ {\text{MBE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - d_{i} } \right), $$
(22)
$$ {\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{n} \left| {\left( {y_{i} - d_{i} } \right)} \right|. $$
(23)

Legate and McCabe’s Index (LMI). Legates and McCabe (1999, 2013) shows the level of divergence in prediction by the model from the actual data:

$$ {\text{LMI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {d_{i} - y_{i} } \right|}}{{\mathop \sum \nolimits_{i = 1}^{N} \left| {d_{i} - d_{{{\text{mean}}}} } \right|}}} \right]. $$
(24)

Expanded uncertainty (U95). Gueymard (2014), Behar et al. (2015) shows the short-term performance of the models in prediction:

$$ U_{95} = 1.96*\left( {{\text{SD}}^{{2}} {\text{ + RMSE}}^{2} } \right)^{1/2} . $$
(25)

t-statistic (Stone 1993) is a tool to indicate the performance of the models:

$$ t{\text{ - stat}} = \sqrt {\frac{{\left( {N - 1} \right){\text{MBE}}^{2} }}{{{\text{RMSE}}^{2} - {\text{MBE}}^{2} }}} . $$
(26)

Global performance indicator (GPI) (Viscarra et al. 2006) incorporate all the parameters to access the performance using single parameter:

$$ {\text{GPI}} = {\text{MBE}} \times {\text{RMSE}} \times U_{95} \times t_{{{\text{stat}}}} \times \left( {1 - R^{2} } \right). $$
(27)

Reliability index (β) value for each model defines the model performance based on the reliability analysis (USACE 1997):

$$ \beta = \frac{{\mu_{{\text{F}}} - 1}}{{\sigma_{{\text{F}}} }}. $$
(28)

Here, di = actual observed data of ith point and yi = predicted data of ith point, dmean = mean value observed data, SD = standard deviation, \(\mu_{{\text{F}}}\) is mean value of factor of safety of soil slope and \(\sigma_{{\text{F}}}\) is standard deviations of factor of safety of soil slope under consideration.

Results and discussion

Reliability analysis of soil slope stability on the considered section done using three soft computing models MARS, GPR and FN by normalizing all the data set value, then dividing them in training and testing data and use them as input and FOS as an output for all the three models. After the predicted values of FOS are obtained from the models, the actual and predicted values are being represented using graph between the actual values and predicted values of FOS of soil slope for both training and testing data values of MARS, GPR and FN models as shown in Figs. 4, 5, 6, respectively. Graphs plots of all the models shows the prediction done by the models are satisfactory, as the all values of both the training and testing data are close to the line depicting actual equal to the predicted value. On comparing the three models, it can be said that MARS model performance is good as the values are more closer to the actual equals to predicted line.

Fig. 4
figure 4

MARS model performance for training and testing dataset

Full size image
Fig. 5
figure 5

GPR model performance for training and testing dataset

Full size image
Fig. 6
figure 6

FN model performance for training and testing dataset

Full size image

All the models are tested using various fitness parameters NS, RMSE, VAF, MAE, RSR, Bias factor, PI, R2, Adj. R2, MAPE, GPI, LMI, U95, tstat and β as mentioned in Table 2. In the Table 2 values of each parameter are mentioned for all the three models MARS, GPR and FN. The value of NS shows that all models prediction power is high as the values of NS are closer to 1. The RMSE and VAF values shows that the MARS model performed good in predicting values of FOS of soil slope as compared to other models, as the prediction error of MARS model is less among the three models. The R2 and Adj. R2 values for all the three model are closer to each other and also closer to 1, but values for MARS model are closest to 1 among the models which shows that the MARS model have included most of the soil parameter variability. On comparing the models based on the values of Bias factor, MAPE, NMBE (%), RSR and PI values, MARS model’s prediction capability is high and also the predicted values are least biased from the actual values of factor of safety of soil slope. WI, MAE, MBE and LMI values for all the three models shows that the models are very less deviated from the actual values of FOS. The RPD value of models shows that the MARS model is good (Table 1) i.e. works accurately among the three models. All the models MARS, GPR and FN performed good as U95 and t-stat values are very small. MARS model is having high accuracy in predicting the FOS of soil slope as GPI value is lowest among the three models. Figure 7 shows the β values for FOSM (first order second moment), FOSM (MARS), FOSM (GPR) and FOSM (FN). The reliability index (β) of all three models MARS, GPR and FN (USACE 1997; Baecher and Christian 2003) shows that the models performance is comparable as shown in Fig. 7. After the development of all the models the advantage of MARS model is that it gives an expression (Eq. 29) as an output result for the dataset for the calculation of factor of safety of soil slope stability using Eq. (1) in which y = FOS, M = 9, a0 = 0.00112 and Bm(x) and am detail in Table 3:

$$ {\text{FOS}} = 0.00112 + \mathop \sum \limits_{m = 1}^{9} a_{m} B_{m} \left( x \right). $$
(29)
Table 2 Performance parameters of MARS, GPR and FN models
Full size table
Fig. 7
figure 7

Reliability index (β) bar chart for MARS, GPR and FN Model

Full size image
Table 3 Estimated values of \(B_{m} \left( x \right)\) and \(a_{m}\) by MARS model
Full size table

Taylor diagram (Taylor 2001) is a statistical summary to know the best match model in terms of standard deviation (SD), RMSE and correlation coefficient. The Taylor curves in Fig. 8 combines together all i.e. standard deviation (SD), RMSE and correlation coefficient together to find the most accurate model. Taylor diagram gives a graphical framework that shows the suitability of variables by the different types models based on the reference data. As per, the training Taylor diagram result (Fig. 8), MARS model shows the best results, and the testing Taylor diagram also MARS model values are closer to the observed actual values. In summary, it indicates that there is a good agreement between the actual and the model results for MARS model.

Fig. 8
figure 8

Taylor diagram a training and b testing plotted for MARS, GPR and FN Model

Full size image

ROC curve (Fawcett 2006) plot for MARS, GPR and FN for the training and testing is shown in Fig. 9 from which AUC (area under curve) value of all three models are calculated and AUC values are shown in Table 4. AUC values from the Table 4 shows that its value for MARS model is highest among the three models, which indicates MARS model is having very high classification accuracy among MARS, GPR and FN models.

Fig. 9
figure 9

ROC curve plot for training and testing values of models

Full size image
Table 4 AUC value of ROC curve for the models
Full size table

Anderson–Darling (A–D) is a statistical test (Anderson and Darling 1952) used to evaluate which whether the model follows the normal distribution or not and also to know the whether the given data is from the same probability distribution or not. Anderson–Darling (A–D) test provides P-value (shown in Table 5), which are greater than 0.05 for all the models MARS, GPR and FN, that shows all the three models works as normal distribution. Among all the three models MARS model follow closest to the normal distribution trend.

Table 5 A–D k-sample test of MARS, GPR and FN models
Full size table

Conclusions

In this article, reliability analysis of soil slope stability was studied using MARS, GPR and FN models. An example of soil slope has been taken to show the procedure of working of the MARS, GPR and FN models. All these models were comprehensively analyzed and compared based on various performance parameters. Values of reliability index of all the models show that models’ prediction capability of factor of safety for the soil slope stability is good. All the models performed satisfactorily, but among three models MARS model outperformed based on the various performance parameters like NS, RMSE, VAF, MAE, RSR, Bias Factor etc. The training and testing data were also accumulated up while graphing Taylor and ROC curves. The results from ROC curve, the largest value of area under curve (AUC) was obtained for MARS model, followed by GPR and FN model. Models were also tested using Anderson–Darling (A–D) statistical test which shows that MARS model followed the closest to normal distribution trend among the models. The developed MARS model is having additional advantage as it provides an equation for determination of factor of safety for soil slope stability analysis. Therefore, it can be concluded that MARS model can be used as reliable tool for the reliability analysis for the prediction of factor of safety of soil slope.