1 Introduction

Understanding the complex physics of turbulence in high-speed flows is critical to enable the prediction of aerothermodynamic loads on hypersonic vehicles. This is already a challenging task, and the presence of shock waves adds significant complexity to the problem. Shock wave/turbulent boundary layer interactions (SWBLIs) are a common example of this combination of phenomena that occur for many hypersonic vehicle geometries. SWBLIs are characterized by the unsteady separation of the boundary layer and increased turbulence fluctuations (Smits and Dussauge 2006; Clemens and Narayanaswamy 2014).

Experimental measurements of the flow velocity in high-speed turbulent flows, and SWBLI in particular, are necessary to fully characterize the complex phenomena that are present. Two of the most common velocimetry techniques for fluid flows are laser Doppler velocimetry (LDV) (Tropea 1995) and particle image velocimetry (PIV) (Raffel et al. 2018). Both of these methods rely on seeding the flow with small tracer particles, which are assumed to faithfully follow the flow. It has been demonstrated, however, that this assumption can fail in low-density flows with large velocity fluctuations, such as turbulent hypersonic flows (Melling 1997; Loth 2008), flows with sudden velocity changes due to shock waves (Williams et al. 2015), and supersonic-nozzle flows (Huffman and Elliott 2009).

Tagging velocimetry (TV) methods are an alternative to LDV and PIV for high-speed flows (Koochesfahani and Nocera 2007), and have been applied in low-speed flows in liquids as well (Park et al. 2000; Fort et al. 2020). Instead of seeding the flow with small solid or liquid particles, TV tracks the fluorescence of excited molecules (or atoms) in the flow. The excited molecules/atoms can be native, seeded, or synthesized, and because the tracer is a gas, or a dye that’s been dissolved into a liquid, there are no issues associated with particle lag as there are for LDV and PIV in high-speed flows. A multitude of TV methods exist depending on the excited species and the method of excitation. Although the experimental details can be quite different for the various TV techniques, the resulting images are similar and so the processing methodology presented in this work could be applied to data from any TV method with minimal modifications. Much like PIV, TV methods produce an initial (“write”) image and a second (“read”) image of the excited gas molecules separated by a short time interval \(\Delta t\). The displacement of the molecules is determined from the image pair, and it is interpreted as a velocity by dividing by the prescribed \(\Delta t\).

The specific TV method exemplified in this work is Krypton Tagging Velocimetry (KTV). First demonstrated by Parziale et al. (2015), KTV excites krypton atoms in a mixture of nitrogen and krypton. Typically, the krypton concentration is low, on the order of 1%, so that the flow can be considered pure nitrogen; any small changes in transport properties may be easily calculated. Krypton atoms are excited using a laser, or more commonly, a single laser beam that has been split into several beams using a microlens array. The beams can be arranged into a variety of patterns, depending on the desired application, but the most widely used to date has been a series of parallel lines orthogonal to the principal flow direction. Only the component of velocity perpendicular to the lines is measured with this type of arrangement, and the method is referred to as KTV-1D. The current state of the art for computing the displacement of the lines in KTV-1D is described by Mustafa et al. (2019). The process is somewhat involved and consists of first finding the centers of the lines in each row of the read and write images by fitting a Gaussian profile to each line, and then computing the displacement of each line center row-by-row between the read and write images. While the produced velocity results are accurate, the procedure involves a significant amount of manual effort and is somewhat slow and painstaking.

Instead of arranging the lines parallel to one another, they can instead be formed into two sets of parallel lines that are oriented at opposite angles to one another such that they cross, forming a set of diamond-shaped intersections (cf. Fig. 2). In theory, this allows both of the in-plane components of the velocity to be measured instead of just the component perpendicular to the lines in KTV-1D. The image data from the resulting two-dimensional KTV (KTV-2D) method are substantially more difficult to analyze in order to extract velocity information compared to KTV-1D, however. Mustafa et al. (2018) use a complex procedure to identify the points of intersections in the grids in the write and read images, and then calculate the displacements by cross-correlation. One velocity vector is produced for each intersection that can be clearly identified in both the write and read images. Besides the complexity of the procedure and the requirement for manual inspection of the data, spatial resolution is sacrificed because much more information concerning the displacement of tracers (and hence velocity) is present in the images than is extracted by calculating only the displacement of the points of intersection on the grids. Other researchers have also sought solutions to finding the translation of grid intersections. This includes the peaking-finding algorithms (Hill and Klewicki 1996), “spatial correlation technique” from Gendrich and Koochesfahani (1996) and Bathel et al. (2011), the “template matching method” from Ramsey and Pitz (2011), the “Hough transform method” from Sánchez-González et al. (2015), and most recently, the work of Pearce et al. which provides continuous flow displacement determinations by parameterization of the entire tagging velocimetry grid (Pearce et al. 2021). The method of Pearce et al. is able to determine displacements along the grid lines as well as at intersection locations for 2D grids, and has shown the potential for automation. Additionally, researchers have used gradient-based optical flow estimation techniques that have incorporated a volumetric model of the liquid in a microchannel to account for non-ideal effects unique to studying microfluidics (Garbe et al. 2008; Brunet et al. 2013).

A potential improvement on these methods is to analyze the 1D or 2D TV images with wavelet-based optical flow velocimetry (wOFV). wOFV is a method that uses optical flow to determine displacements between image pairs in fluid flows. It is applicable to any type of image, so long as they have identifiable features that are displaced by the flow. It has been successfully applied to particle images, such as those produced by PIV (Schmidt and Sutton 2019, 2020; Schmidt et al. 2020; Schmidt and Sutton 2021), as well as continuous scalar images in a simulated two-dimensional flow (Schmidt et al. 2019). wOFV computes displacements by assuming the conservation of brightness (intensity) between images in an image pair and computing a two-dimensional displacement field that minimizes the difference between the image intensities. It is a so-called “dense” velocimetry method, meaning that it produces one velocity vector at each pixel in the images. It is noted that the accuracy at each pixel is not necessarily the same, as it depends strongly on the local image properties, particularly the image intensity gradient. In regions where the magnitude of the gradient is small, the computed velocity is strongly informed by neighboring regions. This allows spatial turbulence spectra and derivative quantities, such as divergence, vorticity, and strain rate to be calculated directly.

wOFV analysis has the potential to extract substantially more information from the write and read images for KTV-2D than previous approaches because it can use entire lines of the excited krypton which make up the grid rather than just the intersection points of lines. Furthermore, it obtains velocity information in the immediate vicinity of intersection points, rather than a single vector at the center of the intersection, because the intersection occupies several pixels in the write and read images. This could allow the computation of quantities such as vorticity at the intersection points, which would be of substantial value in understanding the turbulence characteristics in this flow. wOFV also is an automated procedure, much like PIV algorithms, requiring minimal input from the user and hence substantially simplifying the workflow for processing both 1D and 2D TV images.

The objectives of this paper are to present wOFV as a method to process both 1D and 2D TV images, with a particular emphasis on 2D, and to evaluate its performance. We first present results from a KTV-2D experiment of a SWBLI. Experimental images are processed using the cross-correlation-based method of Mustafa et al. (2018) and with wOFV, and the resulting velocity data are compared. We then present simulated data for both 1D and 2D TV on a turbulent boundary layer and quantify the performance of wOFV to demonstrate its capabilities and assess its limitations.

2 Methods

2.1 Experiment

The experimental data in this work comes from the application of KTV-2D to a SWBLI in a Mach 2.75 flow with a 24\(^\circ\) compression corner. The KTV-2D method generates images to compare over a known time interval by seeding the flow with krypton and exciting the atoms with a grid of tunable laser light, as formed from a beam splitter and a microlens array. The beams enter the test section in the same plane and are oriented at \(\pm 20^\circ\) relative to the vertical axis with a spacing of approximately \(0.1\delta\) in the direction normal to the beams. The beams have an apparent width of 7–8 pixels in the write image. As the krypton is excited, the write image is captured. A short time after the write image is taken (500 ns in this case), the same krypton particles are re-excited by the read laser and the read image is captured. Based on the displacement of the line crossings of the grids, the velocity at various points in the flow field can be determined. We note KTV (-\(1\)D and -\(2\)D) has been performed in many different flows (Zahradka et al. 2016; Mustafa et al. 2017; Mustafa et al. 2018; Mustafa et al. 2019; Shekhtman et al. 2021), with recent improvements in the signal-to-noise ratio (SNR) with advanced write/read strategies (Mustafa and Parziale 2018; Mustafa et al. 2019; Shekhtman et al. 2020) and repetition rate with advanced laser technology (Grib et al. 2019, 2020, 2021).

The experiments were performed in the AEDC Mach 3 Calibration Tunnel (M3CT) in Silver Spring, MD. The tunnel is comprised of a large vacuum tank attached to a converging-diverging nozzle (schematic in Fig. 1; more detail can be found in Zahradka et al. (2016). A flexible isolation bag was added upstream of the orifice to contain the 99% N\(_2\)/1% Kr gas mixture. The flexibility ensured that the mixture stayed at constant ambient pressure. A valve is cycled downstream of the nozzle to run the tunnel. Wind tunnel conditions are listed in Table 1.

Table 1 \(M_\infty\), \(P_\infty\), \(T_\infty\), \(\rho _\infty\), Re\(^{\mathrm{unit}}_\infty\), Re\(_\Theta\), and \(U_\infty\) are the Mach number, pressure, temperature, density, unit Reynolds number, momentum-thickness Reynolds number, and velocity for each experiment
Full size table
Fig. 1
figure 1

Schematic of KTV-2D experimental setup. PDG is pulse-delay generator

Full size image

The experiment was performed using two tunable lasers to provide the 214.7 nm (write) and 769.5 nm (read) laser beams required for KTV. The write laser consisted of a frequency doubled Quanta Ray Pro-350 Nd:YAG laser and a frequency tripled Sirah PrecisionScan Dye Laser. The Nd:YAG laser pumped the dye laser with 1000 mJ/pulse at a wavelength of 532 nm. The dye in the laser was DCM with a dimethyl sulfoxide (DMSO) solvent, and the laser was tuned to output a 644.1 nm beam. Frequency tripling of the dye-laser output was performed using Sirah tripling optics (THU 205).

The write laser beam setup can result in approximately 10–13 mJ/pulse; however, approximately 7 mJ was used for this experiment by reducing the Nd:YAG pump-laser power. The wavelength was 214.7 nm, with a linewidth of approximately 0.045 cm\(^{-1}\), a pulsewidth of approximately 7 ns, and a repetition rate of 10 Hz. The write-laser beam was split into two beams with a beam splitter designed for use with a 193 nm excimer laser (Lambda Research XPR-SWI-4002U-50R-193-45U). To evenly split the laser beams, the beam-splitter mount was rotated slightly about the vertical axis. The two beams were directed into the test section with 1 inch 5th-harmonic Nd:YAG laser mirrors (IDEX Y5-1025-45) and focused to several narrow waists in the test section with a \(f=100\) mm fused-silica microlens array (SUSS MicroOptics Nr. 18-00127) to form the lines in the streamwise direction and a \(f=100\) mm fused-silica cylindrical lens to focus the lines in the spanwise direction. Neglecting losses from the mirrors, lenses, and windows, we estimate that the energy per write line is approximately 300 µJ/pulse.

The read laser consisted of a frequency doubled Quanta Ray Pro-350 Nd:YAG laser and a Sirah PrecisionScan Dye Laser. The Nd:YAG laser pumped the dye laser with 215 mJ/pulse at a wavelength of 532 nm. The dye in the laser was Styryl 8 with a DMSO solvent, and the laser was tuned to output a 769.5 nm beam.

The read laser beam setup resulted in approximately 5 mJ/pulse, with a wavelength of 769.5 nm, a linewidth of approximately 0.025 cm\(^{-1}\), a pulsewidth of approximately 7 ns, and a repetition rate of 10 Hz. The read laser beam was directed into the test section using 2 inch broadband dielectric mirrors (Thorlabs BB2-E02), and expanded to a beam of \(\approx 40\) mm diameter with a \(f=-400\) mm fused silica cylindrical lens. This “read beam” re-excites the metastable krypton tracer atoms so that their displacement can be measured.

The laser and camera timing are controlled by a pulse-delay generator (SRS DG645). The intensified camera used for all experiments is a 16-bit Princeton Instruments PIMAX-4 \(1024\times 1024\) with an 18-mm grade 1, Gen III extended red filmless intensifier with P46 phosphor (PM4-1024i-HR-FG-18-P46-CM). The lens used is a Nikon NIKKOR 24–85 mm f/2.8-4D in “macro” mode and positioned approximately 200 mm from the write/read location. Two high-precision 800 nm long-pass filters (Thorlabs FELH0800, transmission of 3.5e-4% at the read-laser wavelength of 769.5 nm) are placed in series between the lens and the intensifier to minimize the noise resulting from the read-laser pulse reflection and scatter from solid surfaces. The gain is set to 100% with no pixel binning and only recording the read images to ensure a 10 Hz frame rate. A set of write images were recorded with the tunnel off prior to each run. The camera gate was opened for 50 ns immediately following the read-laser pulse to capture the spontaneous emission of \(5p[3/2]_1 \rightarrow 5s[3/2]_{1}^{\text {o}}\) (829.8 nm) transitions.

2.2 Optical flow method

Optical flow is a well-known problem in computer vision that involves computing the motion of objects in an image sequence. Optical flow belongs to the class of ill-posed inverse problems and is typically solved by minimizing a constrained equation to yield the displacement field over the entire image domain. While solutions were originally formulated to resolve the motion of rigid objects in a scene following the seminal work of Horn and Schunck (1981), optical flow methods have since been applied to fluid flows (Tokumaru and Dimotakis 1995; Yuan et al. 2007; Corpetti et al. 2002, 2006; Chen et al. 2015; Liu and Shen 2008; Liu 2017; Cai et al. 2018). In these applications, optical flow solves for the displacement between two images separated by a known time interval \({\Delta } t\) of some flow tracer. The time interval allows the displacement to be interpreted as velocity, and optical flow methods for fluid flow velocimetry are called optical flow velocimetry (OFV) methods. The flow tracer can be particles illuminated by a laser sheet as in PIV, a fluorescent dye or chemical species (i.e., PLIF), or some other flow marker.

OFV methods typically solve some version of a displaced frame difference (DFD) equation, given by

$$\begin{aligned} I_0 \left( {\underline{x}} \right) - I_1 \left( {\underline{x} + \underline{u} \left( {\underline{x}} \right) {\Delta }t} \right) = 0. \end{aligned}$$
(1)

\(I_0\) and \(I_1\) are the first and second images in an image pair, pixel locations are represented by \(\underline{x}\), and the unknown two-component velocity field is \(\underline{u} \left( {\underline{x}} \right)\). This equation simply states that, under stable lighting conditions, the only differences between \(I_0\) and \(I_1\) are due to the transport of image intensity, or brightness, by \(\underline{u}\). Equation (1) has been shown to be equivalent to that of transport of a passive scalar in fluid mechanics by Liu and Shen (2008). As mentioned above, Eq. (1) is typically solved by forming a minimization problem and employing some constraint on the velocity field because of the ill-posedness of the inverse problem. Many forms of the constraint have been employed, depending on the application, but most penalize first- or second-order derivatives of the velocity field.

A subset of OFV methods are wavelet-based OFV, or wOFV methods (Kadri-Harouna et al. 2013; Dérian et al. 2013; Dérian and Almar 2017; Schmidt and Sutton 2019, 2020; Schmidt et al. 2020; Schmidt and Sutton 2021). wOFV methods apply an implicit constraint on the velocity field by solving for the wavelet coefficients of the velocity field \(\underline{\psi }\), instead of the velocity field directly, and enforcing a degree of sparsity on the wavelet decomposition. The resulting minimization equation is

$$\begin{aligned} \hat{\underline{u}} = \underset{\underline{\psi }}{\mathrm {argmin}} \; \; J_D \left( {I_0,I_1,\underline{\psi }} \right) + \lambda J_R \left( {\underline{\psi }} \right) . \end{aligned}$$
(2)

\(J_D\) is a data term based on Eq. (1) that penalizes mismatch between the first image \(I_0 \left( {\underline{x}} \right)\) and a warped second image \(I_1 \left( {\underline{x} + \underline{u} \left( {\underline{x}} \right) {\Delta }t} \right)\), \(J_R\) is a regularization term that forces the solved velocity field to exhibit fluid-like motion by imposing smoothness in an analogous way to viscosity, and \(\lambda\) is a scalar parameter that balances the two terms. Further details on the wOFV algorithm applied in this work are given by Schmidt and Sutton (2020, 2021).

An important feature of OFV methods in general is that, unlike cross-correlation-based approaches or explicit feature tracking methods such as particle tracking velocimetry, OFV methods determine the velocity field that minimizes the mismatch between successive images holistically over the entire image domain. Hence, OFV can be best thought of as pattern matching method, and can accurately determine motion anywhere where the image intensity gradient is sufficiently large in magnitude. Furthermore, the explicit regularization term \(J_R\) used in Eq. (2) in the present work allows the estimation of velocity in regions with small intensity gradients, as long as they are close enough to regions with large intensity gradients. How close they must be depends on the value of \(\lambda\), with larger values increasing the maximum allowable distance but also smoothing the gradients in the estimated velocity field and hence potentially sacrificing resolution of small flow features. This facet of wOFV is demonstrated on tracer particle images by Schmidt et al. (2021)]. In the present application, this means that wOFV may produce accurate results even in the regions between 2D TV write lines, if the line spacing is sufficiently small. This is explored in Sect. 3.4. An important caveat, particularly in the case of high-speed flows, is that large values of \(\lambda\) result in greater smoothing in regions with poor image intensity information, which means that the ability to resolve features with sharp velocity gradients, such as shock waves and the near-wall region of boundary layers, is reduced.

2.3 Image preprocessing

For optimal processing with wOFV, the write and read images should be as similar as possible. Ideally, the only difference between them should be displacement produced by the flow, consistent with Eq. (1). Unlike the write images, the read images in tagging velocimetry methods cannot be averaged to boost SNR, and so their quality is somewhat poor compared to the write images. This necessitates substantial image pre-processing of the read images to apply wOFV. In this work, the read images are processed by a series of steps which (1) denoise the images by smoothing the gradients in image intensity over the image via total variation regularization (TVR) using the Rudin–Osher–Fatemi (ROF) method (Rudin et al. 1992), (2) normalize the intensity along the height of the image (y-axis) to more closely match the write image intensity profile, and (3) set all pixels below a minimum light intensity threshold to zero. This process balances eliminating noise with losing as little information as possible in the form of pixel intensities.

TVR is a variational image denoising method that is based on a total variation prior. In the ROF method, image denoising is performed according to Eq. (3) (Rudin et al. 1992)

$$\begin{aligned} {\hat{I}} = \underset{{\hat{I}}}{\mathrm {argmin}} \; \; \frac{1}{2} \Vert I - {\hat{I}} \Vert _2^2 + \sigma J ({\hat{I}}) \end{aligned}$$
(3)

\({\hat{I}}\) is the denoised version of the original image I, \(\sigma\) is a scalar parameter that balances the first term, which penalizes differences between I and \({\hat{I}}\), with the second term J, which is a prior function that enforces some degree of smoothness on \({\hat{I}}\) to reduce noise. The total variation prior has the form

$$\begin{aligned} J({\hat{I}}) = \int \Vert \underline{\nabla }{\hat{I}}\Vert \, \mathrm {d}\underline{x} . \end{aligned}$$
(4)

The total variation prior preserves edges in the image while reducing fine-scale noise. The minimization of Eq. (3) is performed using an efficient gradient descent algorithm. The smoothing parameter \(\sigma\) is currently tuned using a manual process, based on qualitative image inspection. A balance is sought between reduction in image noise in the image regions away from the read lines and over-smoothing of the lines. Quantified metrics of the processed image may be analyzed in the future to automate the denoising procedure.

An example processed write, unprocessed read, and processed read image set from this experiment are shown in Fig. 2a, b, and c, respectively.

Fig. 2
figure 2

Example a write, b raw (unprocessed) read, and c processed read image used for wOFV analysis. \(\delta\) is the boundary layer thickness measured in a separate experiment with schlieren imaging, and the point \(\left( {x,y} \right) = \left( {0,0} \right)\) is defined as the tip of the compression corner. \(\delta\) = 10 mm

Full size image

The write and processed read image pairs were analyzed with wOFV to determine the flow velocity field for each time instance. Data from individual image pairs, as well as ensemble quantities such as the mean velocity and vorticity, can then be calculated for the flow.

3 Results and discussion

This section is divided into two parts. In Sect. 3.1, images from the KTV-2D experiments of the turbulent SWBLI described in Sect. 2.1 are analyzed using wOFV and cross-correlation. Subsequently, in Sect. 3.2, simulated KTV-1D and -\(2\)D images are advected by velocity fields from a direct numerical simulation (DNS) of a flat plate turbulent boundary layer, and the resulting “read” and “write” image pairs are used to compute a velocity field with wOFV. The accuracy of wOFV is assessed by comparing the computed velocity fields against the true fields from the DNS.

3.1 Experiment

The velocity field was computed for a set of 354 read images from the experiment described in Sect. 2.1. The images are cropped to the region shown in Fig. 2, which is \(623 \times 521\) pixels, and a velocity vector is computed at each pixel. The instantaneous velocity field from the write and read images shown in Fig. 2 is shown in Fig. 3. The excitation lines from the write image are overlaid to aid the eye. The velocity magnitude is represented by the coloration, and individual velocity vectors are shown in green. The vectors are sub-sampled by a factor of 20 in both directions for clarity. The wOFV method produces velocity vectors even where there are no excited krypton atoms, so there is ambiguity at those points when considering only the image intensity data, because perturbations to the value of \(\underline{u} \left( {\underline{x}} \right)\) in Eq. (1) do not produce significant variations in the intensity mismatch between the read and write images at these locations. Velocities at these points are computed instead by enforcing smoothness on the velocity field via \(J_R\) in Eq. (2), because changes to \(\underline{u} \left( {\underline{x}} \right)\) will more strongly impact \(J_R\) at these locations than \(J_D\). The balance of the magnitude of these two terms depends both on the local intensity pattern around each pixel location \(\underline{x}\), specifically whether or not the magnitude of \(J_D\) changes appreciably when the velocity is perturbed during the computation of the solution, and the value of the scalar regularization parameter \(\lambda\). In practice, \(\lambda\) is always small enough that points near locations with large image intensity gradients, i.e., near the write lines, that \(J_R\) does not appreciably contribute to the estimation of \(\underline{u} \left( {\underline{x}} \right)\), and so the estimated velocity is effectively only influenced by the deformation of the lines. While erroneous away from the region in the bottom-center of the image, where there are no lines or intersections, the correct qualitative trend for a turbulent boundary layer of decreasing velocity as one moves downward toward the wall is observed where the density of lines and intersections is high, \(0.25< y/ \delta < 1\) and \(-0.5< x/ \delta < -0.1\).

Fig. 3
figure 3

An instantaneous velocity field of the flow generated by the wOFV method. The excitation lines from the write image are shown overlaid on the velocity field to aid the eye. Coloration represents the velocity magnitude, and sub-sampled velocity vectors are shown in green. \(\delta = 10\,\mathrm{mm}\)

Full size image

The mean velocity field \(\bar{\underline{u}}\) can be computed from the instantaneous velocity fields \(\underline{u}\), and the result is compared to the mean velocity field computed using the previous methodology of Mustafa et al. (2018) in Fig. 4a. Only data from the valid intersection points as determined by the analysis of Mustafa et al. are shown for both methods for easier comparison. Good agreement is observed between the two processing approaches, indicating that the vectors produced by wOFV, at least at the points of intersection, are as reliable as those computed by direct cross-correlation. The mean of the magnitudes of the vectors of the difference between the processing methods is 44 m/s, with a standard deviation of 34 m/s, and the mean relative difference (compared to the magnitudes of the vectors computed with correlation) is 9.9% with a standard deviation of 8.0%.

Fig. 4
figure 4

a Mean, b, instantaneous, and c fluctuating velocity fields produced by the previous correlation-based approach (Mustafa et al. 2018) and the present wOFV results. The edge of the 24\(^\circ\) compression corner is shown as a solid black line in the lower-right of the figure, and the estimated shock position, determined by schlieren imaging, is shown as a dashed line. Vectors in a and b represent velocity magnitudes 4 times larger than ones of equivalent length in c. \(\delta =10\,\mathrm{mm}\)

Full size image

More interesting are the fields of instantaneous and fluctuating velocity \(\underline{u}^\prime = \underline{u} - \bar{\underline{u}}\), which are shown for time instance represented by Figs. 2 and 3 in Fig. 4b and 4c, respectively. The vectors for \(\underline{u}^\prime\) in Fig. 4c have been lengthened by a factor of 4 relative to Fig. 4a and b to aid visualization. While the instantaneous velocity fields again show good agreement, and there is agreement between wOFV and cross-correlation at a few points for the velocity fluctuations, significant differences are observed between the two methods in general for \(\underline{u}^\prime\). The mean of the magnitude of the difference vectors when comparing the instantaneous velocity \(\underline{u}\) is 103 m/s, and the standard deviation is 48 m/s. The mean relative difference is 26% with a standard deviation of 21%. The mean difference vector magnitude for \(\underline{u}^\prime\) is similar: 72 m/s with a standard deviation of 56 m/s, which corresponds to a much larger relative difference: 130% with a standard deviation of 95%.

It is not especially surprising that the disagreement in the velocity fluctuations is larger than in the mean velocity, as the fluctuating streamwise velocity \(u^\prime\) and especially the wall-normal velocity \(v^\prime\) are challenging to measure accurately in turbulent boundary layers, particularly for compressible flows. Given the small number of samples, lack of convergence of the mean velocity may also be a contributing factor to the disagreement. Without further study, either using experiments in a well-characterized flow such as an incompressible turbulent boundary layer on a flat plate, or using synthetic data where the true instantaneous velocities are known, it is not possible to determine which velocimetry algorithm produces more accurate results. The accuracy of wOFV on 2D TV images, including at locations some distance from the laser line intersections, is assessed quantitatively in the next section.

3.2 Synthetic data

To quantify the performance of the wOFV algorithm on TV images, synthetic 1D and 2D TV images were produced and advected using velocity fields from a DNS of a turbulent boundary layer. The DNS data was retrieved from the Johns Hopkins Turbulence Database (JHTDB) (Perlman et al. 2007; Li et al. 2008), and the specific data set used was the “Transitional Boundary Layer” (Zaki 2013). Details regarding the simulation can be found on the JHTDB website. The simulation is of a flat-plate boundary layer that is initially laminar but becomes turbulent as the flow proceeds downstream. Two-dimensional snapshots of the velocity field are retrieved for \(0.891 L< x < 0.947 L\) and \(0< y < 0.0225 L\) where x is the streamwise coordinate, y is the wall-normal coordinate, and L is the length of the plate in the simulation, for four spanwise locations equally spaced with \({\Delta } z = 0.571 L\) for 500 time instances, equally spread throughout the time domain of the simulation, which is \(t_\mathrm {max} = 1.12 \frac{L}{U_\infty }\). These locations are in the fully turbulent region of the simulation, which is \(x > 0.525 L\). The Reynolds number based on x at the start of the snapshot is \(7.49 \times 10^5\), and the 99%, displacement, and momentum thicknesses at that location are \(1.4 \times 10^{-2} L\), \(2.3 \times 10^{-3} L\), and \(1.5 \times 10^{-3} L\), respectively. The resulting 2000 velocity fields are discretized into 512 points in the x and y directions. The 99% boundary layer thickness \(\delta\) is used throughout the following sections to normalize spatial coordinates. In the present simulations, \(\delta\) is approximately equal to 325 pixels, which is similar to the resolution in the experiments in Sect. 3.1 where \(\delta \approx 360\) pixels. Simulated TV images are advected by each of these fields according to Eq. (1) using two-dimensional spline interpolation and symmetric boundary conditions.

3.3 1D line images

Simulated 1D TV write images with a resolution of \(512 \times 512\) pixels were created using a set of vertical lines with Gaussian intensity profiles. The standard deviation was specified to be 3 pixels, to approximate the experimental images in Sect. 2.1, and those from previous studies (Zahradka et al. 2016; Mustafa et al. 2019). All 2000 DNS velocity fields are applied to a noise-free write image to produce 2000 corresponding read images, with a simulated \({\Delta } t\) such that the inter-frame displacement due to the free stream velocity is 7 pixels. The full two-dimensional velocity fields are used to advect the lines in the write images, but only the horizontal component of the velocity fields are used for comparison since wOFV can only provide an estimate of the velocity in the direction orthogonal to the write lines. To quantify the effect of noise on the velocity estimations, random Gaussian noise was independently applied to separate copies of all of the write and read images, resulting in sets with signal-to-noise ratios of infinity (i.e., noise-free), 17, 11, 5, and \(-1\) dB. Using the peak-to-peak quantification of SNR common in the TV literature, e.g., in Ref. (Gendrich and Koochesfahani 1996), these values correspond approximately to SNR values of 26, 13, 6.5, and 3.2. The SNR in the experimental data in Sect. 3.1 is estimated to be between 5 and 10 dB. Example write images are shown in Fig. 5. \(\delta\) is the 99% boundary layer thickness measured at \(x=0\), which is the location of a central write line, corresponding to \(x = 0.917 L\) in the simulation domain.

Fig. 5
figure 5

Example write images with varying levels of added noise, \(\delta\) is the 99% boundary layer thickness at \(x=0\)

Full size image

The mean and RMS horizontal velocity profiles computed from the wOFV results for each noise level are compared against the true profile for the line at \(x = 0\) in the images in Fig. 6a and b, respectively. All profiles computed with wOFV agree very closely with the true result for the mean, and the RMS profiles are similar as well, particularly for image noise levels above 5 dB. Profiles are plotted against \(y^+\), the distance from the wall normalized by the friction length scale \(\delta _\nu\). For these images, each pixel represents approximately \(4 \delta _\nu\).

Fig. 6
figure 6

Calculated a mean and b RMS velocity profiles for the line at \(x = 0\) depicted in Fig. 5 for each noise level, compared against the true profiles

Full size image

The relative error in each metric is computed as a function of \(y^+\) and is shown in Fig. 7. These data quantify the evaluations made from Fig. 6. Except for very close to the wall (\(y^+ \lesssim 100\)), the error is approximately 1% in the mean for all noise levels, and is under 0.1% in the noise-free limit. The relative error in the RMS is higher, approximately 10% for low to moderate noise and under 1% in the noise-free limit. It is furthermore noted that the wOFV solution is largely independent of the SNR, as long as it is above 5 dB. The relative error is high close to the wall for two reasons. First, the true local velocity becomes small, so the relative error increases significantly for small absolute errors. Second, there are very few pixels in the viscous layer, and the velocity gradient is very high in the near-wall region. The condition \(\underline{u} = 0\) at \(y=0\) is not strictly enforced during the computation of velocity, so wOFV is unable to fully resolve the velocity profile within a few pixels of the wall. Other techniques such as PIV suffer from this same effect, except it is worse for PIV because of the finite size of interrogation windows.

Fig. 7
figure 7

Relative error in the a mean and b RMS velocity profiles shown in Fig. 6 for each noise level

Full size image

Turbulence statistics are also extracted from the wOFV results for the full set of lines in the write and read images. The streamwise correlation coefficient \(R_{11}\) at \(y = 0.2 \delta\) and the two-dimensional contours of correlation of the streamwise velocity are shown in Fig. 8a and b, respectively. Each are mean results for the entire 2000-sample data set. Similar to the results for the mean and RMS of the streamwise velocity, the calculated correlation coefficient curves are very close to the true profile for SNR levels above 5 dB. Specifically, the magnitude of the error in the correlation coefficient \(R_{11}\) is less than 0.05 at all write line locations. This is true for the contours of correlation as well, where the curves are observed to be essentially coincident for all but the lowest SNR. These results indicate that wOFV produces sufficiently accurate results to construct statistical turbulence quantities with confidence, with the key advantage of ease of use and repeatable, automated processing compared to more manual methods in the literature for 1D TV data.

Fig. 8
figure 8

a Streamwise correlation coefficient \(R_{11}\) at \(y=0.2 \delta\) for each noise level. b Contours of correlation of the streamwise velocity for each noise level

Full size image

3.4 2D line images

In addition to the 1D TV write images produced and analyzed in the previous section, sets of 2000 write images were produced with simulated 2D TV lines in crossing patterns similar to the experimental images shown in Fig. 2. Unlike 1D TV images, 2D TV images potentially offer the possibility to not only measure both of the in-plane components of the velocity field distributed across the image, but also to acquire derivative quantities such as the out-of-plane component of vorticity, and hence could be considered to be analogous to PIV in terms of the data produced. The accuracy of a full-frame velocity field estimation from 2D TV images, particularly at points between line intersection locations, is likely sensitive to the line inclination and spacing. Therefore, a test matrix with varied line inclination angles of \(\pm 2^\circ\), \(\pm 10^\circ\), \(\pm 20^\circ\), \(\pm 40^\circ\), \(\pm 50^\circ\), and \(\pm 65^\circ\) to the vertical, and varied line spacings of \(0.05 \delta\), \(0.1 \delta\), and \(0.2 \delta\) (normal to the line directions) was created for evaluation. The inclination angle and line spacing in the experimental images are approximately \(20^\circ\) and \(0.1 \delta\), respectively. Different levels of noise were introduced to the set of images with a line inclination angle of \(\pm 20^\circ\) and a line spacing of \(0.1 \delta\) to assess the effects of imaging noise on the accuracy of velocity estimation, as these are most similar to the parameters in the experimental images in Sect. 3.1. A subset of these synthetic images is shown in Fig. 9.

Fig. 9
figure 9

Example synthetic 2D TV write images for various line spacings and inclination angles

Full size image

In addition, a set of 2000 simulated particle images, which represent what would be produced in a PIV experiment, were created and processed with a commercial cross-correlation-based commercial PIV software (TSI Insight4G) for comparison with the 2D TV images processed with wOFV. Simulated particle images were generated using the approach described by Schmidt and Sutton (2020). The particles have a mean diameter of 1 \({\mu }\)m with a standard deviation of 0.5 \({\mu }\)m, and the synthetic particle images are created assuming a magnification of \(M = 0.5\), a camera lens with f/4 and a pixel pitch of 4.5 \({\mu }\)m, using the formulations given by Adrian (1991). The projected particle diameter is 2–4 pixels, and the particle density is 0.25 particles per pixel, which results in 64 particles per final \(16 \times 16\) pixel interrogation window used in the PIV processing. Processing was performed with a multi-pass scheme with deforming interrogation windows and an initial window size of \(32 \times 32\) pixels, which is more than four times the maximum inter-frame particle displacement of 7 pixels. All of these parameters are well within the established experimental guidelines for PIV prescribed in several reference texts, e.g., Raffel et al. (2018), and have been demonstrated to produce optimal results for PIV processing in the literature (Schmidt and Sutton 2019).

As mentioned elsewhere in the paper, the ability of wOFV to resolve small turbulent structures and vorticity depends on the line spacing compared to the relevant length scales in the flow. The most relevant length scale is likely the scale of the large eddies, which can be approximated by the integral scale in isotropic turbulence, although this is a subject for investigation in future work. Such a definition is not as straightforward in boundary layers, where the turbulence scales vary with the wall-normal coordinate y. However, since the outer length scale in boundary layers has been observed to scale with the boundary layer thickness \(\delta\) (Pope 2001), we feel that \(\delta\) is an appropriate length scale to characterize the line spacing in the present work.

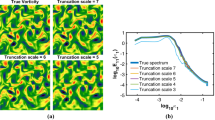
The error in the velocity and vorticity fields is shown in Fig. 10. Throughout the remainder of this paper, “vorticity” and the symbol \(\omega\) refer to the out-of-plane component of the vorticity vector, as this is the only component that can be computed from a two-dimensional velocity field. Errors are reported as the root mean square error (RMSE), which is defined as

$$\begin{aligned} \mathrm {RMSE}=\sqrt{\frac{1}{N} \sum \Vert \underline{u} - \underline{u}_\mathrm {true}\Vert ^2}. \end{aligned}$$
(5)

N is the number of points at which the error is evaluated. Equation (5) can be applied to the vorticity as well by replacing \(\underline{u}\) with \(\omega\). The data points in Fig. 10 represent the mean RMSE over an entire 2000-image set, and the errorbars represent the standard deviation for the set. The vorticity is normalized by the mean vorticity for a given instantaneous velocity field. It is observed from both the RMSE of velocity and vorticity that the accuracy increases as the line spacing is reduced, and the peak accuracy occurs for inclination angles close to \(45^\circ\). If the lines are close enough together, for instance, the \({\Delta }l = 5\% \delta\) case, the error in velocity is nearly insensitive to inclination angle.

Fig. 10
figure 10

Mean root mean square error (RMSE) in a velocity and b vorticity as a function of line inclination and angle for wOFV applied to TV images. Errorbars represent the standard deviation across a 2000-image set. The RMSE in velocity for simulated PIV data is also shown for comparison, as well as RMSE in the velocity field at intersections for a correlation-based approach. RMSE in \(\omega\) is normalized by the true mean vorticity for a given instantaneous velocity field

Full size image

Also shown in Fig. 10a is the RMSE for the correlation-based approach of Mustafa et al. (2018). As might be expected for noise-free images, the correlation results are highly accurate at the line intersection locations, although the accuracy of the two processing methods is very similar for small line spacing and inclination angles larger than 20\(^\circ\). It is also noted that the correlation procedure fails for the smallest line spacing of \({\Delta }l = 5\% \delta\), and for small line inclination angle. The correlation procedure also had a processing time of 10–100 times longer than wOFV when performed on the same images and the same machine. It is also noted that the vorticity cannot be directly calculated from the correlation results, because only one vector per line intersection is returned.

Several other, less intuitive conclusions are drawn from the data in Fig. 10. First, it is noted that both the estimated velocity and vorticity fields have approximately the same accuracy over the entire image as they do at the intersection points, except for \({\Delta } l = 20\% \, \delta\), for large enough line inclination angle. This is because, unlike other methods found in the literature, wOFV does not specifically identify or track lines or intersections. Rather, it matches patterns as a whole, which incorporates the motion of the spaces between lines just as strongly as the motion of the lines and intersections themselves. As the line spacing becomes small, the Gaussian tails of the line intensity profiles contribute small, but meaningful, image intensity information to the spaces between line centers, which improves the overall accuracy.

Second, wOFV applied to TV images is observed to be more accurate than correlation-based PIV applied to particle images for nearly all of the TV write patterns investigated. The RMSE in \(\omega\) for PIV is approximately 1.0, and so is not shown in Fig. 10b. There are several important caveats to this result, however. First, both the TV images and the particle images are noise-free, and wOFV has been observed to be more sensitive to noise than correlation-based PIV (Schmidt et al. 2021). Second, and more significantly, both the TV read images and advected particle images are produced by following Eq. (1), which exactly conserves image intensity at a pixel. Because Eq. (1) is also the equation that is used to estimate the velocity field in wOFV, creating the synthetic images in this way biases the result in favor of wOFV compared to PIV, which does not assume an explicit form of an intensity transport equation. Nonetheless, the results show that wOFV applied to TV images produces comparable accuracy to PIV, even in regions between write lines and intersections, particularly if the lines are closely spaced. Additionally, we speculate that wOFV would be especially effective in TV situations where dense grids can be made, as was done in Fort et al., where those researchers used Talbot-effect structured illumination (Fort et al. 2020).

The spatial distribution of the error magnitude is shown in Fig. 11. For larger line spacings (middle and bottom rows), the error is smaller in regions near the line intersections, and is around 1% of the free stream velocity, or about 0.07 pixels for the specified inter-frame displacement of this data set. For small line spacing, and when the line angle is closer to 45\(^\circ\), however, (upper right quadrant of Fig. 11) the pattern of the write image disappears from the error map, indicating that wOFV is equally accurate across the entire image domain. The output of the measurement becomes analogous to that of PIV in this case, and the uncertainty is independent of the write image pattern.

Fig. 11
figure 11

Mean error magnitude for the write line spacings and inclination angles shown in Fig. 9. The error magnitude has been normalized by the free stream velocity, which corresponds to a displacement of 7 pixels

Full size image

The mean accuracy of the velocity field is not the only quantity of interest, also significant is the ability to calculate derivative quantities such as vorticity. The true vorticity and the vorticity calculated with PIV for a single realization of the velocity field is shown in Fig. 12. Vorticity is computed from each velocity field by approximating partial derivatives using the MaxPol method (Hosseini and Plataniotis 2017a, b). It is observed that PIV under-resolves the true vorticity, which is a well-known effect of the multi-pixel interrogation windows used during PIV processing. The present results were computed using \(16 \times 16\)-pixel interrogation windows with 50% overlap, so the resolution is reduced by 8 pixels in each direction.

Fig. 12
figure 12

Vorticity for a single realization of a the true velocity field and b the velocity field computed with PIV. The magnitude of the vorticity has been normalized to the maximum magnitude of the true vorticity

Full size image

The vorticity computed for TV images using wOFV for each of the write image patterns shown in Fig. 9 is shown in Fig. 13, using the same color scale as Fig. 12. The accuracy of the vorticity calculations is observed to be most sensitive to the line spacing, with only a weak dependence on inclination angle. The vorticity fields for line spacings of \(10\% \delta\) and \(5\% \delta\) and inclination angles greater than \(20^\circ\) (i.e., the upper-right of Fig. 13) appear very similar to the true vorticity field, and appear qualitatively similar or superior to the PIV result. This finding indicates that 2D TV imaging, combined with wOFV, can be used more or less as a direct substitute for PIV in high-speed flows, without sacrificing spatial resolution or suffering a detriment to the ability to compute derivative properties of the velocity field, as long as the line spacing is sufficiently small and the SNR is sufficiently high.

Fig. 13
figure 13

Instantaneous vorticity fields for the write line spacings and inclination angles shown in Fig. 9

Full size image

Finally, results from adding noise to the synthetic 2D TV images are shown in Fig. 14. As for the 1D TV images, the RMSE for wOFV is relatively insensitive to moderate levels of noise, to a SNR of 5, and wOFV and correlation show similar accuracy over this range, with the correlation results slightly more accurate than wOFV (RMSE of approximately 0.033 compared to 0.040). For high levels of noise, the RMSE for wOFV increases and correlation fails to converge to a solution, demonstrating a higher level of robustness for wOFV compared to correlation-based approaches. Instantaneous vorticity fields for the wOFV results also are shown, and these can be compared qualitatively to the noise-free result in the central panel of Fig. 13. The vorticity fields are qualitatively similar that of the noise free limit for SNR values of 11 and 17, and the ultimate effect of noise in these cases is a low-pass filtering of the vorticity field compared to the noise-free results. Increased levels of noise degrade the quality of the vorticity field estimation, as expected.

Fig. 14
figure 14

Left: RMSE for synthetic noisy 2D TV images as a function of signal to noise ratio (SNR). Right: Sample vorticity fields for wOFV as a function of noise level, to be compared to the central panel of Fig. 13

Full size image

4 Conclusions

wOFV was applied in this work to two sets of tagging velocimetry (TV) image data to evaluate its performance. The first set of images were acquired in an experiment of a turbulent shock wave-boundary layer interaction in a Mach 2.75 free stream flow using KTV-2D. An image denoising procedure using total variation regularization (TVR) was applied to the experimental read images to boost the SNR and produce more reliable velocity estimations. Good agreement is observed between velocity estimations using wOFV and cross-correlation for the mean velocity field, but wOFV has several distinct advantages. First, as an automated process, wOFV is much simpler to implement and more adaptable than cross-correlation procedures commonly used in the literature, which require significant manual tuning to identify line intersection locations. Second, wOFV produces a velocity estimation at every point in the image domain, instead of only at line intersection points, and can therefore provide a more complete picture of the turbulent velocity field, as well as potentially enabling the straightforward computation of spatial turbulence spectra and derivative quantities such as vorticity. This advantage can only be realized if the spacing between lines is sufficiently small compared to the relevant turbulent length scale, as the accuracy of wOFV is dependent on the magnitude of the image intensity gradient in the neighborhood of the location at which each velocity vector is computed. Less agreement is observed between wOFV and cross-correlation for the velocity fluctuations, but it is unknown at this time which method is more accurate for this experiment.

A second set of synthetic data was produced to more robustly quantify the accuracy of wOFV applied to TV images. A set of velocity fields from a direct numerical simulation of a turbulent boundary layer was used to advect both 1D and 2D synthetic TV write images. Noise was added to the TV images to assess sensitivity, and it was found that for moderate noise levels such that the SNR is above 5 dB, the wOFV results are relatively insensitive to noise and produce very accurate estimations of the velocity profiles along the write lines as well as turbulence statistics. The chief advantage in this case for wOFV compared to methods from the literature is ease of use and less user-defined inputs, which leads to less ambiguity in the results.

The line spacing and inclination angle were varied in the synthetic 2D TV images to assess their effect on the accuracy of the wOFV estimations. It was found that wOFV produces results that are at least as accurate as PIV for this flow for small enough line spacings (\(<10\% \delta\)) and that the accuracy is less sensitive to line inclination angle, but increases as the angle approaches \(45^\circ\). The accuracy is found to be similar to direct cross-correlation of intersection locations using an advanced line-fitting procedure, except that wOFV is more robust to high levels of noise and more extreme line inclination angles and line spacings. Correlation was found to be more accurate than wOFV in the mean for low-noise images by about 25%. The velocity computed with wOFV is accurate across the entire image, however, not only at line intersection locations, which allows the vorticity to be computed directly. This suggests that, for configurations with closely spaced write lines, 2D TV coupled with wOFV can be substituted directly for PIV in high-speed flows, and the full 2D velocity field, as well as derivative quantities, can be measured with similar accuracy as what would result from PIV. Hence, wOFV offers an additional advantage to most state-of-the-art processing routines in the literature, besides those noted for 1D write images, namely the ability to accurately compute the velocity for the full image, rather than just at the line intersection locations, if the line spacing is sufficiently small.