Improvements in the accuracy of wavelet-based optical flow velocimetry (wOFV) using an efficient and physically based implementation of velocity regularization

Abstract

This manuscript details recent improvements in a wavelet-based optical flow velocimetry (wOFV) method that represents a more physically sound implementation and results in increased accuracy of the velocity estimation. A novel regularization scheme is presented that is based on penalization of directional derivatives of the estimated velocity field or more specifically, second-order penalization of the gradients of divergence and curl, which enforces realistic flow structure. The regularization is performed in the wavelet domain with symmetric boundary conditions for the first time using an alternative wavelet transform approach of matrix multiplications. The method for the computation of full two-dimensional wavelet transforms by a single pair of matrix multiplications is described and shown to be significantly more efficient than a lifting implementation or convolution in MATLAB. Velocity fields are estimated from synthetic tracer particle images generated from 2D DNS of isotropic turbulence and from experimental results from a turbulent flow. Results are compared to an advanced correlation-based PIV algorithm and previous advanced optical flow methods. The velocity results estimated with the new regularization scheme are shown to be more accurate and exhibit a significant reduction in non-physical small-scale artifacts compared to previous results. A significant result from the current method is the ability to generate 2D velocity field images that resolve the dissipative scales in high-Reynolds number, turbulent flows.

Graphic abstract

1 Introduction

Within fluid dynamics research, the visualization of the underlying velocity field and its derivatives yields critical insight into complex phenomena that govern how fluids are transported, how their interactions with immersed bodies will manifest, and how these various processes should be modeled. The most prominent flow visualization technique used to estimate velocity fields is particle image velocimetry (PIV) as described in many available reference texts, e.g. Adrian and Westerweel (2011) and Raffel et al. (2018). In PIV, tracer particles are added into the flow and illuminated with two successive laser pulses with a known time separation, ${\Delta }t$. Light emission from the particles (i.e., scattering or fluorescence) is collected on a camera(s) and the velocity is estimated by dividing the particle field displacements between the two acquired images by the known value of ${\Delta }t$.

The most common approach for determining particle displacement is through cross-correlation of sub-regions within the image domain known as interrogation windows. By finding the peak correlation between two interrogation windows across an acquired image pair, a vector characterizing the average particle displacement within a spatial region corresponding to the interrogation window is determined. This process is well established and there have been numerous advanced PIV correlation-based algorithms published; the discussion of which is beyond the scope of this manuscript. While correlation-based processing is well established, efficient, and robust; there are key limitations to the approach. Since one velocity vector is produced for each interrogation window, the velocity field estimate is “non-dense” and the spatial resolution of the PIV measurement is significantly lower than that of the detector (Kähler et al. 2012). The lower resolution of the cross-correlation-based PIV approach can have some unintended consequences including apparent removal of small-scale flow structure, inaccurate velocity estimates in high-gradient regions, and inaccurate estimations of derivative quantities such as vorticity and strain rate.

An alternative to cross-correlation-based PIV is optical flow motion estimation, first established for addressing rigid motion in the computer vision community (Horn and Schunck 1981), but more recently used for fluid dynamics applications to determine velocity (Liu and Shen 2008). When using optical flow approaches, velocities are determined at each pixel by assuming conservation of brightness (or intensity) from one image to another of a given deformable pattern. The temporal and spatial variations of intensity are used to infer the underlying motion by estimating the velocity that leads an image at time t to evolve to its state at $t+ {\Delta } t$. Recently, there have been many advanced optical flow methods presented that are well suited for the non-linear and multi-scale nature of fluid dynamics (e.g. Corpetti et al. 2006; Atcheson et al. 2009; Regert et al. 2010; Cassisa et al. 2011; Zillé et al. 2014; Chen et al. 2015; Liu et al. 2015; Cai et al. 2018). One particular approach for estimating the fluid velocity via an optical flow approach is to use wavelet transforms in the underlying analysis as first proposed by Wu et al. (2000), and further developed by Bernard (2001), Dérian et al. (2013), Kadri-Harouna et al. (2013), and Schmidt and Sutton (2019). Wavelet-based optical flow has some specific advantages over other optical flow methods, including the inherent multi-resolution analysis characteristic of the wavelet-based estimation strategy; decreased sensitivity to motion ambiguity since the velocity at each pixel is informed by velocity estimations at nearby pixels; and the ability to exploit properties of wavelet transforms to form physically meaningful regularization strategies as discussed in Kadri-Harouna et al. (2013) and in detail below.

Previous work by the current authors described a wavelet-based optical flow method for estimating velocity from pairs of tracer particle images in fluid flows (Schmidt and Sutton 2019). The work demonstrated increased accuracy and spatial resolution compared to a state-of-the-art correlation-based particle image velocimetry (PIV) method and provided recommendations for optimal values of two experimental parameters, particle seeding density and inter-frame displacement, specific to the optical flow method. The current manuscript outlines recent and significant improvements to the wavelet-based optical flow approach presented in Schmidt and Sutton (2019). Specifically, a more physically sound implementation of the regularization scheme is presented that results in increased accuracy of the velocity estimation. The regularization approach is facilitated through an alternative wavelet transform approach of matrix multiplications, which also is shown to be significantly more efficient than the conventional convolution or lifting approaches. The new wavelet-based optical flow approach is applied to synthetic particle images generated from DNS of isotropic turbulence and experimental results from turbulent flows. Results are compared to our previous methodology presented in Schmidt and Sutton (2019), as well as an advanced correlation-based PIV algorithm and other advanced optical flow methods.

2 Brief comments on nomenclature

Although not the primary purpose of the present manuscript, we would like to propose a re-framing of the nomenclature for optical flow methods for estimating velocity in fluid flows. As an alternative to exclusively referring to each optical flow method in the literature by name (e.g. WOF-X (Schmidt and Sutton 2019), Typhoon (Dérian and Almar 2017), DenseMotion (Corpetti et al. 2002), OpenOpticalFlow (Liu 2017), etc.), these methods should be referred to more broadly as optical flow velocimetry (“OFV”), much in the same way as various existing PIV algorithms are all referred to as “PIV.” In addition, a sub-class of OFV methods use a wavelet-based approach, such as the work by Wu et al. (2000), Dérian et al. (2013), Kadri-Harouna et al. (2013), and the previous work presented by Schmidt and Sutton (2019). Wavelet-based approaches utilize a sufficiently different strategy compared to “classical” OFV methods such that they can be referred to separately as “wavelet-based optical flow velocimetry” or “wOFV”. We believe that this re-framing is helpful both for discussing the broader field of OFV and for distinguishing OFV in the context of fluid dynamics measurements from the more classical and widely known applications of optical flow for rigid motion estimation in computer vision à la Horn and Schunck (1981).

3 Wavelet-based optical flow methodology

In our previous work, the wOFV method (referred to as “WOF-X” in Schmidt and Sutton (2019)) was used to estimate velocity from a pair of tracer particle images. Similar to almost all OFV approaches, the image intensity $I\left( \underline{x},t \right)$ is assumed to be conserved such that $I\left( \underline{x},t \right)$ follows an advection equation

$$\begin{aligned} \frac{\partial I\left( \underline{x},t\right) }{\partial t} + \underline{v} \left( \underline{x},t \right) \cdot \underline{\nabla }I \left( \underline{x},t \right) = 0, \end{aligned}$$

(1)

where $\underline{v} \left( \underline{x},t \right)$ is the fluid velocity. Assuming a constant velocity over the time interval between successive images, ${\Delta } t = t_1 - t_0$, Eq. (1) can be integrated in time to yield the displaced frame difference (DFD) equation

$$\begin{aligned} I_0 \left( \underline{x} \right) - I_1 \left( \underline{x} + \underline{v} \left( \underline{x} \right) {\Delta } t \right) = 0 \end{aligned}$$

(2)

and the velocity field $\underline{v}$ is determined through a minimization problem,

$$\begin{aligned} \hat{\underline{v}} = \underset{\underline{v}}{\mathrm {argmin}} \; \; J_D \left( I_0,I_1,\underline{v} \right) + \lambda J_R \left( \underline{v} \right) . \end{aligned}$$

(3)

In Eq. (3), $J_D$ is the data term, which is a penalty function formed from the discrepancy between $I_0$ and the motion-compensated image $I_1$:

$$\begin{aligned} J_D = {\mathcal {P}} \left[ I_0 \left( \underline{x} \right) - I_1 \left( \underline{x} + \underline{v} \left( \underline{x} \right) {\Delta } t \right) \right] . \end{aligned}$$

(4)

${\mathcal {P}}$ represents the functional form of the penalty function, which is a Lorentzian in the current work. $J_R \left( \underline{v} \right)$ is a regularization term that is convex and enforces some amount of smoothness on the velocity field; that is, $J_R$ allows the velocity field estimate to deviate from the constraints of intensity conservation within the data term. This allows elements of fluid physics to be introduced to the velocity estimation. $J_D$ and $J_R$ are balanced by a weighting parameter $\lambda$ that is often determined empirically, but as discussed in Schmidt and Sutton (2019), is determined semi-automatically in the current work.

As described in Schmidt and Sutton (2019), the underlying principle in wOFV is to not perform the minimization outlined in Eq. (3) over the velocity field $\underline{v}$, but to perform the minimization over its wavelet transform $\underline{\psi }$. In this manner, Eq. (3) becomes

$$\begin{aligned} \hat{\underline{v}} = \underset{\underline{\psi }}{\mathrm {argmin}} \; \; J_D \left( I_0,I_1,\underline{\psi } \right) + \lambda J_R \left( \underline{\psi } \right) , \end{aligned}$$

(5)

where $\underline{\psi }$ is the complete set of wavelet coefficients describing the velocity field and is related to the velocity field via

$$\begin{aligned} \underline{\psi } = \varPsi \left( \underline{v}\right) . \end{aligned}$$

(6)

and $\varPsi$ describes an operator representing a wavelet transform. For each image pair, an initial coarse scale, $S=C$, is selected and the algorithm proceeds to a chosen fine scale, $S=F$, subject to $L\le F-1$, where each square image is $2^F \times 2^F$ pixels. The wOFV algorithm used in the present work proceeds according to the following steps at each wavelet decomposition scale S, similar to that presented within Sec. 2.3 of Schmidt and Sutton (2019).

• 1. The wavelet transform of the velocity field from the previous (coarser) scale $\underline{\psi }_{S-1}$ is used to initialize the minimization algorithm.

• 2. Both the regularization term $J_R$ and its gradient $J_R^\prime$ are computed from $\underline{\psi }$ directly in the wavelet domain.

• 3. An estimate of the velocity field $\underline{v}$ is found by performing an inverse wavelet transform of the transformed velocity field $\underline{\psi }$.

• 4. The motion-compensated image $I_1 \left( \underline{x} + \underline{v} \left( \underline{x} \right) {\Delta } t \right)$ in Eq. (4) is computed using bi-cubic spline interpolation.

• 5. The objective function to be minimized in Eq. (5) is evaluated using $J_D$ and $J_R$.

• 6. The gradient of the motion-compensated image is computed using finite differences, which is then used to compute the gradient of the data term $J_D^\prime$.

• 7. $J_D^\prime$ is transformed into the wavelet domain by a forward wavelet transform. Recall that $J_R^\prime$ is computed in the wavelet domain directly in step 2.

• 8. The total objective function and its gradient (steps 5 and 7) are used by the minimization algorithm to obtain a new estimate of $\underline{\psi }$ at scale S and steps 2 through 7 are repeated until the objective function in step 5 is minimized.

The choice of the regularization term $J_R$ is an important component of OFV algorithms in the literature. For non-wavelet-based OFV methods, as well as classical optical flow methods used within the computer vision community, some form of convex regularization is necessary to close the minimization of Eq. (3), as it is ill-posed and under-determined without a regularization term. The most well-known regularization term for rigid motion problems is the first-order regularizer proposed by Horn and Schunck (1981):

$$\begin{aligned} J_R = \int \limits _\varOmega ||\underline{\nabla } v_1 ||^2 + ||\underline{\nabla } v_2||^2 \text {d}\underline{x}. \end{aligned}$$

(7)

This regularization is equivalent to a first-order Tikhonov regularization for generic ill-posed problems (Liu and Shen 2008; Tikhonov and Arsenin 1977) and has also been used in fluid dynamics applications, primarily for its simplicity (Liu et al. 2015). For wOFV methods, explicit regularization is not required since velocity estimates can be determined from truncated wavelet transforms as discussed in Dérian et al. (2013), Kadri-Harouna et al. (2013) and Dérian et al. (2012). In this case, the problem is either determined or over-determined and the truncation can inherently correct for local violations of the DFD equation. However, regularization has been shown to increase accuracy and typically is utilized. Higher order Tikhonov regularization terms also can be considered, and second- and third-order regularizers have been used in wOFV methods in the literature (Kadri-Harouna et al. 2013; Schmidt and Sutton 2019).

Corpetti et al. (2002) argue that the Horn-Schunck regularizer is inappropriate for OFV methods in fluid flows, since it penalizes important derivative quantities and excessively smooths out the physical structure of the flow. Instead, they propose a more physically sound, second-order “div-curl” penalty term, which penalizes the gradients of divergence and curl of the velocity field:

$$\begin{aligned} J_R = \int \limits _\varOmega ||\underline{\nabla } \left( \underline{\nabla } \cdot \underline{v} \right) ||^2 + ||\underline{\nabla } \left( \underline{\nabla } \times \underline{v} \right) ||^2 \text {d}\underline{x}. \end{aligned}$$

(8)

This regularization is consistent with the physical expectation of fluid flows, i.e. that divergence and vorticity form coherent structures, and has been shown to produce very good results for non-wavelet-based OFV methods by a number of researchers (Corpetti et al. 2002, 2006; Yuan et al. 2007). However, it is difficult to implement stably numerically, as the resulting Euler–Lagrange equation is quite complex.

Recently, other strategies for regularization in OFV methods have been investigated, some of which do not include an explicit regularization term $J_R$, but rather constrain $\underline{v}$ in some other way when solving the minimization problem. Constraining $\underline{v}$ to a truncated wavelet basis, as is done in wOFV methods, is itself such an implicit regularization (Dérian et al. 2013) as discussed above. Other regularization strategies include constraining $\underline{v}$ according to a Stokes system (Ruhnau and Schnörr 2007), power-law assumptions about the statistics of the underlying fluid flow (Héas et al. 2012), application of Bayesian statistics to inform the velocity estimation (Héas et al. 2013, 2014), using stochastic transport models (Cai et al. 2018), and employing convolutional neural networks to perform the estimation (Cai et al. 2019).

In our previous work, $J_R$ is a third-order Tikhonov regularization term (Schmidt and Sutton 2019). It is implemented in an approximate way by penalizing the wavelet coefficients of $\underline{v}$ according to their scale as described in Appendix A of Schmidt and Sutton (2019) and in Kadri-Harouna et al. (2013), where it is referred to as the operator discrete approximation method. Although such regularization does improve the velocity estimation compared to no explicit regularization term, it produces unwanted artifacts in the resulting velocity fields due to the fact that wavelet coefficients are penalized globally as a function of their scale, with no consideration given to local flow properties. These artifacts can be observed in results presented in Schmidt and Sutton (2019) and shown below. Similar artifacts are produced by truncation of multiple fine scales as a part of an implicit regularization strategy. This is due to the structure of separable 2-D wavelet transforms that are not translation invariant, and the effect is well documented in wavelet image processing applications (Mallat 2009). Two strategies to alleviate these artifacts in image processing is to use translation invariant (Coifman and Donoho 1995) or non-separable wavelet transforms (Mojsilovic et al. 1998), but both methods have potential drawbacks in terms of computational complexity and numerical stability in a wOFV implementation. Still, they may offer some substantial benefits and are a topic of future research.

In the present work, a more complex regularization scheme is described that penalizes directional derivatives of the velocity field in the wavelet domain in a similar manner to that described in Kadri-Harouna et al. (2013) and in more detail in Dérian (2012), where it is referred to as the operator continuous approximation method. In both of these works (Kadri-Harouna et al. 2013; Dérian 2012), the implementation is for periodic boundary conditions only, which is suitable for DNS test cases with periodic boundary conditions such as that of Carlier and Wieneke (2005), but not necessarily for experimental data. For our current wOFV method, the implementation is for non-periodic boundary conditions, which is more complicated than the methods referenced above and also is more widely applicable and more appropriate for realistic experimental data. For example, the current regularization scheme (described below) allows for general (i.e., zero-padding, periodic, or symmetric) boundary conditions. In the current work, we use the continuous approximation approach to implement the div-curl regularization (Eq. 8) in the wavelet domain, as it is a physically sound regularization term that leads to more accurate velocity estimations with negligible small-scale artifacts compared to the discrete approximation method. The structure of the current manuscript is as follows: first, an alternative method for performing full two-dimensional wavelet transforms by matrix multiplication is described. This involves the construction of transform matrices that allows the computation of the necessary regularization matrices for the continuous approximation method. Second, the speed and efficiency of this approach compared to traditional wavelet transforms by convolution or lifting are examined. Finally, velocimetry results from synthetic and experimental tracer particle images are presented that demonstrate significant improvements facilitated by the new wavelet transform approach and regularization scheme.

4 New methodology

4.1 Wavelet transforms via matrix multiplication

Following Mallat’s algorithm (Mallat 1989), one scale of a discrete wavelet transform of a signal $\underline{x}$ of length $N=2^J$ is performed through (1) convolution of $\underline{x}$ with a low-pass filter $\underline{h}$ and subsampling, yielding a vector of approximation coefficients $\underline{a}_{J-1}$ of length $2^{J-1}$, and (2) convolution of $\underline{x}$ with a high-pass filter $\underline{g}$ and subsampling, yielding a vector of detail coefficients $\underline{d}_{J-1}$ of length $2^{J-1}$. This procedure is repeated at each scale j, on each $\underline{a}_j$ to yield $\underline{a}_{j-1}$ and $\underline{d}_{j-1}$ for as many scales as desired, down to a minimum scale of $j=1$ (maximum of J scales). A non-redundant transform produces N wavelet coefficients (of signal $\underline{x}$), arranged at each scale according to

$$\begin{aligned} \underline{\theta } = \begin{bmatrix} \underline{a}_j \\ \underline{d}_j \\ \underline{d}_{j+1} \\ \vdots \\ \underline{d}_{J-1} \end{bmatrix} . \end{aligned}$$

(9)

The primary outcomes from the current work follow from the representation of wavelet transformations in an alternative manner; that is, as matrix multiplications. It is well known in Mathematics that any linear transformation of a 1-D signal $\underline{x}$ of length N, denoted $\underline{x} = \left[ x_0, x_1, \dots , x_{N-1} \right] ^\mathrm {T}$, can be written as a multiplication of an $N \times N$ matrix by $\underline{x}$ (Smith 1998). Since a wavelet transform $\varPsi \left( \underline{x} \right) = \underline{\theta }$ is a linear operation, there exists an $N \times N$ matrix $\underline{F}$ such that $\underline{F} \, \underline{x} = \varPsi \left( \underline{x} \right)$ is satisfied for a discrete wavelet transform applied down to any minimum scale. In wOFV, full transforms of all scales are performed and cascaded until only one scaling coefficient remains; thus, only this scenario will be considered in the current manuscript to develop the appropriate set of matrices. $\underline{F}$ is found from $\underline{F} = \varPsi \left( \underline{I}_N \right)$, where $\underline{I}_N$ is the $N \times N$ identity matrix and the wavelet transform $\varPsi$ is performed vertically on $I_N$. Subsequently, $\underline{F}$, with $N \times N$ elements, can be formed for any boundary extension desired, including periodic, whole- or half-point (anti-)symmetric, zero-padded, etc., as demonstrated below.

Alternatively, $\underline{F}$ can be formed manually by chain multiplying block matrices which perform downsampling and convolutions with the low- and high-pass decomposition filters, $\underline{h}$ and $\underline{g}$, associated with the chosen wavelet basis. It is necessary to demonstrate the construction of $\underline{F}$ in this manner, since some of the steps of this process are used in Sect. 4.2 to implement continuous regularization. In addition, this process may be insightful for readers less familiar with wavelet analysis in understanding how wavelet transforms are performed.

For finite signals, some form of boundary treatment must be employed. When performing a conventional wavelet transform, periodic boundary conditions are the simplest to implement because the convolution operations can be replaced with circular convolutions. Transforms with other boundary conditions in standard wavelet algorithms found in programs such as Python and MATLAB are redundant, producing extra coefficients during decomposition that are removed during reconstruction. As will be shown below, the use of matrix multiplications to perform the wavelet transforms enables a simple implementation of any desired boundary condition without an increase in redundancy.

The full wavelet transform matrix $\underline{F}$ is constructed from a chain multiplication of matrices $\underline{F}_j$, where $1 \le j \le J$, and each $\underline{F}_j$ operates on approximation coefficients $\underline{a}_j$ to produce $\underline{a}_{j-1}$ and $\underline{d}_{j-1}$ (note that $\underline{a}_J = \underline{x}$). Convolution of $\underline{a}_j$ with the low-pass filter $\underline{h}$ is written as the multiplicative operation $\underline{H}_j \underline{a}_j$, where $\underline{H}_j$ is a $2^j \times 2^j$ matrix with translated copies of $\underline{h}$ as rows. The construction of matrix $\underline{H}_j$ follows naturally from the convolution formula

$$\begin{aligned} \left( \underline{x} \star \underline{h} \right) \left[ n \right] = \sum \limits _{k=-\infty }^\infty x \left[ k \right] h \left[ n-k \right] , \end{aligned}$$

(10)

which is written as $\left( \underline{x} \star \underline{h} \right) = \underline{H} \, \underline{x}$ if $H \left[ n,k \right] = h \left[ n-k \right]$.

More specifically, for a filter of length l, where l is an odd integer, filter elements are indexed from $- \left( l-1 \right) /2 \dots \left( l-1 \right) /2$. Copies of $\underline{h}$ are arranged in $\underline{H}_j$ such that element $h\left[ 0 \right]$ in row k is positioned in column k. If the chosen filter has even length, it can be extended by appending a zero to one end of the filter. The boundary condition for the wavelet transform is then applied at the left and right boundaries of $\underline{H}_j$. This is done by considering the application of a filter of length l to $\underline{a}_j$ that is extended to length $2^j + l -1$ using the appropriate extension for the chosen boundary condition. Example extensions of $\underline{x}$ for a filter of length $l=5$ subject to zero-padding, periodic, and whole-point symmetric boundary conditions are shown below using the notation $x_k \equiv x[k]$.

$$\begin{aligned} \underline{x}_\mathrm {zpd}= & {} \begin{bmatrix} x_{-2} = 0 \\ x_{-1} = 0 \\ x_0 \\ x_1 \\ \vdots \\ x_{N-2} \\ x_{N-1} \\ x_N = 0 \\ x_{N+1} = 0 \end{bmatrix} \quad \underline{x}_\mathrm {per} = \begin{bmatrix} x_{-2} = x_{N-2} \\ x_{-1} = x_{N-1} \\ x_0 \\ x_1 \\ \vdots \\ x_{N-2} \\ x_{N-1} \\ x_N = x_0 \\ x_{N+1} = x_1 \end{bmatrix}\nonumber \\ \underline{x}_\mathrm {sym}= & {} \begin{bmatrix} x_{-2} = x_2 \\ x_{-1} = x_1 \\ x_0 \\ x_1 \\ \vdots \\ x_{N-2} \\ x_{N-1} \\ x_N = x_{N-2} \\ x_{N+1} = x_{N-3} \end{bmatrix} \end{aligned}$$

(11)

When constructing $\underline{H}_j$, the boundary condition is not applied by multiplying by an extended signal, but rather by considering the specific elements of $\underline{h}$ that multiply the corresponding elements of $\underline{a}_j$ at each translation n in Eq. (10), or, equivalently, in each row of $\underline{H}_j$. Example matrices for periodic and whole-point symmetric boundary conditions are shown below for $j=3$ and $l=5$.

$$\begin{aligned} \begin{aligned} \underline{H}_3^\mathrm {per}&= \begin{bmatrix} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} \\ h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 &{} 0 &{} h_{-2} \\ h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 &{} 0 \\ 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 \\ 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 \\ h_2 &{} 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 \\ h_1 &{} h_2 &{} 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 \\ \end{bmatrix} \\ \underline{H}_3^\mathrm {sym}&= \begin{bmatrix} h_0 &{} h_1+h_{-1} &{} h_2+h_{-2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ h_{-1} &{} h_0+h_{-2} &{} h_1 &{} h_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 &{} 0 \\ 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 &{} 0 \\ 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0 &{} h_1 &{} h_2 \\ 0 &{} 0 &{} 0 &{} 0 &{} h_{-2} &{} h_{-1} &{} h_0+h_2 &{} h_1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} h_{-2}+h_2 &{} h_{-1}+h_1 &{} h_0 \\ \end{bmatrix} \end{aligned} \end{aligned}$$

(12)

The same strategy for constructing $\underline{H}_j$ applies even when the filter length is longer than the length of the approximation coefficient vector at scale j, i.e. $l>2^j$. For this case, several copies of $\underline{a}_j$ are needed when constructing extensions (Eq. (11)), which are then considered to populate $\underline{H}_j$.

Referring back to Mallat’s algorithm for reference, the resulting signal must be sub-sampled following the convolution with the filter. This sub-sampling operation also can be written as left multiplication of any matrix by $S_j$, which is simply every other row of the identity matrix, starting from the first row. For example for $j=3$,

$$\begin{aligned} \underline{S}_3 = \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{bmatrix} . \end{aligned}$$

(13)

Hence, the approximation coefficients $\underline{a}_{j-1}$ are determined by $\underline{a}_{j-1} = \underline{S}_j \underline{H}_j \underline{a}_j$. Similarly, the detail coefficients $\underline{d}_{j-1}$ are computed from $\underline{d}_{j-1} = \underline{S}_j^\prime \underline{G}_j \underline{a}_j$, where $\underline{G}_j$ is a matrix constructed from the high-pass filter $\underline{g}$ in an identical way in which $\underline{H}_j$ was constructed from $\underline{h}$. $\underline{S}_j^\prime$ also is a subsampling matrix, which is every other row of the identity matrix, but starting from the second row instead of the first. The use of $\underline{S}_j^\prime$ for the high-pass filter (instead of $\underline{S}_j$) is done only to return the same output as the common wavedec function in MATLAB or Python. The only exception is at the final scale $j=1$, where the final detail coefficient $d_0$ is given by $\underline{S}_1 \underline{G}_1$ to obtain the same result as wavedec. Putting this all together, one step of the wavelet transform decomposition (at scale j) is given by

$$\begin{aligned} \begin{bmatrix} \underline{a}_{j-1} \\ \underline{d}_{j-1} \end{bmatrix}= \begin{bmatrix} \underline{S}_j \underline{H}_j \\ \underline{S}_j^\prime \underline{G}_j \end{bmatrix} \underline{a}_j . \end{aligned}$$

(14)

The matrix multiplying $\underline{a}_j$ on the right hand side of Eq. (14) can be computed in advance from filter elements $\underline{h}$ and $\underline{g}$, and is defined as $\underline{F}_j$, i.e.,

$$\begin{aligned} \underline{F}_j \equiv \begin{bmatrix} \underline{S}_j \underline{H}_j \\ \underline{S}_j^\prime \underline{G}_j \end{bmatrix} . \end{aligned}$$

(15)

$\underline{F}_j$ has size $2^j \times 2^j$, but it must operate on a signal of length N to store the coefficients in the correct position, according to Eq. (9). Since $\underline{F}_j$ is applied only to approximation coefficients $\underline{a}_j$ at each scale in the wavelet transform, and not the detail coefficients from finer scales $\underline{d}_j \dots \underline{d}_{J-1}$, the proper $N \times N$ matrix for $\underline{F}_j$ is a block matrix. The block matrix (at scale j) is formed from $\underline{F}_j$ in the upper left, an identity matrix of size $N-2^j \times N-2^j$ in the lower right, and zeros at other positions:

$$\begin{aligned} \underline{F}_j^\mathrm {B} = \begin{bmatrix} \underline{F}_j &{} 0 \\ 0 &{} \underline{I}_{N-2^j} \end{bmatrix} . \end{aligned}$$

(16)

Finally, the full cascade of low-pass and high-pass filters at all scales is given by the product of $\underline{x}$ with a chain multiplication of the matrices $\underline{F}_j^\mathrm {B}$’s:

$$\begin{aligned} \underline{\theta } = \underline{F}_1^\mathrm {B} \underline{F}_2^\mathrm {B} \dots \underline{F}_J^\mathrm {B} \underline{x} , \end{aligned}$$

(17)

where the resulting matrix chain product is the full wavelet transform matrix $\underline{F}$, defined as

$$\begin{aligned} \underline{F} \equiv \underline{F}_1^\mathrm {B} \underline{F}_2^\mathrm {B} \dots \underline{F}_J^\mathrm {B} \end{aligned}$$

(18)

and the full set of wavelet coefficients is given as $\underline{\theta } = \underline{F} \, \underline{x}$. The matrix chain multiplication can be performed in advance, as it only depends on the chosen filters $\underline{h}$ and $\underline{g}$ and the boundary condition. Thus, $\underline{F}$ is computed once and stored in memory as a dictionary for a given wavelet basis and boundary condition.

$\underline{F}$ has some interesting properties that are worth noting. Intuitively, the inverse transform $\varPsi ^{-1} \left( \underline{\theta } \right)$ is given by $\underline{F}^{-1} \underline{\theta }$, where $^{-1}$ denotes the ordinary matrix inverse. In practice, $\underline{F}^{-1}$ also is computed in advance one time from $\underline{F}$ and stored in memory. For orthogonal wavelets with periodic boundary conditions, $\underline{F}$ is an orthogonal matrix, i.e. $\underline{F}^{-1} = \underline{F}^\mathrm {T}$. For a biorthogonal basis with decomposition filters $\underline{{\tilde{h}}}$ and $\underline{{\tilde{g}}}$ and reconstruction filters $\underline{h}$ and $\underline{g}$, the decomposition matrix $\underline{{\tilde{F}}}$ is formed from from $\underline{{\tilde{h}}}$ and $\underline{{\tilde{g}}}$. Alternatively, a decomposition matrix $\underline{F}$ can be formed from the reconstruction filters h and g, which performs a forward decomposition using the so-called reverse biorthogonal basis associated to a biorthogonal filter pair. For transforms with periodic boundary conditions, $\underline{{\tilde{F}}}$ and $\underline{F}$ are related by $\underline{{\tilde{F}}} = \underline{F}^{-\mathrm {T}}$.

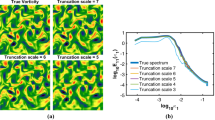
This analysis can be extended to separable, anisotropic transforms of 2-D signals $\underline{X}$ (i.e., “images”) of size $N \times N$ through the relation $\varPsi \left( \underline{X} \right) = \underline{{\tilde{F}}} \, \underline{X} \, \underline{{\tilde{F}}}^\mathrm {T}$. Interestingly, even though the theoretical complexity of matrix multiplication is higher than that of a 2-D wavelet transform using Mallat’s algorithm ($O \left( N^3 \right)$ vs. $O \left( N^2 \right)$), performing full transforms of $\underline{X}$ using $\varPsi \left( \underline{X} \right) = \underline{{\tilde{F}}} \, \underline{X} \, \underline{{\tilde{F}}}^\mathrm {T}$ is much faster than equivalent transforms using MATLAB’s built-in wavelet transform algorithm wavedec2 or a lifting implementation (as used previously in Schmidt and Sutton (2019)) for values of N typically found in image processing ($\le 4$ MP). This is illustrated in Fig. 1 for transforms of a sample image, truncated or extended periodically to the desired sizes. The processing times reported in Fig. 1 include the time to load in $\underline{{\tilde{F}}}$ from memory. The computations used to produce the results shown in Fig. 1 were performed in MATLAB version 9.4 with Wavelet Toolbox version 5.0 on an Intel Core i5 processor with an L1 cache size of 256 kB. The speedup using matrix multiplication is largely due to the highly optimized routines in BLAS/LAPACK used by MATLAB for matrix multiplication. An additional benefit of the matrix multiplication implementation with regard to computational speed is that the number of computations for the wavelet transform becomes independent of the length of the filters, so wavelets with a higher number of vanishing moments can be used without sacrificing speed. This is important for wOFV, since wavelets with more vanishing moments produce more accurate velocity estimations. Finally, because matrix multiplication is ubiquitous in high-performance computing, many algorithms exist for efficient parallelization of matrix multiplication. This includes GPU parallelization, which can enable a further increase in speed with minimal effort. Wavelet transforms by parallel matrix multiplication have been successfully demonstrated previously by researchers in the field of signal processing (Marino et al. 1999).

Fig. 1

a Sample image decomposed by different wavelet transform algorithms. The image was truncated or periodically extended to obtain the various values of N. b Processing time for several 2-D transform implementations in MATLAB on a single processor. Dashed lines for theoretical computational complexity for large N are shown. BLAS uses the Strassen algorithm (Strassen 1969) for matrix multiplication, which has theoretical complexity $O \left( N^{2.8} \right)$

4.2 Continuous regularization

The theory and mathematics underpinning continuous regularization in the wavelet domain is given in detail in Dérian (2012), so only the most pertinent details will be described here. In this work, we describe the implementation of continuous regularization for wavelet transforms with arbitrary boundary conditions, which has not been addressed previously. In essence, continuous regularization seeks to enforce smoothness on the velocity fields by forming a physically sound regularization term $J_R$ that penalizes directional derivatives of the velocity field. In the current work, the div-curl penalization of Corpetti et al. (2002) (Eq. (8)) is used. Instead of approximating the requisite derivatives of $J_R$ with finite difference schemes, differentiation is performed on the smooth wavelet basis functions as described by Beylkin (1992). This is done by constructing filters $\underline{\varGamma }_\varphi ^{\left( n \right) }$ which compute the desired derivatives when applied to components of the velocity field $\underline{v}$ via convolution. $\underline{\varGamma }_\varphi ^{\left( n \right) }$ is the correlation of the wavelet scaling function (father wavelet) $\varphi$ and its n-th order derivative $\varphi ^{\left( n \right) }$:

$$\begin{aligned} \varGamma _\varphi ^{\left( n \right) } \left( x \right) = \int _{\mathbb {R}} \varphi \left( y \right) \varphi ^{\left( n \right) } \left( y-x \right) \text {d}y . \end{aligned}$$

(19)

Using the same approach as described in Sect. 4.1, we describe the formation of matrices $\underline{N}^{\left( n \right) }$ for differentiation order n that produce the appropriate directional derivatives to form $J_R$ when multiplied by components of the wavelet transform of the velocity field $\underline{\psi }$ in matrix triple products of the form $\underline{N}^{\left( n_1 \right) } \underline{\psi } \, \underline{N}^{\left( n_2 \right) \mathrm {T}}$. This implementation is preferred to convolution with $\underline{\varGamma }_\varphi ^{\left( n \right) }$ for two reasons. First, as demonstrated above, matrix multiplication is more efficient for images of sizes relevant to wOFV applications than convolution with a filter. Second, considering the step-by-step implementation of the wOFV algorithm described in Sect. 1, it is much more efficient to compute $J_R$ from the wavelet coefficients of the velocity field directly rather than performing an inverse transform to obtain $\underline{v}$, computing $J_R$ and its gradient, and then performing a forward transform of the gradient when the minimization is performed in the wavelet domain.

To calculate $\underline{N}^{\left( n \right) }$ the vector of wavelet connection coefficients $\underline{\varGamma }_\varphi ^{\left( n \right) }$ must be computed for the chosen wavelet basis reconstruction filter $\underline{h}$ and differentiation order n. In practice, $\underline{\varGamma }_\varphi ^{\left( n \right) }$ can be determined by computing the eigenvector associated with the eigenvalue $1/2^n$ (if it exists) of a matrix $\underline{\varPhi }$, where $\underline{\varPhi }$ is formed from the autocorrelation sequence of $\underline{h}$, $i_h \left[ k \right] =\sum \nolimits _{m \in {\mathbb {Z}}} h[m] h[m-k]$. This follows from the so-called “two-scales relation” satisfied by $\underline{\varGamma }_\varphi ^{\left( n \right) }$ derived from Eq. (19):

$$\begin{aligned} \varGamma _\varphi ^{\left( n \right) } \left( x \right) = 2^n \sum \limits _{k \in {\mathbb {Z}}} i_h \left[ k \right] \varGamma _\varphi ^{\left( n \right) } \left( 2x-k \right) . \end{aligned}$$

(20)

By using a change of variable $k^\prime \equiv 2x-k$, Eq. (20) becomes

$$\begin{aligned} \varGamma _\varphi ^{\left( n \right) } \left( x \right) = 2^n \sum \limits _{k^\prime \in {\mathbb {Z}}} i_h \left[ 2x - k^\prime \right] \varGamma _\varphi ^{\left( n \right) } \left( k^\prime \right) , \end{aligned}$$

(21)

which can be written as a linear system

$$\begin{aligned} \underline{\varPhi } \, \underline{\varGamma }_\varphi ^{\left( n \right) } = \frac{1}{2^n} \underline{\varGamma }_\varphi ^{\left( n \right) } , \end{aligned}$$

(22)

where $\varPhi \left[ x,k^\prime \right] = i_h \left[ 2x-k^\prime \right]$. From this formula, it is apparent that there is a degree of arbitrariness in the construction of $\underline{\varPhi }$.

A simple formulation of $\underline{\varPhi }$ is as a square matrix of size $2l-3$, where l is the length of the filter $\underline{h}$ as described above. Each row of $\underline{\varPhi }$ is a copy of $\underline{i}_h$, with the center value of $\underline{i}_h$ placed in the center column of the center row of the matrix $\underline{\varPhi }$. Copies of $\underline{i}_h$ in the other rows of $\underline{\varPhi }$ are shifted by two columns such that the diagonal of $\underline{\varPhi }$ contains a reversed copy of $\underline{i}_h$. Values of $\underline{i}_h$ outside the bounds of $\underline{\varPhi }$ are truncated and the ends of $\underline{i}_h$ are extended with zeros to fill $\underline{\varPhi }$. For example, if $l=5$, $\underline{i}_h$ has seven elements (indexed from $-3 \dots 3$) and $\underline{\varPhi }$ takes on the form of the following matrix:

$$\begin{aligned} \underline{\varPhi }= \begin{bmatrix} i_h \left[ 3 \right] &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ i_h \left[ 1 \right] &{} i_h \left[ 2 \right] &{} i_h \left[ 3 \right] &{} 0 &{} 0 &{} 0 &{} 0\\ i_h \left[ -1 \right] &{} i_h \left[ 0 \right] &{} i_h \left[ 1 \right] &{} i_h \left[ 2 \right] &{} i_h \left[ 3 \right] &{} 0 &{} 0\\ i_h \left[ -3 \right] &{} i_h \left[ -2 \right] &{} i_h \left[ -1 \right] &{} i_h \left[ 0 \right] &{} i_h \left[ 1 \right] &{} i_h \left[ 2 \right] &{} i_h \left[ 3 \right] \\ 0 &{} 0 &{} i_h \left[ -3 \right] &{} i_h \left[ -2 \right] &{} i_h \left[ -1 \right] &{} i_h \left[ 0 \right] &{} i_h \left[ 1 \right] \\ 0 &{} 0 &{} 0 &{} 0 &{} i_h \left[ -3 \right] &{} i_h \left[ -2 \right] &{} i_h \left[ -1 \right] \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} i_h \left[ -3 \right] \end{bmatrix}. \end{aligned}$$

(23)

Therefore, $\underline{\varGamma }_\varphi ^{\left( n \right) }$ has length $2l-3$, indexed from $2-l \dots l-2$. Values of $\underline{\varGamma }_\varphi ^{\left( n \right) }$ are then normalized according to Beylkin (1992) for proper regularization:

$$\begin{aligned} \underline{{\hat{\varGamma }}}_\varphi ^{\left( n \right) } = \frac{\underline{\varGamma }_\varphi ^{\left( n \right) } n! \left( -1 \right) ^n}{\sum \nolimits _{k \in {\mathbb {Z}}} \nu \left[ k \right] \varGamma _\varphi ^{\left( n \right) } \left[ k \right] } , \end{aligned}$$

(24)

where $\underline{\nu }$ is the sequence $\left[ \left( 2-l \right) ^n \dots \left( l-2 \right) ^n \right]$. Translated copies of $\underline{{\hat{\varGamma }}}_\varphi ^{\left( n \right) }$ are then organized into an $N \times N$ matrix $\underline{M}^{\left( n \right) }$, such that the matrix multiplication $\underline{M}^{\left( n \right) } \underline{X}$ is equivalent to performing a convolution of each column of $\underline{X}$ with $\underline{{\hat{\varGamma }}}_\varphi ^{\left( n \right) }$, as done for $\underline{F}$ in Sect. 4.1. $\underline{M}^{\left( n \right) }$ is structured such that $\varGamma _\varphi ^{\left( n \right) } \left[ 0 \right]$ lies along the diagonal and entries of $\underline{\varGamma }_\varphi ^{\left( n \right) }$ that extend outside the boundaries of $\underline{M}^{\left( n \right) }$ are included according to the chosen boundary condition for the wavelet basis in an identical manner to the example shown for the matrix $\underline{H}_{j}$ in Eq. (12). The same boundary condition used for the wavelet transform must be applied in the construction of $\underline{M}^{\left( n \right) }$.

The desired regularization term $J_R$ could be computed in the physical domain by matrix triple products of the form $\underline{M}^{\left( n_1 \right) } \underline{v}^k \underline{M}^{\left( n_2 \right) \mathrm {T}}$, where $\underline{v}^k$ is the $k^\mathrm {th}$ component $\left( k=1,2 \right)$ of the $N \times N \times 2$ velocity field matrix $\underline{v}$. Subsequently, a 2-D wavelet transform using the reconstruction filters would be performed, since $\underline{M}^{\left( n \right) }$ is formed using $\underline{h}$, not $\underline{{\tilde{h}}}$. However, as stated previously, it is desired to perform the equivalent calculation directly in the wavelet domain on $\underline{\psi }$ for efficiency within the wOFV algorithm. This is performed by computing a matrix $\underline{N}^{\left( n \right) }$ such that

$$\begin{aligned} \underline{N}^{\left( n \right) } \, \underline{\psi } \, \underline{N}^{\left( n \right) \mathrm {T}}&= \underline{F} \, \underline{M}^{\left( n \right) } \underline{v} \, \underline{M}^{\left( n \right) \mathrm {T}} \underline{F}^\mathrm {T}, \nonumber \\&\mathrm {or} \nonumber \\ \underline{N}^{\left( n \right) } \, \underline{{\tilde{F}}} \, \underline{v} \, \underline{{\tilde{F}}}^\mathrm {T} \underline{N}^{\left( n \right) \mathrm {T}}&= \underline{F} \, \underline{M}^{\left( n \right) } \underline{v} \, \underline{M}^{\left( n \right) \mathrm {T}} \underline{F}^\mathrm {T}. \end{aligned}$$

(25)

By examining Eq. (25), it is observed that the matrix product multiplying $\underline{v}$ from the left is the transpose of the product multiplying $\underline{v}$ from the right on both sides of the equation, which yields

$$\begin{aligned} \underline{N}^{\left( n \right) } \underline{{\tilde{F}}} = \underline{F} \, \underline{M}^{\left( n \right) }. \end{aligned}$$

(26)

and

$$\begin{aligned} \underline{N}^{\left( n \right) } = \underline{F} \, \underline{M}^{\left( n \right) } \underline{{\tilde{F}}}^{-1}. \end{aligned}$$

(27)

The regularization term $J_R$ for the div-curl regularization, written via matrix multiplications, is given by a similar format as described in Dérian (2012):

$$\begin{aligned} J_R&= \frac{1}{2} \underline{\psi }_1 : \biggl ( \underline{N}^{\left( 0 \right) } \underline{\psi }_1 \underline{N}^{\left( 4 \right) \mathrm {T}} + 2 \underline{N}^{\left( 2 \right) } \underline{\psi }_1 \underline{N}^{\left( 2 \right) \mathrm {T}} - 2 \underline{N}^{\left( 3 \right) } \underline{\psi }_2 \underline{N}^{\left( 1 \right) \mathrm {T}} \nonumber \\&\quad +\underline{N}^{\left( 4 \right) } \underline{\psi }_1 \underline{N}^{\left( 0 \right) \mathrm {T}} + 2 \underline{N}^{\left( 1 \right) } \underline{\psi }_2 \underline{N}^{\left( 3 \right) \mathrm {T}} \biggr ) + \frac{1}{2} \underline{\psi }_2 : \biggl ( \underline{N}^{\left( 0 \right) } \underline{\psi }_2 \underline{N}^{\left( 4 \right) \mathrm {T}} \nonumber \\&\quad +2 \underline{N}^{\left( 2 \right) } \underline{\psi }_2 \underline{N}^{\left( 2 \right) \mathrm {T}} - 2 \underline{N}^{\left( 1 \right) } \underline{\psi }_1 \underline{N}^{\left( 3 \right) \mathrm {T}} + \underline{N}^{\left( 4 \right) } \underline{\psi }_2 \underline{N}^{\left( 0 \right) \mathrm {T}} \nonumber \\&\quad +2 \underline{N}^{\left( 3 \right) } \underline{\psi }_1 \underline{N}^{\left( 1 \right) \mathrm {T}} \biggr ), \end{aligned}$$

(28)

where  :  denotes the Frobenius inner product. As for the matrices $\underline{{\tilde{F}}}$ and $\underline{F}$, the matrices $\underline{N}^{\left( n \right) }$ depend only on the chosen wavelet basis and the size of the images, so they are computed only once and stored in memory as dictionaries. It should be emphasized here that the development of the continous regularization via matrix multiplication enables an efficient calculation of the regularization parameter with arbitrary boundary conditions. Previously, the continuous regularization has been demonstrated only for periodic boundary conditions when performing the wavelet transforms via convolution (Dérian 2012). The use of non-periodic boundary conditions (as in the current work) is much more accurate for experimental data.

One final note on efficient implementation is addressed here. In the wOFV algorithm, the fact that many of the coefficients of $\underline{\psi }$ are known to be zero a priori can be exploited for speed when computing the matrix triple products and wavelet transforms for $J_D$ and $J_R$ by only considering relevant rows and/or columns of $\underline{F}$, $\underline{{\tilde{F}}}$, and $\underline{N}^{\left( n \right) }$. This is similar to the “smart filter banks” strategy employed by Dérian (2012). For example, at scale S in the wOFV algorithm, all wavelet coefficients in $\underline{\psi }$ at scales finer than S are known to be zero. Therefore, the multiplication $\underline{\psi }^k = \underline{{\tilde{F}}} \, \underline{v}^k \underline{{\tilde{F}}}^\mathrm {T}$ can be performed using only the first $2^S$ rows of $\underline{{\tilde{F}}}$. Similarly, the inverse transform multiplication can be performed only on the $2^S \times 2^S$ non-zero components in the upper-left of $\underline{\psi }^k$ by using the first $2^S$ columns of $\underline{F}$.

5 Results and discussion

Results using the current wOFV method with the continuous div-curl regularization (matrix multiplication implementation) and symmetric boundary conditions¹ are compared to results from the previous implementation using discrete regularization (Schmidt and Sutton 2019), as well as other wOFV approaches and correlation-based PIV. Results are evaluated on both synthetic and experimental data sets. It is noted that the processing time for the current implementation is approximately the same as our previous implementation (Schmidt and Sutton 2019), with significant improvements in accuracy. Although the time required to perform the forward and inverse wavelet transforms decreases for the current method, the computation of $J_R$ is more intensive due to the complexity of the div-curl regularization compared to the third-order Tikhonov regularization used in Schmidt and Sutton (2019). These two aspects essentially offset one another, resulting in no net change in processing time. The improvements of the current method over the previous approach are both quantitative, demonstrated by a reduction in error and an increase in spatial resolution, and qualitative, as demonstrated by a reduction of the small-scale artifacts in the estimated velocity field and its associated gradient quantities.

5.1 Synthetic data

wOFV is first performed on synthetic particle images from the direct numerical simulation (DNS) of 2-D homogeneous, isotropic turbulence of Carlier and Wieneke (2005). The details of the simulation and synthetic particle generation are described in Carlier and Wieneke (2005). This data set has been used by many researchers in the OFV community, including the previous work by the authors (Schmidt and Sutton 2019). The data set consists of 100 sequential images, each with $256 \times 256$ pixels. The accuracy of the velocity estimation is calculated using the root mean square error (RMSE), defined using the standard convention in OFV literature

$$\begin{aligned} \mathrm {RMSE} = \sqrt{\frac{1}{N} \sum ||\underline{v} - \underline{{\hat{v}}}||^2} , \end{aligned}$$

(29)

where $\underline{{\hat{v}}}$ is the estimated velocity at each pixel and $\underline{v}$ is the corresponding true velocity from the DNS. The RMSE from the current and previous (Schmidt and Sutton 2019) wOFV implementations are shown in Fig. 2, along with a comparison to the Typhoon wOFV algorithm of Dérian and Almar (2017). The current wOFV implementation shows a significant improvement in accuracy ($\sim 12\%$) compared to the previous implementation by the same authors, and also is more accurate than the Typhoon algorithm, which uses periodic boundary conditions similar to the DNS. The latter observation is interesting since the use of periodic boundary conditions in wOFV algorithms generally gives lower error on data sets with periodic boundary conditions. The fact that the current wOFV implementation (with non-periodic boundary conditions) outperforms the Typhoon algorithm (with periodic boundary conditions) on a data set with periodic boundary conditions shows the strength of the current wOFV algorithm. If periodic boundary conditions were chosen for the current synthetic data set, the error would be reduced even further. It should also be noted that the estimated velocities in this work have not been projected to divergence-free space as is typically done in other works using this data set, e.g. Kadri-Harouna et al. (2013), Chen et al. (2015), Héas et al. (2013) and Cai et al. (2018). If projected to divergence-free space, the RMSE of our wOFV method is reduced by an additional 20% (or to approximately 0.06 on average). However, this approach only is applicable to specific DNS cases that are divergence-free by construction and thus we choose not to report RMSE in this manner to maintain generality.

Fig. 2

Root mean square error of the velocity estimations from particle images in a 2-D turbulent DNS using wOFV methods

Figure 3 shows the instantaneous vorticity $\left( \omega _z \right)$ and (local) enstrophy $\left( {\mathcal {E}} = \underline{\omega } \cdot \underline{\omega } \right)$ calculated from a single time instance in the simulation. The leftmost image is the 2D vorticity field calculated from the DNS, which is considered as “truth”,while the two middle images are computed from the velocity estimations using both the current and previous wOFV implementations. The synthetic particle images were also processed using a commercial PIV algorithm (LaVision DaVis 8). The images were first pre-processed with a sliding background filter and then a multi-pass approach was used, with interrogation windows of $96 \times 96$ and $16 \times 16$ pixels, each with 75% overlap.The correlation algorithm uses a multi-grid approach with image deformation using 6th-order B-splines and Gaussian weighting of the interrogation windows. The correlation-based PIV results also are shown in Fig. 3 in the rightmost column.

While both wOFV implementations demonstrate increased spatial resolution and fidelity compared to the PIV results, the previous implementation with discrete regularization (3$\mathrm {rd}$ column) shows structural artifacts in the vorticity and enstrophy fields. The artifacts manifest as a square-like pattern imprinted over the actual fields and lead to a “fuzzy” appearance of $\omega _z$ and ${\mathcal {E}}$. The artifacts are due to the equal penalization of wavelet coefficients of the velocity field as a function of scale only, with increasing penalization at finer scales. This produces the regular coarser patterns (lower frequencies) that are observed at the finer scales (higher frequencies) in Fig. 3 and results in behavior similar to truncation of coefficients at fine scales. The current implementation with continuous regularization (2$\mathrm {nd}$ column) does not penalize wavelet coefficients based on scale only, but instead considers the local flow features through penalization of the cross (directional) derivatives as discussed in Sect. 4.2. Since penalization is a local operator in the current approach, the lower-frequency artifacts are no longer observed and the $\omega _z$ and ${\mathcal {E}}$ fields strongly resemble the actual DNS results, even at the smallest scales.

Fig. 3

Two-dimensional vorticity (top) and enstrophy (bottom) fields calculated from DNS results and synthetic particle images. (Left) True vorticity and enstrophy calculated directly from DNS velocity. (2$\mathrm {nd}$–4$\mathrm {th}$ columns) Calculations of $\omega _z$ and ${\mathcal {E}}$ from velocity estimations determined using particle images for three velocimetry methods

Figure 4 shows the normalized one-dimensional energy ($E^*_{11}$) and dissipation ($D^*_{11}$) spectra calculated from the velocity results using the current and previous wOFV methods, as well as correlation-based PIV. Also shown are the spectra determined from the “true” DNS velocity for comparison. All spectra are normalized by their maximum values and are plotted versus the normalized wavenumber, $\eta \kappa _1$, where $\eta$ is the estimated Kolmogorov scale and $\kappa _1$ is the wavenumber in one dimension. The Kolmogorov scale is estimated by considering Pope’s 1D model spectrum (Pope 2001), which shows that $\eta \kappa = 1$ corresponds to the power level where the dissipation spectra drops to 0.9% of its peak value for high Reynolds numbers. The 0.9% position is shown on the dissipation spectrum with a dashed line. As expected, the correlation-based result only resolves the energy and dissipation spectra at lower wavenumbers as evident by its “roll off” at higher frequencies. In contrast, the wOFV approaches faithfully follow the energy and dissipation spectra over a much larger wavenumber range because of the higher spatial resolution of the wOFV methodology. In comparing the current and previous wOFV implementations, the spectra are more faithfully reproduced by the current wOFV approach at higher wavenumbers, where the signature of the artifacts observed in Fig. 3 for discrete regularization (previous wOFV method) are observed as higher-frequency peaks in the dissipation spectrum in Fig. 4. It should be noted that while the deviation between the current and previous wOFV methods in the energy and dissipation spectra primarily occurs for $\eta \kappa _1 > 1$, this only is because of the lower Reynolds number of the DNS. As will be shown below for experimental data, there can be significant improvements at higher Reynolds numbers with the current wOFV approach.

Fig. 4

Normalized energy (a) and dissipation (b) spectra as a function of normalized wavenumber for the 2-D DNS of isotropic turbulence

Finally, we examine the sensitivity of the wOFV results to the regularization parameter $\lambda$ using both the new continuous regularization approach and our previous method with discrete regularization. For both approaches, $\lambda$ is computed using the strategy and heuristic algorithm described in Sect. 2.3 of Schmidt and Sutton (2019). However, no method is exact and since only a single global value of $\lambda$ is used for an entire data set, it is unlikely that the chosen value of $\lambda$ is the optimal value for every local spatial position. In this manner, understanding how the accuracy of the wOFV velocity results is affected by changes (or uncertainty) in $\lambda$ is important. Figure 5 shows the sensitivity of the mean RMSE, computed over the full set of image pairs from the DNS, to variations in the regularization parameter $\lambda$ for the previous and current wOFV implementations. In Fig. 5, $\lambda ^\star$ is the value of the regularization parameter that minimizes the RMSE over the full data set and $\lambda$ represents any other value of the regularization parameter. The results in Fig. 5 show that velocity estimations using the current wOFV method with continuous regularization are much less sensitive to $\lambda$ than the previous implementation with discrete regularization, especially near the “optimal value,” $\lambda ^\star$. For example, to keep the calculated RMSE within 10% of its minimum value (which occurs at $\lambda ^\star$), $\log _{10} \lambda$ must be within 10% of $\log _{10} \lambda ^\star$ for discrete regularization. In contrast, for continuous regularization, $\log _{10}\lambda$ can vary by as much as 30% from $\log _{10}\lambda ^\star$ to keep the RMSE within 10% of its minimum value. This implies that $\lambda$ can vary by as much as a factor of two more for the new approach with continuous regularization compared to the former approach with discrete regularization to keep the RMSE low.

Fig. 5

Sensitivity of calculated RMSE to $\lambda$ for the current and previous wOFV regularization approaches. $\lambda ^\star$ is defined at the value of $\lambda$ at which the mean RMSE is minimized

5.2 Experimental data

Both the current and former wOFV methods are applied to a set of experimental particle image data from a turbulent jet flow to further illustrate improvements brought about by the implementation of continuous regularization. In addition, an advanced correlation-based multi-pass PIV algorithm (LaVision DaVis 8) is applied to the same data for comparison. The PIV results are processed in two ways: (1) a final interrogation window size of $16 \times 16$-pixels with 50% overlap, referred to as “PIV” and (2) a final interrogation window of $12 \times 12$-pixels with 75% overlap, referred to as “High-Res PIV,” meant to show the upper limit of correlation-based PIV estimations.

The turbulent flow under consideration is a non-reacting jet flow case issuing from a burner apparatus that can be used to stabilize a series of turbulent premixed flames as described in Skiba et al. (2018). The main jet consists of a high-velocity air stream that issues into a low-velocity co-flow of air, both at room temperature ($T = 295$ K). The burner has a complex internal structure including a turbulence generation plate that leads to a highly turbulent flow and high turbulent Reynolds numbers. The exit diameter (D) of the jet (burner) outlet is 21.6 mm and the exit velocity is 32 m/s for the case analyzed in the current work, which leads to a Reynolds number based on diameter of 46,000. In a prior experiment, the root mean square of velocity fluctuations $u^\prime _\mathrm {rms}$ and the integral length scale $L_x$ were measured using laser Doppler velocimetry, leading to a turbulent Reynolds number of 8000 (Skiba et al. 2018).

To generate the particle images, the flow is seeded with small titanium dioxide tracer particles with a nominal diameter of 100 nm. The particles are illuminated by a dual-cavity Nd:YAG PIV laser (New-Wave Solo) with 532-nm output. Images are recorded using a 14-bit PCO 1600 interline transfer CCD camera with a resolution of $1612 \times 1210$ pixels; however, images are cropped to the central $1024 \times 1024$-pixel region for velocimetry processing. The field-of-view covers $-0.6<r/D<0.8$ and $0<x/D<1.46$, where r is a radial coordinate and x is the coordinate in the axial direction, corresponding to a magnification of 0.25 and a projected pixel size of 30 $\upmu$m. Further details about the experimental setup are given by Skiba et al. (2018), where the experimental data used for the present study is referred to as Case 3A with cold (non-reacting) flow. Particle images are pre-processed using a sliding background filter with an 8-pixel kernel for both PIV and wOFV.

Instantaneous 2D vorticity fields ($\omega _z$) are shown in Fig. 6 for correlation-based PIV and wOFV processing. Similar to the synthetic cases presented above, the results from four processing methodologies are presented: (1) PIV, (2) High-Res PIV, (3) the previous wOFV approach, and (4) the current wOFV processing approach with improved regularization. The vorticity is computed using the eight-point circular stencil presented by Luff et al. (1999). As with the synthetic data shown above and in previous work (Schmidt and Sutton 2019), the wOFV methods, as applied to the experimental data, show significantly more detailed (fine-scale) structure in the flow field compared to the two correlation-based PIV approaches. However, the most important aspect in the context of the present study is the comparison of the two wOFV approaches with different regularization methods. Figure 6 shows that the current wOFV method using continuous regularization (lower right column) leads to the elimination of the checkerboard-like artifacts that are observed when using the previous wOFV approach (lower left column). Upon examination of the single image calculated using the previous wOFV approach, there is a subtle (but clear) pattern that is imposed over the vorticity field, that even appears to impact the orientations of the vorticity structures. This is clearly observed in the lower-vorticity regions near the coflow (upper right of image) and in greater detail in Fig. 7, which provides a zoomed-in view of the regions marked with white squares in Fig. 6. When comparing the zoomed-in regions shown in Fig. 7, it is clear that the current approach using continuous regularization yields physically realistic topology, whereas the previous wOFV approach yields non-physical structural artifacts that result from the effective truncation of wavelet coefficients based on scale as described in Sect. 5.1. This demonstrates the significance of enforcing a physically sound regularization term in an experimental context.

Fig. 6

Vorticity fields calculated from the estimated velocity fields within the turbulent jet flow using (i) PIV, (ii) High-Res PIV, (iii) the previous wOFV approach with discrete regularization, and (iv) the current wOFV processing approach using continuous regularization. The white squares mark the location of the “zoomed in” regions shown in more detail in Fig. 7

Fig. 7

Zoomed-in views of the wOFV and PIV vorticity fields extracted from the regions marked with white squares shown in Fig. 6. Note the appearance of checkerboard-like structural artifacts in the previous wOFV results (second from right), which are eliminated with the current regularization scheme (far right)

Similar to the synthetic data discussed in Sect. 5.1, the 1D normalized turbulence energy ($E^*_{11}$) and dissipation ($D^*_{11}$) spectra are calculated for the four processing methods and shown in Fig. 8. The spectra are calculated in the axial direction, centered on the jet centerline, and averaged over several columns on either side of the centerline (corresponding to 480 $\upmu$m in width) and over all time instances. In addition, Pope’s 1D model spectrum (Pope 2001) is computed using a Taylor Reynolds number of 260 and is shown for comparison. The first observation of note is the significant enhancement in resolving power of fine scales (high spatial frequencies) of wOFV methods compared to correlation-based PIV processing. As shown in Fig. 8a, both the “PIV” and “High-Res PIV” energy spectra are resolved only through a portion of the inertial range and do not resolve the dissipation scales. This is clearly observed in the dissipation spectra shown in Fig. 8b, where the correlation-based methods “roll off” and depart from the 1D model spectrum at low to moderate frequencies. For example, the PIV processing does not even resolve the peak of the dissipation spectrum and the High-Res PIV only resolves approximately 60% of the total dissipation. This is expected for the high-Reynolds number test conditions considered in the current work.

In contrast, the application of wOFV leads to energy and dissipation spectra that resolve higher frequencies. The energy and dissipation spectra calculated using the previous wOFV approach show evidence of the structural (square-shaped) artifacts observed in the sample images of Figs. 6 and 7 . This manifests itself as a lower frequency modulation imposed over the energy and dissipation spectra. The new wOFV approach, with continuous regularization, eliminates these artifacts, and resolves the highest frequencies present within the flow. Again, estimating the Kolmogorov scale where the power level is $0.9\%$ of the peak of the 1D dissipation spectrum, the current wOFV method appears to fully resolve the dissipative scales. Furthermore, it is noted that the current wOFV method leads to significant increases in measurement dynamic range. The current wOFV method resolves a full range of flow scales ranging from the energy input regime through the inertial range and the dissipation scales.

Fig. 8

a Axial turbulence energy and b dissipation spectra for the turbulent jet flow using four velocimetry approaches. Note the additional local peaks in the spectra for the previous wOFV implementation resulting from the non-physical structural artifacts

In addition to instantaneous fields of kinematic properties, statistical moments (i.e., mean, RMS, etc.) of a turbulent velocity field often are of interest in experimental studies. Here, we compare the effects of the previous and current wOFV regularization approaches (along with correlation-based PIV processing) on the statistics. As an example, Fig. 9 (top) shows the RMS fluctuations of the axial velocity fields using the four velocimetry processing methods, while Fig. 9 (bottom) shows a single slice of the RMS profile at the location denoted by the white, dashed line in the RMS fields. First, it is noted that all four processing methods yield very similar RMS fields, enforcing the quantitative aspect of the wOFV approaches. Second, the structural artifacts resulting from previous discrete regularization approach affect higher-order moments. For example, these are clearly observed as a square-shaped or “grid-like” pattern embedded within the RMS fluctuations of the axial velocity fields (lower left image) shown in Fig. 9. More specifically, when examining the extracted RMS profiles, the previous method (solid, red line) imparts a frequency modulation onto the profile that is approximately 2–3% of the local RMS value. However, these artifacts are eliminated when applying the current approach of continuous regularization, and the current wOFV results yield improved spatial resolution in the extracted statistics, characteristic of the much finer resolvable flow features compared to processing with correlation-based PIV.

Fig. 9

(Top) RMS fluctuations of the axial component of the velocity field for each velocimetry method as applied to the experimental data set from the turbulent jet flow. Note that structural artifacts are present in the RMS fields when using the previous wOFV processing (bottom left) and that they are eliminated using the current wOFV method (bottom right). (Bottom) RMS velocity profiles extracted from the region denoted by a white, dashed line in the images. A periodic modulation of the RMS profile is clearly visible for the previous wOFV method (red line). Symbols in the PIV data indicate the locations of vectors

6 Summary and conclusions

The current manuscript presents recent improvements in a wavelet-based optical flow velocimetry (wOFV) method applied to tracer particle images that leads to increased accuracy through the application of a physically sound regularization procedure. The regularization is based on second-order penalization of the gradients of divergence and curl, which enforces realistic flow structure. The regularization is performed in the wavelet domain and the implementation is described in detail for any general set of boundary conditions for the first time. To derive the “continuous regularization” implementation for any general set of boundary conditions, an alternative method for two-dimensional separable wavelet transforms via matrix multiplication is presented. Not only does this method permit efficient continuous regularization for arbitrary boundary conditions, but it also is shown to be significantly faster than traditional wavelet transform algorithms (i.e., convolution) on a single processor for images smaller than 4 MP, even though its theoretical complexity is higher. The matrix multiplication method also is easily parallelizable for further speedup. Although the use of matrix multiplications for performing wavelet transforms is well-known within the applied mathematics community, the authors are unaware of previous works demonstrating faster computation of transforms via matrix multiplication compared to conventional convolution or lifting methods.

The implementation of continuous regularization (specifically, second-order penalization of the gradients of the divergence and curl) in the current wOFV method is shown to have significant benefits in terms of velocity estimation compared to the previous wOFV method employing discrete regularization. Analysis of velocity estimates using synthetic particle images generated from a 2D DNS of isotropic turbulence show an increase in accuracy through a 10–15% reduction in RMSE error when compared to the actual DNS result. When using the new wOFV methodology (with continuous regularization), the synthetic data and experimental data from a turbulent jet experiment show the elimination of square-shaped structural artifacts that occur when processing with discrete regularization. For example, these artifacts are observed in instantaneous vorticity fields, derived higher-order statistical moments (e.g., RMS fluctuations), and calculated turbulence energy and dissipation spectra at the highest spatial frequencies (finest flow scales). Therefore, the current methodology with continuous regularization allows much more accurate velocity estimations of fine-scale flow features, which is a significant advantage of wOFV compared to correlation-based PIV. In fact, the current methodology allows an increase in dynamic range, with the ability to generate 2D velocity field images that can resolve the dissipative scales in high-Reynolds number, turbulent flows. While the new wOFV method with continuous regularization is shown to significantly improve velocity estimation in turbulent flows, additional work is still needed to assess the sensitivities of wOFV to non-ideal experimental effects (e.g., non-uniform illumination and tracer seeding density, out-of-plane displacement of tracer particles, etc.) and to determine its limits of applicability before it can be used freely to measure velocity from tracer particle images in a broad range of fluid flow experiments.