Keywords

1 Introduction

Chaos is an interesting phenomenon which has been extensively studied in the last three decades. Chaotic systems are characterized by their extreme sensitivity both to initial conditions as well as to parameters changes. The great interest allowed to chaotic systems is motivated by their important applications in various fields including for instance physics, chemistry, biology, ecology, engineering and economics just to name a few (Azar et al. 2015; Hilborn 2001; Lakshmanan and Rajasekhar 2003; Strogatz 1994). In the recent past, there is increasing interest in the study of robust chaotic systems with as simple as possible mathematical model and simple electronic circuit. Some typical examples of this class of chaotic systems have been investigated in Sprott (2000a, b), Vaidyanathan et al. (2016). In these references, the authors studied several new systems with many nonlinearities that show chaotic behavior with easy electronic circuit realization. These systems are modelled by the time evolution of a single scalar variable x given by \(\dddot x\, = \,F(x,\,\dot{x},\,\ddot{x})\) and namely jerk equation. In this equation, \(x,\,\dot{x},\,\ddot{x}\) and \(\dddot x\) represent position, velocity, acceleration and jerk (the time derivative of the acceleration), respectively. According to the simplicity and elegance (in the mathematical model and electronic circuit) of this class of chaotic systems, development of new jerk systems is of great importance. In this point of view, in Benitez et al. (2006), the authors introduced and investigated theoretically and experimentally a new jerk system obtained by converting the well know Van der Pol architecture into a third order differential equation. The proposed mathematical model and electronic circuit are relatively simple. Also, using the same technique, an autonomous chaotic Duffing oscillator based on a jerk architecture is reported in Louodop et al. (2014). The finite-time synchronization of two identical proposed chaotic jerk systems via a simple linear feedback control is examined. The authors used theoretical proofs, numerical and PSpice simulations, as well as practical implementation to demonstrate the feasibility of their proposed scheme. Another interesting works on jerk systems are reported in Kengne et al. (2016, 2017), where the authors introduced and analyzed a new jerk oscillators with hyperbolic sine and smooth piecewise quadratic nonlinearities. They proved through theoretical analysis, numerical simulations and experimental measurements that both systems experience very rich and complex dynamical behaviors such as period-doubling, symmetry recovering crises events, antimonotonicity (i.e. the concurrent creation and annihilation of periodic orbits) and coexistence of multiple attractors.

Motivated by the above mentioned works reported in Sprott (2000a, b), Benitez et al. (2006), Louodop et al. (2014), Kengne et al. (2016, 2017) and many others, in this chapter, we consider an autonomous chaotic jerk oscillator which is obtained by converting the second-order well know Helmholtz oscillator (Del Rio et al. 1992) into a third order differential equations using the jerk architecture. The Helmholtz oscillator is a second order differential equation with a quadratic nonlinearity (Del Rio et al. 1992; Thompson 1989; Gottwald et al. 1995). This oscillator known to naval-architects as the Helmholtz-Thompson equation, provides a simple archetype to describe ship stability to waves in windy situations and its potential and eventual capsize (Thompson et al. 1990). It plays an important role in a large number of developments. In Del Rio et al. (1992) the author provides an overview of the dynamic response of the system which has been studied experimentally by Gottwald et al. (1995). The inhibition of chaotic escape is considered in the context of Balibrea et al. (1998) and a more general approach to the problem is discussed in Lenci and Rega (2001). It is interesting to note that the escape of a dynamical system from a potential well is a common topic in physics and engineering and under periodic forcing it is known that the escape will often be triggered by chaotic motions. The Helmholtz equation finds direct application in the study of bubble dynamics (Kang and Leal 1990) and is much discussed in the naval architecture literature (Thompson 1997). The engineering integrity diagram (Soliman and Thompson 1989) and the use of Melnikov theory to predict parameter values for which erosion of basins of attraction takes place were developed in this context. These concepts continue to find fruitful applications in quantification of capsize resistance, see Spyrou et al. (2002).

Chaos synchronization is one the important issues in nonlinear dynamical science because of its various applications in physics, chemical reactors, control theory, biological networks, artificial neural networks, secure communication, etc. (Blekhman 1988; Pikovsky et al. 2001; Nagaev 2003; Pecora and Carrol 1990; Junde and Parlitz 2000). Various types of synchronization including complete synchronization, generalized synchronization, phase synchronization, lag synchronization, anticipated synchronization and measure synchronization (Vincent et al. 2005; Rullkov et al. 1995; Rosemblum et al. 1997; Voss 2000; Hampton and Zanette 1999) have been investigated in the literature. To achieve these different type of synchronization in dynamical systems, many several methods have been identified and studied. Among these include adaptive control, active control, nonlinear control, sliding mode control and backstepping design. The backstepping technique has been recognized as a powerful design technique for stabilization, tracking and synchronization of chaotic systems. It has been reported in Krstic et al. (1995) that backstepping can guarantee global stability, tracking and transient performance of a broad class of strict-feedback nonlinear systems. Due to the many advantages of backstepping design, in this chapter, we develop an extended backstepping technique to achieve the synchronization of two identical coupled autonomous Helmholtz like-jerk oscillators.

The goal of this chapter is fourfold: (i) to enrich the literature by proposing a relatively simple autonomous chaotic jerk system obtained by converting the second-order well know Helmholtz oscillator into a third order differential equations using the jerk architecture; (ii) to point out the stability and bifurcation analyses in order to reveal different dynamics of the system with respect to its parameter as well as highlighting some of its singularities; (iii) to carry out an experimental study of the system to validate the theoretical analyses and (iv) to investigate the synchronization of a coupled autonomous Helmholtz jerk oscillators via extended backstepping method in order to promote chaos-based synchronization designs of this type of oscillators. Such an approach is particularly useful as it provides important tools for the design of such types of oscillators for relevant engineering applications.

The layout of chapter is as follows. Section 2 describes the system under study and highlights some of its basic properties. The stability of the equilibrium points is also examined and conditions for the occurrence of the Hopf bifurcation are derived. Section 3 deals with numerical study. The bifurcation structures of the system are investigated in order to depict some interesting transitions such as period-doubling and reverse period-doubling scenarios to chaos. Some windows showing the hysteretic dynamics (responsible of the occurrence of the coexistence of multiple attractors) are depicted. The multistability is illustrated by plotting the cross-sections of the basins of attraction of various coexisting attractors. The experimental study is carried out in Sect. 4. The laboratory experimental measurements show a qualitative agreement with numerical results. Section 5 discusses the design of the extended backstepping controllers for synchronization of chaos in the jerk systems. Numerical simulations are given for the illustration and verification of the effectiveness and feasibility of the synchronization technique. Finally in Sect. 6, we summarize our results and draw the conclusions of this chapter.

2 Description and Analytical Analysis of the Proposed Autonomous Helmholtz Like-Jerk Oscillator

2.1 System Description and Basic Properties

In this chapter we consider an autonomous Helmholtz like-jerk oscillator derived from the standard nonautonomous Helmholtz oscillator (Del Rio et al. 1992) described by a two-dimensional differential equation as follows

$$\frac{{d^{2} x}}{{dt^{2} }}\, + \,\delta \frac{dx}{dt}\, + \,x\, + \,x^{2} \, = \,f\,\sin (\omega t)$$
(1)

where \(x\) denotes the vibratory displacement, \(\delta \, > \,0\) is a dimensionless damping coefficient, \(f\) and \(\omega\) are respectively, the amplitude and the pulsation of the harmonic external force. It is demonstrated in Thompson (1989), Gottwald et al. (1995) that Eq. (1) can oscillate chaotically for some specific parameters setting. Motived by the fact that jerk systems are simple in the mathematical representation and easy to realize its corresponding electronic circuit, we propose in this section a three dimensional autonomous Helmholtz oscillator based on jerk architecture. The jerk systems are the third-order equation defined as in Sect. 1. The Helmholtz oscillator defined in Eq. (1) with \(f = 0\) can be converted to a jerk oscillator, as follows

$$\frac{{d^{3} x}}{{dt^{3} }}\, = \, - \left( {\frac{{d^{2} x}}{{dt^{2} }}\, + \,\delta \frac{dx}{dt}\, + \,x\, + \,x^{2} } \right)$$
(2)

where the parameter \(\delta\) has the same signification as in Eq. (1). Obviously, Eq. (2) can be converted to the following set of three coupled first-order nonlinear differential equations:

$$\left\{ {\begin{array}{*{20}l} {\frac{dx}{dt}\, = \,y} \hfill \\ {\frac{dy}{dt}\, = \,\gamma z} \hfill \\ {\frac{dz}{dt}\, = \, - z\, - \delta y\, - x\, - x^{2} } \hfill \\ \end{array} } \right.$$
(3)

where \(dx/dt\, = \,y,\,d^{2} x/dt^{2} \, = \,z\) and \(\gamma\) a new parameter introduced in order to achieve chaotic behavior in Eq. (2). The simplicity of the model is remarkable. It can be implemented experimentally using an appropriate analog electronic circuit as well as integrated circuit technology.

The divergence of system (3) can be obtained as follows

$$\nabla V\; = \;\frac{{\partial \dot{x}}}{\partial x}\; + \;\frac{{\partial \dot{y}}}{\partial y}\; + \;\frac{{\partial \dot{z}}}{\partial z}\; = \; - 1$$
(4)

Obviously, \(\nabla V\) is less than zero and therefore, system (3) is dissipative. This means that the system can support attractors.

2.2 Analytical Analysis of the Proposed Autonomous Helmholtz Jerk Oscillator

It is well known that the equilibrium points play an important role on the dynamics of nonlinear system (Hilborn 1994). By setting the right hand side of system (3) to zero, it is found that there are two equilibrium points \(E_{1} (0,\,0,\,0)\) and \(E_{1} \,( - 1,\,0,\,0)\). The characteristic equation obtained at any equilibrium point \(E^{*} \,(x^{*} ,\,y^{*} ,z^{*} )\) is defined as

$$\lambda^{3} \, + \,\lambda^{2} \, + \,\gamma \delta \lambda \, + \,\gamma (2x^{*} \, + \,1)\, = \,0$$
(5)

The characteristic equation for the equilibrium point \(E_{1} (0,\,0,\,0)\) is

$$\lambda^{3} \, + \,\lambda^{2} \, + \,\gamma \delta \lambda \, + \,\gamma \, = \,0$$
(6)

Based on Routh-Hurwitz conditions, Eq. 6 has all roots with negative real parts if and only if \(\gamma (\delta \; - \;1)\; > \;0\). The equilibrium point \(E_{1} (0,0,0)\) is stable if \(\delta > 1\) and unstable if \(\delta < 1\) provided that the parameters \(\gamma\) and \(\delta\) are strictly positive. The two situations (stable for \(\delta > 1\) and unstable for \(\left. {\delta < 1} \right)\) suggest the existence of the Hopf bifurcation from the equilibrium point \(E_{1} (0,0,0)\) when \(\delta\) is selected as the control parameter.

Theorem

The system under scrutiny undergoes a Hopf bifurcation at the equilibrium point \(E_{1} (0,\,0,\,0)\) when \(\delta\) passes through the critical value \(\delta_{H} \, = \,1\).

Proof

Let a root of the characteristic Eq. (6) as \(\lambda \, = \,i\omega_{0} \left( {\omega_{0} \; > \;0} \right)\). By substituting this root into Eq. (6) and after some manipulations, we have

$$\omega \, = \,\omega_{0} \, = \,\sqrt \gamma$$
(7a)
$$\delta_{H} \, = \,1$$
(7b)

The differentiation of both sides of Eq. (6) with respect to bifurcation parameter \(\delta\) leads to the following expression

$$\frac{d\lambda }{d\delta }\, = \,\frac{ - \gamma \lambda }{{3\lambda^{2} \, + \,2\lambda \, + \,\gamma \delta }}$$
(8)

By substituting \(\lambda\) and \(\delta\) by their corresponding expressions defined above into Eq. (8), the following relation is obtained

$$\left. {\text{Re} \left( {\frac{d\lambda }{d\delta }} \right)} \right|_{\begin{subarray}{l} \lambda = i\omega_{0} \\ \delta = \delta_{H} \end{subarray} } \, = \, - \frac{\gamma }{2(\gamma + 1)}\, \ne \,0$$
(9)

Provided that the characteristic equation of the system at the equilibrium point \(E_{1} (0,\,0,\,0)\) has two purely imaginary eigenvalues and the real part satisfy Eq. (9), thus all the conditions for occurrence of Hopf bifurcation are satisfied. As consequence, system (3) undergoes Hopf bifurcation at critical value of control parameter \(\delta_{H} = 1\) and periodic solutions will exist in a neighbourhood of this critical point. Thus the proof is completed.

The characteristic equation for the equilibrium point \(E_{2} ( - 1,\,0,\,0)\) is

$$\lambda^{3} + \lambda^{2} + \gamma \delta \lambda - \gamma = 0$$
(10)

It is obvious that the equilibrium point \(E_{2} ( - 1,\,0,\,0)\) is always unstable provided that the corresponding characteristic Eq. (10) has coefficients with different signs and the parameters \(\gamma\) and \(\delta\) are positive. Thus, the system under consideration is a self-exited system since its basin of attraction is associated with an unstable equilibrium.

3 Complex Dynamics in the Autonomous Helmholtz Like-Jerk Oscillator

In order to investigate various bifurcation structures in the proposed jerk oscillator, system (3) is integrated numerically using the standard fourth-order Runge-Kutta integration algorithm (Press et al. 1992). Throughout this chapter, the time grid is always \(\Delta t\, = \,0.001\) and the calculations are pointed out using variables and constants parameters in extended mode. The system is integrated for a sufficiently long time and the transient is discarded. The transition to chaos is characterized by the bifurcation diagram and graph of largest Lyapunov exponent noted \(\left( {\lambda_{\hbox{max} } } \right)\). The bifurcation diagram is computed by plotting the local maxima or local minima of the state variable with respect to the control parameter that is changed in tiny steps and the final state at each iteration of the control parameter is used as the initial conditions for the next iteration, while the largest Lyapunov exponent is obtained numerically using the algorithm of Wolf et al. (1985). It measures the exponential rates of divergence or convergence of nearby trajectories in phase space, which can also be used to measure the sensitive dependence of the initial conditions. In particular, the sign of the largest Lyapunov exponent is used to determine the rate of almost all small perturbations to the system’s state, and consequently, the nature of the underlined dynamical attractor. For \(\lambda_{\hbox{max} } \, < \,0\), all perturbations vanish and trajectories starting sufficiently close to each other converge to the same stable fixed point in state space; for \(\lambda_{\hbox{max} } \, = \,0\), initially close orbits remains close but distinct, corresponding to oscillatory dynamics of a limit-cycle or torus; and finally for \(\lambda_{\hbox{max} } \, > \,0\), small perturbations grow exponentially, and the system evolves chaotically within the folded space of a strange attractor. In addition, the complexity of system (3) is examined by using the Lyapunov dimension of the attractors which is computed with the help of the definition proposed by Kaplan and Yorke expressed (Frederickson et al. 1983) as

$$D_{L} \, = \,k\, + \,\frac{1}{{\left| {\lambda_{k + 1} } \right|}}\sum\limits_{j = 1}^{k} {\lambda_{j} }$$
(11)

where \(k\) is the largest integer satisfying the following conditions \(\sum\nolimits_{j = 1}^{k} {\lambda_{j} } \, \ge \,0\) and \(\sum\nolimits_{j = 1}^{k + 1} {\lambda_{j} } \, < \,0\). The Kaplan-Yorke dimension indicates the complexity of the attractor. In other words, it is a measure of the degree of disorder of the points on the attractor. The dynamics of system (3) is also investigated by using another numerical tools such as, the time series of state variables, the frequency spectra as well as the cross sections of the basin of attraction. The latter tool is computed by taking a grid 500 × 500 initial states, testing each initial state on the grid to determine which attractor is goes to, and then plotting those which lead to the chaotic attractors \(\left( {\lambda_{\hbox{max} } \, > \,0} \right)\) and periodic solutions \(\left( {\lambda_{\hbox{max} } \, \le \,0} \right)\). The same strategy is used to compute the two-parameter phase diagram in which we take a grid 500 × 500 points of parameter \(\gamma\) and \(\delta\) with fixed initial states.

3.1 Transition to Chaos

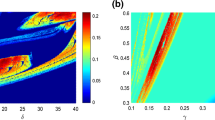
In order to select the values of the system parameters accordingly, we plot in Fig. 1, the two-parameter phase diagram showing the regions of periodic, chaotic and unbounded behaviors in the \(\left( {\gamma ,\,\delta } \right)\) plane with \(4\, \le \,\gamma \, \le \,6\) and \(0.5\, \le \,\delta \, \le \,0.6\).

Fig. 1
figure 1

Two-parameter phase diagram showing different dynamical behaviors of system (3) in the \(\left( {\gamma ,\,\delta } \right)\) plane. The chaotic regions are shown in red, the periodic regions are shown in cyan and unbounded regions are in green

Full size image

In Fig. 1, one can see that different regions of chaotic, periodic and unbounded solutions intertwined intricately. This diagram is of great importance for a practical implementation of system (3). Indeed, it helps to choose the parameters of the system according to the desired bahavior.

We select \(\delta\) as the control parameter in order to examine its sensitivity on the dynamics of the system. To this end, we fix \(\gamma \, = \,4\) and vary \(\delta\) in the range \(0.53\, \le \,\delta \, \le \,1.02\). The bifurcation diagram showing the local maxima (magenta dots) and local minima (blue dots) of coordinate \(x\) associated to the graph of largest Lyapunov exponent versus control parameter \(\delta\) are provided in Fig. 2.

Fig. 2
figure 2

Bifurcation diagram a depicting the local maxima (magenta dots) and local minima (blue dots) of the coordinate \(x\) and the corresponding graph of largest Lyapunov exponent (b) versus control parameter \(\delta\) computed with \(\gamma = 4\). Chaotic and regular behaviors are indicated respectively, by positive and zero largest Lyapunov exponents while fixed points are marked by negative largest Lyapunov exponent

Full size image

It found from Fig. 2 that the system under study can experience various and rich dynamical behaviors such as fixed point motion, Hopf bifurcation, period-doubling bifurcation, periodic and chaotic motions when the control parameter is monitored. For values of \(\delta\) above the critical value \(\delta_{c} \, = \,1\), the system exhibits a fixed point motion (i.e. no oscillations) and the associated largest Lyapunov exponent is negative. By decreasing the control parameter \(\delta\) past this critical value, the system displays a stable period-1 limit cycle born from the Hopf bifurcation. Further decreasing \(\delta\), this period-1 limit cycle metamorphoses to chaos via a series of period-doubling bifurcations. It can be also seen that the bifurcation diagram well coincides with the graph of largest Lyapunov exponent.

To confirm the transition to chaos observed in Fig. 2, sample phase portraits in plane \(\left( {x,\,y} \right)\) accompanied with the corresponding frequency spectra along the control parameter \(\delta\) for \(\gamma \, = \,4\) are shown in Fig. 3.

Fig. 3
figure 3

Phase portraits a(i)–d(i) and corresponding frequency spectra a(ii)–d(ii) depicting routes to chaos in the system with respect to the control parameter \(\delta\) for \(\gamma \, = \,4\). a Period-1 for \(\delta \, = \,0.8\), b period-2 for \(\delta \, = \,0.6\), c period-4 for \(\delta = 0.585\) and d chaos for \(\delta = 0.56\)

Full size image

One can observe that the scenario to chaos predicted by the bifurcation diagram of Fig. 2 is confirmed by the phase portraits of Fig. 3.

Using \(\gamma \, = \,4\) and \(\delta \, = \,0.55\), the corresponding Lyapunov exponents are \(\lambda_{1} \, = \,0.070,\,\lambda_{2} \, = \, - 0.001\) and \(\lambda_{3} \, = \, - 1.069\). From this Lyapunov spectrum, we find that \(\sum\nolimits_{j = 1}^{k + 1} {\lambda_{j} } = \, - 1\, < \,0\), which confirms that system (3) is dissipative. The calculated fractional dimension with the same system parameters setting is

$$D_{L} \, = \,2\, + \,\frac{{\lambda_{1} + \lambda_{2} }}{{\left| {\lambda_{3} } \right|}}\, = \,2.064$$
(12)

Equation (12) clearly indicates that the dissipative system under investigation displays chaotic behavior.

Now, we select also \(\gamma\) as the control parameter in order to investigate its effect on the dynamics of the system. The bifurcation diagram depicting the local maxima of the coordinate \(x\) and corresponding graph of largest Lyapunov exponent with \(\gamma\) varying in the range \(3\, \le \,\gamma \, \le \,14\) are shown in Fig. 4 for \(\delta \, = \,0.55\).

Fig. 4
figure 4

Bifurcation diagram a depicting the local maxima of the coordinate \(x\) with respect to the control parameter \(\gamma\) and the corresponding graph of largest Lyapunov exponent b computed in the range \(3 \le \gamma \le 14\) for \(\delta \, = \,0.55\)

Full size image

The bifurcation diagram (Fig. 4a) and the corresponding graph of largest Lyapunov exponent (Fig. 4b) indicate clearly that there are some windows of periodic and chaotic behaviors. In Fig. 4a, one can observe that two set of data corresponding, respectively, for increasing (blue) and decreasing (magenta) values of control parameter \(\gamma\) are superimposed. This method is a simple way to localize the window in which the system experiences hysteretic phenomenon which is at the origin of multistability (i.e. coexistence of attractors). This striking and exciting phenomenon is examined in the next subsection.

3.2 Coexistence of Attractors in Autonomous Helmholtz Like-Jerk Oscillator

Multistability (i.e. coexistence of multiple attractors) is one of the most striking and exciting phenomenon commonly encountered in dynamical systems. This phenomenon has been reported in almost all natural sciences, including electronics (Maurer and Libchaber 1980; Kamdoum et al. 2016; Kengne et al. 2017; Kengne et al. 2018), optics (Brun et al. 1985), mechanics (Thompson and Stewart 1986), and biology (Foss et al. 1996). During the numerical investigations of the system under consideration, the effects of the initial states on the dynamics of the model were observed. In fact, when we made an enlargement of the bifurcation diagram (Fig. 4a) and the graph of largest Lyapunov exponent (Fig. 4b) in the range \(4\, \le \,\gamma \, \le \,5.8\), the region in which the system experiences hysteretic dynamics (coexisting bifurcation) is clearly visible as shown in Fig. 5.

Fig. 5
figure 5

Enlargement of the bifurcation diagram (a) and corresponding graph of largest Lyapunov exponent (b) of Fig. 4 in the range \(4\, \le \,\gamma \, \le \,5.8\) in order to make more visible the region in which the system exhibits coexisting attractors

Full size image

For the values of \(\gamma\) selected in this window, the dynamics of the system depends on the initial states. For instance, the coexistence of chaotic attractor with period-3 limit cycle obtained respectively, for \(x(0),\,y(0),\,z(0)\, = \,(0.1,\,0.1,\,0.1)\) and \(x(0),\,y(0),\,z(0)\, = \,(0.2,\,0.3,\,0.1)\) is shown in Fig. 6 for \(\delta \, = \,0.55\) and \(\gamma \, = \,5.2\).

Fig. 6
figure 6

Coexistence of two different attractors obtained with \(\delta \, = \,0.55\) and \(\gamma \, = \,5.2\). a Chaotic attractor and b period-3 limit cycle. The initial conditions are respectively, \(x(0),\,y(0),\,z(0)\, = \,(0.1,\,0.1,\,0.1)\) and \(x(0),\,y(0),\,z(0)\, = \,(0.2,\,0.3,\,0.1)\)

Full size image

In order to further characterize the phenomenon of coexisting attractors observed in the system, we provide in Fig. 7 the cross-sections of the basin of attraction, respectively for \(z(0)\, = \,0,\,y(0)\, = \,0\) and \(x(0)\, = \,0\) for \(\delta \, = \,0.55\) and \(\gamma \, = \,5.2\).

Fig. 7
figure 7

(Color online) Cross-sections of the basin of attraction respectively, for \(z(0)\, = \,0\), \(y(0)\, = \,0\) and \(x(0)\, = \,0\) for \(\delta \, = \,0.55\) and \(\gamma = 5.2\) showing the regions of initial conditions leading to chaotic attractors (red) and period-3 limit cycle (cyan). The green dots regions correspond to the unbounded solutions

Full size image

In Fig. 7, the complexity of the basin boundaries is clearly highlighted. It can also be noted that the regions of initial conditions leading to chaotic attractors (red dots) are more abundant than those leading to period-3 limit cycle (cyan dots). This implies that the chaotic behavior in the coexisting windows dominates the period-3 limit cycle. It is known that the occurrence of multiple attractors represents an additional source of randomness (Luo and Small 2007) and system which experience this phenomenon can be used for many applications such as chaos based communication, image encryption and generation of random numbers. However, in many practical situations, this singular phenomenon is not desirable and requires control. Interested readers can see the interesting work of Pisarshik and collaborators (2014) about the review on control of multistability. This direction is an important challenge in the continuation of this work.

4 Electronic Circuit Realization of Proposed Autonomous Helmholtz Like-Jerk Oscillator

The physical realization of theoretical chaotic models is of great importance in various engineering applications such as robotics, chaos based communications, image encryption and random number generation (Banerjee 2010; Volos et al. 2012, 2013a, b). Moreover, the electronic circuit realization of theoretical chaotic models is an effective approach to investigate the dynamics of such systems via for instance the experimental bifurcation diagram obtained by varying the values of variable resistors associated to the control bifurcation parameters (Ma et al. 2014; Buscarino et al. 2009). The dynamics of the system under scrutiny has been examined in preceding paragraphs using theoretical and numerical methods. It is predicted that the system can exhibit very rich and complex behaviors. In this section, to validate the numerical results, we design and realize an electronic circuit capable to emulate the dynamics of system (3). The schematic diagram of the proposed electronic circuit is depicted in Fig. 8.

Fig. 8
figure 8

Electronic circuit realization of the autonomous Helmholtz like-jerk oscillator. The value of electronic components are fixed as \(C\, = \,10\,\text{nF},\,R\, = \,10\,{\text{k}}\Omega ,\,R_{1}\) and \(R_{2}\) variable. The analog multipliers devices are AD633J N-type while operational amplifiers are TL084C N-type ones

Full size image

The electronic circuit of Fig. 8 comprises the analog multipliers used to implement the nonlinear term of the model. They operate over a dynamic range of \(\pm 1\,\text{V}\) with typical tolerance less than \(1\%\). The output signal (W) is connected to those at inputs \(\left( { + X_{1} } \right),\,\left( { - X_{2} } \right),\,\left( { + Y_{1} } \right),\,( - Y_{2} )\), and \(\left( { + Z} \right)\) by the following expression \(W\, = \,(X_{1} - X_{2} )(Y_{1} - Y_{2} )/10\, + \,Z\). The operational amplifiers accompanied with resistors and capacitors which are exploited to implement the basic operations such as addition, subtraction and integration. The bias is provided by a \(15\) V DC symmetry source. By applying the Kirchhoff’s laws into the circuit of Fig. 8, we obtain its mathematical model given by three coupled first-order nonlinear differential equations

$$\left\{ {\begin{array}{*{20}l} {\frac{{dV_{x} }}{dt} = \frac{{V_{y} }}{RC}} \hfill \\ {\frac{{dV_{y} }}{dt} = \frac{{V_{z} }}{{R_{1} C}}} \hfill \\ {\frac{{dV_{z} }}{dt} = - \frac{{V_{z} }}{RC} - \frac{{V_{y} }}{{R_{2} C}} - \frac{{V_{x} }}{RC} - \frac{{V_{x}^{2} }}{{k_{m} RC}}} \hfill \\ \end{array} } \right.$$
(13)

where \(V_{x} ,\,V_{y}\) and \(V_{z}\) are the output voltages of the operational amplifiers. Systems (13) and (3) are equivalent according to the following change of state variables and parameters: \(t = \tau RC;x = V_{x} /1V;y = V_{y} /1V;z = V_{z} /1V;\gamma = R/R_{1} ;\delta = R/R_{2}\). The electronic circuit components are selected as \(C = 10\,\text{nF},\,R = 10\,{\text{k}}\Omega ,\,R_{1} = 2.5\,{\text{k}}\Omega\) and \(R_{2}\) variable. When monitoring the control resistor \(R_{2}\), it is found that the electronic circuit under study displays a rich and striking behaviors including period-doubling route to chaos and coexistence of attractors. A photograph of the experimental hardware on breadboard in operation is shown in Fig. 9. The analog oscilloscope presents the single-band chaotic attractor.

Fig. 9
figure 9

Photograph of the experimental hardware on breadboard in operation. The analog oscilloscope displays the single-band chaotic attractor captured from the experimental circuit

Full size image

The comparison between numerical (left) and experimental (right) phase portraits is provided in Fig. 10 and a very good similarity can be noted.

Fig. 10
figure 10

Experimental phase portraits (right) obtained from the circuit using a dual trace oscilloscope in the XY mode; the corresponding numerical phase portraits are shown in the left obtained by a direct integration of system (3). The scales are \(X\, = \,1\,\text{V}/\text{div}\) and \(X\, = \,2\,\text{V}/\text{div}\) for all pictures

Full size image

In Fig. 10, it clearly appears that the dynamics of the proposed autonomous Helmholtz like-jerk system is well reproduced by the electronic circuit. Moreover, one can note that the experimental circuit displays the same bifurcation scenarios as those obtained numerically.

The phenomenon of coexisting attractors is also validated experimentally for \(R_{1} \, = \,1.92\,{\text{k}}\Omega\) (i.e. \(\left. {\gamma = 5.2} \right)\) and \(R_{2} = 18.18\,{\text{k}}\Omega\) (i.e. \(\left. {\delta = 0.55} \right)\). In Fig. 11, we provide the coexistence between period-3 limit cycle with single band chaotic attractor for different initial states obtained by switching on and off the power supply randomly.

Fig. 11
figure 11

Numerical (left) and experimental (right) phase portraits of coexisting attractors obtained for \(R_{1} \, = \,1.92\,{\text{k}}\Omega\) (i.e. \(\left. {\gamma \, = \,5.2} \right)\) and \(R_{2} \, = \,18.18\,{\text{k}}\Omega\) (i.e. \(\left. {\delta \, = \,0.55} \right)\). Both period-3 limit cycle and chaotic attractor appear randomly in experiment by switching on and off the power supply. The scales are \(X\, = \,1\,\text{V}/\text{div}\) and \(X\, = \,2\,\text{V}/\text{div}\) for all pictures

Full size image

From Fig. 11, one can note the good similarity of experimental portraits of coexisting attractors with those obtained numerically. This serves to proof that the phenomenon of coexisting attractors exists in the proposed autonomous Helmholtz like-jerk oscillator. It should be stressed that system (3) can be also implemented using many other ways such as integrated circuit technology (Trejo Guerra et al. 2012), Field Programmable Gate Array (FPGA) (Koyuncu et al. 2014) and Field Programmable Analog Array (FPAA) technologies (Fatma and Sprott 2016).

5 Synchronization of Two Identical Coupled Autonomous Helmholtz Like-Jerk Oscillators via Extended Backstepping Method

In this section, we synchronize two identical coupled autonomous Helmholtz like-jerk oscillators via extended backstepping method. Based on the proposed approach, generalized weighted controllers are designed to achieve synchronization in chaotic systems. The effectiveness and feasibility of the proposed weighted controllers are verified numerically.

5.1 Design of the Extended Backstepping Controllers for Synchronization in Chaotic Autonomous Helmholtz Like-Jerk Oscillators

Brief recall that the classical backstepping technique has been widely exploited to achieve synchronization in chaotic and hyperchaotic systems. It has the advantage to achieve global stability tracking transient performance for a large class of strict-feedback nonlinear systems (Njah 2010) and the references therein. Moreover, the scheme requires less control effort in comparison to the differential geometric approach (Mascolo 1997). However, the control function designed via this method has been demonstrated to be difficult for practical implementation because of its complexity and high signal strength (Olusola et al. 2011). To overcome these limitations of classical backstepping technique, the improved version of this method namely extended backstepping technique is proposed in Onma et al. (2014). The proposed approach in latter reference is suitable for practical implementation.

To derive the controllers for synchronization in chaotic autonomous Helmholtz like jerk oscillators, we rewrite system (3) in the form

$$\left\{ {\begin{array}{*{20}l} {x_{1} = x_{2} } \hfill \\ {x_{2} = x_{3} } \hfill \\ {x_{3} = - x_{3} - x_{2} - x_{1} - x_{1}^{2} } \hfill \\ \end{array} } \right.$$
(14)

Let system (14) be the drive system and the following be the response

$$\left\{ {\begin{array}{*{20}l} {y_{1} = y_{2} + u_{1} (t)} \hfill \\ {y_{2} = y_{3} + u_{2} (t)} \hfill \\ {y_{3} = - y_{3} - y_{2} - y_{1} - y_{1}^{2} + u_{3} (t)} \hfill \\ \end{array} } \right.$$
(15)

where \(u_{i} (t)i = 1,2,3\) are the control functions.

Let the error state between (14) and (15) defined as

$$e_{i} = y_{i} - x_{i}$$
(16)

From (16), we can obtain the error dynamical system as

$$\left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = e_{2} + u_{1} (t)} \hfill \\ {\dot{e}_{2} = e_{3} + u_{2} (t)} \hfill \\ {\dot{e}_{3} = - e_{3} - \delta e_{2} - e_{1} (1 + e_{1} + 2x_{1} ) + u_{3} (t)} \hfill \\ \end{array} } \right.$$
(17)

The challenge is to determine the control function \(u_{i} (t)\) that can stabilize the error states in (17) at the origin. To this end, we design the controllers in three steps. In the first step, we stabilize the first equation in (17) by considering \(e_{2}\) as controller. Choosing the storage Lyapunov function as \(V_{1} (e_{1} ) = e_{1}^{2} /2\), the time derivative of \(V_{1}\) along the trajectory of error dynamical subsystem \(\dot{e}_{1}\) is

$$\dot{V}_{1} = e_{1} \dot{e}_{1} = e_{1} (e_{2} + u_{1} )$$
(18)

We suppose that the controller \(e_{2}\) has the following form \(e_{2} = \alpha_{1} (e_{1} )\), then (18) can be written as \(\dot{V}_{1} = e_{1} (\alpha_{1} e_{1} + u_{1} )\). The time derivative of Lyapunov function \(\dot{V}_{1}\) is negative definite if the estimate function \(\alpha_{1} (e_{1} ) = - e_{1}\) and \(u_{1} = 0\). Thus, the subsystem \(e_{1}\) is stabilized. In the second step, we choose the error between \(e_{2}\) and \(\alpha_{1} (e_{1} )\) as

$$w_{2} = e_{2} - \alpha_{1} e_{1} = e_{2} + e_{1}$$
(19)

The time derivative of (19) is

$$\dot{w}_{2} = e_{3} + w_{2} - e_{1} + u_{2}$$
(20)

We now stabilize the \(\left( {e_{1} ,\,w_{2} } \right)\) subsystem defined by (20) as follows. Let a Lyapunov function \(V_{2} (e_{1} ,\,w_{2} ) = V_{1} (e_{1} ) + w_{2}^{2} /2\) and its time derivative is

$$\dot{V}_{2} = \dot{V}_{1} (e_{1} ) + w_{2} \dot{w}_{2} = - e_{1}^{2} + w_{2} ( - w_{2} + e_{3} + 2w_{2} - e_{1} + u_{2} )$$
(21)

Estimating that the controller \(e_{3} = \alpha_{2} (e_{1} ,\,w_{2} )\), then (21) can be written as

$$\dot{V}_{2} = - e_{1}^{2} + w_{2} ( - w_{2} + \alpha_{2} + 2w_{2} - e_{1} + u_{2} )$$
(22)

If the estimative function \(\alpha_{2} (e_{1} ,\,w_{2} ) = 0\) and \(u_{2} \, = \,e_{1} \, - 2w_{2}\), then \(\dot{V}_{2} = - e_{1}^{2} - w_{2}^{2}\) is negative definite and hence the \(\left( {e_{1} ,w_{2} } \right)\) subsystem is stabilized. For the last step, we define the error between \(e_{3}\) and \(\alpha_{2} (e_{1} ,\,w_{2} )\) as

$$w_{3} = e_{3} - \alpha_{2} (e_{1} ,w_{2} ) = e_{3}$$
(23)

The time derivative of (23) is

$$\dot{w}_{3} = \dot{e}_{3} = - e_{3} - \delta e_{2} - e_{1} (1 + e_{1} + 2x_{1} ) + u_{3}$$
(24)

We now stabilize the \(\left( {e_{1} ,\,w_{2} ,\,w_{3} } \right)\) complete system defined by (17) as follows. Let a Lyapunov function \(V_{3} (e_{1} ,\,w_{2} ,\,w_{3} ) = V_{2} (e_{1} ,\,w_{2} ) + w_{3}^{2} /2\) and its time derivative is

$$\begin{aligned} \dot{V}_{3} & = \dot{V}_{2} (e_{1} ,\,w_{2} ) + w_{3} \dot{w}_{3} = - e_{1}^{2} - w_{2}^{2} + w_{3} \dot{w}_{3} \\ & = - e_{1}^{2} - w_{2}^{2} + w_{3} [ - w_{3} - \delta e_{2} - e_{1} (1 + e_{1} + 2x_{1} ) + u_{3} ] \\ \end{aligned}$$
(25)

Estimating that \(u_{3} = \delta e_{2} + e_{1} (1 + e_{1} + 2x_{1} )\), (25) becomes

$$\dot{V}_{3} = - e_{1}^{2} - w_{2}^{2} - w_{3}^{2} < 0$$
(26)

Thus, the synchronization goal is realized with the weight added to the control functions as follows

$$\left\{ {\begin{array}{*{20}l} {u_{1} (t) = [0]\varepsilon_{1} } \hfill \\ {u_{2} (t) = [e_{1} - 2w_{2} ]\varepsilon_{1} } \hfill \\ {u_{3} (t) = [\delta e_{2} + e_{1} (1 + e_{1} + 2x_{1} )]\varepsilon_{3} } \hfill \\ \end{array} } \right.$$
(27)

5.2 Numerical Simulations

In this subsection, numerical simulations are given in order to verify and demonstrate the effectiveness and feasibility of the proposed method. The fourth-order Runge-Kutta method is applied to integrate the drive (14) and response (15) system with time step size equal to 0.001. The initial conditions are selected randomly as \(x_{1} (0),\,x_{2} (0),\,x_{3} (0)\, = \,(0.1,\,0.1,\,0.1)\) and \(y_{1} (0),\,y_{2} (0),\,y_{3} (0)\, = \,( - 1,\,1,\, - 0.1)\), respectively for the drive and the response system, while the parameter values are chosen to be \(\gamma = 4\) and \(\delta = 0.56\) so that the systems exhibited chaotic behaviors if no control functions are applied. The time response of the error system and the synchronization quality which is defined by \(e = \sqrt {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} }\) are shown in Fig. 12 for the control function applied after approximately 100 units of time.

Fig. 12
figure 12

Error dynamics between two identical coupled chaotic autonomous Helmholtz like-jerk oscillators (a)–(c) and the synchronization quality (d) with the controller deactivated \(50\, < \,t\, < \,100\). The values of parameters and initial conditions are indicated in the text and \(\varepsilon_{i} \, = \,0.3\) where \(i\, = \,1,\,2,\,3\)

Full size image

From Fig. 12, it is found that the error dynamics moves chaotically with time when the controllers are switched off in the interval \(50\, < \,t\, < \,100\). After this interval, it is very clear that the synchronization is achieved since the error dynamics between the two identical coupled chaotic autonomous Helmholtz like-jerk oscillators approaches zero as \(t\, \to \,\infty\). The synchronization between the drive and the response systems is also confirmed by the synchronization quantity \(e\) which approaches also zero as \(t\, \to \,\infty\). It is important to notice that, the control strength and its complexity are reduced by about \(70\%\) when the extended backstepping method is used compared with the classical backstepping approach (Mascolo 1997; Njah 2010; Olusola et al. 2011). Thus, the new approach investigated in this chapter produces economic controllers with low energy consumption which may be of vital importance for practical applications (Onma et al. 2014). The effectiveness and feasibility of study of synchronization of chaotic systems is verified and is found to be good to be used in secure communication field.

6 Conclusions

This chapter has focused on the dynamical analysis, electronic circuit realization and synchronization of an autonomous oscillator obtained by converting the two-dimensional well know Helmholtz oscillator into a third-order differential equations using the jerk architecture. The stability of the equilibrium points has been examined and conditions for the occurrence of the Hopf bifurcation have been derived. Some basic properties of the model have been studied using standard nonlinear analysis tools. The bifurcation structures of the proposed jerk oscillator were revealed some interesting transitions and phenomena such as period-doubling and reverse period-doubling scenarios to chaos, periodic windows and hysteretic behavior. The latter phenomena has been further illustrated by computing some cross-sections of the basin of attraction showing the domains of initial conditions where coexisting attractors are found. An experimental study has been carried out and the laboratory experimental measurements were in a good qualitative agreement with numerical results. Finally, appropriate controllers have been designed via extended backstepping technique to synchronize the proposed jerk oscillators. Numerical simulations are given to illustrate and verify the effectiveness and feasibility of the synchronization technique. It is worth pointing out that the extended backstepping technique has several advantages over other methods of synchronization as mentioned in Sect. 5. Thus, synchronization of the autonomous proposed jerk oscillators via extended backstepping technique is of practical interest. We stress also that the approach followed in this chapter may be exploited rigorously to the study of any other nonlinear dynamical system exhibiting coexisting bifurcations.