1 Introduction

Chaotic behaviors have been found in many different systems, such as weather and climate [39], economical [19], mechanical [4], biological [14], electronics systems [13], optoelectronics systems [12], optical systems [22] and optomechanics systems [5]. Chaos has been found useful with great potential in many fields, including liquid mixing with low power consumption, human brain and heartbeat regulation and secure communications [3, 18, 32, 33, 45]. One of the important research directions is constructing robust chaotic oscillators with simple structures [31, 35, 42, 43]. There are two kinds of chaotic oscillators: Non-autonomous [44] and autonomous oscillators [37]. Among the existing autonomous chaotic oscillators, there is a family of chaotic oscillators with easy electronic implementation described by a three-dimensional differential equation of the form \(\dddot x = f\left( {x,\,\dot{x},\,\ddot{x}} \right)\). It is called a jerk equation where \(x\), \(\dot{x}\), \(\ddot{x}\) and \(\dddot x\) represent a dynamical variable, first-, second-, third-order time derivative, respectively [42]. Autonomous chaotic jerk oscillators attracted increasingly much attention due to their simplicity. In [42], Sprott proposed many new jerk oscillators with several nonlinearities that show chaotic behavior with easy electronic implementation. The authors of [9, 17, 50] introduced three autonomous chaotic oscillators using the Van der Pol dynamics immersed into a jerk oscillator. In [30], the authors proposed and studied theoretically and experimentally an autonomous chaotic Duffing oscillator based on a jerk oscillator. By converting the autonomous two-dimensional Van der Pol–Duffing oscillator to a jerk oscillator, the authors of [46] obtained a chaotic Van der Pol–Duffing jerk oscillator and investigated the dynamical behavior of the integer proposed chaotic jerk oscillator, chaos control and synchronization in its fractional-order form. The dynamical analysis, electronic circuit realization and synchronization of a proposed autonomous chaotic Helmholtz jerk oscillator has been studied in [36, 47].

Therefore, this paper proposes an autonomous Morse jerk oscillator which is built by converting the two-dimensional autonomous Morse oscillator into a three-dimensional oscillator using the jerk architecture. Morse oscillator is a two-dimensional equation describing an oscillator with two exponential nonlinearities. It is used as a well-known model for molecular vibrations [23, 27, 34, 49]. Despite the simplicity of the Morse oscillator, its dynamical behavior is extremely rich and research on the area is still going on [1]. The rate-equations describing the proposed jerk oscillator has two exponential nonlinearities and its investigation reveals multistability phenomenon. The multistability feature is usually found in nonlinear dynamics [11, 15, 21]. Multistable oscillators are categorized to oscillators with ordinary multistability [24,25,26], oscillators with extreme multistability [6,7,8] and oscillators with megastability [28, 29, 48]. This paper is devoted to the analysis, circuit realization and controls of a proposed autonomous Morse jerk oscillator.

The organization of the paper is as follows: The proposed jerk oscillator is dynamically analysed in the Sect. 2. The circuit realization of the proposed autonomous Morse jerk oscillator is presented in Sect. 3 while Sect. 4 deals with the controls of the signal amplitudes, chaotic behavior and coexisting attractors in proposed jerk oscillator. Finlay, the conclusion is given in Sect. 5.

2 Analytical and numerical analysis of the proposed autonomous Morse jerk oscillator

The autonomous two-dimensional Morse equation is given by [27, 34, 49]:

$$ \ddot{x} + \gamma \dot{x} + \beta \left[ {1 - \exp \left( { - \alpha x} \right)} \right]\exp \left( { - \alpha x} \right) = 0, $$
(1)

where the parameter \(\gamma\) is a dimensionless damping coefficient \(\,\left( {\gamma > 0} \right)\), the parameters \(\beta \,\left( {\beta > 0} \right)\) and \(\alpha \,\left( {\alpha > 0} \right)\) are the dissociation energy and range parameter, respectively. The autonomous Morse Eq. (1) can be converted to a jerk oscillator, as follows:

$$ \dot{x} = y, $$
(2a)
$$ \dot{y} = \delta z, $$
(2b)
$$ \dot{z} = - z - \gamma y - \beta \left[ {1 - \exp \left( { - \alpha x} \right)} \right]\exp \left( { - \alpha x} \right), $$
(2c)

where \(\dot{x}\left( t \right) = y\left( t \right)\) and \(\ddot{x}\left( t \right) = z\left( t \right)\). A positive constant parameter \(\,\delta \,\) is added in Eq. (2b) in order to achieve chaotic behavior in system (2) because for \(\,\delta = \alpha = 1\,,\,\gamma = 0.16\,\) and by varying the parameter \(\,\beta ,\,\) the trajectories of system (2) converge to the equilibrium point \(O = \,\left( {0,0,0} \right)\,\) up to \(\,\beta = \gamma = 0.16\,\) where a Hopf bifurcation occurs followed by period-1-oscillations and periodic spiking oscillations (not shown). By further increasing the value of parameter \(\,\beta ,\) system (2) displays only periodic oscillations. System (2) is dissipative because \(\nabla V\, = \,\frac{{\partial \dot{x}}}{\partial x}\, + \,\frac{{\partial \dot{y}}}{\partial y}\, + \,\frac{{\partial \dot{z}}}{\partial z}\, = \, - 1 < 0\). It has only one equilibrium point \(\,O = (0,0,0)\). The characteristic equation of the Jacobian matrix at the equilibrium point \(\,O = (0,0,0)\) is:

$$ \lambda^{3} \, + \,\,\lambda^{2} + \,\,\gamma \delta \lambda \, + \alpha \beta \delta = \,0. $$
(3)

Using the Routh–Hurwitz conditions, this equation has all roots with negative real parts if and only if:

$$ \alpha \beta \delta > 0, $$
(4a)
$$ \left( {\gamma - \alpha \beta } \right)\delta > 0. $$
(4b)

Since \(\,\delta > 0\), the equilibrium point \(\,O = (0,0,0)\) of system (2) is stable if \(\gamma \, > \,\alpha \beta\) and unstable for \(\gamma \, < \,\alpha \beta\). Since the equilibrium point \(\,O = (0,0,0)\) changes stability properties, system (2) has either a Hopf bifurcation or transcritical bifurcation at the equilibrium point \(\,O\) for \(\,\beta = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\).

Theorem

If \(\,\delta > 0\), then system (3) undergoes a Hopf bifurcation at the equilibrium point \(O\) when \(\,\beta \,\) passes through the critical value \(\beta_{H} = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\).

Proof

Let \(\,\lambda = j\omega \,\)(\(\omega > 0\,\) and \(j^{2} = - 1\)) be a root of Eq. (3). By inserting \(\,\lambda = j\omega \,\) it into Eq. (3) and separating real and imaginary parts, it is obtained

$$ \omega = \omega_{{0_{{}} }} = \sqrt {\alpha \beta \delta } , $$
(5a)
$$ \beta_{H} = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }. $$
(5b)

Differentiating both sides of Eq. (3) with respect to \(\,\beta\), it is obtained

$$ 3\lambda^{2} \frac{d\lambda }{{d\beta }} + 2\lambda \frac{d\lambda }{{d\beta }} + \gamma \delta \frac{d\lambda }{{d\beta }} + \alpha \delta = 0 $$
(6a)

and

$$ \frac{d\lambda }{{d\beta }} = \frac{ - \alpha \delta }{{3\lambda^{2} + 2\lambda + \gamma \delta }} $$
(6b)

then

$$ {\text{Re}} \left( {\left. {\frac{d\lambda }{{d\beta }}} \right|_{{\beta = \beta_{H} ,\,\lambda = i\omega_{0} }} } \right) = - \frac{\alpha }{{2\gamma \left( {1 + \gamma \delta } \right)}} \ne 0. $$
(6c)

Since the Jacobian matrix of system (2) at the equilibrium point \(O\) has two purely imaginary eigenvalues and the real parts of eigenvalues satisfy \(\,{\text{Re}} \left( {\left. {\frac{d\lambda }{{d\beta }}} \right|_{{\beta = \beta_{H} ,\,\lambda = i\omega_{0} }} } \right) \ne 0\); all the conditions for Hopf bifurcation to occur are met. Consequently, system (2) undergoes a Hopf bifurcation at \(O\) when \(\beta = \beta_{H} = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\) and periodic solutions will exist in a neighbourhood of the point \(\beta_{H}\) (provided that \(\,\delta > 0\,\) holds).

The effect of parameters \(\,\alpha ,\,\beta ,\,\gamma \,\) and \(\,\delta \,\) on the dynamics behaviours of system (2) can be studied by using numerical simulations. So, to identify the dynamical behaviours of system (2), the two parameters largest Lyapunov exponents (LLE) diagrams are constructed in Fig. 1.

Fig. 1
figure 1

(Colour online) Two parameters LLE diagrams in: a \(\,\left( {\delta ,\,\beta } \right)\,\) space for \(\,\gamma = 0.16\) and b \(\,\left( {\gamma ,\,\beta } \right)\,\) space for \(\,\delta = 18\). The other parameter is \(\,\alpha = 1\)

Full size image

From Fig. 1a, it is clear that colors are associated with the magnitude of the LLE as follows: blue stands for the negative LLE and positive LLE is indicated by a continuously changing between light blue–red scale passing through green and yellow scales. On LLE diagram in \(\,\left( {\delta ,\,\beta } \right)\,\) space, chaotic regions are characterized as a combination of light blue–green–yellow–red colors and periodic regions are characterized by blue colors. In Fig. 1b, chaotic regions are illustrated as a combination of light blue–green–yellow–red colors and periodic regions are illustrated by blue and light blues on LLE diagram in \(\,\left( {\gamma ,\,\beta } \right)\,\) space. In order to know the route to chaotic behavior exhibited by system (2), the bifurcation diagrams depicting the local extrema of \(x\left( t \right)\) as a function of the parameter \(\,\beta \,\) or \(\,\delta \,\) for specific values of \(\,\delta \,\) or \(\,\beta\) are plotted.

In Fig. 2a, the trajectories of system (2) converge to the equilibrium point \(\,O = \,\left( {0,0,0} \right)\,\) up to \(\,\beta = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha } \approx {0}{\text{.16}},\,\) where a Hopf bifurcation occurs followed by period-1-oscillations and period-doubling to chaos interspersed with periodic windows. Therefore, the above analytical calculations about Hopf bifurcation are confirmed by Fig. 2a. The LLE of Fig. 2b confirms the dynamical behaviors found in Fig. 2a. The phase portraits of chaotic oscillations for specific values of the parameter \(\,\beta\) are plotted in Fig. 3.

Fig. 2
figure 2

The bifurcation diagram depicting the local maxima (black dots) and local minima (gray dots) of \(x\left( t \right)\) (a) and the LLE (b) versus the parameter \(\,\beta \,\) for \(\,\alpha = 1,\,\gamma = 0.16\,\) and \(\,\delta = 18\)

Full size image
Fig. 3
figure 3

The phase portrait of system (2) in planes \(\left( {x,\,y} \right)\), \(\left( {y,\,z} \right)\) and \(\left( {x,\,z} \right)\) with \(\,\beta = {0}{\text{.6,}}\,\) \(\,\alpha = 1,\,\,\gamma = 0.16\,\) and \(\,\delta = 18\). Initial conditions \(\left( {x\left( 0 \right),\,y\left( 0 \right),\,z\left( 0 \right)} \right) =\) \(\left( {0.1,\,0.1,\,0.1} \right)\)

Full size image

System (2) displays one scroll-chaotic attractor as shown in Fig. 3. For \(\,\alpha = 1,\,\gamma = 0.16\,\) and \(\,\beta = 0.4\), the bifurcation diagram of \(x\left( t \right)\) and the corresponding LLE versus the parameter \(\,\delta\) is presented in Fig. 4.

Fig. 4
figure 4

(Colour online) Bifurcation diagram depicting the maxima of \(x\left( t \right)\) (a) and the corresponding LLE (b) versus the parameter \(\,\delta \,\) for \(\,\alpha = 1,\,\gamma = 0.16\,\) and \(\,\beta = 0.4\). Bifurcation diagrams are obtained by scanning the parameter \(\,\delta \,\) upwards (black) and downwards (red)

Full size image

In Fig. 4a, these forward and reverse period doubling sequences when a parameter \(\,\delta \,\) increases (or decreases) in a monotone way, called antimonotonicity [10, 16] is revealed. By comparing the two set of data [for increasing (black) and decreasing (red)] used to plot Fig. 4a, Fig. 4a displays coexistence of attractors between period-6-oscillations and chaotic oscillations for \(\,24.74 \le \delta \le 24.88\,\) and coexistence of attractors between period-3-oscillations and chaotic oscillations in the range \(\,24.88 < \delta \le 25.74\). The dynamical behavior found in Fig. 4a are confirmed by the LLE shown in Fig. 4b.

The bifurcation diagrams depicting the maxima of \(\,x\left( t \right)\,\) versus the parameter \(\,\delta \,\) are computed for some specific values of parameter \(\,\beta \,\) as depicted in Fig. 5 in order to illustrate the mechanism of the antimonotonicity phenomenon found in Fig. 4.

Fig. 5
figure 5

Bifurcation diagrams depicting the maxima of \(\,x\left( t \right)\,\) versus parameter \(\,\delta \,\) for specific values of parameter \(\,\beta\): a The chaotic oscillations at \(\,\beta = 0.37\), b chaotic bubble at \(\,\beta = 0.345\), c bubble of period 16 at \(\,\beta = 0.342\), d bubble of period 8 at \(\,\beta = 0.34\), e bubble of period 4 at \(\,\beta = 0.33\) and f bubble of period 2 at \(\,\beta = 0.32\). The others parameters are given in Fig. 4

Full size image

Chaotic oscillations and bubbles [10] are presented in Fig. 5a, b, respectively while only periodic bubbles are found in Fig. 5c–f. For a specific value of parameters \(\,\beta \,\) and \(\,\delta\), the phase portraits of the chaotic bubble presented in Fig. 5b and the first-return map of the local maxima of \(\,x\left( t \right)\,\) are plotted in Fig. 6.

Fig. 6
figure 6

Phase portraits in plane \(\,\left( {x,\,y} \right)\) (a), \(\left( {y,\,z} \right)\,\) (b), \(\left( {x,\,z} \right)\,\) (c) and the first-return map (\({\text{Max}}_{{\text{n + 1}}} {(}x{\text{) = f (Max}}_{{\text{n}}} {(}x{))}\)) of the maxima of \(\,x\left( t \right)\,\) (d) for \(\,\alpha = 1,\,\) \(\,\gamma = 0.16,\,\) \(\beta = 0.345\,\) and \(\,\delta = 12.85\,\) with the initial conditions \(\left( {x\left( 0 \right),\,y\left( 0 \right),\,z\left( 0 \right)} \right) = \)\(\left ( {0.1,\,0.1,\,0.1} \right)\)

Full size image

The chaotic bubble attractor presented in Fig. 6a–c is confirmed by the numerical calculation of the Lyapunov exponents which gives \(LE_{1} \approx {0}{\text{.0412624}},\,\) \(LE_{2} \approx {0}\,\) and \(LE_{3} \approx { - 1}{\text{.03952}}\,\). The Kaplan–Yorke dimension of the chaotic bubble is \(\,D_{KY} \approx {2}{\text{.0396937}}\). In Fig. 6d, the map is indicative of one-dimensional maps with two critical points \(\,p_{1} \,\) and \(\,p_{2}\), which support the occurrence of antimonotonicity phenomenon in the proposed jerk oscillator according to the results of Dawson et al. [16].

The coexistence of attractors found in Fig. 4 is further detailed in Figs. 7, 8.

Fig. 7
figure 7

Coexistence of attractors for specific values of \(\,\delta \,\) and initial conditions: a1 \(\,\delta = 24.8\,\) and \(\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \)\(\,\left( {{0}{\text{.0545}},\,{0}{\text{.1829}},\,{0}{\text{.0358}}} \right)\), a2 \(\,\delta = 24.8\,\) and \(\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) =\) \(\,\left( {0.1,\,0.1,\,0.1} \right)\), b1\(\,\delta = 25\,\) and \(\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {{0}{\text{.0545}},\,{0}{\text{.1829}},\,{0}{\text{.0358}}} \right)\), b2 \(\,\delta = 25\,\) and \(\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) =\) \(\left( {0.1,\,0.1,\,0.1} \right)\). The remaining parameters are given in Fig. 4

Full size image
Fig. 8
figure 8

(Color online) Cross section of the basin of attraction of system (2) in the (x, y) plane at z = 0. Periodic attractors are in green colour and chaotic attractors are in black colour. The parameters values are \(\,\delta = 25\),\(\,\alpha = 1\),\(\,\gamma = 0.16\) and \(\,\beta = 0.4\)

Full size image

At \(\,\delta = 24.8,\,\) the output \(\,x\left( t \right)\,\) displays period-6-oscillations and one scroll-chaotic attractor for two different initial conditions as shown in Figs. 7a1, a2, respectively. Period-3-oscillations and one scroll-chaotic attractor are revealed in Fig. 7b1, b2, respectively at \(\,\delta = 25\,\) for two different initial conditions. The coexistence of attractors found in Fig. 7 is illustrated in Fig. 8 which depicts the cross section of the basin of attraction of system (2) for specific value of parameter \(\,\delta\).

The black and green regions in Fig. 8 contain initial conditions that lead to the chaotic and periodic behaviors, respectively. The basin of attraction of Fig. 8 shows the possibility of occurrence of chaotic attractors is greater than the one of periodic attractors. The periodic region is located in the range \(\, - 2 \le x\left( 0 \right) < - 1.35\,\) while the chaotic region is found in the range \(- 1.35 < x\left( 0 \right) \le 0\).

3 Electronic realization of the proposed autonomous Morse jerk oscillator

The aim of this section is to realize the electronic circuit describing the proposed jerk oscillator and point out some experimental/PSIM results in order to validate the numerical simulation results of Sect. 2. The circuit of the proposed autonomous Morse jerk oscillator is designed and realized in Fig. 9.

Fig. 9
figure 9

(Color online) Circuit diagram (a) and printed circuit board (b) of the proposed jerk oscillator

Full size image

Figure 9 consists of resistors, capacitors, operational amplifiers, analogue multiplier device M (AD633JN integrated circuit) and diode D (1N4148). The current flowing inside the diode is given by the relation: \(I_{d} = I_{s} \left[ {e^{{\left( { - \frac{{R_{s2} }}{{R_{s1} }}\frac{Vx}{{\eta Vt}}} \right)}} - 1} \right]\) where Is is the reversed satured current, η is an ideal factor and Vt is the thermal temperature of the experimental room. The operations of addition, subtraction and integration are implemented by operational amplifiers OP_4, OP_3 and OP_1 (TL084 integrated circuit) associated with ceramic capacitors and high precision resistors. The resistors R1 and R3 are knob resistors. The nonlinear term in the proposed autonomous Morse jerk oscillator is successfully implemented by combining a diode and an analogue multiplier device. By applying the Kirchhoff’s laws on circuit of Fig. 9, the following nonlinear differential equations are obtained:

$$ \frac{{dV_{x} }}{dt} = \frac{1}{RC}V_{y} , $$
(7a)
$$ \frac{{dV_{y} }}{dt} = \frac{1}{{R_{1} C}}V_{z} , $$
(7b)
$$ \frac{{dV_{z} }}{dt} = - \frac{1}{RC}V_{z} - \frac{1}{{R_{2} C}}V_{y} - \frac{1}{{R_{3} C}}\left[ {1 - R_{S} I_{S} \exp \left( { - \frac{{R_{S2} V_{x} }}{{R_{S1} \eta V_{T} }}} \right)} \right]R_{S} I_{S} \exp \left( { - \frac{{R_{S2} V_{x} }}{{R_{S1} \eta V_{T} }}} \right), $$
(7c)

where \(V_{x}\), \(V_{y}\), \(V_{z}\) are the output voltages of the operational amplifiers OP_1, OP_2 and OP_4, respectively. Adopting a time unit of RC = \(10^{ - 4}\) s, the parameters of system (2) are defined in terms of the values of capacitors and resistors as follows:\(\delta = {{10^{ - 4} } \mathord{\left/ {\vphantom {{10^{ - 4} } {R_{1} C}}} \right. \kern-\nulldelimiterspace} {R_{1} C}}\),\(\,\gamma = {{10^{ - 4} } \mathord{\left/ {\vphantom {{10^{ - 4} } {R_{2} C}}} \right. \kern-\nulldelimiterspace} {R_{2} C}}\), \(\beta = {{10^{ - 4} } \mathord{\left/ {\vphantom {{10^{ - 4} } {R_{3} C}}} \right. \kern-\nulldelimiterspace} {R_{3} C}}\), and \(\alpha = {{10^{ - 4} } \mathord{\left/ {\vphantom {{10^{ - 4} } {RC}}} \right. \kern-\nulldelimiterspace} {RC}}\).We choose convenient values for resistors R = 10 kΩ, capacitor \(\,C = 10\,nF\), RS2 = 0.494 kΩ, RS1 = 10 kΩ and RSIS = 1 V to implement the electronic circuit described by system (3). The observations from the oscilloscope of the phase portraits by using the above values of resistors are shown in Fig. 10.

Fig. 10
figure 10

(Colour online) Phase portraits of chaotic attractors observed on oscilloscope. In panels 1, 2, and 3, we depict the phase portraits in planes \(\,\left( {V_{x} ,\,V_{y} } \right)\), \(\,\left( {V_{y} ,\,V_{z} } \right)\) and \(\,\left( {V_{x} ,\,V_{z} } \right)\), respectively. The values resistances are \(\,R = 10\,{\rm k}\Omega ,\,R_{1} = 0.349\,{\rm k}\Omega ,\,R_{2} = 65.5{\rm k}\Omega ,\,R_{3} = 67.5\,{\rm k}\Omega\) (first line reproduces Fig. 3) and \(\,R = 10\,{\rm k}\Omega ,\,R_{1} = 0.274\,{\rm k}\Omega ,\,R_{2} = 65.5\,{\rm k}\Omega ,\,R_{3} = 67.5\,{\rm k}\Omega\) (second line reproduces Fig. 6a–c)

Full size image

The experimental results of Fig. 10 have in a good qualitative agreement with the numerical results of Figs. 3, 6a–c. PSIM software is used to validate the coexistence between periodic oscillations and one scroll-chaotic attractor as shown in Fig. 11 because it is not easy to achieve special initial voltages of three capacitors in hardware circuit experiment [8].

Fig. 11
figure 11

The phase portraits in plane \(\,\left( {V_{x} ,\,V_{y} } \right)\) of coexisting attractors observed on PSIM. The values resistances are: a \(\,R = 10\,{\rm k}\Omega ,\,R_{1} = 0.73\,{\rm k}\Omega ,\,R_{2} = 60.024\,{\rm k}\Omega ,\,R_{3} = 23\,{\rm k}\Omega\) and b \(\,R = 10\,{\rm k}\Omega ,\,R_{1} = 0.78\,{\rm k}\Omega ,\,R_{2} = 60.024\,{\rm k}\Omega ,\,R_{3} = 23\,{\rm k}\Omega\). Initial conditions are: a1 and b1 \(\,\left( {Vx\left( 0 \right),Vy\left( 0 \right),Vz\left( 0 \right)} \right) = \)\(\,\left( { - 2.0V, - 4.0V,0.0V} \right)\), a2 and b2 \(\,\left( {Vx\left( 0 \right),Vy\left( 0 \right),Vz\left( 0 \right)} \right) = \)\(\,\left( {2.0V,2.0V,2.0V} \right)\)

Full size image

A good qualitative agreement is shown between coexistence attractors illustrated in Fig. 11 using PSIM software and the coexistence attractors obtained during the numerical simulations results of Fig. 7.

4 Controls of the signal amplitudes, chaotic behavior and coexisting attractors in the proposed autonomous Morse jerk oscillator

The goal of this section is to control the signal amplitudes, chaotic behavior and coexisting attractors in the proposed jerk oscillator.

4.1 Partial and total controls of the signal amplitudes

In this subsection, it is demonstrated that system (2) has the feature of partial and total control of the signal amplitudes. The state variable \(\,x\,\) appears only in the third equation of system (2). So, its amplitude can be controlled by replacing \(\,x \to \,x + \zeta \,\,\) into system (2) where \(\,\zeta \,\) is a boosting controller. Then, system (2) becomes:

$$ \dot{x} = y, $$
(8a)
$$ \dot{y} = \delta z, $$
(8b)
$$ \dot{z} = - z - \gamma y - \beta \left[ {1 - e^{{ - \alpha \left( {x + \zeta } \right)}} } \right]e^{{ - \alpha \left( {x + \zeta } \right)}} . $$
(8c)

System (8) has only one equilibrium point \(\,E_{1} = ( - \zeta ,0,0)\,\). The local stability of \(\,E_{1} = ( - \zeta ,0,0)\,\) reveals that if \(\,\delta > 0\), system (8) has a Hopf bifurcation when \(\,\beta \,\) passes through the critical value \(\beta_{H} = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\). So, the stability of equilibrium point \(\,E_{1} = ( - \zeta ,0,0)\,\) is independent from the boosting controller \(\,\zeta\). The average values of the state variables \(x\), \(y\) and \(z\) versus the boosting controller \(\,\zeta\) are plotted in Fig. 12 in order to check the amplitude control of the state variable \(\,x\).

Fig. 12
figure 12

(Color online) The average values of the state variables \(x\) (black), \(y\)(blue) and \(z\) (red) versus the boosting controller \(\,\zeta\) for \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\delta = 18\,\) and \(\,\beta = 0.6\)

Full size image

By increasing the boosting controller \(\,\zeta ,\) the average of the state variable \(x\) decreases while other two state variables \(\,y\) and \(\,z\) remain unchanged as shown in Fig. 12. The phase portraits and time series of the state variable \(x\) of system (8) are presented in Fig. 13 for different values of boosting controller \(\,\zeta .\)

Fig. 13
figure 13

Phase portraits in the plane \((x,\,y)\) and time series of the signal \(x\) of system (9) for \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\delta = 18\),\(\,\beta = 0.6\,\) and different values of boosting controller \(\,\zeta\): \(\zeta = 3\)(black), \(\zeta = 1.5\) (red) and \(\zeta = - 1\) (blue). Initial conditions are(x (0), y (0), z (0)) = (0.1, 0.1, 0.1)

Full size image

The amplitude of chaotic signal \(x\) is boosted from a bipolar signal to unipolar signal by decreasing the boosting controller \(\,\zeta\) as shown in Fig. 13.

The feature of total amplitude control in system (2) can be demonstrated by inserting \(x \to \,{x \mathord{\left/ {\vphantom {x \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon },\,y \to \,{y \mathord{\left/ {\vphantom {y \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }\,\) and \(\,z \to \,{z \mathord{\left/ {\vphantom {z \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }\,\) in system (2) where \(\,\varepsilon \,\) is a control parameter. So, system (3) becomes:

$$ \dot{x} = y, $$
(9a)
$$ \dot{y} = \delta z, $$
(9b)
$$ \dot{z} = - z - \gamma y - \varepsilon \beta \left[ {1 - \exp \left( {{{ - \alpha x} \mathord{\left/ {\vphantom {{ - \alpha x} \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }} \right)} \right]\exp \left( {{{ - \alpha x} \mathord{\left/ {\vphantom {{ - \alpha x} \varepsilon }} \right. \kern-\nulldelimiterspace} \varepsilon }} \right). $$
(9c)

System (9) has only one equilibrium point \(\,O = (0,0,0)\). The local stability of \(\,O = (0,0,0)\,\) shows that if \(\,\delta > 0\), system (9) has a Hopf bifurcation when \(\,\beta \,\) passes through the critical value \(\beta_{H} = {\gamma \mathord{\left/ {\vphantom {\gamma \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\). So the stability of equilibrium point \(\,O = (0,0,0)\,\) is independent from the control parameters \(\,\varepsilon\). In Fig. 14, the phase portraits of system (9) are depicted for different values of control parameter \(\,\varepsilon\).

Fig. 14
figure 14

(Color online) Phase portraits in the planes \((x,\,y)\) and \((y,\,z)\) of system (9) for \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\delta = 18\),\(\,\beta = 0.6\,\) and different values of control parameter \(\,\varepsilon\): \(\varepsilon = 0.85\)(black), \(\varepsilon = 2\) (red) and \(\varepsilon = 3\) (blue). Initial conditions are(x (0), y (0), z (0)) = (0.1, 0.1, 0.1)

Full size image

The amplitudes of chaotic signals \(\,x\), \(y\) and \(\,z\,\) are controlled simultaneously by varying the control parameter \(\,\varepsilon\) as shown in Fig. 14.

4.2 Chaos control in proposed autonomous chaotic Morse jerk oscillator

The aim of this subsection is to suppress chaotic behavior and stabilize system (2) at its equilibrium \(O = \,\,\left( {0,\,0,\,0} \right)\). To achieve this goal, it is introduced an external feedback control law \(u = \left[ {u_{1} \,\,u_{2} \,\,u_{3} } \right]^{T}\) where for simplicity it is chosen \(u_{i \ne 2} = 0\) and \(u_{2} = - k\left( {y - y_{0} } \right)\), \(y_{0}\) being the first coordinate of the equilibrium point \(O\) (\(x_{0} = 0,\,\,y_{0} = 0,\,\,z_{0} = 0\)) and \(\,k\,\) is the positive feedback control gain. The controlled system takes the form:

$$ \frac{dx}{{dt}}\, = \,y, $$
(10a)
$$ \frac{dy}{{dt}}\, = \delta z - k\left( {y - y_{0} } \right), $$
(10b)
$$ \frac{dz}{{dt}} = \, - z - \gamma y - \beta \left[ {1 - \exp \left( { - \alpha x} \right)} \right]\exp \left( { - \alpha x} \right). $$
(10c)

The controlled system (10) has only one equilibrium point \(O = \,\,\left( {0,\,0,\,0} \right)\) and its Jacobian matrix has the characteristic polynomial:

$$ \lambda^{3} \, + \,\left( {\,k + 1} \right)\lambda^{2} + \,\,\left( {k + \delta \gamma \,} \right)\lambda \, + \alpha \beta \delta = \,0. $$
(11)

The Routh–Hurwitz conditions for the stability of the controlled system (10) at its equilibrium are the following:

$$ k + 1 > 0, $$
(12a)
$$ \alpha \beta \delta > 0, $$
(12b)
$$ k^{2} + \left( {1 + \gamma \delta } \right)k + \delta \left( {\gamma - \alpha \beta } \right) > 0. $$
(12c)

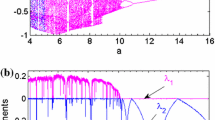
For \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\beta = 0.6\,\) and \(\,\delta = 18\), the inequalities (12c) is positive for \(\,k < - 5.36\,\) and \(\,k > 1.48\). According to the set of inequalities (12), the equilibrium point \(\,O = \,\,\left( {0,\,0,\,0} \right)\,\) is stable for \(\,k > 1.48\,\) and unstable for \(\,k < 1.48\). Using the numerical simulations of system (10) for \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\beta = 0.6\,\) and \(\,\delta = 18\), the bifurcation diagram of \(x\left( t \right)\) and the LLE versus the control gain \(\,k\,\) is plotted in Fig. 15 in order to check the validity of the analytical results found.

Fig. 15
figure 15

Bifurcation diagram depicting the local maxima (black dots) and local minima (gray dots) of \(x\left( t \right)\) (a) and the LLE (b) versus the control gain \(k\) for \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\beta = 0.6\,\) and \(\,\delta = 18\)

Full size image

From Fig. 15a, a reverse period-doubling to chaos interspersed with periodic windows is observed up to \(k \approx \,{1}{\text{.48}}\) where a Hopf bifurcation appears followed by no oscillation (equilibrium point). Therefore, the analytical results confirm the results obtained during numerical integration of controlled system (10) as shown in Fig. 15. The dynamical behaviors found in Fig. 15a are confirmed by the LLE shown in Fig. 15b. For \(\,k = \,{1}{\text{.6}}\), the time series of the outputs of \(x,\,y\) and \(z\) is plotted in Fig. 16.

Fig. 16
figure 16

Time series of the outputs of \(x,\,\,y\,\) and \(z\) for \(k = \,1.{6,}\,\,\alpha = 1,\,\,\gamma = 0.16,\,\,\beta = 0.6\,\) and \(\,\delta = 18\). The initial condition is \(\left( {x\left( 0 \right),\,y\left( 0 \right),\,\,z\left( 0 \right)} \right) = \left( {0.1,\,\,0.1,\,\,0.1} \right)\)

Full size image

The trajectories of controlled system (10) are controlled to the equilibrium point \(\,O = \,\,\left( {0,\,0,\,0} \right)\) as shown in Fig. 16.

4.3 Control of coexisting attractors in proposed autonomous Morse jerk oscillator

In the most dynamical systems, multistability can create inconveniences which contribute to reduce considerably the performances of such systems. Several methods have been proposed and developed for the control of multistabilty in multistable oscillators [2, 20, 38, 40, 41]. It is demonstrated that such methods are capable to stabilize the dynamics of these systems to a monostable state [38, 40, 41]. Among these methods, linear augmentation method is one of the most used methods because of its large applicability, simplicity in designing and physical implementation. In order to destroy the coexistence between periodic and chaotic attractors, system (2) is coupled with a linear system as follows:

$$ \dot{x} = y, $$
(13a)
$$ \dot{y} = \delta z, $$
(13b)
$$ \dot{z} = - z - \gamma y - \beta \left[ {1 - \exp \left( { - \alpha x} \right)} \right]\exp \left( { - \alpha x} \right) + \mu {\text{w}}, $$
(13c)
$$ {\dot{\text{w}}} = - \eta {\text{w}} - \mu \left( {z - \theta } \right), $$
(13d)

where \(\,\mu \,\) is the coupling strength, \(\,\theta\) is the control parameter which serves to locate the position of equilibrium point and \(\,\eta \,\) is the decay parameter of the linear system \(\,{\text{w}}\). System (13) has no-equilibrium point for \(\,{{4\theta \mu^{2} } \mathord{\left/ {\vphantom {{4\theta \mu^{2} } {\eta \beta }}} \right. \kern-\nulldelimiterspace} {\eta \beta }} > 1\,\) while for \(\,{{4\theta \mu^{2} } \mathord{\left/ {\vphantom {{4\theta \mu^{2} } {\eta \beta }}} \right. \kern-\nulldelimiterspace} {\eta \beta }} < 1\,\) two equilibrium points \(\,E_{1} = ({{ - x_{1} } \mathord{\left/ {\vphantom {{ - x_{1} } \alpha }} \right. \kern-\nulldelimiterspace} \alpha },0,0,\,{{\theta \mu } \mathord{\left/ {\vphantom {{\theta \mu } \eta }} \right. \kern-\nulldelimiterspace} \eta }\,)\,\) and \(\,E_{2} = ({{ - x_{2} } \mathord{\left/ {\vphantom {{ - x_{2} } \alpha }} \right. \kern-\nulldelimiterspace} \alpha },0,0,\,{{\theta \mu } \mathord{\left/ {\vphantom {{\theta \mu } \eta }} \right. \kern-\nulldelimiterspace} \eta }\,)\,\) where \(\,x_{1,2} = \ln \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} \pm {{\sqrt {1 - {{4\theta \mu^{2} } \mathord{\left/ {\vphantom {{4\theta \mu^{2} } {\eta \beta }}} \right. \kern-\nulldelimiterspace} {\eta \beta }}} } \mathord{\left/ {\vphantom {{\sqrt {1 - {{4\theta \mu^{2} } \mathord{\left/ {\vphantom {{4\theta \mu^{2} } {\eta \beta }}} \right. \kern-\nulldelimiterspace} {\eta \beta }}} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\,\). The bifurcation diagram depicting local extrema of the controlled system (13) and the corresponding LLE versus the coupling strength \(\,\mu \,\) are shown in Fig. 17.

Fig. 17
figure 17

Bifurcation diagrams depicting the maxima (black shaded areas) and minima (grey shaded areas) of \(\,x\left( t \right)\,\) a and b the corresponding LLE versus the coupling strength \(\,\mu \,\) for \(\,\eta = 0.7\), \(\,\theta = 0.5\), \(\,\alpha = 1,\,\,\gamma = 0.16,\,\,\beta = 0.6\,\) and \(\,\delta = 25\)

Full size image

By increasing the coupling strength \(\,\mu\), the bifurcation diagram of the controlled system (13) in Fig. 17a displays a reverse period-doubling bifurcation to chaotic behavior interspersed with periodic windows. By further increasing the coupling strength \(\,\mu\), a limit cycle is observed up to µ ≈ 0.3156 where a Hopf bifurcation occurs followed by converging of the trajectories of the controlled system (13) to the equilibrium point E2. The dynamical behaviors found in Fig. 17a are confirmed by the LLE shown in Fig. 17b. Therefore, the controlled system (13) transforms the multistable attractors to desired monostable attractors.

5 Conclusion

In this paper, an autonomous Morse jerk oscillator was proposed and analyzed. It was demonstrated that the proposed jerk oscillator displays Hopf bifurcation, antimonotonicity, one scroll-chaotic attractor, periodic and chaotic bubbles and coexistence between periodic and one scroll-chaotic attractors by tuning the parameters. Then, an analogue circuit was designed to realize the rate-equations describing the proposed autonomous Morse jerk oscillator. The experimental/PSIM results were shown consistency with numerical simulations results. Then, a flexible chaotic autonomous jerk oscillator with partial and total amplitude controls was achieved by adding two new parameters in the rate-equations describing the proposed Morse jerk oscillator. Moreover, a single linear feedback controller was used to stabilize the chaotic proposed jerk oscillator to its unique equilibrium point. Finally, the coexisting of attractors found in the proposed jerk oscillator was controlled to a desired trajectory by using a linear augmentation method.