Dynamics, Circuitry Implementation and Control of an Autonomous Helmholtz Jerk Oscillator

Abstract

In this paper, an autonomous three-dimensional Helmholtz-type oscillator is designed based on conversion of an autonomous Helmholtz two-dimensional oscillator to a jerk oscillator. For a suitable choice of the parameters, the proposed autonomous Helmholtz jerk oscillator can generate Hopf bifurcation, bistable period-2 limit cycles, two types of one-scroll chaotic attractors and coexistence between period-3 limit cycle and one-scroll chaotic attractors. Using a weak modulation of a parameter of the proposed Helmholtz jerk oscillator, it is possible to destroy the coexisting attractors found and transform the proposed Helmholtz jerk oscillator to period-3 oscillations. Moreover using experiments and OrCAD-PSpice software, circuit implementation of the proposed autonomous Helmholtz jerk oscillator is realized in order to check the one-scroll chaotic attractors and the coexisting attractors found during the numerical simulations. Numerical and experimental/OrCAD-PSpice results have a good qualitative agreement. Finally, by adding two new parameters in the proposed autonomous Helmholtz jerk oscillator, it is possible to control the amplitude of the attractor and the largest Lyapunov exponent.

1 Introduction

Chaotic behavior in nonlinear oscillators has been investigated in the past four decades, but the systems considered lead to difficult electronic implementations. Since 2000, the development of new autonomous chaotic oscillators with easy electronic implementation has been of interest, as it can be seen in Sprott papers (Sprott 2000a, b). These circuits are described by simple three-dimensional equations, which can be easily scaled to different frequencies, and have simple electronic elements such as diodes, operational amplifiers and resistors. The class of such oscillators given by ${{{\text{d}}^{3} x} \mathord{\left/ {\vphantom {{{\text{d}}^{3} x} {{\text{d}}t^{3} }}} \right. \kern-0pt} {{\text{d}}t^{3} }} = j\left( {x,{{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}},{{{\text{d}}^{2} x} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x} {{\text{d}}t^{2} }}} \right. \kern-0pt} {{\text{d}}t^{2} }}} \right)$ was called by Gottlieb jerk oscillators (Gottlieb 1996; Malasoma 2000; Sprott 1997a, b; 2011). Practically, jerk oscillators may be used for the modeling of some real phenomena such as a special case of the Nosé–Hoover thermostated dynamic system which exhibits time-reversible Hamiltonian chaos (Sprott 1997a, b). Following these ideas, development of new jerk oscillators with easy electronic implementation and the chaotification of non-chaotic oscillators, the authors of Ref. Benitez et al. (2006) introduced, theoretically studied and experimented an autonomous chaotic oscillator using the Van der Pol dynamics immersed into a jerk oscillator. In Refs. Louodop et al. (2014) and Kengne et al. (2016), the authors proposed, studied theoretically and experimented an autonomous chaotic Duffing oscillator based on a jerk architecture. Recently Tamba et al. have proposed a chaotic Van der Pol–Duffing jerk oscillator based on jerk architecture and studied the dynamical behaviors, chaos control and synchronization in its integer and fractional-order form (Tamba et al. 2018a).

Motivated by the studies reported in Refs. Benitez et al. (2006), Louodop et al. (2014), Kengne et al. (2016) and Tamba et al. (2018a, b), in this paper we consider an autonomous jerk oscillator which is obtained by converting the second-order Helmholtz oscillator into a three-dimensional oscillator using the jerk model. Helmholtz oscillator is a two-dimensional oscillator with a quadratic nonlinearity. The Helmholtz oscillator known to naval architects as the Helmholtz–Thompson equation gives the possibility to investigate the escape phenomenon. Thompson’s paper (Thompson 1989) presented a detailed dynamical analysis of the system which has been investigated experimentally by Gottwald et al. (1995). The equation finds direct application in the investigation of the bubble dynamics (Kang and Leal 1990) and is much discussed in the naval architecture literature, see Ref. Thompson (1997). These concepts continue to find fruitful applications in quantification of capsize resistance, see Spyrou et al. (2002).

This paper is structured as follows: Sect. 2 is devoted to the analytical and numerical analysis of proposed autonomous Helmholtz jerk oscillator. In Sect. 3, an electronic circuit realization is suggested for the investigation of the dynamical behavior of the proposed autonomous Helmholtz jerk oscillator. Amplitude and largest Lyapunov exponent (LLE) controls of the proposed autonomous Helmholtz jerk oscillator are presented in Sect. 4. The conclusion is given in Sect. 5.

2 Analysis of the Proposed Autonomous Helmholtz Jerk Oscillator

The Helmholtz oscillator described by a second-order differential equation with an external periodic drive term (Helmholtz 1954; Thompson 1989; del Río et al. 1992; Gottwald et al. 1995) is given by:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} + \delta \frac{{{\text{d}}x}}{{{\text{d}}t}} + x - x^{2} = f_{0} \sin \left( {\omega t} \right), $$

(1)

where $\,\delta \,$ is a dimensionless damping coefficient $\,\left( {\delta > 0} \right)$, $\,f_{0} \,,\omega$ is the amplitude and the pulsation of the periodic signal. The general form of the $\,\phi^{3}$ potential associated with Eq. (1) is defined by $\,V(x) = {{a_{1} x^{2} } \mathord{\left/ {\vphantom {{a_{1} x^{2} } 2}} \right. \kern-0pt} 2} + {{bx^{3} } \mathord{\left/ {\vphantom {{bx^{3} } 3}} \right. \kern-0pt} 3}$ where $\,a_{1} \,$ and $\,b\,$ are real parameters. The potential $\,V(x)\,$ can have four different forms depending on the sign of the parameters $\,a_{1} \,$ and $\,b$. Indeed, if the parameters $\,a_{1} \,$ and $\,b\,$ are positive, the potential $V(x)$ has a single well at $\,x = 0\,$ and a single hump at $\,x < 0$. If the parameters $\,a_{1} \,$ and $\,b\,$ are negative, the potential $V(x)$ has a single well at $\,x < 0\,$ and a single hump at $\,x = 0$. If the parameter $\,a\,$ is negative and the parameter $\,b\,$ is positive, the potential $\,V(x)\,$ has a single well at $\,x > 0\,$ and a single hump at $\,x = 0$. If the situation is reversed, the potential $\,V(x)\,$ has a single well at $\,x = 0\,$ and a single hump at $\,x > 0$. Each configuration corresponds to a physical situation of the Helmholtz oscillator. Very recently, Tamba et al. (2018b) proposed and investigated the dynamics and synchronization of a Helmholtz oscillator with a potential having a single well at $\,x = 0\,$ and a single hump at $\,x < 0$. The model exhibited some interesting behaviors including Hopf bifurcation, period-doubling and reversals period-doubling bifurcations and coexisting attractors. In the present work, in order to check the effects of the form of the potential on the dynamics of the Helmholtz oscillator, we introduce an autonomous Helmholtz jerk oscillator with a potential having a single well at $\,x = 0\,$ and a single hump at $\,x > 0$.

For $\,f_{0} \, = 0$, Eq. (1) has two equilibrium points $\left( {x^{*} ,y^{*} = {{{\text{d}}x^{*} } \mathord{\left/ {\vphantom {{{\text{d}}x^{*} } {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}}} \right) = \left( {0,0} \right)$ and $\,\left( {1,0} \right)\,$. The stability of the equilibrium points is determined by the damping coefficient $\,\delta$. When $\delta > 0$, the fixed point $\,\left( {0,0} \right)\,$ is stable while the equilibrium point $\,\left( {1,0} \right)\,$ is unstable. For $\,f_{0} \, = 0\,$ and any value of parameter $\,\delta \,$, the trajectories of Eq. (1) converge to one or the other equilibrium point $\,\left( {0,0} \right)\,$ either to the equilibrium point $\,\left( {1,0} \right)$.While for $\,f_{0} \, \ne 0\,$ and $\,\omega \, \ne 0$, Eq. (1) can exhibit complex behavior such as chaos.

Inspired by the works reported in Benitez et al. (2006), Louodop et al. (2014), Kengne et al. (2016), Tamba et al. (2018a) and in order to convert the second-order non-autonomous Helmholtz oscillator [see Eq. (1)] to an autonomous form which can display interesting and complex features, the following model is introduced

$$ \frac{{{\text{d}}^{3} x}}{{{\text{d}}t^{3} }} = - \left( {\frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} + \delta \frac{{{\text{d}}x}}{{{\text{d}}t}} + x - x^{2} } \right), $$

(2)

where $\,\delta \,$ is a dimensionless damping coefficient $\,\left( {\delta > 0} \right)$. The state space representation of Eq. (2) yields:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = y, $$

(3a)

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = z, $$

(3b)

$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = - z - \delta y - x + x^{2} , $$

(3c)

where ${{{\text{d}}x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}x\left( t \right)} {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}} = y\left( t \right)$ and ${{{\text{d}}^{2} x\left( t \right)} \mathord{\left/ {\vphantom {{{\text{d}}^{2} x\left( t \right)} {{\text{d}}t^{2} }}} \right. \kern-0pt} {{\text{d}}t^{2} }} = z\left( t \right)$. By varying the parameter $\,\delta ,\,$ system (3) exhibits period-1 oscillations and period-2 oscillations. A positive constant parameter $\,a\,$ is added in Eq. (3b) to find chaos in system (3). System (3) can be rewritten as:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = y, $$

(4a)

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = az, $$

(4b)

$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = - z - \delta y - x + x^{2} . $$

(4c)

System (4) is dissipative because $\nabla V\, = \,\frac{{\partial \dot{x}}}{\partial x}\, + \,\frac{{\partial \dot{y}}}{\partial y}\, + \,\frac{{\partial \dot{z}}}{\partial z}\, = \, - 1$. System (4) has two equilibrium points $\,E_{1} = (0,0,0)\,$ and $\,E_{2} = (1,0,0)$. The characteristic equation associated to $\,E^{*} \left( {x^{*} ,\,y^{*} ,\,z^{*} } \right)\,$ is:

$$ \lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, - \left( {2x^{*} - 1} \right)a = \,0. $$

(5)

For the equilibrium $\,E_{1} = (0,0,0)$, the characteristic equation is $\,\lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, + a = \,0$. According to Routh–Hurwitz criteria, this characteristic equation has all roots with negative real parts if and only if $A > 0,\,C > 0,\,AB - C > 0$ where $A = 1$, $B = a\delta$ and $C = a$, namely:

$$ a > 0, $$

(6a)

$$ a\left( {\delta - 1} \right) > 0. $$

(6b)

Since $\,a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{1} = (0,0,0)\,$ of system (4) is stable if $\delta \, > \,1$ and unstable for $\,\delta \, < \,1$.

Theorem

If$\,a > 0$, system (4) has a Hopf bifurcation at equilibrium point$\,E_{1} = (0,0,0)\,$when$\,\delta \,$passes through the critical value$\delta_{H} = 1$.

Proof

By replacing $\,\lambda = i\omega \,\left( {\omega > 0} \right)\,$ into the characteristic Eq. (5) associated to $\,E_{1} = (0,0,0)\,$ and separating real and imaginary parts, we obtain

$$ \omega = \omega_{{0_{{}} }} = \sqrt a , $$

(7a)

$$ \delta_{H} = 1. $$

(7b)

Differentiating both sides of the characteristic Eq. (5) associated to $\,E_{1} = (0,0,0)\,$ with respect to $\,\delta_{H}$, we can obtain

$$ 3\lambda^{2} \frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }} + 2\lambda \frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }} + a\delta \frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }} + a\lambda = 0, $$

(8a)

and

$$ \frac{{{\text{d}}\lambda }}{E\delta } = \frac{ - a\lambda }{{3\lambda^{2} + 2\lambda + a\delta }}, $$

(8b)

then

$$ \text{Re} \left( {\left. {\frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }}} \right|_{{\delta = \delta_{H} ,\lambda = i\omega_{0} }} } \right) = - \frac{1}{{2\left( {a + 1} \right)}} \ne 0. $$

(9)

Since the characteristic Eq. (5) associated to $\,E_{1} = (0,0,0)\,$ has two purely imaginary eigenvalues and the real parts of eigenvalues satisfy $\text{Re} \left( {\left. {\frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }}} \right|_{{\delta = \delta_{H} ,\lambda = i\omega_{0} }} } \right) \ne 0$, all the conditions for Hopf bifurcation to occur are met. Consequently, system (4) has a Hopf bifurcation at $\,E_{1} = (0,0,0)\,$ when $\,\delta = \delta_{H} = 1$. Next, substituting the equilibrium $\,E_{2} \,$ in the characteristic Eq. (5) yields the following characteristic equation: $\lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, - a = \,0$. Using Routh–Hurwitz conditions, this equation has all roots with negative real parts if and only if: $a < 0$ and $a\left( {\delta + 1} \right) > 0$. Since $\,a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{2} \,$ of system (4) is always unstable.

2.1 Dynamical Analysis of Proposed Autonomous Helmholtz Jerk Oscillator

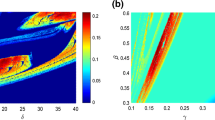
System (4) has two parameters $\,a\,$ and $\,\delta$, we construct the two parameters ($\delta$, $\,a$) bifurcation diagram by examining the Lyapunov exponents and time series for each cell as illustrated in Fig. 1.

Fig. 1

Regions of dynamical behaviors in the parameters space $\,\delta \,$ and $\,a$. Periodic oscillations are in cyan regions and chaotic behaviors are in red regions. The values of parameters chosen in gray regions lead to unbounded orbits (Color figure online)

From Fig. 1, we can see that system (4) can display not only periodic and chaotic behaviors but it can also lead to unbounded orbits. In order to know the route to chaos exhibited by system (4), we plot the bifurcation diagrams showing the local extrema of state variable $x\left( t \right)$ when one of the parameters $\,\delta \,$ or $\,a\,$ is fixed and the other one is varied. We fix $\,a = 5\,$ and present the bifurcation diagram and the LLE versus the parameter $\,\delta$ as shown in Fig. 2.

Fig. 2

Bifurcation diagram depicting the local maxima (black dots) and local minima (gray dots) of $x\left( t \right)$ (a) and the LLE (b) versus the parameter $\,\delta \,$ for $\,a = 5$

When the parameter $\,\delta \,$ varies from 0.52 to 1.1, the bifurcation diagram of the output $\,x\left( t \right)\,$ in Fig. 2a displays chaos interspersed with periodic windows followed by a reverse period-doubling bifurcation to period-1 oscillations. The period-1 oscillations is observed up to $\,\delta \approx 1$, where a Hopf bifurcation occurs followed by converging of the trajectories of system (4) to the equilibrium point $\,E_{1} = (0,0,0)$. The bifurcation diagram in Fig. 2a is confirmed by the LLE shown in Fig. 2b.

For $\delta = 0.55$, bifurcation diagram of $x\left( t \right)$ and the LLE versus the parameter $\,a$ is plotted in Fig. 3.

Fig. 3

(Color online) Bifurcation diagram depicting the maxima of $x\left( t \right)$ (a) and the LLE (b) versus the parameter $\,a$ for $\,\delta = 0.55$. Bifurcation diagrams are obtained by scanning the parameter $\,a\,$ upwards (black) and downwards (red)

When the parameter $\,a\,$ varies from 2.6 to 13 (see black dot in Fig. 3a), the bifurcation diagram of the output $\,x\left( t \right)\,$ exhibits a period-2 oscillations followed by a period-doubling bifurcation to chaos interspersed with periodic windows for $\,2.6 < a < 4.27$. Then a period-3 oscillations window is observed for $\,4.27 \le a < 5.44$. By further increasing the parameter $\,a$, the system (4) undergoes a reverse period-doubling bifurcation and a period-1 oscillations is observed for $\,a > 12.26$. By ramping the parameter $\,a\,$ (see red dot in Fig. 3a), the output $x\left( t \right)$ displays the same dynamical behaviors as in Fig. 3a (see black dot) in the ranges $\,2.6 \le a \le 5.075$ and $5.44 \le a \le 13$. While in the range $5.075 < a < 5.44,$ the output $x\left( t \right)$ exhibits chaotic behavior. By comparing the two sets of data [for increasing (black) and decreasing (red)] used to plot Fig. 3a, one can notice that system (4) displays coexistence of period-3 oscillations and chaotic behavior in the range $\,5.075 < a < 5.44$. It is important to note that in the range $\,2.635 < a < 2.745\,$ the output $x\left( t \right)$ displays the same dynamical behaviors as in Fig. 3a (see black dot), but the amplitudes of the output $x\left( t \right)$ are not the same. Therefore, one can notice that system (4) shows bistability. The bifurcation diagram in Fig. 3a is confirmed by the LLE shown in Fig. 3b. The phase portraits of chaotic oscillations found in Figs. 2a and 3a are plotted in Fig. 4 for specific values of $\,\delta$ and $\,a$.

Fig. 4

Phase portrait of system (4) in planes $\,\left( {x,\,y} \right)$, $\left( {y,\,z} \right)$ and $\left( {x,\,z} \right)$ for specific values of $\,\delta \,$ and $\,a$:$\,\delta = 0.56$, $\,a = 5\,$ and $\,\delta = 0.55$, $\,a = 3.2\,$ with the initial conditions $\,\left( {x\left( 0 \right),\,y\left( 0 \right),\,z\left( 0 \right)} \right) =$$\left( {0.1,\,0.1,\,0.1} \right)$

From Fig. 4, we observe that system (4) exhibits two types of one-scroll chaotic attractor. The trajectories of one-scroll chaotic attractor shown in Fig. 4a are constituted of large spikes with randomly distributed amplitudes. The trajectories of one-scroll chaotic attractor depicted in Fig. 4b are constituted of large spikes with randomly distributed amplitudes, alternatively followed by irregular burst of smaller amplitudes.

The coexisting and bistability phenomena found in Fig. 3a are further detailed in Fig. 5 which depicts the phase portrait of the resulting attractors of system (4) in plane $\,\left( {x,\,y} \right)\,$ and time series of the output $\,x\left( t \right)\,$ for specific value of parameter $\,a\,$ and initial conditions.

Fig. 5

Bistable and coexisting attractors for specific value of parameter $\,a\,$ and the initial conditions: (a1) $\,a = 2.7\,$ and $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {0.1,\,0.1,\,0.1} \right)$, (a2) $\,a = 2.7\,$ and $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {0.6,\,0.6,\,0.0} \right)$ and (b1) $\,a = 5.08\,$ and $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) =$$\left( {0.0,\,0.1,\,0.0} \right)$, (b2) $\,a = 5.08\,$ and $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {0.6,\,0.6,\,0.0} \right)$. The remaining parameter is $\,\delta = 0.55$

In Fig. 5a, the output $\,x\left( t \right)\,$ displays period-2 oscillations for the initial conditions $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {0.1,\,0.1,\,0.1} \right)$ while in Fig. 5b for the initial conditions $\,\left( {x\left( 0 \right),y\left( 0 \right),\,z\left( 0 \right)} \right) = \left( {0.6,\,0.6,\,0.0} \right)$, the output $\,x\left( t \right)\,$ exhibits also period-2 oscillations but with higher amplitude than in Fig. 5a. At $\,a = 5.08,\,$, the output $\,x\left( t \right)\,$ displays period-3 oscillations and chaotic attractor for two special initial conditions as shown in Fig. 5b1 and b2, respectively. The coexistence of attractors is shown in Fig. 6 which presents the basin of attraction of system (4) in the plane $\,z = 0\,$ for $\,a = 5.08\,$ and $\,\delta = 0.55$.

Fig. 6

(Color online) Cross section of the basin of attraction of system (4) in the xy-plane at z = 0 for $\,a = 5.08\,$ and $\,\delta = 0.55$. The values of the initial conditions selected in gray regions lead to unbounded solutions. While the red and cyan regions correspond, respectively, to chaotic and periodic behaviors

From Fig. 6, it can be observed that system (4) can exhibit either unbounded solutions or chaotic or periodic attractor depending on the initial conditions.

2.2 Control of Coexisting Attractors

Multistability is a wonderful phenomenon found in immense majority of areas of science (e.g., physics, chemistry, biology, economy) and in nature (Pisarchik and Feudel 2014). This complex and striking behavior can introduce additional randomness in dynamical systems and therefore can be exploited for a few applications such as image processing and random bits generation (Mortu et al. 2007). However, in the most dynamical systems, this phenomenon can create inconveniences which reduce the performances of such systems. For instance, if a system is designed to remain at a certain dynamical equilibrium (i.e., with a predictable behavior), a small perturbation-induced jump to a coexisting states may change the performance and spoil the reproducibility and hence reliability (Goswami and Pisarchik 2008). The multistability can also create the well-known green problem in a laser system with intracavity second harmonic generation (Baer 1986). Many other examples explaining the inconveniences of multistability in dynamical systems are reported in Pisarchik and Feudel (2014). These examples illustrate sufficiently the necessity to control this phenomenon in nonlinear dynamical systems. Different methods have been currently used to control multistability including stochastic control, combined control, feedback control and non-feedback control (Pisarchik and Feudel 2014). The latter method is applied in the present work to control multistability since it is simple and requires no feedback loop or a permanent tracking of the phase-space trajectory compared to feedback ones. A slow harmonic modulation is applied to the parameter a of system (4) as

$$ a = a_{0} + a_{c} \sin (2\pi f_{c} t) $$

(10)

where $a_{0}$ is the initial value of the parameter in the uncontrolled system, $a_{c}$ and $f_{c}$ are, respectively, the amplitude and frequency of the control modulation. We assume that this additional modulation is slow ($a_{c} \ll a_{0}$) and weak ($f_{c} \ll f_{0} = {{\sqrt {a_{0} } } \mathord{\left/ {\vphantom {{\sqrt {a_{0} } } {2\pi }}} \right. \kern-0pt} {2\pi }}$). To illustrate the destruction of the coexisting attractors in system (4), we compute the bifurcation diagram depicting the local maxima of variable $x$ versus control amplitude parameter $a_{c}$ for $\delta = 0.55$, $a_{0} = 5.08$, $f_{c} = 0.05$ as shown in Fig. 7.

Fig. 7

(Color online) Bifurcation diagram depicting the local maxima $x$ with respect to the control amplitude parameter $a_{c}$ for $\delta = 0.55$, $a_{0} = 5.08$, $f_{c} = 0.05$. The upward and downward bifurcations are indicated, respectively, by red and blue color branches

From Fig. 7, we can obviously find that system (4) displays multistability at the beginning, next converts to period-3 oscillations when the control amplitude parameter $a_{c}$ is increased and decreased. These results confirm that a weak harmonic modulation converts system (4) from multistable attractors to monostable one. Moreover, the effects of the control of multistability in system (4) are more illustrated by plotting the cross section of the basin of attraction as shown in Fig. 8 for $z(0)$, $\delta = 0.55$, $a_{0} = 5.08$, $f_{c} = 0.05$ and $a_{c} = 0.05$.

Fig. 8

(Color online) Cross section of the basin of attraction of system (4) in the $x - y$ plane $z(0)$, $\delta = 0.55$, $a_{0} = 5.08$, $f_{c} = 0.05$ and $a_{c} = 0.05$. The unbounded solutions and period-3 oscillations are marked with gray and cyan, respectively

Form Fig. 8, it can be seen that system (4) is actually monostable. The chaotic behavior previously represented by red regions in Fig. 6 (uncontrolled system) was converted to period-3 oscillations because of a slow harmonic modulation to parameter $a$.

Compared to other jerk systems based on Van der Pol, Duffing, Van der Pol–Duffing oscillators (Benitez et al. 2006; Louodop et al. 2014; Kengne et al. 2016; Tamba et al. 2018a) investigated in the literature, the proposed autonomous Helmholtz jerk system (4) has a relatively simple mathematic description and can be easily implemented with some available electronic components such as resistors, capacitors, analogue multipliers and operational amplifiers.

3 Circuit Realization of Proposed Autonomous Helmholtz Jerk Oscillator

In this section, we design an electronic circuit to realize the proposed autonomous Helmholtz jerk oscillator. Using the operational amplifiers approach (Tamba et al. 2015; Jafari et al. 2016; Kingni et al. 2014; Pham et al. 2016), our circuit is designed and presented in Fig. 9.

Fig. 9

a The schematic diagram of the designed circuit modeling the proposed autonomous Helmholtz jerk oscillator described by the system (4) and b its experimental jerk circuit in operation

The designed circuit of Fig. 9 includes five operational amplifiers, one analog multiplier, ten resistors and three capacitors. The voltages at the outputs of three operational amplifiers ($U_{1} ,$$U_{2}$, $\,U_{3}$) are denoted as X, Y, Z. From Fig. 9, it is easy to derive the circuital equations of the circuit as follows

$$ \frac{{{\text{d}}X}}{{{\text{d}}t}} = \frac{1}{\text{RC}}Y $$

(11a)

$$ \frac{{{\text{d}}Y}}{{{\text{d}}t}} = \frac{1}{\text{RC}}\frac{R}{{R_{a} }}Z $$

(11b)

$$ \frac{{{\text{d}}Z}}{{{\text{d}}t}} = \frac{1}{\text{RC}}\left( { - Z - \frac{R}{{R_{\delta } }}Y - X + \frac{{X^{2} }}{1V}} \right) $$

(11c)

The circuital equation of the circuit (11) corresponds to the theoretical proposed Helmholtz jerk oscillator (4) with $a = \frac{R}{{R_{a} }},$$\delta = \frac{R}{{R_{\delta } }}.$ The values of the resistors and capacitors are chosen as $R = 10\,{\text{k}}\varOmega ,$$C = 10\,{\text{nF}}.$ The values of two resistors $R_{a} ,$$R_{\delta } \,$ can be changed to match with the values of the parameters a and $\delta .$ Figure 10 presents the observations on the oscilloscope of one-scroll chaotic attractor obtained by the circuit of Fig. 9.

Fig. 10

(Color online) Phase portraits of the one-scroll chaotic attractor observed on the oscilloscope. The values resistances are $\,R_{a} = 2\,{\text{k}}\varOmega ,$$R_{\delta } = 17.86\,{\text{k}}\varOmega .$

A good qualitative agreement is shown between one-scroll chaotic attractor illustrated in Fig. 4a and the one-scroll chaotic attractor obtained during the hardware experiments in Fig. 10. Orcard-PSpice software is utilized to validate the coexistence between period-3 oscillations and one-scroll chaotic attractor for some given initial voltages, see Fig. 11 because it is not easy to achieve special initial voltages of three capacitors in hardware circuit experiment (Argyris and Andreadis 2000; Bao et al.2016; Bao et al. 2017).

Fig. 11

(Color online) Coexisting attractors in planes $\left( {V_{x} = X,V_{y} = Y} \right)$ observed on Orcard-PSPICE. The values resistances and capacitors are $\,R_{a} = 1.96\,{\text{k}}\varOmega ,\,$$R_{\delta } = 18.18\,{\text{k}}\varOmega$

Figure 11 reproduces Fig. 5b. From Fig. 11, it can be noted that there is a good agreement between the numerical simulations and the PSpice results.

4 Amplitude and Largest Lyapunov Exponent Control of Proposed Autonomous Helmholtz Jerk Oscillator

Designing oscillators with adjustable properties is of interest in the literature (Munmuangsaen et al. 2015; Li and Sprott 2014; Li et al. 2015; Li and Sprott 2013; de la Fraga et al. 2012; Carbajal-Gomez et al. 2014; de la Fraga and Tlelo-Cuautle 2014). Amplitude control of chaotic oscillators is essential to obtain the desired size of the attractor in some engineering applications (Munmuangsaen et al. 2015; Li and Sprott 2014; Li et al. 2015; Li and Sprott 2013). Another important feature in chaotic oscillators is LLE. In Refs. de la Fraga et al. (2012), Carbajal-Gomez et al. (2014) and de la Fraga and Tlelo-Cuautle (2014), the authors designed oscillators with desired LLE. In the following subsections, a more flexible chaotic autonomous oscillator is constructed by modifying the proposed autonomous Helmholtz jerk oscillator. To improve this jerk oscillator and achieve more adjustable properties, two control parameters are added to the system describing this jerk oscillator. The first parameter controls the amplitude. The second control parameter is added to achieve changeable LLE.

4.1 Total Amplitude Control

An amplitude control parameter $\,\gamma_{1} \,$ in the form of a total amplitude controller is considered to adjust attractor amplitude. By inserting $x \to \,{x \mathord{\left/ {\vphantom {x {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }},\,y \to \,{y \mathord{\left/ {\vphantom {y {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}\,$ and $\,z \to \,{z \mathord{\left/ {\vphantom {z {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}\,$ in system (4), $\,\gamma_{1} \,$ remains only in the quadratic term $\,x^{2}$ as shown in the following system:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = y, $$

(12a)

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = az, $$

(12b)

$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = - z - \delta y - x + {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}. $$

(12c)

The set of Eq. (12) has two equilibrium points $\,E_{1} = (0,0,0)\,$ and $\,E_{2} = (1,0,0)$. The characteristic equation associated to $\,E^{*} \left( {x^{*} ,\,y^{*} ,\,z^{*} } \right)\,$ is:

$$ \lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, + \left( {1 - 2{{x^{*} } \mathord{\left/ {\vphantom {{x^{*} } {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}} \right)a = \,0 $$

(13)

For the equilibrium $\,E_{1} = (0,0,0)$, the characteristic equation is $\lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, + a = \,0$. Using Routh–Hurwitz criteria, this equation has all roots with negative real parts if and only if: $a > 0$ and $a\left( {\delta - 1} \right) > 0$. Since $\,a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{1} = (0,0,0)\,$ of system (12) is stable if $\delta \, > \,1$ and unstable for $\,\delta \, < \,1$. For the equilibrium point, $\,E_{2} \,$ in the characteristic Eq. (13) yields the following characteristic equation: $\lambda^{3} \, + \,\lambda^{2} + \,a\delta \lambda \, - a = \,0$. Using Routh–Hurwitz criteria, this equation has all roots with negative real parts if and only if: $a < 0$ and $a\left( {\delta + 1} \right) > 0$. Since $\,a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{2} \,$ of system (12) is always unstable. So the equilibrium points and their stability are independent from the parameter $\,\gamma_{1}$.

To examine the dynamical properties of system (12), bifurcation diagrams and Lyapunov exponents are considered as depicted in Fig. 12.

Fig. 12

(Color online) Bifurcation diagram depicting the maxima of $x\left( t \right)$ and the Lyapunov exponents versus the parameter $\,\gamma_{1} \,$ for specific values of $\,\delta$: a$\,\delta = 0.56\,$ and b$\,\delta = 0.8$. The remaining parameter is $\,a = 5$

In Fig. 12, the amplitude of $x\left( t \right)$ depends on the parameter $\,\gamma_{1}$. The amplitudes of variables $x\left( t \right)$, $y\left( t \right)$ and $z\left( t \right)$ are simultaneously controlled by parameter $\,\gamma_{1}$. In case $\,\gamma_{1} > 1$, the amplitude of the variables is enlarged and if $\,\gamma_{1} < 1$, it is shrunk. While the Lyapunov exponents are independent on the parameter $\,\gamma_{1}$, so it means that dynamical behavior of attractor do not change in consequence of the parameter $\,\gamma_{1}$.

4.2 Largest Lyapunov Exponent Control

A control parameter which adjusts the speed of the oscillator to reach the attractor is used in order to achieve desirable LLE. Therefore by taking ${\text{d}}t \to {{{\text{d}}t} \mathord{\left/ {\vphantom {{{\text{d}}t} {\gamma_{2} }}} \right. \kern-0pt} {\gamma_{2} }}\,$ in system (12), it can be rewritten as

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = \gamma_{2} y $$

(14a)

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = \gamma_{2} az $$

(14b)

$$ \frac{{{\text{d}}z}}{{{\text{d}}t}} = \gamma_{2} \left( { - z - \delta y - x + {{x^{2} } \mathord{\left/ {\vphantom {{x^{2} } {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}} \right) $$

(14c)

By this way, it is possible to control the LLE by choosing appropriate $\,\gamma_{2}$. System (14) has two equilibrium points $\,E_{1} = (0,0,0)\,$ and $\,E_{3} = (\gamma_{1} ,0,0)$. The characteristic equation associated to $\,E^{*} \left( {x^{*} ,\,y^{*} ,\,z^{*} } \right)\,$ is:

$$ \lambda^{3} \, + \,\gamma_{2} \lambda^{2} + \,a\gamma_{2}^{2} \delta \lambda \, + \gamma_{2}^{3} \left( {1 - 2{{x^{*} } \mathord{\left/ {\vphantom {{x^{*} } {\gamma_{1} }}} \right. \kern-0pt} {\gamma_{1} }}} \right)a = \,0 $$

(15)

For the equilibrium $\,E_{1} = (0,0,0)$, the characteristic equation is $\lambda^{3} \, + \,\gamma_{2} \lambda^{2} + \,a\gamma_{2}^{2} \delta \lambda \, + \gamma_{2}^{3} a = \,0$.

Using Routh–Hurwitz criteria, this equation has all roots with negative real parts if: $\gamma_{2} > 0$, $\gamma_{2}^{3} > 0$ and $a\gamma_{2}^{3} \left( {\delta - 1} \right) > 0$. Since $\,\gamma_{2} > 0,\,$$a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{1} = (0,0,0)\,$ of system (14) is stable if $\delta \, > \,1$ and unstable for $\,\delta \, < \,1$. For the equilibrium point, $\,E_{3} \,$ in the characteristic Eq. (15) yields the following characteristic equation: $\lambda^{3} \, + \,\gamma_{2} \lambda^{2} + \,a\delta \gamma_{2}^{2} \lambda \, - \gamma_{2}^{3} a = \,0$. Using Routh–Hurwitz criteria, this equation has all roots with negative real parts if and only if: $\gamma_{2} > 0$, $a\gamma_{2}^{3} < 0$ and $a\gamma_{2}^{3} \left( {\delta + 1} \right) > 0$. Since $\,\gamma_{2} > 0,\,$$a > 0\,$ and $\,\delta > 0$, the equilibrium point $\,E_{3} \,$ of system (14) is unstable.

To investigate the dynamical behavior of system (14), we represent in Fig. 13, the bifurcation diagrams and the LLE versus the parameter $\,\gamma_{2}$.

Fig. 13

Bifurcation diagram depicting the maxima of $x\left( t \right)$ (a) and the LLE (b) versus the parameter $\,\gamma_{2} \,$ for $\,\delta = 0.56,\,$$a = 5\,$ and $\,\gamma_{1} = 1$

The output of $x\left( t \right)$ is independent on the parameter $\,\gamma_{2} \,$ in Fig. 13a. While the LLE increases linearly with the parameter $\,\gamma_{2}$.

Before the conclusion, one can note that the proposed Helmholtz jerk oscillator studied here can generate Hopf bifurcation, periodic attractors, one-scroll chaotic attractor and coexisting attractors as the Universal Chua circuit or the Duffing-like jerk oscillator (Kengne et al. 2016) or, a similar Helmholtz jerk oscillator investigated previously by some authors of this work Tamba et al. (2018b). The new results found in the proposed Helmholtz jerk oscillator studied are bistable period-2 limit cycles, two types of one-scroll chaotic attractor and the control of the coexisting attractors, amplitude and largest Lyapunov exponents. Investigating control in dynamical systems is very important because it helps to design a system with desired features. Control can also help to improve the performances of the existing dynamical systems with undesired behaviors.

5 Conclusion

This paper reports on the analytical, numerical and experimental analyses of the proposed autonomous Helmholtz jerk oscillator. For specific parameters, the proposed autonomous Helmholtz jerk oscillator exhibited Hopf bifurcation, bistable period-2 limit cycles and two types of one-scroll chaotic attractors. The trajectories of one type of one-scroll chaotic attractor are characterized by large spikes with randomly distributed amplitudes. While the trajectories of the other type of one-scroll chaotic attractor are constituted of large spikes with randomly distributed amplitudes, alternatively followed by irregular burst of smaller amplitudes, the coexistence between period-3 limit cycle and one-scroll chaotic attractor was also found in the proposed autonomous Helmholtz jerk oscillator. The coexistence of attractors found in proposed autonomous Helmholtz jerk oscillator was controlled to a desired trajectory by using the parameter modulation method. Furthermore, hardware experiments and PSpice circuit simulations were performed to well verify the numerical simulations. Finally by adding two new parameters: the first parameter for total amplitude control without any change in largest Lyapunov exponent and the second parameter for controlling the largest Lyapunov exponent, the proposed autonomous Helmholtz jerk oscillator was controlled. The flexible chaotic autonomous Helmholtz jerk oscillator with amplitude and largest Lyapunov exponent controls would be benefitted especially in electronic, communication and information engineering.