Nondeterministic Complexity of Operations on Closed and Ideal Languages

Abstract

We study the nondeterministic state complexity of basic regular operations on the classes of prefix-, suffix-, factor-, and subword-closed regular languages and on the classes of right, left, two-sided, and all-sided ideal regular languages. For the operations of union, intersection, complementation, concatenation, square, star, and reversal, we get the tight upper bounds for all considered classes.

P. Mlynárčik—Research supported by VEGA grant 2/0084/15.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The nondeterministic state complexity of a regular language L, nsc(L), is the smallest number of states in any nondeterministic finite automaton (NFA) with a single initial state recognizing the language L. The nondeterministic state complexity of a regular operation is defined as the maximal nondeterministic state complexity of languages resulting from the operation, considered as a function of nondeterministic state complexities of the operands.

The nondeterministic state complexity of basic operations on regular languages has been investigated in [8, 9], and on prefix-free and suffix-free languages in [6, 7]. In this paper we continue this research and study the nondeterministic complexity of operations on closed and ideal languages. The (deterministic) state complexity of operations on the classes of closed and ideal languages has been studied by Brzozowski et al. in [2, 3]. Čevorová in [4] examined the state complexity of the square operation on these classes. The class of prefix-closed languages has been investigated in [5].

In this paper we get the tight upper bounds on the nondeterministic state complexity of operations of union, intersection, complementation, concatenation, square, star, and reversal on the classes of prefix-, suffix-, factor-, and subword-closed languages. We also study the operations on left, right, two-sided and all sided ideals and get tight upper bounds for these classes as well.

To prove tightness, we use a fooling set method [1]. Although the gap between a fooling set for a regular language and the size of a minimal NFA for this language may be exponential [10], here this method is successfully used to get tight upper bounds in all the cases. In most cases we describe witness languages over a binary alphabet.

2 Preliminaries

A language L is prefix (suffix, factor, subword)-closed iff for every $w\in L$ every prefix (suffix, factor, subword) of w is in L.

Let L be a language over an alphabet $\varSigma$. Then we have four classes of ideals. The language L is a right ideal iff $L=L\varSigma ^*$. The language L is a left ideal iff $L=\varSigma ^*L$. The language L is two-sided ideal iff $L=\varSigma ^*L\varSigma ^*$. The language L is all-sided ideal iff , where operation is the shuffle operation.

In the paper we investigate the nondeterministic complexity of basic operations on the above mentioned subclasses of regular languages. To prove the minimality of NFAs, we use a fooling set lower-bound technique [1, 13].

Definition 1

A set of pairs of strings $\{(x_1,y_1),(x_2,y_2),\ldots ,(x_n,y_n)\}$ is called a fooling set for a language L if for all i, j in $\{1,2,\ldots ,n\}$,

(F1) $x_iy_i\in L$, and

(F2) if $i\ne j$, then $x_iy_j\notin L$ or $x_jy_i \notin L$.

Lemma 2

([1, 13]). Let $\mathcal {F}$ be a fooling set for a language L. Then every NFA (with multiple initial states) for the language L has at least $|\mathcal {F}|$ states.

Lemma 3

([11]). Let $\mathcal {A}$ and $\mathcal {B}$ be sets of pairs of strings and let u and v be two strings such that $\mathcal {A}\cup \mathcal {B}$, $\mathcal {A}\cup \{(\varepsilon ,u)\}$, and $\mathcal {B}\cup \{(\varepsilon ,v)\}$ are fooling sets for a language L. Then every NFA with a single initial state for L has at least $|\mathcal {A}|+|\mathcal {B}|+1$ states.

3 Closed Languages

We start with union and intersection on the class of closed languages.

Theorem 4

Let $m,n\ge 2$. Let K and L be closed languages with $\mathrm {nsc}{(K)} = m$ and $\mathrm {nsc}{(L)} = n$. Then $\mathrm {nsc}{(K\cup L)} \le m+n+1$. The bound is met by binary subword closed languages.

Fig. 1.

The DFAs of subword closed languages K and L with $\mathrm {nsc}(K\cup L)=m+n+1$.

Proof

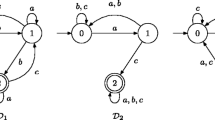
The upper bound is the same as for regular languages. To prove tightness, consider the binary subword-closed languages shown in Fig. 1.

Consider the following sets of pairs of strings:

$\mathcal {A} = \{(b^na^i, a^{m-1-i}b) \mid 0 \le i \le m-1 \}$, $\mathcal {B} = \{(ab^{n-1-j}, b^ja^m) \mid 0 \le j \le n-1 \}$

Let us show that $\mathcal A\cup \mathcal B$ is a fooling set. Condition (F1) is satisfied since for each i, j, the strings $b^na^i \cdot a^{m-1-i}b$ and $ab^{n-1-j} \cdot b^ja^m$ are in $K\cup L$. To prove (F2), we consider three cases:

(1) if $0 \le i < k \le m-1$, then $b^na^k \cdot a^{m-1-i}b$ is not in $K \cup L$;

(2) if $0 \le j < \ell \le n-1$, then $ab^{n-1-j} \cdot b^\ell a^m$ is not in $K \cup L$;

(3) if $0 \le i \le m-1$ and $0 \le j \le n-1$, then $b^na^i \cdot b^ja^m$ is not in $K \cup L$.

In addition, $\mathcal A\cup \{(\varepsilon , a^{m}b^{n-1})\}$ and $\mathcal B\cup \{(\varepsilon , a^{m-1}b^{n})\}$ are fooling sets for $K \cup L$. By Lemma 3, we have that $\mathrm {nsc}{(K \cup L)} \ge m+n+1$. This holds also for classes of factor-, prefix-, and suffix-closed languages.    $\square$

Theorem 5

Let $m, n\ge 2$. Let K and L be closed languages with $\mathrm {nsc}{(K)} = m$ and $\mathrm {nsc}{(L)} = n$. Then $\mathrm {nsc}{(K\cap L)} \le mn$. The bound is met by binary subword-closed languages.

Proof

The upper bound is the same as for regular languages. To prove tightness, consider the binary subword-closed languages shown in Fig. 1. Consider the following set of pairs of strings: $\mathcal {F} = \{(a^ib^j, a^{m-1-i}b^{n-1-j}) \mid 0 \le i\le m-1, 0 \le j \le n-1 \}$. Let us show that $\mathcal {F}$ is a fooling set for $K \cap L$. Condition (F1) is satisfied since for each i, j, the string $a^ib^j \cdot a^{m-1-i}b^{n-1-j}$ is in $K\cap L$. To prove (F2), let $(i,j) \ne (k,\ell )$. (1) If $i < k$, then $a^kb^\ell \cdot a^{m-1-i}b^{n-1-j}$ is not in $K\cap L$. (2) If $i = k$ and $j < \ell$, then $a^kb^\ell \cdot a^{m-1-i}b^{n-1-j}$ is not in $K\cap L$.

Hence $\mathcal {F}$ is a fooling set for $K \cap L$, so $\mathrm {nsc}{(K \cap L)} \ge mn$.    $\square$

Fig. 2.

The subword-closed witnesses K, L for concatenation meeting the bound $m+n$.

Let us continue with concatenation and square.

Theorem 6

Let K and L be closed languages with $\mathrm {nsc}{(K)} = m$ and $\mathrm {nsc}{(L)} = n$. Then $\mathrm {nsc}{(KL)} \le m+n$. The bound is met by ternary subword-closed languages.

Proof

The upper bound is the same as for regular languages. To prove tightness, consider the ternary subword-closed languages shown in Fig. 2.

Consider the following set of pairs of strings:

$\mathcal {F} = \{(a^i, a^{m-1-i}cba^{n-1}) \mid 0 \le i\le m-1 \} \, \cup \, \{(a^{m-1}cba^j, a^{n-1-j}) \mid 0 \le j \le n-1 \}$.

Let us show that $\mathcal {F}$ is a fooling set for KL. Condition (F1) is satisfied since for each i, j, the strings $a^i \cdot a^{m-1-i}cba^{n-1}$ and $a^{m-1}cba^j \cdot a^{n-1-j}$ are in KL. To prove (F2), notice that KL is a subset of $b^*a^*c^*b^*a^*c^*$ and every string in KL has at most $m-1+n-1$ letters a. We consider three cases.

(1) If $0 \le i < k \le m-1$, then $a^k \cdot a^{m-1-i}cba^{n-1}$ is not in KL, because it has more than $m-1+n-1$ letters a.

(2) If $0 \le j < \ell \le n-1$, then $a^{m-1}cba^\ell \cdot a^{n-1-j}$ is not in KL, because it has more than $m-1+n-1$ letters a.

(3) If $0 \le i \le m-1$ and $0 \le j \le n-1$, then $a^{m-1}cba^j \cdot a^{m-1-i}cba^{n-1}$ is not in KL, because this string is not in the form $b^*a^*c^*b^*a^*c^*$.

Hence $\mathcal {F}$ is a fooling set for KL, so $\mathrm {nsc}{(KL)} \ge m+n$.    $\square$

If $m=n$, then $K=L$ in the proof above, so we get the next result.

Corollary 7

Let L be a closed language with $\mathrm {nsc}{(L)} = n$. Then $\mathrm {nsc}{(L^2)} \le 2n$. The bound is met by a ternary subword-closed language.

Fig. 3.

The prefix-closed witness language L for star and reversal.

Fig. 4.

The suffix-closed witness language L for star meeting the bound n.

Theorem 8

Let L be a closed language over $\varSigma$ with $\mathrm {nsc}{(L)} = n$. Then

(a) if L is prefix-closed, then $\mathrm {nsc}{(L^*)} \le n$, and the bound is tight if $|\varSigma | \ge 2$;

(b) if L is suffix-closed, then $\mathrm {nsc}{(L^*)} \le n$, and the bound is tight if $|\varSigma | \ge 2$;

(c) if L is factor- or subword-closed, then $\mathrm {nsc}{(L^*)} = 1$.

Proof

If L is a closed language, then $\varepsilon \in L$. It follows that $\mathrm {nsc}{(L^*)} \le n$. To prove tightness, consider a prefix-closed language shown in Fig. 3 and a suffix-closed language shown in Fig. 4. Lower bound for prefix-closed was proven in [5], lower bound for suffix-closed is n because $L = L^*$. For factor- or subword-closed, let $\varGamma$ be set of letters present in any string of L. While $L \subseteq \varGamma ^*$, every single-letter string from $\varGamma$ is in L. It follows that $L^* = \varGamma ^*$, hence $\mathrm {nsc}{(L^*)} = 1$.    $\square$

Fig. 5.

The factor-closed witness language L for reversal meeting the bound $n+1$.

Theorem 9

Let $n\ge 3$ and L be a closed language with $\mathrm {nsc}{(L)}=n$. Then $\mathrm {nsc}{(L^R)}\le n+1$. The bound is met by a binary prefix-closed language, by a ternary factor-closed language and by a subword-closed language over an alphabet of size $2n-2$.

Proof

The upper bound is the same as for regular languages. To prove tightness, consider the binary prefix-closed language shown in Fig. 3. It was shown in [5] that the reversal of this language requires $n+1$ states. Now consider the ternary factor-closed language shown in Fig. 5. Consider the following sets of pairs of strings: $\mathcal A= \{(b, a^{n-2}c)\} \text { and } \mathcal B= \{(ba^i, a^{n-2-i}c) \mid 1 \le i \le n-2\} \, \cup \,\{(ca^{n-1},\varepsilon )\}.$ Let us show that $\mathcal A\,\cup \, \mathcal B$, $\mathcal A\,\cup \,\{(\varepsilon ,a^{n-3}c)\}$, and $\mathcal B\,\cup \,\{(\varepsilon ,a^{n-2}c)\}$ are fooling sets for $L^R$. Condition (F1) is satisfied since for each i, the string $ba^i \cdot a^{n-2-i}c$ equals $ba^{n-2}c$ that is in $L^R$ since $ca^{n-2}b$ is in L. String $ca^{n-1}$ is also in $L^R$ since $a^{n-1}c$ is in L. To prove (F2), notice that every string of L has at most $n-2$ continual occurences of a after any c. Thus we consider cases:

(1) If $0 \le i < j \le n-2$, then $ba^j \cdot a^{n-2-i}c$ is not in $L^R$, because it has more than $n-2$ continual occurences of a after c. (2) If $0 \le i \le n-2$, then $ca^{n-1} \cdot a^{n-2-i}c$ is not in $L^R$, because it has more than $n-2$ continual occurences of a after c.

Sets $\mathcal A\cup \{(\varepsilon ,a^{n-3}c)\}$ and $\mathcal B\cup \{(\varepsilon ,a^{n-2}c)\}$ are fooling sets for $L^R$, because the strings $b \cdot a^{n-3}c$ and $ba^{i} \cdot a^{n-2}c, i\ge 1$ are not in $L^R$. Therefore by Lemma 3 $\mathrm {nsc}(L^R)\ge n+1$. This proof holds also for the class of suffix-closed languages since every factor-closed language is also suffix-closed.

Finally consider the subword-closed language accepted by the DFA shown in Fig. 6. Consider the following sets:

$\mathcal A= \{(b_2b_3\cdots b_{n-1}, a_1)\}$, $\mathcal B= \{(b_1\cdots b_{i-1}b_{i+1}\cdots b_{n-1}, a_i) \mid 2 \le i \le n-1\} \cup \{(b_1a_2,\varepsilon )\}$. Let us show that $\mathcal A\cup \mathcal B$, $\mathcal A\cup \{(\varepsilon , a_2)\}$ and $\mathcal B\cup \{(\varepsilon , a_1)\}$ are fooling sets for $L^R$. Condition (F1) for $\mathcal A\cup \mathcal B$ is satisfied because for every i the string $b_1\cdots b_{i-1}b_{i+1}\cdots b_{n-1} \cdot a_i$ is in $L^R$. Next, for every $i \ne j$ the string $b_1\cdots b_{i-1}b_{i+1}\cdots b_{n-1}\cdot a_j$ is not in $L^R$, because it has $b_j$ before $a_j$. Hence (F2) is satisfied. The condition (F1) for $\mathcal A\cup \{(\varepsilon , a_2)\}$ and for $\mathcal B\cup \{(\varepsilon , a_1)\}$ is satisfied, because the strings $a_2$ and $a_1$ are in $L^R$. The proof of condition (F2) uses the same strings as for $\mathcal A\cup \mathcal B$.    $\square$

Fig. 6.

The DFA of subword-closed language L where $B=\{b_1, \ldots , b_{n-1}\}$.

We conclude this section with the complementation operation. In [5], a ternary prefix-closed language meeting the upper bound $2^n$ for complement was described. Now we describe a binary witness language.

Theorem 10

Let L be a closed language over $\varSigma$ with $\mathrm {nsc}(L)=n$. Then

(a) if L is prefix-closed, then $\mathrm {nsc}(L^c)\le 2^n$, and the bound is tight if $|\varSigma |\ge 2$; (b) if L is suffix-closed, then $\mathrm {nsc}(L^c)\le 2^{n-1}+1$, and the bound is met by a binary factor-closed language;

(c) if L is subword-closed, then $\mathrm {nsc}(L^c)\le 2^{n-1}+1$, and the bound is tight if $|\varSigma |\ge 2^n$.

Fig. 7.

The NFA of binary witness prefix-closed language L with $\mathrm {nsc}(L^c)=2^n$.

Proof

(a) The upper bound is the same as for regular languages. To prove tightness, let L be the binary language accepted by the NFA A shown in Fig. 7. First, we prove the reachability of every subset of $\{1,2,\ldots , n\}$ in the subset automaton of A. Notice that we have $\{1\} \xrightarrow {a^{n-1}} \{n\} \xrightarrow {a^{n-1}} \{1,2,\ldots ,n\}$. Next, we can shift cyclically by one every subset S: we use the string a if $n\notin S$ or if $n\in S$ and $n-1\in S$, and we use the string ab otherwise. Finally, we can remove state n from any subset containing n by b. It follows that every subset of $\{1,2,\ldots ,n\}$ is reachable. Thus for every set S, there exists a string $u_S$ such that $u_S$ leads the subset automaton from $\{1\}$ to S.

Now, we define a fooling set for complement of L. For every set S we define a string $v_S$ as follows. First we define $\sigma (i)$, where $i\in \{1,2,\ldots , n\}$ as

$$\begin{aligned} \sigma (i) ={\left\{ \begin{array}{ll} ba, &{}\text {if} \, i \,\in S,\\ a, &{}\text {if} \, i \, \not \in S. \end{array}\right. } \end{aligned}$$

Let $v_S=\sigma (n)\sigma (n-1)\ldots \sigma (2)\sigma (1)$. We show, that such a string is rejected by A from every $i\in S$ and accepted from every $i\not \in S$. Let $i\notin S$, then $\sigma (i)=a$, and $i \xrightarrow {\sigma (n)} i+1 \xrightarrow {\sigma (n-1)} i+2 \xrightarrow {\sigma (n-2)} \cdots \xrightarrow {\sigma (i+1)} n \xrightarrow {a} 1 \xrightarrow {\sigma (i-1)\ldots \sigma (1)} i$,

so $v_S$ is accepted since every state is final. If $i\in S$, then $\sigma (i)=ba$, and $i \xrightarrow {\sigma (n)} \{i+1 \} \xrightarrow {\sigma (n-1)} \{ i+2\} \xrightarrow {\sigma (n-2)} \cdots \xrightarrow {\sigma (i+1)} \{n\}$,

and now A reads the first symbol of $\sigma (i)$ which is b. However, transition on b is not defined in state n, therefore the string $v_S$ is rejected.

Now we show that

$\mathcal {F}=\{(u_S,v_S)\mid S\subseteq \{1,2,\ldots , n\}\}$ is a fooling set for $L^c$.

(F1) Let $S\subseteq \{1,2,\ldots , n\}$. The NFA A reaches subset S by $u_S$, and from every state $q\in S$ the string $v_S$ is rejected. So $u_Sv_S$ is rejected by A, so $u_Sv_S\in L^c$.

(F2) Let $S, T \subseteq \{1,2,\ldots , n\}$ and $S\ne T$. Without loss of generality, there exists a state i, such that $i\in S$ and $i\not \in T$. So $v_T$ is accepted from i. Hence $u_Sv_T$ is accepted by A, and therefore $u_Sv_T\not \in L^c$. This completes the proof of (a).

(b) We first prove the upper bound. Let $A=(Q,\varSigma ,\delta ,s,F)$ be a minimal NFA, such that $L(A)=L$. Since A is a minimal NFA, every q in Q is reachable from s and also some final state is reachable from q. Let a state $q\in Q$ be reachable from s by a string u. If a final state is reachable from q by string v, then also uv reaches a final state, so uv is accepted. Since L is suffix-closed, the string v reaches a final state from s. Therefore every subset of Q containing s is equivalent to $\{s\}$ in the subset automaton of NFA A. So subset automaton of A has at most $2^{n-1}+1$, so $\mathrm {nsc}(L^c)\le 2^{n-1}+1$.

Fig. 8.

The factor-closed witness L for complement, with $\mathrm {nsc}(L^c)=2^{n-1}+1$.

To prove tightness, consider the language L accepted by automaton in Fig. 8. If there is an accepting computation from a state q on a string u such that $q\xrightarrow {a(b)}q'\xrightarrow {u'}f$, where $u=au'$ or $u=bu'$ and f is a final state, then there is a computation $s\xrightarrow {a(b)}q'\xrightarrow {u'}f$. It follows that L is suffix-closed. Therefore L is factor-closed. First, we prove the reachability of every subset of $\{1,2,\ldots , n-1\}$ in the subset automaton of A. Notice that we have $\{0\} \xrightarrow {a} \{1,2,\ldots ,n-1\}$. Next, we can shift cyclically by one every subset S by using the string a. Finally, we can remove state $n-1$ from any subset containing $n-1$ by b. It follows that every subset of $\{1,2,\ldots ,n-1\}$ is reachable. Thus for every set S, there exists a string $u_S$ such that $u_S$ leads the subset automaton from $\{0\}$ to S. Now, we define a fooling set for complement of L. For every set S we define a string $v_S$ as follows. First we define $\sigma (i)$, where $i\in \{1,2,\ldots , n-1\}$ as $\sigma (i) =ba$ if $i\in S$, and $\sigma (i)=a$ if $i\notin S$. Let $v_S=\sigma (n-1)\sigma (n-2)\cdots \sigma (2)\sigma (1)$. Similarly as in proof in case of prefix-closed in (a) we can show that such a string is rejected by A from every $i\in S$ and accepted from every $i\not \in S$. Let $\mathcal {A}=\{(u_S,v_S)\mid S\subseteq \{1,2,\ldots , n-1\}\}$. We can show that $\mathcal {F}=\mathcal {A}\cup \{(\varepsilon ,(ba)^n)\}$ is a fooling set for $L^c$.

(c) Since subword-closed language is also factor-closed, the upper bound is $2^{n-1}+1$. To prove tightness consider an NFA A, defined as follows:

$A=(Q,\varSigma ,\delta ,s,F)$, where $Q=\{0,1,2,\ldots ,n-1\}, s=0, F=Q$ and $\varSigma =\{a_S, b_S\mid S\subseteq \{1,2,\ldots ,n-1\}\}$, $\delta (0,a_S)=S$, for $i>0$ $\delta (i,a_S)=\emptyset$, $\delta (0,b_S)=0$, for $i>0$: if $i\notin S$, then $\delta (i,b_S)=\{i\}$ and if $i\in S$, then $\delta (i,b_S)=\emptyset$ . Such an NFA is shown in Fig. 9. Consider now the language $L=L(A)$. Let $w \in L$. The string w is accepted in a $i \in S$. Any substring of w is accepted also in the i. Hence L is subword-closed. We can show that $\mathcal {A}=\{(a_S,b_S)\mid S\subseteq \{1,2,\ldots , n-1\}\} \,\cup \,\{(\varepsilon ,a_{\emptyset }\}$ is fooling set for $L^c$. Therefore $\mathrm {nsc}(L^c)\ge 2^{n-1}+1$.    $\square$

Fig. 9.

The subword-closed witness language L with $\mathrm {nsc}(L)=3$ and $|\varSigma |=2^n$.

In the end of this section we pay attention to unary closed languages. Consider prefix-closed languages and two cases, finite languages and infinite languages. In the case of finite languages, there is a string with maximum length, so every shorter string also must be in the language. In the case of infinite languages, for arbitrary positive integer i, there is a string w with length at least i and with this string every its prefixes, so such a language is $a^*$. Moreover suffix-closed, factor-closed and subword-closed coincide.

Theorem 11

Let K and L be two unary closed languages with $\mathrm {nsc}{(K)}=m$ and $\mathrm {nsc}{(L)}=n$. Then $\mathrm {nsc}{(K\cup L)} \le \mathrm {max}\{m,n\}$, $\mathrm {nsc}{(K\cap L)} \le \mathrm {min}\{m,n\}$, $\mathrm {nsc}{(KL)} \le m+n-1$, $\mathrm {nsc}{(L^2)} \le 2n-1$, $\mathrm {nsc}{(L^*)} \le 1$, $\mathrm {nsc}{(L^R)} \le n$, and $\mathrm {nsc}{(L^c)} \le n+1$. All these bounds are tight.

4 Ideal Languages

Let us begin with a useful proposition about some features of automata for left and right ideals.

Proposition 12

Let L be a regular language. (1) If L is a left ideal, then there exists a minimal NFA A such that $L(A)=L$ and there is a loop on each symbol in the initial state and no transition goes to the initial state from any other state. (2) If L is a right ideal, then there exists a minimal NFA A such that $L(A)=L$ and there is a unique final state in which there is a loop on each symbol and from which no transition goes to any other state.

Theorem 13

Let $m,n\ge 1$. Let K and L be ideal languages with $\mathrm {nsc}(K)=m$ and $nsc(L)=n$. Then $\mathrm {nsc}(K\cap L)\le mn$. The bound is met by binary all-sided ideals.

Theorem 14

Let $m,n\ge 3$. Let K and L be ideal languages over an alphabet $\varSigma$ with $\mathrm {nsc}(K)=m$ and $nsc(L)=n$. Then

(a) if K, L are right ideals, then $\mathrm {nsc}(K\cup L)\le m+n$,

(b) if K, L are left ideals, then $\mathrm {nsc}(K\cup L)\le m+n-1$,

(c) if K, L are two-sided or all-sided ideals, then $\mathrm {nsc}(K\cup L)\le m+n-2$,

and all the bounds are tight if $|\varSigma |\ge 2$.

Proof

(a) We first prove the upper bound. Let A be a minimal m-state NFA for K and B be a minimal n-state NFA for L. Since K and L are right ideals, A and B have exactly one final state which goes to itself on each symbol. We can get an $\varepsilon$-NFA for $K\cup L$ from NFAs A and B by merging the final states of A and B and by adding a new initial state connnected to the initial states of A and B by $\varepsilon$-transitions. The resulting $\varepsilon$-NFA has $m+n$ states, so the corresponding NFA for $K\cup L$ has also $m+n$ states.

Fig. 10.

Witnesses right ideals for union.

To prove tightness, consider the binary right ideals K and L shown in Fig. 10. Now we show that minimal NFA for $K\cup L$ needs $m+n$ states. To this aim let

$\mathcal {A}=\{(a^{m-1+i},a^{m-2-i}b)\mid 0\le i \le m-2\}\cup \{(a^{m-2}b,\varepsilon )\},$ and

$\mathcal {B}=\{(b^{n-1+j},b^{n-2-j}a)\mid 0\le j \le n-2\}.$

The sets $\mathcal {A}\,\cup \,\mathcal {B}$, $\mathcal {A}\,\cup \,\{(\varepsilon ,b^{n-2}a)\}$ and $\mathcal {B}\cup \{(\varepsilon ,a^{m-2}b)\}$ are fooling sets. By Lemma 3 we have $\mathrm {nsc}({K\cup L})\ge |\mathcal {A}|+|\mathcal {B}|+1 =m+n$.

Fig. 11.

Witnesses left ideals for union.

(b) We first prove the upper bound. Let A be a minimal m-state NFA for K and B be a minimal n-state NFA for L. Since K and L are left ideals, we may assume by Proposition 12 that A and B have a loop on each symbol in the initial state, and no transition from some other state goes to the initial state.

We can get an NFA for $K\cup L$ from NFAs A and B by merging the initial states. All original transitions from initial states of NFAs A, B go from new merged state to states as before merging. The resulting NFA has $m+n-1$ states, so $\mathrm {nsc}(K\cup L)\le m+n-1$.

To prove tightness, consider two left ideals shown in Fig. 11. Now we show that minimal NFA for $K\cup L$ needs $m+n-1$ states. To this aim let $\mathcal {A}=\{(a^i,a^{m-1-i})\mid 0\le i \le m-1\}$ and $\mathcal {B}=\{(b^j,b^{n-1-j})\mid 1\le j \le n-2\}\cup \{(b^{n-1},ab^{n-2})\}.$ The set $\mathcal {A}\,\cup \,\mathcal {B}$ is fooling set for $K\,\cup \, L$, so $\mathrm {nsc}(K\,\cup \,L)\ge m+n-1$, therefore $\mathrm {nsc}(K\cup L)=m+n-1$.

(c) For upper bound, let A be a minimal m-state NFA for K and B be a minimal n-state NFA for L. Since K and L are left ideals and also right ideals, we may assume by Proposition 12 that A and B have properties claimed there. We can get an NFA for $K\cup L$ from NFAs A and B by merging the initial states, and by merging the final states of A and B. The resulting NFA has $m+n-2$ states and we leave to the reader to verify the correctness of the construction. To prove tightness, consider languages $K=\{w\in \{a,b\}^*\mid \#_a(w)\ge m-1\}$ and $L=\{w\in \{a,b\}^*\mid \#_b(w)\ge n-1\}$, so K and L are all-sided ideals. Notice that each string in $K\cup L$ has at least $m-1$ symbols a or at least $n-1$ symbols b. The set $\{(a^i,a^{m-1-i})\mid 0\le i \le m-1\} \cup \{(b^j,b^{n-1-j})\mid 1\le j \le n-2\}$ is fooling set for $K\cup L$ and contains $m+n-2$ pairs, so $\mathrm {nsc}(K\cup L)\ge n+m-2$.    $\square$

In the next theorem we use unary languages to prove tightness.

Theorem 15

Let $m,n\ge 3$. Let K and L be ideal languages over $\varSigma$ with $\mathrm {nsc}(K)=m$ and $\mathrm {nsc}(L)=n$. Then $\mathrm {nsc}(KL)\le m+n-1$ and the bound is tight if $|\varSigma |\ge 1$. Moreover, $\mathrm {nsc}(L^2)\le 2n-1$ and the bound is tight if $|\varSigma |\ge 1$ .

Proof

First, let K, L be left ideals. Let $A=(Q_A,\varSigma ,\delta _A,s_A,F_A)$ and $B=(Q_B,\varSigma ,\delta _B,s_B,F_B)$ be minimal NFAs for K, L. Since K and L are left ideals, we may assume by Proposition 12 that A and B have a loop on each symbol in the initial state, and no transition from some other state goes to the initial state. We can get an NFA C for KL from NFAs A and B as follows: For every f in $F_A$ add a loop on every symbol and add transitions (f, a, q) when there is a transition $(s_B,a,q)$ in B, where $f\in F_A, a\in \varSigma , q\in Q_B\setminus \{s_B\}$. Set $F_C=F_B, Q_C=Q_A\cup Q_B\setminus \{s_B\}$. The resulting NFA has $m+n-1$ states, so $\mathrm {nsc}(KL)\le m+n-1$.

Now, let K, L be right ideals. Let $A=(Q_A,\varSigma ,\delta _A,s_A,\{q_f\})$ be a minimal m-state NFA for K and $B=(Q_B,\varSigma ,\delta _B,s_B,\{p_f\})$ be a minimal n-state NFA for L. Since K and L are right ideals, we may assume by Proposition 12 that A and B have a loop on each symbol in a unique final state, and no transition goes from the final state to some other state. We can get an NFA C for KL from NFAs A and B by merging final state of A with initial state of B and excluding of merged state from set of final states as follows: $C=(Q_C,\varSigma ,\delta _C,s_A,\{p_f\})$, where $Q_C=(Q_A\setminus \{q_f\})\cup (Q_B\setminus \{s_B\})\cup \{n_{AB}\}$ and for every a in $\varSigma$ we have $\delta _C(n_{AB},a)=\delta _A(q_f,a)\cup \delta _B(s_B,a)$. The resulting NFA has $m+n-1$ states, so $\mathrm {nsc}(KL)\le m+n-1$.

Two-sided and all-sided ideals are also right ideals, so upper bound is the same as in that cases. To prove tightness, consider all-sided ideal languages $K=\{a^{m-1}a^k\mid k\ge 0 \}$ and $L=~\{a^{n-1}a^k\mid k\ge 0 \}$, with $\mathrm {nsc}(K)=m$ and $\mathrm {nsc}(L)=n$. The set $\mathcal {F}=\{(a^i, a^{m+n-2-i})\mid 0\le i\le m+n-2\}$ is fooling set for KL, so $\mathrm {nsc}(KL)\ge |\mathcal {F}|=m+n-1$. It remains to show the case for square. The upper bound follows from general concatenation, when $m=n$. The tightness follows from a coincidence of the forms of witness languages.    $\square$

Theorem 16

Let $n\ge 2$. Let L be ideal languages over $\varSigma$ with $nsc(L)=n$. Then $\mathrm {nsc}(L^*)\le n+1$ and the bound is met by a binary all-sided ideal.

Theorem 17

Let $n\ge 3$. Let L be ideal languages over $\varSigma$ with $\mathrm {nsc}(L)=n$. (a) If L is right or two-sided or all-sided ideal, then $\mathrm {nsc}(L^R)\le n$ and the bound is tight if $|\varSigma |\ge 1$. (b) If L is left ideal, then $\mathrm {nsc}(L^R)\le n+1$ and the bound is tight if $|\varSigma |\ge 3$.

Theorem 18

([14]). Let $n\ge 3$. Let L be language over $\varSigma$ with $nsc(L)=n$.

(a) If L is a right or left ideal, then $\mathrm {nsc}(L^c)\le 2^{n-1}$. The bound is tight if $|\varSigma |\ge 2$.

(b) If L is a two-sided ideal, then $\mathrm {nsc}(L^c)\le 2^{n-2}$. The bound is tight if $|\varSigma |\ge 2$.

(c) If L is an all-sided ideal, then $\mathrm {nsc}(L^c)\le 2^{n-2}$. The bound is tight if $|\varSigma |\ge 2^{n-2}$.

In the end we pay attention to unary ideal languages. Let $\varSigma =\{a\}$. If L is a right ideal and $a^i$ is its shortest string, then $L=a^ia^*$. Moreover , hence left, right, two-sided and all-sided ideals coincide.

Theorem 19

Let $m, n\ge 2$. Let K, L be unary ideals with $\mathrm {nsc}(K)=m, \mathrm {nsc}(L)=~n$. Then $\mathrm {nsc}(K\cap L)=\max \{m,n\}$, $\mathrm {nsc}(K\cup L)=\min \{m,n\}$, $\mathrm {nsc}(KL)=m+n-1$, $\mathrm {nsc}(L^2)=2n-1$, $\mathrm {nsc}(L^*)=n-1$, $\mathrm {nsc}(L^R)=n$, $\mathrm {nsc}(L^c)=n-1$.

5 Conclusions

We investigated the nondeterministic state complexity of basic regular operations on the classes of closed and ideal languages. For each class and for each operation, we obtained the tight upper bounds. To prove tightness we usually used a binary alphabet. In all the cases where we used a larger alphabet for describing witness languages, we do not know whether the obtained upper bounds can be met also by languages defined over smaller alphabets. For both closed and ideal languages, we also considered the unary case. Our results are summarized in the following tables.

Class	$K\cap L$, $\varSigma$	$K\cup L$, $\varSigma$	$K\cdot L$, $\varSigma$
Prefix-closed	mn, 2	$m+n+1$, 2	$m+n$, 3
Suffix-closed	mn, 2	$m+n+1$, 2	$m+n$, 3
Factor-closed	mn, 2	$m+n+1$, 2	$m+n$, 3
Subword-closed	mn, 2	$m+n+1$, 2	$m+n$, 3
Unary closed	min$\{m,n\}$	max$\{m,n\}$	$m+n-1$
Right ideal	mn, 2	$m+n$, 2	$m+n-1$, 1
Left ideal	mn, 2	$m+n-1$, 2	$m+n-1$, 1
Two-sided ideal	mn, 2	$m+n-2$, 2	$m+n-1$, 1
All-sided ideal	mn, 2	$m+n-2$, 2	$m+n-1$, 1
Unary ideal	max$\{m,n\}$	min$\{m,n\}$	$m+n-1$
Regular	mn, 2	$m+n+1$, 2	$m+n$, 2
Unary regular	mn; gcd$(m,n)=1$	$m+n$; gcd$(m,n)=1$	$m+n(-1)$

Class	$L^2$, $\varSigma$	$L^*$, $\varSigma$	$L^R$, $\varSigma$	$L^c$, $\varSigma$
Prefix-closed	2n, 3	n, 2	$n+1$, 2	$2^n$, 2
Suffix-closed	2n, 3	n, 2	$n+1$, 3	$1+2^{n-1}$, 2
Factor-closed	2n, 3	1, 1	$n+1$, 3	$1+2^{n-1}$, 2
Subword-closed	2n, 3	1, 1	$n+1$, $2n-2$	$1+2^{n-1}$, $2^{n}$
Unary closed	$2n-1$	1	n	$n+1$
Right ideal	$2n-1$, 1	$n+1$, 2	n, 1	$2^{n-1}$, 2
Left ideal	$2n-1$, 1	$n+1$, 2	$n+1$, 3	$2^{n-1}$, 2
Two-sided ideal	$2n-1$, 1	$n+1$, 2	n, 1	$2^{n-2}$, 2
All-sided ideal	$2n-1$, 1	$n+1$, 2	n, 1	$2^{n-2}$, $2^{n-2}$
Unary ideal	$2n-1$	$n-1$	n	$n-1$
Regular	2n, 2	$n+1$, 1	$n+1$, 2	$2^n$, 2
Unary regular	$2n(-1)$	$n+1$	n	$2^{\varTheta (\sqrt{n\log {n}})}$