Square on Ideal, Closed and Free Languages

Abstract

We study the deterministic state complexity of a language accepted by an $n$-state DFA concatenated with itself for languages from certain subregular classes. Tight upper bounds are obtained on optimal alphabets for prefix-closed, xsided-ideal and xfix-free languages, except for suffix-free, where a ternary alphabet is used.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Janusz Brzozowski and his coauthors have recently published a series of articles concerning quotient complexity of basic operations such as concatenation, Kleene closure or boolean operations on ideal [1], free [2], and closed [3] languages. The results were usually significantly smaller compared to the state complexity of general languages, despite the fact that quotient and state complexity is numerically always the same.

None of these articles considered the operation square. Since it is a special case of concatenation – a product of language with itself – results for concatenation provide an immediate upper bound on state complexity of operation square. On the other hand, the state complexity of square on general languages has been studied by Rampersad [4]. He showed, that in the binary case it is $n2^{n}-2^{n-1}$, whereas in unary $2n-1$. Our aim was to study the state complexity of a square on certain ideal, free or closed subclasses of regular languages and compare results with these upper bounds.

The study of these subregular classes is not isolated. Determination of many classes of NFAs was considered in [5], including free and closed languages. Syntactic complexity was studied for ideal and closed languages [6]. A more specialized study of suffix-free languages is in [7], of prefix-free languages in [8] and of prefix-closed languages in [9] and [10].

This paper is organized as follows. In next section we give the most important definitions. In Sect. 3 we study ideal languages, Sect. 4 is dedicated to prefix-closed languages and then, in Sect. 5, we discuss free languages. In the conclusion, we compare our results with results for concatenation on the same classes and for general regular languages.

2 Preliminaries

We assume, that the reader is familiar with basic notions from automata theory, for reference see [11]. Here we recall only the most important definitions.

Let $[c,d]$ denote the set $\{c,c+1,\ldots ,d\}$ if $c\le d$. A binary operation $\oplus$ called symmetric difference is defined on sets as $S\oplus S' = S\cup S\ -(S \cap S')$. Cardinality of set $S$ is denoted by $|S|$.

An incomplete DFA is an NFA $A = (Q,\varSigma ,\delta , \{q_0\},F)$ with single initial state and with the property that for every $q \in Q$ and $a\in \varSigma$ the inequality $|\delta (q,a)| \le 1$ holds. Thus some transitions may be not defined, but this is the only trace of nondeterminism. It could be made deterministic by adding one nonfinal dead state, where all previously undefined transitions are incoming.

Let $L$ be a regular language. The state complexity is denoted by ${{\mathrm{sc}}}(L)$, and is defined as the number of states of its minimal DFA, whereas the incomplete state complexity $\mathrm {isc}(L)$, is the number of states of its minimal incomplete DFA.

Let $u,v,x,w$ be words. If $w = uvx$, then we call $u$ a prefix, $x$ a suffix and $v$ a factor of word $w$. If $w = u_1v_1u_2v_2\cdots u_kv_k$, for some words $u_i,v_i$, then word $u = u_1u_1\cdots u_k$ is called subword of $w$.

We call $L$ xfix-free for xfix $\in \{\text {prefix, suffix, factor, subword}\}$, if whenever $u,v \in L$ and $u$ is xfix of $v$, then $u = v$. Similarly, $L$ is xfix-closed, if whenever $u$ is xfix of $v$ and $v \in L$, then also $u \in L$. And lastly we call $L$ an xsided ideal for xsided $\in \{\text {left, right, 2-sided, all-sided}\}$, when $L = \varSigma ^*L$, $L = L\varSigma ^*$, $L=\varSigma ^*L\varSigma ^*$, respectively, where is the shuffle operation. Square of $L$ is language $L\cdot L$, denoted as $L^2$.

Sometimes we will think of letters as of a function $Q\longrightarrow Q$. In particular, this allows us to define for each letter $a$ inverse function $a^{-1}$ for all states with exactly one incoming transition on $a$. This can be naturally generalized for words.

Proposition 1

Note that in the case $w^{-1}(q)$ exists, there is a unique state, from which state $q$ could be reached on the word $w$.

Fig. 1.

NFA for square

The standard construction of DFA for square of DFA $A = (Q,\varSigma ,\delta ,s,F)$. At first, we define an NFA accepting $L^2(A)$ as shown in Fig. 1. If $A$ has a dead state, we remove it, to obtain an incomplete DFA. Then we take two exact copies of the DFA $A$ with all transitions and change labels of states so they are unique and a state $t$ becomes $q_t$. Other changes are, that $s$ will not be initial and we change the finality of all states in the first copy to nonfinal. Lastly, we will add transitions. Whenever $f \in F$, then we add a transition $q_f\overset{\varepsilon }{\longrightarrow }s$.

Now we determine this NFA by the standard subset construction to obtain DFA accepting $L^2(A)$. Note that all reachable states contain at most one state from the first copy, because this copy is deterministic and there is no transition to it from the second copy.

3 Xsided Ideal Languages

A concatenation of left ideal languages has a quotient, i.e., also state complexity $m+n-1$ [1]. Witness languages are unary $a^{n-1}a^*$ and $a^{m-1}a^*$; thus the upper bound on the state complexity of square of left ideal language is $2n-1$ and is tight with the witness $a^{n-1}a^*$. Moreover, since 2-sided and all-sided ideals are also left ideals, this upper bound also holds for them. Because in the unary case the 2-sided or all-sided ideal is the same as left ideal, this bound is tight. Only nonunary right ideals remain unresolved by this reasoning.

Proposition 2

A language $L$ is right ideal if and only if the minimal DFA that recognizes $L$ has exactly one final state with all outcoming transitions leading back to this final state.

Lemma 3

Let $L$ be a right ideal language with ${{\mathrm{sc}}}(L) = n$. Then ${{\mathrm{sc}}}(L^2) \le n+2^{n-2}$.

Proof

This is a direct consequence of Theorem 9 in [1], which states, that product (concatenation) of two right ideal languages with quotient complexities $m$ and $n$ has quotient complexity at most $m+2^{n-2}$. We will also provide an elementary proof, since it provides the insight necessary for the following lemmata. Let $n-1$ be the only final state of a minimal DFA for a right-ideal language. Consider the standard construction of an NFA for a square and then the subset determination of it as described in the preliminaries. What kind of subsets are reachable?

Since $n-1$ loops to itself on all letters, states reachable from the state $S$ containing $q_{n-1}$ again contain $q_{n-1}$. The state $n-1$ is a final state, thus, that $0 \in S$. Moreover, it is the only final state, thus if $i < n-1$ and $q_{i}\in S$ is reachable, then $S = \{q_i\}$.

Finally, consider the case when $n-1 \in S$. It is a final state and all states reachable from such state contain $n-1$, therefore are final. Hence, all such states are equivalent.

Summed up, that is $n-1$ states in form $\{q_i\}$, $2^{n-2}$ for states in form $\{q_{n-1},0\}\cup S$, where $S \subseteq \{1,2,\dots , n-2\}$ and 1 state for all accepting subsets, in total $n+2^{n-2}$ states.    $\square$

Lemma 4

For every $n \ge 2$, there exists a binary right ideal language $L$ with ${{\mathrm{sc}}}(L) = n$ and ${{\mathrm{sc}}}(L^2)=n+2^{n-2}$.

Proof

Consider the DFA $A = (\{0,1,\dots ,n-1\},\{a,b\},\delta ,0,\{n-1\})$ shown in Fig. 2, where $\delta$ is defined as follows:

$$ \delta (i,a) = {\left\{ \begin{array}{ll} i+1, &{}\text {if}\, i<n-1;\\ n-1, &{}\text {if}\, i=n-1. \end{array}\right. }\;\;\;\;\;\;\;\; \delta (i,b) = {\left\{ \begin{array}{ll} 0, &{}\text {if}\, i = 0; \\ i+1, &{}\text {if}\, 1\le i \le n-3;\\ 0, &{}\text {if}\, i = n-2; \\ n-1, &{}\text {if}\, i=n-1. \end{array}\right. } $$

Fig. 2.

Witness for right-ideal bound optimality

We will show that all subsets considered in Lemma  3 are reachable and distinguishable. We will start with reachability.

For $i < n-1$ states $\{q_i\}$ are reachable by word $a^i$. We have to accept word $a^{2(n-1)}$, thus final state could be also reached. The reachability of states of the form $\{q_{n-1},0,j_1,j_2,\dots ,j_k$}, where $1\le j_1 < j_2 < \dots < j_k$ is proven by induction on the size of maximal element of this set – the element $j_k$. The state $\{q_{n-1},0\}$ is reached by the word $a^{n-1}$.

The induction hypothesis is, that all states $S$ with $\max S = j_k-1$ are reachable. If $j_1 = 1$, then $\{q_{n-1},0,1,j_2,\dots , j_k\} = a(\{q_{n-1},0,j_2-1,\dots ,j_k-1\})$; otherwise $\{q_{n-1},0,j_1,\dots ,j_k\} = a(\{q_{n-1},0,j_1-1,\dots , j_k-1\})$.

Proof of distinguishability is necessary only for nonfinal states. We will start by distinguishing states $S$ and $S'$, where $S \cap [1,n-1] \ne \varnothing$.

Let $m = \max (S\oplus S')$ – this is well-defined and $m \ge 0$, since $S \ne S'$. Without loss of generality let $m \in S$. Denote $B = \delta (S,b^{n-2-m})$ and $B' = \delta (S',b^{n-2-m})$. Note that the state $n-1$ is not reachable from the state $0$ by any word shorter than $n-2$ and $m \le n-2$ and the transition function on states other than $n-1$ is injective. Therefore a state reached by $b^{n-2-m}$ contains $n-2$ iff we started in a state containing $m$ and thus $n-2 \in B$, while $n-2 \in B'$. On the other hand, neither $B$ nor $B'$ does contain $n-1$, since $n-1$ has no incoming transition by $b$. And since the final state $n-1$ is reachable by $a$ only from $n-1$ and $n-2$, the state $\delta (B,a)$ is final, while $\delta (B',a)$ is not. Therefore the word $b^{n-2-m}a$ distinguishes these two states.

Now we will distinguish states $\{q_i\}$ and $\{q_k\}$ for $0\le i<k\le n-1$ (we treat $\{q_{n-1},0\}$ as $\{q_{n-1}\}$). The word $a^{2k-2-k}$ is accepted from $\{q_k\}$, but not from $\{q_i\}$, since it is too short.    $\square$

Combination of two previous lemmata yields the following result.

Theorem 5

Let $n$ be integer with $n \ge 2$ and $L$ be a right ideal language with ${{\mathrm{sc}}}(L)=n$. Then ${{\mathrm{sc}}}(L^2) \le n+2^{n-2}$, and this bound is tight for an alphabet of size at least two.

4 Prefix-Closed Languages

Since minimal DFA for prefix-closed has all states final [9], except for one dead state, it is much more convenient to use incomplete DFA. We will do so, and in the end, we will derive results for standard state complexity.

Lemma 6

Let $L$ be a prefix-closed language with $\mathrm {isc}(L)=n$. Then $\mathrm {isc}(L^2) \le (n+5)2^{n-2}-2$.

Proof

Let $A$ be the minimal DFA for the language $L$ and let $S$ be a reachable subset state of the standard square DFA construction. Let us label states of $A$ with integers from $[0,n-1]$ so that $0$ is the initial state of $A$. We will show that if $q_i \in S$, then also $i \in S$ and $s \in S$.

The initial subset state is $\{q_0,0\}$. Let $w$ be a word such that $\{q_0,0\} \overset{w}{\longrightarrow }S$. Then if $q_i \in S$, it means that $s \overset{w}{\longrightarrow } i$ in $A$ and therefore $\{q_i,i\}\subseteq S$. Since $q_i$ is final, $0 \in S$. Moreover, state $\{0,1,\dots , n-1\}$ is unreachable, because it could be reached only from some state $S'$ with some $q_i\in S$ on a letter $a$ with an undefinied transition from $i$, but that results in a state with at most $n-1$ states.

Summing up, there are $(n-1)2^{n-2}$ states containing $q_i$ other than $q_0$ plus $2^{n-1}$ for those with $q_0$ plus $2^n-2$ for subsets of $[0,n-1]$, not counting the unreachable full state and the empty dead state uncounted in incomplete DFAs.

   $\square$

Lemma 7

Let $n \ge 2$. There exists a binary language $L$ with $\mathrm {isc}(L) = n$ and $\mathrm {isc}(L^2) = (n+5)2^{n-2}-2$.

Proof

If $n = 2$, consider the DFA $(\{0,1\},\{a,b\},\delta ,0,\{0,1\})$ with transitions defined as $\delta (0,a) = 1$, $\delta (0,b) = \varnothing$ and $\delta (1,a) = \delta (1,b) = 0$.

For $n > 2$ consider the DFA $A = ([0,n-1],\{a,b\},\delta ,0,[0,n-1])$ shown in Fig. 3 where

$$ \delta (i,a) = {\left\{ \begin{array}{ll} \varnothing , &{}\text {if}\,i=0;\\ 0, &{}\text {if}\, i=1;\\ i+1, &{}\text {if}\, 2\le i \le n-2;\\ 2, &{}\text {if}\, i=n-1. \end{array}\right. }\;\;\;\;\;\;\; \delta (i,b) = {\left\{ \begin{array}{ll} i+1, &{}\text {if}\, 1\le i \le n-2;\\ 0, &{}\text {if}\, i=n-1. \end{array}\right. } $$

Fig. 3.

The witness for prefix-closed bound optimality

Note that in the standard square DFA construction for this witness DFA (see preliminaries), if $n-1$ is a member of set $S$, then $|b(S)| = |S|$. Moreover,

$$ |a(S)| = {\left\{ \begin{array}{ll} |S|, &{}\text {if}\, 1 \notin S;\\ |S|-1, &{}\text {if}\, 1 \in S.\\ \end{array}\right. } $$

To prove reachability, we will use a variation on an inductive proof. Largest sets will be used as the base of the induction and in an inductive step, we will show, how to reach smaller sets. As the base of the induction we will show that all sets in form $\{q_i,0,1,\dots ,n-2,n-1\}$ are reachable from the start state as follows:

$$\{q_0,0\} \overset{b^{n-1}}{\longrightarrow } \{q_{n-1},0,1,\dots ,n-2,n-1\}\overset{b^{i+1}}{\longrightarrow } \{q_i,0,1,\dots ,n-2,n-1\}.$$

The induction hypothesis is that all states $S$ with $|S\cap [1,n-1]|\ge k+1$ with property $q_i\in S$ implies that $i \in S$ are reachable. We will show that all such states $S'$ with $|S'\cap [1,n-1]|= k$ are also reachable. The proof is divided into four cases in all of them we suppose that $0<j_r<j_{r+1}$ ($r$ is used as an arbitrary index $1\le r$ in this proof).

• 1. $S = \{q_i,0,j_1, \dots ,j_k\}$ and $j_1 > 1$ and $i \in S$. Since $j_r \ne 1$, necessarily also $i \ne 1$ (see the proof of Lemma 6). In that case is $a^{-1}(S)$ well defined and we have $a^{-1}(S)=\{q_{a^{-1}(i)},0,1,a^{-1}(j_1),\dots ,a^{-1}(j_k)\} \overset{a}{\longrightarrow } \{q_i, 0, j_1,\dots , j_k\} .$ Both $q_{a^{-1}(i)}\in S$ and $a^{-1}(i)\in S$. Moreover since $a$ is bijection on $[2,n-1]$, set $a^{-1}(S)$ has $k+1$ elements from $[0,n-1]$.

• 2. $S = \{q_i,0,1, j_2, \dots ,j_k\}$. Let $m = \min \{b\,|~b > 0 ~\text { and }~ b \ne j_r\}$. Then, since $b$ is a bijection, the set $B= \{q_{b^{-(m-1)}(i)},b^{-(m-1)}(0), b^{-(m-1)}(j_1),\dots ,b^{-(m-1)}(j_k)\}$ is well-defined. Then we have $B \overset{b^{m-1}}{\longrightarrow } \{q_i, 0, 1,j_2,\dots ,j_k \}.$ The choice of the exponent $m-1$ was deliberate so that $1 \notin B$. Moreover, since $0$ is a member of each state $b^l(B)$ in this computing path, the state $b^{-1}(0) = n-1$ is also a member of $b^l(B)$. Therefore, as noted at the beginning of this proof, this implies that $|B| =|b(B)|=\dots =|b^{m-1}(B)| = |S|$. This shows how $S$ can be reached from a state of the same size containing $1$, which has already been shown to be reachable in case 1.

• 3. $S = \{0,j_1, \dots ,j_k\}$. Then $\{q_0, 0,a^{-1}(j_1),\dots ,a^{-1}(j_k)\} \overset{a}{\longrightarrow } \{j_1,\dots , j_k\}$. Since letter $a$ is an injection on states other than $0$, the state on the left was shown to be reachable in 2.

• 4. $S = \{j_1, \dots ,j_k\}$. Then $\{0,j_2-j_1,\dots ,j_k-j_1\} \overset{b^{j_1}}{\longrightarrow } \{j_1, \dots ,j_k\}$. Since $b$ is a bijection, the state on the left was shown to be reachable in 3.

The proof of distinguishability of states $S$ and $S'$ is divided into four cases. The empty state is the only nonfinal state; therefore in each of these cases, our aim is to find a word that leads to the empty state from one of these states, whereas from the other does not.

• 1. Both $S$ and $S'$ are subsets of $[0,n-1]$. Without loss of generality there exists $s \in S$ such that $s \notin S'$. The transition on $b$ in states that are subsets of $[0,n-1]$ never changes the size of a resulting state, while a transition on $a$ changes it iff $1$ is its member. We will call a state the successor of a given state on a word $w$, if it is reached on this word without using $\varepsilon$ transition. State $i \in S'$ will have no successors on words with prefix $b^{n-i}a$. In this manner, we gradually construct word removing successors of all states in $S'$ so it will have no successor and we reach the empty state. On the same word, we removed all states in $S$ that are in $S\cap S'$. But we did not remove $s$, so the resulting state is not empty.

• 2. $S$ is a subset of $[0,n-1]$. Let $q_i \in S'$. If $i \notin S$, then we just erase the state $S$ as in case 1. The successor of $q_i$ was not erased, so the result is an non-empty state. If $i \in S$, we erase everything except $i$. In the successor of $S'$, there are still at least the states $0$ and successor of $i$ and $q_i$. We will not remove successors of states other than $i$ while removing $i$. There always is some other state, unless we have states $\{q_0,0\}$ and $\{0\}$. But the word $b^{n}a$ distinguishes these two.

• 3. $q_i \in S$, $q_j \in S'$ and $i < j$. Then $q_0 \in b^{n-j}(S')$ while $q_{i+n-j} \in b^{n-j}(S)$. The state $q_0$ has no successor on $a$, therefore $b^{n-j}a(S') \subseteq [0,n-1]$, while $b^{n-j}a(S) \nsubseteq [0,n-1]$. We distinguished these types of states in the case 2.

• 4. $q_i \in S$ and $q_i \in S'$ for some $i$. At first, suppose that $S\oplus S' \ne \{1\}$; we will resolve the opposite later. A transition on $a^{n-1-i}ba$ leads from both states to two different states in $[0,n-1]$. Since any difference other than $1$ between $S$ and $S'$ is preserved by transitions on $a$, following a transition on $b$ adds $1$, but this leaves the difference (which is in the cycle $[2,n-1]$) untouched and so does the last transition on $a$. So we reduced this to case 1. Lastly, if $S\oplus S' \ne \{1\}$, that is $S = S'\cup \{1\}$, then $b(S)\oplus b(S') = \{2\}$ and this case was treated in previous paragraph.    $\square$

Now we will combine previous results for incomplete state complexity to get a tight upper bound on the standard deterministic state complexity.

Theorem 8

Let $n\ge 3$ and $L$ be prefix-closed language with ${{\mathrm{sc}}}(L) = n$. Then ${{\mathrm{sc}}}(L^2) \le (n+4)2^{n-3}-1$, and this bound is tight for an alphabet of size at least two.

Proof

Since all prefix-closed languages $L$ with ${{\mathrm{sc}}}(L)=n \ge 2$ have a dead state, $\mathrm {isc}(L) = n-1$. Prefix-closed languages are closed under the operation square. Therefore ${{\mathrm{sc}}}(L^2) = \mathrm {isc}(L^2)+1 = (n-1+5)2^{n-1-2}-2+1 = (n+4)2^{n-3}-1$.    $\square$

5 Xfix-Free Languages

The state complexity of a concatenation of prefix-free languages is $m+n-2$ [12]. In fact, this is not only a tight upper bound, but also a lower bound. Beside that witness languages are unary $\{a^{n-1}\}$ and $\{a^{m-1}\}$, so $\{a^{n-1}\}$ is also a unary witness for a prefix-free square. Moreover, bifix-, factor- and subword-free languages are also prefix-free and in the unary case all of these properties are the same, so the state complexity is the same for all of these classes. It remains to investigate suffix-free languages.

Lemma 9

If $L$ is a suffix-free regular language with ${{\mathrm{sc}}}(L) = n$, then ${{\mathrm{sc}}}(L^2)\le n2^{n-3}+1$.

Proof

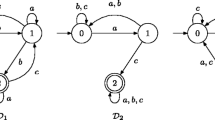
By [13], every DFA accepting $L$ is nonreturning with a dead state. Let $A = ([0,n-3]\cup \{s,d\},\varSigma ,\delta ,s,F)$ be the minimal DFA for $L$, where $d$ denotes the dead state.

Let $S$ be a reachable set in the standard square construction on $A$. Suffix-freeness imposes certain restrictions on $S$. Since $A$ is nonreturning, $s \in S$ iff $S\cap F \ne \varnothing$ and, for the same reason, if $q_s \in S$, then $S=\{q_s\}$. Note that states $S$ and $S \cup \{d\}$ are equivalent. Finally, we will show that if for index $i$ with $i \ne d$ holds that if $q_i \in S$, then $i \notin S$.

Fig. 4.

Sketch of proof

Suppose that there exists reachable subset $S$ and index $i$, such that both $i$ and $q_i$ are members of $S$. Consider a computation that shows reachability of $S$. Since $i$ is in $S$, there was a step when the first copy of an DFA $A$ was in state $q_f$ corresponding to final state of $A$ and from this step, the computation led from $s$ to $i$ and from $q_f$ to $q_i$. Let $u$ and $v$ denote words corresponding to these two parts of the computation, respectively. Note that $u \ne \varepsilon$, because $s$ is not final. If $i \ne d$, then $i$ is a useful state and some final state $f'$ is reachable from it on word $w$. So there are these two paths $q_s \overset{uvw}{\longrightarrow } q_{f'}$ and $s \overset{vw}{\longrightarrow } f'$. But this means that $A$ accepts both $uvw$ and $vw$, and that is impossible, because $A$ accepts suffix-free language and $u \ne \varepsilon$.

This sums up to $(n-2)2^{n-3}$ equivalence classes of subset states when $q_d \notin S$ and $q_s\notin {S}$, plus $2^{n-2}$ classes of states such that $q_d \in S$ and plus one initial state $\{q_s\}$, in total $n2^{n-3}+1$ states.    $\square$

Lemma 10

There exists a suffix-free language $L$ with ${{\mathrm{sc}}}(L) = n$ and ${{\mathrm{sc}}}(L^2) = n2^{n-3}+1$.

Proof

Consider the DFA in Fig. 5, note that we did not draw transitions leading to the dead state $d$. This automaton satisfies requirements of Lemma 1 in [7], so it accepts a suffix-free language.

Fig. 5.

Witness for suffix-free bound optimality

At first, we will show that all equivalence classes considered in the Lemma 9 are reachable. As presence of the dead state in a subset is unimportant and the presence of $s$ determined, we will usually omit them, unless they are important. The initial state $\{q_s\}$ is reachable. For the reachability of $S$, we will use a variation of a mathematical induction on a size of $S$.

As the base of the induction we will show that the largest sets, that is sets such that $|S \cap [0,n-3]| = n-3$ are reachable.

$$\begin{aligned}\{q_s\} \overset{c}{\longrightarrow } \{q_{n-3},s\} \overset{a^{n-3}}{\longrightarrow } \{&q_{n-3},0,1,\dots ,n-4\}\overset{b^{i-1}}{\longrightarrow }\{q_i,0,1,\dots ,i-1,i+1,\dots ,n-3\}\\ \{q_s\} \overset{c}{\longrightarrow } \{q_{n-3},s\} \overset{a^{n-3}}{\longrightarrow } \{&q_{n-3},0,1,\dots ,n-4\}\overset{c}{\longrightarrow }\\&\quad \overset{c}{\longrightarrow }\{0,1,\dots ,n-4\}\overset{b^{i-1}}{\longrightarrow }\{0,1,\dots ,i-1,i+1,\dots ,n-3\}.\end{aligned}$$

The inductive hypothesis now is that all sets $S$ with $|S \cap [0,n-3]| = k+1$ are reachable. First, let it be the case that the set $S=\{j_1,j_2,\dots ,j_k\}$ and let $m = \min \{p\,|~p\in [0,n-1]\text { and }p\notin S\}$. Then $S = \{j_1,\dots ,j_{k-(n-3-m),m+1,m+2,\dots ,n-3}\}$. Then the following computation shows reachability:

$$ \{j_{m+1}-(m+1),\dots ,j_k-(m+1),n-3-m,\dots ,n-4,n-3\} \overset{c}{\longrightarrow }\\ \overset{c}{\longrightarrow }\{j_{m+1}-(m+1),\dots ,j_k-(m+1),n-3-m,\dots ,n-4\} \overset{b^{m+1}}{\longrightarrow }\\ \overset{b^{m+1}}{\longrightarrow }\{0,1,\dots ,m-1,j_{m+1},\dots ,j_k\}. $$

The proof for states of the form $\{q_i,j_1,\dots ,j_k\}$ is similar, with redefinition of $m = \min \{p\,|~p\in [0,n-1]\text { and }p\notin S \text { and } p \ne i\}$. Just note that whenever we reach state $q_{n-3}$ there is indeed $0$ in the following state. The empty i.e., dead state, is reached from $\{n-1\}$ on $c$ and lastly,

$$\{q_{n-3},s,0,1,\dots ,n-4\} \overset{c}{\longrightarrow }\{0,1,\dots ,n-3\}.$$

Now we will prove distinguishability. Notice that the NFA for the square has the following properties:

• 1. the string $\varepsilon$ is accepted only from state $n-1$;

• 2. the string $b^{n-1-i}$ is accepted only from state $i$;

• 3. the string $ab^{n-1}$ is accepted only from $0$;

• 4. the string $cab^{n-1}$ is accepted only from $q_{n-3}$;

• 5. the string $a^{n-1-i}cab^{n-1}$ is accepted only from $q_i$.

Hence for each state $q$ of this NFA, there is a string $w_q$ which is accepted from $q$, but rejected from any other state. Now let $S$ and $S'$ be two distinct subsets in the subset automaton of this NFA. Then $S$ and $S'$ differ in a state $q$ and the string $w_q$ distinguishes them.    $\square$

Theorem 11

Let $L$ be a suffix-free language with ${{\mathrm{sc}}}(L) = n$. Then ${{\mathrm{sc}}}(L^2) \le n2^{n-3}+1$, and this bound is tight for an alphabet of size at least three.

Proof

This is a corollary of Lemmata 9 and 10.    $\square$

6 Conclusions

Table 1 is a summary of our results and comparison with catenation and regular languages [14].

Table 1. Comparison of results for square and concatenation.

The state complexity of square for all closed languages, except for prefix-closed, remains open.