Operations on Subregular Languages and Nondeterministic State Complexity

Abstract

We study the nondeterministic state complexity of basic regular operations on subregular language families. In particular, we focus on the classes of combinational, finitely generated left ideal, group, star, comet, two-sided comet, ordered, and power-separating languages, and consider the operations of intersection, union, concatenation, power, Kleene star, reversal, and complementation. We get the exact complexity in all cases, except for complementation of group languages where we only have an exponential lower bound. The complexity of all operations on combinational languages is given by a constant function, except for the k-th power where it is $k+1$. For all considered operations, the known upper bounds for left ideals are met by finitely generated left ideal languages. The nondeterministic state complexity of the k-th power, star, and reversal on star languages is n. In all the remaining cases, the nondeterministic state complexity of all considered operations is the same as in the regular case, although sometimes we need to use a larger alphabet to describe the corresponding witnesses.

Research supported by VEGA grant 2/0132/19 and grant APVV-15-0091.

1 Introduction

The fields of study at the intersection of mathematics and computer science, known as formal language theory and automata theory, contain a rich history of publications interesting both from a practical and theoretical point of view. One of the primary investigated language classes in the field, regular languages, have a number of combinatorial, algebraic, and computational properties still prominently investigated today. The topic of interest in this publication are the notions of nondeterministic finite automata (NFA) accepting some subregular languages and operational state complexity.

The definition of NFAs originates from the seminal paper by Rabin and Scott [15]. A conversion procedure to deterministic finite automata (DFA) called “subset construction” was provided as well, showing that an NFA with n states can be simulated by a DFA with at most $2^n$ states. This model is connected to the measure of nondeterministic state complexity of a given language L, which represents the number of states of the smallest NFA accepting L. The nondeterministic state complexity of a given regular operation is the nondeterministic state complexity of the language resulting from this operation, considered as a function of the sizes of NFAs for operands. A more rigorous investigation of this measure comes from Holzer and Kutrib [8] for the Boolean operations, concatenation, iteration, and reversal.

By restricting the operands to certain subclasses of regular languages, it turns out that the resulting nondeterministic state complexities of these operations might differ from the general case to various degrees. This observation motivated several publications focusing on specific subregular language classes. Han et al. [5, 6] considered the complexities of some of the mentioned basic operations for prefix-free and suffix-free languages. Additional results were provided for star-free languages by Holzer et al. [9], for union-free languages by Jirásková and Masopust [14], and recently Hospodár et al. [12] examined various subclasses of convex languages.

In this paper, we continue with such investigations focusing on the operations of intersection, union, concatenation, power, Kleene star, reversal, and complementation. We consider the language classes mainly from [2], more specifically combinational languages, finitely generated left ideals, group languages, stars, comets, two-sided comets, ordered languages, and power-separating languages.

We get the exact complexity for each pair of operation and class except for complementation on group languages where we obtain only a lower bound. For combinational languages, the complexity does not depend on the size of input NFAs. In most other cases, the complexity is the same as for regular languages, except for finitely generated left ideals where the complexity of all operations is the same as for general left ideals [12]. To get lower bounds, instead of commonly used fooling sets for regular languages, we rather use fooling sets for MNFAs consisting of pairs of a reachable and a co-reachable set for each state. Then, we only test the emptiness of intersection of finite sets instead of deciding whether or not a string is in a language.

2 Preliminaries

We assume that the reader is familiar with the standard notation and definitions in formal language and automata theory. For details and a more thorough introduction, refer to [10].

We denote the set of positive integers by $\mathbb {N}$. Let $\varSigma$ be a non-empty alphabet of symbols. Then $\varSigma ^*$ denotes the set of all strings over $\varSigma$, including the empty string $\varepsilon$. A language over $\varSigma$ is any subset of $\varSigma ^*$.

The reversal of a string w over $\varSigma$ denoted $w^R$ is defined as $\varepsilon ^R = \varepsilon$ if $w=\varepsilon$, and $w^R=a_na_{n-1}\cdots a_2a_1$ if $w=a_1a_2\cdots a_{n-1}a_n$ with $a_i\in \varSigma$. The reversal of a language L is the language $L^R = \{ w^R \mid w\in L \}$. The complement of a language L over $\varSigma$ is the language $L^c=\varSigma ^*\setminus L$. The intersection of languages K and L is the language $K\cap L = \{w \mid w\in K\;\text {and}\;w\in L\}$, while the union of K and L is $K\cup L = \{w \mid w\in K\;\text {or}\;w\in L\}$. The concatenation of languages K and L is the language $KL=\{uv\mid u\in K\;\text {and}\;v\in L\}$. For a given positive integer k, the k-th power of a language L is the language $L^{k} =LL^{k-1}$ with $L^0 = \{ \varepsilon \}$. The positive closure of a given language L is $L^+=\bigcup _{k\ge 1}L^k$, while the Kleene star of L is defined as $L^* = \bigcup _{k\ge 0} L^k$ and it is equal to $\{ \varepsilon \} \cup L^+$. We use the notation of regular expressions over $\varSigma$ in a standard way with $\emptyset$ (empty set), $\varepsilon$, and each $\sigma \in \varSigma$ being regular expressions; furthermore if r and s are regular expressions, then rs (concatenation), $r + s$ (union), and $r^*$ (star) are also regular expressions. For a regular expression r, the expression $r^k$ denotes the k-th power of the language of r, and $r^{\le k}$ denotes the expression $r^0 + r^1 + \cdots r^k$.

A nondeterministic finite automaton with multiple initial states (MNFA) is a quintuple $M=(Q,\varSigma ,\cdot ,I,F)$ where Q is a finite non-empty set of states, $\varSigma$ is a finite set of input symbols (i.e., input alphabet), $I\subseteq Q$ is the set of initial states, $F\subseteq Q$ is the set of final (accepting) states, and $\cdot :Q\times \varSigma \rightarrow 2^Q$ is the transition function which can be naturally extended to the domain $2^Q\times \varSigma ^*$. The language accepted by the MNFA M is $L(M)=\{w\in \varSigma ^* \mid I \cdot w \cap F\ne \emptyset \}.$ If R and S are two sets of states of M, then $R\xrightarrow {\sigma }S$ denotes that $R\cdot \sigma = S$.

An MNFA whose set of initial states is a singleton is called a nondeterministic finite automaton (NFA). An NFA is a (complete) deterministic finite automaton (DFA) if $|q\cdot \sigma |=1$ for each $q \in Q$ and each $\sigma \in \varSigma$; in such a case, $\cdot$ is a mapping from $Q \times \varSigma$ to Q. A non-final state q with transitions $(q,\sigma ,q)$ for each $\sigma$ in $\varSigma$ is called a dead state.

A given language L is called regular if and only if there exists an MNFA M for which $L=L(M)$. Two MNFAs A and B are equivalent if they accept the same language. Every MNFA $M=(Q,\varSigma ,\cdot ,I,F)$ can be converted into an equivalent complete DFA $\mathcal {D}(M)=(2^Q,\varSigma ,\cdot ,I,\{S\in 2^Q\mid S\cap F\ne \emptyset \})$, by the subset construction [10] where $\cdot$ is the extension of the transition function of M to the domain $2^Q\times \varSigma$. The DFA $\mathcal {D}(M)$ is referred to as the subset automaton.

The reverse of an MNFA M, denoted $M^R$, is the MNFA obtained from M by reversing all transitions and by swapping the roles of initial and final states. A subset S of states of M for which exists a string w such that $I\cdot w = S$ is called reachable in M. If a set is reachable in $M^R$, we say it is co-reachable in M.

Sometimes we allow an MNFA to have $\varepsilon$-transitions, and then a set S is reached from a set R on a symbol $\sigma$ if $S=E(\{q\cdot \sigma \mid q\in R\})$ where E(P) is the set of states reachable from a state in the set P via $\varepsilon$-transitions.

The nondeterministic state complexity of a regular language L, denoted by $\mathrm {nsc}(L)$, is the smallest number of states in any NFA for L. The nondeterministic state complexity of a unary regular operation $^\circ$ is a mapping from $\mathbb {N}$ to $\mathbb {N}$ defined as

$$n \mapsto \max \{ \mathrm {nsc}(L^\circ )\mid L\; \text {is accepted by an}\;n\text {-state NFA} \}.$$

The nondeterministic state complexity of a binary regular operation $\circ$ is a mapping from $\mathbb {N}^2$ to $\mathbb {N}$ defined as

$$(m,n) \mapsto \max \{ \mathrm {nsc}(K\circ L)\mid K,L\; \text {accepted by}\;m\text {-state and}\;n\;\text {-state NFAs, resp.} \}.$$

In order to obtain lower bounds on the nondeterministic state complexity of regular languages, the so-called fooling set method is usually used. A set of pairs of strings $\{(x_i,y_i)\mid 1\le i\le n\}$ is called a fooling set for some given language L if (1) $x_i y_i\in L$ for each i, and (2) if $i\ne j$, then $x_i y_j\notin L$ or $x_j y_i\notin L$. It is well known that if $\mathcal {F}$ is a fooling set for the given regular language L, then $\mathrm {nsc}(L)\ge |\mathcal {F}|$ [1, Lemma, p. 188].

To describe fooling sets for languages can be tedious and checking whether or not a string $x_i y_j$ is in L may be hard. To avoid such difficulties, we use the technique of fooling sets for MNFAs where to each state of a given MNFA M, we assign a pair of subsets of the state set of M.

Definition 1

Let $M=(Q,\varSigma ,\cdot ,I,F)$ be an MNFA. A set $\{(R_q,C_q) \mid q\in Q\}$, where $R_q$ and $C_q$ are subsets of Q, is a fooling set for the MNFA M if for all states p, q,

• (1) $R_q$ is reachable and $C_q$ is co-reachable in M,

• (2) $q\in R_q\cap C_q$,

• (3) if $p\ne q$, then $R_p\cap C_q=\emptyset$ or $R_q\cap C_p=\emptyset$.

Notice that by the definition above, a fooling set for L(M) exists if and only if a fooling set for M of the same size exists; if each set $R_q$ is reached by $x_q$ and each set $C_q$ is co-reached by $y_q$, then $\{(x_q,y_q^R) \mid q\in Q\}$ is a fooling set for L(M), and vice versa. Therefore, we immediately get the following observation.

Lemma 2

([11, Lemma 4], [12, Lemma 4]). Let $M=(Q,\varSigma ,\cdot ,I,F)$ be an MNFA such that at least one of the following conditions holds:

• (a) there exists a fooling set $\{(R_q,C_q) \mid q\in Q\}$,

• (b) each singleton subset of Q is reachable and co-reachable in M.

Then $\mathrm {nsc}(L(M))\ge |Q|$.   $\square$

To describe a fooling set for the complement of a language may be cumbersome, cf. [13, Theorem 5]. The condition in the following lemma guarantees the existence of such a fooling set.

Lemma 3

([12, Proposition 6]). Let L be a language accepted by an NFA in which k subsets of the state set are reachable and each of their complements is co-reachable. Then $\mathrm {nsc}(L^c)\ge k$.    $\square$

So if we prove that each subset of states of an NFA A is both reachable and co-reachable, then $\mathrm {nsc}(L(A)^c)=2^n$. Notice that the reachability of all subsets in the NFA M from [13, Theorem 5] can be easily shown, and since M is isomorphic to its reverse, so can be the co-reachability. This immediately gives a lower bound $2^n$ for the complement of L(M).

The union of two NFAs of m and n states is accepted by an $(m+n)$-state MNFA. To get an NFA for union, one more state may be needed. However, we cannot construct a fooling set for union of size $m+n+1$ since we already have an MNFA of size $m+n$. A similar observation works for reversal as well. In [14, Lemma 4], a modified fooling set method has been described. Now we present it using the reachable and co-reachable sets instead of strings.

Lemma 4

($\mathcal {S}\mathcal {T}$-Lemma, cf. [11, Lemma 8]). Let Q be a set of states. Let $\mathcal {S}$ and $\mathcal {T}$ be disjoint sets of pairs of subsets of Q and let U and V be two subsets of Q such that $\mathcal {S}\cup \mathcal {T}$, $\mathcal {S}\cup \{(I,U)\}$, and $\mathcal {T}\cup \{(I,V)\}$ are fooling sets for the MNFA $M=(Q,\varSigma ,\cdot ,I,F)$. Then $\mathrm {nsc}(L(M))\ge |\mathcal {S}|+|\mathcal {T}|+1$.    $\square$

Next, we introduce the language classes considered in this paper. These languages were already examined to some extent in [2], with the exception of group languages which were investigated in [7]. A language L is

• combinational (class abbreviation CB): if $L=\varSigma ^*H$ for $H\subseteq \varSigma$;

• finitely generated left ideal (FGLID): if $L=\varSigma ^*H$ for some finite language H (in [2] called noninitial definite);

• left ideal (LID): if $L=\varSigma ^*L$ (in [2] called ultimate definite);

• group language (GRP): if it is accepted by a permutation DFA (equivalently, if the minimal DFA for L is a permutation one);

• star (STAR): if $L=G^*$ for a regular language G [3] (equivalently, $L=L^*$);

• comet (COM): if $L{=}G^*H$ for some regular languages G, H with $G{\notin }\{\emptyset ,\{\varepsilon \}\}$;

• two-sided comet (2COM): if $L{=}EG^*H$ for regular E, G, H with $G{\notin }\{\emptyset ,\{\varepsilon \}\}$;

• ordered (ORD): if it is accepted by a (possibly non-minimal) DFA with ordered states such that $p \preceq q$ implies $p\cdot \sigma \preceq q\cdot \sigma$ for each symbol $\sigma$ [17];

• star-free (SFREE): if L is constructable from finite languages, concatenation, union, and complementation (equivalently, if L has an aperiodic DFA) [16];

• power-separating (PSEP): if for every x in $\varSigma ^*$ there exists an integer m such that $\bigcup _{i\ge m} \{x^i\} \subseteq L$ or $\bigcup _{i\ge m} \{x^i\} \subseteq L^c$ [18].

We have $\text {CB}\subsetneq \text {FGLID}\subsetneq \text {LID}$, $\text {STAR}\subsetneq \text {COM}\subsetneq \text {2COM}$, and $\text {ORD}\subsetneq \text {STFR}\subsetneq \text {PSEP}$ [2]; the only star language that is not a comet is $\{\varepsilon \}$.

3 Results

In this section, we gradually present our obtained results by lemmas individually focusing on the considered operations and language classes. They are grouped together based on their proof structure, with summarizing tables included in the Conclusions section. We proceed with the proposition considering all operations on the class of combinational languages. This class is special since every combinational language has nondeterministic state complexity at most two.

Proposition 5

Let $m,n\ge 2$. Let K and L be combinational languages over $\varSigma$ accepted by m-state and n-state NFAs. Then

• (1) $\mathrm {nsc}(K),\mathrm {nsc}(L)\le 2$,

• (2) $\mathrm {nsc}(K\cap L),\mathrm {nsc}(K\cup L),\mathrm {nsc}(L^R)\le 2$, and this bound is tight if $|\varSigma |\ge 1$,

• (3) $\mathrm {nsc}(L^*),\mathrm {nsc}(L^c)\le 2$, and this bound is tight if $|\varSigma |\ge 2$,

• (4) $\mathrm {nsc}(KL)\le 3$ and $\mathrm {nsc}(L^k)\le k+1$, and these bounds are tight if $|\varSigma |\ge 1$.

The next two lemmas consider intersection and union on finitely generated left ideal languages.

Lemma 6

Let $m,n\ge 3$ and $\varSigma =\{a_1,a_2,\ldots ,a_{m-1},b_1,b_2,\ldots ,b_{n-1},c,d,e\}$. Let A, B, C, and D be the NFAs from Fig. 1. Then L(A), L(B), L(C), and L(D) are finitely generated left ideal languages such that $\mathrm {nsc}(L(A)\cap L(B))=mn$ and $\mathrm {nsc}(L(C)\cup L(D))=m+n-1$.

Proof

First we consider intersection. We can get an NFA accepting a finite generator of L(A) from A by removing loops in the initial state, adding final states $m+1,m+2,\ldots ,2m$ connected through transitions $m+1\xrightarrow {b_j}m+2\xrightarrow {b_j}\cdots \xrightarrow {b_j}2m$ for each j, and adding transitions $(q,\sigma ,m+1)$ for each transition $(q,\sigma ,m)$ in A. A similar construction can be done for B. Hence L(A) and L(B) are finitely generated left ideals. Consider the product automaton $A\times B$ for $L(A)\cap L(B)$. For each (i, j) in $\{1,2,\ldots ,m\}\times \{1,2,\ldots ,n\}$, define the following sets:

$[i,j]~~=\{1,2,\ldots ,i\}\times \{1,2,\ldots ,j\}$ if $1\le i\le m-1$ and $1\le j\le n-1$;

$\llbracket i,n\rrbracket ~=\{1,2,\ldots ,i\}\times \{1,n\}$ if $1\le i\le m-1$;

$\llbracket m,j\rrbracket =\{1,m\}\times \{1,2,\ldots ,j\}$ if $1\le j\le n-1$;

$\llbracket m,n\rrbracket =\{1,m\}\times \{1,2,\ldots ,n\}$.

To each state (i, j) in $A\times B$, we assign a pair of sets $R_{i,j}$ and $C_{i,j}$ as follows:

$$ (R_{i,j},C_{i,j})= {\left\{ \begin{array}{ll} ([i,j],\{(i,j)\}),&{} \text {if}\; 1\le i\le m{-}1\; \text {and}\; 1\le j\le n{-}1; \\ (\!\!\llbracket i,n\rrbracket ,\{(i,n{-}1),(i,n)\}),&{} \text {if}\; 1\le i\le m{-}1\; \text {and}\; j=n; \\ (\!\!\llbracket m,j\rrbracket ,\{(m{-}1,j),(m,j)\}),&{} \text {if}\; i=m\; \text {and}\; 1\le j\le n{-}1; \\ (\!\!\llbracket m,n\rrbracket ,\{(m,n)\}),&{} \text {if}\; i=m\; and \;j=n. \end{array}\right. } $$

It can be shown that the set $\{(R_{i,j},C_{i,j})\mid 1\le i\le m\;\text { and }\;1\le j\le n\}$ is a fooling set for $A\times B$ of size mn. Hence $\mathrm {nsc}(K\cap L)=mn$ by Lemma 2(a).

Now we consider union. We have $L(C)=(a+b+c+d)^*a(a+b)^{m-2}a^* = (a+b+c+d)^*a(a+b)^{m-2}a^{\le m-1}$, so L(C) is a finitely generated left ideal. By a similar argument, the language L(D) is a finitely generated left ideal as well. Construct the NFA N for $L(C)\cup L(D)$ from automata C and D by omitting the state 0 and by adding the transition $(1,c,m+1)$. For each state of N, define the following pairs of sets:

$$ (R_i,C_i)= {\left\{ \begin{array}{ll} (\{1,i\},\{i\}), &{} \text {if}\; 1\le i\le m+n-2 \text {and}\;i\ne m; \\ (\{1,i\},\{i-1,i\}), &{} \text {if}\;i\in \{m,m+n-1\}. \end{array}\right. } $$

Then $\{(R_i,C_i)\mid 1\le i\le m+n-1\}$ is a fooling set for the NFA N of size $m+n-1$. Hence $\mathrm {nsc}(L(C)\cup L(D))=m+n-1$ by Lemma 2(a).    $\square$

Fig. 1.

Finitely generated left ideal witnesses for intersection and for union.

The next lemma considers intersection, union, and concatenation on the class of group languages; notice that we use the same witnesses for all three operations.

Lemma 7

Let $m,n\ge 2$. Let A and B be the NFAs from Fig. 2. Then L(A) and L(B) are group languages, and $\mathrm {nsc}(L(A)\cap L(B))=mn$, $\mathrm {nsc}(L(A)\cup L(B))=m+n+1$, and $\mathrm {nsc}(L(A)L(B))=m+n$.

Proof

In the product automaton for $L(A)\cap L(B)$, each singleton set is reachable and co-reachable, so $\mathrm {nsc}(L(A)\cap L(B))=mn$ by Lemma 2(b).

In the case of union, we may assume that $m\le n$. Construct the MNFA M for $L(A)\cup L(B)$ in the standard way. In M, each set $\{p_i,q_j\}$ is reachable and co-reachable. For each state q of M, we define the pair of sets $(R_q,C_q)$ as follows:

$(R_{p_i},C_{p_i})=(\{p_i,q_{(i-1)\bmod m}\},\{p_i,q_{(i-2)\bmod m}\})$,

$(R_{q_j},C_{q_j})=(\{q_j,p_{(j+2)\bmod m}\},\{q_j,p_{(j+1)\bmod m}\})$.

Then $\mathcal {S}=\{(R_{p_i},C_{p_i})\mid i=0,1,\ldots ,m{-}1\}$, $\mathcal {T}=\{(R_{q_j},C_{q_j})\mid j=0,1,\ldots ,n{-}1\}$, $I=\{p_0,q_0\}$, $U=\{q_0,p_1\}$, and $V=\{p_0,q_{m-2}\}$ satisfy the conditions of Lemma 4, so $\mathrm {nsc}(L(A)\cup L(B))=m+n+1$.

To get an NFA N for L(A)L(B) from NFAs A and B, add the transition $(p_{m-1},\varepsilon ,q_0)$, and make the state $p_{m-1}$ non-final and the state $q_0$ non-initial. Then the set $\{(\{p_i\},\{p_i,q_{n-1}\})\mid 0\le i\le m-2\}\cup \{(\{p_{m-1},q_0\},\{p_{m-1},q_{n-1}\})\} \cup \{(\{p_0,q_0\},\{p_{m-1},q_0\})\}\cup \{(\{p_0,q_j\},\{q_j\})\mid 1\le j\le n-1\}$ is a fooling set for N of size $m+n$, so $\mathrm {nsc}(L(A)L(B))$ by Lemma 2(a).    $\square$

Fig. 2.

Binary group witnesses for intersection, union, and concatenation.

To get star witnesses, construct the NFAs $A'$ and $B'$ from A and B in Fig. 2 by making the initial state final and all other states non-final. Then $L(A')$ and $L(B')$ are star languages. Moreover, all the sets from the proof above are still reachable and co-reachable, so we have $\mathrm {nsc}(L(A')\cap L(B'))=mn$ and $\mathrm {nsc}(L(A')\cup L(B'))=m+n+1$. The concatenation of star languages $(a^m)^*$ and $(b^n)^*$ has nondeterministic state complexity $m+n$, as shown in [8, Theorem 7]. The next lemma considers intersection, union, and concatenation on ordered languages.

Lemma 8

Let $m,n\ge 2$, $K=(b^*a)^{m-1}b^*$, and $L=(a^*b)^{n-1}a^*$. Then K and L are ordered languages accepted by m-state and n-state NFAs, $\mathrm {nsc}(K\cap L)=mn$, $\mathrm {nsc}(K\cup L)=m+n+1$, and $\mathrm {nsc}(KL)=m+n$.

Proof

The languages K and L are accepted by DFAs A and B from Fig. 3. In the product automaton $A\times B$ for $K\cap L$, each singleton set is reachable and co-reachable. This gives the tight lower bound mn by Lemma 2(b).

Let M be the MNFA containing all states and transitions of A and B. Then $L(M)=K\cup L$. In the MNFA M, the initial set is $\{p_1,q_1\}$, and each singleton set is both reachable and co-reachable by a string in $a^*b^*$ or in $b^*a^*$. Let $\mathcal {S}=\{(\{p_i\},\{p_i\})\mid 1\le i\le m\}$, $\mathcal {T}=\{(\{q_j\},\{q_j\})\mid 1\le j\le n\}$. $I=\{p_1,q_1\}$, $U=\{q_1\}$, and $V=\{p_1\}$. Then the sets $\mathcal {S}\cup \mathcal {T}$, $\mathcal {S}\cup \{(I,U)\}$, and $\mathcal {T}\cup \{(I,V)\}$ are fooling sets for $A\cup B$. Hence $\mathrm {nsc}(K\cup L)=m+n+1$ by Lemma 4.

Construct the NFA N from M by adding the transition $(p_m, \varepsilon , q_1)$, making the state $q_1$ non-initial, and making the state $p_m$ non-final. Then $L(N)=KL$, and the set $\{(\{p_i\},\{p_i\})\mid 1\le i\le m-1\}\cup \{(\{p_m,q_1\},\{p_m\})\} \cup \{(\{q_1\},\{p_m,q_1\})\}\cup \{(\{q_j\},\{q_j\})\mid 2\le j\le n\}$ is a fooling set for N. Hence $\mathrm {nsc}(KL)=m+n$.    $\square$

Fig. 3.

Binary ordered witnesses for intersection, union, and concatenation.

In what follows, we consider the unary operations of the k-th power, star, reversal, and complementation. We start with the class of star languages.

Lemma 9

Let L be a star language. Then $L^k=L^*=L$ and $\mathrm {nsc}(L^R)=\mathrm {nsc}(L)$.

Proof

We have $L^k\subseteq L^*=L$ by definition. To show that $L\subseteq L^k$, let $w\in L$. Since $L=L^*$, we have $\varepsilon \in L$. Set $u_1=w$ and $u_2=u_3=\cdots =u_k=\varepsilon$. Then $w=u_1u_2\cdots u_k$ with $u_i\in L$, so $w\in L^k$. Thus $L^k=L^*=L$.

For reversal, notice that each star language is accepted by an NFA A with a single final state which is the initial state. Then $L^R$ is accepted by the NFA $A^R$ which has the same number of states and the same initial and final state. Hence $\mathrm {nsc}(L^R)\le \mathrm {nsc}(L)$. Since $(L^R)^R=L$, we have $\mathrm {nsc}(L^R)=\mathrm {nsc}(L)$.    $\square$

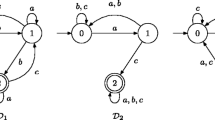
The language $(a^{n-1}b)^*a^{n-1}$ is a comet and ordered language and it meets the upper bound kn on the complexity of the k-th power if $n\ge 2$ [4, Theorem 3]. Now we consider the k-th power on the class of group languages and we show that the complexity in this class is kn as well.

Lemma 10

Let $k\ge 2$ and $n\ge 3$. Let A be the binary NFA from Fig. 4. Then L(A) is a group language and $\mathrm {nsc}(L(A)^k)=kn$.

Proof

Construct the NFA N for $L(A)^k$ from k copies of A in the standard way; assume that the copies are numbered from 1 to k and the state j in the i-th copy is denoted (i, j). For each state (i, j) with $j\ne n-1$, set

$$R_{i,j}= \{(i,j)\}\cup \{(i-\ell ,(j-\ell )\bmod (n-1)) \mid 1\le \ell \le i-1\}, $$

that is, in $R_{i,j}$ we have states $(i,j),(i-1,j-1),(i-2,j-2),\ldots$ where the second component is modulo $n-1$. Next, set

$$\begin{aligned} R_{i,n-1} =&\{(p,q) \mid q\le n-3 \text{ and } (p,q)\in R_{i,n-2} \} \cup \\&\{(p,n-1) \mid (p,n-2)\in R_{i,n-2} \} \cup \{(i+1,0)\}, \end{aligned}$$

that is, to get $R_{i,n-1}$, we move each state of $R_{i,n-2}$ in column $n-2$ to the corresponding state in column $n-1$, and we add the state $(i+1,0)$, so we have $R_{i,n-2}\xrightarrow {b}R_{i,n-1}$. Moreover $R_{i,n-1}\xrightarrow {b} R_{i,n-2}\cup \{(i+1,0)\}=R_{i+1,0}$.

Denote by $\llbracket i,j\rrbracket$ the set $\{(i,j),(i+2,j),\ldots ,(i+2p,j)\}$ where $i+2p$ is either $k-1$ or k, that is, the set containing the state j in copies $i,i+2,\ldots ,i+2p$. Set

$$C_{i,j}= {\left\{ \begin{array}{ll} \!\!\llbracket i,j\rrbracket \cup \llbracket i+1,n-1\rrbracket , &{}\text {if}\; 1\le j\le n-2\; \text {or}\; (i,j)=(1,0); \\ \!\!\llbracket i,n-1\rrbracket \cup \llbracket i+1,n-2\rrbracket , &{}\text {if}\; j= n-1; \\ \!\!\llbracket i,0\rrbracket \cup \llbracket i-1,n-1\rrbracket , &{}\text { if} \;j=0 \; \text {and}\; i\ne 1. \end{array}\right. }$$

The set $\{(R_{i,j},C_{i,j})\mid 1\le i\le k \text { and } 0\le j\le n-1\}$ is a fooling set for N of size kn. Hence $\mathrm {nsc}(L(A)^k)=kn$ by Lemma 2(a).    $\square$

Fig. 4.

A binary group witness for power meeting the upper bound kn.

It was shown in [8, Theorem 9] that for the language $L=(a^n)^*a^{n-1}$, we have $\mathrm {nsc}(L^*)=n+1$. Since L is a group and comet language, $L^+$ is ordered, and $(L^+)^*=L^*$, the nondeterministic state complexity of star in the classes of group, comet, and ordered languages is $n+1$. The next lemma shows that the complexity of star on finitely generated left ideal languages is $n+1$ as well.

Lemma 11

Let $n\ge 4$. Let $K=(a+b)^*a^{n-2}(a+b)a^*$. Then K is a finitely generated left ideal language accepted by an n-state NFA, and $\mathrm {nsc}(K^*)= n+1$.

Proof

Since we have $(a+b)^*a^{n-2}(a+b)a^* = (a+b)^*a^{n-2}(a+b)a^{\le n-1}$, the language K is a finitely generated left ideal accepted by the NFA A from Fig. 5. Construct the MNFA $A^*$ for $L(A)^*$ by adding a new initial and final state 0 and the transitions $(n-1,a,1),(n-1,b,1),(n,a,1)$. To each state i of $A^*$, we assign the following pair of sets:

$$ (R_i,C_i)= {\left\{ \begin{array}{ll} (\{0,1\},\{0,n\}),&{}\text {if}\; i=0; \\ (\{1,2,\ldots ,i\},\{i\}),&{}\text {if}\;1\le i\le n-1; \\ (\{1,n\},\{n-1,n\}),&{}\text {if}\;i=n. \end{array}\right. } $$

Then $\{(R_i,C_i)\mid 0\le i\le n\}$ is a fooling set for $A^*$. Hence $\mathrm {nsc}(L(A)^*)=n+1$.    $\square$

Fig. 5.

A binary finitely generated left ideal witness for star meeting the bound $n+1$.

The following two lemmas consider the reversal on classes of finitely generated left ideal and group languages.

Lemma 12

Let $n\ge 4$. Consider the NFAs A and B from Fig. 6 and the language $L=(a^{n-1}b)^*a^{\le n-1}$. Then L(A) is a finitely generated left ideal language, L(B) is a group language, L is a comet and ordered language accepted by an n-state NFA, and we have $\mathrm {nsc}(L(A)^R)=\mathrm {nsc}(L(B)^R)=\mathrm {nsc}(L^R)=n+1$.

Proof

In the lemma statement, we consider three witness languages. We present the proofs gradually, starting with $L(A)=(a+b+c)^* \big (c+(cc+a^{n-3}(a+b))a^*\big ) =(a+b+c)^*\big (c+(cc+a^{n-3}(a+b))a^{\le n-2}\big )$, so L(A) is a finitely generated left ideal. For each state i of $A^R$, define the sets

$$ R_i= {\left\{ \begin{array}{ll} \{i\},&{} \text {if}\; 1\le i\le n-1; \\ \{n-1,n\},&{} \text {if}\; i=n, \end{array}\right. } ~~~ C_i= {\left\{ \begin{array}{ll} \{1,3,4,\ldots ,i\},&{} \text {if}\; 3\le i\le n-1, \\ \{1\}\cup \{i\},&{} \text {if}\; i\in \{1,2,n\}. \end{array}\right. } $$

Next, let $\mathcal {S}=\{(R_i,C_i) \mid 1\le i\le 2\}$, $\mathcal {T}=\{(R_i,C_i) \mid 3\le i\le n\}$, $I=\{2,n\}$, $U=\{1,n\}$, and $V=\{1,2\}$. Then $\mathcal {S}\cup \mathcal {T}$, $\mathcal {S}\cup \{(I,U)\}$, and $\mathcal {T}\cup \{(I,V)\}$ satisfy the conditions of Lemma 4, so $\mathrm {nsc}(L(A)^R)=n+1$.

Now let us consider the witness for reversal on group languages, i.e., NFA B, which is actually a DFA. Since the symbols a and b perform permutations on the state set of B, the language L(B) is a group language. Consider the following pairs of subsets of states of B:

$$ (R_i,C_i)= {\left\{ \begin{array}{ll} (\{i,i+1\},\{i\}),&{} \text {if}\; 1\le i\le n-1; \\ (\{n,2\},\{n\}),&{} \text {if}\; i= n, \end{array}\right. } $$

and set $\mathcal {S}=\{(R_i,C_i)\mid i=1,2,\ldots ,n-1\}$, $\mathcal {T}=\{(R_n,C_n)\}$, $I=\{n,1\}$, $U=\{n\}$, and $V=\{1\}$. Then $\mathcal {S}\cup \mathcal {T}$, $\mathcal {S}\cup \{(I,U)\}$, and $\mathcal {T}\cup \{(I,V)\}$ satisfy the conditions of Lemma 4, so $\mathrm {nsc}(L(B)^R)=n+1$.

Finally, consider the comet language $L=(a^{n-1}b)^*a^{\le n-1}$. It is accepted by the NFA C shown in Fig. 6. To get an ordered DFA for L from C, add the dead states 0 and $n+1$ and the transitions $(n,a,n+1)$ and (i, b, 0) for $i=1,2,\ldots ,n-1$. Hence L is ordered. In C, each singleton set $\{i\}$ is reachable by $a^{i-1}$, and in $C^R$, the initial set is $I=\{1,2,\ldots ,n\}$ and each singleton set $\{i\}$ is reachable by $ba^{n-i}$. Set $\mathcal {S}=\{(\{1\},\{1\})\}, \mathcal {T}=\{(\{i\},\{i\})\mid 2\le i\le n\}, U=\{2\}, \text {and}~V=\{1\}.$ Then $\mathcal {S}\cup \mathcal {T}$, $\mathcal {S}\cup \{(I,U)\}$, and $\mathcal {T}\cup \{(I,V)\}$ are fooling sets for $C^R$. It follows that $\mathrm {nsc}(L^R)=n+1$ by Lemma 4.    $\square$

Fig. 6.

A finitely generated left ideal, group, and ordered witnesses for reversal.

In the last two lemmas, we consider complementation. The upper bound on left ideals is known to be $2^{n-1}$ [12, Theorem 37(1)] and we provide a finitely generated witness for this bound. For stars and ordered languages, the complexity is $2^n$, and for group language, we have a hyperpolynomial lower bound $\left( {\begin{array}{c}n-1\\ \lfloor n/2\rfloor \end{array}}\right)$.

Lemma 13

Let $n\ge 3$. Let A, B, C be the NFAs from Fig. 7; $a_{i..j}$ denotes the transitions on $a_i, a_{i+1}, \ldots , a_j$. Then L(A) is a finitely generated left ideal, L(B) is a star language, L(C) is ordered, and we have $\mathrm {nsc}(L(A)^c)=2^{n-1}$ and $\mathrm {nsc}(L(B)^c)=\mathrm {nsc}(L(C)^c)=2^n$.

Fig. 7.

Finitely generated left ideal, star, and ordered witnesses for complementation.

Proof

We provide a proof only for the ordered witness L(C). In the subset automaton $\mathcal {D}(C)$, let us assign the value $p_S=2^{i_1}+2^{i_2}+\cdots +2^{i_k}$ to a set $S=\{{i_1},{i_2},\ldots ,{i_k}\}$ with $n-1\ge i_1>i_2>\cdots >i_k\ge 0$. It follows from the transitions defined in the NFA C that in $\mathcal {D}(C)$, we have $p_S \xrightarrow {a} \lfloor p_S/2\rfloor$, $p_S \xrightarrow {b} 0$ if $p_S\in \{0,1\}$ and $p_S \xrightarrow {b} 2^{n-1}+\lfloor p_S/2\rfloor$ otherwise, and $p_S\xrightarrow {c_j} p_S$ if $j\notin S$ or $0\in S$, and $p_S\xrightarrow {c_j} p_S+1$ otherwise. Since all these transformations preserve the order of states in $\mathcal {D}(C)$ given by their corresponding values, the language L(C) is ordered. In C, the empty set and each singleton set is reachable by a string in $a^*$. Each set $\{{n-1}\}\cup S$ of size k is reached from the set $\{{i+1}\mid i\in S\}$ of size $k-1$ by b, and each set S with ${n-1}\notin S$ of size k is reached from a set of size k containing ${n-1}$ by a string in $a^*$. This proves the reachability of all subsets in C by induction. To get co-reachability, we use the symbols $c_j$. The empty set and each singleton set is co-reachable by a string in $a^*$. Each set S with $0\in S$ and $\max S=j$ is co-reached from $S\setminus \{j\}$ by $c_j$. Each set S with $0\notin S$ is co-reached from a set of the same size containing 0 by a string in $a^*$. It follows that all sets are co-reachable. Hence by Lemma 3, we have $\mathrm {nsc}(L(C)^c)=2^n$.    $\square$

Fig. 8.

A binary group language meeting the lower bound $\left( {\begin{array}{c}n-1\\ \lfloor n/2\rfloor \end{array}}\right)$ for complementation.

Lemma 14

Let $n\ge 4$. Let M be the binary MNFA from Fig. 8 with $k=\lfloor n/2\rfloor$. Then L(M) is a group language with $\mathrm {nsc}(L(M))\le n$ and $\mathrm {nsc}(L(M)^c)=\left( {\begin{array}{c}n-1\\ k\end{array}}\right)$.

Proof

Since in M, the symbols a and b form a generator of all permutations on states from 1 to $n-1$, each subset of $\{1,2,\ldots ,n-1\}$ of size k is reachable and each subset of $\{1,2,\ldots ,n-1\}$ of size $n-1-k$ is co-reachable in M. In total we have $\left( {\begin{array}{c}n-1\\ k\end{array}}\right) =\left( {\begin{array}{c}n-1\\ \lfloor n/2\rfloor \end{array}}\right)$ reachable sets and their co-reachable complements. This gives the lower bound for $\mathrm {nsc}(L(M)^c)$ by Lemma 3. To get an equivalent n-state NFA A from M, add the initial state 0, make all other states non-initial, and add transitions (0, b, i) and $(0,a,i+1)$ for each $i=1,2,\ldots ,k$. Then $\mathrm {nsc}(L(A)^c)=\mathrm {nsc}(L(M)^c)\ge \left( {\begin{array}{c}n-1\\ \lfloor n/2\rfloor \end{array}}\right)$.    $\square$

4 Conclusions

Our results are summarized in the following two theorems and tables. Recall $\text {CB}\subsetneq \text {FGLID}\subsetneq \text {LID}$, $\text {STAR}\subsetneq \text {COM}\subsetneq \text {2COM}$, $\text {ORD}\subsetneq \text {STFR}\subsetneq \text {PSEP}$ [2].

Theorem 15

The nondeterministic state complexity of intersection, union, and concatenation on some subclasses of regular languages is given by Table 1.

Proof

The results for combinational languages follow from Proposition 5.

For the remaining classes, first we handle intersection. The upper bounds are the same as for regular languages. Finitely generated left ideal witnesses are described in Lemma 6. Group witnesses are given in Lemma 7; notice that if we modify them such that only the initial state is final, they are star (so also comet and two-sided comet) witness languages. Ordered (so also power-separating) witnesses are provided in Lemma 8.

Now consider union. The finitely generated left ideals from Lemma 6 meet the upper bound for left ideals. In the remaining classes, the upper bounds are the same as in the regular case. Group witnesses that can be modified to star (so also comet and two-sided comet) languages are described in Lemma 7. Ordered (so also power-separating) witnesses are given by Lemma 8.

Finally we discuss concatenation. The result for finitely generated left ideals follows from [12, Theorem 16] where it is shown that the upper bound for left ideals is $m+n-1$; the unary witnesses $a^*a^{m-1}$ and $a^*a^{n-1}$ described in this theorem are finitely generated left ideals. In all the remaining cases, we have the regular upper bounds. The group witnesses are given in Lemma 7. A proof using the same fooling set as for the group languages works also for the star (so also comet and two-sided comet) witnesses $(a^m)^*$ and $(b^n)^*$, cf. [8, Theorem 7]. The ordered (so also power-separating) witnesses are defined in Lemma 8.    $\square$

Table 1. Results for binary operations; $\diamond$ means the witness from above can be used.

Theorem 16

The nondeterministic state complexity of power, star, reversal, and complementation on some subclasses of regular languages is given by Table 2.

Proof

The results for combinational languages follow from Proposition 5. Now let us examine the remaining classes.

First we consider the k-th power. The upper bound $k(n-1)+1$ for left ideals is met by the unary finitely generated left ideal $a^*a^{n-1}$ [11, Theorem 12(c)]. The tight upper bound for star languages is n by Lemma 9. The general upper bound kn is met by the group language described in Lemma 10. The ordered language $(a^{n-1}b)^*a^{n-1}$ is also a comet (and two-sided comet) language and it meets the upper bound kn as shown in [4, Theorem 3].

The complexity of the star and reversal operations on star languages is n by Lemma 9. For the other classes, the upper bound $n+1$ for star is met by binary finitely generated left ideal language from Lemma 11 which is also a comet and two-sided comet language, by unary group and comet language $(a^n)^*a^{n-1}$, and by unary ordered (so also power-separating) language $(a^{n-1}+a^n)^*a^{n-1}$, as shown in [8, Theorem 9]. This upper bound for reversal is met by a ternary finitely generated left ideal language, a binary group language, and the binary comet and ordered language $(a^{n-1}b)^*a^{\le n-1}$, as shown in Lemma 12.

The upper bound $2^{n-1}$ for complement on left ideals from [12, Theorem 37(1)] is met by the finitely generated left ideal over an alphabet of size $n-1$ from Lemma 13. The regular upper bound $2^n$ is met by a binary star (so also comet and two-sided comet) language and by ordered language over an alphabet of size $n+1$, as shown in Lemma 13, and by the binary star-free (so also power-separating) language from [9, Theorem 5]. Finally, a binary group language meeting the lower bound $n-1\atopwithdelims ()\lfloor n/2\rfloor$ for complementation is described in Lemma 14.    $\square$

Table 2. Results for unary operations;$\diamond$ means the witness from above can be used.