Template Attacks on Different Devices

Abstract

Template attacks remain a most powerful side-channel technique to eavesdrop on tamper-resistant hardware. They use a profiling step to compute the parameters of a multivariate normal distribution from a training device and an attack step in which the parameters obtained during profiling are used to infer some secret value (e.g. cryptographic key) on a target device. Evaluations using the same device for both profiling and attack can miss practical problems that appear when using different devices. Recent studies showed that variability caused by the use of either different devices or different acquisition campaigns on the same device can have a strong impact on the performance of template attacks. In this paper, we explore further the effects that lead to this decrease of performance, using four different Atmel XMEGA 256 A3U 8-bit devices. We show that a main difference between devices is a DC offset and we show that this appears even if we use the same device in different acquisition campaigns. We then explore several variants of the template attack to compensate for these differences. Our results show that a careful choice of compression method and parameters is the key to improving the performance of these attacks across different devices. In particular we show how to maximise the performance of template attacks when using Fisher’s Linear Discriminant Analysis or Principal Component Analysis. Overall, we can reduce the entropy of an unknown 8-bit value below 1.5 bits even when using different devices.

1 Introduction

Side-channel attacks are powerful tools for inferring secret algorithms or data (passwords, cryptographic keys, etc.) processed inside tamper-resistant hardware, if an attacker can monitor a channel leaking such information, most notably the power-supply current and unintended electromagnetic emissions.

One of the most powerful side-channel attacks is the template attack [2], which consists of a profiling step to compute some parameters (the templates) on a training device and an attack step in which the templates are used to infer some secret data on a target device (Sect. 2). However, most previous studies [2, 5, 8, 10, 17] used the same device (and possibly acquisition campaign) for the profiling and attack phases. Only recently, Renauld et al. [12] performed an extensive study on 20 different devices, showing that the template attack may not work at all when the profiling and attack steps are performed on different devices; Elaabid et al. [14] showed that acquisition campaigns on the same device, but conducted at different times, also lead to worse template-attack results; and Lomné et al. [16] evaluated this scenario using electromagnetic leakage.

In this paper, we explore further the causes that make template attacks perform worse across different devices. For this purpose, we evaluate the template attacks with four different Atmel XMEGA 256 A3U 8-bit devices, using different compression methods and parameters.

We show that, for our experiments, a main difference across devices and acquisition campaigns is a DC offset, and this difference decreases very much the performance of template attacks (Sect. 4). To compensate for differences between devices or campaigns we evaluate several variants of the template attack (Sect. 5). One of them needs multiple profiling devices, but can improve significantly the performance of template attacks when using sample selection as the compression method (Sect. 5.3). However, based on detailed analysis of Fisher’s Linear Discriminant Analysis (LDA) and Principal Component Analysis (PCA), we explain how to use these compression techniques to maximise the performance of template attacks on different devices, even when profiling on a single device (Sect. 5.4).

Overall, our results show that a good choice of compression method and parameters can dramatically improve template attacks across different devices or acquisition campaigns. Previous studies [12, 14] may have missed this by evaluating only one compression method.

2 Template Attacks

To implement a template attack, we need physical access to a pair of devices of the same model, which we refer to as the profiling and the attacked device. We wish to infer some secret value ${k}{\star }\in \mathcal {S}$, processed by the attacked device at some point. For an 8-bit microcontroller, $\mathcal {S}=\{0,\ldots ,255\}$ might be the set of possible byte values manipulated by a particular machine instruction.

We assume that we determined the approximate moments of time when the secret value ${k}{\star }$ is manipulated and we are able to record signal traces (e.g., supply current or electromagnetic waveforms) around these moments. We refer to these traces as leakage vectors. Let $\{t_1,\ldots ,t_{{m}^{\mathrm {\text {r}}}}\}$ be the set of time samples and $\mathbf {x}^\text {r}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ be the random vector from which leakage traces are drawn.

During the profiling phase we record $n_{\mathrm {p}}$ leakage vectors ${\mathbf {x}}^{\text {r}}_{{k}{i}}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ from the profiling device for each possible value $k\in \mathcal {S}$, and combine these as row vectors ${{\mathbf {x}}^{\text {r}}_{{k}{i}}}'$ in the leakage matrix $\mathbf {X}^{\text {r}}_{k}\in \mathbb {R}^{n_{\mathrm {p}}\times {m}^{\mathrm {\text {r}}}}$.¹

Typically, the raw leakage vectors ${\mathbf {x}}^{\text {r}}_{{k}{i}}$ provided by the data acquisition device contain a very large number ${m}^{\mathrm {\text {r}}}$ of samples (random variables), due to high sampling rates used. Therefore, we might compress them before further processing, either by selecting only a subset of ${m}^{\mathrm {}}\ll {m}^{\mathrm {\text {r}}}$ of those samples, or by applying some other data-dimensionality reduction method, such as Principal Component Analysis (PCA) or Fisher’s Linear Discriminant Analysis (LDA).

We refer to such compressed leakage vectors as ${\mathbf {x}}_{{k}{i}}\in \mathbb {R}^{{m}^{\mathrm {}}}$ and combine all of these as rows into the compressed leakage matrix $\mathbf {X}_{k}\in \mathbb {R}^{n_{\mathrm {p}}\times {m}^{\mathrm {}}}$. (Without any such compression step, we would have $\mathbf {X}_{k}=\mathbf {X}^{\text {r}}_{k}$ and ${m}^{\mathrm {}}={m}^{\mathrm {\text {r}}}$.)

Using $\mathbf {X}_{k}$ we can compute the template parameters $\bar{\mathbf {x}}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}}$ and $\mathbf {S}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$ for each possible value $k\in \mathcal {S}$ as

$$\begin{aligned} \bar{\mathbf {x}}_{k}= \frac{1}{n_{\mathrm {p}}} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} {\mathbf {x}}_{{k}{i}},\qquad \mathbf {S}_{k}= \frac{1}{n_{\mathrm {p}}-1} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k}){({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k})}', \end{aligned}$$

(1)

where the sample mean $\bar{\mathbf {x}}_{k}$ and the sample covariance matrix $\mathbf {S}_{k}$ are the estimates of the true mean $\mathbf {\mu }_{k}$ and true covariance $\mathbf {\Sigma }_{k}$. Note that

$$\begin{aligned} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k}){({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k})}' = {\widetilde{\mathbf {X}}_{k}}' \widetilde{\mathbf {X}}_{k}, \end{aligned}$$

(2)

where $\widetilde{\mathbf {X}}_{k}$ is $\mathbf {X}_{k}$ with ${\bar{\mathbf {x}}_{k}}'$ subtracted from each row, and the latter form allows fast vectorised computation of the covariance matrices in (1).

In our experiments we observed that the particular covariance matrices $\mathbf {S}_{k}$ are very similar and seem to be independent of the candidate $k$. In this case, as explained in a previous paper [17], we can use a pooled covariance matrix

$$\begin{aligned} \mathbf {S}_{\mathrm {pooled}}= \frac{1}{|\mathcal {S}|(n_{\mathrm {p}}-1)} \displaystyle \sum _{k\in \mathcal {S}} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k}){({\mathbf {x}}_{{k}{i}}-\bar{\mathbf {x}}_{k})}', \end{aligned}$$

(3)

to obtain a much better estimate of the true covariance matrix $\mathbf {\Sigma }_{}$.

In the attack phase, we try to infer the secret value ${k}{\star }\in \mathcal {S}$ processed by the attacked device. We obtain $n_{\mathrm {a}}$ leakage vectors ${\mathbf {x}}_{i}\in \mathbb {R}^{{m}^{\mathrm {}}}$ from the attacked device, using the same recording technique and compression method as in the profiling phase, resulting in the leakage matrix $\mathbf {X}_{{k}{\star }}\in \mathbb {R}^{n_{\mathrm {a}}\times {m}^{\mathrm {}}}$. Then, using $\mathbf {S}_{\mathrm {pooled}}$, we can compute a linear discriminant score [17], namely

$$\begin{aligned} \mathrm {d}_{\mathrm {LINEAR}}^{\mathrm {joint}}(k\mid \mathbf {X}_{{k}{\star }}) = {\bar{\mathbf {x}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\displaystyle \sum _{{\mathbf {x}}_{i}\in \mathbf {X}_{{k}{\star }}} {\mathbf {x}}_{i}\bigg ) - \frac{n_{\mathrm {a}}}{2}{\bar{\mathbf {x}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{\mathbf {x}}_{k}, \end{aligned}$$

(4)

for each $k\in \mathcal {S}$, and try all $k\in \mathcal {S}$ on the attacked device, in order of decreasing score (optimized brute-force search, e.g. for a password or cryptographic key), until we find the correct ${k}{\star }$.

2.1 Guessing Entropy

In this work we are interested in evaluating the overall practical success of the template attacks when using different devices. For this purpose we use the guessing entropy, which estimates the (logarithmic) average cost of an optimized brute-force search. The guessing entropy gives the expected number of bits of uncertainty remaining about the target value ${k}{\star }$, by averaging the results of the attack over all ${k}{\star }\in \mathcal {S}$. The lower the guessing entropy, the more successful the attack has been and the less effort remains to search for the correct ${k}{\star }$. We compute the guessing entropy $g$ as shown in our previous work [17]. For all the results shown in this paper, we compute the guessing entropy on 10 random selections of traces $\mathbf {X}_{{k}{\star }}$ and plot the average guessing entropy over these 10 iterations.

2.2 Compression Methods

Previously [17], we provided a detailed comparison of the most common compression methods: sample selection (1ppc, 3ppc, 20ppc, allap), Principal Component Analysis (PCA) and Fisher’s Linear Discriminant Analysis (LDA), which we summarise here. For the sample selection methods 1ppc, 3ppc, 20ppc and allap, we first compute a signal-strength estimate $\mathbf {s}(t)$ for each sample $j\in \{1,\ldots ,{m}^{\mathrm {\text {r}}}\}$, by summing the absolute differences² between the mean vectors $\bar{\mathbf {x}}_{k}^{\text {r}}$, and then select the 1 sample per clock cycle (1ppc, $6\le {m}^{\mathrm {}}\le 10$), 3 samples per clock cycle (3ppc , $18\le {m}^{\mathrm {}}\le 30$), 20 samples per clock cycle (20ppc, $75\le {m}^{\mathrm {}}\le 79$) or the 5 % samples (allap, ${m}^{\mathrm {}}=125$) having the largest $\mathbf {s}(t)$. For PCA, we first combine the first ${m}^{\mathrm {}}$ eigenvectors $\mathbf {u}_j\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ of the between-groups matrix $\mathbf {B}= \sum _{k\in \mathcal {S}} (\bar{\mathbf {x}}_{k}^{\text {r}}-\bar{\mathbf {x}}_{}^{\text {r}}) {(\bar{\mathbf {x}}_{k}^{\text {r}}-\bar{\mathbf {x}}_{}^{\text {r}})}',$ where $\bar{\mathbf {x}}_{}^{\text {r}} = \frac{1}{|\mathcal {S}|} \sum _{k\in \mathcal {S}}\bar{\mathbf {x}}_{k}^{\text {r}},$ into the matrix of eigenvectors $\mathbf {U}= [\mathbf {u}_1,\ldots ,\mathbf {u}_{m}^{\mathrm {}}]$, and then we project the raw leakage matrices $\mathbf {X}^{\text {r}}_{k}$ into a lower-dimensional space as $\mathbf {X}_{k}= \mathbf {X}^{\text {r}}_{k}\mathbf {U}$. For LDA, we use the matrix $\mathbf {B}$ and the pooled covariance $\mathbf {S}_{\mathrm {pooled}}$ from (3), computed from the uncompressed traces ${\mathbf {x}}^{\text {r}}_{i}$, and combine the eigenvectors $\mathbf {a}_j\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ of $\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$ into the matrix $\mathbf {A}=[\mathbf {a}_1,\ldots ,\mathbf {a}_{m}^{\mathrm {}}]$. Then, we use the diagonal matrix $\mathbf {Q}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$, with $\mathbf {Q}_{jj} = ({\mathbf {a}_{j}}' \mathbf {S}_{\mathrm {pooled}}\mathbf {a}_{j})^{-\frac{1}{2}},$ to scale the matrix of eigenvectors $\mathbf {A}$ and use $\mathbf {U}= \mathbf {A}\mathbf {Q}$ to project the raw leakage matrices as $\mathbf {X}_{k}= \mathbf {X}^{\text {r}}_{k}\mathbf {U}$. In this case, the compressed covariances $\mathbf {S}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$ and $\mathbf {S}_{\mathrm {pooled}}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$ reduce to the identity matrix $\mathbf {I}$, resulting in more efficient template attacks.

For most of the results shown in Sects. 4 and 5, we used PCA and LDA with ${m}^{\mathrm {}}=4$, based on the elbow rule (visual inspection of eigenvalues) derived from a standard implementation of PCA and LDA. However, as we will then show in Sect. 5.4, a careful choice of ${m}^{\mathrm {}}$ is the key to good results.

2.3 Standard Method

Using the definitions from the previous sections, we can define the following standard method for implementing template attacks.

Method 1

(Standard)

• 1. Obtain the $n_{\mathrm {p}}$ leakage traces in $\mathbf {X}_{k}$ from the profiling device, for each $k$.

• 2. Compute the template parameters $(\bar{\mathbf {x}}_{k}$,$\mathbf {S}_{\mathrm {pooled}})$ using (1) and (3).

• 3. Obtain the leakage traces $\mathbf {X}_{{k}{\star }}$ from the attacked device.

• 4. Compute the guessing entropy as described in Sect. 2.1.

3 Evaluation Setup

For our experimental research we produced four custom PCBs (named Alpha, Beta, Gamma and Delta) for the unprotected 8-bit Atmel XMEGA 256 A3U microcontroller. The current consumption across all CPU ground pins is measured through a single 10-ohm resistor. We powered the devices from a battery via a 3.3 V linear regulator and supplied a 1 MHz sine wave clock signal. We used a Tektronix TDS 7054 8-bit oscilloscope with P6243 active probe, at 250 MS/s, with 500 MHz bandwidth in SAMPLE mode. Devices Alpha and Beta used a CPU with week batch ID 1145, while Gamma and Delta had 1230.

For the analysis presented in this paper we run five acquisition campaigns: one for each of the devices, which we call Alpha, Beta, Gamma and Delta (i.e. the same name as the device), and another one at a later time for Beta, which we call Beta Bis. For all the acquisition campaigns we used the settings described above. Then, for each campaign and each candidate value $k\in \{0,\ldots ,255\}$ we recorded $3072$ traces ${\mathbf {x}}^{\text {r}}_{{k}{i}}$ (i.e., $786\,432$ traces per acquisition campaign), which we randomly divided into a training set (for the profiling phase) and an evaluation set (for the attack phase). Each acquisition campaign took about 2 h. We note a very important detail for our experiments: instead of acquiring all the traces per $k$ sequentially (i.e. first the $3072$ traces for $k=0$, then $3072$ traces for $k=1$, and so on), we used random permutations of all the $256$ values $k$ and acquired $256$ traces at a time (corresponding to a random permutation of all the $256$ values $k$), for a total of $3072$ iterations. This method distributes equally any external noise (e.g. due to temperature variation) across the traces of all the values $k$. As a result, the covariances $\mathbf {S}_{k}$ will be similar and the mean vectors $\bar{\mathbf {x}}_{k}$ will be affected in the same manner so they will not be dependent on factors such as low-frequency temperature variation.

For all the results shown in this paper we used $n_{\mathrm {p}}=1000$ traces ${\mathbf {x}}^{\text {r}}_{{k}{i}}$ per candidate $k$ during the profiling phase. Each trace contains ${m}^{\mathrm {\text {r}}}=2500$ samples, recorded while the target microcontroller executed the same sequence of instructions loaded from the same addresses: a MOV instruction, followed by several LOAD instructions. All the LOAD instructions require two clock cycles to transfer a value from RAM into a register, using indirect addressing. In all the experiments our goal was to determine the success of the template attacks in recovering the byte $k$ processed by the second LOAD instruction. All the other instructions were processing the value zero, meaning that in our traces none of the variability should be caused by variable data in other nearby instructions that may be processed concurrently in various pipeline stages. This approach, also used in other studies [8, 13, 17], provides a general setting for the evaluation of the template attacks. Specific algorithm attacks (e.g. on the S-box output of a block cipher such as AES) may be mounted on top of this.

4 Ideal vs Real Scenario

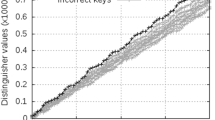
Most publications on template attacks [2, 5, 8, 10, 17] used the same device (and most probably the same acquisition campaign) for the profiling and attack phase in their evaluation. The results of the standard Method 1 in this ideal case, where we used the same acquisition data for profiling and attack (but disjoint sets of traces), are shown in Fig. 1 (top-left). We can see that most compression methods perform very well for large $n_{\mathrm {a}}$, while for smaller $n_{\mathrm {a}}$ LDA is generally the best. This is in line with our previous results [17].

Fig. 1.

Template attacks using Method 1 in different scenarios. Top-left (ideal): using same device and acquisition campaign (Beta) for profiling and attack. Top-right: using Alpha for profiling and Beta for attack. Bottom-left: arithmetic average of guessing entropy over all combinations of different pairs of devices for profile and attack. Bottom-right: using same device (Beta) but different acquisition campaigns for profile (Beta) and attack (Beta Bis).

However, in a more realistic scenario, an attacker who wants to infer some secret data from a target device may be forced to use a different device for profiling. Indeed, there are situations where we could use non-profiled attacks, such as DPA [1], CPA [3], or MIA [9], to infer secret data using a single device (e.g. by targeting values that represent a known relationship between key and plaintext). But these methods cannot be used in more general situations where we want to infer a single secret data value that does not depend on any other values, which is the setting of our experiments. In such cases the template attacks or the stochastic approach [4] might be the only viable side-channel attack.³ Moreover, the template attacks are expected to perform better than the other attacks when provided with enough profiling data [11]. Therefore, we would like to use template attacks also with different devices for profiling and attack.

As we show in Fig. 1 (top-right), the efficacy of template attacks using the standard Method 1 drops dramatically when using different devices for the profiling and attack steps. This was also observed by Renauld et al. [12], by testing the success of template attacks on 20 different devices with 65 nm CMOS transistor technology. Moreover, Elaabid et al. [14] mentioned that even if the profiling and attack steps are performed on the same device but on different acquisition campaigns we will also observe weak success of the template attacks. In Fig. 1 (bottom-right) we confirm that indeed, even when using the same device but different acquisition campaigns (same acquisition settings), we get results as bad or even worse as when using different devices. In Sect. 5, we offer an explanation for why LDA can perform well across different devices.

4.1 Causes of Trouble

In order to explore the causes that lead to worse attack performance on different acquisition campaigns, we start by looking at two measures of standard deviation (std), that we call std devices and std data.

Let $\bar{x}_{kj}^{(i)}$ be the mean value of sample $j\in \{1,\ldots ,{m}^{\mathrm {}}\}$ for the candidate $k\in \mathcal {S}$ on the campaign $i\in \{1,\ldots ,n_{\mathrm {c}}\}$, $\bar{x}_{j}^{(i)} = \frac{1}{|\mathcal {S}|}\sum _{k\in \mathcal {S}} \bar{x}_{kj}^{(i)}$, $\mathbf {z}_k(j) = [ (\bar{x}_{kj}^{(1)} - \bar{x}_{j}^{(1)}), \ldots , (\bar{x}_{kj}^{(n_{\mathrm {c}})} - \bar{x}_{j}^{(n_{\mathrm {c}})}) ] = [ z_{k}^{(1)}(j), \ldots , z_{k}^{(n_{\mathrm {c}})}(j) ]$ and $\bar{z}_{k}(j) = \frac{1}{n_{\mathrm {c}}} \sum _{i=1}^{n_{\mathrm {c}}} z_{k}^{(i)}(j)$. Then,

$$\begin{aligned} \text {std devices}(j) = \frac{1}{|\mathcal {S}|} \displaystyle \sum _{k\in \mathcal {S}} \sqrt{ \frac{1}{n_{\mathrm {c}}-1} \sum _{i=1}^{n_{\mathrm {c}}} {(z_{k}^{(i)}(j) - \bar{z}_{k}(j))}^2 }, \end{aligned}$$

(5)

and

$$\begin{aligned} \text {std data}(j) = \frac{1}{n_{\mathrm {c}}} \sum _{i=1}^{n_{\mathrm {c}}} \sqrt{ \frac{1}{|\mathcal {S}|-1} \sum _{k\in \mathcal {S}} {(\bar{x}_{kj}^{(i)}- \bar{x}_{j}^{(i)})}^2 }. \end{aligned}$$

(6)

We show these values in Fig. 2. The results on the left plot are from the four campaigns on different devices, while the results on the right plot are from the two campaigns on the device Beta. We can observe that both plots are very similar, which suggests that the differences between campaigns are not entirely due to different devices being used, but largely due to different sources of noise (e.g., temperature, interference, etc.) that may affect in a particular manner each acquisition campaign. Using a similar type of plots, Renauld et al. [12, Fig. 1] observed a much stronger difference, attributed to physical variability. Their observed differences are not evident in our experiments, possibly because our devices use a larger transistor size (around 0.12 $\upmu$m)⁴.

Fig. 2.

std devices($j$) and std data($j$), along with clock signal for a selection of samples around the first clock cycle of our target LOAD instruction. Left: using the 4 campaigns on different devices. Right: using Beta and Beta Bis.

4.2 How It Differs

Next we look at how the overall power consumption differs between acquisition campaigns. In Fig. 3, we show the overall mean vectors $\bar{\mathbf {x}}_{} = \frac{1}{|\mathcal {S}|} \sum _{k\in \mathcal {S}} \bar{\mathbf {x}}_{k}$ for each campaign, from which we removed the overall mean vector of Beta (hence the vector for Beta is 0). From this figure we see that all overall mean vectors $\bar{\mathbf {x}}_{}$ (except the one for Beta) are far outside the confidence region of Beta ($\alpha =0.05$). Moreover, we see that the overall mean vector $\bar{\mathbf {x}}_{}$ for Beta Bis is the most distant from the overall mean vector of Beta. This confirms our previous assumption that the main difference between acquisition campaigns is caused by campaign-dependent factors, such as temperature drift, environmental noise, etc. and not necessarily by the use of different devices. A similar observation was made by Elaabid et al. [14], however they used different setups for the different campaigns on the same devices. In our study we have used the exact same setup for the acquisition of data, while replacing only the tested device (evaluation board).

Fig. 3.

Overall mean vectors $\bar{\mathbf {x}}_{}$ for all campaigns, from which the overall mean vector of Beta was subtracted. $Beta{+}ci$ and $Beta{-}ci$ represent the confidence region ($\alpha =0.05$) for the overall mean vector of Beta. SNR of Beta is the Signal-to-Noise signal strength estimate of Beta (rescaled). Samples at first clock cycle of target LOAD instruction.

It is clear from Fig. 3 that a main difference between the different campaigns is an overall offset. We see that this is also the case over the samples corresponding to the highest SNR. If we now look at the distributions of our data, as shown in Fig. 4 for Alpha and Beta, we observe that the distributions are very similar (in particular the ordering of the different candidates $k$ is generally the same) but differ mainly by an overall offset. This suggests that, for our experiments, this offset is the main reason why template attacks perform badly when using different campaigns for the profiling and attack steps.

Fig. 4.

Normal distribution at sample index $j=884$ based on the template parameters ($\bar{\mathbf {x}}_{k},\mathbf {S}_{\mathrm {pooled}}$) for $k\in \{0,1,\ldots ,9\}$. Left: on Alpha. Right: on Beta.

4.3 Misalignment

We also mention that in some circumstances the recorded traces might be misaligned, e.g. due to lack of a good trigger signal, or random delays introduced by some countermeasure. In such cases, we should first apply a resynchronisation method, such as those proposed by Homma et al. [7]. In our experiments we used a very stable trigger, as shown by the exact alignments of sharp peaks in Fig. 3.

5 Improved Attacks on Different Devices

In this section, we explore ways to improve the success of template attacks when using different devices (or different campaigns), in particular by dealing with the campaign-specific offset noted in Sect. 4. We assume that the attacker can profile well a particular device or set of devices, i.e. can get a large number $n_{\mathrm {p}}$ of traces for each candidate $k$, but needs to attack a different device for which he only has access to a set of $n_{\mathrm {a}}$ traces for a particular unknown target value ${k}{\star }$. Unless otherwise mentioned, in the following evaluations we considered all possible combinations of the campaigns Alpha, Beta, Gamma and Delta, always ensuring that the campaign of one device is only used in either the profiling or attack phases, but not in both.

5.1 Profiling on Multiple Devices

Renauld et al. [12] proposed to accumulate the sample means $\bar{\mathbf {x}}_{k}$ and variances $S_{jj}$ (where $\mathbf {S}_{}$ can be either $\mathbf {S}_{k}$ or $\mathbf {S}_{\mathrm {pooled}}$) of each sample $x_j$ across multiple devices in order to make the templates more robust against differences between different devices. That is, for each candidate $k$ and sample $j$, and given the sample means $\bar{\mathbf {x}}_{k}$ and covariances $\mathbf {S}_{}$ from $n_{\mathrm {c}}$ training devices, they compute the robust sample means $\bar{x}_{kj}^{(\mathrm {robust})} = \frac{1}{n_{\mathrm {c}}} ( \bar{x}_{kj}^{(1)} + \ldots + \bar{x}_{kj}^{(n_{\mathrm {c}})} )$ (i.e. an average over the sample means of each device), and the robust variance as $S_{jj}^{(\mathrm {robust})} = S_{jj}^{(1)} + \frac{1}{n_{\mathrm {c}}-1} \displaystyle \sum _{i=1}^{n_{\mathrm {c}}} {(\bar{x}_{kj}^{(i)}- \bar{x}_{kj}^{(\mathrm {robust})})}^2$ (i.e. they add the variance of one device with the variance of the noise-free sample mean across devices, using simulated univariate noise for each device). However, this approach does not consider the correlation between samples or the differences between the covariances of different devices. Therefore, we instead use the following method, where we use the traces from all available campaigns.

Method 2

(Robust Templates from Multiple Devices)

• 1. Obtain the leakage traces $\mathbf {X}_{k}^{(i)}$ from each profiling device $i\in \{1,\ldots ,n_{\mathrm {c}}\}$, for each $k$.

• 2. Pull together the leakage traces of each candidate $k$ from all $n_{\mathrm {c}}$ devices into an overall leakage matrix $\mathbf {X}_{k}^{(\mathrm {robust})}\in \mathbb {R}^{n_{\mathrm {p}}n_{\mathrm {c}}\times {m}^{\mathrm {}}}$ composed as

  $$\begin{aligned} {\mathbf {X}_{k}^{(\mathrm {robust})}}' = [ {\mathbf {X}_{k}^{(1)}}', \ldots , {\mathbf {X}_{k}^{(n_{\mathrm {c}})}}' ]. \end{aligned}$$

  (7)

• 3. Compute the template parameters $(\bar{\mathbf {x}}_{k}, \mathbf {S}_{\mathrm {pooled}})$ using (1) and (3) on $\mathbf {X}_{k}^{(\mathrm {robust})}$.

• 4. Obtain the leakage traces $\mathbf {X}_{{k}{\star }}$ from the attacked device.

• 5. Compute the guessing entropy as described in Sect. 2.1.

Fig. 5.

Results of Method 2, profiling on three devices and attacking the fourth one. Top-left: attack on Alpha; top-right: attack on Beta; bottom-left: arithmetic average of guessing entropy over all four combinations; bottom-right: attack on Delta.

In our evaluation of Method 2, we used the data from the campaigns on the four devices (Alpha, Beta, Gamma, Delta), by profiling on three devices and attacking the fourth. The results are shown in Fig. 5. We can see that, on average, all the compression methods perform better than using Method 1 (Figs. 1 and 5, bottom-left). This is because, with Method 2, the pooled covariance $\mathbf {S}_{\mathrm {pooled}}$ captures noise from many different devices, allowing more variability in the attack traces. However, the additional noise from different devices also has the negative effect of increasing the variability of each leakage sample [12, Fig. 4]. As a result, we can see that for the attacks on Beta, LDA performs better when we profile on a single device (Alpha) than when we use three devices (Figs. 1 and 5, top-right).

5.2 Compensating for the Offset

In Sect. 4.2 we showed that a main difference between acquisition campaigns (and devices) is a constant offset between the overall mean vector $\bar{\mathbf {x}}_{}$. Therefore, we expect that a template attack that removes this offset should provide better results. Elaabid et al. [14] have shown that, indeed, if we replace each trace from each campaign by the difference between itself and the overall mean $\bar{\mathbf {x}}_{}$ of that campaign (they refer to this process as normalisation, and this process may also include division by the overall standard deviation), we can obtain results very similar to those in the ideal case (profiling and attack on the same campaign). However, this approach does not work straight away in a more realistic scenario in which the attacker only has access to a limited number of traces from the target device for a particular target value ${k}{\star }$, and hence he cannot compute the overall mean $\bar{\mathbf {x}}_{}$ of the campaign. Nevertheless, if the difference between campaigns is mainly a constant overall offset (as we showed in Sect. 4.2), then an attacker may still use the subset of available attack traces $\mathbf {X}_{{k}{\star }}$ to improve the template attack. The method we propose is the following.

Method 3

(Adapt for the Offset)

• 1. Obtain the raw leakage traces $\mathbf {X}^{\text {r}}_{k}$ from the profiling device, for each $k$.

• 2. Compress the raw leakage traces $\mathbf {X}^{\text {r}}_{k}$ to obtain $\mathbf {X}_{k}$, for each $k$.

• 3. Compute the template parameters $(\bar{\mathbf {x}}_{k}$,$\mathbf {S}_{\mathrm {pooled}})$ using (1) and (3) on $\mathbf {X}_{k}$.

• 4. Compute the overall mean vector $\bar{\mathbf {x}}_{}^{\text {r}(\mathrm {profile})} = \frac{1}{|\mathcal {S}|} \sum _{k} \bar{\mathbf {x}}_{k}^{\text {r}}$ from $\mathbf {X}^{\text {r}}_{k}$.

• 5. Compute the constant offset $\mathrm {c}^{(\mathrm {profile})} = \mathrm {offset}(\bar{\mathbf {x}}_{}^{\text {r}(\mathrm {profile})}) \in \mathbb {R}^{}$.⁵

• 6. Obtain the leakage traces $\mathbf {X}_{{k}{\star }}$ from the attacked device.

• 7. Compute the offset $\mathrm {c}^{(\mathrm {attack})} = \mathrm {offset}(\mathbf {x}^\text {r}) \in \mathbb {R}^{}$ from each raw attack trace $\mathbf {x}^\text {r}$ (row of $\mathbf {X}_{{k}{\star }}^\text {r}$). As in step 5, for our data we used the median of $\mathbf {x}^\text {r}$.

• 8. Replace each trace $\mathbf {x}^\text {r}$ (row of $\mathbf {X}_{{k}{\star }}^\text {r}$) by $\mathbf {x}^{\text {r}(\mathrm {robust})} = \mathbf {x}^\text {r}- \mathbf {1}^\text {r}\cdot (\mathrm {c}^{(\mathrm {attack})} - \mathrm {c}^{(\mathrm {profile})})$, where $\mathbf {1}^\text {r}=[1,1,\ldots ,1]\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$.

• 9. Apply the compression method to each of the modified attack traces $\mathbf {x}^{\text {r}(\mathrm {robust})}$, obtaining the robust attack leakage matrix $\mathbf {X}_{{k}{\star }}^{(\mathrm {robust})}$.

• 10. Compute the guessing entropy as described in Sect. 2.1 using $\mathbf {X}_{{k}{\star }}^{(\mathrm {robust})}$.

Note that instead of Method 3 we could also compensate for the offset $(\mathrm {c}^{(\mathrm {attack})} - \mathrm {c}^{(\mathrm {profile})})$ in the template parameters ($\bar{\mathbf {x}}_{k},\mathbf {S}_{\mathrm {pooled}}$), but that would require much more computation, especially if we want to evaluate the expected success of an attacker using this method with an arbitrary number of attack traces, as we do in this paper. Note also that in our evaluation, each additional attack trace improves the offset difference estimation of the attacker: the use of the linear discriminant from (4) in our evaluation implies that, as we get more attack traces, we are basically averaging the differences $(\mathrm {c}^{(\mathrm {attack})} - \mathrm {c}^{(\mathrm {profile})})$, thus getting a better estimate of this difference.

Fig. 6.

Results of Method 3, profiling on one device and attacking a different device. Top-left: worst case (profiling on Beta, attack on Delta); top-right: best case (profiling on Alpha, attack on Beta); bottom-left: average over all possible 12 combinations using campaigns Alpha, Beta, Gamma, Delta.

In Fig. 6 we show the results of Method 3. We can see that, on average, we get a similar pattern as with Method 2, but slightly worse results. For the best case (top-right), LDA is now achieving less than 1 bit of entropy at $n_{\mathrm {a}}=1000$, thus approaching the results on the ideal scenario. On the other hand, we also see that for the worst case (top-left) we get very bad results, where even using LDA with $n_{\mathrm {a}}=1000$ doesn’t provide any real improvement. This large difference between the best and worst cases can be explained by looking at Fig. 3. There we see that the difference between the overall means $\bar{\mathbf {x}}_{}$ of Alpha and Beta is constant across the regions of high SNR (e.g. around samples 878 and 884), while the difference between Beta and Delta varies around these samples. This suggests that, in general, there is more than a simple DC offset involved between different campaigns and therefore this offset compensation method alone is not likely to be helpful.

We could also try to use a high-pass filter, but note that a simple DC block has a non-local effect, i.e. a far-away bump in the trace not related to $k$ can affect the leakage samples that matter most. Another possibility, to deal with the low-frequency offset, might be to use electromagnetic leakage, as this leakage is not affected by low-frequency components, so it may provide better results [16].

5.3 Profiling on Multiple Devices and Compensating for the Offset

If an attacker can use multiple devices during profiling, and since compensating for the offset may help where this offset is the main difference between campaigns, a possible option is to combine the previous methods. This leads to the following.

Method 4

(Robust Templates and Adapt for the Offset)

• 1. Obtain the overall raw leakage matrix $\mathbf {X}_{k}^{r(\mathrm {robust})}$ using Steps (1, 2) of Method 2.

• 2. Use Method 3 with $\mathbf {X}_{k}^{r(\mathrm {robust})}$ instead of $\mathbf {X}^{\text {r}}_{k}$.

Fig. 7.

Results of Method 4, profiling three devices and attacking the fourth one. Top-left: attack on Alpha; top-right: attack on Beta; bottom-left: average over all 4 combinations; bottom-right: attack on Delta.

The results from Method 4 are shown in Fig. 7. We can see that using this method the sample selections (in particular 20ppc, allap) perform much better than using the previous methods, and in most cases even better than LDA. This can be explained as follows: the profiling on multiple devices allows the estimation of a more robust covariance matrix (which helps both the sample selection methods and LDA), while the offset compensation helps more the sample selection methods than LDA. We also notice that PCA still performs poorly, which was somewhat expected since the standard PCA compression method does not take advantage of the robust covariance matrix. In the following sections, we show how to improve template attacks when using LDA or PCA.

5.4 Efficient Use of LDA and PCA

In the previous sections, we showed that LDA did not benefit much from profiling on different devices or adapting the attack traces for a DC offset. In fact, using the standard Method 1, LDA was already able to provide good results across different devices (see Fig. 1). To understand why this happens, we need to look at the implementation of LDA, summarised in Sect. 2.2. There we can see that LDA takes into consideration the raw pooled covariance $\mathbf {S}_{\mathrm {pooled}}$. Also, as we explained in Sect. 3, we acquired traces for random permutations of all values $k$ at a time and our acquisition campaigns took a few hours to complete. Therefore, the pooled covariance $\mathbf {S}_{\mathrm {pooled}}$ of a given campaign contains information about the different noise sources that have influenced the current consumption of our microcontrollers over the acquisition period. But one of the major sources of low-frequency noise is temperature variation (which can affect the CPU, the voltage regulator of our boards, the voltage reference of the oscilloscope, our measurement resistor; see also the study by Heuser et al. [15]), and we expect this temperature variation to be similar within a campaign as it is across campaigns, if each acquisition campaign takes several hours. As a result, the temperature variation captured by the covariance matrix $\mathbf {S}_{\mathrm {pooled}}$ of one campaign should be similar across different campaigns. However, the mean vectors $\bar{\mathbf {x}}_{k}$ across different campaigns can be different due to different DC offsets (even if the overall temperature variation is similar), and this is why the sample selection methods (e.g. 20ppc, allap) perform poorly across different campaigns. Nevertheless, the LDA algorithm is able to remove the DC component and use only the rest of the trace for the attack. This, combined with the fact that with LDA we no longer need a covariance matrix after compression, allows LDA to filter out temperature variations and other noise sources that are similar across campaigns, and provide good results even across different devices.

Fig. 8.

Top: DC components of eigenvectors of LDA ($\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$), PCA ($\mathbf {B}$) and $\mathbf {S}_{\mathrm {pooled}}$. Middle: First six eigenvectors of LDA ($\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$), PCA ($\mathbf {B}$) and $\mathbf {S}_{\mathrm {pooled}}$. Bottom: eigenvalues (log y axis) of LDA and PCA.

In order to show how LDA and PCA deal with the DC offset, we show in Fig. 8 (top) the DC components (mean) of the LDA and PCA eigenvectors. For LDA we can see that there is a peak at the fifth DC component, which shows that our choice of ${m}^{\mathrm {}}=4$ avoided the component with largest DC offset by chance. For PCA we can see a similar peak, also for the fifth component, and again our choice ${m}^{\mathrm {}}=4$ avoided this component. However, for PCA this turned out to be bad, because PCA does use a covariance matrix after projection and therefore it would benefit from getting knowledge of the temperature variation from the samples. This temperature variation will be given by the eigenvector with a high DC offset and therefore we expect that adding this eigenvector may provide better results. We also show in Fig. 8 the first six eigenvectors of LDA ($\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$), PCA ($\mathbf {B}$) and $\mathbf {S}_{\mathrm {pooled}}$, along with the first $20$ eigenvalues of LDA and PCA. The fifth eigenvector of PCA clearly contains a DC offset, while this is not obvious in LDA. Also, we see that the division by $\mathbf {S}_{\mathrm {pooled}}$ in LDA has removed much of the noise found in the PCA eigenvectors, and it appears that LDA has reduced the number of components extracting most information from four (in PCA) down to three.

Fig. 9.

Template attack on different campaigns (profiling on Alpha, attack on Beta). Left: using various compressions with Method 1. Right: using PCA and LDA with Method 5.

To confirm the above observations, we show in Fig. 9 (left) the results of template attacks when using PCA and LDA with different values of ${m}^{\mathrm {}}$. We see that for LDA there is a great gap between using ${m}^{\mathrm {}}=4$ and ${m}^{\mathrm {}}=5$, no gap between ${m}^{\mathrm {}}=3$ and ${m}^{\mathrm {}}=4$, while the gap between ${m}^{\mathrm {}}=5$ and ${m}^{\mathrm {}}=40$ is very small. This confirms our previous observation that with LDA we should ignore the eigenvector containing a strong DC coefficient. Also, we see that for PCA there is a huge gap between using ${m}^{\mathrm {}}=4$ and ${m}^{\mathrm {}}=5$ (in the opposite sense as with LDA), but the gap between ${m}^{\mathrm {}}=5$ and ${m}^{\mathrm {}}=40$ is negligible. Therefore, PCA can work well across devices if we include the eigenvectors containing the DC offset information. These results provide an important lesson for implementing template attacks across different devices or campaigns: the choice of components should consider the DC offset contribution of each eigenvector. This suggests that previous studies may have missed important information, by using only sample selections with one to three samples [12] or only the first PCA component [14].

5.5 Add DC Offset Variation to PCA

Renauld et al. [12] mentioned that “physical variability makes the application of PCA irrelevant, as it cannot distinguish between inter-plaintext and inter-chip variances”. While it is true that the standard PCA approach [6] is not aimed at distinguishing between the two types of variance, we showed in Sect. 5.4 that PCA can actually provide good results if we select the eigenvectors carefully. Starting from this observation, we can try to enhance the PCA algorithm by deliberately adding DC noise, in the hope of concentrating the DC sensitivity in one of the first eigenvectors, thereby making the other eigenvectors less DC sensitive (as all eigenvectors are orthogonal).

Method 5

(Add Random Offsets to the Matrix $\mathbf {B}$ – PCA and LDA only)

• 1. Obtain the raw leakage traces $\mathbf {X}^{\text {r}}_{k}$ from the profiling device, for each $k$.

• 2. Obtain the raw pooled covariance matrix $\mathbf {S}_{\mathrm {pooled}}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}\times {m}^{\mathrm {\text {r}}}}$.

• 3. Pick a random offset $c_k$ for each mean vector $\bar{\mathbf {x}}_{k}$.⁶

• 4. Compute the between-groups matrix as $\mathbf {B}= \sum _{k\in \mathcal {S}} (\bar{\mathbf {x}}_{k}^{\text {r}}- \bar{\mathbf {x}}_{}^{\text {r}} + \mathbf {1}^\text {r}\cdot c_k) {(\bar{\mathbf {x}}_{k}^{\text {r}}- \bar{\mathbf {x}}_{}^{\text {r}} + \mathbf {1}^\text {r}\cdot c_k)}'$.

• 5. Use PCA (uses $\mathbf {B}$ only) or LDA (uses both $\mathbf {B}$ and $\mathbf {S}_{\mathrm {pooled}}$) to compress the raw leakage traces and obtain $\mathbf {X}_{k}$ for each $k$.

• 6. Compute the template parameters $(\bar{\mathbf {x}}_{k}, \mathbf {S}_{\mathrm {pooled}})$ using (1) and (3).

• 7. Obtain the compressed leakage traces $\mathbf {X}_{{k}{\star }}$ from the attacked device.

• 8. Compute the guessing entropy as described in Sect. 2.1.

The results of this method are shown in Fig. 9 (right). We see that now PCA provides good results even with ${m}^{\mathrm {}}=4$. However, in this case LDA gives bad results with ${m}^{\mathrm {}}=4$. In Fig. 10 we show the eigenvectors from LDA and PCA, along with their DC component. We can see that, by using this method, we managed to push the eigenvector having the strongest DC component first, and this was useful for PCA. However, LDA does not benefit from including a noise eigenvector into $\mathbf {B}$, so we propose this method only for use with PCA.

Fig. 10.

Top: DC components of eigenvectors of LDA ($\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$) and PCA ($\mathbf {B}$) after using Method 5. Bottom: First six eigenvectors of LDA ($\mathbf {S}_{\mathrm {pooled}}^{-1}\mathbf {B}$) and PCA ($\mathbf {B}$).

6 Conclusions

In this paper, we explored the efficacy of template attacks when using different devices for the profiling and attack steps.

We observed that, for our Atmel XMEGA 256 A3U 8-bit microcontroller and particular setup, the campaign-dependent parameters (temperature, environmental noise, etc.) appear to be the dominant factors in differences between campaign data, not the inter-device variability. These differences rendered the standard template attack useless for all common compression methods except Fisher’s Linear Discriminant Analysis (LDA). To improve the performance of the attack across different devices, we explored several variants of the template attack, that compensate for a DC offset in the attack phase, or profile across multiple devices. By combining these options, we can improve the results of template attacks. However, these methods did not provide a great advantage when using Principal Component Analysis (PCA) or LDA.

Based on detailed analysis of LDA, we offered an explanation why this compression method works well across different devices: LDA is able to compensate temperature variation captured by the pooled covariance matrix and this temperature variation is similar across campaigns. From this analysis, we were able to provide guidance for an efficient use of both LDA and PCA across different devices or campaigns: for LDA we should ignore the eigenvectors starting with the one having the strongest DC contribution, while for PCA we should choose enough components to include at least the one with the strongest DC contribution. Based on these observations we also proposed a method to enhance the PCA algorithm such that the eigenvector with the strongest DC contribution corresponds to the largest eigenvalue and this allows PCA to provide good results across different devices even when using a small number of eigenvectors.

Our results show that the choice of compression method and parameters (e.g. choice of eigenvectors for PCA and LDA) has a strong impact on the success of template attacks across different devices, a fact that was not evidenced in previous studies. As a guideline, when using sample selection we should use a large number of samples, profile on multiple devices and adapt for a DC offset, but with LDA and PCA we may use the standard template attack and perform the profiling on a single device, if we select the eigenvectors according to their DC component. Overall, LDA seems the best compression method when using template attacks across different devices, but it requires to invert a possibly large covariance matrix, which might not be possible with a small number of profiling traces. In such cases, PCA might be a better alternative.

We conclude that with a careful choice of compression method we can obtain template attacks that are efficient also across different devices, reducing the guessing entropy of an unknown 8-bit value below 1.5 bits.

Data and Code Availability: In the interest of reproducible research we make available our data and related MATLAB scripts at:

http://www.cl.cam.ac.uk/research/security/datasets/grizzly/