Efficient Template Attacks

Abstract

Template attacks remain a powerful side-channel technique to eavesdrop on tamper-resistant hardware. They model the probability distribution of leaking signals and noise to guide a search for secret data values. In practice, several numerical obstacles can arise when implementing such attacks with multivariate normal distributions. We propose efficient methods to avoid these. We also demonstrate how to achieve significant performance improvements, both in terms of information extracted and computational cost, by pooling covariance estimates across all data values. We provide a detailed and systematic overview of many different options for implementing such attacks. Our experimental evaluation of all these methods based on measuring the supply current of a byte-load instruction executed in an unprotected 8-bit microcontroller leads to practical guidance for choosing an attack algorithm.

1 Introduction

Side-channel attacks are powerful tools for inferring secret algorithms or data (passwords, cryptographic keys, etc.) processed inside tamper-resistant hardware, if an attacker can monitor some channel leaking such information out of the device, most notably the power-supply current and unintended electromagnetic emissions.

One of the most powerful techniques for evaluating side-channel information is the template attack [4], which relies on a multivariate model of the side-channel traces. While the basic algorithm is comparatively simple (Sect. 2), there are a number of additional steps that must be performed in order to obtain a practical and efficient implementation.

In this paper we examine several problems that can arise in the implementation of template attacks (Sect. 3), especially when using a large number of voltage samples. We explain how to solve them in two steps: (a) using compression techniques, i.e. methods to reduce the number of samples involved, either by throwing away most, or by projecting them into a lower-dimensional space, using only a few linear combinations (Sect. 4); and (b) we contribute efficient variants of the template-attack algorithm, which can avoid numerical limitations of the standard approach, provide better results and execute faster (Sect. 5).

We evaluate all these methods in practice, against an unprotected 8-bit microcontroller, comparing their effectiveness using the guessing entropy (Sect. 6). We focus on gathering information about individual data values, independent of what algorithm these are part of. Other algorithm-specific attacks that use dependencies between different data values, e.g. to recover keys from a specific cipher, could be implemented on top of that, but are outside the scope of this paper. We show that PCA and LDA provide the best results overall, and that a previous guideline of selecting at most one point per clock cycle is not optimal in general. Based on these experiments and theoretical background, we provide practical guidance for the choice of template-attack algorithm.

2 Template Attacks

To implement a template attack, we need physical access to a pair of identical devices, which we refer to as the profiling and the attacked device. We wish to infer some secret value $k{\star }\in {\mathcal {S}}$, processed by the attacked device at some point. For an 8-bit microcontroller, ${\mathcal {S}}=\{0,\ldots ,255\}$ might be the set of possible byte values manipulated by a particular machine instruction.

We assume that we determined the approximate moments of time when the secret value $k{\star }$ is manipulated and we are able to record signal traces (e.g., supply current or electro-magnetic waveforms) around these moments. We refer to these traces as leakage vectors. Let $\{t_1,\ldots ,t_{{m}^{\mathrm {\text {r}}}}\}$ be the set of time samples and ${\mathbf {x}}^\text {r}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ be the random vector from which leakage traces are drawn.

During the profiling phase we record $n_{\mathrm {p}}$ leakage vectors ${{\mathbf {x}}}^{\text {r}}_{{k}{i}}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ from the profiling device for each possible value $k\in {\mathcal {S}}$, and combine these as row vectors ${{{\mathbf {x}}}^{\text {r}}_{{k}{i}}}'$ in the leakage matrix ${\mathbf {X}}^{\text {r}}_{k}\in \mathbb {R}^{n_{\mathrm {p}}\times {m}^{\mathrm {\text {r}}}}$.¹

Typically, the raw leakage vectors ${{\mathbf {x}}}^{\text {r}}_{{k}{i}}$ provided by the data acquisition device contain a large number ${m}^{\mathrm {\text {r}}}$ of samples (random variables), due to high sampling rates used. Therefore, we might compress them before further processing, either by selecting only a subset of ${m}^{\mathrm {}}\ll {m}^{\mathrm {\text {r}}}$ of those samples, or by applying some other data-dimensionality reduction method (see Sect. 4). We refer to such compressed leakage vectors as ${{\mathbf {x}}}_{{k}{i}}\in \mathbb {R}^{{m}^{\mathrm {}}}$ and combine all of these as rows into the compressed leakage matrix ${\mathbf {X}}_{k}\in \mathbb {R}^{n_{\mathrm {p}}\times {m}^{\mathrm {}}}$. (Without any such compression step, we would have ${\mathbf {X}}_{k}={\mathbf {X}}^{\text {r}}_{k}$ and ${m}^{\mathrm {}}={m}^{\mathrm {\text {r}}}$.)

Using ${\mathbf {X}}_{k}$ we can compute the template parameters $\bar{{\mathbf {x}}}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}}$ and $\mathbf {S}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$ for each possible value $k\in {\mathcal {S}}$ as

$$\begin{aligned} {\begin{array}{l@{}r} \bar{{\mathbf {x}}}_{k}= \frac{1}{n_{\mathrm {p}}} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} {{\mathbf {x}}}_{{k}{i}},&\mathbf {S}_{k}= \frac{1}{n_{\mathrm {p}}-1} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k}){({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k})}', \end{array}} \end{aligned}$$

(1)

where the sample mean $\bar{{\mathbf {x}}}_{k}$ and the sample unbiased ² covariance matrix $\mathbf {S}_{k}$ are the estimates of the true mean $\mathbf {\mu }_{k}$ and true covariance $\mathbf {\Sigma }_{k}$. Note that a sum of squares and cross products matrix such as $\displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k}){({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k})}',$ from (1) can also be written as

$$\begin{aligned} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k}){({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k})}' = {\widetilde{{\mathbf {X}}}_{k}}' \widetilde{{\mathbf {X}}}_{k}, \end{aligned}$$

(2)

where $\widetilde{{\mathbf {X}}}_{k}$ is ${\mathbf {X}}_{k}$ with ${\bar{{\mathbf {x}}}_{k}}'$ subtracted from each row.³

Side-channel leakage traces can generally be modeled well by a multivariate normal distribution [4], which we also observed in our experiments. In this case, the sample mean $\bar{{\mathbf {x}}}_{k}$ and sample covariance $\mathbf {S}_{k}$ are sufficient statistics: they completely define the underlying distribution [10, Chap. 4]. Then the probability density function (pdf) of a leakage vector ${\mathbf {x}}$, given $\bar{{\mathbf {x}}}_{k}$ and $\mathbf {S}_{k}$, is

$$\begin{aligned} \mathrm {f}({\mathbf {x}}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k}) = \frac{1}{\sqrt{(2\pi )^{{m}^{\mathrm {}}} |\mathbf {S}_{k}|}} \exp {\left( -\frac{1}{2} {({\mathbf {x}}-\bar{{\mathbf {x}}}_{k})}' \mathbf {S}_{k}^{-1} ({\mathbf {x}}-\bar{{\mathbf {x}}}_{k}) \right) }. \end{aligned}$$

(3)

In the attack phase, we try to infer the secret value $k{\star }\in {\mathcal {S}}$ processed by the attacked device. We obtain $n_{{\mathrm {a}}}$ leakage vectors ${{\mathbf {x}}}_{i}\in \mathbb {R}^{{m}^{\mathrm {}}}$ from the attacked device, using the same recording technique and compression method as in the profiling phase, resulting in the leakage matrix ${\mathbf {X}}_{k{\star }}\in \mathbb {R}^{n_{{\mathrm {a}}}\times {m}^{\mathrm {}}}$. Then, for each $k\in {\mathcal {S}}$, we compute a discriminant score $\mathrm {d}(k\mid {\mathbf {X}}_{k{\star }})$. Finally, we try all $k\in {\mathcal {S}}$ on the attacked device, in order of decreasing score (optimized brute-force search, e.g. for a password or cryptographic key), until we find the correct $k{\star }$. Given a trace ${{\mathbf {x}}}_{i}$ from ${\mathbf {X}}_{k{\star }}$, a commonly used discriminant [8, 11, 14], derived from Bayes’ rule, is

$$\begin{aligned} \mathrm {d}(k\mid {{\mathbf {x}}}_{i}) = \mathrm {f}({{\mathbf {x}}}_{i}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k}) P(k), \end{aligned}$$

(4)

where the denominator from Bayes’ rule is omitted, as it is the same for each $k$. Assuming a uniform a-priori probability $P(k) = |{\mathcal {S}}|^{-1}$, applying Bayes’ rule becomes equivalent to computing the likelihood

$$\begin{aligned} \mathrm {l}(k\mid {{\mathbf {x}}}_{i}) = \mathrm {d}(k\mid {{\mathbf {x}}}_{i}) = \mathrm {l}(\bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k}\mid {{\mathbf {x}}}_{i}) = \mathrm {f}({{\mathbf {x}}}_{i}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k}), \end{aligned}$$

(5)

where the latter can be computed from (3). However, we do not need to compute a proper a-posteriori probability for each candidate $k$ given a trace ${{\mathbf {x}}}_{i}$, but only a discriminant function that allows us to sort scores and identify the most likely candidates. Section 5 shows how the latter can be much more efficient.

3 Implementation Caveats

We now present several problems that can appear when implementing the template attack, especially when using a large number of samples ${m}^{\mathrm {}}$.

3.1 Inverse of Covariance Matrix

Several authors [14, 15] noted that inverting the covariance matrix $\mathbf {S}_{k}$ from (1), as needed in (3), can cause numerical problems for large ${m}^{\mathrm {}}$. However, we consider it important to explain why $\mathbf {S}_{k}$ can become singular ($|\mathbf {S}_{k}|\approx 0$), causing these problems.

Since $\mathbf {S}_{k}$ is essentially the matrix product ${\widetilde{{\mathbf {X}}}_{k}}' \widetilde{{\mathbf {X}}}_{k}$ (2), both $\mathbf {S}_{k}$ and $\widetilde{{\mathbf {X}}}_{k}$ have the same rank. Therefore $\mathbf {S}_{k}$ is singular iff $\widetilde{{\mathbf {X}}}_{k}$ has dependent columns, which is guaranteed if $n_{\mathrm {p}}< {m}^{\mathrm {}}$. The constraint on $\widetilde{{\mathbf {X}}}_{k}$ to have zero-mean rows implies that it has dependent columns even for $n_{\mathrm {p}}= {m}^{\mathrm {}}$. Therefore, $n_{\mathrm {p}}> {m}^{\mathrm {}}$ is a necessary condition for $\mathbf {S}_{k}$ to be non-singular. See [10, Result 3.3] for a more detailed proof.

The restriction ${m}^{\mathrm {}}< n_{\mathrm {p}}$ is one main reason for reducing ${m}^{\mathrm {}}$ through compression (see Sect. 4). However, it is not mandatory to compress ${m}^{\mathrm {}}$ further than what is needed to keep the columns of $\widetilde{{\mathbf {X}}}_{k}$ independent. Note that in practice some samples can be highly correlated, in which case $n_{\mathrm {p}}$ needs to be somewhat larger than ${m}^{\mathrm {}}$ (e.g., $n_{\mathrm {p}}\ge 3000$ for ${m}^{\mathrm {}}=1250$ with our Sect. 6 data).

If we cannot obtain $n_{\mathrm {p}}> {m}^{\mathrm {}}$ then we can try the covariance estimator of Ledoit and Wolf [5], which gave us a non-singular $\mathbf {S}_{k}$ even for $n_{\mathrm {p}}< {m}^{\mathrm {}}$. However, a much better option is to use the pooled covariance matrix (see Sect. 5.2) when possible.

3.2 Floating-Point Limitations

One practical problem with (3) is that for large ${m}^{\mathrm {}}$ the statistical distance

$$ {({\mathbf {x}}-\bar{{\mathbf {x}}}_{k})}' \mathbf {S}_{k}^{-1} ({\mathbf {x}}-\bar{{\mathbf {x}}}_{k}) $$

can reach values that cause the subsequent exponentiation operation to overflow. For example, in IEEE double precision, $\exp (x)$ is only safe with $|x| < 710$, easily exceeded for large ${m}^{\mathrm {}}$.

Another problem is that for large ${m}^{\mathrm {}}$ the determinant $|\mathbf {S}_{k}|$ can overflow. For example, considering that $|\mathbf {S}_{k}|$ is the product of the eigenvalues of $\mathbf {S}_{k}$, in some of our experiments the 100 largest eigenvalues were at least $10^{6}$ and multiplying merely 52 such values again overflows the IEEE double precision format.

Fig. 1.

Signal-strength estimates from DOM, SOSD and SNR (identical to SOST) for a LOAD instruction processing all possible 8-bit values, along with the average standard deviation (STD) of the traces and clock signal. We used 2000 traces per value. All estimates are rescaled to fit into the plot, so the vertical axis (linear) has no scale.

4 Compression Methods

A compression method can be used to reduce the length (dimensionality) of leakage vectors from ${m}^{\mathrm {\text {r}}}$ to ${m}^{\mathrm {}}$. As detailed in Sect. 3, this may be needed if we do not have enough traces for a full rank covariance matrix or to cope with computational or memory restrictions. Several approaches are described in the literature, which can be divided into two categories: (a) selecting some of the samples based on some criteria; (b) using some linear combinations of the leakage vectors, based on the principal components or Fisher’s linear discriminant. All of the following techniques evaluate the differences $\bar{{\mathbf {x}}}_{k}-\bar{{\mathbf {x}}}_{}$ where

$$\begin{aligned} \bar{{\mathbf {x}}}_{} = \frac{1}{|{\mathcal {S}}|} \displaystyle \sum _{k\in {\mathcal {S}}} \bar{{\mathbf {x}}}_{k}. \end{aligned}$$

(6)

4.1 Selection of Samples

In this method we first compute a signal-strength estimate ${\mathbf {s}}(t), t\in \{t_1,\cdots ,t_{{m}^{\mathrm {\text {r}}}}\}$, and then we select a subset of ${m}^{\mathrm {}}$ points based on this estimate.

There are several proposals for producing ${\mathbf {s}}(t)$, such as difference of means (DOM) [4, Sect. 2.1], the sum of squared differences (SOSD) [9], the Signal to Noise Ratio (SNR) [15] and SOST [9]. All these are similar, with the notable difference that the first two do no take the variance of the traces into consideration, while the latter two do. We show the difference between these estimates for our experiments in Fig. 1. The methods SNR and SOST are in fact the same if we consider the variance at each sample point to be independent of the candidate $k$, which is expected in our setting. Under this condition SNR and SOST reduce to computing the following value used by the F-test in the Analysis of Variance [10]:

$$\begin{aligned} {\mathrm {F}}(t) = \frac{ \left( n_{\mathrm {p}}\displaystyle \sum _{k\in {\mathcal {S}}} (\bar{{\mathbf {x}}}_{k}(t)-\bar{{\mathbf {x}}}_{}(t))^2 \right) \big / (|{\mathcal {S}}| - 1)}{\left( \displaystyle \sum _{k\in {\mathcal {S}}} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({{\mathbf {x}}}_{{k}{i}}(t)-\bar{{\mathbf {x}}}_{k}(t))^2 \right) \big / (|{\mathcal {S}}|(n_{\mathrm {p}}-1))}. \end{aligned}$$

(7)

${\mathrm {F}}(t)$ can be used to reject, at any desired significance level, the hypothesis that the sample mean values at sample point $t$ are equal, therefore providing a good indication of which samples contain more information about the means.

In the second step of this compression method we need to choose ${m}^{\mathrm {}}$ samples based on the signal-strength estimate ${\mathbf {s}}$. The goal is to select the smallest set of samples that contains most of the information about our target. An accepted guideline, by Rechberger and Oswald [7, Sect. 3.2], is to select at most one sample per clock cycle among the samples with highest ${\mathbf {s}}$. In Sect. 6 we evaluate several other options, and we show that this guideline is not optimal in general.

4.2 Principal Component Analysis (PCA)

Archambeau et al. [8] proposed the following method for using PCA as a compression method for template attacks. First compute the sample between groups matrix ${\mathbf {B}}$:

$$\begin{aligned} {\mathbf {B}}= n_{\mathrm {p}}\displaystyle \sum _{k\in {\mathcal {S}}} (\bar{{\mathbf {x}}}_{k}^{\text {r}}-\bar{{\mathbf {x}}}_{}^{\text {r}}) {(\bar{{\mathbf {x}}}_{k}^{\text {r}}-\bar{{\mathbf {x}}}_{}^{\text {r}})}'. \end{aligned}$$

(8)

Next obtain the singular value decomposition (SVD) ${\mathbf {B}}= {\mathbf {U}}\mathbf {D} {{\mathbf {U}}}'$, where each column of ${\mathbf {U}}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}\times {m}^{\mathrm {\text {r}}}}$ is an eigenvector ${\mathbf {u}}_{j}$ of ${\mathbf {B}}$, and $\mathbf {D}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}\times {m}^{\mathrm {\text {r}}}}$ contains the corresponding eigenvalues $\delta _{j}$ on its diagonal.⁴ The crucial point is that only the first ${m}^{\mathrm {}}$ eigenvectors ${[{\mathbf {u}}_1 \ldots {\mathbf {u}}_{m}^{\mathrm {}}]} = {{\mathbf {U}}}^m$ are needed in order to preserve most of the information from the mean vectors $\bar{{\mathbf {x}}}_{k}^{\text {r}}$. Therefore we can restrict ${\mathbf {U}}$ to ${{\mathbf {U}}}^m\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}\times {m}^{\mathrm {}}}$. Finally, we can project the mean vectors $\bar{{\mathbf {x}}}_{k}^{\text {r}}$ and covariance matrices $\mathbf {S}^{\text {r}}_{k}$ (computed with (1) on the raw traces ${{\mathbf {x}}}^{\text {r}}_{i}$) into the new coordinate system defined by ${{\mathbf {U}}}^m$ to obtain the PCA template parameters $\bar{{\mathbf {x}}}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}}$ and $\mathbf {S}_{k}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$:

$$\begin{aligned} {\begin{array}{l@{}r} \bar{{\mathbf {x}}}_{k}= {{{\mathbf {U}}}^m}' \bar{{\mathbf {x}}}_{k}^{\text {r}},&\mathbf {S}_{k}= {{{\mathbf {U}}}^m}' \mathbf {S}^{\text {r}}_{k}{{\mathbf {U}}}^m. \end{array}} \end{aligned}$$

(9)

Choice of PCA Components. Archambeau et al. [8] propose to select only those first ${m}^{\mathrm {}}$ eigenvectors ${\mathbf {u}}_{j}$ for which the corresponding eigenvalues $\delta _j$ are a few orders of magnitude larger than the rest. This technique, also known as elbow rule or Scree Graph [6], requires manual inspection of the eigenvalues. Another technique, which does not require manual inspection of the eigenvalues, is known as the Cumulative Percentage of Total Variation [6]. It selects those ${m}^{\mathrm {}}$ eigenvectors that retain at least fraction $f$ of the total variance, by computing the score

$$\begin{aligned} \phi ({m}^{\mathrm {}}) = \frac{\sum _{1\le j\le {m}^{\mathrm {}}} \delta _j}{\sum _{1\le j\le {m}^{\mathrm {\text {r}}}} \delta _j}, \quad 1\le {m}^{\mathrm {}}\le {m}^{\mathrm {\text {r}}}, \end{aligned}$$

(10)

and selecting the lowest ${m}^{\mathrm {}}$ for which $\phi ({m}^{\mathrm {}}) > f$.⁵ We recommend trying both approaches, as “there is no definitive answer [to the question of how many components to choose]” [10, Chap. 8].

Alternative Computation of PCA Templates. Even though in [11, Sect. 4.1] the authors mention that PCA can help where computing the full covariance matrix $\mathbf {S}^{\text {r}}_{k}$ is prohibitive (due to large ${m}^{\mathrm {\text {r}}}$), their approach still requires the computation of $\mathbf {S}^{\text {r}}_{k}$ (see (9)). Also, numerical artifacts during the double matrix multiplication in (9) can make $\mathbf {S}_{k}$ non-symmetric. One way to avoid the latter is to use the Cholesky decomposition $\mathbf {S}^{\text {r}}_{k}= {{\mathbf {C}}}' {\mathbf {C}}$ and compute

$$\begin{aligned} \mathbf {S}_{k}= {{{\mathbf {U}}}^m}' \mathbf {S}^{\text {r}}_{k}{{\mathbf {U}}}^m= {{{\mathbf {U}}}^m}' {{\mathbf {C}}}' {\mathbf {C}}{{\mathbf {U}}}^m= {({\mathbf {C}}{{\mathbf {U}}}^m)}' ({\mathbf {C}}{{\mathbf {U}}}^m) = {\mathbf {V}}' \mathbf {V}. \end{aligned}$$

(11)

However, to avoid both the numerical artifacts and the computation of large covariance matrices, we propose an alternative PCA method, based on the following result: given the leakage matrix ${\mathbf {X}}^{\text {r}}_{k}$ and the PCA projection matrix ${{\mathbf {U}}}^m$, it can be shown [10, Eq. (2-45)] that

$$\begin{aligned} \mathbf {S}_{k}= \mathrm {Cov}({\mathbf {X}}^{\text {r}}_{k}{{\mathbf {U}}}^m) = {{{\mathbf {U}}}^m}' \mathrm {Cov}({\mathbf {X}}^{\text {r}}_{k}) {{\mathbf {U}}}^m= {{{\mathbf {U}}}^m}' \mathbf {S}^{\text {r}}_{k}{{\mathbf {U}}}^m. \end{aligned}$$

(12)

Therefore, instead of first computing $\mathbf {S}^{\text {r}}_{k}$ and then applying (9) or (11), we can first compute the projected leakage matrix

$$\begin{aligned} {\mathbf {X}}_{k}= {\mathbf {X}}^{\text {r}}_{k}{{\mathbf {U}}}^m\end{aligned}$$

(13)

and then compute the PCA-based template parameters using (1). We use this method for all the results shown in Sect. 6.

4.3 Fisher’s Linear Discriminant Analysis (LDA)

Given the leakage traces ${{\mathbf {x}}}^{\text {r}}_{{k}{i}}$ (rows of ${\mathbf {X}}^{\text {r}}_{k}$), Fisher’s idea [2, 10] was to find some coefficients ${\mathbf {a}}_{j} \in \mathbb {R}^{{m}^{\mathrm {\text {r}}}}$ that maximise the following ratio:

$$\begin{aligned} \frac{ \displaystyle \sum _{k\in {\mathcal {S}}} (\bar{y}_{kj} - \bar{y}_{j})^2}{\mathrm {Var}(y_j)} = \frac{ \displaystyle \sum _{k\in {\mathcal {S}}} ({{\mathbf {a}}_{j}}' (\bar{{\mathbf {x}}}_{k}^{\text {r}}-\bar{{\mathbf {x}}}_{}^{\text {r}}))^2}{\mathrm {Var}({{\mathbf {a}}_{j}}' {\mathbf {x}})} = \frac{ {{\mathbf {a}}_{j}}' {\mathbf {B}}{\mathbf {a}}_{j}}{{{\mathbf {a}}_{j}}' \mathbf {S}_{\mathrm {pooled}}{\mathbf {a}}_{j}}, \end{aligned}$$

(14)

where the linear combinations ${y}_{j} = {{\mathbf {a}}_{j}}' {\mathbf {x}}$ are known as sample discriminants, ${\mathbf {B}}$ is the treatment matrix from (8) and $\mathbf {S}_{\mathrm {pooled}}= \frac{1}{|{\mathcal {S}}|} \sum _{k\in {\mathcal {S}}} \mathbf {S}_{k}^{\text {r}}$ is the common covariance of all groups (see also Sect. 5.2). Note the similarity between the left hand side of (14) and (7) which is used by the F-test, SNR and SOST. This allows us to make an interesting observation: while in the sample selection method we first compute (7) for each sample and then select the samples with the highest ${\mathrm {F}}(t)$, Fisher’s method finds the linear combinations of the trace samples that maximise (14). The coefficients ${\mathbf {a}}_{j}$ that maximise (14) are the eigenvectors $[{\mathbf {u}}_1 \ldots {\mathbf {u}}_{{m}^{\mathrm {\text {r}}}}] = {\mathbf {U}}$ corresponding to the largest eigenvalues of $\mathbf {S}_{\mathrm {pooled}}^{-1}{\mathbf {B}}$.⁶

As with PCA, we only need to use the first ${m}^{\mathrm {}}$ coefficients ${\mathbf {a}}_1, \ldots , {\mathbf {a}}_{{m}^{\mathrm {}}}$, which can be selected using the same rules discussed in Sect. 4.2. If we let ${\mathbf {A}}= [{\mathbf {a}}_1 \ldots {\mathbf {a}}_{{m}^{\mathrm {}}}] = {{\mathbf {U}}}^m$ be the matrix of coefficients, we can project each leakage matrix as:

$$\begin{aligned} {\mathbf {X}}_{k}= {\mathbf {X}}^{\text {r}}_{k}{\mathbf {A}}= {\mathbf {X}}^{\text {r}}_{k}{{\mathbf {U}}}^m\end{aligned}$$

(15)

and compute the LDA-based template parameters using (1).

Several authors [11, 14] have used Fisher’s LDA for template attacks, but without mentioning two important aspects. Firstly, the condition of equal covariances (known as homoscedasticity) may be important for the success of Fisher’s LDA. Therefore, the PCA method (Sect. 4.2), which does not depend on this condition, might be a better choice in some settings. Secondly, the coefficients that maximise (14) can be obtained using scaled versions of $\mathbf {S}_{\mathrm {pooled}}$ ⁷ or different approaches [11, 14], which will result in a different scale of the coefficients ${\mathbf {a}}_{j}$. This difference has a major impact on the template attack: only when we scale the coefficients ${\mathbf {a}}_{j}$, such that ${{\mathbf {a}}_{j}}' \mathbf {S}_{\mathrm {pooled}}{\mathbf {a}}_{j} = 1$, the covariance between discriminants becomes the identity matrix [10], i.e. $\mathbf {S}_{k}=\mathbf {I}$. That means the sample means in (1) suffice and we can discard the covariance matrix from the discriminant scores in Sect. 5, which greatly reduces computation and storage requirements.

Continuing the steps that led to (15), we can compute the diagonal matrix $\mathbf {Q}\in \mathbb {R}^{{m}^{\mathrm {}}\times {m}^{\mathrm {}}}$, having the values $q_{jj} = (\frac{1}{{{\mathbf {a}}_{j}}' \mathbf {S}_{\mathrm {pooled}}{\mathbf {a}}_{j}})^{\frac{1}{2}} = (\frac{1}{{{\mathbf {u}}_{j}}' \mathbf {S}_{\mathrm {pooled}}{\mathbf {u}}_{j}})^{\frac{1}{2}}$ on its diagonal, to obtain the scaled coefficients ${\mathbf {A}}\mathbf {Q} = {{\mathbf {U}}}^m\mathbf {Q}$, and replace (15) by

$$\begin{aligned} {\mathbf {X}}_{k}= {\mathbf {X}}^{\text {r}}_{k}{\mathbf {A}}\mathbf {Q} = {\mathbf {X}}^{\text {r}}_{k}{{\mathbf {U}}}^m\mathbf {Q}. \end{aligned}$$

(16)

An alternative approach is to compute the eigenvectors ${\mathbf {u}}_{j}$ of $\mathbf {S}_{\mathrm {pooled}}^{-\frac{1}{2}} {\mathbf {B}}\mathbf {S}_{\mathrm {pooled}}^{-\frac{1}{2}}$ and then obtain the coefficients ${\mathbf {a}}_{j} = \mathbf {S}_{\mathrm {pooled}}^{-\frac{1}{2}} {\mathbf {u}}_{j}$, which leads directly to coefficients that satisfy ${{\mathbf {a}}_{j}}' \mathbf {S}_{\mathrm {pooled}}{\mathbf {a}}_{j} = 1$.

5 Efficient Implementation of Template Attacks

In this section we introduce methods that avoid the problems identified in Sect. 3 and implement template attacks very efficiently.

5.1 Using the Logarithm of the Multivariate Normal Distribution

Mangard et al. [15, p. 108] suggested calculating the logarithm of (3), as in

$$\begin{aligned} \log {\mathrm {f}({\mathbf {x}}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k})} = -\frac{1}{2} \left( \log {[(2\pi )^{{m}^{\mathrm {}}} |\mathbf {S}_{k}|]} + {({\mathbf {x}}-\bar{{\mathbf {x}}}_{k})}'\mathbf {S}_{k}^{-1}({\mathbf {x}}-\bar{{\mathbf {x}}}_{k}) \right) . \end{aligned}$$

(17)

They then claim that “the template that leads to the smallest absolute value [of ( 17 )] indicates the correct [candidate]”.

The first problem with this approach is that (17) does not avoid the computation of $|\mathbf {S}_{k}|$, which we have shown to be problematic. Therefore we propose to compute the logarithm of the multivariate normal pdf as

$$\begin{aligned} \log {\mathrm {f}({\mathbf {x}}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k})} = -\frac{{m}^{\mathrm {}}}{2} \log {2\pi } - \frac{1}{2} \log {|\mathbf {S}_{k}|} -\frac{1}{2} {({\mathbf {x}}-\bar{{\mathbf {x}}}_{k})}'\mathbf {S}_{k}^{-1}({\mathbf {x}}-\bar{{\mathbf {x}}}_{k}), \end{aligned}$$

(18)

where we compute the logarithm of the determinant as

$$\begin{aligned} \log {|\mathbf {S}_{k}|} = 2 \sum _{c_{ii}\in \mathrm {diag}({\mathbf {C}})} \log {c_{ii}}, \end{aligned}$$

(19)

using the Cholesky decomposition $\mathbf {S}_{k}= {{\mathbf {C}}}' {\mathbf {C}}$ of the symmetric matrix $\mathbf {S}_{k}$. (Since ${\mathbf {C}}$ is triangular, its determinant is the product of its diagonal elements.)

Secondly, it is incorrect to choose the candidate $k$ that leads to the “smallest absolute value” of (17, 18), since the logarithm is a monotonic function and preserves the property that the largest value corresponds to the correct $k$.⁸

We can use (18, 19), dropping the first term which is constant across all $k$, to compute a discriminant score based on the log-likelihood:

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LOG}}(k\mid {{\mathbf {x}}}_{i})&= -\frac{1}{2} \log {|\mathbf {S}_{k}|} -\frac{1}{2} {({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k})}' \mathbf {S}_{k}^{-1}({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k}) \\&= \log \mathrm {f}({{\mathbf {x}}}_{i}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{k}) + \frac{{m}^{\mathrm {}}}{2} \log {2\pi } = \log \mathrm {l}(k\mid {{\mathbf {x}}}_{i}) + \text {const}. \nonumber \end{aligned}$$

(20)

5.2 Using a Pooled Covariance Matrix

When the leakages from different candidates $k$ have different means but the same covariance $\mathbf {\Sigma }_{}=\mathbf {\Sigma }_{1}=\mathbf {\Sigma }_{2}=\cdots =\mathbf {\Sigma }_{k}$, it is possible to pool the covariance estimates $\mathbf {S}_{k}$ into a $pooled$ covariance matrix [10, Sect. 6.3]

$$\begin{aligned} \mathbf {S}_{\mathrm {pooled}}= \frac{1}{|{\mathcal {S}}|(n_{\mathrm {p}}-1)} \displaystyle \sum _{k\in {\mathcal {S}}} \displaystyle \sum _{i=1}^{n_{\mathrm {p}}} ({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k}){({{\mathbf {x}}}_{{k}{i}}-\bar{{\mathbf {x}}}_{k})}', \end{aligned}$$

(21)

an average of the covariances $\mathbf {S}_{k}$ from (1). The great advantage of $\mathbf {S}_{\mathrm {pooled}}$ over $\mathbf {S}_{k}$ is that it represents a much better estimator of the real covariance $\mathbf {\Sigma }_{}$, since $\mathbf {S}_{\mathrm {pooled}}$ estimates the covariance using $n_{\mathrm {p}}|{\mathcal {S}}|$ traces, while $\mathbf {S}_{k}$ uses only $n_{\mathrm {p}}$. This in turn means that the condition for a non-singular matrix (see Sect. 3.1) relaxes to $n_{\mathrm {p}}|{\mathcal {S}}| > {m}^{\mathrm {}}$ or $n_{\mathrm {p}}> \frac{{m}^{\mathrm {}}}{|{\mathcal {S}}|}$. Therefore the number of traces that we must obtain for each candidate $k$ is reduced by a factor of $|{\mathcal {S}}|$, a great advantage in practice. Nevertheless, the quality of the mean estimate $\bar{{\mathbf {x}}}_{k}$ still depends directly on $n_{\mathrm {p}}$. Also note that for Fisher’s LDA (Sect. 4.3) we need to compute the inverse of $\mathbf {S}_{\mathrm {pooled}}\in \mathbb {R}^{{m}^{\mathrm {\text {r}}}\times {m}^{\mathrm {\text {r}}}}$, which requires $n_{\mathrm {p}}|{\mathcal {S}}| > {m}^{\mathrm {\text {r}}}$.

Several authors used $\mathbf {S}_{\mathrm {pooled}}$ with template attacks [12, 16], but gave no motivation for its use. We would expect the assumption of equal covariances to hold for many side-channel applications, because $\mathbf {S}_{k}$ captures primarily information about how noise, that is variation in the recorded traces unrelated to $k$, is correlated across trace samples. After all, the data-dependent signal $\bar{{\mathbf {x}}}_{k}$ was already subtracted. As a result, we should not expect substantial differences between the $\mathbf {S}_{k}$ for different candidate values $k$, unless the targeted device contains a mechanism by which $k$ can modify the correlation between samples (which we do not completely exclude).

Box’s test [3] can be used to reject the hypothesis of equal covariances, although it can be misleading for large $|{\mathcal {S}}|$ or large ${m}^{\mathrm {}}$. In our experiments, with $|{\mathcal {S}}|=2^8$, ${m}^{\mathrm {}}=6$ and $n_{\mathrm {p}}=2000$, Box’s variable $C \sim F_{f1,f2}(\alpha )$ had the value $2.03$, which was above the rejection threshold for any realistic significance level (e.g. $F_{f1,f2}(0.99)=1.045$). Nevertheless, we found the different $\mathbf {S}_{k}$ to be visually similar (viewed as bitmaps with linear colour mapping), and we consider that our hypothesis was confirmed by the superior results from using the pooled estimate (Sect. 6).

Using $\mathbf {S}_{\mathrm {pooled}}$, we can discard the first two terms in (18) and use the generalized statistical distance

$$\begin{aligned} d_{\text{ M }}^2({\mathbf {x}}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{\mathrm {pooled}}) = {({\mathbf {x}}-\bar{{\mathbf {x}}}_{k})}'\mathbf {S}_{\mathrm {pooled}}^{-1}({\mathbf {x}}-\bar{{\mathbf {x}}}_{k}) \ge 0, \end{aligned}$$

(22)

also known as the Mahalanobis distance [1], to compare the candidates $k$. The inequality in (22) holds because the covariance matrix is positive semidefinite. From (18, 22) we can derive the discriminant score

$$\begin{aligned} {\mathrm {d}}_{\mathrm {MD}}(k\mid {{\mathbf {x}}}_{i}) = -\frac{1}{2}d_{\text{ M }}^2({{\mathbf {x}}}_{i}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{\mathrm {pooled}}) = {\mathrm {d}}_{\mathrm {LOG}}(k\mid {{\mathbf {x}}}_{i}) + \text {const.}, \end{aligned}$$

(23)

where the constant does not vary with $k$.

5.3 Linear Discriminant Score

When using the pooled covariance matrix $\mathbf {S}_{\mathrm {pooled}}$ we can rewrite the distance from (22) as:

$$\begin{aligned} d_{\text{ M }}^2({\mathbf {x}}\mid \bar{{\mathbf {x}}}_{k}, \mathbf {S}_{\mathrm {pooled}}) = {{\mathbf {x}}}'\mathbf {S}_{\mathrm {pooled}}^{-1}{\mathbf {x}}- 2 {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}{\mathbf {x}}+ {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}, \end{aligned}$$

(24)

and observe that the first term is constant for all groups $k$ so we can discard it. That means, that we can now use the following linear discriminant score:

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LINEAR}}(k\mid {{\mathbf {x}}}_{i}) = {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}{{\mathbf {x}}}_{i}- \frac{1}{2}{\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}= {\mathrm {d}}_{\mathrm {MD}}(k\mid {{\mathbf {x}}}_{i}) + \text{ const. }, \end{aligned}$$

(25)

which depends linearly on ${{\mathbf {x}}}_{i}$ (where const. does not depend on $k$). Although equivalent, the linear discriminant ${\mathrm {d}}_{\mathrm {LINEAR}}$ can be far more efficient to compute than the quadratic ${\mathrm {d}}_{\mathrm {MD}}$.

5.4 Combining Multiple Attack Traces

We have to combine the $n_{{\mathrm {a}}}$ individual leakage traces ${{\mathbf {x}}}_{i}$ from ${\mathbf {X}}_{k{\star }}$ into the final discriminant score $\mathrm {d}(k\mid {\mathbf {X}}_{k{\star }})$. We present two sound options for doing so:

Option 1: Average all the traces in ${\mathbf {X}}_{k{\star }}$ (similar to the mean computation in (1)) in order to remove as much noise as possible and then use this single mean trace $\bar{{\mathbf {x}}}_{k{\star }}$ to compute

$$\begin{aligned} \mathrm {d}^{\mathrm {avg}}(k\mid {\mathbf {X}}_{k{\star }}) = \mathrm {d}(k\mid \bar{{\mathbf {x}}}_{k{\star }}). \end{aligned}$$

(26)

This option is computationally fast, requiring $O(n_{{\mathrm {a}}}+ {{m}^{\mathrm {}}}^2)$ time for any presented discriminant, but it does not use all the information from the available attack traces (in particular the noise).

Option 2:Compute the joint likelihood $\mathrm {l}(k\mid {\mathbf {X}}_{k{\star }}) = \displaystyle \prod _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} \mathrm {l}(k\mid {{\mathbf {x}}}_{i}).$ By applying the logarithm to both sides we have $\log \mathrm {l}(k\mid {\mathbf {X}}_{k{\star }}) = \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} \log \mathrm {l}(k\mid {{\mathbf {x}}}_{i})$ and we obtain the derived scores:

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LOG}}^{\mathrm {joint}}(k\mid {\mathbf {X}}_{k{\star }})&= -\frac{n_{{\mathrm {a}}}}{2} \log {|\mathbf {S}_{k}|} -\frac{1}{2} \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k})}'\mathbf {S}_{k}^{-1}({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k}),\end{aligned}$$

(27)

$$\begin{aligned} {\mathrm {d}}_{\mathrm {MD}}^{\mathrm {joint}}(k\mid {\mathbf {X}}_{k{\star }})&= -\frac{1}{2} \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k})}'\mathbf {S}_{k}^{-1}({{\mathbf {x}}}_{i}-\bar{{\mathbf {x}}}_{k}),\end{aligned}$$

(28)

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {joint}}(k\mid {\mathbf {X}}_{k{\star }})&= {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) - \frac{n_{{\mathrm {a}}}}{2}{\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}. \end{aligned}$$

(29)

Given the $n_{{\mathrm {a}}}$ leakage traces ${{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}$, ${\mathrm {d}}_{\mathrm {LOG}}$ and ${\mathrm {d}}_{\mathrm {MD}}$ require time $O(n_{{\mathrm {a}}}{{m}^{\mathrm {}}}^2)$ while ${\mathrm {d}}_{\mathrm {LINEAR}}$ only requires $O(n_{{\mathrm {a}}}+ {{m}^{\mathrm {}}}^2)$, since the operations ${\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}$ and ${\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}$ only need to be done once, which is a great advantage in practice. As a practical example, our evaluations of the guessing entropy (see Sect. 6) for ${m}^{\mathrm {}}= 125$ and $1\le n_{{\mathrm {a}}}\le 1000$ took about 3.5 days with ${\mathrm {d}}_{\mathrm {LOG}}$ but only 30 min with ${\mathrm {d}}_{\mathrm {LINEAR}}$.⁹ We note that for ${\mathrm {d}}_{\mathrm {LINEAR}}$ the computation time is the same regardless of which option we use to combine the traces, and both give the same results for the template attack.

5.5 Unequal Prior Probabilities

In the previous descriptions we have assumed equal prior probabilities among the candidates $k$. When this is not the case, we only need to add the term $\log P(k)$ to the discriminant scores ${\mathrm {d}}_{\mathrm {LOG}}^{\mathrm {avg}}$, ${\mathrm {d}}_{\mathrm {MD}}^{\mathrm {avg}}$, ${\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {avg}}$, or $n_{{\mathrm {a}}}\log P(k)$ to the discriminant scores ${\mathrm {d}}_{\mathrm {LOG}}^{\mathrm {joint}}$, ${\mathrm {d}}_{\mathrm {MD}}^{\mathrm {joint}}$, ${\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {joint}}$.

6 Evaluation of Methods

We evaluated the efficiency of many template-attack variants on a real hardware platform, comparing all the compression methods from Table 1 ¹⁰ and all the implementation options from Sect. 5. We compare the commonly used high-compression methods, such as PCA, LDA and sample selection using the guideline [7] of 1 sample per clock at most (1ppc), against weak compressions providing a larger number of samples: the 3ppc, 20ppc and allap selections.¹¹

Table 1. List of compression methods evaluated in this paper.

6.1 Experimental Setup

Our target is the 8-bit CPU Atmel XMEGA 256 A3U, an easily available microcontroller without side-channel countermeasures, mounted on our own evaluation board to monitor the total current in all CPU ground pins via a $10\,\Omega$ resistor. We powered it from a battery via a 3.3 V regulator and supplied a 1 MHz sine clock. We used a Tektronix TDS 7054 8-bit oscilloscope with P6243 active probe, at 250 MS/s, with 500 MHz bandwidth in SAMPLE mode. We used the same device for both the profiling and the attack phase, which provides a good setting for the focus of our work.

For each candidate value $k\in \{0,\cdots ,255\}$ we recorded $3072$ traces ${{\mathbf {x}}}^{\text {r}}_{{k}{i}}$ (i.e., $786\,432$ traces in total), which we divided into a training set (for the profiling phase) and an evaluation set (for the attack phase). Each trace contains ${m}^{\mathrm {\text {r}}}=2500$ samples, recorded while the target microcontroller executed the same sequence of instructions loaded from the same addresses: a MOV instruction, followed by several LOAD instructions. All the LOAD instructions require two clock cycles to transfer a value from RAM into a register, using indirect addressing. In all the experiments our goal was to determine the success of the template attacks in recovering the byte $k$ processed by the second LOAD instruction. All the other instructions were processing the value zero, meaning that in our traces none of the variability should be caused by variable data in other nearby instructions that may be processed concurrently in various pipeline stages.¹²

6.2 Guessing Entropy

We use the guessing entropy as the sole figure of merit to compare all methods. It estimates the (logarithmic) cost of any optimized search following a template attack to find the correct $k{\star }$ among the values $k$ with the highest discriminant scores. It gives the expected number of bits of uncertainty remaining about the target value $k{\star }$. The lower the guessing entropy, the more successful the attack has been and the less effort remains to search for the correct $k{\star }$.

To compute the guessing entropy, we compute the score $\mathrm {d}(k\mid {\mathbf {X}}_{k{\star }})$ (see Sect. 5) for each combination of candidate value $k$ and target value $k{\star }$, resulting in a score matrix ${\mathbf {M}}\in \mathbb {R}^{|{\mathcal {S}}|\times |{\mathcal {S}}|}$ with ${\mathbf {M}}(k{\star }, k) = {\mathrm {d}}(k\mid {\mathbf {X}}_{k{\star }}).$ Each row in $\mathbf {M}$ contains the score of each candidate value $k$ given the traces ${\mathbf {X}}_{k{\star }}$ corresponding to a given target value $k{\star }$. Next we sort each row of $\mathbf {M}$, in decreasing order, to obtain a depth matrix ${\mathbf {D}}\in \mathbb {N}^{|{\mathcal {S}}|\times |{\mathcal {S}}|}$ with

$$\begin{aligned} {\mathbf {D}}(k{\star }, k) = \text {position of}~\mathrm {d}(k\mid {\mathbf {X}}_{k{\star }})~\text {in the sorted row of}~\mathbf {M}(k{\star }, \cdot ). \end{aligned}$$

(30)

Finally, using the matrix ${\mathbf {D}}$ we define the guessing entropy

$$\begin{aligned} g= \log _2 \frac{1}{|{\mathcal {S}}|} \sum _{k\in {\mathcal {S}}} {\mathbf {D}}(k, k). \end{aligned}$$

(31)

Standaert et al. [13] also used this measure, but without the logarithm.

6.3 Experimental Results and Practical Guidance

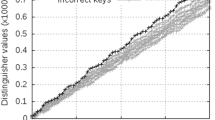
We performed each attack 10 times for each combination of $n_{{\mathrm {a}}}$, $k$ and $k{\star }$, using a different random selection of ${\mathbf {X}}_{k{\star }}$ for each $n_{{\mathrm {a}}}$ and $k{\star }$. We plot in Figs. 2 and 3 the averaged guessing entropy, resulting in highly reproducible graphs. The standard deviation across all experiments is around 0.1 bits.

Fig. 2.

Guessing entropy remaining after template attacks, with different compressions, for $n_{\mathrm {p}}=200$ (left) and $n_{\mathrm {p}}=2000$ (right) profiling traces, using individual covariances $\mathbf {S}_{k}$ with ${\mathrm {d}}_{\mathrm {LOG}}$ (top) or a pooled covariance $\mathbf {S}_{\mathrm {pooled}}$ with ${\mathrm {d}}_{\mathrm {LINEAR}}$ (bottom).

Fig. 3.

Guessing entropy from the methods discussed, for $n_{{\mathrm {a}}}=1$ (left) and $n_{{\mathrm {a}}}=1000$ (right), using $\mathrm {d}^{\mathrm {joint}}$ (at $n_{\mathrm {p}}\in \{200,500,1000,1500,2000\}$, linearly interpolated).

These results, as well as the considerations discussed earlier, allow us to provide the following practical guidance regarding the choice of algorithm:

• 1. Use Option 2 ( $\mathrm {d}^{\mathrm {joint}}$ ) in preference to Option 1 ( $\mathrm {d}^{\mathrm {avg}}$ ) to combine the discriminant scores for $n_{{\mathrm {a}}}>1$ attack traces. For $n_{{\mathrm {a}}}=1$ or when using $\mathbf {S}_{\mathrm {pooled}}$, these options are equivalent. Otherwise, as the number $n_{{\mathrm {a}}}$ of attack traces increases and the covariance matrix is better estimated (e.g. due to a large number $n_{\mathrm {p}}$ of profiling traces or small number ${m}^{\mathrm {}}$ of variables) $\mathrm {d}^{\mathrm {joint}}$ outperforms $\mathrm {d}^{\mathrm {avg}}$ for all compression methods.

• 2. Try using a common covariance matrix $\mathbf {S}_{\mathrm {pooled}}$ with ${\mathrm {d}}_{\mathrm {LINEAR}}$ (unless differences between individual estimates $\mathbf {S}_{k}$ are very evident, e.g. from visual inspection). Failing a statistical test for homoscedasticity (e.g., Box’s test) alone does not imply that using individual estimates $\mathbf {S}_{k}$ will improve the template attack. Using individual estimates $\mathbf {S}_{k}$ prevents use of the significantly faster and more robust discriminant ${\mathrm {d}}_{\mathrm {LINEAR}}$. Then:

  • (a) If your target allows you to acquire a large number of traces ( $n_{{\mathrm {a}}}>100$ ): try the compression methods PCA, LDA and sample-selection with large ${m}^{\mathrm {}}$ since they may perform differently based on the level of noise from the profiling traces ${\mathbf {X}}_{k}$.

  • (b) If your target allows only acquisition of a limited number of attack traces ( $n_{{\mathrm {a}}}<10$ ): use LDA. Note that in this case, as the covariance estimate improves due to large $|{\mathcal {S}}|n_{\mathrm {p}}$, performance increases with larger ${m}^{\mathrm {}}$ (cf. 3ppc, 20ppc, allap). In particular, for $n_{{\mathrm {a}}}<10$, we see in Fig. 2 (bottom) that we got more than 1 bit of data from 20ppc and allap compared to 1ppc, which contradicts the claim [7, Sect. 3.2] that “additional [samples] in the same clock cycle do not provide additional information”. In this setting, 20ppc and allap can outperform PCA.

• 3. If you cannot use the pooled covariance $\mathbf {S}_{\mathrm {pooled}}$, then use the individual covariances $\mathbf {S}_{k}$ with ${\mathrm {d}}_{\mathrm {LOG}}$ and use PCA as the compression method.

This guidance should work well in situations similar to our experimental conditions. Further research is needed to also consider pipelining, where other data in neighbour instructions can partially overlap in the side-channel.

7 Conclusions

In this paper, we have explored in detail the implementation of template attacks based on the multivariate normal distribution, comparing different compression methods, discriminant scores, and number of profiling and attack traces.

We explained why several numerical obstacles arise when dealing with a large number ${m}^{\mathrm {}}$ of variables (e.g. when retaining a large part of the leakage vectors), and we presented efficient methods that can be used in this case, such as the discriminant ${\mathrm {d}}_{\mathrm {LOG}}$.

Based on the observation that the covariance matrices $\mathbf {S}_{k}$ of each candidate $k$ are similar, we explained the use of the pooled covariance estimate $\mathbf {S}_{\mathrm {pooled}}$ and we showed how $\mathbf {S}_{\mathrm {pooled}}$ allows us to derive a linear discriminant ${\mathrm {d}}_{\mathrm {LINEAR}}$ which is much more efficient than ${\mathrm {d}}_{\mathrm {LOG}}$. For $n_{{\mathrm {a}}}=1000$ attack traces and ${m}^{\mathrm {}}=125$ samples, the computation of the guessing entropy remaining after the template attacks can be reduced from 3 days (using ${\mathrm {d}}_{\mathrm {LOG}}$) to 30 min (using ${\mathrm {d}}_{\mathrm {LINEAR}}$). This is a great advantage for the evaluation of template attacks, which is often a requirement to obtain Common Criteria certification.

We applied all the methods presented in this paper on real traces from an unprotected 8-bit microcontroller and we evaluated the results using the guessing entropy. Using the efficient methods presented in this paper we were able to obtain a guessing entropy close to 0, i.e. we are able to extract all 8 bits processed by a single LOAD instruction, not just their Hamming weight.

Based on these results and theoretical arguments, we proposed a practical guideline for the choice of algorithm when implementing template attacks.

Data and Code Availability: In the interest of reproducible research we make available our data and associated MATLAB scripts at:

http://www.cl.cam.ac.uk/research/security/datasets/grizzly/

Appendices

Evaluation Board

For our experiments, we built a custom PCB for the Atmel microcontroller (see Fig. 4, left). This 4-layer PCB has inputs for the clock signal and supply voltage, a USB port to communicate with a PC, and a $10\,\Omega$ resistor in the ground line for power measurements. The PCB connects all the ground pins of the microcontroller to the same line, which leads to the measurement resistor.

Fig. 4.

Left: the device used during our experiments. Right: A single example trace ${{\mathbf {x}}}^{\text {r}}_{i}$ from our experimental setup.

Executed Code

During all our experiments we recorded traces with 2500 samples, covering the execution of several instructions, as shown in Fig. 4 (right). The executed instruction sequence is

The load instructions use the Z pointer (which refers to registers r31:r30) for indirect RAM addressing. The initial value of registers r8–r12 before the load operations is zero. The initial value of Z before the first load instruction is 2020.

Some Proofs

In Sect. 5.3 we rewrote (22) as (24). This is possible because

$$\begin{aligned} {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}{\mathbf {x}}= {({\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}{\mathbf {x}})}' = {{\mathbf {x}}}'{\mathbf {S}_{\mathrm {pooled}}^{-1}}'\bar{{\mathbf {x}}}_{k}= {{\mathbf {x}}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}. \end{aligned}$$

(32)

In Sect. 5.4 we state that ${\mathrm {d}}_{\mathrm {LINEAR}}$ provides the same results for both options of combining the traces (from average trace and based on joint likelihood). This happens because if we let $c_{k} = -\frac{1}{2}{\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1}\bar{{\mathbf {x}}}_{k}$ for any $k$, then we have

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {joint}}(k\mid {\mathbf {X}}_{k{\star }})&= {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + n_{{\mathrm {a}}}c_{k}, \end{aligned}$$

(33)

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {avg}}(k\mid {\mathbf {X}}_{k{\star }})&= {\bar{{\mathbf {x}}}_{k}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\frac{1}{n_{{\mathrm {a}}}} \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + c_{k}, \end{aligned}$$

(34)

and therefore for any $u, v\in {\mathcal {S}}$ it is true that

$$\begin{aligned} {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {avg}}(u \mid {\mathbf {X}}_{k{\star }})&> {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {avg}}(v \mid {\mathbf {X}}_{k{\star }}) \Leftrightarrow \\ {\bar{{\mathbf {x}}}_{u}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\frac{1}{n_{{\mathrm {a}}}} \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + c_u&> {\bar{{\mathbf {x}}}_{v}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\frac{1}{n_{{\mathrm {a}}}} \displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + c_v \Leftrightarrow \\ {\bar{{\mathbf {x}}}_{u}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + n_{{\mathrm {a}}}c_u&> {\bar{{\mathbf {x}}}_{v}}'\mathbf {S}_{\mathrm {pooled}}^{-1} \bigg (\displaystyle \sum _{{{\mathbf {x}}}_{i}\in {\mathbf {X}}_{k{\star }}} {{\mathbf {x}}}_{i}\bigg ) + n_{{\mathrm {a}}}c_v \Leftrightarrow \\ {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {joint}}(u \mid {\mathbf {X}}_{k{\star }})&> {\mathrm {d}}_{\mathrm {LINEAR}}^{\mathrm {joint}}(v \mid {\mathbf {X}}_{k{\star }}). \end{aligned}$$