Non-deterministic Calibration of Crystal Plasticity Model Parameters

Abstract

Crystal plasticity constitutive models are frequently used with finite elements for modeling metallic grain-scale phenomena. The accuracy of these models is directly a function of the calibrated parameters, which fully define a crystal plasticity model. A number of techniques exist for the calibration of these parameters. In the current study, a comparison of results using deterministic and non-deterministic calibration methods is made. Additionally, the effect of the type of measured data on calibrated material parameters, global (homogenized) or local, is also presented. Included in the study is a new approach to parameter calibration based on combined digital image correlation and high angular resolution electron backscatter diffraction. Utilizing data from these experimental techniques allows for local evaluation of both strain and relative stress: essentially giving stress-strain curves from numerous point locations in a single coupon. The overall result is that calibration based on sub-grain-scale measurements is preferable when sub-grain-scale phenomena are of primary interest.

1 Introduction

The use of crystal plasticity (CP) to model grain-scale mechanical behavior of metallic microstructures has become widely used, especially in the finite element context. A major motivation has been observations made during experiment regarding the microstructure dependence of crack initiation on microstructural features and the general understanding that microstructure variation underpins variability observed at larger length scales. CP models aid in the fundamental understanding of those observations through their capability to model the effect of microscale heterogeneity by capturing the orientation-dependent behavior of each grain in a polycrystalline material. The aggregate effect of each grain, assembled in a polycrystal model, can then be analyzed upon CP model implementation within numerical methods for the solution of differential equations with complex geometry and imposed boundary conditions, e.g., finite element or fast Fourier transform methods.

Recently, the importance of CP-based models for engineering applications has been highlighted, especially in aerospace applications where increased demands on efficiency and speed are driving increased complexity in structural configuration and reductions in thickness for fracture-critical components [31, 36]. While this change in paradigm is exciting and is enabling a new era in aerospace vehicles, it also defines specific challenges for researchers. A major challenge currently is that traditional standard practice models for material constitutive behavior and crack growth rates become invalidated for these next-generation applications. For example, the application of traditional fracture mechanics approaches does not apply when crack growth is in the microstructurally small regime throughout life with only several grains through thickness.

At the center of these engineering challenges is CP-based modeling for grain-scale constitutive and cracking behavior. An ultimate goal of the Integrated Computational Materials Engineering community is to provide physics-based models for materials, enabled through multiscale modeling of fundamental material behavior, propagated to a continuum representation of a material. However, until CP model parameters can be provided without a need for any experimental measurements, calibration will play a fundamental role in the application of CP models for engineering applications.

Simply put, parameter calibration is an inverse problem that aims to determine a set of material model parameters that minimize some measure of error between a model, which is a function of the parameters, and measured data. The field of applying inverse problem methodologies for the calibration of material parameters is broad. Many of the approaches to date are based on the same variational and virtual work principles upon which the fundamental principles of continuum solid mechanics are based, such as the reciprocity gap or error in constitutive equations methods. For an overview of the more general area of inverse problem methodologies applied to material parameter calibration, see [3]. For understanding the work in this chapter, it is important to identify the additional complexities imposed by working with CP models specifically. As the material model becomes more complex or requires more parameters, which is characteristic of CP models, the computational demand of calibration increases. Additionally, more data is required in such cases to mitigate issues of uniqueness. This notion becomes especially important upon consideration of the need to identify distributions of material parameters, where it is expected that the parameters are not single deterministic values.

The current literature, pertaining to discussion in this chapter, typically involves a hybrid approach to CP model parameter calibration, in which local strains from digital image correlation (DIC) and global (homogenized) stresses from testing are combined to form a cost function. An interesting approach to calibration using such data is the integrated DIC (IDIC) method. Early work of Leclerc et al. [24] formulated a two-stage process, whereby the correlation and parameter identification optimization was solved simultaneously. While the formulation is general, that work studied identification of elastic material parameters and presented a study of the effect of signal-to-noise ratio on the calibrated parameters. That initial work was later extended to the calibration of elastic-plastic material model parameters, with comparison to the commonly used finite element model updating (FEMU) method [26]. Local DIC strain data was also used to calibrate spatial variations of yield stress within a weld nugget and heat-affected zone using uniform stress and virtual fields methods [39]. Recently, Rokoš et al. [32] addressed the known issue of boundary condition sensitivity within the IDIC method, by formulating a procedure to combine material parameters with kinematic boundary conditions as degrees of freedom at the model boundary. For an in-depth description of parameter identification methods using local DIC strain and global stress data, see [1].

The application of parameter identification methods to CP models is relatively limited. Early work of Hoc et al. [17] studied the calibration of CP parameters for an ARMCO oligocrystal specimen using deterministic optimization. In that work, the local DIC strain field was homogenized to produce a statistical distribution of their component values. Additionally, global stress values were measured during experiment. A cost function was formed by a weighted sum of both sets of data: summing the differences between the measured and computed strain distributions, at eight sampling points, and the measured and computed global stresses. More recently, local DIC strain and global stress data have been used to calibrate CP parameters from in situ tensile tests. By comparing two different CP models with experimental data at various length scales (global stress-strain curve and strain map from DIC), Sangid et al. [37] showed that although the two CP models agreed with each other and the experimental data with regard to the global stress-strain behavior, their local agreement was relatively poor at the spatial length scale of the slip system. Guery et al. [15] used FEMU to calibrate CP parameters for AISI 316LN steel using 2D simulations of microstructures with varying grain size. Grain size-dependent CP parameters were calibrated and illustrated the ability to reproduce the expected Hall-Petch behavior. Bertin et al. [2] also studied CP parameter calibration, using the IDIC method. In comparison with the study previously mentioned, the work of Bertin et al. was on a smaller scale, focused on the deformation of a bicrystal tensile sample fabricated using a focused ion beam (FIB).

The use of CP models within the finite element framework has largely focused on the propagation of uncertainty via representative volume elements (RVEs), formed by statistical instantiations of microstructure morphology. In these studies, the CP model parameters are, however, deterministic, and their variations are not considered in the ultimate prediction of variation in mechanical behavior. This is likely due to two fundamental difficulties. First, there are currently no proven methods for the non-deterministic identification of CP model parameters, and preliminary developments are required. Second, the inclusion of CP model parameter uncertainties adds to an already computationally intensive problem, when considering variations in microstructure morphology. A goal of this chapter is to illustrate that there are now methods available for the non-deterministic calibration of CP model parameters and that those parameters can be considered in the forward propagation from microscale uncertainties to predicted variation in component scale mechanical behavior.

This chapter first covers the common methods for acquiring and processing experimental data, when calibrating CP model parameters. The methods are organized into global and local approaches. Subsequently, a brief introduction to CP is given, mainly to provide sufficient understanding of the CP parameters to be calibrated and how they are involved in the model. Common numerical methods for CP model parameter calibration are then discussed in context of the global and local data that can be acquired and processed. The fundamental concepts of uncertainty quantification, with focus on the context of CP model parameter calibration, are then provided. Lastly, each of the discussed methods for calibration is evaluated on a simulated experiment with known CP parameters. This provides a clear quantification of the practical issues of uniqueness of the identified parameters.

2 Acquiring and Processing Experiment Data

The experimental measurements that must be made and post-processing methods to prepare the acquired data are overviewed here. There are two general categories, global and local, by which the acquiring and processing methods can be binned. The fundamental definitions for each of these types of acquired data are given here because they are important for understanding of the subsequently described calibration methods.

2.1 Global Data

Global data here is defined by any measurement or post-processing method that quantifies the bulk behavior of a mechanical test coupon. An example of a directly measured global data set would be the applied or reaction force provided by a load cell during testing. Similarly, this data could then be post-processed to produce either the engineering or true stress by considering the initial or current cross-section area, respectively. While displacements can similarly be obtained from the stroke of the test stand during testing, typically a displacement or strain gauge is attached to the test coupon for this data. Using gauges in this way means that any test-stand compliance is inherently filtered out of the displacement or strain data. Because these gauges homogenize underlying coupon deformation over their length, they are also considered global data.

2.2 Local Data

Local data here is defined as any measurement or post-processing method that extracts data as a field across the coupon surface or volume. An example of a directly measured local data set would be displacements or strain obtained through the use of DIC, which is explained in Sect. 2.2.1. The full-field data could also be used to produce global data by extracting displacements or strains from virtual strain gauges, which extract averaged values over their length during post-processing of the DIC data. In the context of deformation of polycrystalline materials, local DIC data can be used to quantify deformations within each grain in the polycrystalline aggregate. This approach requires that the underlying microstructural features be aligned with the DIC data. The underlying microstructure morphology can be measured using electron backscatter diffraction (EBSD), which provides quantification of the surface grain shapes and their orientations. Additionally, high-resolution EBSD (HREBSD) can be used to compute the elastic deformation gradient locally on the surface of a specimen. An overview of EBSD and HREBSD is provided in Sect. 2.2.2.

2.2.1 Digital Image Correlation

DIC is a metrological tool used for quantifying motion/deformation that occurs between a reference image f(x, y) and a deformed image g(x′, y′) (see Fig. 1). By maximizing the correlation of features within f and g, a mapping can be found between (x, y) and (x′y′). Ultimately, that mapping comes in the form of a displacement field (usually a spatial array of displacements) [28, 40]. The displacements can be further processed to give estimates of local strains. A limitation in the above-described two-dimensional DIC is that displacements can only be measured in the plane of the image, i.e., displacements and strains with components in the Z-direction are not identified. Stereo-DIC is able to identify out-of-plane motion with the use of a two-camera setup. However, because images can only be taken of the surface of a specimen, strains with respect to the through-thickness dimension, i.e., into the specimen, are still not identified.

Fig. 1

Digital image correlation example

A fundamental aspect of DIC is that the specimen surface must contain sufficient features such that obtained images can be used to perform the correlation. While there are examples of using natural surface variation for DIC in the literature, cf. [19, 46], it is more common that a pattern must be applied to the specimen to make up for sparse natural features. The applied surface pattern plays a large role in DIC, namely, it affects the possible spatial resolution and accuracy of the measurements. There are several patterning options available for measurements of deformations at the grain scale, e.g., microstamping, lithography, and nanoparticle placement. For a full review of available techniques, the reader is referred to the recent review article of Dong and Pan [10]. Most importantly, the pattern needs to be visible to the image capturing device; optical cameras and scanning electron microscopes (SEM) are the two most common means of image capture for appropriately scaled DIC of polycrystalline metals. Furthermore, those methods require different pattern characteristics, e.g., pattern features must be opaque to electrons for optimal image contrast in SEM and opaque to visible light with optical cameras.

2.2.2 High-Resolution EBSD

EBSD is a well-established scanning electron microscope-based diffraction technique that may be used to determine local crystallographic orientation on a specimen surface. With respect to modeling, it may be used to determine the grain structure of a specific specimen [47] or to acquire statistical data about grain texture and morphology for a given material [8, 45]. HREBSD is a means of extracting the elastic deformation gradient of one diffraction pattern compared to another via cross-correlation [44]. This deformation gradient, F, is related to a feature shift between the patterns measured by cross-correlation, q, as follows:

$$\displaystyle \begin{aligned} \mathbf{q} = \mathbf{F}(\mathbf{x}-\mathbf{PC})\frac{-\mathbf{PC} \cdot \hat{z}}{\mathbf{F}(\mathbf{x}-\mathbf{PC}) \cdot \hat{z}} - \mathbf{x} + \mathbf{PC} , \end{aligned} $$

(1)

where x is the location of the feature on the reference pattern, PC is the location of origin of the diffraction pattern relative to the detector (also known as the pattern center), and $\hat {z}$ is a unit vector normal to the detector surface. If shifts are measured from four or more non-collinear points, eight of the nine components of F may be calculated via least squares. The missing degree of freedom is approximately the relative dilatory strain (it may not be recovered as a consequence of projecting the diffraction pattern onto a 2D detector) and is recovered by assuming zero traction or by determining only the deviatoric component of the strain. Note that HREBSD recovers the relative deformation gradient between two patterns. In order to determine the absolute deformation gradient of a material, it is necessary to simulate a strain-free reference pattern of known orientation [18, 20]. This method is more sensitive to error in PC and requires careful calibration [5]. Once recovered, the local elastic deformation gradient may be used to determine a number of useful variables concerning the local material state, including elastic strain, orientation (much more accurately than conventional EBSD), and stress via Hooke’s law (if the elastic parameters of the material are well-known). By looking at the curl of the deformation gradient, HREBSD measurements may even be used to calculate Nye’s tensor, a continuum representation of geometrically necessary dislocation density [34].

2.2.3 Combining DIC and HREBSD

Recently, a new measurement method has been developed which allows for the simultaneous acquisition of DIC and HREBSD on a specimen surface. The integration of these two, previously mutually exclusive, experimental methods is made possible by the application of an amorphous DIC-pattern material, such as urethane rubber [35], that provides good contrast for DIC in a SEM at low acceleration voltage (at about 5 keV) using secondary electron imaging, but has negligible interference with the primary electrons that form diffraction patterns at high-accelerating voltage (20 keV). An example of this stamp, imaged in two different modes, is shown in Fig. 2. This combination of methods enables decomposition of deformation within the same surface domain during loading. In other words, DIC can be used to quantify the total deformation, while HREBSD can be used to quantify the elastic part of that total deformation, allowing for a decomposition of the elastic and plastic parts. Note that the current feature size of the stamp is approximately 1 micron and the spatial resolution of the patterning technique is expected to improve with further development. The implications of this new measurement method on calibration methods are provided in Sect. 6.3.

Fig. 2

Images on of a urethane residual layer stamp applied to an aluminum oligocrystal sample imaged at 5 keV using secondary electron imaging (a) and at 20 keV using backscattered electrons (b)

3 Crystal Plasticity

As motivated in Sect. 1 of this chapter, CP models are becoming increasingly used when microstructure dependence in engineering use cases is observed. There are at least two driving factors for that increased adoption. First, CP models are reaching maturity where even complex micromechanism multiphysics simulations can be completed in a reasonable amount of time and with well-supported computational toolsets. Second, in many engineering applications, component size reduction is common. Examples of such applications are microelectromechanical systems, electronic devices, and thinning of structural components in aerospace vehicle components. Furthermore, material processing of Ni- and Al-based metals in aerospace applications, e.g., turbine blades and pressure vessels, can result in grain growth resulting in grain sizes approaching the structural scale. In these cases, and others like them, the micromechanics plays a governing role in the behavior, size effect, and variability in component performance and reliability and, hence, must be considered during design and certification.

While the general area of CP modeling and their applications is large, a focus here is given to phenomenological models. Such models are characterized by the consideration of the shear stress resolved on each crystallographic slip system, τ ^α, and its current strength, g ^α, that causes plastic slip, γ ^α, to occur. Similarly, the discussion is limited to CP models that represent a single phase with lattice dislocations as the sole deformation mechanism. The objective of this section is to provide sufficient background for CP modeling such that the subsequent discussion of non-deterministic calibration of CP parameters can be understood. For an encompassing review of CP modeling, see [33].

3.1 Concepts

For the remainder of this chapter, consideration is given to CP as a model for the homogenization of the underlying motion of dislocations on each slip system. As such, the primary parts of a CP model are the kinematics of slip and a constitutive model relating the external forces to slip rates through resolved shear stress. The mathematical model of the kinematics of finite deformation relates the original reference configuration of a continuum to a current configuration that is obtained through the application of external loads and displacements. The total deformation gradient, F, relates the reference and current configurations directly.

The decomposition of F into its elastic and plastic parts can be thought of as a multiplicative transformation, Eq. 3. Therein, F _e represents the reversible component of deformation, while F _p represents the deformation that remains upon removal of the external forces and displacements. If irreversible deformation is present, an intermediate configuration is obtained upon removal of external forces and displacements. This intermediate configuration is related to the reference configuration by F _p. Furthermore, the lattice orientation remains unchanged in the intermediate configuration, resulting in a stress-free configuration. Effectively, this relies on an assumption that any dislocations formed must be passed beyond its local neighborhood. The intermediate and current configurations are related by F _e, where lattice distortions lead to material stresses. This concept that the stress is induced by the elastic portion of the deformation is fundamental both to the development of the following constitutive equations and to the calibration method presented in Sect. 4.4.

$$\displaystyle \begin{aligned} F = F_e F_p . \end{aligned} $$

(2)

However, this decomposition does not yet have information regarding the underlying crystallography essential for CP modeling. To capture crystallographic kinematics, the plastic velocity gradient, L _p, is defined as a tensor that transforms the plastic deformation gradient, F _p, to its time rate of change:

$$\displaystyle \begin{aligned} \dot{F}_p = L_p F_p . \end{aligned} $$

(3)

Since the consideration here is limited to dislocation slip as the only plastic deformation process, L _p is formulated as the sum of rates of slip on each system, $\dot {\gamma }^{\alpha }$, along with the slip direction for each system, m ^α, and its corresponding plane normal, n ^α:

$$\displaystyle \begin{aligned} L_p = \sum_{\alpha=1}^n \dot{\gamma}^{\alpha} m^{\alpha} \otimes n^{\alpha} . \end{aligned} $$

(4)

It is with this definition that the crystallographic kinematics are modeled.

The constitutive models in CP relate F _e to the resolved shear stress on each system, τ ^α, through the elastic stiffness tensor, C, using second Piola-Kirchhoff stress and Green elastic strain:

$$\displaystyle \begin{aligned} \tau^{\alpha} = 0.5C[F_{e}^{T}F_{e} - I] : m^{\alpha} \otimes n^{\alpha} , \end{aligned} $$

(5)

where T denotes the transpose. With τ ^α computed, the rate of slip on each system, $\dot {\gamma }^{\alpha }$, is computed herein as:

$$\displaystyle \begin{aligned} \dot{\gamma}^{\alpha} = \dot{\gamma}_{o}\frac{\tau^{\alpha}}{g^{\alpha}}\left|\frac{\tau^{\alpha}}{g^{\alpha}}\right|{}^{\frac{1}{m}-1} . \end{aligned} $$

(6)

And, lastly, the evolution of hardening on each system, $\dot {g}^{\alpha }$, is integrated as a function of the current hardness, g ^α; the saturation hardness, g _s; and the initial hardness, g _o.

$$\displaystyle \begin{aligned} \dot{g}^{\alpha} = G_o \left(\frac{g_{s} - g^{\alpha}}{g_{s} - g_{o}}\right)\left|\dot{\gamma}^{\mathrm{tot}}\right| . \end{aligned} $$

(7)

In Eq. 7, $\dot {\gamma }^{\mathrm {tot}}$ refers to the total slip rate across all the slip systems and can be represented mathematically per Eq. 8:

$$\displaystyle \begin{aligned} \dot{\gamma}^{\mathrm{tot}} = \sum_{\alpha=1}^{N_{SS}}\dot{\gamma}^{\alpha} , {} \end{aligned} $$

(8)

where N _SS refers to the number of slip systems, which is 12 for an FCC system. Since Eq. 7 incorporates the total accumulated slip rate, the hardening on each system is equivalent.

Further, the saturation hardness term, g _s, in Eq. 7 can be expressed as:

$$\displaystyle \begin{aligned} g_s=g_{so}{\left|\frac{\dot{\gamma}^{\mathrm{tot}}}{\dot{\gamma}_{s}}\right|}^{\omega} , {} \end{aligned} $$

(9)

where g _so, $\dot {\gamma }_{s}$, and ω are three input parameters for the reference saturation hardness, the reference saturation slip rate, and the saturation rate exponent, respectively.

For the purpose of simplicity and tractability of both global-local and local calibration studies, the saturation hardness, g _s, can further be expressed as:

$$\displaystyle \begin{aligned} g_{s}=(g_{o} + g^{*}_{s}){\left|{\dot{\gamma}^{\mathrm{tot}}}\right|}^{\omega} , \end{aligned} $$

(10)

where $g^{*}_{s}$ is a normalized reference saturation hardness. Although $g^{*}_{s}$ is a function of both g _so and $\dot {\gamma }_{s}$, for the purpose of calibration studies, it is expressed as an independent variable. Additionally, parameters $\dot {\gamma }_{o}$ and ω are treated as “fixed parameters” – not included as calibration parameters – as their respective influence on slip rates and hardening of each slip system can be emulated by parameters m and $g^{*}_s$, respectively. Therefore, the set of calibration parameters involved in the current work include g _o, m, G _o, and $g^{*}_{s}$.

The CP model presented in this section is used throughout the remainder of the chapter. First, the model is used to represent a collection of grains, Sect. 4.2, within a Taylor model where the grains deform independently. Subsequently, in Sects. 4.3 and 4.4, these equations are implemented within a finite element framework for higher-fidelity modeling of the interaction among grains in a polycrystal. This aggregation of the deformation of multiple grains with varying crystallographic orientations leads to an anisotropic behavior with heterogeneous stress and strain fields throughout the continuum. As discussed in the subsequent sections, these heterogeneities are important aspects of the calibration process.

Finally, model selection is an important preliminary step to calibrating parameters. In other words, no calibration process can function adequately if an inaccurate or invalid model is selected. Consequently, care should be taken in identifying an appropriate model, before the calibration process is considered. In this chapter, simulated experiments are completed to serve as a surrogate for physical test data. As such, the model selection is inherently prescribed, which allows for a focus on issues regarding non-deterministic calibration (and not model selection).

4 Calibration

In this section, an overview of the general methods for CP material model calibration is provided in the context of local and global, measured and computed, data. Subsequently, in Sect. 6, issues of uniqueness and precision are illustrated through application of several calibration methods, using a simulated experiment.

4.1 General Process

The core of model calibration is the inference of model parameters, θ, adjusted to match some set of measured data. The inference is centered on the comparison of the predicted model response and measured response, where the model is subjected to some measured loading (see the flowchart in Fig. 3). To put this in context of the uncertainty quantification framework, which is described in Sect. 5, the comparison is used in the calculation of the likelihood of a set of calibration parameters.

Fig. 3

Model calibration flowchart

The measurements, model, and comparison parts of the process are where customization for a particular calibration method are made. The experimental measurements, which provide loading and geometry input to the model, can be global, local, or a combination. Similarly, the model itself can be global, local, or a combination in its scale. The comparison of the model and measured response can be either deterministic or non-deterministic in its formulation. In this section, a discussion of available experimental measurement and modeling approaches are discussed in the context of global and local variations. Subsequently, in Sect. 5, a method for non-deterministic comparison is presented.

Model choice plays an important role in the ability to generate accurate and precise calibrations. The inability of a model to fit a given data set during calibration suggests that the model is missing necessary physics and will exhibit poor predictive performance. This is known as model discrepancy and is discussed in detail in [22]. It is the responsibility of the analyst to check for model discrepancy as part of the calibration process.

In the context of CP calibration, three general categories of models can be used. The categories are differentiated by the types of data that are used for both the input loading and output response. Global and local calibration methods are differentiated by their use of global and local data, respectively (see Sect. 2). Global-local methods use a combination of global and local data.

4.2 Global Methods

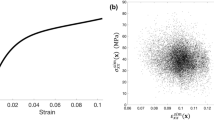
In the case of isotropic materials, calibrating material parameters is readily achieved using a uniaxial, one-dimensional, stress-strain curve. However, because of the anisotropic nature of CP models, the resulting yield surface being evolved during computational simulation is six-dimensional. In the case of anisotropic material models, as is the focus here, the reduction of a six-dimensional yield surface to a measured scalar (one-dimensional) surface can be problematic. For example, Fig. 4 illustrates global uniaxial tension stress-strain behavior measured on a pure Al coupon. Also shown are the computed stress-strain results, using a Taylor model, from two disparate sets of CP parameters; see Table 1. Note, the parameters in Table 1 are chosen to illustrate this issue of uniqueness, where ω is permitted to vary (unlike other calibration exercises in this chapter). Upon studying the goodness of fit produced by either set of CP parameters, it would be reasonable to accept either set as accurately reproducing the measured data because both produce a nearly identical aggregate response. Consequently, more advanced methods should be considered for calibration of CP parameters to resolve this issue of uniqueness.

Fig. 4

Multiple CP parameters sets with nearly identical one-dimensional stress-strain response

Table 1 Two disparate sets of CP model parameter definitions. These sets were used to produce the global stress-strain curves in Fig. 4

Nonetheless, global methods are commonly used for CP model calibration. It is largely the practicality of these methods that make them attractive: less sample preparation and specialized equipment is required to complete the calibrations. In the most typical form, calibration is performed based on the stress-strain relationship of a polycrystalline coupon in uniaxial tension. In cases where only bulk behavior is of interest, the lack of uniqueness poses no real issue. However, when local, microstructurally controlled quantities are of interest, the lack of uniqueness becomes more problematic. The fundamental problem is that the local response may be very different between predictions made with two sets of CP parameters despite the fact that their global response is similar.

4.2.1 Data Flow

In a global calibration method, both the measured and computed data are the result of a homogenization; see Fig. 5. Typically, the experimental measurement is force and displacement over the gauge length for a uniaxial mechanical test. This provides a one-dimensional slice of the larger yield surface. To inform the CP model, crystallographic texture must also be measured, for example, using EBSD. The measured force or displacement (or stress and strain) is used, along with the current iterate for material parameters as input to the computational model, discussed in Sect. 4.2.2. The output of the model must produce data that is directly comparable to the measured data to enable the computation of difference and drive updates to iterated material parameters.

Fig. 5

Example of a global calibration based on a Taylor model

4.2.2 Computational Model

In global calibration methods, two approaches can be used. First, simplified (not explicitly representing specific grain structure or compatibility) models, like that developed by Taylor [41], are often used because of their relative simplicity and computational efficiency. In this case, the equations presented in Sect. 3 are integrated using the measured strains and texture as input. Orientations are then sampled for each material point to be modeled with the measured strain applied to each sampled orientation. After integrating the constitutive equations, to evolve slip rates and resistance to slip, stresses are computed for each material point. Those stresses are then averaged to compute an homogenized, global scalar value to be compared to the measured stress-strain curve.

Second, a higher-fidelity model of the polycrystalline aggregate can be generated using finite element (FE) models. In this approach, either a statistically representative volume can be instantiated by sampling measured microstructure morphology distributions, or a replicated volume can be produced by measuring the specific microstructure of the coupon. The advantage of these models, over the Taylor model, is that the complex interactions among grains in the polycrystal is inherently captured. The disadvantage is that these models are computationally more demanding. Consequently, calibration will take longer, will require additional computational resources, and limits the number of grains that can be modeled. Upon an iterative update to the CP material parameters being calibrated, the global forces and displacements are post-processed from reactions at the boundary for comparison with measured data.

Taylor approximations and FE models represent bounding scenarios between ease of use (Taylor) and high fidelity (FE). However, approaches such as the visco-plastic self-consistent (VPSC) model [23] can provide accurate results by accounting for the effect of grain shape while maintaining a tractable computational effort. Additionally, while not exercised in this chapter, it is important to note that stress-strain curves could be extracted from a variety of directions with respect to the bulk material texture. This additional data would serve to improve the global calibration approach.

4.3 Global-Local Methods

Like purely global methods, hybrid global-local methods use homogenized stress as a target for the calibration method. A major difference, and improvement, comes from the acquiring and integration of full-field displacement or strain data from DIC. This additional full-field data fundamentally changes the numerical aspects of the calibration. Instead of fitting a relatively simple (approximately a second-order polynomial) global stress-strain curve using many (often greater than 5) CP parameters, the DIC dataset helps alleviate the issue of uniqueness that plagues global methods. Because of this, global-local methods are an improvement over global methods.

4.3.1 Data Flow

In a global-local calibration method, the measured global force is combined with local DIC data; see Fig. 6. Consequently, compared to the standard global methods, global-local methods require additional DIC hardware and software to acquire and process the acquired images. To inform the CP model, it is ideal to measure the particular microstructure throughout the test coupon. Most commonly, this data is acquired before mechanical testing using EBSD. While acquiring EBSD data provides data beneficial to the calibration process, it is incomplete in the sense that only surface microstructure is measured, leaving uncertainty about the underlying microstructure. This not only means that subsurface grain orientations are unknown but further means that subsurface defects could also influence the acquired surface strain data. While volumetric methods for measuring microstructure are possible, their availability is currently lacking in general common usage and less commonly used for calibration.

Fig. 6

Example of a global-local calibration based on a finite element model

4.3.2 Computational Model

Because the DIC data acquired in this method is local, local values for displacement or strain must be computed using a FE model. To most closely match the acquired DIC data, the FE model should be constrained on its boundaries with measured DIC displacement data within a region of interest (ROI). Rokoš et al. [32] have recently studied the high sensitivity of calibrated CP parameters on applied boundary conditions and investigated methods to mitigate this source of noise. The FE model should also be defined to replicate the measured grains and their orientations. Upon simulation of the FE model, the computed global stress can be homogenized and compared in the same manner as global methods. Additionally, the local displacement or strain data should also be compared and requires the spatial alignment of the measured and computed displacement or strain data. Alignment of multiple data sets in this context is typically done using fiducial markers as discussed in Lim et al. [25] and Chen et al. [9]. The relative error is typically defined mathematically as a weighted summation of the global and local components.

4.4 Local Methods

Purely local methods are characterized by utilization of local DIC data and local stress data. These methods are somewhat specific to calibrating CP models for crystalline structures in that HREBSD is used to compute local stress; recall Sect. 2.2.2. This improves upon both previously discussed methods in that no global homogenization of mechanical behavior is required. Also, since local stresses and strains are acquired coincidentally, there is no need to generate a FE model to compute homogenized stress. The main disadvantage of the purely local approach is that acquiring and processing HREBSD data is time-consuming, which means that the test must be periodically paused for relatively long periods to acquire the data, which can have implications for rate-dependent materials.

4.4.1 Data Flow

The local calibration method requires that the mechanical test be paused periodically to acquire and process HREBSD and compute local stress at various microstructure locations; see Fig. 7. At the same time, DIC data is acquired to provide local strain data. The DIC data is used as input to the CP model, where each local strain tensor is used to drive deformation. The CP model is then used to compute stress at each coincident point. Those computed stress values are compared directly with the local stress values acquired by HREBSD. In this process, the CP model must be constrained to follow the same local strain and strain rate as the test. This way, there is no discrepancy in the history between acquired and computed data. Lastly, because acquiring HREBSD data is relatively time-consuming, it is practical to repeat this measurement only several times during loading. The increment in time between these measurements will likely be large relative to the numerical integration time stepping required by the CP model. However, the CP model need not increment in one step to times where DIC data was acquired, but may instead subdivide that increment into sufficiently small time steps to achieve convergence.

Fig. 7

Example of a local calibration based on a direct use of a CP model

4.4.2 Computational Model

Since no FE model is required for the local method, there is also no need to extract boundary conditions from DIC for application to the FE model, and the previously discussed issues regarding sensitivity of calibrated CP parameters to boundary conditions in the global and global-local methods are precluded. Instead, each material point is completely defined, in terms of deformation gradient and stress, as decoupled material tests. Because these material points exist throughout a heterogeneous stress-strain field, each of these decoupled material behavior datasets is under different loading scenarios, with respect to their local crystallography. In effect, this is equivalent to running many mechanical tests and measuring the stress-strain response.

5 Uncertainty Quantification Model for Calibration

Model calibration in the presence of uncertainty requires a non-deterministic approach to parameter estimation. For cases where measurement errors, ε _i, are unbiased, independent, and identically distributed (iid), the statistical model describing the relationship between measurements, model, and errors can be defined as:

$$\displaystyle \begin{aligned} \mathrm{Y}_i = \mathcal{M}_i(\Theta) + \varepsilon_i , \end{aligned} $$

(11)

for i = 1, …, M, where Y_i, Θ, and ε _i are random variables representing the measurements, model parameters, and measurement errors, respectively. In the context of the CP model calibration herein, $\Theta =[g_0, m, G_0, g_s^*]$ and the measurements are local or global observations, as discussed in previous sections. M is the total number of measurements available, and $\mathcal {M}_i(\Theta )$ denotes the model response corresponding to a time and location, represented by i, at which the measurements were obtained.

The goal of model calibration is to solve the inverse problem posed by Eq. 11; that is, determine the probability distribution of the model parameters given a set of measurements. Formally, this involves determining the posterior density, π(θ|y), where y and θ are realizations of the random variables Y and Θ, respectively. Using Bayes’ theorem, the posterior density can be expressed as:

$$\displaystyle \begin{aligned} \pi(\theta|y)=\frac{\pi(y|\theta)\pi(\theta)}{\pi(y)}=\frac{\pi(y|\theta)\pi(\theta)}{\int_{\mathbb{R}^p} \pi(y|\theta)\pi(\theta)d\theta} . \end{aligned} $$

(12)

The numerator of Eq. 12 is a multiplication of two densities, the likelihood function, π(y|θ), and the prior density, π(θ). The latter represents any a priori knowledge regarding the parameters, Θ. The prior density is assumed to be known and is often derived from expert knowledge or previous experiments. If unknown, a noninformative prior can be used such that the prior is an improper uniform density over the known parameter support; e.g., a parameter known to be positive would be distributed uniformly over the space bounded by zero and infinity.

The likelihood function is dependent on assumptions about the errors in Eq. 11. A common assumption is that errors are iid and ε _i ∼ N(0, σ ²) where the variance, σ ², is fixed. In this case, the likelihood function becomes:

$$\displaystyle \begin{aligned} \pi(y|\theta) = \frac{1}{(2\pi\sigma^2)^{M/2}}\exp{\bigg (-\frac{1}{2\sigma^2}\sum_{i=1}^M \big [y_i-\mathcal{M}_i(\theta) \big ]^2 \bigg )} , \end{aligned} $$

(13)

which is a function of the sum of squared errors between the model and the measurements. Therefore, both the prior density and the likelihood function can be evaluated at any given point in the parameter space.

The denominator, on the other hand, is more complex as it involves integration over the entire parameter space, with $\theta \in \mathbb {R}^p$ and p denoting the dimensionality of θ. Computing this denominator and, hence, the posterior density can be challenging if not intractable, especially as p increases. While classical quadrature can be used in some cases, an alternative is to construct a Markov chain through the parameter space that has a stationary distribution equal to the posterior density. This approach is called Markov chain Monte Carlo (MCMC) and was chosen in this work to obtain an approximation of the posterior density, π(θ|y).

A detailed explanation of MCMC is beyond the scope of this section, but interested readers are referred to [21, 38] for more information on implementation. In short, MCMC avoids computing the denominator of Eq. 12 and instead utilizes the proportionality:

$$\displaystyle \begin{aligned} \pi(\theta|y) \propto \pi(y|\theta)\pi(\theta) , \end{aligned} $$

(14)

which can be computed at any point $\theta \in \mathbb {R}^p$. An iterative sampling procedure is implemented to form the Markov chain. Since realizations of the chain are samples of the posterior by definition, a sample-based approximation of the posterior density can be obtained. As with standard Monte Carlo sampling, this sample-based estimate of the posterior density converges as the number of samples in the chain, N →∞. In practice, N << ∞, and thus MCMC yields an approximation of the posterior density.

A multitude of algorithms exist for forming this Markov chain. In general, they involve a proposal distribution, J(θ ^∗|θ ^k−1), that depends only on the previous sample in the chain, θ ^k−1. A common choice is J(θ ^∗|θ ^k−1) = N(θ ^k−1, V ), a normal distribution centered at the previous sample with some covariance, V . The candidate sample, θ ^∗, is either accepted or rejected based on the value of the acceptance ratio:

$$\displaystyle \begin{aligned} \mathcal{A}(\theta^{*}, \theta^{k-1}) = \frac{\pi(\theta^*|y)}{\pi(\theta^{k-1}|y)}=\frac{\pi(y|\theta^*)\pi(\theta^*)}{\pi(y|\theta^{k-1})\pi(\theta^{k-1})} . \end{aligned} $$

(15)

A new sample yielding $\mathcal {A}(\theta ^{*}, \theta ^{k-1}) > 1$ is always accepted into the chain as it has a high posterior probability than the previous sample. Accepting a sample implies θ ^k = θ ^∗. If not, the new sample is accepted with probability $\mathcal {A}(\theta ^{*}, \theta ^{k-1})$, meaning that the sample is more likely to be accepted the closer π(θ ^∗|y) is to π(θ ^k−1|y). If rejected, θ ^k = θ ^k−1. This process is iterated until chain convergence.¹

The dependence of J(⋅) on θ ^k−1 means MCMC algorithms require initialization. In this work, a least squares optimization was conducted to deterministically fit the model parameters to available data and generate an initial guess in a region of high posterior probability. This method accelerates chain convergence by reducing the time spent searching for this region of high probability by a random walk over the parameter space. Adaptive tuning of the proposal covariance V  is typically required during the initial stage of chain development as well. The resulting, non-stationary period of searching and tuning is referred to as the burn-in period. The end of the burn-in is defined by the point at which the Markov chain reaches a stationary condition. By definition, samples obtained from the burn-in period are not drawn from the targeted posterior distribution. In practice, an initial percentage of the chain is attributed to burn-in and discarded.

A flowchart of the calibration process is shown in Fig. 8. Upon completion of MCMC sampling, approximations of Θ are available. If the variance in the assumed measurement error distribution is unknown, it can be included in the parameter vector and estimated; e.g., $\Theta =[g_0, m, G_0, g_s^*, \sigma ^2]$. The end result is a non-deterministic calibration of the CP model as well as an estimate of measurement noise. Then, according to Eq. 11, samples drawn from the joint posterior parameter density can be fed through the model to form a non-deterministic prediction of a given quantity of interest via Monte Carlo simulation. Examples of a quantity of interest in the context of CP model calibration might be mechanical response at a larger scale or under new boundary conditions.

Fig. 8

Flowchart of the MCMC-based model calibration

6 Demonstration Using Simulated Experiments

A numerical experiment was performed in order to generate a synthetic dataset on which a calibration can be performed. An advantage to a numerical experiment and synthetic data is that the true values of the parameters will be known. The proceeding calibration demonstrations can thus be judged relative to the known values.

A coarse-grain microstructure model representing an aluminum oligocrystal was created using DREAM.3D [14], an open-source microstructure modeling and analysis package. Zhao et al. [47] observed that a significant portion of grain boundaries in an oligocrystal sample remained perpendicular to the surface of the sample, thereby maintaining a nearly columnar shape. For simplicity, an idealized perfectly columnar grain structure is considered in the current study, thereby resulting in the generation of a 2.5D microstructure. The columnar grain assumption serves to reduce a source of uncertainty that arises due to the through-thickness variation in grain structure [30, 42]. Based on the observations of Zhao et al. [47], the texture of the microstructure was assumed to be random, and an average grain size of 3.5 mm was used in creating the microstructure model. A 2.5D microstructure model of an aluminum oligocrystal (shown in Fig. 9a) was used in the current study. Figure 9b, c are the {001} and {111} pole figures, respectively, showing the orientations assigned to the 51 grains in the microstructure model. The dimensions of the microstructure model shown in Fig. 9a are 200 × 800 × 20 voxels, with each voxel having a resolution of 70 μm.

Fig. 9

(a) Front view of the 2.5D microstructure model used in the current work. Each unique color represents an individual grain. (b) {001} pole figure showing the overall orientation distribution of all the grains in the polycrystal model. (c) {111} pole figure showing the overall orientation distribution of all the grains in the polycrystal model

To prepare the geometry for finite element simulation, the “quick mesh” filter in DREAM.3D is applied to convert the grid geometry of the voxelated microstructure to a triangle geometry by inserting a pair of triangles on the face of each voxel or cell. Following the “quick mesh” filter, the “Laplacian smoothing” filter is applied to smooth out the stair stepped grain boundary profiles. The smoothed surface mesh of each grain is then output to a binary stereolithography file. Surface meshes of all the grains were input into Gmsh [12] to generate a volume mesh of the microstructure. The finite element volume mesh of the microstructure model was discretized into 5.837 million quadratic tetrahedral elements and contained 8.509 million nodes. The volume mesh is then input into the finite element code, ScIFEi [43], to carry out the computationally intensive CP simulations to solve for the heterogeneous stress and strain state within the microstructure.

The microstructure model is subjected to a 1% global strain by prescribing displacement-controlled loading conditions along with the other boundary conditions as depicted schematically in Fig. 10. Fully fixed constraints were applied on the bottom (−Y) face, whereas the top (+ Y) face, on which the displacement was prescribed, was constrained from any displacements in the X- and Z-directions. The remaining four faces (+ X, −X, + Z, and −Z) of the cuboidal microstructure domain were set to deform freely. The simulation was run in parallel on 400 processors using NASA Langley’s K cluster for about 38 h.

Fig. 10

(a) Front view of the microstructure domain showing the boundary conditions on + X, + Y, −X, and −Y faces. (b) Side view of the microstructure domain showing the boundary conditions on the + Z and −Z faces

The complex heterogeneous stress and strain fields developed within the microstructure are computed using a built-in anisotropic elasticity and CP framework in ScIFEi, Sect. 3.1. The grains were assigned anisotropic elastic properties, through three cubic elastic constants C ₁₁,C ₁₂, and C ₄₄, which were assigned the values 101.9, 58.9, and 26.3 GPa, respectively. Rate-dependent and length scale-independent CP kinematics (flow and hardening laws), discussed in Sect. 3, were assigned to the grains. The values of the calibration constants used for the CP model were chosen in such a way that they are in the range of the values assigned for corresponding parameters in CP models of aluminum alloys [4, 47], but do not pertain to any specific study.

As discussed in Sect. 3, the six fitting parameters present in the CP equations shown in Eq. 6 through Eq. 10 include g _o, ω, G _o, $\dot {\gamma }_{o}$, ${g}^*_{s}$, and m. The values of the six fitting parameters that serve as the target for calibration studies are shown in Table 2. It must be noted that since the non-deterministic local calibration model is insensitive to the values of the fitting parameters used, the chosen values will not influence the output of the calibration model. In order to mimic the lower yield strength of oligocrystal alloy, g _o and G _o were assigned lower values compared to the relatively finer grain material, Al 7075-T651 [4]. The lower g _o and G _o signify the lower yield strength of the aluminum oligocrystal, which is the material of choice in the current study.

Table 2 Fitting parameters used in the CP model

The heterogeneous distributions of stress and strain components in the loading direction, obtained at 1% global strain, are shown in Fig. 11. The stress and strain data obtained from the free surface of the microstructure model serves as the simulated DIC data.

Fig. 11

(a) Strain map on the free surface of the microstructure model showing the strain component in the loading direction obtained at a global strain of 1%. (b) Stress map on the free surface of the microstructure model showing stress component in the loading direction obtained at a global strain of 1%

In all of the proceeding calibration demonstrations, model inputs that are derived from the simulated experiments (i.e., geometry and loading) are noise-free. Measurement noise has been lumped into the measurement fields Y_i. For example, the stress-strain curve used in the global calibration has Gaussian noise added to the homogenized stress with a standard deviation of 0.5% of the maximum stress, Fig. 12. The strain values and the grain orientations for that case are noise-free and taken directly from the simulation. Gaussian noise with standard deviations of 0.07 microns and 5 MPa are added to each component of the simulated experiment’s DIC displacement and HREBSD stress, respectively, when these are used as data for model calibration. Note that the stress fields in simulated HREBSD have more added noise than the homogenized stress (standard deviation of 5 MPa compared to about 1.2 MPa, respectively) to reflect higher measurement error in the local method.

Fig. 12

Stress-strain curve from simulated experiment, including added measurement noise

6.1 Using Global Calibration

The demonstration of non-deterministic global calibration was performed using the Taylor model (see Sect. 4.2.2) and the uncertainty quantification framework described in Sect. 5. In this case, the measurements, Y_i, are the homogenized stresses from the simulated experiment. The model response $\mathcal {M}_i(\Theta )$ is the homogenized stresses of the Taylor model.

Before approximating the posterior parameter distribution with MCMC sampling, a deterministic optimization was performed to initialize the Markov chain. A Broyden-Fletcher-Goldfarb-Shanno (BFGS) [27] optimization was chosen with the initial guesses of the parameters at 105% of their true values. The open-source python package PyMC [29] was used to perform MCMC sampling with the delayed rejection adaptive Metropolis (DRAM) [16] step method. In total, 25,000 samples were generated, with the first 10,000 samples discarded as burn-in. The covariance of the proposal distribution was adapted every 1,000 accepted samples to accelerate convergence of the Markov chain to a stationary condition. The calibration took about 82 h on a single core of a 3.50 GHz Intel Xeon E5-1650 v3 CPU, corresponding to about 12 s per sample, although it should be noted that up to two samples can be evaluated for each new addition to the Markov chain due to the delayed rejection aspect of the DRAM algorithm.

The resulting marginal probability density functions of Θ are illustrated in Fig. 13. In general and with respect to the initial bounds, the distributions of the parameters are wide, corresponding to high uncertainty in the parameter values. Also, all of the distributions of the calibrated parameters are biased away from the true values (black triangles). This bias has been linked to model discrepancy [7], which generally leads to a violation of assumptions made in Sect. 5. The overestimation of the measurement noise variance supports this and points toward an inability of the Taylor model to accurately reproduce the measurements. Additionally, the lack of uniqueness of the calibration parameters and their corresponding high degree of correlation also plays a part in the large uncertainty in the parameters.

Fig. 13

The result of global calibration. The marginal probability density functions of the calibration parameters, including the estimate of the variance of the error. The triangle denotes the true values of each calibration parameter

The marginal probability density function for $g_s^*$ is relatively flat and spans the complete range specified by the bounds of the uninformative (uniform) prior. Essentially, the uncertainty in $g_s^*$ is similar to the prior, which indicates that the test used in the calibration did not provide significant insight on $g_s^*$. Because $g_s^*$ is related to saturation hardness, the above might indicate that the applied strain loading of the experiment was too small to see saturation; repeating the test to higher strains might help identify $g_s^*$. It is worth noting that, if a deterministic calibration was performed, a single value of $g_s^*$ would result, without knowing that the parameter was essentially unidentifiable by the test. Apart from gathering additional data to aid identification, a more informative prior could have been used to regularize the inverse problem. However, this was beyond the scope of this work, and the uncertainty in the calibrated $g_s^*$ was accepted as uniform over the given bounds.

6.2 Using Global-Local Calibration

The global-local calibration was set up using a finite element model with the same geometry as the simulated experiment. In order to remove the effect of erroneous boundary conditions, the same boundary conditions were applied as the simulated experiment.

The model was coarsened to decrease the model evaluation time. The coarse mesh contained 25,500 quadratic tetrahedral elements and 45,700 nodes. The time discretization of the model was also decreased by a factor of 2 compared to the simulated experiment. Model evaluation of the coarsened finite element model took approximately 9 min on 40 cores of a Dual socket 20 core 2.40 GHz Intel Gold 6148 Skylake Processor. Because a non-deterministic calibration akin to the one in Sect. 6.1 would take at least 156 days, a deterministic optimization was pursued instead. This means that a single deterministic set of calibration parameters is obtained, without an idea of how certain that calibration is.

The error metric for the optimization was the weighted sum of the error norms of the global (homogenized stress) and local (displacement) fields. The weighting was performed in the fashion of [26] which weights the errors at each scale based on the resolution of the measurement technique. In this case, the magnitude of the added measurement noise was used. After normalization of the two fields, equal weight was placed on global and local measurements.

The optimization was performed via Nelder-Mead simplex method [11] with the initial guesses of the parameters at 105% of their true values. The optimization took about 50 h to complete. The resulting optimal parameters are shown in Table 3. Example comparisons of the global and local response from the simulated experiment and optimal parameters are shown in Figs. 14 and 15. The global response is close to the simulated data with a slight under prediction. Presumably the bias seen in the global response was compensated by a more accurate local field, i.e., a balance of the global and local errors would be found.

Fig. 14

Global response comparison of the global-local optimization using finite element model updating. For these data, the mean absolute error is 1.32 MPa

Fig. 15

Local response comparisons for the global-local optimization using finite element model updating. Displacement fields are shown at the point locations of the simulated DIC (reference)

Table 3 Results of global-local deterministic calibration

From Figs. 14 and 15, it can be seen that overall the calibration was somewhat successful in matching the global and local behavior of the model; however, it is difficult to place confidence in the calibration without a measure of uncertainty. Furthermore, there is no guarantee that the optimized values represent global optimal values; it is possible they only correspond to a local optimum. No insight on $g_s^*$ is gained besides a single optimum value.

6.3 Using Local Calibration

The demonstration of non-deterministic local calibration was performed by directly integrating the CP model given a local grain orientation from EBSD and local deformation gradients stemming from simulated DIC. In this case, the measurements, Y_i, are the deviatoric stresses fields from the simulated experiment (i.e., simulated HREBSD). The model response, $\mathcal {M}_i(\Theta )$, is the deviatoric part of the stress resulting from the CP model integration. It is worth noting that in this demonstration, the full deformation gradient is imposed on the CP model, which assumes unrealistically that all components of strain can be identified with DIC. With addition of a plane-stress constraint, the result is not expected to be altered significantly by the restriction of the DIC information to the planar strains.

The local calibration was again non-deterministic. As in the global calibration, a deterministic optimization was performed to initialize the Markov chain prior to MCMC sampling. The same optimization and MCMC options were used for this local calibration as before. This includes the generation of 25,000 samples with a 10,000 sample burn-in. The calibration took about 116 h to run on a single core of a 3.50 GHz Intel Xeon E5-1650 v3 CPU, corresponding to about 17 s per sample. Again, the effect of rejection on this per-sample estimate should be noted.

The resulting marginal probability density functions of Θ are illustrated in Fig. 16. The distributions are now much tighter when compared to the global posterior. More importantly, these distributions now encompass the true values. The local calibration is better able to identify the parameters for two reasons: first, an increased amount of data acquired and second, the CP model is directly probed rather than utilizing homogenized values, which diminishes the model discrepancy. As in the local calibration, the probability density function of $g_s^*$ looks similar to the uniform prior, illustrating that the simulated experiment was not very informative for this parameter. The σ ² probability density functions in Fig. 16 should not be compared to those shown in Fig. 13 because they correspond to noise estimates of different data sets (i.e., noise in homogenized stress vs. noise in HREBSD stress).

Fig. 16

The results of local calibration. The marginal probability density functions of the calibration parameters, including the estimate of the variance of the error. The triangle denotes the true values of each calibration parameter

7 Summary

The objective of this chapter is to motivate the use of CP models in microstructure-dependent engineering problems and to provide a comprehensive study of calibrating CP model parameters. Historical perspective and background is provided for understanding what methods have been published, in terms of both generalized parameter identification methods and specific methods studied for use with CP models. A review of the literature illustrates that the methods for CP parameter calibration studied to date have largely focused on global-local methods, where a combination of global (homogenized) stresses are combined with local DIC displacements or strain to form the comparison between measured and computed data.

Various methods for acquiring and post-processing data are also overviewed. Global data, as would come directly from test-stand data or attached gauges, are relatively cheap and easy to apply. Consequently, especially when many tests are being performed, acquiring global data may be the only affordable method. Acquiring local DIC displacement and strain data provides a significant improvement on the measured data set. But, this comes with a cost of additional equipment and setup time. Additionally, application of this data in the global-local approach also implies the need to acquire EBSD data before testing. Local stress data can also be measured using HREBSD to analyze shifts in diffraction patterns. Combining both local methods, DIC and HREBSD, is now possible with selectively transparent stamping as the means to apply a DIC speckle pattern to the test specimen surface. However, this method requires the highest level of infrastructure and time since both HREBSD and DIC must be completed multiple times during testing.

Three classes of calibration methods can be used, differing by the type of acquired data. While global data is the easiest and cheapest to acquire, CP model parameter calibration using that data has fundamental issues. Namely, because many sets of CP model parameters can reproduce nearly equivalent global stress-strain curves, there should be no expectation that the calibrated parameters are unique. Adding local DIC displacement data aids in the mitigation of this uniqueness issue, but there are still local minima that exist in this case. Because of the hybrid approach, with both global and local data, the computational model in this case must represent the particular microstructure being tested. Running these full simulations, for example, as a finite element model, is computationally intensive and intractable for a non-deterministic approach. Additionally, this leads to the need for assumptions or direct measurement of the microstructure underlying the surface and high sensitivities to applied boundary conditions. Purely local data enables a computationally tractable method for non-deterministic calibration. Furthermore, this method precludes issues of generating a model of the microstructure aggregate, does not incorporate boundary conditions, and helps resolve the issue of uniqueness. However, as illustrated by the calibration of $g_s^*$, the model parameters cannot be determined accurately without adequate data that has sensitivity to the parameter.

As complexity in acquiring data is added, the computational cost of the calibration and issues surrounding uniqueness can be resolved. The combination of the results from Fig. 13, Table 3, and Fig. 16 is shown in Fig. 17; it illustrates the calibrated parameters from each approach. The two distributions represent the calibrated parameters for the purely global (red) and purely local (blue) methods. This clarifies the relative uncertainty and inaccuracy in calibrating CP model parameters using only global data. On the other hand, the purely local method results in very little uncertainty and accurately reproduces the correct parameters (black triangles). Because it is computationally intractable to run the global-local calibration because of the costly computational model required, the single deterministic value for each parameter is shown (downward-pointing magenta triangle). As mentioned above, the inclusion of local DIC data improves significantly the calibrated result of a purely global approach, but still suffers from inaccuracy because of local minima.

Fig. 17

The results of all calibrations. The marginal probability density functions of the calibration parameters for the global calibration (red) and local calibration (blue). The upward-pointing black triangle denotes the true values of each calibration parameter. The downward-pointing magenta triangle denotes the deterministic result of global-local optimization

8 Outlook

The ability to make high-resolution and volumetric observations and measurements of material microstructures is ever-increasing. The measurement techniques described in this chapter were chosen to represent methods that could be employed in a common materials research laboratory at the present. Consequently, data acquisition methods were mainly focused on high-resolution surface measurements, EBSD and DIC, along with load-displacement data acquired through mechanical testing. However, volumetric acquisition methods, such as X-ray computed tomography (CT) and high-energy X-ray diffraction (HEDM), are becoming increasingly valuable and available.

With these improved data acquisition methods, the various global and local calibration methods presented in this chapter may still be used. Utilizing only surfaced-based approaches includes uncertainties to the calibration process due to unknown subsurface features, such as grain variations and defects. For example, a subsurface defect can influence the local strain on the surface as measured by DIC. Using only a surface-based approach, this would manifest as additional (inaccurate) variation in the calibrated parameter distribution. However, if that same subsurface feature was detected using X-ray CT and included in the computational model, a more accurate calibrated parameter distribution would be expected. Consequently, an important next step is to quantify the improvement in calibration that can be expected with volumetric acquisition methods and weigh those against the added costs and time associated with acquiring that data.