Development of an in situ method for measuring elastic and total strain fields at the grain scale with an estimation of accuracy

Abstract

Identifying the parameters of a crystal plasticity model requires the use of grain scale experimental data. The objective of our work is to develop a robust procedure to identify the model using information at the scale of the crystals. In this study, an in situ experimental measurement has been developed for the parameter identification of crystal plasticity models. During the experimental stage, the total ${\left( \epsilon ^t\right) }$ and elastic ${\left( \epsilon ^e\right) }$ strain fields of an Al-alloy specimen with around 12 grains were measured at the same time. The total strain fields were determined by digital image correlation. For this, a speckle-painting was applied on the sample surface which was tracked to derive the total deformation of the specimen surface under loading. The elastic strains were calculated from X-ray diffraction measurements. Yet certain experimental difficulties had to be solved in order to achieve these simultaneous measurements. Besides results and analysis, the corresponding uncertainties during each measurement were quantified as well.

Introduction

Crystal plasticity models allow one to describe the changes of the microstructure of a crystalline material and predict its local behaviour. As the physical mechanisms—on which the constitutive equations are based—are the main causes of material deformation, these equations are able to predict the strain and stress heterogeneities under thermomechanical loading [2, 14, 30, 31]. For example, the local disorientations due to forming [9] or the localisation of the plastic deformation which leads to crack initiation in fatigue [22, 33] can be predicted.

However, the parameters of these models are difficult to identify because the mechanisms they describe are at a small scale and are thus difficult to measure directly (e.g. evolution of dislocation density, strain hardening, pile-ups at grain boundaries, changes in dislocation microstrutures, etc.). Identification of the parameters of these models is usually performed by an inverse method from macroscopic tests curves [12, 15]. There are two feasible approaches.

The first approach uses a self-consistent method based on [11, 20] wherein the mechanical behaviour is described using a micromechanical model, in which grains are considered as inclusions embedded in a homogeneous equivalent medium [1, 13, 21, 26]. In this approach, the texture and elongation ratio of grains can be taken into account. Yet neither a specific shape of the grains nor specific grain boundary misorientation are dealt with.

Another approach consists of modelling representative 3D polycrystalline aggregates which can be obtained experimentally by FIB-SEM serial-sectioning [6], by tomography [23] or by Voronoi tessellation (CVT) [3–5, 34, 35]. In order to account for the mean behaviour of the material, it is necessary to include a sufficient number of configurations (e.g. grain orientations and positions, neighbouring grains and shapes). These configurations can be included in a unique aggregate if it is sufficiently large [the representative volume element (RVE)] or in several smaller aggregates. The mean behaviour of these small aggregates, if not too small, converges to the behaviour of the RVE [18]. This method, although the calculations are more time-consuming, allows one to take specific characteristics of the microstructure (realistic shape of the grains, specific neighbouring misorientation, percolation of one or several phases, etc.) into consideration.

These two methods allow one to simulate the macroscopic stress–strain response and to perform the parameter identification by comparison with experimental measurements. However, minimising a cost function based on macroscopic measurements may lead to local minima, and not to a global one. The validity of such an identification is thus generally limited to the experimental tests used during the identification stage. In order to increase the robustness of the identification, it is necessary to give a physical meaning to the parameters. To accomplish this, local experimental data at the grain scale were used. The richness of the data provided by the experimental fields measured on the surface of the specimen should allow one to constrain the values of the parameters to be identified. The objective of the present work is to access local information, which will be used in a second step as input to allow the identification of a crystal plasticity model. This information is needed not only in a single point but in a wider field as the more measurement points used, the more precise the identification will be.

Several methods allow one to assess elastic strain locally, and they are all based on diffraction of crystalline planes. They can use either electron backscatter diffraction patterns [17, 19] or Laue microdiffraction [29]. As we wanted to carry out in situ mechanical tests and be able to determine the strain field in the whole specimen, an X-ray method was preferred and is detailed in the section of experimental methods.

The present paper focuses on in situ experimental measurements at the intragranular scale. Total ${\left( \epsilon ^t\right) }$ and elastic ${\left( \epsilon ^e\right) }$ strain fields of a specimen with around 12 grains were measured simultaneously at each imposed loading level (Fig. 1). The total strain fields were determined by Digital Image Correlation (DIC) using ${Correli\_Q4}$ software [16]. For this, a speckle-painting was applied on the sample surface. The elastic strains were calculated from X-ray diffraction (XRD) measurements [10]. At the same time, some experimental difficulties had to be solved in order to achieve these simultaneous measurements. Besides results and analysis, the corresponding uncertainties during each measurement were quantified as well.

This paper is organised as follows. “Materials and sample preparation” section describes the sample preparation and the material. Experimental methods and measuring techniques are introduced in “Experimental methods” section. “Results and discussion” section presents and discusses the results and the corresponding uncertainties. Finally, “Conclusion” section closes the paper with a short summary, conclusions and a perspective.

Fig. 1

Principle of simultaneous kinematic full-field measurements

Materials and sample preparation

For the experiments, a specimen in aluminium alloy (5052) was used. The chemical composition is given in Table 1.

Table 1 Chemical composition (in wt%) of the aluminium alloy used (5052)

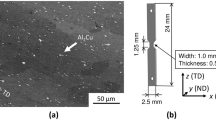
The dimension of the tested specimen is given in Fig. 2. To facilitate the measurements of strain gradients inside the grains, a polycrystalline structure with the grain sizes ranging from 5 to 20 mm were obtained by recrystallization after critical work hardening. The sample contains around 12 grains per side and 2 grains in the thickness of 0.55 mm (Fig. 3) [7].

Fig. 2

Sketch of the sample used showing its large grains (in mm)

Fig. 3

Thickness view of the sample. Grain boundaries (in dashed lines) between the two layers are at mid-thickness

Experimental methods

Simultaneous $\epsilon ^t$ and $\epsilon ^e$ measurements

Implementation

The experimental device was set up (Fig. 4) to conduct the tests in situ in a diffractometer [7]. The micro-tensile machine designed by Deben and a single-lens reflex camera are installed inside. The reflex camera faces the specimen vertically during DIC measurement. The XRD measurements were performed on a Panalytical X’Pert Pro MRD 7-axis goniometer. The description of the XRD apparatus is given in [7]. A cable guide has been designed around the micro-tensile machine to prevent it from crossing the beam during diffraction measurements. The experimental setup provided an observation area of ${17 \times 8}$ ${\mathrm{mm^2}}$ for DIC measurement and ${15 \times 8}$ ${\mathrm{mm^2}}$ for XRD measurement (Fig. 5).

Fig. 4

Experimental setup

Fig. 5

Useful part of XRD measurement (in dashed line)

Initial microstructure

Initial shape of the grains

Knowing the initial microstructure of the sample is essential for positioning the sample with respect to the X-ray beam during characterisation process. As mentioned in “Materials and sample preparation” section, there are two layers of grains in the useful part of the sample, the mechanical response of a grain is not only affected by its own crystalline orientation [32] but also by the surrounding grains with different crystal orientations [24].

Each grain position in the sample was measured using an optical microscope (Fig. 6). To better distinguish the grain boundaries, photos of the sample at the same position were captured with different lighting directions. The accurate grain cartography facilitated the XRD scanning programming. Trading off with the grain size and measuring time, there are approximately 20 points of XRD measurement per grain and the spatial resolution is ${1 \times 1}$ ${\mathrm{mm^2}}$. The spatial resolution for DIC is much finer and is 326.4$\mu$m (=32pixels). The choice of the spatial resolution for DIC will be presented later.

In this paper, half of the useful part was measured with XRD, in order to validate the methodology. DIC measurements were carried out on the entire useful part (Fig. 6).

Fig. 6

The spots indicate the X-ray measuring positions

The crystallographic orientation

The crystal orientations are represented by three Euler angles ($\varphi _1$, $\Phi$, $\varphi _2$) defined by the relative orientations of the sample and the crystal coordinate systems. The crystal orientations of every grain were firstly characterised by XRD using inverse method (Fig. 7) [7].

Fig. 7

Logic diagram for finding Euler angles of a given grain which match the results measured by XRD

Fig. 8

Front view of the sample with its grains numbered

Fig. 9

Back view of the sample with its grains numbered

The coordinate system of the sample was defined as in Fig. 8. When measuring the Euler angles of the grains on the back side ($\varphi _1^\prime$, $\Phi^\prime$ , $\varphi _2^\prime$ )$_{grain}$ of the sample, the sample is rotated 180° along y-axis (Fig. 9). Therefore, the actual grain orientations ($\varphi _1$, $\Phi$, $\varphi _2$)$_{grain}$ on this side need to take the rotation of 180^° along y-axis Ry into account. There are two options for this transformation:

$$\begin{aligned} \varphi _1 = \pi - \varphi _1^{\prime } ; \quad \Phi = \pi + \Phi ^{\prime } ; \quad \varphi _2 = \varphi _2^{\prime } \end{aligned}$$

(1)

or

$$\begin{aligned} \varphi _1 = - \varphi _1^{\prime } ; \quad \Phi = \pi - \Phi ^{\prime } ; \quad \varphi _2 = \pi + \varphi _2^{\prime } \end{aligned}$$

(2)

In this article, the first option was used and the crystal orientations of both sides of the sample are shown in Appendix 6.

Unlike EBSD scanning which requires a high quality of polishing on the sample surface, this is a non-destructive and residual-stress-free method to determine the material’s texture.

$\epsilon ^t$ field measurement

DIC measuring method and quality of the speckle paint

Total strain $\epsilon ^t$ field was derived using the digital image correlation. A speckle pattern painting in black and white (top left Fig. 10) was sprayed on the sample surface and images of the same region of the sample were taken regularly during mechanical tests for comparison. The software ${Correli\_Q4}$ [16] was used for image analysis and the displacement field calculation. To ensure the quality of the speckle paint, the painting thickness, grey histogram and measurement errors were quantified using the same software (Fig. 10). In addition, a glass sample coated with the same thickness of speckle was diffracted by X-ray to ensure the absence of metallic components which may disturb the XRD [7].

Fig. 10

Speckle verification conducted by ${Correli\_{Q4}}$. A polycrystalline sample covered by speckle-painting and a zone of 10.5 × 5.1mm² was selected for speckle verification. The resolution captured by camera is 10.2 ${\mu }$m/pixel (Top left). The speckle pattern is made of two colours: black and white. The high resolution of the image enables one to distinguish the black/white edges easily and avoids averaging blurred black–white area to a grey one (Top right). Hence, there is a superposition of two grey level distributions (a Gaussian function for each colour) in the histogram (Bottom left). A large grey level distribution improves the accuracy of displacement field measurements. For the element size 362.4 ${\mu }$m (=32 pixels), the average error is 3.1 nm (=$2.75\times 10^{-4}$  pixels) (Bottom right)

$\epsilon ^e$ field measurement

Application of Bragg’s law

The interreticular plane distance $d_{hkl}$ can be used as a gauge to measure the local elastic strain $\epsilon ^e$ (Fig. 11) through the application of Bragg’s law (Eq. 3):

$$\begin{aligned} d_{hkl} = \frac{\lambda }{2{\rm sin}(\theta )} \end{aligned},$$

(3)

where $\theta$ is the diffraction angle and $\lambda$ is the wavelength of the X-ray source.

Differentiating Eq. 3 by using the product rule, we get

$$\begin{aligned} \epsilon _{hkl} = \frac{\delta {d_{hkl}}}{d_{hkl}} = -{\mathrm{cot}}\theta \cdot \delta \theta \end{aligned}.$$

(4)

Therefore, if $d_{hkl}$ increases (which corresponds to a tension state, $\epsilon _{hkl}>0$), $2\theta _{hkl}$ value of the peak decreases with respect to its initial position (Fig. 12), and vice versa. The lattice parameter $a_0$ (= 0.4067nm) of our Al-alloy was characterised by XRD in its initial state, with the powder method.

Fig. 11

Illustration of X-ray diffraction method

Fig. 12

$2\theta _{\left( -2-22\right) }$ of Grain3 ($X=-1,Y=-1$) in its initial state (blue line with markers ‘$\cdot$’) and at ${\overline{\epsilon }^t_{xx}}$ = ${7.4\times 10^{-3}}$ (red line with markers ‘x’) (Color figure online)

X-ray diffraction technique: first Ortner method [28]

The metric tensor G can be calculated during a tensile test knowing the peak positions for each ($\phi$, $\psi$)$_{\{hkl\}}$, so that the strain tensor $\epsilon$ can be deduced. The relationship between the selected $\{hkl\}$ plane distance (vector ${D^*}$ in the reciprocal lattice) and reciprocal metric tensor ${G^*}$ can be described with a matrix H, which is constructed using the co-ordinates of the diffraction vectors of these $\{hkl\}$ planes in the reciprocal lattice (Eq. 6).

$$\begin{aligned} D^* = d^{-2} = \frac{4{{\mathrm{sin}}(\theta )}^2}{\lambda ^2} \end{aligned}$$

(5)

$$\begin{aligned} \left( \begin{array}{c} D_1^*\\ D_2^*\\ D_3^*\\ \vdots \\ \vdots \\ D_n^*\end{array} \right) = \left( \begin{array}{ccccccccc} h_1^2 &{}\quad k_1^2 &{}\quad l_1^2 &{}\quad 2{k_1}{l_1} &{}\quad 2{h_1}{l_1} &{}\quad 2{h_1}{k_1}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ h_n^2 &{}\quad k_n^2 &{}\quad l_n^2 &{}\quad 2{k_n}{l_n} &{}\quad 2{h_n}{l_n} &{}\quad 2{h_n}{k_n}\end{array} \right) \left( \begin{array}{c} G_1^*\\ G_2^*\\ G_3^*\\ G_4^*\\ G_5^*\\ G_6^*\end{array} \right) \end{aligned}.$$

(6)

In Eq. 6, ${G_1^*}={g^{11}}$, ${G_2^*}={g^{22}}$, ${G_3^*}={g^{33}}$, ${G_4^*}={g^{23}}$, ${G_5^*}={g^{31}}$ and ${G_6^*}={g^{12}}$. And this equation can be rewritten as

$$\begin{aligned} D_{n\times 1}^* = H_{n\times 6} G_{6\times 1}^* \end{aligned}.$$

(7)

At least 6 $\{hkl\}$ planes are required to determine ${G^*}$ in Eq. 7. In order to enhance the measurement precision, more than 6 planes are desired. The method of least squares has been used to determine ${G^*}$ as follows:

$$\begin{aligned} G^*_{6\times 1} = \left[ \left( H^T\cdot H\right) ^{-1}H^{T}\right] _{6\times n} \cdot D_{n\times 1}^* \end{aligned}.$$

(8)

The advantage of this method is its independence with respect to the $2\theta$ rotation. The strain tensor $\epsilon$ is then determined by

$$\begin{aligned} \epsilon _{ij} = \epsilon ^{ij} = \frac{g^{ij}-g_0^{ij}}{{2}\sqrt{g_0^{ii}}\sqrt{g_0^{jj}}} \end{aligned},$$

(9)

where $g_0^{ij}$ et $g^{ij}$ are the contra-variant co-ordinates of the initial and the deformed metric tensor G*.

Choice of $\{hkl\}$ planes and criteria associated

Besides the requirement to determine the six components of ${G^*}$, measurement of additional $\{hkl\}$ planes will improve the precision of the calculation. Moreover, errors and existing limitations of the experimental apparatus should be taken into consideration. Crystal planes with a larger diffracting plane distance will have a smaller diffraction Bragg angle and correspond to higher intensity. However, $\{hkl\}$ planes with large values of $2\theta$ improve measurement precision (Table 2). The choice of $\{hkl\}$ planes results in a compromise between peak intensity and precision of $2\theta$ variation. Thus, for a sample of Al-alloy with FCC structure, only $\{220\}$, $\{311\}$ and $\{222\}$ planes are considered. According to the limits of the goniometer, 18 $\{hkl\}$ planes fulfil the above requirements. Yet, the grips of the micro-tensile machine restrict the accessible angle for X-ray beam diffracting towards the sample. Even so, a weak diffraction beam intensity is obtained once the cradle inclines more than $75^{\circ }$ along the $\psi$-axis. In the remaining $\{hkl\}$ planes, planes forming a circle in the pole figure are preferred since this combination minimises the uncertainty [27]. As a result, after eliminating all the inaccessible ($\phi$,$\psi$)$_{hkl}$, 13 $\{hkl\}$ planes are left to be analysed at every XRD measuring point (Fig. 13).

Table 2 Theoretical variation of $2\theta$ corresponding to various $\{hkl\}$ planes of a crystal submitted to a strain of ${4.29\times 10^{-3}}$ in the ${\left\langle 100 \right\rangle }$ direction

Fig. 13

Location of the $\{hkl\}$ planes summarised for XRD measurement in grain 7. Only accessible $\{220\}$, $\{311\}$ and $\{222\}$ planes are considered

XRD measuring method

As it will be necessary to determine small $2\theta$ variations of the order of ${0.4^{\circ }}$–${0.6^{\circ }}$ during the mechanical loading (see Table 2), the initial ($\phi$,$\psi$)$_{hkl}$ should be measured with high accuracy before determining the tensor $\epsilon ^e$. The diffraction peak of an $\{hkl\}$ plane in a monocrystal is very fine (width ${<\! 1^{\circ }}$). To measure $\epsilon ^e$ with accuracy, each peak position should be cautiously measured at each step. As such, the position of the diffraction peak is searched for along $\phi$, $\psi$ and $2\theta$ successively around an initial position determined by the initial texture. This optimisation procedure is repeated until convergence [10].

The stability of the optimisation process has been tested and validated in a crystal of an Al-alloy sample. Several sets of parameters ($\phi$, $\psi$ and $2\theta$) in the vicinity of a given peak were considered as initial positions (Fig. 14). The optimisation process was carried out from these various initial positions to determine the peak position along $\phi$, $\psi$ and $2\theta$. After 3 iterations, all of the processes converged to nearly the same $2\theta$ value with a variation of ${0.005^{\circ }}$(Fig. 15).

Fig. 14

Method used for testing the stability of the optimisation process

Fig. 15

Changes in ${2\theta }$ after several iterations of measurement starting from various initial positions. The final variance ${\Delta 2\theta }$ is about 0.005${^\circ }$

Once the tensile test has started, the sample deforms elastically and plastically. The elastic deformation induces peak translation, as shown in Fig. 12. After plastic deformation, one or more crystal re-orientations can be found inside a grain, which is called mosaicity. The mosaicity development as well as dislocation accumulation during plastic deformation cause XRD peak broadening and intensity decrease (Fig. 16). The grain disorientation and peak broadening are the evidence of heterogeneous deformation in materials [8]. The objective of the experimental procedure developed here is to measure peak translation without the interference due to plastic deformation. In some conditions, the plastic deformation may be so large that several distinct peaks may appear (Fig. 16). We decided to consider only the peak with the highest intensity. In order to limit this mosaicity [25], the beam size has been refined to $0.1\times 0.1$ ${\mathrm{mm^2}}$. The intensity is sufficient for the peak measurement and optimisation, as the signal to noise ratio remains higher than 60. Furthermore, as the strain levels remain small during the experiment presented, the displacement of the peaks was small enough to consider the position associated with the previous loading step as a starting point for searching for the peak position after deformation.

The final $2\theta$ peak position determination is presented in the following subsection.

Fig. 16

Evolution of a peak of $(-222)_{Grain7}$ from its inital state (left) to ${\overline{\epsilon }^t_{xx}}$ = ${7.4\times 10^{-3}}$ (middle) and ${\overline{\epsilon }^t_{xx}}$ = 0.0356 (right). Intensity drops as strain level increases due to the crystal orientation dispersion during plastic deformation

Accuracy of $2\theta$ positioning

The X-ray $K_\alpha$ line is by far the strongest emitted X-ray spectral line. It contains 2 lines: $K_{\alpha 1}$ and $K_{\alpha 2}$ with wavelengths relatively close ($\lambda _{K\alpha 1(Co)}$= 0.178897 nm and $\lambda _{K\alpha 2(Co)}$= 0.179285 nm). These components are not easily resolved. During $2\theta$ measurement, both $K_{\alpha 1}$ and $K_{\alpha 2}$ interact with $\{hkl\}$ crystalline planes (Fig. 17b), and therefore, a diffraction peak doublet is obtained.

Fig. 17

a Scheme of X-ray diffraction. b $2\theta$ measured by XRD (solid line) contains peak doublets. Simulation of the peak (dashed line)

Owing to the complicated form of the peak, the $2\theta$ position is not able to be determined immediately. The peak position is sought through an inverse method by modelling the diffracted peak as the sum of two Gaussian functions ${{\mathcal {G}}}$ (Eq. 10).

Gaussian function ${\mathcal {G}}$ for each spectral line is defined as

$$\begin{aligned} {\mathcal {G}}\big (A_{\rm p},h_{\rm p},2\theta _p\big ) = \frac{2A_p}{h_p}\sqrt{\frac{ln2}{\pi }}{\rm e}^{\frac{-4{\rm ln}2}{h_p^2}\big (2\theta _{\rm p}-2\theta \big )^2} \end{aligned}$$

(10)

with the properties:

• (1) $h_{p}$ is the full width at half maximum (FWHM)

• (2) Amplitude $A_{p}$ of $K_{\alpha 1}$ is always twice as large as that of $K_{\alpha 2}$

  $$\begin{aligned} A_{p\_K\alpha 1} = 2A_{p\_K\alpha 2} \end{aligned}$$

  (11)

• (3) $2\theta _{p}$ is the simulated final peak position. The Gaussian function ${\mathcal {G}}$ is defined in the range $[2\theta _p-2\theta ,2\theta _p+2\theta ]$. As $d_{hkl}$ is the same for $K_{\alpha 1}$ and $K_{\alpha 2}$, Bragg’s law (Eq. 3) can be applied to describe the relationship of the peak position between $K_{\alpha 1}$ (${\theta _{K\alpha 1}}$) and $K_{\alpha 2}$ (${\theta _{K\alpha 2}}$).

  $$\begin{aligned} \frac{\lambda _{K\alpha 1}}{{\rm sin}(\theta _{p\_K\alpha 1})} = \frac{\lambda _{K\alpha 2}}{{\rm sin}(\theta _{p\_K\alpha 2})} \end{aligned}.$$

  (12)

Several peak forms were tested, Gaussian functions were the most appropriate to predict experimental diffraction peaks. After minimising the difference between experimental and simulated data, the optimised ${2\theta _{p\_K\alpha 1}}$ was used to calculate elastic strain tensor.

Results and discussion

In-plane strain fields were measured on the upper surface of the oligo-crystal specimen at two successive loadings. $\epsilon ^t$ and $\epsilon ^e$ fields are plotted in the initial configuration with grain boundaries superimposed.

Tensile tests

During the in situ experiment, the sample was subjected to a symmetric loading in the x-direction. The micro-tensile machine was stopped twice for XRD measurements at increasing levels of strain—once was just after the yield stress at 81.1 MPa, ① ${\epsilon }^t_{xx}$ = 0.0074 and the second was at 118.6 MPa, ② ${\epsilon }^t_{xx}$ = 0.0356. Photos were taken throughout the entire tensile test and the total strain fields were calculated using $Correli\_{Q4}$. The tensile stress measured during the test is plotted in Fig. 18 versus the mean strain averaged over the useful part of the specimen.

Fig. 18

Stress–strain curve. The micro-tensile machine was stopped once at ① ${\epsilon }^t_{xx}$ = 0.0074 and then at ② ${\epsilon }^t_{xx}$ = 0.0356

Total strain field measurement $\epsilon ^t$

Map of $\epsilon ^t$

The in-plane components ${\epsilon }^t_{xx}$ and ${\epsilon }^t_{yy}$ are plotted in Figs. 19, 20, 21 and 22. As shown in Figs. 19 and 21, relatively homogeneous fields are observed per grain but are heterogeneous when compared to each another. This heterogeneity increases with the imposed loading. The magnitude of the axial strain is much higher on the left-hand side of the sample than on the right-hand side. This difference can be explained by the initial crystallographic orientation of grains on both the front and the back sides of the sample, since grains with favourable orientation to the loading direction and thus the highest Schmid Factor (SF) deform first. For example, grains 2, 3 and 7 on the left have a SF of about 0.5 (7) while grains 4, 12 and 13 on the right have a SF of about 0.4. Although the SF of grains 5 and 9 on the right-hand side are high, the grains right behind then (grain 1bi, 1bii and 14b) have low SFs, which explains why the strain is globally much lower on this side.

Fig. 19

Map of $\epsilon ^t_{xx}$ at level ① $\big ({\overline{\epsilon }^t_{xx}}$ = ${7.4\times 10^{-3}}\big )$

Fig. 20

Map of $\epsilon ^t_{yy}$ at level ① $\big ({\overline{\epsilon }^t_{yy}}$= ${-4.8\times 10^{-3}}\big )$

Fig. 21

Map of $\epsilon ^t_{xx}$ at level ② $\big ({\overline{\epsilon }^t_{xx}} = 0.0356\big )$

Fig. 22

Map of $\epsilon ^t_{yy}$ at level ② $\big ({\overline{\epsilon }^t_{yy}} = -0.0221\big )$

Uncertainties of DIC

In order to quantify DIC uncertainties, 38 photos of the sample surface covered with speckled painting were taken in the same conditions of loading and lighting (initial state). Digital correlation was performed between images taken in pairs (Fig. 23). The total error amplitude of the strain field calculated was $\pm 4\times 10^{-4}$.

Fig. 23

Error maps of 2 photos taken (1 photo/s) in the initial state under the same experimental environment. It shows that the background noise gives DIC a random total strain error of $\pm 4\times 10^{-4}$ at each measuring point

Elastic strain field measurement $\epsilon ^e$

Map of $\epsilon ^e$

Fields of components $\epsilon ^e_{xx}$ and $\epsilon ^e_{yy}$ obtained at levels ① and ② are shown in Figs. 24, 25, 26 and 27. Similar to the $\epsilon ^t$ results, heterogeneous elastic deformation was observed on the sample surface. Due to local grain disorientation during plastic deformation (mentioned in “XRD measuring method” section), the intensity of some $\{hkl\}$ peaks for some measuring points was too low to allow their measurement and thus elastic strain tensor calculation. This explains the absence of some strain field measurements in Figs. 26 and 27.

Fig. 24

Map of $\epsilon ^e_{xx}$ at level ① $\big ({\overline{\epsilon }^e_{xx}}$ = ${1.1\times 10^{-3}}\big )$

Fig. 25

Map of $\epsilon ^e_{yy}$ at level ① $\big ({\overline{\epsilon }^e_{yy}}$= ${-0.2\times 10^{-3}}\big )$

Fig. 26

Map of $\epsilon ^e_{xx}$ at level ② $\big ({\overline{\epsilon }^e_{xx}} = {1.6\times 10^{-3}}\big )$

Fig. 27

Map of $\epsilon ^e_{yy}$ at level ② $\big ({\overline{\epsilon }^e_{yy}}= {-0.2\times 10^{-3}}\big )$

Uncertainty estimation of the elastic strain tensor $\sigma _{\epsilon ^e}$

Two steps are necessary to determine the uncertainty of the elastic strain tensor $\sigma _{\epsilon ^e}$. It is first necessary to evaluate the uncertainty of peak position measurement $\sigma _{\theta }$, and then, by knowing this value, $\sigma _{\epsilon ^e}$ can be calculated. It is assumed that the error of the peak position $\sigma _{\theta }$ has two main sources: one is related to the peak repositioning by the diffractometer ${\Delta 2\theta }$, and another is linked to the discretization of the intensity curve in ${\delta 2\theta }$. So, a priori, both of these sources of error have to be quantified. Moreover, although the method chosen to estimate $\sigma _{\epsilon ^e}$ is discretization-related (Eq. 22), if the repositioning error shows a more significant value, it should be taken into account instead of the discretization error.

• (1) Uncertainty of peak position $\sigma _{\theta }$

  To evaluate $\sigma _{\theta }$, two approaches were used. The first approach consisted in determining the position of a given peak from various initial positions, and comparing the final peak positions obtained. As mentioned in “XRD measuring method” section, the error obtained is ${\Delta 2\theta = \pm 0.0025^{\circ }}$.

  $$\begin{aligned} \Delta \theta \le 0.00125^{\circ } \end{aligned}.$$

  (13)

However, this approach took into account only one part of the measurement chain. It was also necessary to evaluate the accuracy of the method used to determine the peak position from the distribution of intensities around a peak. Inspired by the method for calculating displacement and total strain field uncertainties [16], an evaluation of the precision of peak position measurement with small shifts in $\theta$ was conducted as follows:

• (a) For existing XRD data measured with a scanning step of $0.05^{\circ }$ (blue line with markers $\times$), a shift of ${\delta \theta }$ ($\le 0.05^{\circ }$) was imposed, i.e., $2\theta ^\prime$ = $2\theta$ + ${\delta \theta }$ (black markers $+$) (Fig. 28).

• (b) The discrete experimental points were projected on the shifted line by linear interpolation (green points with markers $*$).

• (c) The peak simulation process presented in “Accuracy of $2\theta$ positioning” section was carried out to determine the peak positions for both the initial measurement ${2\theta _{\mathrm{XRD}}}$ and shifted-projected measurement ${2\theta _{\mathrm{shifted}}}$ .

• (d) The change between the imposed ${\delta \theta }$ and the calculated ${\delta \theta }$ (${\delta \theta }$ = ${2\theta _{\mathrm{XRD}}}$ and ${2\theta _{\mathrm{shifted}}}$) was calculated.

Fig. 28

Method to evaluate the ability of detecting small peak displacements along $\theta$

A measuring point in Grain7 was taken as an example in results of Table 3. Errors in ${\delta \theta _{-202}}$, ${\delta \theta _{-131}}$ and ${\delta \theta _{-222}}$ were observed for small peak displacements along $\theta$ (Table 3). The fractional changes between imposed and obtained ${\delta \theta }$ were calculated. This error was insignificant starting from ${\delta \theta }_{\mathrm{imposed}}$ = $0.025^{\circ }$—half of the scanning step size—until $0.0001^{\circ }$ as the criterion of $5\,\%$ of error was firstly reached using ${\delta \theta _{-222}}$ (Fig. 29). As a result, the smallest measurable shift is $0.0001^{\circ }$ (Eq. 14).

The error in the measurement of $\theta$ is thus

$$\begin{aligned} \delta \theta \le 0.0001^{\circ } \end{aligned}.$$

(14)

Table 3 Errors in ${\delta \theta _{-202}}$, ${\delta \theta _{-131}}$ and ${\delta \theta _{-222}}$ were observed for small peak displacement along $\theta$

Fig. 29

Error between ${\delta \theta _{\mathrm{imposed}}}$ and ${\delta \theta _{hkl}}$ in Grain 7 at a measuring point

Since the error from peak repositioning $\Delta \theta$ ($\le \!0.00125^{\circ }$) is much larger than the one caused by the limitation of our peak simulation equation $\delta \theta$ ($\le \!0.0001^{\circ }$), $\Delta \theta$ is considered as the major contribution to the uncertainty of elastic strain tensor $\sigma _{\epsilon ^e}$. Assuming that $\Delta \theta$ follows normal distribution law and 99.7 % of the values are within 3 standard deviations of the mean; therefore, its standard deviation $\sigma _\theta$ is one-third of $\Delta \theta$

$$\begin{aligned} \sigma _\theta = 0.00042^{\circ } \end{aligned}.$$

(15)

• (2) Uncertainty of the elastic strain tensor $\sigma _{\epsilon ^e}$

  Given the uncertainty of the diffracting angles evaluated in Eq. 15, the uncertainty for elastic strain tensor ${\sigma _{\epsilon ^e}}$ were quantified.

• (a) The range of uncertainty for elastic strain tensor ${\sigma _{\epsilon ^e}}$

  Eq. (8) can be rewritten as

  $$\begin{aligned} G_{6 \times 1}^* = B_{6 \times n }^{} D_{n \times 1}^* \end{aligned},$$

  (16)

  where ${B=(H^{T} H)^{-1}H^T}$ is known as the pseudoinverse of H.

  $$\begin{aligned} \left( \begin{array}{c} G_1^*\\ G_2^*\\ \vdots \\ G_6^*\end{array} \right) = \left( \begin{array}{ccccccccc} B_{11} &{}\quad B_{12} &{}\quad B_{13} &{}\quad \cdots &{}\quad B_{1n}\\ B_{21} &{}\quad B_{22} &{}\quad B_{23} &{}\quad \cdots &{}\quad B_{2n}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ B_{61} &{}\quad B_{62} &{}\quad B_{63} &{}\quad \cdots &{}\quad B_{6n}\end{array} \right) \left( \begin{array}{c} D_1^*\\ D_2^*\\ \vdots \\ D_n^*\end{array} \right) \end{aligned}.$$

  (17)

  ${G_{m}^*}$ is a linear function of ${D_{n}^*}$ :

  $$\begin{aligned} G_{m}^* = {B_{m1}^{}}{D_{1}^*}+{B_{m2}^{}}{D_{2}^*}+\cdots +{B_{mn}^{}}{D_{n}^*},\quad {m =1,2,\ldots ,6} \end{aligned}$$

  (18)
  $$\begin{aligned} G_{m}^* = \sum\limits ^{n}_{i=1}{B_{mi}^{}}D_{i}^* \end{aligned}.$$

  (19)

  By expressing ${D_i^*}$ as a function of $\theta$ using Eq. 5, one obtains

  $$\begin{aligned} G_{m}^* = \frac{4}{\lambda ^2}\sum\limits ^{n}_{i=1}{B_{mi}^{}}{\rm sin}^2\theta _i \end{aligned},$$

  (20)

  where ${\theta _i}$ is a diffraction angle measured during the experiment. Let ${\theta _{i=1,\ldots ,n}}$ and ${\theta _{i=n+1,\ldots ,2n}}$ be n diffraction angles measured (actual value) in the deformed and initial states, respectively, so that ${\theta _1}$ corresponds to the evolution of ${\theta _{n+1}}$, ${\theta _2}$ corresponds to the evolution of ${\theta _{n+2}}$, etc. Now, $\epsilon ^e$ in Eq. 9 can be also expressed in terms of ${\theta _i}$ by

  $$\begin{aligned} \epsilon _{m=1,\ldots ,6}^{e} = \left( \begin{array}{c} \frac{\sum\limits ^{n}_{i=1}B_{1i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{2\sum\limits ^{n}_{i=1}B_{1i}{\rm sin}^2\theta _{n+i}}\\ \frac{\sum\limits ^{n}_{i=1}B_{2i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{2\sum\limits ^{n}_{i=1}B_{2i}{\rm sin}^2\theta _{n+i}}\\ \frac{\sum\limits ^{n}_{i=1}B_{3i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{2\sum\limits ^{n}_{i=1}B_{3i}{\rm sin}^2\theta _{n+i}}\\ \frac{\sum\limits ^{n}_{i=1}B_{4i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{\sqrt{2\sum\limits ^{n}_{i=1}B_{2i}{\rm sin}^2\theta _{n+i}}\sqrt{2\sum\limits ^{n}_{i=1}B_{3i}{\rm sin}^2\theta _{n+i}}}\\ \frac{\sum\limits ^{n}_{i=1}B_{5i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{\sqrt{2\sum\limits ^{n}_{i=1}B_{1i}{\rm sin}^2\theta _{n+i}}\sqrt{2\sum\limits ^{n}_{i=1}B_{3i}{\rm sin}^2\theta _{n+i}}}\\ \frac{\sum\limits ^{n}_{i=1}B_{6i}\big ({\rm sin}^2\theta _i-{\rm sin}^2\theta _{n+i}\big )}{\sqrt{2\sum\limits ^{n}_{i=1}B_{1i}{\rm sin}^2\theta _{n+i}}\sqrt{2\sum\limits ^{n}_{i=1}B_{2i}sin^2\theta _{n+i}}} \end{array} \right) \end{aligned},$$

  (21)

  where ${\epsilon _1^{e}}={\epsilon _{11}}$ , ${\epsilon _2^{e}}={\epsilon _{22}}$, ${\epsilon _3^{e}}={\epsilon _{33}}$, ${\epsilon _4^{e}}={\epsilon _{23}}$, ${\epsilon _5^{e}}={\epsilon _{31}}$ and ${\epsilon _6^{e}}={\epsilon _{12}}$. When $\epsilon ^e$ is represented by its first-order Taylor series expansion around the true values ${\mu _1,\mu _2,\ldots ,\mu _{2n}}$, it becomes

  $$\begin{aligned} \epsilon _{m=1,\ldots ,6}^{e} \approx \epsilon _{m}(\mu _1,\mu _2,\ldots ,\mu _{2n}) + \sum\limits ^{2n}_{i=1}\left[ \frac{\partial {\epsilon _{m}}}{\partial {\theta _i}}(\mu _1,\mu _2,\ldots \mu _{2n})\right] \left[ \theta _i-\mu _i\right] \end{aligned}.$$

  (22)

  Equation (22) is of the form ${\epsilon _{m}^{e} \approx a_{m0} + \sum\limits ^{2n}_{i=1}a_{mi}\left( \theta _i-\mu _i\right) }$ with

  $$\begin{aligned} a_{m0} = \epsilon _{m}(\mu _1,\mu _2,\ldots ,\mu _{2n}) \end{aligned}$$

  (23)

  and

  $$\begin{aligned} a_{mi} = \frac{\partial {}}{\partial {\theta _i}}B_{m}\epsilon _{m}(\mu _1,\mu _2,\ldots ,\mu _{2n}) \end{aligned}.$$

  (24)

  The mean ${\overline{\epsilon _m^{e}}}$ and the standard derivation ${\sigma _{\epsilon _m^{e}}^2}$ can be calculated as follows:

  $$\begin{aligned} \mu _{\epsilon _m^{e}}&= E\left[ \epsilon _m^{e}\right] \\&= E\left[ a_{m0}+\sum\limits ^{2n}_{i=1}a_{mi}\left( \theta _i-\mu _i\right) \right] \\&= E\left[ a_{m0}\right] +\sum\limits ^{2n}_{i=1}\left( E\left[ a_{mi}\theta _i\right] -E\left[ a_{mi}\mu _i\right] \right) \\&= a_0+\sum\limits ^{2n}_{i=1}\left( a_{mi}E\left[ \theta _i\right] -a_{mi}E\left[ \mu _i\right] \right) \\&= a_{m0}+\sum\limits ^{2n}_{i=1}\left( a_{mi}\mu _i-a_{mi}\mu _i\right) \\&= a_{m0} \end{aligned}$$

  (25)
  $$\begin{aligned} \sigma ^2_{\epsilon _m^{e}}&= E\left[ \left( \epsilon _m^{e}-\overline{\epsilon _m^{e}}\right) ^2\right] \\&= E\left[ \left( \sum\limits ^{2n}_{i=1}a_{mi}\left( \theta _i-\mu _i\right) \right) ^2\right] \\&= E\left[ \sum\limits ^{2n}_{i=1}a_{mi}\left( \theta _i-\mu _i\right) \sum\limits ^{2n}_{j=1}a_j\left( \theta _j-\mu _j\right) \right] \\&= E\left[ \sum\limits ^{2n}_{i=1}a_{mi}^2\left( \theta _i-\mu _i\right) ^2+{\mathop {\sum\limits \sum\limits }}_{i\ne j}{a_{mi}}{a_{mj}}\left( \theta _i-\mu _i\right) \left( \theta _j-\mu _j\right) \right] \\&= \sum\limits ^{2n}_{i=1}a_{mi}^2E\left[ \left( \theta _i-\mu _i\right) ^2\right] +{\mathop {\sum \sum\limits }}_{i\ne j}{a_{mi}}{a_{mj}}E\left[ \left( \theta _i-\mu _i\right) \left( \theta _j-\mu _j\right) \right] \\&= \sum\limits ^{2n}_{i=1}a_{mi}^2\sigma ^2_{\theta \_mi}+{\mathop {\sum \sum\limits }}_{i\ne j}{a_{mi}}{a_{mj}}\sigma _{ij} \end{aligned}.$$

  (26)

  Although ${{\theta _i}\left( s\right) }$ are dependent, the source of measuring error are independent ($\sigma ^2_{\theta \_mi} = \sigma ^2_{\theta }$), the covariance $\sigma _{ij}$ then disappears and the resulting approximated variance is

  $$\begin{aligned} \sigma ^2_{\epsilon _m^e}= \sum\limits ^{n}_{i=1}\left( \frac{\partial {}}{\partial {}\theta _i}\epsilon _m^e\right) ^2\sigma _\theta ^2 \end{aligned}.$$

  (27)

  For example, elastic strain tensor ${\epsilon ^e}$ calculated with 13 diffraction planes in Grain 7 at the same measuring point is in sample co-ordinate system:

  $$\begin{aligned} \epsilon ^e = \left( \begin{array}{r r r } 0.0011 &{}\quad 0.0003 &{}\quad 0.0003\\ 0.0003 &{}\quad -0.0002 &{}\quad 0.0002\\ 0.0003 &{}\quad 0.0002 &{}\quad 0.0001 \end{array}\right) \end{aligned}.$$

  (28)

  The uncertainty ${\sigma _{\epsilon ^e}}$ associated is

  $$\begin{aligned} \sigma _{\epsilon ^e} \le \left( \begin{array}{r r r } 8.7 &{}\quad 6.8 &{}\quad 5.8\\ 6.8 &{}\quad 10.7 &{} \quad 7.2\\ 5.8 &{}\quad 7.2 &{}\quad 6.4\\ \end{array}\right) \times 10^{-6} \end{aligned}.$$

  (29)

• (b) Influence of the number of measuring planes on $\epsilon ^e$ uncertainty

  However, not every measuring point presents 13 diffraction planes since mosaicity increases during plastic deformation, as shown in Fig. 16. In some regions of the specimens, the number of diffraction planes of a given point decreases during the test as plasticity and mosaicity increases. For example, the ${\epsilon ^e}$ calculated with minimum 6 diffraction planes for the same measuring point in sample co-ordinate system is

  $$\begin{aligned} \epsilon ^e = \left( \begin{array}{r r r } 0.0017 &{}\quad -0.0007 &{}\quad -0.0003\\ -0.0007 &{}\quad 0.0000 &{}\quad 0.0003\\ -0.0003 &{}\quad 0.0003 &{}\quad 0.0001 \end{array}\right) \end{aligned}$$

  (30)

  and its ${\sigma _{\epsilon ^e}}$ range is

  $$\begin{aligned} \sigma _{\epsilon ^e} \le \left( \begin{array}{r r r } 3.9 &{}\quad 5.7 &{}\quad 6.1\\ 5.7 &{}\quad 5.1 &{}\quad 4.2\\ 6.1 &{}\quad 4.0 &{}\quad 1.8\\ \end{array}\right) \times 10^{-5} \end{aligned}.$$

  (31)

The uncertainty of ${\epsilon ^e}$ calculated with 6 $\{hkl\}$ planes is much larger than those with 13 $\{hkl\}$ planes. Therefore, the number of $\{hkl\}$ planes used gives an influence towards ${\epsilon ^e}$ accuracy. The more planes used for ${\epsilon ^e}$ calculation, the more accurate the answer.

As the number of measuring planes depends on the point considered, the $\sigma _{\epsilon ^e}$ range of each XRD measuring point was calculated according to the number of diffractable $\{hkl\}$ planes left over. The maps of $\sigma _{\epsilon ^e}$ at each strain level are shown in Figs. 30, 31, 32 and 33. It can be seen that the ${\epsilon ^e}$ uncertainties $\sigma _{\epsilon ^e}$ are always smaller than $10^{-5}$. Considering a Gaussian distribution, it implies a total error range in ${\epsilon ^e}$ smaller than $\pm 3\times 10^{-5}$.

Fig. 30

Map of $\sigma _{\epsilon ^e_{xx}}$ uncertainties at level ①

Fig. 31

Map of $\sigma _{\epsilon ^e_{yy}}$ uncertainties at level ①

Fig. 32

Map of $\sigma _{\epsilon ^e_{xx}}$ uncertainties at level ②

Fig. 33

Map of $\sigma _{\epsilon ^e_{yy}}$ uncertainties at level ②

Conclusion

An in situ method has been developed to measure $\epsilon ^t$ and $\epsilon ^e$ strain fields at the grain scale. The specifically developed device was introduced, the measurement concept was presented and the testing procedure was described. The analysis method as well as the precautions taken to minimise experimental errors were stated. After the first comparison between $\epsilon ^t$ and $\epsilon ^e$, heterogeneity was quantified. This heterogeneity increased with the imposed loading from 81.1 to 118.6 MPa. The level of heterogeneity of $\epsilon ^t_{xx}$ increased from 0.022 to 0.088. Meanwhile, for $\epsilon ^e_{xx}$, there was a rise from $1.2\times 10^{-3}$ to $1.9\times 10^{-3}$. Moreover, the location of heterogeneity of the sample for $\epsilon ^t$ and $\epsilon ^e$ were not necessary identical. The area less deformed during the elastic deformation could be greatly deformed in the plastic stage. Apart from the results and analysis, the corresponding uncertainty for each measurement were analysed. The uncertainty in ${\epsilon ^t}$ and in ${\epsilon ^e}$ were $\pm 4\times 10^{-4}$ and $\pm 3\times 10^{-5},$ respectively.

These experimental results and methodology provide a basis for determining for future development of a crystal plasticity model that better accounts microstructural effects.

Appendices

Appendix A: Crystal orientations of both sides of the sample

See Table 4.

Table 4 Crystal orientations of the front (left) and back (right) sides of the sample

Appendix B: Schmid factor of each grain of both sides of the sample

See Table 5.

Table 5 Schmid factor of each grain of the front (left) and back (right) sides of the sample