Keywords

Introduction

The development in material mechanics reveals that the plastic behavior of a crystal alloy is based on the concurrent operations of plastic deformation mechanisms such as slip systems, deformation twinning, and phase transformation. As for alloy systems where multiple mechanisms are active, the quantitative analysis of the constitutions of the plastic deformation would be difficult [1,2,3]. The method is to fit the respective macroscopic polycrystalline data by a polycrystalline model based on crystal plasticity theory. The well-fitted model can provide the single-crystal properties in the crystallographic scale, such as slip system activities, texture evolution, and deformation twin expansion [4,5,6,7]. The viscoplastic self-consistent model with twinning and de-twinning scheme (VPSC-TDT) is an accurate model and is feasible to describe plenty of alloy systems [5, 7]. However, the model parameters are hard to be calibrated manually due to the large number of them, especially in systems with HCP crystal structures like magnesium alloys. For such a system where the plastic deformation mechanisms consist of 3 types of slip systems and extension twinning, the number of parameters that require calibration can reach at least 10. To promote the application of the crystal plasticity models, an effective method to the parameter auto-calibration is in great demand.

An auto-calibration problem can be transformed into an optimization problem aimed to minimize the difference between the model results and the experimental macroscopic results. However, the relationship between the parameter inputs and the results of the self-consistent model is not analytic, therefore the conventional optimization algorithms based on the gradient method are not efficient enough. To solve this “black-box” optimization problem, the genetic algorithm and some variants have been used in previous works, but hundreds to thousands of trials are needed and it still costs days to weeks to finish [8,9,10]. Recently, the algorithm Bayesian Optimization has been widely used in neural network-related works and materials science works. It can initialize its searching domain by small numbers of random samples but find all possible optima globally. This algorithm is expected to behave well in such a physical principle-based black-box optimization problem studied here.

In this work, a Bayesian Optimization algorithm is adapted to solve the auto-calibration problem in the viscoplastic self-consistent polycrystalline plasticity model with twinning and de-twinning scheme (VPSC-TDT). A relatively complex alloy system, the rare-earth magnesium alloy ZEK100, is selected to represent the effect of Bayesian Optimization on the model calibration problem. An extended Voce hardening law that is proven to be able to describe the hardening behavior of the Mg alloys is employed. Besides, a practical tactic is also proposed to contract the searching domain of the model parameters, resulting in an optimized auto-calibration procedure.

Problem Formulation and Solution Method

VPSC-TDT

As mentioned previously, the crystal plastic model adopted here to model the mechanical behavior of the rare-earth magnesium alloy ZEK100 is the VPSC-TDT model. Detailed descriptions can be found in the previous works [5, 7]. For a deformation system \(\alpha\) related to ZEK100 like a slip system or a twinning system, the shear rate follows a power-law form:

$$ \dot{\gamma }^{\alpha } = \dot{\gamma }_{0} |\tau^{\alpha } /\tau_{cr}^{\alpha } |^{{\frac{1}{{m^{\alpha } }}}} sgn(\tau^{\alpha } ) $$
(1)

where \(\dot{\gamma }_{0}\) is a reference shear rate, \(\tau^{\alpha }\), \(\tau_{cr}^{\alpha }\), and \(m^{\alpha }\) are the resolve shear stress, the critical resolved shear stress (CRSS), and the strain rate sensitivity associated with the system \(\alpha\), respectively. Note that for the deformation twinning system, Eq. 1 is only adopted with the RSS in the right direction, otherwise the strain rate will be set as zero. To describe the twin nucleation, the new grain with a twin orientation updated via the rotation matrix will be created and serve as the twinned portion of the original grain. The new grain (twin) and the original grain (matrix) are treated as independent grains that interact with the homogeneous effective medium. As the distortion proceeds, the twin will evolve through growth (twinning) or shrinkage (de-twinning) with their summed volume fraction unchanged.

Considering that a grain is rarely twinned entirely, a threshold to terminate twinning is defined as

$$ V^{th} = \min \left( {1.0,A_{1} + A_{2} \frac{{V^{{\text{eff }}} }}{{V^{acc} }}} \right) $$
(2)

where Vacc and Veff are the weighted volume fraction of the twinned region and the volume fraction of twin terminated grains, respectively. A1 and A2 are two material constants controlling the terminating threshold Vth. More specifically, A1 essentially controls the strain level before the twinning mechanism begins to undergo exhaustion, and A2 controls the rate at which this exhaustion takes place.

For both slip and twinning systems, the CRSS \(\tau_{cr}^{\alpha }\) is updated as

$$ \tau_{cr}^{\alpha } = \frac{{d\hat{\tau }^{\alpha } }}{d\Gamma }\sum\limits_{\beta } {\theta^{\alpha \beta } } \left| {\dot{\gamma }^{\beta } } \right| $$
(3)

where Γ is the accumulated shear strain in the crystal and is calculated as \(\Gamma = \sum\limits_{\alpha } {\int {\left| {\dot{\gamma }^{\alpha } } \right|} } dt\), and \(\theta^{\alpha \beta }\) is the latent hardening coupling coefficients, which empirically account for the obstacles on system α associated with system β. \(\hat{\tau }^{\alpha }\) is the threshold stress for the system α defined by an extended Voce law as

$$ \hat{\tau }^{\alpha } = \tau_{0}^{\alpha } + \left( {\tau_{1}^{\alpha } + h_{1}^{\alpha } \Gamma } \right)\left( {1 - \exp \left( { - \frac{{h_{0}^{\alpha } }}{{\tau_{1}^{\alpha } }}\Gamma } \right)} \right) $$
(4)

where \(\tau_{0}^{\alpha }\) and \(\tau_{0}^{\alpha } + \tau_{1}^{\alpha }\) are the initial and back-extrapolated CRSSes, and\(h_{0}^{\alpha }\) and \(h_{1}^{\alpha }\) are the initial and asymptotic hardening rates for the system α, respectively.

Model Parameter Calibration Method

The model parameter calibration problem here is to modulate the parameters in the Voce hardening law (Eq. 4) to reach a consistency between the mechanical behavior curves provided by the VPSC-TDT model and that given by the experiments. The investigated object, ZEK100 magnesium alloy (1.3%Zn, 0.2%Nd, 0.25%Zr, and 0.01% Mn), is studied in the quasi-static tension and compression experiment with the hydraulic servo tensile tester (Instron 1331). The sample size and specific test procedure can be referred to in Kurukuri et al. [11]. Mechanical tests were conducted along four orientations, namely the rolling direction (RD), transverse direction (TD), 45° with respect to RD and TD (45), and normal direction (ND), with the strain rate 0.001 s−1 and the maximum strain level 0.2. Seven experimental datasets for ZEK100 sheet (compression along the RD (C-RD), the transverse direction (C-TD), 45° with respect to RD (C-45), and the normal direction (C-ND), as well as tension along the RD (T-RD), the TD (T-TD), and 45° with respect to RD (T-45)) are used.

In the Voce hardening law (Eq. 4), there are 4 parameters mainly influencing the behavior for each deformation system, \(\tau_{0}^{\alpha }\),\(\tau_{1}^{\alpha }\), \(h_{0}^{\alpha }\), and \(h_{1}^{\alpha }\). The system α here refers to one of the main concurrent deformation mechanisms in ZEK100, including basal slip, prismatic slip, pyramidal slip, and extension twinning. Among these 16 parameters, \(h_{1}^{\alpha }\) in all systems are set as zero as this parameter matters at relatively large deformation. Moreover, in most magnesium alloy stress–strain curves, the extension twinning usually results in a plateau. Therefore, it is reasonable to use a zero-hardening mechanism to approximate the extension twinning to furtherly simplify the calibration problem. Consequently, \(\tau_{1}^{twin}\), \(h_{0}^{twin}\), and \(h_{1}^{twin}\) are zero, and the total number of parameters to be calibrated is reduced from 16 to 10.

This 10-dimensional parameter calibration problem can be converted to an optimization problem to minimize the difference between the simulation stress–strain curves and the experimental curves. The normalized root mean square error (NRMSE) between the stress values in two curves is adopted to measure the difference. The mean NRMSE for the stress–strain curves corresponding to the seven loading cases is calculated as the objective to minimize for the optimization:

$$ NRMSE_{i} = \left[ {\sqrt {\sum\limits_{j} {\frac{{(\sigma_{j}^{exp} - \sigma_{j}^{sim} )^{2} }}{{(\sigma_{max}^{exp} - \sigma_{min}^{exp} )^{2} }}} } } \right]_{case:i} $$
(5)
$$ {\text{Objective}} = \frac{1}{N}\sum\limits_{i = 0}^{N} N RMSE_{i} $$
(6)

where i refers to one of the loading cases and N = 7, and j in Eq. 5 refers to each point in curves.

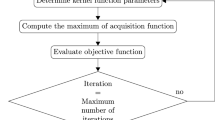
The algorithm Bayesian Optimization is applied to search for the optimum to minimize the objective. The detailed principle and realization can be found in [12] and the GPyOpt site [13]. A basic concept will be illustrated here. Based on the initial samples (means the trials of possible parameter sets) in the searching domain and the corresponding return value (means the objective), a surrogate model for the VPSC-TDT model using Gaussian Process (GP) will be established first. An acquisition function is used to find the potential optimum of the GP model, which will be the parameter set for the next trial. The additional one sample and the result will be passed to update the GP model. Each iteration will generate a more representative GP model to the VPSC-TDT model and a more reasonable candidate for the optimum. The optimization process will terminate when the objective reaches a specified criterion.

The acquisition function selected in this work is the Expected Improvement (EI) acquisition function. At the nth iteration, EI is defined as

$$ EI_{n} ({\mathbf{x}}) = E_{n} [[GP({\mathbf{x}}) - f_{n}^{*} ]^{ - } ] $$
(7)

where \({\mathbf{x}}\) refers to a 10-dimensional parameter set, and \(f_{n}^{*}\) is the current optimum at step n. Note that the GP model provides a Gaussian distribution for a certain \({\mathbf{x}}\) so the expectation is meaningful. The []− operator filters out the possible sets resulting in GP(\({\mathbf{x}}\)) larger than \(f_{n}^{*}\). The next sample is obtained by

$$ x_{n + 1} = \arg \min EI_{n} ({\mathbf{x}}) $$
(8)

Apparently, the EI function will traverse the entire searching domain at each iteration, and this makes the Bayesian Optimization a global optimization algorithm. Moreover, more steps of iteration will be needed for a larger searching domain. However, the parameter domain won’t be so specific and a rather large searching domain is usually possible. To exemplify this, the searching domain of the parameters based on the papers relevant to the magnesium alloy [14,15,16,17] are given in Table 1, which is also used for obtaining the optimum for ZEK100. To solve this problem, a tactic to contract the searching domain based on the Monte Carlo Markov Chain (MCMC) method will be delivered as follows.

Table 1 Range of material parameters for the magnesium alloy sheets
Full size table

At the initial 2% of the plastic strain, the stress response can provide some information about the model parameters, especially the \(\tau_{0}^{\alpha }\) s which control the initial yielding. This knowledge tells that it is expected to use the initial sections of the curves to determine a more contracted searching domain of the parameters. After an optimization process only to minimize the objective based on the initial 2% of plastic strain and the corresponding stress data in seven loading cases, the parameter set candidates which have smaller objectives can be selected. The selected candidates should be within a range around the target optimum. In this tactic, each selected candidate is regarded as a sample from a 10-dimensional Gaussian distribution whose mean value is the optimal solution. To reconstruct this 10-dimensional distribution, thousands or more samples are necessary so only the selected candidates are not enough. However, the MCMC method can be used to generate plenty of samples so the reconstruction becomes possible.

With each parameter normalized with the parameter domain listed in Table 1 to the interval [−0.5, 0.5], each parameter set can be considered as a 10-dimensional vector \({\mathbf{x}}\) of which the component \(x_{m}\) follows the Gaussian distribution \(N(\mu_{m} ,\sigma_{m} )\). The Gaussian distribution parameters are supposed to follow the uniform prior:

$$ \mu_{m} \sim {\text{Uniform}}( - 0.5,0.5),\sigma_{m} \sim {\text{Uniform}}(0,1) $$
(9)

The selected candidates serve as the observed data. The No-U-Turn Sampler is used to sample 10,000 reasonable \(\mu_{m}\) s and \(\sigma_{m}\) s from the uniform priors to maximize the probability that the vector \({\mathbf{x}}\) equals the selected candidates. The posterior distribution of \(\mu_{m}\) and \(\sigma_{m}\) are obtained from the 10,000 samples. This update is navigated by the probabilistic programming engine PyMC3 [18]. Then the values for each \(\mu_{m}\) and \(\sigma_{m}\) with maximum probability are adopted and the distribution of \(x_{m}\) is determined. The original interval [−0.5, 0.5] for \(x_{m}\) can be updated to the interval \([\widehat{\mu }_{m} - \widehat{\sigma }_{m} ,\widehat{\mu }_{m} + \widehat{\sigma }_{m} ]\), which is reasonable enough. The new interval for \(x_{m}\) is then converted back from the normalization. In the contracted searching domain, the Bayesian Optimization process can be accelerated, and the acceptable optimum can appear at earlier iteration steps. A schematic diagram of the whole calibration method is given in Fig. 1, and the concrete process will be discussed in section “Optimization Process”.

Fig. 1
figure 1

Schematic diagram of the VPSC-TDT model parameter calibration method

Full size image

Results and Discussion

Mechanical Behavior

The optimum of the parameter sets adopted to model the ZEK100 mechanical behavior is listed in Table 2. The simulated stress–strain curves under both tension and compression cases are plotted in Fig. 2 with the corresponding experimental data points. Good consistency is committed. Moreover, to evaluate the relative contribution of each deformation mode to the shear strain, the relative activity is usually calculated as the ratio of the shear strain rate of the respective deformation mode to the total shear strain rate. The relative activities of the deformation systems in all loading cases are also given in Fig. 3. Clearly, in the tension cases, pyramidal slip is nearly absent, and basal and prismatic slip systems are usually dominating from the beginning. In the compression cases, basal slip and extension twinning are more active than the other two systems. Pyramidal slip participates more at a higher plastic strain level, but it also helps accommodate a little deformation at the beginning in C-TD and C-ND cases. Note the discussion here is related to the tactic to contract the searching domain, and the relationship will be discussed in section “Optimization Process”.

Table 2 The selected optimum parameter sets in VPSC-TDT
Full size table
Fig. 2
figure 2

The initial texture of the studied ZEK100 sheet (a) and the plastic strain–true stress data in compression cases (b) and tension cases (c) given in experiments (scatters) and VPSC-TDT model (lines)

Full size image
Fig. 3
figure 3

The relative activity of the deformation systems, including basal slip (a), prismatic slip (b), pyramidal slip (c), and extension twinning (d), in all loading cases

Full size image

Optimization Process

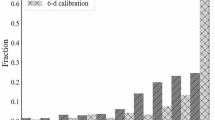
The optimization processes in the original searching domain and the contracted domain are illustrated in Fig. 4. The lines are the current minimal objective during the optimization and the scatters are the objective values near the current minimal objective (within a 5% derivation). The yellow dot line represents a threshold value for the reasonable objective 0.10. Clearly, it is not stable to reach an objective under the threshold within 200 trials when searching in the original domain. While in the domain contracted with the tactic mentioned previously, solutions with an objective less than 0.10 can be obtained within 30 iterations in all 3 example processes. Even with a reduced threshold like 0.095, around 100 iterations are completely enough. Therefore, the domain contracting tactic can drastically promote the convergence of the Bayesian Optimization to the target optimum.

Fig. 4
figure 4

The current optimal objective during the optimization processes searching in the original domain (a) and the contracted domain (b); 3 example processes in each circumstance are plotted with the scatters representing trials with nearly optimal objective values

Full size image

To obtain the contracted domain, as introduced in section “Model Parameter Calibration Method”, an optimization process with only the data in the initial 2% of the plastic strain should be conducted first. After 100 iterations, 10 parameter sets with the minimal objective values are selected as the candidates. Then the posterior distributions of the parameters \(\mu_{m}\) and \(\sigma_{m}\) are updated based on the selected candidates. The respective probability density functions are estimated from the MCMC results by the kernel density estimation (KDE) and the profiles are shown in Fig. 5a, b. The values with maximum probability are chosen as the estimated values \(\widehat{\mu }_{m}\) and \(\widehat{\sigma }_{m}\), and the contracted intervals \([\widehat{\mu }_{m} - \widehat{\sigma }_{m} ,\widehat{\mu }_{m} + \widehat{\sigma }_{m} ]\) are therefore obtained. For the 3 processes in Fig. 4b, the corresponding contracted domains are also given in Fig. 5c as the updated normalized intervals for each parameter to optimize.

Fig. 5
figure 5

The KDE graphs of \(\mu_{m}\) and \(\sigma_{m}\) (a, b) and the updated intervals of the VPSC-TDT model parameters (c)

Full size image

The performance of the tactic is highly relevant to the initial 100 iterations. Only the data within the initial 2% plastic strain are adopted, and they provide more information about the \(\tau_{0}^{\alpha }\) s than the other parameters. This is reflected in Fig. 5a, b as the relatively narrow distributions of \(\mu_{m}\) corresponding to \(\tau_{0}^{\alpha }\) s (plotted in solid lines) as well as the lower values of the \(\sigma_{m}\) s. Also, the contracted intervals for \(\tau_{0}^{\alpha }\) s are more consistent in 3 processes, shown in Fig. 5c, compared to the more obvious fluctuations in the updated intervals of the parameters \(\tau_{1}^{\alpha }\) s and \(h_{0}^{\alpha }\) s. Moreover, as the basal and prismatic slips dominate in the initial plastic deformations in these loading cases (Fig. 2), this tactic is more efficient in contracting the intervals of \(\tau_{0}^{bas}\) and \(\tau_{0}^{pri}\) than that of other \(\tau_{0}^{\alpha }\) s. But as a whole, the searching domain can be contracted to around 0.1% of the initial domain (evaluated in a 10-dimensional hyperspace), and the updated intervals in the 3 processes can be regarded as similar. This proves the efficiency and stability of this tactic.

Conclusions

In this paper, a new method to calibrate the model parameters for a certain alloy system in the polycrystalline crystal plasticity model is proposed. This method is based on Bayesian Optimization and is equipped with a practical tactic based on the MCMC method to efficiently contract the searching domain of the model parameters. This method performs well in calibrating the parameters in the VPSC-TDT model to simulate the magnesium alloy ZEK100, and the total trial number can be reduced to around 100 or even less. This result can be realized because the MCMC tactic contracts the parameters’ domain to around 0.1% of the initial guess. In the evaluation provided here, this method is of great efficiency and stability. This method does not rely on the constitutive model used and can be applied to any other crystal plasticity models or hardening laws. Therefore, it is believed that this method can greatly accelerate the works relative to crystal plasticity models.