LFT Bond Graph Model-Based Robust Fault Detection and Isolation

Abstract

Diagnosis of uncertain systems has been the subject of several recent research works (Djeziri et al. Proceeding of the 2007 American Control Conference 3017–3022, 2007; Han et al. 15th IFAC World Congress 1887–1892, 2002; Henry and Zolghari Control Engineering Practice 14:1081–1097, 2006; Hsing-Chia and Hui-Kuo Engineering Applications of Artificial Intelligence 17:919–930, 2004; Ploix Ph.D. de I.N.P.L, C.R.A.N 1998; Yan and Edwards Automatica 43:1605–1614, 2007). This interest is reflected by the fact that physical systems are complex and non-stationary and require more security and performance. The bond graph model in LFT form allows the generation of analytical redundancy relations (ARRs) composed of two completely separated parts: a nominal part, which represents the residuals, and an uncertain part which serves for both the calculation of adaptive thresholds and sensitivity analysis.

1 Introduction

Diagnosis of uncertain systems has been the subject of several recent research works [1–6]. This interest is reflected by the fact that physical systems are complex and non-stationary and require more security and performance. The bond graph model in LFT form allows the generation of analytical redundancy relations (ARRs) composed of two completely separated parts: a nominal part, which represents the residuals, and an uncertain part which serves for both the calculation of adaptive thresholds and sensitivity analysis.

The chapter is composed of three parts. In the first one, the LFT BG is defined and its building procedure is presented. The second part shows how to use LFT BG for diagnosis of uncertain systems. This methodology is implemented on an electromechanical system and simulation and experimentation results are compared.

2 Bond Graph Modeling in LFT Form

Before developing the methodology for diagnosis of uncertain systems using the bond graph (BG) model in linear fractional transformation (LFT) form, BG modeling in LFT form of elements with parameter uncertainties is presented in this section. Linear fractional transformation was introduced on mathematical models by R. Redheffer in 1960 [7] and on bond graph models by G. Dauphin-Tanguy in 1999 [8]. This kind of modeling offers several advantages for robust control and fault detection and isolation (FDI) of uncertain systems.

2.1 LFT Representation

Linear fractional transformations (LFT) represented in Fig. 3.1 are generic objects, widely used for uncertain systems modeling. Genericity of the LFT is due to the fact that any rational expression can be written under this form [9, 10]. It is used for stability analysis and for control law synthesis using μ-analysis and synthesis principles, by separating the nominal part of the model from its uncertain part as shown in Fig. 3.1. The nominal values are grouped in an augmented matrix denoted M, supposed proper and all uncertainties (structured and unstructured uncertainties, measurement noise, etc.) are gathered in a matrix Δ with a diagonal structure.

Fig. 3.1

LFT representation

In the linear case, this standard form leads to a state-space representation as follows:

$$\left\{ \begin{array}{l} \overset{\cdot }{x}=A.x+B_{1}.w+B_{2}.u \\z=C_{1}.x+D_{11}.w+D_{12}.u \\ y=C_{2}.x+D_{21}.w+D_{22}.u \end{array} \right.$$

((3.1))

with $x\in R^{n}$ the state vector of the system, $u\in R^{m}$ and $y\in R^{p}$ vectors gathering, respectively, the control inputs and the measured outputs of the system. $w\in R^{l}$ and $z\in R^{l}$ include, respectively, auxiliary inputs and outputs. n, m, l, and p are positive integers.

$(A, B_{1}, B_{2}, C_{1}, C_{2}, D_{11}, D_{12}, D_{21}, D_{22})$ are matrices of appropriate dimensions. Equations (3.1) are not easy to obtain in case of complex systems, particularly because of the constraint on Δ which has to be diagonal.

2.2 LFT Modeling of Bond Graph Elements

An uncertainty on a parameter value θ can be introduced under either an additive form or a multiplicative one, as follows:

$$\begin{array}{lll}\theta &=\theta _{n}+\varDelta \theta & (a) \\ \theta &=\theta _{n}.\left( 1+\delta _{\theta }\right) & (b) \end{array}$$

((3.2))

where Δθ and $\delta _{\theta }={\varDelta \theta }/{\theta _{n}}$ are, respectively, absolute and relative deviations around nominal value θ _n .

When the element characteristic law is written in terms of ${1}/{\theta }$, (3.2) becomes

$$\frac{1}{\theta }=\frac{1}{\theta _{n}}.\left( 1+\delta _{{1}/{\theta } }\right)$$

((3.3))

with $\delta _{{1}/{\theta }}=-\frac{\varDelta \theta }{\theta _{n}+\varDelta \theta }$.

Only LFT models of uncertain R-element, RS-element, and TF-element in flow and effort causality are developed here. Figure 3.8 regroups all the LFT BG models of passive and junction elements. The sources are supposed to be known without uncertainty, except in the case of closed-loop models.

Consider R-element in resistance (imposed flow) causality. The characteristic law corresponding to R-element in the linear case (Fig. 3.2a) is given as follows:

$$e_{R}=R.f_{R}$$

((3.4))

Fig. 3.2

(a) R-element in resistance causality. (b) Uncertain R-element in resistance causality in LFT form

In case of uncertainty on a parameter R, (3.4) becomes

$$e_{R}=R_{n}.\left( 1+\delta _{R}\right) .f_{R}=R_{n}.f_{R}+\delta _{R}.R_{n}.f_{R}=e_{R_{n}}+e_{R_{\mathrm{unc}}}$$

((3.5))

Constitutive equation (3.5) can be represented by the LFT BG of uncertain R-element in Fig. 3.2b by introducing a modulated source MSe associated with auxiliary input w _R and a virtual effort sensor associated with auxiliary output z _R .

For an R-element in conductance (imposed effort) causality, the procedure is the same

$$f_{R}=\frac{1}{R}.e_{R}$$

((3.6))

which can be written as follows and leads to Fig. 3.3b:

$$f_{R}=\frac{1}{R_{n}}.\left( 1+\delta _{{1}/{R}}\right) .e_{R}=\frac{1}{ R_{n}}.e_{R}+\frac{\delta _{{1}/{R}}}{R_{n}}.e_{R}=f_{R_{n}}+f_{R_{\mathrm{unc}}}$$

((3.7))

Fig. 3.3

(a) R-element in conductance causality. (b) Uncertain R-element in conductance causality in LFT form

Fig. 3.4

LFT BG model of a pipe transporting water in ambient temperature

In non-linear case, the non-linearities do not appear explicitly on the BG, but on the characteristic law governing the BG element dynamic. Let us consider the LFT BG of a pipe transporting water at ambient temperature as given in Fig. 3.4.

The mathematical equation characterizing the system is given as follows:

$$\dot{m}_{Rz}=\frac{1}{Rz}.\sqrt{P_{\mathrm{in}}-P_{\mathrm{out}}}$$

((3.8))

Rz-element depends on the manufacturing of the pipe and it is a function of the valve opening z. The nominal value Rz _n and uncertainty value δ _Rz can be calculated as follows by considering a Poiseuille law:

$$Rz=\frac{8.\rho _{l}.L_{\mathrm{p}}}{\pi .r_{\mathrm{p}}{}^{4}}$$

((3.9))

where L _p is the length of the pipe, r _p the pipe radius, assumed uncertain.

Using a logarithmic derivative we obtain

$$\delta _{_{{1}/{Rz}}}=-\delta _{\rho _{l}}-\delta _{L\mathrm{p}}+4.\delta _{r\mathrm{p}}$$

((3.10))

The uncertainty on flow at the output of the pipe can be calculated as follows:

$$w_{Rz}=-\delta _{\frac{1}{Rz}}.\frac{\sqrt{P_{\mathrm{in}}-P_{\mathrm{out}}}}{Rz}$$

((3.11))

Let us consider an RS multi-port (well developed in Thoma and Ould Bouamama [11]). This element can be considered as an active resistance which generates entropy. The typical example is an electrical heating resistance (Fig. 3.5a). Using thermal pseudo-bond graph developed initially by Karnopp [12] and later by Thoma and Ould Bouamana [11], the flow and effort variables are, respectively, thermal flow $\dot{\phi}$ (J/s) and temperature T. For an electrical resistance $(e_{1\mathrm{RS}},\;f_{1\mathrm{RS}})$ corresponds to the pair (voltage (u), current (i)) and $(e_{2\mathrm{RS}},\;f_{2\mathrm{RS}})$ corresponds to $\left( T,\dot{\phi}\right)$. The thermal flow f _2RS can be expressed as

$$f_{2\mathrm{RS}}=e_{1\mathrm{RS}}.f_{1\mathrm{RS}}$$

((3.12))

The bond graph model of an RS-element is given in Fig. 3.5b.

Fig. 3.5

RS-element. (a) Heating resistance. (b) Bond graph model of the heating resistance

When the power variables are both known at the left bond input of the multi-port RS, the principle of power conservation allows the determination of the heat flow with precision, without using the value of the parameter RS. The generated heat flow $\ dot{Q}$ is thus given by the expression

$$\dot{Q}=u.i$$

When only one of the two variables (e _1RS or f _1RS) is known, power output is a nonlinear function of the known power variable and the value of parameter RS, which could be known with uncertainty.

When $e_{1_{\mathrm{RS}}}$ is known, expression of f _2RS is given as follows:

$$\begin{array}{rcl}f_{2\mathrm{RS}} &=&\varPhi \left( \mathrm{RS}_{n},e_{1\mathrm{RS}}\right) .\left( 1+\delta _{{1}/{\mathrm{RS}} }\right) \\ &=&\varPhi \left( \mathrm{RS}_{n},e_{1\mathrm{RS}}\right) +\delta _{{1}/{\mathrm{RS}}}.\varPhi \left( \mathrm{RS}_{n},e_{1\mathrm{RS}}\right) =f_{2\mathrm{RS}_{n}}+f_{2\mathrm{RS}_{\mathrm{unc}}} \end{array}$$

((3.13))

The bond graph model in LFT form of the multi-port RS equivalent to the mathematical model of (3.13) is given in Fig. 3.6a.

Fig. 3.6

Bond graph model in LFT form of RS-element with two different causalities

When the flow variable is known, expression of f _2RS is given as follows:

$$\begin{array}{rcl}f_{2\mathrm{RS}}&=&\varPhi \left( \mathrm{RS}_{n},f_{1\mathrm{RS}}\right) .\left( 1+\delta _{\mathrm{RS}}\right)\nonumber\\ &=&\varPhi \left( \mathrm{RS}_{n},f_{1\mathrm{RS}}\right) +\delta _{\mathrm{RS}}.\varPhi \left( \mathrm{RS}_{n},f_{1\mathrm{RS}}\right) =f_{2\mathrm{RS}_{n}}+f_{2\mathrm{RS}_{\mathrm{unc}}} \end{array}$$

((3.14))

The bond graph model in LFT form of the multi-port RS equivalent to the mathematical model of (3.14) is given in Fig. 3.6b.

The characteristic law of an uncertain TF-element in m causality is written as follows:

$$\begin{array}{rcl}e_{1} &=&m_{n}.\left( 1+\delta _{m}\right) .e_{2} \\ e_{1} &=&m_{n}.\left( e_{2}-w_{b}\right) \textrm{ with }w_{b}=-\delta _{m}.e_{2} \nonumber \\ f_{2} &=&m_{n}.\left( 1+\delta _{m}\right) .f_{1} \nonumber \\ f_{2} &=&m_{n}.\left( f_{1}+w_{a}\right) \textrm{ with }w_{a}=\delta _{m}.f_{1} \end{array}$$

((3.15))

with $\delta _{m}={\varDelta m}/{m_{n}}$.

Fig. 3.7

LFT bond graph model of TF-element with two different causalities

Fig. 3.8

LFT BG of uncertain elements: (a) R element in resistance causality, (b) R element in conductance causality, (c) I element in integral causality, (d) C element in derivative causality, (e) C element in integral causality, (f) I element in derivative causality, (g) TF element in m causality, (h) TF element in 1/m causality, (i) GY element in r causality, (j) GY element in 1/r causality, (k) RS element in resistance causality, (l) RS element in conductance causality

m _n , δ _m , and Δm represent, respectively, the nominal value, multiplicative uncertainty, and additive uncertainty on the module m of the TF-element. e ₁, f ₁ and e ₂, f ₂, are, respectively, the effort and the flow at the two bonds of TF-element. w _a , w _b are the fictive inputs.

The bond graph model of TF-element in m causality with multiplicative uncertainty is given in Fig. 3.7a.

The characteristic law of the uncertain TF-element in 1/m causality is given as follows and the corresponding LFT BG is given in Fig. 3.7b:

$$\begin{array}{rcl}e_{2} &=&\frac{1}{m_{n}}.\left( 1+\delta _{{1}/{m}}\right) .e_{1} \\ e_{2} &=&\frac{1}{m_{n}}.\left( e_{1}+w_{a}\right) \textrm{ with }w_{a}=\delta _{{1}/{m}}.e_{1} \\ f_{1} &=&\frac{1}{m_{n}}.\left( 1+\delta _{{1}/{m}}\right) .f_{2} \\ f_{1} &=&\frac{1}{m_{n}}.\left( f_{2}-w_{b}\right) \textrm{ with } w_{b}=-\delta _{{1}/{m}}.f_{2} \end{array}$$

((3.16))

with $\delta _{{1}/{m}}=\dfrac{-\Delta m}{m_{n}+\Delta m}$.

All the LFT BG elementary elements are regrouped in Fig. 3.8.

2.3 LFT BG of a Global Model

Modeling in LFT form requires for the model to be proper and observable [13]. The bond graph methodology allows by causal manipulations, the verification of these properties directly on the bond graph model.

Property 1.1 A bond graph model is proper if and only if it does not contain any dynamic element in derivative causality when the bond graph model is in preferred integral causality, and vice versa [14].

Property 1.2 A bond graph model is structurally state-observable if and only if the following conditions are satisfied:

• (i) On the bond graph model in integral causality, there is a causal path between all the dynamic elements I and C in integral causality and a detector De or Df;

• (ii) All dynamic elements I and C admit a derivative causality on the bond graph model in preferred derivative causality. If some dynamic elements I and C remain in integral causality, the dualization of the detectors De and Df should enable to assign them derivative causality [14].

Proposition 3.1

The LFT representation of a global model can be derived from a BG model, by replacing each uncertain element by its LFT BG model.

2.4 Example

The example of Fig. 3.9a represents an oleopneumatic suspension for a quarter of vehicle. The oleopneumatic element combines the functions of suspension and damping. Oleopneumatic compliance of the gas is expressed as $\ C_{\mathrm{sph}}={\nu .P_{e}^{2}}/({P_{0}V_{0}})$ with $P_{\mathrm{e}}={M_{s}.g}/{S_{P}}$, C _sph being the capacity of the sphere. P _e is the static pressure at equilibrium state, $\nu =1.4$ is the isentropic constant of the nitrogen. P ₀ and V ₀ represent, respectively, the inflation pressure of the sphere and the volume of the sphere vacuum, M _s is the mass of the body, g is gravity.

Fig. 3.9

Oleopneumatic suspension for a quarter of vehicle and its bond graph model in integral causality

Fig. 3.10

Bond graph model in LFT form of an oleopneumatic suspension for a quarter of vehicle. Uncertainties on C _Sph, R _a , M _ns , M _s , S _p

The bond graph model of the system in integral causality is given in Fig. 3.9b, and the bond graph model in LFT form of the system is given in Fig. 3.10 [15]. The model represents the movements around the static equilibrium with respect to gravity, neglecting initial conditions. Multiplicative uncertainties are introduced in elements: C _sph, R _a , M _ns and M _s , and S _p .

The state variables are associated with the I- and C-elements with nominal values:

$$x=\left[ \begin{array}{c} p_{M_{ns}} \\ p_{M_{s}} \\ q_{k_{p}}=\Delta l_{k_{p}} \\ q_{C_{\mathrm{sph}}}=V_{\mathrm{sph}} \end{array} \right]$$

((3.17))

The auxiliary variables corresponding to parameter uncertainties satisfy the following:

$$\left\{ \begin{array}{l} {\small w}_{\frac{1}{M_{ns}}}={\small -\delta }_{\frac{1}{M_{ns}}}.z_{\frac{1 }{M_{ns}}} \\ {\small w}_{\frac{1}{M_{s}}}={\small -\delta }_{\frac{1}{M_{s}}}.{\small z}_{ \frac{1}{M_{s}}} \\ {\small w}_{R_{a}}={\small -\delta }_{R_{a}}.{\small z}_{_{R_{a}}} \\ {\small w}_{\frac{1}{C_{\mathrm{sph}}}}={\small -\delta }_{\frac{1}{C_{\mathrm{sph}}}}.{\small z}_{\frac{1}{C_{\mathrm{sph}}}} \\ {\small w}_{a}=\delta _{S_{p}}.z_{a} \\ {\small w}_{b}=-\delta _{S_{p}}.z_{b} \end{array} \right.$$

((3.18))

with ${\small \delta }_{{1}/{M_{s}}}=\frac{-\Delta M_{s}}{M_{sn}+\Delta M_{s}},$ ${\small \delta }_{{1}/{M_{ns}}}=\frac{-\Delta M_{ns}}{ M_{ns_{n}}+\Delta M_{ns}},$ ${\small \delta }_{{1}/{C_{\mathrm{sph}}}}=\frac{ -\Delta C_{\mathrm{sph}}}{C_{\mathrm{sph}_{n}}+\Delta C_{\mathrm{sph}}},$ ${\small \delta }_{R_{a}}= \frac{\Delta R_{a}}{R_{a_{n}}},$ ${\small \delta }_{S_{p}}=\frac{\Delta S_{p} }{S_{p_{n}}}$.

The fictive outputs $z_{{1}/{Mns}},\ z_{{1}/{Ms}},\ z_{a},\ z_{b},\ z_{\frac{1}{C_{\mathrm{sph}}}}$, and $z_{R_{a}}$ are determined from the bond graph model of Fig. 3.10 and expressed as follows:

$$\left\{ \begin{array}{l} z_{\frac{1}{Mns}}=\frac{1}{Mns_{n}}.p_{Mns} \\ z_{\frac{1}{Ms}}=\frac{1}{Ms_{n}}.p_{Ms} \\ z_{a}=\frac{1}{Mns_{n}}.p_{Mns}-\frac{1}{Ms_{n}}.p_{Ms} \\ z_{b}=\frac{1}{C_{\mathrm{sph}_{n}}}.q_{\frac{1}{C_{\mathrm{sph}}}}-w_{\frac{1}{C_{\mathrm{sph}}} }-w_{R_{a}}w_{a}+Sp_{n}.R_{a_{n}}.w_{\frac{1}{Ms}}+Sp_{n}.R_{a_{n}}.\frac{1}{ Mns_{n}}.p_{Mns} \\ \textrm{ \ \ \ \ \ \ }-Sp_{n}.R_{a_{n}}.\frac{1}{Ms_{n}} .p_{Ms}-Sp_{n}.R_{a_{n}}.w_{\frac{1}{Mns}} \\ z_{\frac{1}{C_{\mathrm{sph}}}}=\frac{1}{C_{\mathrm{sph}_{n}}}.q_{\frac{1}{C_{\mathrm{sph}}}} \\ z_{R_{a}}=w_{a}+Sp_{n}.R_{a_{n}}.w_{\frac{1}{Ms}}+Sp_{n}.R_{a_{n}}.\frac{1}{ Mns_{n}}.p_{Mns} \\ \textrm{ \ \ \ \ \ \ \ \ }-Sp_{n}.R_{a_{n}}.\frac{1}{Ms_{n}} .p_{Ms}-Sp_{n}.R_{a_{n}}.w_{\frac{1}{Mns}} \end{array} \right.$$

((3.19))

The state model deduced from the LFT BG of Fig. 3.10 is now under the form of (3.1) with

$$\begin{array}{lll}\begin{array}{ccc} A &=&\left[{\arraycolsep6pt \begin{array}{cccc} -\frac{Sp_{n}^{2}.R_{a_{n}}}{Mns_{n}} & \frac{Sp_{n}^{2}.R_{a_{n}}}{Ms_{n}} & k_{p_{n}} & -\frac{Sp_{n}}{C_{\mathrm{sph}_{n}}}0 \\\\[-6pt] \frac{Sp_{n}^{2}.R_{a_{n}}}{Mns_{n}} & -\frac{Sp_{n}^{2}.R_{a_{n}}}{Ms_{n}} & 0 & \frac{Sp_{n}}{C_{\mathrm{sph}_{n}}} \\\\[-6pt] -\frac{1}{Mns_{n}} & 0 & 0 & 0 \\\\[-6pt] \frac{Sp_{n}}{Mns_{n}} & -\frac{Sp_{n}}{Ms_{n}} & 0 & 0 \end{array}} \right] ; \\\\[-6pt] B_{1}&=&\left[ {\arraycolsep6pt\begin{array}{cccccc} 0 & 0 & 0 & Sp_{n} & Sp_{n} & Sp_{n} \\\\[-6pt] 0 & 0 & 0 & -Sp_{n} & -Sp_{n} & -Sp_{n} \\\\[-6pt] 1 & 0 & 0 & 0 & 0 & 0 \\\\[-6pt] -Sp_{n} & Sp_{n} & Sp_{n} & 0 & 0 & 0 \end{array}} \right] \end{array} \\\nonumber\\ C_1 &=&\left[ {\arraycolsep6pt\begin{array}{cccc} \frac{1}{Mns_{n}} & 0 & 0 & 0 \\\\[-6pt] 0 & \frac{1}{Ms_{n}} & 0 & 0 \\\\[-6pt] \frac{1}{Mns_{n}} & -\frac{1}{Ms_{n}} & 0 & 0 \\\\[-6pt] \frac{Sp_{n}.R_{a_{n}}}{Mns_{n}} & \frac{-Sp_{n}.R_{a_{n}}}{Ms_{n}} & 0 & \frac{1}{C_{\mathrm{sph}_{n}}} \\\\[-6pt] 0 & 0 & 0 & \frac{1}{C_{\mathrm{sph}_{n}}} \\\\[-6pt] \frac{Sp_{n}.R_{a_{n}}}{Mns_{n}} & \frac{-Sp_{n}.R_{a_{n}}}{Ms_{n}} & 0 & 0 \end{array}} \right] ;\nonumber\\\nonumber\\ D_{11}&=&\left[ {\arraycolsep6pt\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\\\[-6pt] 0 & 0 & 0 & 0 & 0 & 0 \\\\[-6pt] 0 & 0 & 0 & 0 & 0 & 0 \\\\[-6pt] Sp_{n}.R_{a_{n}} & Sp_{n}.R_{a_{n}} & 0 & Sp_{n}.R_{a_{n}} & -1 & -1 \\\\[-6pt] 0 & 0 & 0 & 0 & 0 & 0 \\\\[-6pt] -Sp_{n}.R_{a_{n}} & Sp_{n}.R_{a_{n}} & Sp_{n}.R_{a_{n}} & 0 & 0 & 0 \end{array}} \right]\end{array}$$

((3.20))

$$w=\left[ \begin{array}{c} w_{\frac{1}{Mns}} \\\\[-9pt] w\frac{1}{Ms} \\\\[-9pt] w_{a} \\\\[-9pt] w_{b} \\\\[-9pt] w_{\frac{1}{C_{\mathrm{sph}}}} \\\\[-9pt] w_{R_{a}} \end{array} \right] =\left[ \begin{array}{cccccc} \delta _{\frac{1}{Mns}} & 0 & 0 & 0 & 0 & 0 \\\\[-9pt] 0 & \delta \frac{1}{Ms} & 0 & 0 & 0 & 0 \\\\[-9pt] 0 & 0 & \delta _{a} & 0 & 0 & 0 \\\\[-9pt] 0 & 0 & 0 & \delta _{b} & 0 & 0 \\\\[-9pt] 0 & 0 & 0 & 0 & \delta _{\frac{1}{C_{\mathrm{sph}}}} & 0 \\\\[-9pt] 0 & 0 & 0 & 0 & 0 & \delta _{R_{a}} \end{array} \right] .\left[ \begin{array}{c} z_{\frac{1}{Mns}} \\\\[-9pt] z\frac{1}{Ms} \\\\[-9pt] z_{a} \\\\[-9pt] z_{b} \\\\[-9pt] z_{\frac{1}{C_{\mathrm{sph}}}} \\\\[-9pt] z_{R_{a}} \end{array} \right] ; D_{12}=0; B_{2}=\left[ \begin{array}{c} 0 \\\\[-9pt] 0 \\\\[-9pt] 1 \\\\[-9pt] 0 \end{array} \right]$$

((3.21))

3 LFT Bond Graphs for Robust FDI

Diagnosis of uncertain systems has been the subject of several recent research works [1–6]. This interest is reflected by the fact that physical systems are complex and non-stationary and require more security and performance. The bond graph model in LFT form allows the generation of analytical redundancy relations (ARRs) composed of two completely separated parts: a nominal part, which represents the residuals, and an uncertain part which serves both for the calculation of adaptive thresholds and sensitivity analysis.

In a BG (as in a bi-partite graph) can be defined a set of variables $Z=K\cup X$, composed of known variables (K) associated with measured variables (De and Df) and input ones (Se, Sf, MSe, MSf) and of unknown variables $X=x_{a}\cup x_{d}\cup \dot{x}_{d}\cup x_{i}\cup \dot{x} _{i}$ (variables associated with all the elements of a BG). a, d, i refer, respectively, to algebraic, derivative, and integral constraints.

The determination of ARRs on a bond graph model is done by elimination of unknown variables contained in the structural constraints of junctions 0 and 1. The equations of power balance on the junctions constitute the ARRs [16].

To avoid initial conditions problem which are not known in real processes, ARRs are directly generated from the BG model in derivative causality. Dualizing effort (or flow ) detector transforms it into a signal source $SSe= \tilde{De}$ (or $SSf=\tilde{Df}$) modulated by the measured value, as illustrated in Fig. 3.11. This imposed signal is the starting point for the elimination of unknown variables. Thus, models in integral causality of Figs. 3.11a and 3.12a are aimed at physical simulation while those in derivative causality of Figs. 3.11b and 3.12b are used for ARRs generation.

Fig. 3.11

(a) BG model in integral causality with a flow sensor. (b) BG model in derivative causality with a dualized flow sensor

Fig. 3.12

(a) BG model in integral causality with an effort sensor. (b) BG model in derivative causality with a dualized effort sensor

From the BG model of Figs. 3.11b and 3.12b we can write

$$\begin{array}{rcl}SSf+\sum b_{i}.e_{i}&=0 \\[6pt] SSe+\sum b_{i}.f_{i}&=0 \end{array}$$

with i the number of the links connected to the junction and $b_{i}=\pm 1$ following the half-arrow orientation.

ARRs generation consists in eliminating unknown variables e _i and f _i by following the causal path from a known variable to an unknown one. However, the elimination of the unknown variable on the considered causal constraint is not always possible. In the algebraic case where the equation is nonlinear, calculating the variable can be done only in one way.

Consider first a junction with I- and R-elements (Fig. 3.13a).

By dualizing the flow detector (on the model of Fig. 3.13a) which becomes a flow source SSf, I-element can be assigned with derivative causality. The ARR of (3.22) is then derived by eliminating the unknown variables in junction 1 using causal paths from known variable SSf (imposed) to the unknown variables:

$$Se-I_1\frac{dSSf}{dt}-R_1.SSf=0$$

((3.22))

In the presence of a C-element (Fig. 3.13b), a conflict of causality appears on the bond graph when trying to put both dynamic elements in derivative causality. It means that C element has to stay in integral causality. ARR will depend on initial effort e _C(0).

Fig. 3.13

(a) Bond graph model causally correct after dualizing the sensor. (b) Bond graph model with a conflict of causality (under-constrained)

3.1 Generation of Robust Residuals

3.1.1 General Form of Uncertain ARRs

The generation of robust analytical redundancy relations from a bond graph model proper and observable is summarized by the following steps:

• 1st step: Try to assign a preferred derivative causality on the nominal BG; if it is possible (the model is over-constrained), then continue the following steps;

• 2nd step: Build the LFT BG model;

• 3rd step: Derive ARRs by writing junction equations, as

  $$\sum b_{i}.f_{i_{\rm n}}+\sum Sf+\sum w_{i}=0$$

  for a junction 0 and

  $$\sum b_{i}.e_{i_{\textrm{n}}}+\sum Se+\sum w_{i}=0$$

  for a junction 1.

  The unknown variables are $e_{i_{\mathrm{n}}}$ and $f_{i_{\mathrm{n}}}$.

• 4th step: Eliminate the unknown variables by following the causal paths from sensors and sources to unknown variables;

• 5th step: Write the uncertain ARRs as follows:

  $$\mathrm{ARR}:\varPhi \left( \sum Se, \sum Sf, De, Df, \overset{\sim }{De}, \overset{\sim }{Df}, \sum w_{i}, R_{n}, C_{n}, I_{n}, \mathrm{TF}_{n}, \mathrm{GY}_{n}, \mathrm{RS}_{n}\right) =0$$

  ((3.23))

  where TF _n and GY _n are, respectively, the nominal values of TF and GY moduli. R _n , C _n , I _n , and RS _n are the nominal values of elements R, C, I, and RS. $\sum w_{i}$ is the sum of modulated inputs corresponding to uncertainties on the elements related to the considered junction.

3.1.2 Generation of Adaptive Thresholds

The generated ARR consists of two parts well separated due to the using of LFT model, a nominal part noted r:

$$r=\varPhi \left( \sum Se, \sum Sf, De, Df, \overset{ \sim }{De}, \overset{\sim }{Df}, R_{n}, C_{n}, I_{n}, \mathrm{TF}_{n}, \mathrm{GY}_{n}, \mathrm{RS}_{n}\right)$$

((3.24))

and an uncertain part noted $b=\sum w_{i}$ with

$$w_{i}=\varPhi \left( De, Df, \overset{\sim }{De}, \overset{ \sim }{Df}, R_{n}, C_{n}, I_{n}, \mathrm{TF}_{n}, \mathrm{GY}_{n}, \mathrm{RS}_{n}, \delta _{R}, \delta _{I}, \delta _{C}, \delta _{\mathrm{RS}}, \delta _{\mathrm{TF}}, \delta _{\mathrm{GY}}\right)$$

((3.25))

where δ _R , δ _I , δ _C , δ _RS, Δ _TF, Δ _GY are respectively, the values of multiplicative uncertainties on the elements R, I, C, RS, TF, and GY.

The uncertain part of the ARR is used to generate adaptive thresholds under an envelope form that contains residuals in the absence of faults.

Parameter uncertainty can be defined as a slight deviation of the parameter from its nominal value, without any effect on the functioning of the system. It may be constant or variable and may vary randomly in a positive or in a negative sense.

From (3.23), (3.24), and (3.25), it gives

$$r+\sum w_{i}=0\Rightarrow r=-\sum w_{i}$$

Let us define a threshold of the residual noted a as

$$a=\sum \left\vert w_{i}\right\vert$$

((3.26))

with $r\leqslant a$.

Thus an adaptive threshold of the residual is generated in the form of an envelope (3.27):

$$-a\leqslant r\leqslant a$$

((3.27))

The use of absolute values to generate the thresholds of normal operation ensures the robustness of this algorithm to false alarms. To control the non-detections and delays in the detection of the faults, sensitivity analysis of the residuals to faults and uncertainties allows the estimation of the fault detectable values.

3.2 Sensitivity Analysis

Several methods of model-based robust FDI have been developed in recent years [2, 3, 6, 17–19], for residual generation and evaluation. Evaluation methods depend on the approaches used for residual generation, and assumptions on the nature and type of uncertainties in the model. If we assume that uncertainties are not involved at the same frequency as faults, filtering methods are well suited [3]. In the case where the variation of the residual is assumed normally distributed around a known mean value, statistical methods are used to generate normal operating thresholds. After a judicious choice of a confidence degree, it is possible to calculate the probability of false alarms and non-detections [17]. Parity space is used for the fault detection of sensors and actuators, where the evaluation of the residuals is performed by considering uncertainties bounded by a norm or an interval. With this method, it is difficult to find a good compromise between robustness to uncertainty and sensitivity to faults, since the elimination of the influence of uncertainties in the residual may cause insensitivity to faults, especially actuators’ faults [2]. Since it is often difficult to reduce or eliminate the impact of uncertainties on the residuals using the space parity, it is useful to exploit the uncertain part of the model to derive thresholds for normal operation [2, 18]. Unfortunately, in case of parameter dependency, the thresholds are overvalued and likely differ, then they are usually generated by neglecting the parameter correlation.

LFT bond graph model allows to generate automatically residuals and adaptive thresholds; these thresholds provide robustness to uncertainties and are automatically adapted to changes in the operating modes of the system. The bond graph tool provides a practical solution to the problem of parameter dependency, because it is possible to track the spread of the influence of uncertainties in terms of effort or flow across the model through causal paths.

The sensitivity analysis of residuals to uncertainties and faults depends on sensitivity indices and fault detectability indices, to be defined. They allow control and improvement of diagnosis performance. In practice, the knowledge of fault detectable value allows the user to measure the damage that this fault can cause on the system, and the knowledge of uncertainties that could mask the appearance of faults may induce additional measurements to control their changes and achieve the desired performance.

3.2.1 Normalized Sensitivity Index

Sensitivity analysis of a residual to a parameter uncertainty can be done by deriving the uncertain part a of the ARR according to uncertainty δ _i as shown by (3.28) and (3.29). The result is a power variable (effort or flow), derived using the nominal value of the parameter. The sensitivity of the ARRs generated from 1 junction and 0 junction are

$$S_{\delta _{i}} =\frac{\partial a}{\partial \left\vert \delta _{i}\right\vert }=\frac{\partial \left( \sum \left\vert w_{i}\right\vert \right) }{\partial \left\vert \delta _{i}\right\vert }=\frac{\partial \left( \sum \left\vert \delta _{i}.e_{i_{\mathrm{n}}}\right\vert \right) }{\partial \left\vert \delta _{i}\right\vert }=\left\vert e_{i_{\mathrm{n}}}\right\vert$$

((3.28))

$$S_{\delta _{i}} =\frac{\partial a}{\partial \left\vert \delta _{i}\right\vert }=\frac{\partial \left( \sum \left\vert w_{i}\right\vert \right) }{\partial \left\vert \delta _{i}\right\vert }=\frac{\partial \left( \sum \left\vert \delta _{i}.f_{i_{\mathrm{n}}}\right\vert \right) }{\partial \left\vert \delta _{i}\right\vert }=\left\vert f_{i_{\mathrm{n}}}\right\vert$$

((3.29))

$i\in \left\{ R, C, I, \mathrm{RS}, \mathrm{TF}, \mathrm{GY}\right\}$. δ _i is the multiplicative uncertainty on parameter i.

The normalized sensitivity index of the residual to a parametric uncertainty δ _i is the ratio between effort (or flow) given by the uncertainty δ _i and the effort (or flow) contributed by all the parameter uncertainties a. Thus, the sum of these indices gives

$$\sum \mathrm{SI}_{\delta _{i}}=\sum \frac{\left\vert w_{i}\right\vert }{a}=\frac{\sum \left\vert w_{i}\right\vert }{a}=1$$

((3.30))

The residual sensitivity to parameter uncertainty is proportional to the normalized sensitivity indices, i.e., the residual is most sensitive to the uncertainty that has the greatest normalized sensitivity index.

3.2.2 Fault Detectability Index

In this section, we focus on two types of faults, parameter fault noted Y _i and structural fault noted Y _s. The parameter fault Y _i represents a rate of abnormal deviation of the parameter i of the system from its nominal value. It differs from the multiplicative parameter uncertainty noted δ _i , which is a slight deviation rate of the parameter from its nominal value, without any influence on the normal operation of the system. A parameter fault causes a degradation of system performances and may cause its total failure.

An example of parameter fault is given in Fig. 3.14. The system consists of a tank driven by an external source; the fluid then passes through a pipe to outside. The bond graph model of the system without fault is given in Fig.3.14a. Figure 3.14b shows the system with a plug in the pipe, considered as parameter fault because it changes the value of the element $R:Rz,$ but does not modify the model structure. It is modeled in the same way as a multiplicative uncertainty, as a percentage of the nominal value of the parameter.

Fig. 3.14

(a) Bond graph model of a system without fault. (b) Bond graph model of a system with a parameter fault

A structural fault noted Y _s corresponds to a new effort (or flow) source that causes a change in the structure of the model. Thus, the nominal model of the system is not conserved and its dynamic is altered by the presence of the fault. This difference between the system and the model generates an unbalance in the flow, mass and energy conservation laws, calculated from junctions 0 and 1 of the bond graph model. For example, a water leakage in the tank of Fig. 3.15b is a structural fault. It can be modeled by a flow source $Sf:Y_{\mathrm{s}}$. The model structure has changed from the bond graph model of the system without fault of Fig 3.15a.

Fig. 3.15

(a) Bond graph model of a system without fault. (b) Bond graph model of a system with a structural fault

The fault detectability index DI is defined as follows:

Definition 3.1

The fault detectability index DI is the difference in absolute value between the effort (or flow) provided by faults and those granted by all the uncertainties:

$$\begin{array}{rcl}\mathrm{DI} &=&\left\vert Y_{i}\right\vert .\left\vert e_{i_{\mathrm{n}}}\right\vert +\left\vert Y_{\mathrm{s}}\right\vert -a\textrm{ \ in a junction }1 \\ \mathrm{DI} &=&\left\vert Y_{i}\right\vert .\left\vert f_{i_{\mathrm{n}}}\right\vert +\left\vert Y_{\mathrm{s}}\right\vert -a\textrm{ \ in a junction }0\end{array}$$

((3.31))

where $\left( \left\vert Y_{i}\right\vert .\left\vert e_{i_{n}}\right\vert +\left\vert Y_{\mathrm{s}}\right\vert \right )$ corresponds to the contribution of all faults. Y _i is the rate of detectable fault on the parameter i, Y _s is detectable value of a structural fault and a is deducted from the uncertain part of the ARR. $e_{i_{\mathrm{n}}}$ is the effort brought by element with nominal parameter value i _n.

Proposition 3.3

Fault detectability condition

$$\left\{ \begin{array}{l} \textrm{if }DI\leqslant 0:\textrm{ The fault is not detectable} \\ \textrm{if }DI>0:\textrm{ The fault is detectable} \end{array} \right.$$

Assumption 3.3

The effort (or flow) provided to the residual by the occurrence of multiple faults is greater than the effort (or flow) contributed to the residual by the occurrence of a single fault.

Given this assumption, detectable value of a fault can be calculated assuming that this fault is the only one present in the system. The detectable rate Y _i of the fault on the parameter i can be defined by one of inequalities (3.32) and (3.33), assuming $Y_{\mathrm{s}}=0$.

• From the ARR generated from a junction 1, we deduce

  $$\left\vert Y_{i}\right\vert >\frac{a}{\left\vert e_{i_{\mathrm{n}}}\right\vert }$$

  ((3.32))

• From the ARR generated from a junction 0, we deduce

  $$\left\vert Y_{i}\right\vert >\frac{a}{\left\vert f_{i_{\mathrm{n}}}\right\vert }$$

  ((3.33))

Given Definition 3.1, Proposition 3.2 and Assumption 3.3, the detectable value of a structural fault Y _s can be defined by the following inequality, assuming $Y_{i}=0$:

$$\left\vert Y_{s}\right\vert >a$$

((3.34))

4 Application to a Mechatronic System

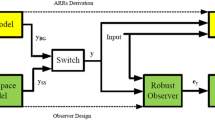
The mechatronic test bench of Fig. 3.16 consists of a computer, communicating with the power part of the system through DSpace acquisition card. The system consists of a DC motor which delivers a maximum power of 900 W and equipped with an incremental encoder on its main axle. The mechanical part of the system consists of a transmission mechanism (Fig. 3.17), defined by two moving parts linked to the engine axle by means of springs of different stiffnesses. The two parts can communicate through a dead zone varying between 0 and 0.5 rad. The position of the output axle is measured by an incremental encoder, which gives the relative position of the external load.

Fig. 3.16

Overview of the test bench

Fig. 3.17

The backlash mechanism

The bond graph model of the nominal system in integral causality is given in Fig. 3.18. The mechanical part of the engine is characterized by the viscous friction f _m and inertia J _m . Load part is characterized by friction f _s and inertia J _s . Reducer part is represented by TF, and the axles’ stiffness at the input and output of the reducer is represented by $C:{1}/{K}$ element. Modulated effort sources d and d _s are the disturbing torques caused by the presence of the backlash. Axle velocities are represented on the bond graph model of Fig. 3.18 by two flow sensors $Df:\dot{\theta}_{e}$ and $Df:\dot{\theta}_{s}$.

Fig. 3.18

Bond graph model of the nominal system in preferred integral causality

4.1 Robust FDI Procedure

1st step: Verification of structural properties of the system on the nominal bond graph model of Fig. 3.18.

On the bond graph model of Fig. 3.19, all dynamic elements are linked by causal paths to at least one detector, and all the dynamic elements I and C admit derivative causality on the bond graph model in preferred derivative causality. The model is thus proper and observable [20].

Fig. 3.19

Nominal bond graph model of the system in derivative causality

Fig. 3.20

Bond graph model of the system in derivative causality with dualized flow sensors

Fig. 3.21

LFT BG model of the test bench

Dualization of the two sensors (Fig. 3.20) causes a problem of causality on the part of the system located before the transformer TF.

Since initial conditions are known as the real system is equipped with position detectors, we can generate two ARRs from both 1 junctions, by keeping the element $C:{1}/{K}$ in integral causality.

2nd step: The LFT bond graph model of the test bench is given in Fig. 3.21.

Fictive inputs $w_{i}(i=1,\ldots,7)$ are linked to fictive outputs $z_{i}(i=1,\ldots,7)$ by the following relations:

$$\left\{ \begin{array}{l} {\small w}_{1}=\left( {\small \delta }_{K}{\small .\delta }_{j_{0}}{\small +\delta }_{K}{\small +\delta }_{j_{0}}\right) .{\small z}_{1}{\small \ ;} {\small z}_{1}{\small =d}_{{\small n}} \\\\[-6pt] {\small w}_{2}={\small -\delta }_{f_{m}}.{\small z}_{2}{\small \ ;} {\small z}_{2}{\small =f}_{m_{n}}.{\small \dot{\theta}}_{e} \\\\[-6pt] {\small w}_{3}={\small -\delta }_{J_{m}}.{\small z}_{3}{\small \ ;} {\small z}_{3}{\small =J}_{m_{n}}.{\small \ddot{\theta}}_{e} \\\\[-6pt] {\small w}_{4}={\small -\delta }_{K}.{\small z}_{4}{\small \ ;} {\small z}_{4}{\small =K}_{{\small n}}{\small .}\left( \theta _{e}-N.\theta _{s}\right) \\\\[-6pt] {\small w}_{5}=\left( \delta _{K}.\delta _{j_{0}}+\delta _{K}+\delta _{j_{0}}\right) .{\small z}_{5}{\small \ ;z}_{5}{\small =d}_{s_{n}} \\\\[-6pt] {\small w}_{6}={\small -\delta }_{f_{s}}.{\small z}_{6}{\small \ ;} {\small z}_{6}{\small =f}_{s_{n}}.{\small \dot{\theta}}_{s} \\\\[-6pt] {\small w}_{7}={\small -\delta }_{J_{s}}.{\small z}_{7}{\small \ ;} {\small z}_{7}{\small =J}_{s_{n}}.{\small \ddot{\theta}}_{s} \end{array} \right.$$

${\small \delta }_{J_{m}}$, ${\small \delta }_{f_{m}}$, ${\small \delta } _{J_{s}}$, ${\small \delta }_{f_{s}}$ represent, respectively, the multiplicative uncertainties on the inertia and viscous friction of the engine and the load. δ _K is the multiplicative uncertainty on the stiffness constant.

Disturbing torques d and d _s are considered as known inputs, estimated by (3.35), and represented on the bond graph model of Fig. 3.21 by two modulated inputs, with multiplicative uncertainties $\delta _{d}=\delta _{K}.\delta _{j_{0}}+\delta _{K}+\delta _{j_{0}}$ and $\delta _{d_{s}}=N.\left( \delta _{K}.\delta _{j_{0}}+\delta _{K}+\delta _{j_{0}}\right)$. The torque U and the reduction constant N ₀ are considered well known.

$$\left\{ \begin{array}{l} d=-4.K.j_{_{0}}.\frac{1-e^{-\gamma \beta }}{1+e^{-\gamma \beta }} \\\\[-6pt] d_{s}=N.d \end{array} \right.$$

((3.35))

3rd step: On the bond graph model of Fig. 3.21, ARRs of (3.36) are generated from the energy balance on the two 1 junctions:

$$\begin{array}{rcl}{\small \mathrm{ARR}}_{{\small 1}} &:&{\small U-f}_{m_{n}}{\small .\dot{\theta}}_{e} {\small -J}_{m_{n}}{\small .\ddot{\theta}}_{e}{\small -K}_{{\small n}} {\small .}\left( {\small \theta }_{e}{\small -N}_{0}{\small .\theta } _{s}\right) {\small +w}_{1}{\small +w}_{2}{\small +w}_{3}{\small +w}_{4} {\small =0} \\[6pt] {\small \mathrm{ARR}}_{{\small 2}} &:&{\small N}_{{\small 0}}{\small .K}_{{\small n}} {\small .}\left( {\small \theta }_{e}{\small -N}_{{\small 0}}{\small .\theta }_{s}\right) {\small +d}_{s_{n}}{\small -f}_{s_{n}}{\small .\dot{\theta}}_{s} {\small -J}_{s_{n}}{\small .\ddot{\theta}}_{s}{\small -N}_{{\small 0}} {\small .w}_{4}{\small +w}_{5}{\small +w}_{6}{\small +w}_{7}{\small =0} \end{array}$$

((3.36))

4th step: The ARRs obtained in the previous step are composed of two separated parts, given as follows:

$$\begin{array}{rcl}{\small r}_{{\small 1}} &=&U{\small -f}_{m_{n}}.\dot{\theta}_{e}{\small -J} _{m_{n}}.\ddot{\theta}_{e}{\small -K}_{{\small n}}{\small .}\left( \theta _{e}-N.\theta _{s}\right) \\[6pt] a_{1} &=&\left\vert w_{1}\right\vert +\left\vert w_{2}\right\vert +\left\vert w_{3}\right\vert {\small +}\left\vert w_{4}\right\vert {\small +} \left\vert {\small d}_{{\small n}}\right\vert \nonumber \\[6pt] {\small r}_{{\small 2}} &=&{\small N}.{\small K}_{{\small n}}{\small .} \left( \theta _{e}-N.\theta _{s}\right) {\small -f}_{s_{n}}.\dot{\theta}_{s} {\small -J}_{s_{n}}.\ddot{\theta}_{s} \nonumber \\[6pt] a_{2} &=&\left\vert N.w_{4}\right\vert +\left\vert w_{5}\right\vert +\left\vert w_{6}\right\vert +\left\vert w_{7}\right\vert {\small +} \left\vert d_{s_{n}}\right\vert\end{array}$$

((3.37))

4.2 Simulation Results

The original backlash is considered as a model uncertainty, whose contributed efforts are estimated using the equation set (3.35 ); its variation cannot be associated with the variation of one of elements R, I, and C of a BG model. An abnormal variation of the backlash is treated as a structural fault; its detectable value is determined using (3.31):

• Detectability index DIr ₁

  $$\begin{array}{rcl}\mathrm{DI}r_{1} &=&\left\vert Y_{\mathrm{s}}\right\vert -\sum \left\vert w_{i}\right\vert \\ &=&\left\vert Y_{\mathrm{s}}\right\vert -\left( \left\vert w_{1}\right\vert +\left\vert w_{2}\right\vert +\left\vert w_{3}\right\vert {\small +} \left\vert w_{4}\right\vert {\small +}\left\vert {\small d}_{{\small n} }\right\vert \right) \end{array}$$
  $$\mathrm{DI}r_{1}>0\Longrightarrow \left\vert Y_{\mathrm{s}}\right\vert >\left( \left\vert w_{1}\right\vert +\left\vert w_{2}\right\vert +\left\vert w_{3}\right\vert {\small +}\left\vert w_{4}\right\vert {\small +}\left\vert {\small d}_{ {\small n}}\right\vert \right)$$

• Detectability index DIr ₂

  $$\begin{array}{rcl}\mathrm{DI}r_{1} &=&\left\vert Y_{\mathrm{s}}\right\vert -\sum \left\vert w_{i}\right\vert \\ &=&\left\vert Y_{\mathrm{s}}\right\vert -\left( \left\vert N.w_{4}\right\vert +\left\vert w_{5}\right\vert +\left\vert w_{6}\right\vert +\left\vert w_{7}\right\vert {\small +}\left\vert d_{s_{n}}\right\vert \right) \end{array}$$
  $$\mathrm{DI}r_{2}>0\Longrightarrow \left\vert Y_{\mathrm{s}}\right\vert >\left( \left\vert N.w_{4}\right\vert +\left\vert w_{5}\right\vert +\left\vert w_{6}\right\vert +\left\vert w_{7}\right\vert {\small +}\left\vert d_{s_{n}}\right\vert \right)$$

with

$$\left\vert Y_{s}\right\vert =\left\vert -4K\left( j_{_{0}}+Y_{J_{0}}\right) .\frac{1-e^{-\gamma \beta }}{1+e^{-\gamma \beta }} \right\vert$$

((3.38))

where $Y_{J_{0}}$ is the fault. In the absence of fault $Y_{J_{0}}$ is equal to zero.

Fig. 3.22

Residuals and fault detectability indices in the absence of faults and uncertainties. (a) Residual r ₁, (b) residual r ₂, (c) fault detectability index of r ₁, and (d) fault detectability index of r ₂

Figure 3.22 shows the residuals and fault detectability indices without any fault and any uncertainty.

Figure 3.23 presents the residuals in the presence of modeling uncertainties ($j_{0}=0.2 \, \mathrm{rad}$ which is the maximum backlash allowed on the system in normal operation) and parameter uncertainties, and in the absence of fault $\left( Y_{J_{0}}=0\right)$. The fault detectability indices DIr ₁ and DIr ₂ are negative as shown in Fig. 3.23c, d. The residual values are equal to the torque provided by the initial disturbing torque, estimated by (3.35).

Figure 3.25 represents the residuals r ₁ and r ₂ in the presence of fault. The fault is gradually added to the original backlash j ₀ (3.38) between time $t=4\,\mathrm{s}$ and $t=16\,\mathrm{s}$ as shown in Fig. 3.24. The fault detectability index DIr ₂ becomes positive at time $t=6\,\mathrm{s}$ (Fig. 3.25d) and the fault amplitude at this time is 0.00038 rad (Fig. 3.24). Indeed, residual r ₂ begins to detect the presence of the fault at time $t=6\,\mathrm{s}$. The fault detectability index DIr ₁ becomes positive at time $t=7.8\,\mathrm{s}$ (Fig. 3.25c); at this time the residual r ₁ detects the presence of the fault. So, we conclude that the fault detectable value is 0.00038 rad, and it will be detected by the residual r ₂ with a slight lead over the residual r ₁.

Fig. 3.23

Residuals and fault detectability indices in the absence of faults and in the presence of uncertainties. (a) Residual r ₁, (b) residual r ₂, (c) fault detectability index of r ₁, and (d) fault detectability index of r ₂

Fig. 3.24

Profile of the fault Y _j

Fig. 3.25

Residuals and fault detectability indices in the presence of fault. (a) Residual r ₁, (b) residual r ₂, (c) fault detectability index of r ₁, and (d) fault detectability index of r ₂

Fig. 3.26

(a) Position difference between θ _e and θ _s . (b) Reducer input θ _e and output θ _s

4.3 Experimental Results

On the real system, the residual values in normal operation are not equal to zero because of parameter uncertainties and the value of the model uncertainty corresponding to an initial backlash j ₀. This latter causes a slight difference between the input and output of the reducer as shown in Fig. 3.26a, b. Residuals given in Fig. 3.27, the system being in normal operation, remain inside thresholds and no alarm is generated.

The structure of the test bench does not allow introducing a progressive fault to accurately reproduce the previous simulation. The fault is introduced by removing a metal plate at the reducer level.

Fig. 3.27

Residuals and thresholds in normal operation. (a) Residual r ₁ and (b) residual r ₂

Fig. 3.28

(a) Position difference between θ _e and θ _s . (b) Reducer input θ _e and output θ _s

Fig. 3.29

Residuals and thresholds in faulty situation. (a) Residual r ₁ and (b) residual r ₂

The backlash variation causes a large difference between the reducer input and output as shown in Fig. 3.28a, b. Overlaying Fig. 3.28a with Fig. 3.29a, b shows that the residuals begin to detect the fault as soon as its amplitude becomes slightly higher, 0.2 rad, which corresponds to the estimated value by the fault detectability indices.

5 Conclusion

Modeling is an important step in fault diagnosis scheme design, because the desired performances depend heavily on the model accuracy. The choice of the bond graph tool for robust FDI of uncertain systems is due to its multi-energy aspect and its causal and structural properties. The LFT BG modeling does not introduce new bond graph elements on the model; therefore, no change occurs in the order of the model and its structural properties. Structural analysis can thus be done directly on the deterministic model. The transformation from the deterministic to LFT bond graph model is easily made by just replacing the deterministic elements R, I, C, TF, GY, and RS by their corresponding LFT element.

The presented FDI method allows by using a bond graph model in LFT form, to generate residuals and adaptive thresholds. To improve and monitor the performances of the diagnosis, a method of residual sensitivity analysis is proposed to estimate the detectable values of the faults.

The proposed application shows the robustness of an FDI algorithm on mechatronic systems. Indeed, simulation and experimental results show that the algorithm is robust to false alarms, because residues remain inside the thresholds when the system is in normal operation. The performance of the algorithm against the non-detections and delays in fault detection is controlled by estimation of the fault detectable values.