1 Introduction

The word composite implies a material consisting of at least two distinct constituents (phases/materials) of entirely different physical/chemical properties. They are also referred to as engineered materials and some of them are inspired from natural composites, viz., wood, human teeth, bone, muscle, to name a few. The salient feature of such engineered materials is that the equivalent property of composite is better than its individual constituents. Within the composite, however, the constituent elements can be easily identified as they do not dissolve/blend into each other [1]completely. This is because, a composite material is manufactured by embedding the matrix (host) material, with reinforcements, such as filaments or stacking of laminae [2]. A careful choice of constituents can lead to a composite materials that is lighter, increased fatigue life, improved wear and corrosion resistance [3].

Of these, laminated composites are preferred as they have better mechanical characteristics and are more convenient to manufacture than the particle-reinforced composites; further, the volume fraction of the constituent components is easy to control [4, 5]. In addition, due to the presence of interface (matrix-fiber interface), the mechanical properties are improved. The interfaces act as barriers to crack propagation and deflect the cracks at the interface, thus enabling more fracture energy consumption [6, 7]. The laminated composite can be categorized as: (a) constant stiffness composite laminates (CSCL), and (b) tow-steered composite laminates (TSCL) based on the stiffness variation within the laminates. The CSCL is considered as a single domain with uniform staking sequence, fiber density, fiber orientation, and ply thickness. Whereas, TSCL is regarded as a domain consisting of multiple elements with different stacking sequence and modifies the load-carrying directions within the laminate, such that the stress distributions are within design tolerances and uniform; further, it improves the global response of structures in terms of failure stress, critical buckling load, and stiffness [8]. The flexibility offered by the TSCL, i.e., it allows the fiber to be placed at any angle, also increases the computational complexity of adequately predicting their response. Several approaches are presented to predict their response accurately [9,10,11].

In spite of the improved material properties that the composites offer, the presence of different constituents introduces interface macroscopically. The presence of an interface can lead to stress raisers and potential region for crack initiation; further, this can lead to failure of the structure. Typical failure processes in composite laminates include cracking of fibers, crack formation in the matrix, and debonding of matrix-fiber interface and/or delamination of plies [12, 13]. The catastrophic collapse of the system is associated to the matrix cracking, while, loss of strength is associated to stiffness and strength degradation  [14]. Experiments have shown that the free edges or the presence of discontinuities is the prominent region for the delamination to start [15]. Such diverse damage mechanisms cause the composite to lose strength gradually and eventually to catastrophic failures [16]. Brittle fracture is the prominent failure mode of unidirectional composites and the energy release mechanisms are by the deflection of the crack at the interface, shielding of crack by interfaces/other discontinuities, and branching of cracks [17, 18]. The crack orientation and propagation is highly influenced by the strength of the interface and the fracture toughness [19].

Complex fracture mechanisms in composites prohibit theoretical studies and often numerical approaches combined with experimental tests are employed. There are various numerical approaches that have been adopted in the literature to model the fracture characteristics in a composite laminate, some of them are: cohesive zone models [20], discrete element method [21], the eXtended finite element method [22, 23], and diffuse crack approach [24]. Aforementioned approaches requires a priori knowledge of the crack path, a criteria for changing crack morphology. This is circumvented by the introduction of phase field method for fracture by the seminal work of Francfort and Marigo [25], and Bourdin et al. [26]. The phase field method (PFM) was originally developed for interface problems and applied to the material solidification process [27,28,29,30]. Within the PFM framework, sharp interfaces are approximated by a scalar field variable that is continuous that distinguishes between multiple phases within the system through a smooth transition. In the last decade, the PFM is used by the physics and mechanics community to simulate fracture problems. In the context of fracture, order the parameter (termed as the phase field parameter) used to represent the fully broken and intact material phase with smooth transition (see Fig. 1c). The physics community models are generally based on the Landau-Ginzburg phase transition [31], and the mechanic’s community uses a model based on Griffith’s theory. Different models used by

  • physics community: Aranson et al. model [32], Karma et al. model [33], Henry and Levine model [34],

  • mechanics communityFootnote 1: Francfort and Marigo model [25], Bourdin model [26], Kuhn and Müller model [35, 36], Amor, Marigo and Maurini model [37], Miehe model [38, 39], Borden model [40], Hybrid model [41].

Due to its attractive features, the PFM is applied to wider range of engineering problems; some of them include: ductile fracture [42], thermal fracture [43], brittle fracture in functionally graded materials [44, 45], failure in composites [46, 47] and ceramics [48], crack growth in rocks [49], strength prediction in fiber-reinforced composite [12, 50, 51], and laminated composite [52], to name a few. Some researchers have used the UEL feature of the commercial software Abaqus [53, 54] to implement the phase field method, while Hirhikesh et al. [55] implemented the method in the open source finite element software, FEniCS.

The primary objective of this chapter is to discuss the implementation aspects of the PFM for an orthotropic material, and constant and tow-steered stiffness composite laminates in FEniCS. The effect of different parameters, such as, the inter-matrix spacing and the angle of the fiber on the load-carrying capacity is discussed with a few carefully chosen examples. This will enhance the understanding of fracture in composites.

2 Overview of Phase Field Method

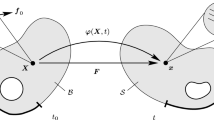
A linear elastic body with a discontinuity (material and crack) occupying the domain \(\Omega \subset \mathbb {R}^d\), where \(d=\) 2,3, represents the dimension of the problem (See Fig. 1). The domain is bounded by \(\Gamma \) with a unit outward normal \(\mathbf {n}\), accommodates the following disjoint sets, viz., \(\Gamma = \Gamma _\mathrm{D} \cup \Gamma _\mathrm{t} \cup \Gamma _c\) and \(\Gamma _\mathrm{D} \cap \Gamma _\mathrm{t} = \emptyset \), where on \(\Gamma _\mathrm{D}\) represents the region over which Dirichlet boundary conditions are specified and Neumann conditions are enforced on \(\Gamma _\mathrm{t}\). The discontinuous surface that denotes the crack is represented by \(\Gamma _c\), which in this study is denoted by a phase field variable \(\phi \in [0,1]\) with \(\phi =\) 1 represents the completely damaged state (see Fig. 1b, c).

Fig. 1
figure 1

a A discrete representation of the interface \(\Gamma \) and a sharp crack \(\Gamma _c\) in a domain \(\Omega \), b conforming representation of the interface, while a diffuse representation for the crack and c schematic of the scalar field variable \(\phi \), used to represent crack. Note that width of the crack is controlled by \(\ell _o\)

Full size image

2.1 Governing Balance Equations

The evolution of the fracture topology within PFM is captured by minimizing the total potential energy [25]. The total potential energy is given by the sum of bulk and surface energy as:

$$\begin{aligned} \Psi = \Psi _b + \Psi _s = \underbrace{\int \limits _\Omega \psi (\varvec{\varepsilon }) \mathrm {d} \Omega }_\mathrm{bulk~energy} + \underbrace{\int \limits _{\Gamma } {\mathcal {G}}_{c} \mathrm{{d}} \Gamma }_\mathrm{surface~energy}, \end{aligned}$$
(2.1)

where the small strain tensor is \(\varvec{\varepsilon } = \frac{1}{2} \left( \nabla ^{e} \varvec{\mathrm {u}}^\mathrm{{T}} + \nabla ^{e} \varvec{\mathrm {u}}\right) \), \(\mathcal {G}_c\) is the critical energy release rate, \(\psi (\varvec{\varepsilon })=\frac{1}{2} \lambda \left( \mathrm {tr} \quad \varvec{\varepsilon } \right) ^2 + \mu \mathrm {tr}( \varvec{\varepsilon }^2)\) is the elastic energy density and Lamé constants are denoted by \(\mu \) and \(\lambda \). where \(\nabla ^{e^T}\) is a vector Laplacian which is defined as

$$\begin{aligned} \nabla ^{e^T} = \left[ \begin{array}[c]{ccc} \frac{\partial }{\partial x} &{} 0 &{} \frac{\partial }{\partial y} \\ 0 &{} \frac{\partial }{\partial y}&{} \frac{\partial }{\partial x} \end{array}\right] . \end{aligned}$$

Upon introducing a damage variable to the strain energy, \(\Psi _b\) is modified as:

$$\begin{aligned} \Psi _b = \int \limits _\Omega \left[ (1- \phi )^2 + k \right] \psi (\varvec{\varepsilon }) \mathrm {d} \Omega , \end{aligned}$$
(2.2)

where \(k < 0\) is introduced for numerical stability. Further, by constructing a crack density functional \(\Gamma _{\ell _o}\) using a scalar field variable (\(\phi \)), \(\Psi _s\) in Eq. (2.1) can be written as [56]:

$$\begin{aligned} \int \limits _\Gamma \mathcal {G}_c \mathrm {d} \Gamma \approx \int \limits _\Omega \mathcal {G}_c \left( \frac{1}{2\ell _o}\phi ^2 + \frac{\ell _o}{2} |\nabla \phi |^2 \right) \mathrm {d} \Omega . \end{aligned}$$
(2.3)

With these modifications to the surface and the bulk energy, \(\Psi \) is rewritten as:

$$\begin{aligned} \Psi = \int \limits _\Omega \left[ (1-\phi )^2 + k \right] \psi (\varvec{\varepsilon }) + \mathcal {G}_c \left( \frac{1}{2\ell _o} \phi ^2 + \frac{\ell _o}{2} |\nabla \phi |^2\right) \mathrm {d}\Omega . \end{aligned}$$
(2.4)

Governing differential equations are derived by employing the variational principle that includes the internal and the external work; \(\delta \mathcal {W}_\mathrm{{int}}\) and \(\delta \mathcal {W}_\mathrm{{ext}}\). The internal energy \(\delta \mathcal {W}_\mathrm{{int}}\) is computed by taking the variation of \(\Psi \) as

$$\begin{aligned} \delta \mathcal {W}_\mathrm{{int}} = \int \limits _\Omega \left[ \varvec{\sigma } \delta \varvec{\varepsilon } - (2-2\phi ) \delta \phi ~\psi (\varvec{\varepsilon }) + \mathcal {G}_c \left( \frac{1}{\ell _o} \phi \delta \phi + \ell _o \nabla \phi \cdot \nabla \delta \phi \right) \right] \mathrm {d} \Omega . \end{aligned}$$
(2.5)

The variation of the external work \(\delta \mathcal {W}_\mathrm{{ext}}\) is obtained as

$$\begin{aligned} \delta \mathcal {W}_{\mathrm {ext}} = \int \limits _\Gamma \bar{\varvec{\mathrm {t}}} \cdot \delta \varvec{\mathrm {u}}~\mathrm {d} \Gamma , \end{aligned}$$
(2.6)

where \(\bar{\mathbf {t}}\) is the external traction imposed on \(\Gamma _\mathrm{t}\). In the above equation, it is assumed that there are no body forces and inertial forces. Imposing the constraint \(\delta \mathcal {W}_\mathrm{{int}} - \delta \mathcal {W}_\mathrm{{ext}}=0\), results, find \((\varvec{\mathrm {u}},\phi ): \Omega \rightarrow \mathbb {R}^d\) such that:

$$\begin{aligned} \varvec{\nabla } \cdot \varvec{\sigma } =&~ \varvec{0} \quad \text {in} \quad \Omega , \end{aligned}$$
(2.7a)
$$\begin{aligned} -\mathcal {G}_c \ell _o \nabla ^2 \phi + \left[ \frac{\mathcal {G}_c}{\ell _o} + 2 H \right] \phi =&~ 2 H \quad \mathrm {in} \quad \Omega , \end{aligned}$$
(2.7b)
$$\begin{aligned} \varvec{\sigma } \cdot \varvec{n} =&\overline{\mathbf {t}} \quad \mathrm {on} \quad \Gamma _\mathrm{t}, \end{aligned}$$
(2.7c)
$$\begin{aligned} \varvec{\mathrm {u}}=&\overline{\varvec{\mathrm {u}}} \quad \mathrm {on} \quad \Gamma _\mathrm{D}, \end{aligned}$$
(2.7d)
$$\begin{aligned} \nabla \phi \cdot \varvec{n} =&0 \quad \mathrm {on} \quad \Gamma _\mathrm{}, \end{aligned}$$
(2.7e)

where H is the history variable that depends on the strain energy, \(\psi (\varvec{\varepsilon })\) and is given by:

$$\begin{aligned} H ={\left\{ \begin{array}{ll} \psi (\varvec{\varepsilon }), &{} \text {if}~\psi (\varvec{\varepsilon })>H_n,\\ H_n, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(2.8)

where n denotes the load step and \(\varvec{\sigma }= \left[ (1-\phi )^2 + k \right] \frac{\partial \psi (\varvec{\varepsilon })}{\partial \varvec{\varepsilon }}\) is the modified Cauchy stress tensor. This model is known as an isotropic model in the literature [41]. The shortcoming of this model is that if fails to distinguish between the crack propagation in the tensile and compressive regions. Table 1 presents the various approaches that been postulated in the literature to alleviate some of the difficulties associated with the conventional PFM, such as: (a) prevent crack propagation in the compressive region, (b) non-physical crack propagation at the boundary and (c) length scale sensitivity. Readers are referred to [41, 57] that gives a comprehensive overview of different phase field approaches.

Table 1 Difficulties associated with the phase field method and proposed advances
Full size table

In this chapter, we employ the hybrid formulation that has the advantages of an isotropic model (i.e., the elastic equilibrium equation remains linear) and anisotropic model, that ensures that the crack propagates only by the tensile elastic energy, \(\psi ^+\).

$$\begin{aligned} -\mathcal {G}_c \ell _o \nabla ^2 \phi + \left[ \frac{\mathcal {G}_c}{\ell _o} + 2 H^+ \right] \phi =&~ 2 H^+ \quad \text {in} \quad \Omega , \end{aligned}$$
(2.9)
$$\begin{aligned} \forall \varvec{x}: \Psi ^+ < \Psi ^- \Rightarrow \phi :=&0 \end{aligned}$$
(2.10)

\(H^+\) in Eq. (2.10) is give by: \(H^+:=\text {max}_{\tau \in [0, t]} \Psi ^+(\varvec{\varepsilon }(\mathbf{x} , \tau ))\) and second constrain in Eq. (2.10) ensures that the crack faces do not inter penetrate. and

$$\begin{aligned} \Psi ^{\pm }(\varvec{\varepsilon }) = \frac{1}{2} \lambda \langle \mathrm {tr} (\varvec{\varepsilon }) \rangle ^{2}_{\pm } + \mu \mathrm {tr} (\varvec{\varepsilon }^{2}_{\pm }), \end{aligned}$$
(2.11)

with \(\langle \cdot \rangle _{\pm }:= \frac{1}{2}(\cdot \pm |\cdot |)\), \(\varvec{\varepsilon }_{\pm }:= \sum \limits ^3_{I = 1} \langle \varepsilon _I \rangle _{\pm } \varvec{n}_I \otimes \varvec{n}_I \) and \(\varepsilon = \sum \nolimits ^{3}_{I = 1} \langle \varepsilon _I \rangle \varvec{n}_I \otimes \varvec{n}_I,\) where \(\varepsilon _I\) and \(\varvec{n}_I\) are the principal strains and the principal strain directions, respectively.

2.2 Numerical Implementation

A Bubnov-Galerkin procedure is adopted to develop the weak form for the coupled Eq. (2.7). The domain is decomposed into non-overlapping regions called elements and a polynomial representation is adopted for the unknown field and the geometry. In this chapter, the unknown fields \((\mathbf {u},~\phi )\) is represented by Lagrange basis functions as:

$$\begin{aligned} \mathbf {u}&= \left\{ u,v \right\} = \sum \limits _I^n N_I \{ u_I,v_I \} \end{aligned}$$
(2.12a)
$$\begin{aligned} \phi&= \sum \limits _I^n N_I \phi _I \end{aligned}$$
(2.12b)

where \(N_I\) are the hat functions, n is the total number of nodes in the domain and \(\mathbf {u}_I,~\phi _I\) denotes nodal variables. The corresponding weak form is given by: Find \((\, \varvec{\mathrm {u}}, \, \phi )\) such that:

$$\begin{aligned} \int \limits _{\Omega } \varvec{\sigma }(\varvec{\mathrm {u}}):\varvec{\varepsilon }(\varvec{\mathrm {v}})\,\mathrm {d}\Omega&= \int \limits _{\Gamma _t}\hat{\varvec{\mathrm {t}}}\cdot \varvec{\mathrm {v}}\,\mathrm {d}\Gamma , \end{aligned}$$
(2.13a)
$$\begin{aligned} \int \limits _{\Omega } \left\{ \nabla \theta \, G_c \ell _o \nabla \phi + \theta \left[ \frac{G_c}{\ell _o} + 2 H^+ \right] \phi \right\} \, \mathrm {d}\Omega&= \int \limits _{\Omega } 2 H^+ \theta \, \mathrm {d}\Omega + \int \limits _{\Gamma } \nabla \phi \cdot \varvec{\mathrm {n}} \, \theta \, \mathrm {d}\Gamma \end{aligned}$$
(2.13b)

The unknown field variables \((\varvec{\mathrm {u}},\phi )\) are computed by solving the coupled equations (Eq. 2.13). Typical choices are Newton-Raphson and staggered approach. Due to the different nature of the equations, the Newton-Raphson approach has been known to yield converged results, and hence, the staggered approach is employed. Algorithm 1 shows the pseudo code for the staggered approach, where the unknown variables are solved sequentially within each time step until the convergence. For convergence, a user defined tolerance is specified and the convergence for the displacement and the phase field variable between successive staggered iteration steps is checked using max { \(\frac{||\{\mathbf {u}^h_{i+1}-\mathbf {u}^h_i\}||}{||\{\mathbf {u}^h_{i+1}\}||}\), \(\frac{||\{\phi _{i+1}-\phi _i\}||}{||\{\phi _{i+1}\}|| }\) } \(\le \) tolerance. Once the convergence is achieved, \(\phi ,~H\) and \(\varvec{\mathrm {u}}\) is updated and then the next load increment is applied. In this work, we use FEniCS, an open source finite element package is used to solve.

figure a

2.3 Implementation Aspects in FEniCS

The nice feature of FEniCS is that it is independent of the dimension of the problem and takes weak form directly as an input (see Listings 16.1 and 16.2). By using the unified form language embedded in Python, the weak from and the required finite element discretization is specified. Upon invoking \(\text {V = FunctionSpace(mesh,`P',m)}\), the domain is discretized with 3-noded triangular or 4-noded tetrahedra elements in two and three dimensions, respectively, ‘P’ defines the family of Lagrange elements and ‘m’ the order of polynomial that needs to employed to represent the unknown field variables. Listings 16.1 to 16.3 depicts the Python code for the staggered scheme adopted in FEniCS.

figure b
figure c
figure d

A three-dimensional domain with three holes subjected to far field tension (see Fig. 2a is solved first to show the capability of FEniCS to handle three dimensional problems and can also do parallel processing. The crack trajectory computed through the phase field framework is compared against the solution available in the literature [70]. The material properties used for the analysis: Young’s modulus E = 210 \(\times 10^3\) N/mm\(^2\), Poisson’s ratio \(\nu \) = 0.3 and strain energy release rate \(\mathcal {G}_c =\) 1.0 N/m. Four noded tetrahedra elements are used to discretized the domain, this is done using Gmsh. The mesh is then converted to FEniCS readable format by using the following command: dolfin-convert inputmesh.msh outputmesh.xml. The simulation is performed on an Intel Core i5-4590 CPU@3.30GHz \(\times \) 4 using 3 cores. Figure 2c shows the corresponding splitting of the domain in the three parallel cores.

Fig. 2
figure 2

Three-dimensional edge crack specimen with holes: a domain description with boundary conditions, b domain discretization, and c domain discretization using parallel core

Full size image
Fig. 3
figure 3

Crack propagation trajectory from a final crack trajectory as reported in Msekh [70], b FEniCS implementation

Full size image
Fig. 4
figure 4

Plate with circular hole in tension: a problem description and boundary conditions, crack trajectory for b 45\(^\circ \), c 0\(^\circ \), and d \(-45^\circ \) fiber orientation

Full size image

Figure 3 shows the crack trajectory. The crack trajectory is compared with the work of [70] and the results show very good agreement. The crack is initially attracted toward the first hole and then resumes to propagate between the holes. Hence, larger size problems can be solved using the parallel computation in FEniCS with the same accuracy. In the following, the implementation is verified for the orthotropic materials. For an orthotropic material, the Cauchy stress tensor in Eq. (2.13a) is defined as: \(\varvec{\sigma } = \left[ (1-\phi )^2 + k\right] \mathbb {D} \varvec{\varepsilon }\), where

$$\begin{aligned} \mathbb {D} = \begin{bmatrix} \cos \theta &{} -\sin \theta &{} 0 \\ \sin \theta &{} \cos \theta &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} \dfrac{E_1}{1-\nu _{12} \nu _{21}} &{} \dfrac{\nu _{12} E_2}{1-\nu _{12} \nu _{21}} &{} 0 \\ \dfrac{\nu _{12} E_2}{1-\nu _{12} \nu _{21}} &{} \dfrac{E_2}{1-\nu _{12} \nu _{21}} &{} 0 \\ 0 &{} 0 &{} G_{12} \end{bmatrix} \begin{bmatrix} \cos \theta &{} \sin \theta &{} 0 \\ -\sin \theta &{} \cos \theta &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$
(2.14)

where \(\nu _{21} = \dfrac{E_2}{E_1} \nu _{12}\), the Young’s modulus along the transverse and longitudinal direction is represented by \(E_2\) and \(E_1\), Shear modulus is represented by \(G_{12}\), \(\nu _{21}\) and \(\nu _{12}\) are the minor and the major Poisson’s ratio, respectively. To account for the material orientation, we introduce \(\mathbb {A} = \mathbf {I} + \beta \left[ \mathbf {I} - \mathbf {n} \otimes \mathbf {n}\right] \) with \(\mathbf {n}=\left\{ \cos \theta , \sin \theta \right\} ^\mathrm{T}\) into Eq. (2.10) to give:

$$\begin{aligned} -\mathcal {G}_c \ell _o \nabla \phi \mathbb {A} \nabla \phi + \left[ \frac{\mathcal {G}_c}{\ell _o} + 2 H^+\right] \phi =2H^+~\mathrm {in}~\Omega , \end{aligned}$$
(2.15)

The parameter \(\beta \) ensures that the crack propagates perpendicular to the cleavage plane orientation. For the current study, \(\beta =\) 20 is used for anisotropic case and for isotropic case, Eq. (2.10) is employed. The domain and the boundary conditions for a plate with circular hole subjected to tension is considered (see, Fig. 4a). Unidirectional fibers are embedded in the plate with an angle \(\theta \) with the vertical axis (see Fig. 4). The material properties are chosen as, \((E_1,E_2,G_{12},\nu _{12})=\) (114.8, 11.7,  9.66,  0.21 GPa). Figures 4b–d show the crack propagation trajectory for different material orientations. The crack path depends on the material orientations which agrees well with results presented in [71, 72].

3 Laminated Composite Fracture

In this section, we study the fracture processes in a two-dimensional CSCL/TSCL using the presented framework (see Fig. 5). The influence of the matrix thickness, \(t_m\) and fiber orientations on the crack propagation path and the maximum load for fracture is systematically studied. In all the examples, the domain is subjected to a far field tension, with \(a=\) 0.25 mm as the initial crack length, \(\ell _o = 2h\) (where h denotes the diameter of the smallest element in the domain) is employed, unless mentioned otherwise. The displacement increment is set to \(\Delta u=\) 1\(\times \)10\(^{-5}\) until complete fracture. Further, a no-slip condition is assumed between the fiber-matrix interface and the fibers inclined at an angle \(\vartheta (\varvec{x})\). In case of TSCL, the fiber angle is dictated by the angle at the center of the plate, \(\theta _O\) and angle at the free edge, \(\theta _1\). The variation of the fiber angle within the laminae is then given by [73,74,75]:

$$\begin{aligned} {\vartheta (\varvec{x}) = \frac{2(\theta _1 - \theta _0)}{2W} \mathrm{abs}(\varvec{x}) + \theta _0,} \end{aligned}$$
(3.1)

where W is half-width of the plate. For the present study, we assume \(2W=\) 3 mm and \(2L=\) 6 mm.

Fig. 5
figure 5

Schematic representation boundary value problem for: a CSCL, b TSCL

Full size image

The TSCL with different fiber orientations is represented as \(\langle \theta _1, \theta _0 \rangle \), and the CSCL fiber orientation is represented for a particular choice of the TSCL with \(\theta _1 \equiv \theta _0\) (see Fig. 5a). The material properties for the individual layered constituents are given in Table 2. In the model considered, alternate layers of fiber and matrix are arranged and assumes absence of the interface cracking and the micro-cracking mechanisms.

Remark 1

The mode mixity at the crack tip is discussed through the fringe pattern, which is the given: \(\sigma _1 - \sigma _2 = n \frac{f_\sigma }{t}\), where h is the plate thickness, \(f_\sigma \) is the fringe constant and the maximum and the minimum principal stresses are given by \(\sigma _1\) and \(\sigma _2\), respectively. The orientation of the fringes ahead of the crack tip is an indicator of the crack propagation direction and the fringes can be used to identify the fracture modes [76].

The fracture characteristics of CSCL is discussed first. After the application of the load, when \(\mathcal {G} = \mathcal {G}_c\) of the domain, the crack starts to propagate. For a pure far field tension, in case of an isotropic material, the direction of the crack is perpendicular to the loading direction. However, in case of laminates, due the presence of the matrix and the fiber with different material properties, the crack path deviates. This depends on the relative fracture toughness of the matrix and the fiber. In this present study, as the fracture toughness of the fiber is less than that of the matrix, the crack easily propagates in the fiber than the matrix. Figure 6 shows the crack path for CSCL with different fiber orientations, \(30^\circ ,~45^\circ \) and \(60^{\circ }\). In all the different cases, the crack growth is along the interface. It is seen that for fiber orientations \(45^{\circ }\) and \(60^{\circ }\), as the initial crack tip is inside the matrix, the crack propagates in the matrix, until it reaches the interface and upon further increase in the load, the propagation is along the interface. Figures 8 and 9 shows the fringe pattern for fiber orientations \(45^\circ \) and \(60^{\circ }\). A symmetric pattern is an indicator of mode I fracture whilst an anti-symmetric indicates mixed mode. This is seen in Fig. 8a. It is seen that the crack growth in the matrix is because the influence of the mode-mixity is greater than the fracture toughness of the matrix (see  Fig. 6b). Similar behavior has been observed in Fig. 6c, e, f.

Table 2 Material parameters for the fiber and the matrix [12]
Full size table
Fig. 6
figure 6

Phase field variable evolution for CSCL with different fiber orientation and for a–c \(t_\mathrm {m} =\) 0.25, d–f \(t_\mathrm {m} =\) 0.5, g–i \(t_\mathrm {m} =\) 0.75, the interface between the matrix and the fiber is represented by white line

Full size image

Figures 7a, b shows the load-carrying capacity of CSCL for different fiber orientations, viz., \(30^{\circ },~45^{\circ }\) and \(60^{\circ }\) and for different matrix thickness, \(t_m=\) 0.25, 0.5 and 0.75. The stress state experienced by the crack tip is strongly influenced by the fiber orientation. Fiber angle with \(\theta =\) 60\(^{\circ }\) experiences higher mode-mixity than other orientations. Thus, a laminate with fiber orientation 60\(^{\circ }\) offers higher resistance to crack propagation for a constant matrix thickness. However, the peak load at which the propagation starts is almost independent of the matrix thickness. This is because, as the matrix thickness increases, the inter-matrix spacing increases and the crack grows without the influence of the interface. The evolution of the damage variable, an indicator of the crack propagation, is shown in Fig. 6 for different fiber orientations and for different matrix thicknesses. The while line in Fig. 6 represents the fiber-matrix interface. As seen from Fig. 6 that as the matrix thickness increases, the crack tip is mostly in the matrix, an isotropic material. Hence, the crack grows perpendicular to the direction of the load and independent of the fiber orientation. The presence of the fiber offers less resistance to the crack path.

Fig. 7
figure 7

CSCL subjected to tension: load-displacement for the various fiber orientations for different matrix thickness: a \(t_\mathrm{m}= \) 0.25 ([the symbols (a–d) are the instances at which \(\sigma _{\mathrm {max}}-\sigma _{\mathrm {min}}\) are plotted in Figs. 8 and 9), b \(t_\mathrm {m}=\) 0.5, c \(t_\mathrm{m}=\) 0.75

Full size image
Fig. 8
figure 8

Fringe pattern for CSCL with fibers at 45\(^{\circ }\) at selected points on the load-displacement curve (c.f. Fig. 7a) for the matrix thickness, \(t_\mathrm {m}=\) 0.25

Full size image
Fig. 9
figure 9

Fringe pattern for CSCL with fibers at 60\(^{\circ }\) at selected points on the load-displacement curve (c.f.Fig. 7a) for the matrix thickness, \(t_\mathrm {m}=\) 0.25

Full size image
Fig. 10
figure 10

Dependence of the fiber orientation on the crack length (on the interface) for different matrix thickness, \(t_\mathrm {m}\)

Full size image

As seen earlier, for particular fiber orientations and matrix thickness, the growth of the crack is along the matrix-fiber interface. The influence of the fiber orientation on this is depicted in Fig. 10. From the numerical study, it is observed that the greater the matrix thickness and fiber orientation, the longer the crack length along the interface. The mode mixity experienced by the crack tip in case of fiber oriented at 60\(^\circ \) is less when compared to the fiber oriented at 45\(^\circ \) (see Figs. 8b and 9b). It is also seen that for a particular matrix thickness and fiber orientation 30\(^\circ \), the crack first propagates along the matrix-fiber interface before propagating further in the fiber and this is because, \(\mathcal {G}_c^\mathrm{fiber} < \mathcal {G}_c^\mathrm{matrix}\).

Fig. 11
figure 11

Representation of an initial crack in TSCL, a initial crack in matrix and b initial crack tip in the fiber

Full size image

3.1 Tow-Steered Composite Laminates (TSCL)

Next, the crack propagation in the TSCL is analyzed. The domain, the initial crack location, and the essential conditions are shown in Fig. 11. For the analysis, two cases are considered: the initial crack is in the matrix (see, Fig. 11a) and the initial crack is in the fiber (see, Fig. 11b). These are referred to as case I and case II whilst discussing the results. The aim of this is to study the influence of the initial location on the crack trajectory and the load-carrying capacity.

Fig. 12
figure 12

Crack propagation in TSCL with different fiber orientations ( \(\langle -30^\circ , 0^\circ \rangle \), \(\langle -45^\circ , 0^\circ \rangle \), \(\langle -60^\circ , 0^\circ \rangle \))

Full size image
Fig. 13
figure 13

Load-displacement for CSCL and the TSCL: a \(\langle -30^{\circ },~0^{\circ }\rangle \) and b \(\langle -45^{\circ }, 0^{\circ } \rangle \). In case of TSCL, both the cases are considered

Full size image

For both cases, the crack growth is in the direction that minimizes mode-II stress intensity factor, until it reaches the fiber-matrix interface (see Fig. 12. However, in case of Case I, the crack kinks into the soft compliant material (fiber) (see, Fig. 12a). This is because the fracture toughness of the fiber is less when compared to the matrix and so it offers less resistance, while it propagates along the interface for case II (see Fig. 12b). This can be attributed to the relatively higher fracture toughness of the matrix. It is further opined that the angle of the fiber does not have a strong influence on the crack propagation path for both cases as seen in Fig. 12.

The influence of the applied displacement on the reaction force for TSCL (both cases) with fiber orientations \(\langle -30^\circ , 0^\circ \rangle \) and \(\langle -45^\circ , 0^\circ \rangle \) are shown in Fig. 13. The results for CSCL with fiber orientations \(30^\circ \) and \(45^\circ \) is also shown for comparison. In both cases, the peak load-carrying capacity is higher and this is due to the stiffer matrix material that resists crack propagation. It is inferred that the peak load for TSCL is independent of the cases considered here and significantly higher than the CSCL. Figure 14 shows the effect of the combination of center angle \(\theta _0\) and \(\theta _1\) on the damage evolution and shows that the fiber orientation strongly influences the crack path. The corresponding load-displacement is shown in Fig. 14d.

Fig. 14
figure 14

a–c evolution of damage for different fiber orientations: \(\langle \)0\(^\circ ,\) 30\(^\circ \rangle \), \(\langle \)15\(^\circ ,\) 45\(^\circ \rangle \) \(\langle \)30\(^\circ ,\) 60\(^\circ \rangle \), respectively, and d load-displacement curve for TSCL

Full size image

4 Concluding Remarks

In this chapter, using the phase field method, the fracture characteristics of laminated composites (both straight fibers and tow-steered) are studied. The open source finite element software, FEniCS was used to solve the coupled phase field-elasticity equations. Fracture processes in the homogeneous and orthotropic material are compared against the available results in the literature. The influence of the fiber orientation, tow angle, inter-matrix spacing on the peak load at which the crack starts to propagate and the crack morphology are systematically studied. It can be inferred that for the cases considered, mode-mixity and the matrix material properties significantly influence the crack propagation. The maximum load at which the fracture happens for the CSCL is strongly influenced by the fiber angle for small fiber thickness and is relatively less sensitive for higher inter-fiber spacing. Further, the inter-matrix spacing and the fiber angle directly influences the crack length along the matrix-fiber interface.