Parametric Instability of an Electromechanically Coupled Rotor-Bearing System Subjected to Periodic Axial Loads: A Preliminary Theoretical Analysis

Abstract

The parametric instability of an electromechanically coupled single-span rotor-bearing system subjected to periodic axial loads is studied. Here, the rotor system is equipped with two piezoelectric dampers, which has been developed in our previous work. The so-called electromechanically coupled characteristic is namely derived from that damper. By using assumed mode method and Lagrange equation, the equations of motion are derived. The multiple scales method is utilized to obtain the analytical instability boundaries. Numerical simulations based on the discrete state transition matrix method (DSTM) are conducted to verify the analytical results. With the comparison between analytical results and simulated results, we find that the additional combination instability regions are created due to the usage of piezoelectric dampers.

1 Introduction

When the rotating slender structures, such as cylindrical shell or shaft are subjected to periodic axial forces, they may experience unstable transverse vibrations in some case. Such vibrations are so-called parametrically excited vibrations. It is very necessary to study the dynamic stability of these structures. On one hand, the rotating shaft or shell under periodic axial load can be found from many actual mechanical systems, e.g., marine propulsion shafting, aero-engine and so on. On the other hand, as above mentioned, these structures may be unstable due to certain combinations of the values of load parameters and natural frequency of transverse vibration. The final consequences will vary from economic loss to risk of catastrophic events. Thus, the dynamic stability of periodic axial loaded shafts or shells has received considerable attention over the years [3,4,5,6,7,8,9,10,11,12].

For example, Chen et al. [3] used the Timoshenko beam theory and FE method to build the rotor model, and then applied the Bolotin’s method to construct the instability regions. Their results showed that due to the Coriolis effect, the boundaries of the regions of dynamic instability were shifted out and the sizes of these regions were increased as the rotational speed increased. However, whether the Bolotin’s method is applicable to the rotating structure or not, there seems to have some disputes. Pei [6] found that using the Bolotin’s method may enlarge the instability region for the gyroscopic system, which may contradict the results based upon the Floquet’s method. Song et al. [9] presented a new method—discrete singular convolution. In their research, the external viscous damping and internal material damping were considered so as to analyze their influence on the stability of axial loaded rotating shaft. Qaderi et al. [10] investigated the dynamic responses of a rotating unbalanced shaft with geometrical nonlinearity under periodic axial loads. There the resonances, bifurcations, and stability of the response were analyzed. Phadatare et al. [12] studied the vibration and bifurcation analysis of a spinning rotor-disk-bearing system so as to reveal the effect of unbalance eccentricity and pulsating axial load on the dynamic stability. All of these papers are based on the rotor system. In addition, some research activities based on the rotating cylindrical shell model also have great reference value. For instance, Han et al. [7] investigated the parametric instability of a rotating cylindrical shell under periodic axial loads. By using the multiple scale method, the analytical expressions of instability boundaries for various modes were obtained. Their theoretical analysis demonstrated that as long as rotation is considered, only combination instability regions exist for such rotating shell.

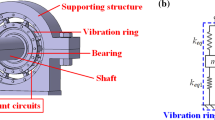
Although there have been many research activities focused on the dynamic stability analysis of parametrically excited rotating shafts or shells, there seems to be little reference about how to control the parametric resonances. In our previous research [1, 2], a novel piezoelectric damper has been developed for the lateral vibration control of rotor system. Through the preliminary experiment, the authors realize that this damper may also be used for the parametric resonance. However, how the damper’s performance is for the parametric excited rotor is not very clear. Thus, in this paper, its influence on the rotor’s dynamic behavior is studied. Certainly, as a preliminary theoretical analysis, only the dynamic stability analysis is presented here, where the analytical expressions of instability boundaries are also derived.

The content of this paper can be listed as follows: In Sect. 2, the mathematical model is given. In Sect. 3, the solving process of obtained mathematical model based on the multiple scales method is proposed, where the instability boundaries are derived analytically. Moreover, the existence condition of instability regions is presented there. In Sect. 4, the numerical simulations are carried out with comparison between analytical results and numerical results. There, the influence of shunt circuit parameters on the instability regions are analyzed in detail. Finally, some conclusions are given.

2 The Mathematical Model

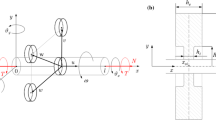
When the rotor system is mounted with the proposed damper, the whole dynamic model can be shown in Fig. 1. Note that all of supporting structures are linear. The electromechanically coupled boundary conditions which are generalized as spring-mass-damper systems are namely derived from the proposed damper. For the detailed description about this damper, one can refer to Refs. [1, 2]. Consider a spinning circular Rayleigh beam, through introducing two transverse (v, w) and two rotational (B, Γ) displacements in a fixed reference coordinate, as shown in Fig. 1, the deflection of a point in the shaft can be described.

Fig. 1.

The dynamic model of rotor system mounted with vibration ring

where Ω is the rotating speed of shaft and ω is the whirl speed of that. The strain energy of a rotating shaft can be expressed as

$$ U_{s} = \frac{1}{2}\int_{0}^{L} {EI_{D} } \left( {v^{{\prime\prime}{2}} + w^{{\prime\prime}{2}} } \right){\text{d}}x - \frac{1}{2}\int_{0}^{L} {P\left( t \right)} \left( {v^{{\prime}{2}} + w^{{\prime}{2}} } \right){\text{d}}x $$

(1)

where E is the Young’s modulus, I_D is the diametrical moment of inertia and L is the length of the shaft. The prime denotes the partial differentiation with respect to location x. Here, the periodic axial force P(t) is

$$ P\left( t \right) = P_{cr} \left( {\chi + \varepsilon \cos \theta t} \right) $$

(2)

where P_cr, χ, ε and θ represent the fundamental static buckling load, static load coefficient, dynamic load coefficient and excitation frequency, respectively. The total strain energy of springs at the end of shaft is

$$ \begin{gathered} U_{k} = \frac{1}{2}k_{eq} \left( {w\left| {_{x = 0} } \right. - a_{lz} } \right)^{2} + \frac{1}{2}k_{eq1} a_{lz}^{2} + \frac{1}{2}k_{eq2} \left( {a_{lz} - \tilde{q}_{lz} } \right)^{2} \hfill \\ \;\;\;\;\;\;\; + \frac{1}{2}k_{eq} \left( {v\left| {_{x = 0} } \right. - a_{ly} } \right)^{2} + \frac{1}{2}k_{eq1} a_{ly}^{2} + \frac{1}{2}k_{eq2} \left( {a_{ly} - \tilde{q}_{ly} } \right)^{2} \hfill \\ \;\;\;\;\;\;\; + \frac{1}{2}k_{eq} \left( {w\left| {_{x = L} } \right. - a_{rz} } \right)^{2} + \frac{1}{2}k_{eq1} a_{rz}^{2} + \frac{1}{2}k_{eq2} \left( {a_{rz} - \tilde{q}_{rz} } \right)^{2} \hfill \\ \;\;\;\;\;\;\; + \frac{1}{2}k_{eq} \left( {v\left| {_{x = L} } \right. - a_{ry} } \right)^{2} + \frac{1}{2}k_{eq1} a_{ry}^{2} + \frac{1}{2}k_{eq2} \left( {a_{ry} - \tilde{q}_{ry} } \right)^{2} \hfill \\ \end{gathered} $$

(3)

The total kinetic energy of the whole system is

$$ \begin{gathered} T = \frac{1}{2}\int_{0}^{L} {\left[ {\rho A\left( {\dot{v}^{2} + \dot{w}^{2} } \right) + \rho I_{D} \left( {\dot{B}^{2} + \dot{\Gamma }^{2} } \right) - 2\rho \Omega I_{p} \dot{\Gamma }B + \rho \Omega^{2} I_{p} } \right]} {\text{d}}x \hfill \\ \;\;\;\;\; + \frac{1}{2}\int_{0}^{L} {\left[ {M\left( {\dot{v}^{2} + \dot{w}^{2} } \right) + J_{p} \left( {\dot{B}^{2} + \dot{\Gamma }^{2} } \right) - 2J_{p} \Omega \dot{\Gamma }B + J_{p} \Omega^{2} } \right]} \delta \left( {x - x_{0} } \right){\text{d}}x \hfill \\ \;\;\;\;\; + \int_{0}^{L} {\left\{ {Me\left[ { - \dot{v}\sin \left( {\Omega t + \varphi } \right) + \dot{w}\cos \left( {\Omega t + \varphi } \right)} \right]\delta \left( {x - x_{0} } \right) + \frac{1}{2}M\Omega^{2} e^{2} \delta^{2} \left( {x - x_{0} } \right)} \right\}{\text{d}}x} \hfill \\ \end{gathered} $$

(4)

where the first term represents the kinetic energy of rotating shaft, the second and third terms represent that of eccentric disk. The symbols ρ, A, I_p, M, J_p, e, φ, x₀ and δ(x) are the mass density, area of cross section of shaft, polar moment of inertia of shaft, disk mass, polar moment of inertia of disk, mass eccentricity and its phase of disk, location of disk and Dirac delta function, respectively. The Rayleigh’s dissipation function due to the damping can be formulated as

$$ \begin{gathered} \Phi = \frac{1}{2}\eta \left( {\dot{w}\left| {_{x = 0} } \right. - \dot{a}_{lz} } \right)^{2} + \frac{1}{2}\eta \left( {\dot{v}\left| {_{x = 0} } \right. - \dot{a}_{ly} } \right)^{2} + \frac{1}{2}\eta \left( {\dot{w}\left| {_{x = L} } \right. - \dot{a}_{rz} } \right)^{2} \hfill \\ \;\;\;\;\;\; + \frac{1}{2}\eta \left( {\dot{v}\left| {_{x = L} } \right. - \dot{a}_{ry} } \right)^{2} + \frac{1}{2}\zeta \dot{\tilde{q}}_{lz}^{2} + \frac{1}{2}\zeta \dot{\tilde{q}}_{ly}^{2} + \frac{1}{2}\zeta \dot{\tilde{q}}_{rz}^{2} + \frac{1}{2}\zeta \dot{\tilde{q}}_{ry}^{2} \hfill \\ \end{gathered} $$

(5)

The assumed mode method is used to discretize the elastic displacements in space and time as

$$ v\left( {x,t} \right) = \sum\limits_{i = 1}^{n} {\phi_{i} \left( x \right)p_{i} \left( t \right)} = {{\varvec{\Phi}}}\left( x \right){\mathbf{p}}\left( t \right),\;\;w\left( {x,t} \right) = \sum\limits_{i = 1}^{n} {\phi_{i} \left( x \right)q_{i} \left( t \right)} = {{\varvec{\Phi}}}\left( x \right){\mathbf{q}}\left( t \right) $$

(6)

where Φ(x) = [ϕ₁(x), ϕ₂(x), …, ϕ_n(x)], p(t) = [p₁(t), p₂(t), …, p_n(t)]^T, q(t) = [q₁(t), q₂(t), …, q_n(t)]^T. ϕ_i(x) is the corresponding shape function of the beam bending under the short circuit condition. The variable n represent the number of the corresponding mode shapes used for spatial discretization. The time-dependent variables p_i(t) and q_i(t) are the corresponding generalized coordinates to be determined. In this paper, two mode shapes are used, i.e., n = 2. By combining Eqs. (1)–(6) and then substituting them into the Lagrange’s equation, that is

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial {\dot{\mathbf{s}}}}}} \right) - \left( {\frac{\partial L}{{\partial {\mathbf{s}}}}} \right) + \frac{\partial \Phi }{{\partial {\dot{\mathbf{s}}}}} = {\mathbf{0}} $$

(7)

where L = T − U_k − U_s and s = [p₁(t), p₂(t), q₁(t), q₂(t), a_lz, a_ly, a_rz, a_ry, $\tilde{q}_{lz} ,\, \tilde{q}_{ly} ,\,\tilde{q}_{rz} ,\,\tilde{q}_{ry}$]^T is the vector of the flexible generalized coordinates of size 12, the equations of motion can be obtained

$$ \begin{gathered} {\mathbf{M}}_{r} {{\ddot{\mathbf{p}}}} + {\mathbf{G}}_{r} {\dot{\mathbf{q}}} + {\mathbf{D}}_{r} {\dot{\mathbf{p}}} + \left[ {{\mathbf{K}}_{r} - P\left( t \right){\mathbf{S}}_{r} } \right]{\mathbf{p}} - \eta {{\varvec{\Phi}}}^{{\text{T}}} \left( 0 \right)\dot{a}_{ly} - \eta {{\varvec{\Phi}}}^{{\text{T}}} \left( L \right)\dot{a}_{ry} - k_{eq} {{\varvec{\Phi}}}^{{\text{T}}} \left( 0 \right)a_{ly} \hfill \\ \;\;\;\;\;\; - \,k_{eq} {{\varvec{\Phi}}}^{{\text{T}}} \left( L \right)a_{ry} = {{\varvec{\Phi}}}^{{\text{T}}} \left( {x_{0} } \right) \cdot M\Omega^{2} e\cos \left( {\Omega t + \varphi } \right) \hfill \\ {\mathbf{M}}_{r} {{\ddot{\mathbf{q}}}} - {\mathbf{G}}_{r} {\dot{\mathbf{p}}} + {\mathbf{D}}_{r} {\dot{\mathbf{q}}} + \left[ {{\mathbf{K}}_{r} - P\left( t \right){\mathbf{S}}_{r} } \right]{\mathbf{q}} - \eta {{\varvec{\Phi}}}^{{\text{T}}} \left( 0 \right)\dot{a}_{lz} - \eta {{\varvec{\Phi}}}^{{\text{T}}} \left( L \right)\dot{a}_{rz} - k_{eq} {{\varvec{\Phi}}}^{{\text{T}}} \left( 0 \right)a_{lz} \hfill \\ \;\;\;\;\;\; - \,k_{eq} {{\varvec{\Phi}}}^{{\text{T}}} \left( L \right)a_{rz} = {{\varvec{\Phi}}}^{{\text{T}}} \left( {x_{0} } \right) \cdot M\Omega^{2} e\sin \left( {\Omega t + \varphi } \right) \hfill \\ \end{gathered} $$

(8a)

$$ \begin{gathered} \eta \dot{a}_{ly} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{ly} - k_{eq2} \tilde{q}_{ly} = k_{eq} {{\varvec{\Phi}}}\left( 0 \right){\mathbf{p}} + \eta {{\varvec{\Phi}}}\left( 0 \right){\dot{\mathbf{p}}} \hfill \\ \eta \dot{a}_{lz} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{lz} - k_{eq2} \tilde{q}_{lz} = k_{eq} {{\varvec{\Phi}}}\left( 0 \right){\mathbf{q}} + \eta {{\varvec{\Phi}}}\left( 0 \right){\dot{\mathbf{q}}} \hfill \\ \eta \dot{a}_{ry} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{ry} - k_{eq2} \tilde{q}_{ry} = k_{eq} {{\varvec{\Phi}}}\left( L \right){\mathbf{p}} + \eta {{\varvec{\Phi}}}\left( L \right){\dot{\mathbf{p}}} \hfill \\ \eta \dot{a}_{rz} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{rz} - k_{eq2} \tilde{q}_{rz} = k_{eq} {{\varvec{\Phi}}}\left( L \right){\mathbf{q}} + \eta {{\varvec{\Phi}}}\left( L \right){\dot{\mathbf{q}}} \hfill \\ \end{gathered} $$

(8b)

$$ \begin{gathered} k_{eq2} \left( {a_{ly} - \tilde{q}_{ly} } \right) = \zeta \dot{\tilde{q}}_{ly} \hfill \\ k_{eq2} \left( {a_{lz} - \tilde{q}_{lz} } \right) = \zeta \dot{\tilde{q}}_{lz} \hfill \\ k_{eq2} \left( {a_{ry} - \tilde{q}_{ry} } \right) = \zeta \dot{\tilde{q}}_{ry} \hfill \\ k_{eq2} \left( {a_{rz} - \tilde{q}_{rz} } \right) = \zeta \dot{\tilde{q}}_{rz} \hfill \\ \end{gathered} $$

(8c)

Here, Eq. (8a) is the governing equation of the whole system and Eqs. (8b) and (8c) are the boundary conditions. If the piezo stacks are shunted with a single resonant RLC circuit, the electrical damping ζ will have the Laplace form: $\zeta \,{ = }\,2\cot^{2} \beta \theta_{p}^{2} \;{\text{(sL + R + }}\frac{{1}}{{{\text{sC}}}}{)}$, where s is the Laplace variable. Substituting its expression into Eq. (8c), these equations can then be expressed as

$$ \left\{ \begin{gathered} 2\cot^{2} \beta \theta_{p}^{2} L \cdot \ddot{\tilde{q}}_{ly} + 2\cot^{2} \beta \theta_{p}^{2} R \cdot \dot{\tilde{q}}_{ly} + \left( {k_{eq2} + \frac{{2\cot^{2} \beta \theta_{p}^{2} }}{C}} \right)\tilde{q}_{ly} - k_{eq2} a_{ly} = 0 \hfill \\ 2\cot^{2} \beta \theta_{p}^{2} L \cdot \ddot{\tilde{q}}_{lz} + 2\cot^{2} \beta \theta_{p}^{2} R \cdot \dot{\tilde{q}}_{lz} + \left( {k_{eq2} + \frac{{2\cot^{2} \beta \theta_{p}^{2} }}{C}} \right)\tilde{q}_{lz} - k_{eq2} a_{lz} = 0 \hfill \\ 2\cot^{2} \beta \theta_{p}^{2} L \cdot \ddot{\tilde{q}}_{ry} + 2\cot^{2} \beta \theta_{p}^{2} R \cdot \dot{\tilde{q}}_{ry} + \left( {k_{eq2} + \frac{{2\cot^{2} \beta \theta_{p}^{2} }}{C}} \right)\tilde{q}_{ry} - k_{eq2} a_{ry} = 0 \hfill \\ 2\cot^{2} \beta \theta_{p}^{2} L \cdot \ddot{\tilde{q}}_{rz} + 2\cot^{2} \beta \theta_{p}^{2} R \cdot \dot{\tilde{q}}_{rz} + \left( {k_{eq2} + \frac{{2\cot^{2} \beta \theta_{p}^{2} }}{C}} \right)\tilde{q}_{rz} - k_{eq2} a_{rz} = 0 \hfill \\ \end{gathered} \right. $$

(9)

By combining Eq. (8) and Eq. (9), the following matrix form of equations of motion can be obtained

$$ \begin{gathered} {\tilde{\mathbf{M}}\ddot{\mathbf{y}}}_{v} + {\tilde{\mathbf{D}}\dot{y}}_{v} + {\tilde{\mathbf{G}}\dot{y}}_{v} + \left( {{\tilde{\mathbf{K}}} - \varepsilon P_{cr} \cos \theta t \cdot {\tilde{\mathbf{S}}}} \right){\mathbf{y}}_{v} = {\tilde{\mathbf{F}}}_{v} \hfill \\ {\tilde{\mathbf{M}}\ddot{\mathbf{y}}}_{w} + {\tilde{\mathbf{D}}\dot{y}}_{w} - {\tilde{\mathbf{G}}\dot{y}}_{v} + \left( {{\tilde{\mathbf{K}}} - \varepsilon P_{cr} \cos \theta t \cdot {\tilde{\mathbf{S}}}} \right){\mathbf{y}}_{w} = {\tilde{\mathbf{F}}}_{w} \hfill \\ \end{gathered} $$

(10)

where y_v = [p₁(t), p₂(t), a_ly, a_ry, $\tilde{q}_{ly} ,\, \tilde{q}_{ry}$]^T and y_w = [q₁(t), q₂(t), a_lz, a_rz, $\tilde{q}_{lz} ,\, \tilde{q}_{rz}$]^T. Here, the matrices ${\tilde{\mathbf{M}}},\,{\tilde{\mathbf{G}}},\,{\tilde{\mathbf{K}}},\,{\tilde{\mathbf{D}}},\,{\tilde{\mathbf{S}}},\,{\tilde{\mathbf{F}}}_{v} ,\,{\tilde{\mathbf{F}}}_{w}$ represent the mass matrix, gyroscopic matrix, stiffness matrix, damping matrix, axial stiffness matrix, generalized unbalance vector force along v direction and w direction, respectively. The dimensions of these matrices are all 6 × 6. The detailed expressions of them are provided in Appendix A. It should be mentioned that the stiffness matrix K has included the effect of static axial load. In fact, Eq. (10) can be further simplified. For the isotropic boundary condition, the following definition could be introduced

$$ \begin{gathered} y_{1} = p_{1} + {\text{j}}q_{1} ,\;\;y_{2} = p_{2} + {\text{j}}q_{2} ,\;\; \cdots ,\;\;y_{n} = p_{n} + {\text{j}}q_{n} ,\;\; \hfill \\ a_{l} = a_{ly} + {\text{j}}a_{lz} ,\;\;a_{r} = a_{ry} + {\text{j}}a_{rz} ,\;\;\tilde{q}_{l} = \tilde{q}_{ly} + {\text{j}}\tilde{q}_{lz} ,\;\;\tilde{q}_{r} = \tilde{q}_{ry} + {\text{j}}\tilde{q}_{rz} \hfill \\ \end{gathered} $$

Then Eq. (10) can be simplified as

$$ {\tilde{\mathbf{M}}\ddot{\mathbf{y}}} + \left( {{\tilde{\mathbf{D}}} - {\text{j}}{\tilde{\mathbf{G}}}} \right){\dot{\mathbf{y}}} + \left( {{\tilde{\mathbf{K}}} - \varepsilon P_{{cr}} \cos \theta t \cdot {\tilde{\mathbf{S}}}} \right){\mathbf{y}} = {\tilde{\mathbf{F}}} $$

(11)

where j = $\sqrt{-{1}}$, y = y_v + jy_w = [y₁, y₂, a_l, a_r, $\tilde{q}_{l} ,\, \tilde{q}_{r}$]^T and ${\tilde{\mathbf{F}}}$ = ${{\tilde{\mathbf{F}}}}_{\text{v}}$+j ${{\tilde{\mathbf{F}}}}_{\text{w}}$ = MΩ²e[ϕ₁(x₀)e^j(Ωt+φ), ϕ₂(x₀), 0, 0, 0, 0]^T.

From the expressions of matrices ${\tilde{\mathbf{M}}}$, ${\tilde{\mathbf{G}}}$, ${\tilde{\mathbf{K}}}$, ${\tilde{\mathbf{D}}}$ and ${\tilde{\mathbf{S}}}$, it can be found that these matrices are non-diagonal due to the assumed approximate mode shapes. Thus, one can diagonalize some ones of them and reduce their scales by using the eigenvectors ψ of eigenvalue problem: (${\tilde{\mathbf{K}}}$−λ ${\tilde{\mathbf{M}}}$)ψ = 0. It should be pointed out that this eigenvalue problem represents the rotor system is non-rotating and only suffered by the static axial load. This problem should be solved in two case, that is, the short-circuit case (L = 0) and closed-circuit case (L ≠ 0). Note that the mass matrix ${\tilde{\mathbf{M}}}$ is always singular due to the massless degree of freedoms a_l and a_r. Hence, it is easy to be concluded that the rotor system has 2 useful eigenvectors in the short-circuit case and 4 useful eigenvectors in the closed-circuit case. Then these eigenvectors are combined to form the modal matrix Ψ = [ψ₁, ψ₂, …, ψ_N], where N = 2 or 4. Here, the eigenvectors are the weighted normal modal vectors which have been divided by the square roots of the generalized masses. Assume that the modal displacement vector y has the form: y(t) = Ψq(t). Substituting it into Eq. (11) and premultiplying each side by Ψ^T, one can obtain

$$ {\mathbf{I}}\ddot{\mathbf{q}} + \left( {{\overline{\mathbf{D}}} - {\text{j}}{\overline{\mathbf{G}}}} \right){\dot{\mathbf{q}}} + \left( {{\overline{\mathbf{K}}} - 2\varepsilon \cos \theta t \cdot {\overline{\mathbf{S}}}} \right){\mathbf{q}} = {\overline{\mathbf{F}}} $$

(12)

where I is the identity matrix, ${\overline{\mathbf{K}}} = {{\varvec{\Psi}}}^{{\text{T}}} {\mathbf{K\Psi }}$ = diag[α₁, α₂, …, α_N] is the diagonal matrix consists of the rotor system’s square of eigenvalues α_i (i = 1, 2, …, N) under the static condition, ${\overline{\mathbf{D}}} = {{\varvec{\Psi}}}^{{\text{T}}} {\tilde{\mathbf{D}\Psi }}$, ${\overline{\mathbf{G}}} = {\boldsymbol{\Psi}} \tilde{\mathbf{G}\boldsymbol{\Psi }}^{{\text{T}}}$, ${\overline{\mathbf{S}}} = \frac{{P_{cr} }}{{2}}{{\varvec{\Psi}}}^{{\text{T}}} {\tilde{\mathbf{S}\Psi }}$ and ${\overline{\mathbf{F}}} = {{\varvec{\Psi}}}^{{\text{T}}} {\tilde{\mathbf{F}}}$.

3 Multiple Scales Method for Dynamic Analysis

In this section, the method of multiple scales [13] is applied to Eq. (12). Note that for the instability regions analysis, only the homogeneous form of Eq. (12) need to be used. Introducing two time scales T₀ = t and T₁ = εt, a perturbation solution is sought in the form

$$ {\mathbf{q}}\left( t \right) = {\mathbf{q}}_{0} \left( {T_{0} ,T_{1} } \right) + \varepsilon {\mathbf{q}}_{1} \left( {T_{0} ,T_{1} } \right) + \user2{\rm O}\left( {\varepsilon^{2} ,\;\varepsilon^{3} ,\; \cdots } \right) $$

(13)

Then

$$ {\dot{\mathbf{q}}} = D_{0} {\mathbf{q}} + \varepsilon D_{1} {\mathbf{q}},\;\;{{\ddot{\mathbf{q}}}} = D_{0}^{2} {\mathbf{q}} + 2\varepsilon D_{0} D_{1} {\mathbf{q}} + \user2{\rm O}\left( {\varepsilon^{2} ,\;\varepsilon^{3} ,\; \cdots } \right) $$

(14)

where D₀ = ∂/∂T₀ and D₁ = ∂/∂T₁. Note that the small dimensionless parameter ε is same with the dynamic load coefficient of periodic axial force P(t), which is for the purpose of balancing the influence of dynamic load coefficient ε, damping coefficient η, and resistance value R. Therefore, one can write

$$ \eta \to \varepsilon \eta ,\;\;R \to \varepsilon R $$

(15)

Then, ${\overline{\mathbf{D}}} = \varepsilon {\overline{\mathbf{D}}}$. In this case, Eq. (12) can be transformed into

$$ {\mathbf{I}}\ddot{\mathbf{q}} - {\text{j}}{\overline{\mathbf{G}}}\dot{\mathbf{q}} + {\overline{\mathbf{K}}}{\mathbf{q}} = \varepsilon \left[ { - {\overline{\mathbf{D}}\dot{\mathbf{q}}} + \left( {{\text{e}}^{{{\text{j}}\theta t}} + {\text{e}}^{{ - {\text{j}}\theta t}} } \right){\overline{\mathbf{S}}\mathbf{q}}} \right] $$

(16)

By substituting Eq. (13) and (14) into Eq. (16), replacing θt by θT₀ and equating coefficients of the same power of ε⁰ and ε¹, one obtains

$$ D_{0}^{2} {\mathbf{q}}_{0} - {\text{j}}{\overline{\mathbf{G}}}D_{0} {\mathbf{q}}_{0} + {\overline{\mathbf{K}}\mathbf{q}}_{0} = {\mathbf{0}} $$

(17)

and

$$ D_{0}^{2} {\mathbf{q}}_{1} - {\text{j}}{\overline{\mathbf{G}}}D_{0} {\mathbf{q}}_{1} + {\overline{\mathbf{K}}\mathbf{q}}_{1} = - 2D_{0} D_{1} {\mathbf{q}}_{0} + {\text{j}}{\overline{\mathbf{G}}}D_{1} {\mathbf{q}}_{0} - {\overline{\mathbf{D}}}D_{0} {\mathbf{q}}_{0} + \left( {{\text{e}}^{{{\text{j}}\theta t}} + {\text{e}}^{{ - {\text{j}}\theta t}} } \right){\overline{\mathbf{S}}\mathbf{q}}_{0} $$

(18)

Equation (17) defines a standard linear time-independent damped gyroscopic system that can be solved via the modal analysis. Its modal solution [10] is

$$ {\mathbf{q}}_{0} = \sum\limits_{i = 1}^{N} {A_{i} \left( {T_{1} } \right){\mathbf{r}}_{i} {\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }} } + \sum\limits_{k = 1}^{N} {B_{k} \left( {T_{1} } \right){\mathbf{s}}_{k} } {\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }} $$

(19)

where A_i(T₁) and B_k(T₁) represent a complex function with respect to T₁ to be determined later, ω_Fi > 0 and ω_Bk > 0 are the ith (i = 1, 2, …, N) forward whirl frequency and kth (k = 1, 2, …, N) backward whirl frequency with respect to the specific rotating speed Ω, which are solved respectively from

$$ \det \left( { - \omega_{F}^{2} {\mathbf{I}} + \omega_{F} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right) = 0 $$

(20a)

and

$$ \det \left( { - \omega_{B}^{2} {\mathbf{I}} - \omega_{B} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right) = 0 $$

(20b)

Actually Eq. (20a) or Eq. (20b) has 2N solutions which contain all of the synchronous whirl frequencies. Equation (20a) has N positive solutions which represent the synchronous forward whirl frequencies and N negative ones which represent the synchronous backward whirl frequencies; whereas Eq. (20b) is quite the opposite. Thus, in this paper, only the positive solutions of these two equations are considered to avoid confusion. Following this stipulation, the ith or kth mode r_i or s_k which is used in Eq. (19) can be solved respectively from

$$ \left( { - \omega_{Fi}^{2} {\mathbf{I}} + \omega_{Fi} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right){\mathbf{r}}_{i} = {\mathbf{0}} $$

(21a)

and

$$ \left( { - \omega_{Bk}^{2} {\mathbf{I}} - \omega_{Bk} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right){\mathbf{s}}_{k} = {\mathbf{0}} $$

(21b)

Substituting Eq. (19) into Eq. (18), which will lead to

$$ \begin{gathered} \;\;\;D_{0}^{2} {\mathbf{q}}_{1} - {\text{j}}{\overline{\mathbf{G}}}D_{0} {\mathbf{q}}_{1} + {\overline{\mathbf{K}}\mathbf{q}}_{1} \hfill \\ = \sum\limits_{i = 1}^{N} {\dot{A}_{i} \left( {T_{1} } \right)\left( { - 2{\text{j}}\omega_{Fi} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{r}}_{i} {\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }} } + \sum\limits_{k = 1}^{N} {\dot{B}_{k} \left( {T_{1} } \right)\left( {2{\text{j}}\omega_{Bk} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{s}}_{k} {\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }} } \hfill \\ \;\;\; -\, {\text{j}}\sum\limits_{i = 1}^{N} {\omega_{Fi} A_{i} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{r}}_{i} {\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }} } + {\text{j}}\sum\limits_{k = 1}^{N} {\omega_{Bk} B_{k} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{s}}_{k} {\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }} } \hfill \\ \;\;\; +\, {\overline{\mathbf{S}}}\left[ {\sum\limits_{i = 1}^{N} {A_{i} \left( {T_{1} } \right)\left( {{\text{e}}^{{{\text{j}}\left( {\theta + \omega_{Fi} } \right)T_{0} }} + {\text{e}}^{{{\text{j}}\left( { - \theta + \omega_{Fi} } \right)T_{0} }} } \right){\mathbf{r}}_{i} } + \sum\limits_{k = 1}^{N} {B_{k} \left( {T_{1} } \right)\left( {{\text{e}}^{{{\text{j}}\left( {\theta - \omega_{Bk} } \right)T_{0} }} + {\text{e}}^{{ - {\text{j}}\left( {\theta + \omega_{Bk} } \right)T_{0} }} } \right){\mathbf{s}}_{k} } } \right] \hfill \\ \end{gathered} $$

(22)

where the superscript dot denotes the derivative with respect to T₁ to indicate the fact that A_i or B_k is independent of T₀. In Eq. (22), one can find that the forced term ${\text{e}}^{{{\text{j}}\Omega T_{{0}} }}$ and the other terms ${\text{e}}^{{{\text{j}}\left( {\theta - \omega_{Bk} } \right)T_{0} }}$, ${\text{e}}^{{{\text{j}}\left( { - \theta + \omega_{Fi} } \right)T_{0} }}$ and so on can form the secular terms if and only if they satisfy that: Ω, θ + ω_Fi, –θ + ω_Fi, θ–ω_Bk and –θ–ω_Bk equal to ω_Fi or –ω_Bk. Thus, it is easy to find that only the shaft rotating speed Ω equals to ω_Fi or –ω_Bk and axial excitation frequency θ equals to ω_Fi + ω_Bk can produce the resonances. That is to say, only the combination instability regions may exist. This phenomenon is consistent with many references proposed, for example, Refs. [7, 11]. It is also can be concluded that the new combination instability regions will be formed in the closed-circuit case because the additional whirl frequencies are introduced by the shunt circuit. Section 4 will enhance the readers’ comprehension about this phenomenon.

Assume that there are resonances defined by

$$ \begin{gathered} \Omega = \omega_{Fi} + \varepsilon \sigma_{1} \hfill \\ \theta = \omega_{Fi} + \omega_{Bk} + \varepsilon \sigma_{0} \hfill \\ \end{gathered} $$

(23)

where σ₀ and σ₁ are the detuning parameters. Substituting Eq. (23) into Eq. (22) and rearranging the resulting terms on the right hand of Eq. (22) yield

$$ \begin{gathered} D_{0}^{2} {\mathbf{q}}_{1} - {\text{j}}{\overline{\mathbf{G}}}D_{0} {\mathbf{q}}_{1} + {\overline{\mathbf{K}}\mathbf{q}}_{1} \hfill \\ = \left[ {\dot{A}_{i} \left( {T_{1} } \right)\left( { - 2{\text{j}}\omega_{Fi} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{r}}_{i} - {\text{j}}\omega_{Fi} A_{i} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{r}}_{i} + B_{k} \left( {T_{1} } \right){\overline{\mathbf{S}}\mathbf{s}}_{k} {\text{e}}^{{{\text{j}}\sigma_{0} T_{1} }} } \right]{\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }} \hfill \\ \;\;\; +\, \left[ {\dot{B}_{k} \left( {T_{1} } \right)\left( {2{\text{j}}\omega_{Bk} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{s}}_{k} + {\text{j}}\omega_{Bk} B_{k} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{s}}_{k} + A_{i} \left( {T_{1} } \right){\overline{\mathbf{S}}\mathbf{r}}_{i} {\text{e}}^{{ - {\text{j}}\sigma_{0} T_{1} }} } \right]{\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }} + {\text{NST}} \hfill \\ \end{gathered} $$

(24)

where NST stands for non-secular generating terms. To derive the solvability conditions, assume that the solution of Eq. (24) takes the form

$$ {\mathbf{q}}_{1} \left( {T_{0} ,T_{1} } \right) = {\mathbf{P}}_{i} \left( {T_{1} } \right){\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }} + {\mathbf{Q}}_{k} \left( {T_{1} } \right){\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }} $$

(25)

where P_i and Q_k is the T₁-dependent vector to be determined. Substituting Eq. (25) into Eq. (24) and then equating each coefficient of ${\text{e}}^{{{\text{j}}\omega_{Fi} T_{0} }}$ and ${\text{e}}^{{ - {\text{j}}\omega_{Bk} T_{0} }}$ in the resulting equation, one can obtain

$$ \begin{gathered} \left( { - \omega_{Fi}^{2} {\mathbf{I}} + \omega_{Fi} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right){\mathbf{P}}_{i} = {\mathbf{R}}_{i}^{F} = \dot{A}_{i} \left( {T_{1} } \right)\left( { - 2{\text{j}}\omega_{Fi} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{r}}_{i} \hfill \\ -\, {\text{j}}\omega_{Fi} A_{i} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{r}}_{i} + B_{k} \left( {T_{1} } \right){\overline{\mathbf{S}}\mathbf{s}}_{k} {\text{e}}^{{{\text{j}}\sigma_{0} T_{1} }} \hfill \\ \end{gathered} $$

(26a)

and

$$ \begin{gathered} \left( { - \omega_{Bk}^{2} {\mathbf{I}} - \omega_{Bk} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right){\mathbf{Q}}_{k} = {\mathbf{R}}_{k}^{B} = \dot{B}_{k} \left( {T_{1} } \right)\left( {2{\text{j}}\omega_{Bk} {\mathbf{I}} + {\text{j}}{\overline{\mathbf{G}}}} \right){\mathbf{s}}_{k} \hfill \\ +\, {\text{j}}\omega_{Bk} B_{k} \left( {T_{1} } \right){\overline{\mathbf{D}}\mathbf{s}}_{k} + A_{i} \left( {T_{1} } \right){\overline{\mathbf{S}}\mathbf{r}}_{i} {\text{e}}^{{ - {\text{j}}\sigma_{0} T_{1} }} \hfill \\ \end{gathered} $$

(26b)

Equation (26a) or (26b) can be seen as a system of N linear equations in N unknowns P_i or Q_k. According to Eq. (20), its coefficient determinants vanishes. Hence, to ensure the existence of solutions P_i and Q_k, each matrix in which the residual vector ${\text{R}}_{\text{i}}^{\text{F}}$ or ${\text{R}}_{\text{k}}^{\text{B}}$ replaces column a or b (a, b = 1, 2, …, N) of $\left( { - \omega_{Fi}^{2} {\mathbf{I}} + \omega_{Fi} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}} \right)$ or $- \omega_{Bk}^{2} {\mathbf{I}} \,- \,\omega_{Bk} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}$ should be degenerated. If denoting such matrix as ${{\varvec{\Delta}}}_{ia}^{F}$ or ${{\varvec{\Delta}}}_{kb}^{B}$, the solvability conditions will be written as

$$ \det \left( {{{\varvec{\Delta}}}_{ia}^{F} } \right) = 0,\,\,\,\left( {a = 1,\;2,\; \cdots ,\;N} \right) $$

(27a)

and

$$ \det \left( {{{\varvec{\Delta}}}_{kb}^{B} } \right) = 0,\,\,\,\left( {b = 1,\;2,\; \cdots ,\;N} \right) $$

(27b)

It should be mentioned that Eq. (27a) or (27b) yields a solvability condition consists of N ordinary differential equations with the respect of A_i(T₁) and B_k(T₁). Therefore, there are totally a set of N ordinary differential equations derived from the solvability conditions for an N degree-of-freedom system.

Specifically, this paper only gives the detailed dynamic analysis for the closed-circuit case and the resonances near first whirl mode are considered. The other cases are similar. Then we have Ω = $\omega_{F1}^{cc} \, +$εσ1 and θ = $\omega_{F1}^{cc} \, + \,\omega_{B1}^{cc} \, +$εσ₀ (i = k = 1), where ‘cc’ represents the closed-circuit case. Ref. [14] has demonstrated that the solvability conditions are unchanged as one chooses the different columns of $- \left( {\omega_{F1}^{cc} } \right)^{2} {\mathbf{I}} + \omega_{F1}^{cc} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}$ or $- \left( {\omega_{B1}^{cc} } \right)^{2} {\mathbf{I}} - \omega_{B1}^{cc} {\overline{\mathbf{G}}} + {\overline{\mathbf{K}}}$ to form the matrix ${{\varvec{\Delta}}}_{1a}^{F}$ or ${{\varvec{\Delta}}}_{1b}^{B}$, and thus, this paper chooses the first column, i.e., a = b = 1. By following the solving process from Eq. (13) to Eq. (27), one can obtain the detailed expressions of the residual vectors ${\mathbf{R}}_{1}^{\text{F}}$ and ${\mathbf{R}}_{1}^{\text{B}}$

$$ {\mathbf{R}}_{1}^{F} = \left( {\begin{array}{*{20}c} {R_{11}^{F} } \\ {R_{21}^{F} } \\ {R_{31}^{F} } \\ {R_{41}^{F} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \begin{gathered} {\text{j}}\dot{A}_{1} \left( {\overline{g}_{11} + \overline{g}_{12} r_{21} + \overline{g}_{13} r_{31} + \overline{g}_{14} r_{41} - 2\left( {\omega_{F1}^{cc} } \right)^{2} } \right) \hfill \\ - \,{\text{j}}A_{1} \left( {\overline{d}_{11} + \overline{d}_{12} r_{21} + \overline{d}_{13} r_{31} + \overline{d}_{14} r_{41} } \right)\omega_{F1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{11} + \overline{s}_{12} s_{21} + \overline{s}_{13} s_{31} + \overline{s}_{14} s_{41} } \right)B_{1} {\text{e}}^{{\sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{A}_{1} \left( {\overline{g}_{21} + \overline{g}_{23} r_{31} + \overline{g}_{24} r_{41} + \overline{g}_{22} r_{21} - 2r_{21} \left( {\omega_{F1}^{cc} } \right)^{2} } \right) \hfill \\ - \,{\text{j}}A_{1} \left( {\overline{d}_{21} + \overline{d}_{22} r_{21} + \overline{d}_{23} r_{31} + \overline{d}_{23} r_{41} } \right)\omega_{F1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \,\left( {\overline{s}_{21} + \overline{s}_{22} s_{21} + \overline{s}_{23} s_{31} + \overline{s}_{24} s_{41} } \right)B_{1} {\text{e}}^{{\sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{A}_{1} \left( {\overline{g}_{31} + \overline{g}_{32} r_{21} + \overline{g}_{34} r_{41} + \overline{g}_{33} r_{31} - 2r_{31} \left( {\omega_{F1}^{cc} } \right)^{2} } \right) \hfill \\ -\, {\text{j}}A_{1} \left( {\overline{d}_{31} + \overline{d}_{32} r_{21} + \overline{d}_{33} r_{31} + \overline{d}_{34} r_{41} } \right)\omega_{F1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{31} + \overline{s}_{21} s_{32} + \overline{s}_{33} s_{31} + \overline{s}_{34} s_{41} } \right)B_{1} {\text{e}}^{{\sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{A}_{1} \left( {\overline{g}_{41} + \overline{g}_{42} r_{21} + \overline{g}_{43} r_{31} + \overline{g}_{44} r_{41} - 2r_{41} \left( {\omega_{F1}^{cc} } \right)^{2} } \right) \hfill \\ -\, {\text{j}}A_{1} \left( {\overline{d}_{41} + \overline{d}_{42} r_{21} + \overline{d}_{43} r_{31} + \overline{d}_{44} r_{41} } \right)\omega_{F1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{41} + \overline{s}_{42} s_{21} + \overline{s}_{43} s_{31} + \overline{s}_{44} s_{41} } \right)B_{1} {\text{e}}^{{\sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \end{array} } \right) $$

(28a)

and

$$ {\mathbf{R}}_{1}^{B} = \left( {\begin{array}{*{20}c} {R_{11}^{B} } \\ {R_{21}^{B} } \\ {R_{31}^{B} } \\ {R_{41}^{B} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \begin{gathered} {\text{j}}\dot{B}_{1} \left( {\overline{g}_{11} + \overline{g}_{12} s_{21} + \overline{g}_{13} s_{31} + \overline{g}_{14} s_{41} + 2\left( {\omega_{B1}^{cc} } \right)^{2} } \right) \hfill \\ { + }\,{\text{j}}B_{1} \left( {\overline{d}_{11} + \overline{d}_{12} s_{21} + \overline{d}_{13} s_{31} + \overline{d}_{14} s_{41} } \right)\omega_{B1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{11} + \overline{s}_{12} r_{21} + \overline{s}_{13} r_{31} + \overline{s}_{14} r_{41} } \right)A_{1} {\text{e}}^{{ - \sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{B}_{1} \left( {\overline{g}_{21} + \overline{g}_{23} s_{31} + \overline{g}_{24} s_{41} + \overline{g}_{22} s_{21} + 2s_{21} \left( {\omega_{B1}^{cc} } \right)^{2} } \right) \hfill \\ +\, {\text{j}}B_{1} \left( {\overline{d}_{21} + \overline{d}_{22} s_{21} + \overline{d}_{23} s_{31} + \overline{d}_{23} s_{41} } \right)\omega_{B1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{21} + \overline{s}_{22} r_{21} + \overline{s}_{23} r_{31} + \overline{s}_{24} r_{41} } \right)A_{1} {\text{e}}^{{ - \sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{B}_{1} \left( {\overline{g}_{31} + \overline{g}_{32} s_{21} + \overline{g}_{34} s_{41} + \overline{g}_{33} s_{31} + 2s_{31} \left( {\omega_{B1}^{cc} } \right)^{2} } \right) \hfill \\ + \,{\text{j}}B_{1} \left( {\overline{d}_{31} + \overline{d}_{32} s_{21} + \overline{d}_{33} s_{31} + \overline{d}_{34} s_{41} } \right)\omega_{B1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; +\, \left( {\overline{s}_{31} + \overline{s}_{21} r_{32} + \overline{s}_{33} r_{31} + \overline{s}_{34} r_{41} } \right)A_{1} {\text{e}}^{{ - \sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \begin{gathered} {\text{j}}\dot{B}_{1} \left( {\overline{g}_{41} + \overline{g}_{42} s_{21} + \overline{g}_{43} s_{31} + \overline{g}_{44} s_{41} + 2s_{41} \left( {\omega_{B1}^{cc} } \right)^{2} } \right) \hfill \\ +\, {\text{j}}B_{1} \left( {\overline{d}_{41} + \overline{d}_{42} s_{21} + \overline{d}_{43} s_{31} + \overline{d}_{44} s_{41} } \right)\omega_{B1}^{cc} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \left( {\overline{s}_{41} + \overline{s}_{42} r_{21} + \overline{s}_{43} r_{31} + \overline{s}_{44} r_{41} } \right)A_{1} {\text{e}}^{{ - \sigma_{0} T_{1} }} \hfill \\ \end{gathered} \\ \end{array} } \right) $$

(28b)

where r₁ = [r₁₁, r₂₁, r₃₁, r₄₁]^T and s₁ = [s₁₁, s₂₁, s₃₁, s₄₁]^T are the mode vectors which can be derived from Appendix B. The matrices ${\Delta }_{{{11}}}^{F}$ and ${\Delta }_{{{11}}}^{B}$ in solvability condition (27) are

$$ \Delta_{11}^{F} = \left( {\begin{array}{*{20}c} {R_{11}^{F} } & {\omega_{F1}^{cc} \overline{g}_{12} } & {\omega_{F1}^{cc} \overline{g}_{13} } & {\omega_{F1}^{cc} \overline{g}_{14} } \\ {R_{21}^{F} } & {\alpha_{2} + \omega_{F1}^{cc} \overline{g}_{22} - \left( {\omega_{F1}^{cc} } \right)^{2} } & {\omega_{F1}^{cc} \overline{g}_{23} } & {\omega_{F1}^{cc} \overline{g}_{24} } \\ {R_{31}^{F} } & {\omega_{F1}^{cc} \overline{g}_{32} } & {\alpha_{3} + \omega_{F1}^{cc} \overline{g}_{33} - \left( {\omega_{F1}^{cc} } \right)^{2} } & {\omega_{F1}^{cc} \overline{g}_{34} } \\ {R_{41}^{F} } & {\omega_{F1}^{cc} \overline{g}_{42} } & {\omega_{F1}^{cc} \overline{g}_{43} } & {\alpha_{4} + \omega_{F1}^{cc} \overline{g}_{44} - \left( {\omega_{F1}^{cc} } \right)^{2} } \\ \end{array} } \right) $$

(29a)

and

$$ \Delta_{11}^{B} = \left( {\begin{array}{*{20}c} {R_{11}^{B} } & { - \omega_{B1}^{cc} \overline{g}_{12} } & { - \omega_{B1}^{cc} \overline{g}_{13} } & { - \omega_{B1}^{cc} \overline{g}_{14} } \\ {R_{21}^{B} } & {\alpha_{2} - \omega_{B1}^{cc} \overline{g}_{22} - \left( {\omega_{B1}^{cc} } \right)^{2} } & { - \omega_{B1}^{cc} \overline{g}_{23} } & { - \omega_{B1}^{cc} \overline{g}_{24} } \\ {R_{31}^{B} } & { - \omega_{B1}^{cc} \overline{g}_{32} } & {\alpha_{3} - \omega_{B1}^{cc} \overline{g}_{33} - \left( {\omega_{B1}^{cc} } \right)^{2} } & { - \omega_{B1}^{cc} \overline{g}_{34} } \\ {R_{41}^{B} } & { - \omega_{B1}^{cc} \overline{g}_{42} } & { - \omega_{B1}^{cc} \overline{g}_{43} } & {\alpha_{4} - \omega_{B1}^{cc} \overline{g}_{44} - \left( {\omega_{B1}^{cc} } \right)^{2} } \\ \end{array} } \right) $$

(29b)

Substitution of Eq. (29) into Eq. (27) yields a set of 2 first order ordinary differential equations with respect to A₁(T₁) and B₁(T₁), which are written as

$$ \begin{gathered} \frac{{\partial A_{1} }}{{\partial T_{1} }} + \Theta_{1} A_{1} - \Gamma_{1} B_{1} {\text{e}}^{{{\text{j}}\sigma_{0} T_{1} }} = 0 \hfill \\ \frac{{\partial B_{1} }}{{\partial T_{1} }} + \Theta_{2} B_{1} - \Gamma_{2} A_{1} {\text{e}}^{{ - {\text{j}}\sigma_{0} T_{1} }} = 0 \hfill \\ \end{gathered} $$

(30)

Here, the detailed expressions of Θ₁, Θ₂, Γ₁ and Γ₂ are so complicated that this paper doesn’t show them. However, it can be sure that Θ₁ and Θ₂ are associated with the mechanical or electrical damping. If the system’s damping is eliminated, one have Θ₁ = Θ₂ = 0. The nontrivial solutions of Eq. (30) have the form

$$ A_{1} \left( {T_{1} } \right) = a_{1} {\text{e}}^{{\lambda_{a} T_{1} }} ,\;\;B_{1} \left( {T_{1} } \right) = b_{1} {\text{e}}^{{\left( {\lambda_{a} - {\text{j}}\sigma_{0} } \right)T_{1} }} $$

(31)

where a₁ and b₁ are the complex constants and λ_a are roots of the associated characteristic equation, which are

$$ \lambda_{a} = - \frac{{\text{j}}}{2}\sigma_{0} - \frac{1}{2}\left( {\Theta_{1} + \Theta_{2} } \right) \pm \frac{1}{2}\sqrt { - \sigma_{0}^{2} + \Lambda + \left( {\Theta_{1} - \Theta_{2} } \right)^{2} + 2{\text{j}}\sigma_{0} \left( {\Theta_{1} - \Theta_{2} } \right)} $$

(32)

with Λ = 4|Γ₁Γ₂|. For the undamped case, Eq. (32) can be reduced as

$$ \lambda_{a} = - \frac{{\text{j}}}{2}\sigma_{0} \pm \frac{1}{2}\sqrt { - \sigma_{0}^{2} + \Lambda } $$

(33)

From Eq. (33), it is easy to be concluded that A₁ and B₁ are bounded when $\sigma_{0}^{2} \ge \Lambda$ and unbounded when $\sigma_{0}^{2} \ge \Lambda$. Thus, the boundaries of the instability regions are

$$ \theta = \omega_{F1}^{cc} + \omega_{B1}^{cc} + \varepsilon \sqrt \Lambda $$

(34)

4 Numerical Simulation

In this subsection, by applying the DSTM method and above solving process, the unstable regions in the case of eliminating damping effect are respectively determined. Here, the conclusion that only the combination instability regions exist for such a rotating slender component subjected to periodic axial load is further confirmed. The model parameters which are used in the following analyses are provided in Table 1. Here, it should be mentioned that the fundamental static buckling load P_cr is the minimum axial static load which will lead to buckling for the non-rotating beam. In the instability regions analysis, the inductance value is set to 1.542H so that the resonance frequency of shunt circuit will approach to 700 rad/s. About why we use this specific frequency, the readers will understand this in the following analysis.

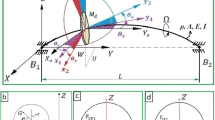
Before carrying out the instability regions analysis, it is necessary to determine the rotor’s whirl characteristics. The Campbell diagrams for the short-circuit case and closed-circuit case, which graphically show the relationship between rotating speed Ω and whirl frequencies ω, are respectively shown in Fig. 2a and Fig. 2b. Here, the sign ‘o’ represents the synchronous forward whirl frequencies and signs ‘ ×’ and ‘□’ respectively indicate the forward and backward whirl frequencies under specific rotating speed Ω. In this subsection, the rotating speed Ω is set to 359.3 rad/s. Because only the ‘ ×’ and ‘□’ whirl frequencies are used in the instability regions analysis, all of them have been collected in Table. 2 for simplicity. From Fig. 2, one can see that the whirl frequencies in the closed-circuit case are changed little by comparison with that in the short-circuit case. Thus, we can eliminate the superscript ‘sc’ and ‘cc’, which are used to distinguish the short-circuit or closed-circuit case. Moreover, due to the introduction of shunt circuit, the additional synchronous whirl modes, i.e., 2nd and 3rd synchronous whirl modes can be observed. These two whirl modes are so closed that we can merge them into one mode, which is denoted by r, and hence, all of the additional whirl frequencies can be denoted by ω_r. Actually these two modes are respectively derived from the left and right supporting structures. Then according to these whirl characteristics, the instability regions can be determined and plotted, as shown in Fig. 3 and Fig. 4. Figure 3 represents the short-circuit case and Fig. 4 represents the closed-circuit case. The blue shaded regions represent the instability regions which are numerically determined by using the discrete state transition matrix method (DSTM) [8]. The red solid lines represent the unstable boundaries which are analytically determined by using Eq. (34). It can be found from Fig. 3 and Fig. 4 that two new combination instability regions, i.e., region ‘A’ and ‘C’ in Fig. 4, are produced. Their starting points are formed by combining the new whirl frequencies ω_r with original whirl frequencies. That is namely the influence of circuit on the instability regions. Furthermore, this phenomenon also confirms that only the combination instability regions exist for the rotating slender component suffer from periodic axial load. Now, the readers may understand why the electrical resonance frequency is set to 700 rad/s, which distinguish from all of the rotor system’s whirling frequencies. This behavior is aimed at separating the new instability regions from the original regions more clearly.

Table 1. Model parameters used in the numerical simulation

Table 2. The whirling frequencies (rad/s) under Ω = 359.3 rad/s condition.

Fig. 2.

The Campbell diagrams for the (a) short-circuit case and (b) closed-circuit case

Fig. 3.

The instability regions for the short-circuit case

Fig. 4.

The instability regions for the closed-circuit case

5 Conclusion

In this paper, the dynamic behavior of a rotor-bearing system with electromechanically coupled boundary conditions under harmonic axial load is analyzed. Specifically, the influence of shunt circuit on the rotor system’s instability regions is analyzed. Both the analytical and simulated results show that only the combination instability regions exist when the rotor is rotating, which is consistent with the previous research activities. Furthermore, the instability regions analyses show that the rotation effect erases the primary instability region. As long as the shaft starts to rotate, only the combination instability region which is located by the combined whirling frequencies can be observed. The external shunt circuits introduce the additional synchronous whirl modes. These additional whirling frequencies ω_ej (j = 1, 2, …) are combined with the original frequencies ω_fi or ω_bi (i = 1, 2, …) to form the new combination instability regions. Their start points can be written as: ω_fi + ω_ej and ω_bi + ω_ej.

Appendices

Appendix A

The detailed expressions of ${\tilde{\mathbf{M}}}$, ${\tilde{\mathbf{G}}}$, ${\tilde{\mathbf{K}}}$, $\stackrel{\mathrm{\sim }}{\text{D}}$, $\stackrel{\mathrm{\sim }}{\text{S}}$, ${{\tilde{\mathbf{F}}}}_{\text{v}}$, ${{\tilde{\mathbf{F}}}}_{\text{w}}$ are given as follows:

where

$$ \begin{gathered} \tilde{m}_{ij} = \int_{0}^{L} {\rho A\;\phi_{i} \left( x \right)\phi_{j} \left( x \right){\text{d}}x} + \int_{0}^{L} {\rho I_{D} \phi^{\prime}_{i} \left( x \right)\phi^{\prime}_{j} \left( x \right){\text{d}}x} + M\phi_{i} \left( {x_{0} } \right)\phi_{j} \left( {x_{0} } \right) + J_{d} \phi^{\prime}_{i} \left( {x_{0} } \right)\phi^{\prime}_{j} \left( {x_{0} } \right) \hfill \\ \tilde{m}_{55} = \tilde{m}_{66} = 2\cot^{2} \beta \theta_{p}^{2} L \hfill \\ \tilde{g}_{ij} = \int_{0}^{L} {\rho \Omega I_{p} \phi^{\prime}_{i} \left( x \right)\phi^{\prime}_{j} \left( x \right){\text{d}}x} + J_{p} \Omega \phi^{\prime}_{i} \left( {x_{0} } \right)\phi^{\prime}_{j} \left( {x_{0} } \right)\;\;\left( {i,j = 1,\;2} \right) \hfill \\ \end{gathered} $$

where

$$ \begin{gathered} \tilde{k}_{ij} = \int_{0}^{L} {EI_{D} \phi^{\prime\prime}_{i} \left( x \right)\phi^{\prime\prime}_{j} \left( x \right){\text{d}}x} + k_{eq} \left[ {\phi_{i} \left( 0 \right)\phi_{j} \left( 0 \right) + \phi_{i} \left( L \right)\phi_{j} \left( L \right)} \right] - \chi P_{cr} \tilde{s}_{ij} \hfill \\ \tilde{k}_{55} = \tilde{k}_{66} = k_{eq2} + \frac{{2\cot^{2} \beta \theta_{p}^{2} }}{C},\;\;\tilde{k}_{13} = \tilde{k}_{31} = - k_{eq} \phi_{1} \left( 0 \right),\;\;\tilde{k}_{14} = \tilde{k}_{41} = - k_{eq} \phi_{1} \left( L \right),\;\; \hfill \\ \tilde{k}_{23} = \tilde{k}_{32} = - k_{eq} \phi_{2} \left( 0 \right),\;\;\tilde{k}_{24} = \tilde{k}_{42} = - k_{eq} \phi_{2} \left( L \right) \hfill \\ \tilde{d}_{ij} = \eta \left[ {\phi_{i} \left( 0 \right)\phi_{j} \left( 0 \right) + \phi_{i} \left( L \right)\phi_{j} \left( L \right)} \right] \hfill \\ \tilde{d}_{55} = \tilde{d}_{66} = 2\cot^{2} \beta \theta_{p}^{2} R,\;\;\tilde{d}_{13} = \tilde{d}_{31} = - \eta \phi_{1} \left( 0 \right),\;\;\tilde{d}_{14} = \tilde{d}_{41} = - \eta \phi_{1} \left( L \right),\;\; \hfill \\ \tilde{d}_{23} = \tilde{d}_{32} = - \eta \phi_{2} \left( 0 \right),\;\;\tilde{d}_{24} = \tilde{d}_{42} = - \eta \phi_{2} \left( L \right) \hfill \\ \end{gathered} $$

and

$$ \left\{ \begin{gathered} {\tilde{\mathbf{F}}}_{v} = M\Omega^{2} e\left[ {\phi_{1} \left( {x_{0} } \right)\cos \left( {\Omega t + \phi } \right),\;\phi_{2} \left( {x_{0} } \right)\cos \left( {\Omega t + \phi } \right),\;0,\;0,\;0,\;0} \right]^{{\text{T}}} \hfill \\ {\tilde{\mathbf{F}}}_{w} = M\Omega^{2} e\left[ {\phi_{1} \left( {x_{0} } \right)\sin \left( {\Omega t + \phi } \right),\;\phi_{2} \left( {x_{0} } \right)\sin \left( {\Omega t + \phi } \right),\;0,\;0,\;0,\;0} \right]^{{\text{T}}} \hfill \\ \end{gathered} \right. $$

Appendix B

For simplicity, only the mode vector r_i is derived here and the derivation process of s_k is similar. In Eq. (21a), the matrix equation can be detailedly expressed as

$$ \left( {\begin{array}{*{20}c} { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{11} + \alpha_{1} } & {\omega_{Fi} \overline{g}_{12} } & \cdots & {\omega_{Fi} \overline{g}_{1N} } \\ {\omega_{Fi} \overline{g}_{21} } & { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{11} + \alpha_{1} } & \cdots & {\omega_{Fi} \overline{g}_{2N} } \\ \vdots & \vdots & \ddots & \vdots \\ {\omega_{Fi} \overline{g}_{N1} } & {\omega_{Fi} \overline{g}_{N2} } & \cdots & { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{NN} + \alpha_{N} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {r_{1i} } \\ {r_{2i} } \\ \vdots \\ {r_{Ni} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right) $$

Assume r_1i = 1, then the other elements of r_i can be calculated by the following N − 1 linear algebraic equations

$$ \begin{gathered} \left( {\begin{array}{*{20}c} { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{22} + \alpha_{2} } & {\omega_{Fi} \overline{g}_{22} } & \cdots & {\omega_{Fi} \overline{g}_{2N} } \\ {\omega_{Fi} \overline{g}_{32} } & { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{33} + \alpha_{3} } & \cdots & {\omega_{Fi} \overline{g}_{3N} } \\ \vdots & \vdots & \ddots & \vdots \\ {\omega_{Fi} \overline{g}_{N2} } & {\omega_{Fi} \overline{g}_{N3} } & \cdots & { - \omega_{Fi}^{2} + \omega_{Fi} \overline{g}_{NN} + \alpha_{N} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {r_{2i} } \\ {r_{3i} } \\ \vdots \\ {r_{Ni} } \\ \end{array} } \right) \hfill \\ = \left( {\begin{array}{*{20}c} { - \omega_{Fi} \overline{g}_{21} } \\ { - \omega_{Fi} \overline{g}_{31} } \\ \vdots \\ { - \omega_{Fi} \overline{g}_{N1} } \\ \end{array} } \right) \hfill \\ \end{gathered} $$