Investigation of Resonance Frequency and Stability of Solutions in a Continuous Rotor System

Abstract

Purpose

The primary objective of this work is to analyze the effect of different system parameters on the resonance frequency of the linear rotor system. The effect of internal damping on the stability of the system is also investigated and a critical frequency ratio separating the stable and unstable regions is obtained.

Methods

A continuous rotor system is modeled by considering some critical factors, like the gyroscopic and rotary inertia effects of disc and shaft cross-sections, internal damping, large shaft deformation, and restriction to shaft axial motion at the bearings. The bearings are replaced by spring-dashpot systems along both horizontal and vertical directions. The governing partial differential equations (PDE’s) for the vibrations of the disc along the horizontal and vertical directions are derived by employing Hamilton's principle. The governing equations are then reduced to a set of ordinary differential equations (ODEs) using the method of modal projection. The large deformation, restriction to axial motion of the shaft, and the nonlinear stiffness of the end springs yield nonlinearities in the system governing equations. However, only the linear system is considered in this paper.

Results and Conclusion

The parameters in the dimensionless form of the governing equations are functions of some independent variables. These independent variables, on the other hand, are associated with the material and geometrical properties of the rotor system. The effect of the independent parameters on the system dynamics is analysed wherein the variation of the dependent parameters is also monitored. An appropriate design of a rotor system can be achieved through a methodical analysis, like the one this study addresses.

Introduction

Rotating machinery such as turbines, compressors, and pumps are extensively used in various sectors like energy generation, power transmission, etc. Unavoidable eccentricity between the center of mass of the disc away from the center of rotation causes unwanted vibrations in high-speed rotating systems, resulting in unsafe working conditions as well as the depreciation of expensive equipment and infrastructure. These vibrations in rotating machinery may also lead to catastrophic fatigue failure. Many researchers attempt to identify an approach that can effectively control vibrations in the rotor system to avoid unwanted failure and minimize the energy loss. This can somewhat be achieved at the preliminary stages of design of a rotating system. An extensive analysis is performed in this paper to understand the effect of different parameters on the system response. The parameters in the rotor system modelled in this paper are functions of geometrical and material properties. Hence, the system vibrations can be related to these geometrical and material properties which, on the other hand, will help to achieve an effective design to minimize the amplitude of vibrations of the rotating system.

The literature consists of preliminary investigations on both linear and nonlinear rotor dynamics [1,2,3,4,5]. Several models are available in the literature for analysis of rotor system vibrations. They can be categorized into: (i) continuous model [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28], and (ii) discrete or lumped parameter model [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. In the lumped parameter model, inertia of the shaft is neglected in comparison to the inertia of the disc. The restoring force of the shaft is considered either a linear [45] or a nonlinear function [6, 7, 32, 34, 43, 47] of displacement of the disc. The bearing clearance is also assumed to provide a restoring force [5, 31, 39, 43, 47, 48]. Different models for the gyroscopic effect [29,30,31,32, 34, 35, 38, 40, 43, 45], hydrodynamic forces in the journal bearings [32, 43], internal damping [32, 33, 35, 43,44,45,46,47,48], etc., are available in the literature which can be conveniently used for the analysis of a discrete rotor system.

There is a considerable number of literatures on the analysis of continuous rotor systems [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] wherein the inertia of the shaft is also considered along with the inertia of the disc. In the continuous model, the governing equations of the shaft-rotor system are first derived in the form of partial differential equations (PDE’s) either by using Lagrange’s principle [3, 9, 12, 23] or Hamilton’s principle [6, 11,12,13,14,15, 18, 21, 49,50,51]. Several important factors, like the large beam deflection [13,14,15], rotary inertia [11, 13, 14, 19, 22, 23], internal damping [6, 7, 23,24,25,26], etc., can be incorporated in the continuous system model. The transformation of the governing PDEs into a set of ODEs can be achieved by either Galerkin method [6, 18, 21], or Raleigh–Ritz method [3, 9, 11, 16, 23], or any other dimensionality reduction technique. In this paper, a continuous rotor system is modelled by considering the effect of rotary inertia and gyroscopic moment of the disc and shaft cross sections, internal damping, large beam deflection and constraints to shaft’s axial motion at bearings. The PDE’s governing the system vibrations are obtained using Hamilton’s principle for which the energy terms are derived by following the reference [3]. One of the novelties of this work is the reduction of PDEs to ODEs by Galerkin type method of modal projection using orthonormal mode shapes of a beam supported by Kelvin–Voigt model at both ends [22, 28].

The sources of nonlinearities in a rotor system model are: (i) the large deflection of the shaft [13,14,15], (ii) restriction to axial motion of the shaft at the bearings [3, 13,14,15], (iii) restoring force due to bearing clearance [5, 31, 32, 39, 43, 47], (iv) hydrodynamic forces in journal bearings [33, 44], etc. The effect of the geometric nonlinearities due to the large deflection of the shaft is negligible for small amplitude vibrations. In many practical cases, the effect of nonlinearities is negligibly small and the linear systems might provide reasonably accurate results. A lot of work on the analysis of linear systems are available in literatures [20, 22, 28, 45]. Analysis of the linear rotor system is essential to determine the effect of system parameters on the frequency response curves [22, 28], phase angle plot [22], critical speeds [20, 28, 45], forward and backward whirling motion [20, 28, 45], etc.

The geometric nonlinearities are triggered for large amplitude of oscillations in a rotor system. The analysis of a nonlinear rotor system may lead to some interesting results, such as fluttering [26], multivalued solutions [13,14,15, 25, 28, 37, 43, 47], subharmonic motion [30, 31, 35], quasiperiodic motion [16, 35], chaotic behaviour [16, 35], jump phenomena [13,14,15, 25, 28, 35, 43, 47], Hopf bifurcation [31, 43, 47], forward and backward whirling motion [18, 20, 28,29,30,31, 34, 38, 40, 41, 49,50,51], multiple loops [43, 47], Spring hardening [13,14,15, 28, 43, 48], etc. The study of linear and nonlinear rotor systems has distinct advantages, and both yields meaningful insights. Both analyses should be performed to have a better understanding of a rotor system. In this study, only the linear system is addressed, serving as a foundation for future analyses of the nonlinear system. The derivation of the continuous rotor system with the addition of various nonlinearities, as well as the effect of independent factors on the linear response, are discussed in this work.

The rest of the paper is organized as follows. In the section "Mathematical Modeling", the mathematical model of the rotor system is derived. The analytical method for obtaining the closed form solutions and the analysis of free vibration of the rotor system is covered in the section "Exact Analytical Solution and Analysis of Free Vibrations" followed by results and discussions in the section "Results and Discussion". At the end, some conclusions about this present work are drawn and scopes for future work are presented.

Mathematical Modeling

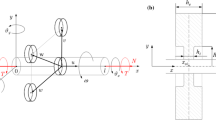
The modelling of the rotor system and the derivation of the governing equations of motion are discussed in this section. The physical system is shown in Fig. 1 wherein a rigid disc is mounted on a flexible shaft supported by two bearings ${B}_{1}$ and ${B}_{2}$. The flexibility of each of these two bearings is modelled by spring-dashpot systems along horizontal and vertical directions as shown in Fig. 1c and d. These springs at each bearing are assumed to be isotropic with cubic nonlinear stiffness. This cubic nonlinearity will result in the intended symmetric bending of the shaft in the $X-Y$ and $Z-Y$ planes [11]. The linear and nonlinear spring coefficients at bearing ${B}_{1}$ are ${K}_{11}$ and ${K}_{13}$, respectively, and at bearing ${B}_{2}$ are ${K}_{21}$ and ${K}_{23}$, respectively. Accordingly, the spring forces at bearings ${B}_{1}$ and ${B}_{2}$ along horizontal ($X-$) direction are ${F}_{sX1}={K}_{11}U\left(0,t\right)+{K}_{13}{U}^{3}\left(0,t\right)$, and ${F}_{sX2}={K}_{21}U\left(L,t\right)+{K}_{23}{U}^{3}\left(L,t\right)$, respectively, where $U\left(Y,t\right)$ is the displacement of the shaft along $X-$ direction. The centrifugal force due to the eccentricity ($e$) of the center of mass (G) away from the geometric center (S) induces vibrations in the rotor system. The rotor system is modelled as a continuous system with the inclusion of several factors like (i) tilting motion of disc and shaft, (ii) gyroscopic effect of disc and shaft, (iii) internal damping, (iv) large deformation of shaft, and (v) restriction of shaft axial motion at the bearings. The partial differential equations governing the vibrations of the rotor system are derived by using the extended Hamilton’s principle. The energy terms needed in the extended Hamilton’s principle are obtained from [13,14,15]. The governing partial differential equations are reduced to a set of ordinary differential equations by the method of modal projection. In what follows, each of these steps are discussed in separate sections (“Derivation of Governing Equations Using Hamilton’s Principle” and “Derivation of the Governing Ordinary Differential Equations by the Method of Modal Projection”) for proper understanding of the development of the mathematical model.

Fig. 1

Schematic representation of a disk rotating on a flexible shaft, b rotor eccentricity, c bearing ${B}_{1}$ (Left), and d bearing ${B}_{2}$ (Right)

Derivation of Governing Equations Using Hamilton’s Principle

According to the Extended Hamilton’s principle,

$${\int }_{{t}_{1}}^{{t}_{2}}\left(\delta T-\delta V+\delta {\overline{W} }_{nc}\right){\text{dt}}=0,$$

(1)

where $T$ and $V$ are the total kinetic and potential energy of the rotor system, respectively, ${\overline{W} }_{nc}$ is the work done by the nonconservative forces and $\delta$ represents the variation. The kinetic energy of the disc and the shaft are given by [13,14,15].

$$ \begin{aligned} {\text{T}}_{{\text{d}}} = & {\text{T}}_{{{\text{d1}}}} + {\text{T}}_{{{\text{d}}2}} + {\text{T}}_{{{\text{d}}3}} + {\text{T}}_{{{\text{d}}4}} \\ = & \left[ {\frac{{M_{d} }}{2}\left( {\dot{U}^{2} + \dot{W}^{2} } \right) + \frac{{I_{dx} }}{2}\left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{z}^{2} } \right) + I_{dy} \Omega \dot{\theta }_{z} \theta_{x} + M_{d} \Omega e\left( {\dot{U}\cos \Omega t - \dot{W}\sin \Omega t} \right)} \right]_{{L_{1} }} , \\ \end{aligned} $$

(2a)

$$ \begin{aligned} T_{s} = & T_{{s1}} + T_{{s2}} + T_{{s3}} \\ = & \mathop \smallint \limits_{0}^{L} \frac{{\rho I}}{2}\left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{z}^{2} } \right)dY + \mathop \smallint \limits_{0}^{L} \frac{{\rho A}}{2}\left( {\dot{U}^{2} + \dot{W}^{2} } \right)dY + \mathop \smallint \limits_{0}^{L} 2\rho I\Omega \dot{\theta }_{z} \theta _{x} dY, \\ \end{aligned} $$

(2b)

respectively, where $\dot{U}=\frac{\partial U}{\partial t}$, $\dot{W}=\frac{\partial W}{\partial t}$, ${\theta }_{x}=\frac{\partial W}{\partial Y}$, ${\theta }_{z}=-\frac{\partial U}{\partial Y}$, ${\dot{\theta }}_{x}=\frac{\partial {\theta }_{x}}{\partial t}=\frac{{\partial }^{2}W}{\partial t\partial Y}$, and ${\dot{\theta }}_{z}=\frac{\partial {\theta }_{z}}{\partial t}=-\frac{{\partial }^{2}U}{\partial t\partial Y}$. The subscript ${L}_{1}$ in Eq. (2a) indicates that the quantities $\dot{U}$, $\dot{W}$, ${\theta }_{x}$, ${\theta }_{z}$, ${\dot{\theta }}_{x}$, and ${\dot{\theta }}_{z}$ are evaluated at $Y={L}_{1}$, which is the location of the disk on the shaft. The total kinetic energy of the rotor system is $T={T}_{d}+{T}_{s}$. ${T}_{d1}$ refers to kinetic energy due to the translational motion of the disk, ${T}_{d2}$ refers to kinetic energy due to the rotational motion of the disk, ${T}_{d3}$ refers to the gyroscopic effect of the disk, ${T}_{d4}$ refers to the centrifugal force acting on the disk, ${T}_{s1}$ refers to kinetic energy of the shaft in bending, ${T}_{s2}$ refers to the rotary inertia of the shaft, and ${T}_{s3}$ refers to the gyroscopic effect of the shaft.

The strain energy of the shaft $({V}_{sh})$ and spring $({V}_{sp})$ are given by [13,14,15]

$${V}_{sh}={\int }_{0}^{L} \frac{EI}{2}\left\{{\left(\frac{\partial {\theta }_{x}}{\partial {\text{Y}}}\right)}^{2}+{\left(\frac{\partial {\theta }_{z}}{\partial Y}\right)}^{2}\right\}{\text{dY}}+{\int }_{0}^{L} \frac{EA}{2}\left(\frac{1}{4}{\theta }_{x}^{4}+\frac{1}{4}{\theta }_{z}^{4}+\frac{1}{2}{\theta }_{x}^{2}{\theta }_{z}^{2}\right){\text{dY}}+{\int }_{0}^{L} \frac{EA}{4{\text{L}}}\left({\int }_{0}^{L}\left({\theta }_{x}^{2}+{\theta }_{z}^{2}\right)dY\right)\left({\theta }_{x}^{2}+{\theta }_{z}^{2}\right){\text{dY}},$$

(3a)

$${V}_{sp}={\int }_{0}^{L}\left\{\frac{1}{2}{K}_{11}\left({U}^{2}+{{\text{W}}}^{2}\right)+\frac{1}{4}{K}_{13}\left({U}^{4}+{{\text{W}}}^{4}\right)\right\}{\varvec{\updelta}}\left(Y\right){\text{dY}} +{\int }_{0}^{L} \left\{\frac{1}{2}{K}_{21}\left({U}^{2}+{{\text{W}}}^{2}\right)+\frac{1}{4}{K}_{23}\left({U}^{4}+{{\text{W}}}^{4}\right)\right\}{\varvec{\updelta}}\left(Y-L\right){\text{dY}} ,$$

(3b)

respectively, where ${\varvec{\updelta}}$ is the Dirac delta function. The first and second integrals in Eq. (3a) are the strain energy of the shaft with the second integral being associated with the higher order deformation of the shaft. The third integral is the strain energy due to the constraint to axial motion of the shaft at the bearings. As mentioned earlier, both the bearings at $Y=0$ and $Y=L$ are considered to be flexible and are replaced by springs with nonlinear stiffness. Moreover, the stiffness of the two bearings are assumed to be different. The potential energy due to the deformation of the springs at the supports are given by Eq. (3b).

The variation in work done by the nonconservative forces are given by [16, 21, 27, 28]

$$\delta {\overline{W} }_{nc}={\int }_{0}^{L}\left({C}_{ex}\frac{\partial U}{\partial t}\delta U+{C}_{ez}\frac{\partial W}{\partial t}\delta W\right){\text{dY}} +{\int }_{0}^{L}{C}_{1}\left(\frac{\partial U}{\partial t}\delta U+\frac{\partial W}{\partial t}\delta W\right){\varvec{\updelta}}\left(Y\right){\text{dY}} +{\int }_{0}^{L}{C}_{2}\left(\frac{\partial U}{\partial t}\delta U+\frac{\partial W}{\partial t}\delta W\right){\varvec{\updelta}}\left(Y-L\right){\text{dY}} ,$$

(4)

where ${C}_{ex}$ and ${C}_{ez}$ are the external damping coefficients along horizontal and vertical directions, respectively. These external damping are caused by the resistance of the surrounding fluid (air or steam) on the rotor system. They are assumed to be viscous in nature for the simplicity of analysis. The bearings are considered to be isotropic with damping coefficients ${C}_{1}$ and ${C}_{2}$ for the left (at $Y=0$) and right (at $Y=L$) bearings, respectively.

Substitution of Eqs. (2)–(4) into Eq. (1) leads to the partial differential equations governing the vibrations of the rotor system along horizontal and vertical directions as

$$ \begin{gathered} \rho A\frac{{\partial^{2} U}}{{\partial t^{2} }} + EI\frac{{\partial^{4} U}}{{\partial Y^{4} }} + M_{d} \frac{{\partial^{2} U}}{{\partial t^{2} }}{{\varvec{\updelta}}}_{{L_{1} }} - I_{dx} \frac{\partial }{\partial Y}\left( {\frac{{\partial^{3} U}}{{\partial t^{2} \partial Y}}{{\varvec{\updelta}}}_{{L_{1} }} } \right) + I_{dy} \Omega \frac{\partial }{\partial Y}\left( {\frac{{\partial^{2} W}}{\partial t\partial Y}{{\varvec{\updelta}}}_{{L_{1} }} } \right) \hfill \\ -\rho I\frac{{\partial }^{4}U}{\partial {t}^{2}\partial {Y}^{2}}+2\rho I\Omega \frac{{\partial }^{3}W}{\partial t\partial {Y}^{2}}-\frac{EA}{2}\frac{\partial }{\partial {\text{Y}}}\left\{\frac{\partial {\text{U}}}{\partial {\text{Y}}}\left({\left(\frac{\partial {\text{U}}}{\partial {\text{Y}}}\right)}^{2}+{\left(\frac{\partial {\text{W}}}{\partial {\text{Y}}}\right)}^{2}\right)\right\} \hfill \\ - \frac{EA}{{\text{L}}}\frac{{\partial^{2} U}}{{\partial {\text{Y}}^{2} }}\mathop \smallint \limits_{0}^{L} \left( {\left( {\frac{{\partial {\text{U}}}}{{\partial {\text{Y}}}}} \right)^{2} + \left( {\frac{{\partial {\text{W}}}}{{\partial {\text{Y}}}}} \right)^{2} } \right)dY + \left( {K_{11} U + K_{13} U^{3} } \right){{\varvec{\updelta}}}\left( Y \right) + \left( {K_{21} U + K_{23} U^{3} } \right){{\varvec{\updelta}}}_{L} \hfill \\ +{C}_{ex}\frac{\partial U}{\partial t}+{C}_{1}\frac{\partial U}{\partial t}{\varvec{\updelta}}\left(Y\right)+{C}_{2}\frac{\partial U}{\partial t}{{\varvec{\updelta}}}_{L}+{C}_{i}I\frac{{\partial }^{5}U}{\partial {Y}^{4}\partial t}+\Omega {C}_{i}I\frac{{\partial }^{4}W}{\partial {Y}^{4}}={M}_{d}{\Omega }^{2}e{\text{sin}}\Omega t{{\varvec{\updelta}}}_{{L}_{1}}, {\text{and}} \hfill \\ \end{gathered} $$

(5a)

$$\begin{gathered}{\rho A\frac{{\partial }^{2}W}{\partial {t}^{2}}+EI\frac{{\partial }^{4}W}{\partial {Y}^{4}}+M}_{d}\frac{{\partial }^{2}W}{\partial {t}^{2}}{{\varvec{\updelta}}}_{{L}_{1}}-{I}_{dx}\frac{\partial }{\partial Y}\left(\frac{{\partial }^{3}W}{\partial Y\partial {t}^{2}}{{\varvec{\updelta}}}_{{L}_{1}}\right)-{I}_{dy}\Omega \frac{\partial }{\partial Y}\left(\frac{{\partial }^{2}U}{\partial t\partial Y}{{\varvec{\updelta}}}_{{L}_{1}}\right) \hfill \\ -\rho I\frac{{\partial }^{4}W}{\partial {t}^{2}\partial {Y}^{2}}-2\rho I\Omega \frac{{\partial }^{3}U}{\partial t\partial {Y}^{2}}-\frac{EA}{2}\frac{\partial }{\partial Y}\left\{\frac{\partial W}{\partial Y}\left\{{\left(\frac{\partial U}{\partial Y}\right)}^{2}+{\left(\frac{\partial W}{\partial Y}\right)}^{2}\right\}\right\} \hfill \\ -\frac{EA}{L}\frac{{\partial }^{2}W}{{\partial Y}^{2}}{\int }_{0}^{L}\left({\left(\frac{\partial U}{\partial Y}\right)}^{2}+{\left(\frac{\partial W}{\partial Y}\right)}^{2}\right)dY+\left({K}_{11}W+{K}_{13}{W}^{3}\right){\varvec{\updelta}}\left(Y\right)+\left({K}_{21}W+{K}_{23}{W}^{3}\right){{\varvec{\updelta}}}_{L} \hfill \\ +{C}_{ez}\frac{\partial W}{\partial t}+{C}_{1}\frac{\partial W}{\partial t}{\varvec{\updelta}}\left(Y\right)+{C}_{2}\frac{\partial W}{\partial t}{{\varvec{\updelta}}}_{L}+{C}_{i}I\frac{{\partial }^{5}W}{\partial {Y}^{4}\partial t}-\Omega {C}_{i}I\frac{{\partial }^{4}U}{\partial {Y}^{4}}={M}_{d}{\Omega }^{2}e{\text{cos}}\Omega t{{\varvec{\updelta}}}_{{L}_{1}}, \hfill \\ \end{gathered}$$

(5b)

respectively, where ${{\varvec{\updelta}}}_{{L}_{1}}={\varvec{\updelta}}\left(Y-{L}_{1}\right)$, and ${{\varvec{\updelta}}}_{L}={\varvec{\updelta}}\left(Y-L\right)$. Note the difference between the symbols $\delta$ (in Eq. (1)) and ${\varvec{\updelta}}$; the first one is used to represent the variation and the second one for the Dirac delta function. Also note that the last two terms associated with ${C}_{i}$ in Eqs. (5a) and (5b) are the bending moments due to the strain rate dependent internal damping along $X$ and $Z$ axes, respectively [23,24,25,26]. Introducing the dimensionless parameters.

$u=\frac{U}{L}$, $y=\frac{Y}{L}$, $w=\frac{W}{L}$, $\tau = \Upsilon t$, $\Upsilon=\sqrt{\frac{EI}{\rho A{L}^{4}}}$, ${l}_{1}=\frac{{L}_{1}}{L}$,${r}_{m}=\frac{\rho AL}{{M}_{d}}$, ${r}_{dx}=\frac{{I}_{dx}}{{\rho AL}^{3}}$, ${r}_{dy}=\frac{{I}_{dy}}{{\rho AL}^{3}}$, ${r}_{e}=\frac{e}{L}$, ${r}_{f}=\frac{\Omega }{\Upsilon}$, ${r}_{g}=\frac{I}{{\text{A}}{L}^{2}}=\frac{{\text{A}}{R}_{s}^{2}}{A{L}^{2}}={{\text{r}}}^{2}$,${k}_{11}=\frac{{K}_{11}{L}^{3}}{EI}$, ${k}_{21}=\frac{{K}_{21}{L}^{3}}{EI}$, ${k}_{13}=\frac{{K}_{13}{L}^{2}}{{M}_{d}{\Upsilon}^{2}}$, ${k}_{23}=\frac{{K}_{23}{L}^{2}}{{M}_{d}{\Upsilon}^{2}}$, ${c}_{ex}=\frac{{C}_{eX}L}{{M}_{d}\Upsilon}$, ${c}_{ez}=\frac{{C}_{eZ}L}{{M}_{d}\Upsilon}$, ${c}_{1}=\frac{{C}_{1}}{{M}_{d}\Upsilon}$, ${c}_{2}=\frac{{C}_{2}}{{M}_{d}\Upsilon}$, ${c}_{i}=\frac{{C}_{i}I}{{M}_{d}\Upsilon{L}^{3}}$,

the governing Eq. (5) are reduced to the dimensionless forms as

$$\begin{gathered} \left({r}_{m}+{{\varvec{\updelta}}}_{{l}_{1}}\right)\frac{{\partial }^{2}u}{\partial {\tau }^{2}}+{r}_{m}\frac{{\partial }^{4}u}{{\partial y}^{4}}-{ r}_{m}{r}_{dx}\frac{\partial }{\partial y}\left(\frac{{\partial }^{3}u}{\partial {\tau }^{2}\partial y}{{\varvec{\updelta}}}_{{l}_{1}}\right)+{ r}_{m}{r}_{dy}{r}_{f}\frac{\partial }{\partial y}\left(\frac{{\partial }^{2}w}{\partial \tau \partial y}{{\varvec{\updelta}}}_{{l}_{1}}\right) -{r}_{g}{r}_{m}\frac{{\partial }^{4}u}{\partial {\tau }^{2}\partial {y}^{2}}\hfill \\+2{ r}_{m}{r}_{g}{ r}_{f}\frac{{\partial }^{3}w}{\partial \tau \partial {y}^{2}} -\frac{{ r}_{m}}{2{r}_{g}}\frac{\partial }{\partial y}\left(\frac{\partial u}{\partial y}\left({\left(\frac{\partial u}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial y}\right)}^{2}\right)\right)-\frac{{ r}_{m}}{{r}_{g}}\frac{{\partial }^{2}u}{{\partial y}^{2}}{\int }_{0}^{L}\left({\left(\frac{\partial u}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial y}\right)}^{2}\right)dy+\hfill \\ \left({k}_{11}{r}_{m}u+{k}_{13}{u}^{3}\right){\varvec{\updelta}}\left(y\right)+\left({k}_{21}{r}_{m}u+{k}_{23}{u}^{3}\right){{\varvec{\updelta}}}_{{\varvec{l}}}+{c}_{ex}\frac{\partial u}{\partial \tau }+{c}_{1}\frac{\partial u}{\partial \tau }{\varvec{\updelta}}\left(y\right)+{c}_{2}\frac{\partial u}{\partial \tau }{{\varvec{\updelta}}}_{l}\hfill \\+{c}_{i}\frac{{\partial }^{5}u}{\partial y\partial \tau }+{r}_{f}{c}_{i}\frac{{\partial }^{4}w}{\partial {y}^{4}}={r}_{e}{{r}_{f}}^{2}{\text{sin}}\left({r}_{f}\tau \right){{\varvec{\updelta}}}_{{l}_{1}}, {\text{and}} \hfill \\ \end{gathered}$$

(6a)

$$\begin{gathered} \left({r}_{m}+{{\varvec{\updelta}}}_{{l}_{1}}\right)\frac{{\partial }^{2}w}{\partial {\tau }^{2}}+{ r}_{m}\frac{{\partial }^{4}w}{{\partial y}^{4}}-{ r}_{m}{r}_{dx}\frac{\partial }{\partial y}\left(\frac{{\partial }^{3}w}{\partial {\tau }^{2}\partial y}{{\varvec{\updelta}}}_{{l}_{1}}\right)-{ r}_{m}{r}_{dy}{r}_{f}\frac{\partial }{\partial y}\left(\frac{{\partial }^{2}u}{\partial \tau \partial y}{{\varvec{\updelta}}}_{{l}_{1}}\right) -{r}_{m}{r}_{g}\frac{{\partial }^{4}w}{\partial {\tau }^{2}\partial {y}^{2}} \hfill \\-2{ r}_{m}{r}_{g}{ r}_{f}\frac{{\partial }^{3}u}{\partial \tau \partial {y}^{2}}-\frac{{ r}_{m}}{2{r}_{g}}\frac{\partial }{\partial y}\left(\frac{\partial w}{\partial y}\left({\left(\frac{\partial u}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial y}\right)}^{2}\right)\right)-\frac{{ r}_{m}}{{r}_{g}}\frac{{\partial }^{2}w}{{\partial y}^{2}}{\int }_{0}^{L}\left({\left(\frac{\partial u}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial y}\right)}^{2}\right)dy \hfill \\+\left({k}_{11}{r}_{m}w+{k}_{13}{w}^{3}\right){\varvec{\updelta}}\left(y\right)+\left({k}_{21}{r}_{m}w+{k}_{23}{w}^{3}\right){{\varvec{\updelta}}}_{{\varvec{l}}}+{c}_{ez}\frac{\partial w}{\partial \tau }+{c}_{1}\frac{\partial w}{\partial \tau }{\varvec{\updelta}}\left(y\right)+{c}_{2}\frac{\partial w}{\partial \tau }{{\varvec{\updelta}}}_{l}\hfill \\+{c}_{i}\frac{{\partial }^{5}w}{\partial y\partial \tau }-{r}_{f}{c}_{i}\frac{{\partial }^{4}u}{\partial {y}^{4}}={r}_{e}{{r}_{f}}^{2}{\text{cos}}\left({r}_{f}\tau \right){{\varvec{\updelta}}}_{{l}_{1}}, \hfill \\ \end{gathered}$$

(6b)

where the following scaling property of the Dirac delta function is used: ${\varvec{\updelta}}\left(y\right)=L{\varvec{\updelta}}\left(Y\right).$ These dimensionless equations are reduced to a set of ordinary differential equations by applying the method of modal projection in the section "Derivation of the Governing Ordinary Differential Equations by the Method of Modal Projection".

Derivation of the Governing Ordinary Differential Equations by the Method of Modal Projection

In this section, the partial differential Eq. (6) governing the vibrations of the rotor system are reduced to a set of ordinary differential equations (ODEs) by the method of modal projection. Following the Galerkin type method of modal projection, the solution of the partial differential Eq. (6) is assumed in the variable separation form as

$$u\left(y,\tau \right)=\sum_{i=1}^{n}{\Psi }_{i}\left(y\right){u}_{i}\left(\tau \right), {\text{and}} w\left(y,\tau \right)=\sum_{i=1}^{n}{\Psi }_{i}\left(y\right){w}_{i}\left(\tau \right),$$

(7)

where ${\Psi }_{i}\left(y\right)$ is the ith orthonormal mode shape of a reduced system consisting of a beam supported by springs at the ends. For motion along $x$-direction, the beam is subjected to the boundary conditions: ${\left.\frac{{\partial }^{2}u}{\partial {y}^{2}}\right|}_{y=0}=0$, ${\left.\frac{{\partial }^{3}u}{\partial {y}^{3}}\right|}_{y=0}=-{k}_{11}u$, ${\left.\frac{{\partial }^{2}u}{\partial {y}^{2}}\right|}_{y=1}=0$, and ${\left.\frac{{\partial }^{3}u}{\partial {y}^{3}}\right|}_{y=1}={k}_{21}u$. The boundary conditions for motion along $z$-direction is obtained by replacing $u$ by $w$ in these expressions. The ith orthonormal mode shape ${\Psi }_{i}\left(y\right)$ is obtained as [22]

$${\Psi }_{i}\left(y\right)={C}_{1}\left[\left({\text{sin}}{p}_{i}y+{\text{sinh}}{p}_{i}y\right)+{C}_{2}\left({\text{cos}}{p}_{i}y+{\text{cosh}}{p}_{i}y-\frac{2{k}_{11}}{{p}_{i}^{3}}{\text{sinh}}{p}_{i}y\right)\right].$$

(8)

where ${C}_{2}={p}_{i}^{3}\left({\text{sinh}}{p}_{i}-{\text{sin}}{p}_{i}\right)/\left(2{k}_{11}{\text{sinh}}{p}_{i}+{p}_{i}^{3}\left({\text{cos}}{p}_{i}-{\text{cosh}}{p}_{i}\right)\right)$. The eigenvalue ${p}_{i}$ can be determined from the following characteristic equation

$${p}_{i}^{6}\left(1-{\text{cos}}{p}_{i}{\text{cosh}}{p}_{i}\right)+{p}_{i}^{3}\left({k}_{11}+{k}_{21}\right)\left({\text{cos}}{p}_{i}{\text{sinh}}{p}_{i}-{\text{sin}}{p}_{i}{\text{cosh}}{p}_{i}\right)+2{k}_{11}{k}_{21}{\text{sin}}{p}_{i}{\text{sinh}}{p}_{i}=0.$$

(9)

Imposing the conditions ${k}_{11}\to \infty$, and ${k}_{21}\to \infty$ for hard bearings in Eq. (9) leads to

$${\text{sin}}{p}_{i}=0.$$

(10)

This is the characteristic equation for a simply supported beam (SSB). The ith eigenvalue obtained from Eq. (10) is ${p}_{i}=i\pi$. The mode shape ${\Psi }_{i}\left(y\right)$ satisfy the following orthonormality conditions

$${\int }_{0}^{1}{\Psi }_{i}\left(y\right){\Psi }_{j}\left(y\right){\text{d}}y={\delta }_{ij}, \mathrm{and }{\int }_{0}^{1}{\Psi }_{i}\frac{{d}^{4}{\Psi }_{j}}{d{y}^{4}}dy={\int }_{0}^{1}{\Psi }_{j}\frac{{d}^{4}{\Psi }_{i}}{d{y}^{4}}dy={p}_{i}^{4}{\delta }_{ij}.$$

(11)

The arbitrary constant ${C}_{1}$ in Eq. (8) is rendered unique through the normalization scheme ${\int }_{0}^{1}{\Psi }_{i}^{2}\left(y\right){\text{d}}y=1$. The expression for this constant ${C}_{1}$ obtained using the software package “MAPLE” is long and not shown in this paper.

The orthonormal mode shape for the first mode (${\Psi }_{1}\left(y\right)$) is plotted in Fig. 2 for different values of spring constants and compared with that for a simply supported beam (SSB). The bearings are assumed to be identical (${k}_{11}={k}_{21}$) in Fig. 2a. As a result, the mode shape is symmetric about $y=0.5$. In Fig. 2b, the stiffness of the bearings differs causing the symmetry of the mode shape about $y=0.5$ to break down. As shown in Fig. 2, the curve for ${\Psi }_{1}\left(y\right)$ for the beam with springs at both ends gradually approaches the mode shape curve for the simply supported beam and the difference is hardly noticeable for ${k}_{11}={k}_{21}=6000$. It is to be noted that the natural frequency for the first mode of vibrations for a SSB obtained from Eq. (10) is ${p}_{1}=\pi$. Also, the orthonormal mode shapes for a SSB can be obtained as ${\Psi }_{i}\left(y\right)=\sqrt{2}{\text{sin}}{p}_{i}y.$

Fig. 2

Comparison of mode shapes of a beam with springs attached at both ends with that for a simply supported beam (SSB)

To derive the governing ODEs, solutions (7) are first substituted into Eq. (6). The resulting equations are multiplied by the jth mode shape ${\Psi }_{j}\left(y\right)$ and integrated over the domain [0, 1]. The governing ODEs are then obtained by applying the orthonormality conditions (11). For the first mode of analysis ($i=j=1$), the ODEs are obtained as

$${u}_{1}^{\prime\prime}+{\mu }_{x}{u}_{1}^{\mathrm{^{\prime}}}+G{r}_{f}{w}_{1}^{\mathrm{^{\prime}}}+{\omega }_{n}^{2}{u}_{1}+{\mu }_{i}{r}_{f}{w}_{1}+\left(\left(\lambda +\nu \right){u}_{1}^{3}+\lambda {u}_{1}{w}_{1}^{2}\right)={q}_{0}{\text{sin}}\left({r}_{f}\tau \right),$$

(12a)

$${w}_{1}^{{\prime\prime}}+{\mu }_{z}{w}_{1}^{\mathrm{^{\prime}}}-G{r}_{f}{u}_{1}^{\mathrm{^{\prime}}}+{\omega }_{n}^{2}{w}_{1}-{\mu }_{i}{r}_{f}{u}_{1}+\left(\lambda {w}_{1}{u}_{1}^{2}+\left(\lambda +\nu \right){w}_{1}^{3}\right)={q}_{0}{\text{cos}}\left({r}_{f}\tau \right),$$

(12b)

where the primes ($\mathrm{^{\prime}}$) denote derivative with respect to the dimensionless time $\tau$ and

$${\mu }_{x,z}={\left({c}_{eq}\right)}_{x,z}/{m}_{e}, {\left({c}_{eq}\right)}_{x,z}={c}_{ex,ez}+{c}_{i}{p}_{1}^{4}+{c}_{1}{\left({\Psi }_{1}\left(0\right)\right)}^{2}+{c}_{2}{\left({\Psi }_{1}\left(1\right)\right)}^{2},$$

(13a)

$${\mu }_{i}={c}_{i}{p}_{1}^{4}/{m}_{e},{\omega }_{n}^{2}=\frac{{r}_{m}}{{m}_{e}}\left({p}_{1}^{4}+{k}_{11}{\left({\Psi }_{1}\left(0\right)\right)}^{2}+{k}_{21}{\left({\Psi }_{1}\left(1\right)\right)}^{2}\right),{q}_{0}=\frac{{\Psi }_{1}({l}_{1})}{{m}_{e}}{r}_{e}{r}_{f}^{2},$$

(13b)

$${m}_{e}=\left({r}_{m} + {t}_{4}-{D}_{r}{r}_{dx}{r}_{m} \left({t}_{5}- {t}_{6}\right)-{S}_{r}{r}_{g}{r}_{m}{t}_{1}\right), \lambda =-\frac{{ r}_{m}}{{m}_{e}{ r}_{g}}\left(\frac{3}{2}{t}_{3}{ L}_{b}+{S}_{ra}{t}_{1}{t}_{2}\right),$$

(13c)

$$G=\frac{{r}_{m}}{{m}_{e}}\left({D}_{g}{r}_{dy} ({t}_{5}- {t}_{6})+2{S}_{g}{r}_{g}{t}_{1}\right), \nu ={k}_{13}{\left({\Psi }_{1}\left(0\right)\right)}^{4}+{k}_{23}{\left({\Psi }_{1}\left(1\right)\right)}^{4},$$

(13d)

$${t}_{1}={\int }_{0}^{1}{\psi }_{1}\frac{{d}^{2}{\Psi }_{1}}{d{y}^{2}}dy, {t}_{2}={\int }_{0}^{1}{\left(\frac{d{\Psi }_{1}}{dy}\right)}^{2}dy, {t}_{3}={\int }_{0}^{1}{{\Psi }_{1}\left(\frac{d{\Psi }_{1}}{dy}\right)}^{2}\left(\frac{{d}^{2}{\Psi }_{1}}{d{y}^{2}}\right)dy, {t}_{4}={\Psi }_{1}^{2}\left({l}_{1}\right), {t}_{5}={\Psi }_{1}\left({l}_{1}\right){\left.\frac{{d}^{2}{\Psi }_{1}}{d{y}^{2}}\right|}_{y={l}_{1}}, {t}_{6}={\left.\frac{d}{dy}\left({\Psi }_{1}\frac{d{\Psi }_{1}}{dy}\right)\right|}_{y={l}_{1}}.$$

(13e)

In Eq. (13c), the terms ${D}_{r}$ and ${S}_{r}$ are associated with the rotary inertia of the disc and shaft, respectively. Similarly, the terms ${D}_{g}$ and ${S}_{g}$ in Eq. (13d) are associated with the gyroscopic effects of the disc and shaft cross-sections, respectively. Moreover ${L}_{b}$ is associated with the large beam deflection criterion, and ${S}_{ra}$ is associated with the effect of restricting the shaft axial motion at the bearings. These terms may take a value of either 1 or 0 depending on whether the related effect is considered in the analysis or not, e.g., ${D}_{r}=1$ if the disc rotary is considered in the analysis, and ${L}_{b}=0$ if the large beam defection criterion is not considered in the analysis. The expressions for ${t}_{1}$ to ${t}_{6}$ in Eq. (13e) are obtained using the software package “MAPLE”. They are long and are not presented in this paper.

The nonlinearities in the rotor system governed by Eq. (12) are associated with the parameters $\lambda$ and$\nu$. The large beam deflection and the shaft's confinement to axial motion are two elements that contribute to the nonlinearities related to$\lambda$. The parameter $\nu$ is a function of the cubic stiffness of the bearings (${k}_{13}$ and${k}_{23}$). A rotor system associated with such nonlinear terms show some interesting results, like multiple solutions, jump phenomena, multiple loops, etc. [11, 13,14,15, 28, 43, 47]. The system parameters like$\lambda$,$\nu$,$G$, etc., are treated as independent in many literatures [31, 38]. However, it is clear from Eqs. (12) and (13) that these parameters depend on the material and geometric properties of the rotor system. Arbitrarily choosing these parameters ($\lambda$,$\nu$,$G$, etc.) may yield some undesired system dynamics.

In many practical applications, the deflection of the shaft may not be large enough and the shaft may move freely inside the bearings along axial direction. On top of that, if hard bearings are used, the nonlinearities may not be triggered. The system dynamics can then be predicted from the analysis of the linear system only (considering $\lambda =0$ and $\nu =0$). The analysis of the linear system is much easier compared to that for the nonlinear system as an exact analytical solution can easily be obtained. Moreover, the primary resonance condition of a linear system can easily be predicted. Considering all these important factors, a separate study is conducted in this paper on the analysis of a linear system for the continuous rotor model developed in this section. We primarily focus on the influence of different system parameters on the natural frequency of the continuous rotor system. The stability of the rotor system is additionally discussed in relation to the impact of internal damping. The exact analytical solution of the linear system is derived in the next section.

Exact Analytical Solution and Analysis of Free Vibrations

The exact closed form solutions of the linear system are first obtained in this section. The governing equations of the linear system obtained by substituting $\lambda =0$ and $\nu =0$ in Eq. (12) is written in the matrix form as

$$\mathbf{I}{\widetilde{\mathbf{x}}}^{{\prime}{\prime}}+\mathbf{D}{\widetilde{\mathbf{x}}}{\prime}+\mathbf{F}\widetilde{\mathbf{x}}={\tilde{\mathbf{Q}}}_{1}{\text{Im}}\left({e}^{i{ r}_{f }\tau }\right)+{\tilde{\mathbf{Q}}}_{2}{\text{Re}}\left({e}^{i{ r}_{f }\tau }\right),$$

(14)

where $\mathbf{I}$ is a $2\times 2$ identity matrix and

$$\widetilde{\mathbf{x}}=\left\{\begin{array}{c}{u}_{1}\\ {w}_{1}\end{array}\right\}, \mathbf{D}=\left[\begin{array}{cc}{\mu }_{x}& G{r}_{f}\\ -G{r}_{f}& {\mu }_{z}\end{array}\right], \mathbf{F}=\left[\begin{array}{cc}{\omega }_{n}^{2}& {\mu }_{i}{r}_{f}\\ -{\mu }_{i}{r}_{f}& {\omega }_{n}^{2}\end{array}\right], {\tilde{\mathbf{Q}}}_{1}=\left\{\begin{array}{c}{q}_{0}\\ 0\end{array}\right\}, {\tilde{\mathbf{Q}}}_{2}=\left\{\begin{array}{c}0\\ {q}_{0}\end{array}\right\},$$

(15)

where ${q}_{0}= \gamma {r}_{e}{r}_{f}^{2}$, and ${\text{Im}}\left({e}^{{\text{i}}{ r}_{f }\tau }\right)$ $\left(={\text{sin}}\left({r}_{f}\tau \right)\right)$ and ${\text{Re}}\left({e}^{{\text{i}}{ r}_{f }\tau }\right)$ $\left(={\text{cos}}\left({r}_{f}\tau \right)\right)$ are the imaginary and real parts of ${e}^{{\text{i}}{ r}_{f }\tau }$, respectively. The solution of the linear system is first obtained for the excitations ${\tilde{\mathbf{Q}}}_{1}{\text{Im}}\left({e}^{{\text{i}}{ r}_{f }\tau }\right)$ and ${\tilde{\mathbf{Q}}}_{2}{\text{Re}}\left({e}^{{\text{i}}{ r}_{f }\tau }\right)$. Applying the principle of superposition, the solutions of Eq. (14) are finally obtained as [2]

$${u}_{1}\left(\tau \right)={u}_{11}\left(\tau \right)+{u}_{12}\left(\tau \right)={U}_{1}{\text{sin}}\left({r}_{f}\tau -{\phi }_{{\text{x}}}\right),$$

(16a)

$${w}_{1}\left(\tau \right)={w}_{11}\left(\tau \right)+{w}_{12}\left(\tau \right)={{\text{W}}}_{1}{\text{cos}}\left({r}_{f}\tau -{\phi }_{{\text{z}}}\right),$$

(16b)

where

$${U}_{1}{\text{sin}}{\phi }_{{\text{x}}}=\frac{{q}_{0}}{\Delta }\left[{\Delta }_{r}\left({{\left({z}_{12}\right)}_{r}-\left({z}_{22}\right)}_{i}\right)+{\Delta }_{i}\left({{\left({z}_{22}\right)}_{r}+\left({z}_{12}\right)}_{i}\right)\right],$$

(17a)

$${U}_{1}{\text{cos}}{\phi }_{{\text{x}}}=\frac{{q}_{0}}{\Delta }\left[{\Delta }_{r}\left({{\left({z}_{22}\right)}_{r}+\left({z}_{12}\right)}_{i}\right)+{\Delta }_{i}\left({{\left({z}_{22}\right)}_{i}-\left({z}_{12}\right)}_{r}\right)\right],$$

(17b)

$${W}_{1}{\text{sin}}{\phi }_{z}=\frac{{q}_{0}}{\Delta }\left[{\Delta }_{r}\left({{\left({z}_{12}\right)}_{r}-\left({z}_{11}\right)}_{i}\right)+{\Delta }_{i}\left({{\left({z}_{11}\right)}_{r}+\left({z}_{12}\right)}_{i}\right)\right],$$

(17c)

$${W}_{1}{\text{cos}}{\phi }_{z}=\frac{{q}_{0}}{\Delta }\left[{\Delta }_{r}\left({{\left({z}_{11}\right)}_{r}+\left({z}_{12}\right)}_{i}\right)+{\Delta }_{i}\left({{\left({z}_{11}\right)}_{i}-\left({z}_{12}\right)}_{r}\right)\right],\Delta ={\Delta }_{r}^{2}+{\Delta }_{i}^{2},$$

(17d)

$$ \begin{aligned} \Delta _{r} = & \left( {z_{{11}} } \right)_{r} \left( {z_{{22}} } \right)_{r} - \left( {z_{{11}} } \right)_{i} \left( {z_{{22}} } \right)_{i} + \left( {z_{{12}} } \right)_{r}^{2} - \left( {z_{{12}} } \right)_{i}^{2} , \\ \Delta _{i} = & \left( {z_{{11}} } \right)_{r} \left( {z_{{22}} } \right)_{i} + \left( {z_{{11}} } \right)_{i} \left( {z_{{22}} } \right)_{r} + 2\left( {z_{{12}} } \right)_{r} \left( {z_{{12}} } \right)_{i} , \\ \end{aligned} $$

(17e)

$${\left({z}_{11}\right)}_{r}={\left({z}_{22}\right)}_{r}={\omega }_{n}^{2}-{r}_{f}^{2},{\left({z}_{11}\right)}_{i}={r}_{f}{\mu }_{x},{\left({z}_{22}\right)}_{i}={r}_{f}{\mu }_{z},{\left({z}_{12}\right)}_{r}={\mu }_{i}{r}_{f}, {\left({z}_{12}\right)}_{i}={r}_{f}^{2}G,$$

(17f)

$${U}_{1}=\sqrt{{{\left({U}_{1}{\text{sin}}{\phi }_{{\text{x}}}\right)}^{2}+\left({U}_{1}{\text{cos}}{\phi }_{{\text{x}}}\right)}^{2}},{\phi }_{{\text{x}}}={{\text{tan}}}^{-1}\left(\frac{{U}_{1}{\text{sin}}{\phi }_{{\text{x}}}}{{U}_{1}{\text{cos}}{\phi }_{{\text{x}}}}\right),$$

(17g)

$${W}_{1}=\sqrt{{\left({W}_{1}{\text{sin}}{\phi }_{{\text{z}}}\right)}^{2}+{\left({W}_{1}{\text{cos}}{\phi }_{{\text{z}}}\right)}^{2}},{\phi }_{{\text{z}}}={{\text{tan}}}^{-1}\left(\frac{{W}_{1}{\text{sin}}{\phi }_{{\text{z}}}}{{W}_{1}{\text{cos}}{\phi }_{{\text{z}}}}\right).$$

(17h)

To plot the Campbell diagram, it is necessary to first derive the expression for the damped natural frequency. Equations governing the free vibrations are obtained in matrix form from Eq. (14) as

$$\mathbf{I}{\widetilde{\mathbf{x}}}^{{\prime}{\prime}}+\mathbf{D}{\widetilde{\mathbf{x}}}{\prime}+\mathbf{F}\widetilde{\mathbf{x}}=0.$$

(18)

The solution of Eq. (18) can be assumed in the form as $\widetilde{\mathbf{x}}={\left(\begin{array}{cc}{u}_{1}& {w}_{1}\end{array}\right)}^{T}={\left(\begin{array}{cc}{u}_{10}& {w}_{10}\end{array}\right)}^{T}{e}^{\beta \tau }={\widetilde{\mathbf{x}}}_{0}{e}^{\beta \tau }$. Substitution of this assumed solution in Eq. (18) leads to

$$\mathbf{B}{\widetilde{\mathbf{x}}}_{0}=0,$$

(19)

where $\mathbf{B}=\left[\begin{array}{cc}{\beta }^{2}+{\mu }_{x}\beta +{\omega }_{n}^{2}& G{r}_{f}\beta +{\mu }_{i}{r}_{f}\\ -G{r}_{f}\beta -{\mu }_{i}{r}_{f}& {\beta }^{2}+{\mu }_{z}\beta +{\omega }_{n}^{2}\end{array}\right]$. For nontrivial solutions of ${\widetilde{\mathbf{x}}}_{0}$ (${u}_{10}$, and ${w}_{10}$), the determinant of matrix $\mathbf{B}$ should be zero ($\left|\mathbf{B}\right|=0$). This leads to a quartic equation of $\beta$ as

$${\beta }^{4}+\left({\mu }_{x}+{\mu }_{z}\right){\beta }^{3}+\left({\mu }_{x}{\mu }_{z}+2{\omega }_{n}^{2}+{G}^{2}{r}_{f}^{2}\right){\beta }^{2}+\left(\left({\mu }_{x}+{\mu }_{z}\right){\omega }_{n}^{2}+2G{r}_{f}^{2}{\mu }_{i}\right)\beta +{\omega }_{n}^{4}+{\mu }_{i}^{2}{r}_{f}^{2}=0.$$

(20)

The roots of Eq. (20) are obtained numerically. Two sets of complex conjugate roots are obtained for the set of parameters chosen for the analysis. The imaginary parts of the roots correspond to the damped natural frequency. These are used to plot the Campbell diagrams to be discussed in the next section.

A closed form solution for the damped natural frequency can be determined for a special case of equal damping along horizontal and vertical directions (${\mu }_{x}={\mu }_{z}= \mu$). For ${\mu }_{x}={\mu }_{z}= \mu$, Eq. (18) can be represented in terms of a complex variable $\eta \left(\tau \right)={w}_{1}\left(\tau \right)+i{u}_{1}\left(\tau \right)$ as

$${\eta }^{{\prime\prime}}+\mu {\eta }^{\mathrm{^{\prime}}}+{\omega }_{n}^{2}\eta +iG{r}_{f}{\eta }^{\mathrm{^{\prime}}}+i{\mu }_{i}=0.$$

(21)

Substituting the solution of the form of $\eta ={\eta }_{0}{e}^{\beta \tau }$ in Eq. (21) yields

$${\beta }^{2}+\left(\mu +iG{r}_{f}\right)\beta +{\omega }_{n}^{2}+i{\mu }_{i}=0.$$

(22)

To separate the real and imaginary parts, $\beta$ is written in terms of complex number form as

$$\beta ={\beta }_{r}+i{\beta }_{i}.$$

(23)

Substituting Eq. (23) into Eq. (21) and separating the real and imaginary parts leads to two equations which are solved to get

$${\beta }_{r}=-\frac{\mu }{2}\pm \frac{\sqrt{\left({\mu }^{2}-4{\omega }_{n}^{2}-{G}^{2}{r}_{f}^{2}\right)+\sqrt{{\left({\mu }^{2}-4{\omega }_{n}^{2}-{G}^{2}{r}_{f}^{2}\right)}^{2}+4{r}_{f}^{2}{\left(\mu G-2{\mu }_{i}\right)}^{2}}}}{2\sqrt{2}},$$

(24a)

$${\beta }_{i}=-\frac{G{r}_{f}}{2}\mp \frac{\sqrt{-\left({\mu }^{2}-4{\omega }_{n}^{2}-{G}^{2}{r}_{f}^{2}\right)+\sqrt{{\left({\mu }^{2}-4{\omega }_{n}^{2}-{G}^{2}{r}_{f}^{2}\right)}^{2}+4{{r}_{f}^{2}\left(\mu G-2{\mu }_{i}\right)}^{2}}}}{2\sqrt{2}} .$$

(24b)

These expressions are obtained by imposing the condition that ${\beta }_{r}$ and ${\beta }_{i}$ are real numbers. It is to be noted that ${\beta }_{i}$ is the damped natural frequency of the linear system (18). Moreover, the solution of (18) is stable for a negative value of ${\beta }_{r}$. Positive value of ${\beta }_{r}$ will lead to an exponentially growing solution. Imposing the condition for stable solution (${\beta }_{r}\le 0$) leads to

$${r}_{f}\le {\left({r}_{f}\right)}_{c}, {\left({r}_{f}\right)}_{c}=\frac{\left(\frac{{\mu }_{i}+{\mu }_{o}}{{\mu }_{i}}\right){\omega }_{n}}{\sqrt{1-\left(\frac{{\mu }_{i}+{\mu }_{o}}{{\mu }_{i}}\right)G}} ,$$

(25)

where ${\mu }_{o}=\left({c}_{e}+{c}_{1}{\left({\Psi }_{1}\left(0\right)\right)}^{2}+{c}_{2}{\left({\Psi }_{1}\left(1\right)\right)}^{2}\right)/{m}_{e}$, ${c}_{e}={c}_{ex}={c}_{ez}$. Hence, the solution of Eq. (19) is unstable (exponentially growing) for frequency ratios above the critical value ${\left({r}_{f}\right)}_{c}$. Solution of Eq. (21) is the homogeneous solution of Eq. (14) for ${\mu }_{x}={\mu }_{z}= \mu$. As a consequence, the response of the rotor system governed by Eq. (14) (for ${\mu }_{x}={\mu }_{z}= \mu$) will be unstable for ${r}_{f}>{\left({r}_{f}\right)}_{c}$. Since ${\left({r}_{f}\right)}_{c}=\infty$ for ${\mu }_{i}=0$, the rotor system will always be stable in the absence of internal damping.

If the gyroscopic effect is neglected ($G=0$), the critical frequency ratio is reduced to

$${\left({r}_{f}\right)}_{c}=\left(\frac{{\mu }_{i}+{\mu }_{o}}{{\mu }_{i}}\right){\omega }_{n}.$$

(26)

Further, if all the external damping effects are neglected (${\mu }_{o}=0$),

$${\left({r}_{f}\right)}_{c}={\omega }_{n}.$$

(27)

All the relevant and important results are discussed in the next section. In most of the cases, the rotor system dynamics are analyzed through the frequency response and phase angle plots.

Results and Discussion

In this section, the effects of different system parameters on the vibration characteristics of the rotor system are analyzed. The critical parameters in the equations governing the vibrations of the linear system (Eq. (12) with $\uplambda =0$, $\nu =0$) are: internal damping factor (${\mu }_{i}$), damping factors (${\upmu }_{x}$, ${\upmu }_{z}$), undamped natural frequencies (${\omega }_{x}$, ${\omega }_{z}$), gyroscopic coefficient ($G$), the amplitude of excitation (${q}_{0}=\gamma {r}_{e}{r}_{f}^{2}$), and the effective mass (${m}_{e}$). Damping factors (${\upmu }_{x}$, ${\upmu }_{z}$) are functions of the external damping coefficients (${{\text{c}}}_{ex}$, ${c}_{ez}$), internal damping coefficient (${\mu }_{i}$), and the damping coefficients of the bearings (${{\text{c}}}_{1}$, ${c}_{2}$). These parameters depend on other system parameters, like the eccentricity ratio (${r}_{e}$), mass ratio (${r}_{m}$), mass moment of inertia of the disc about $x$-axis (${r}_{dx}$), polar moment of the disc about $y$-axis (${r}_{dy}$), radius of gyration ($r$), end spring stiffness (${k}_{11}$, ${k}_{21}$), etc. Henceforth, for convenience, the first set of parameters (${\omega }_{x}$, ${\omega }_{z}$, $G$, ${q}_{0}$, ${m}_{e}$, ${\upmu }_{x}$, ${\upmu }_{z}$, ${\mu }_{i}$) will be called as the dependent parameters and the second set of parameters (${c}_{1}$, ${c}_{2}$, ${c}_{ex}$, ${c}_{ez}$, ${c}_{i}$, ${r}_{e}$, ${r}_{m}$, ${r}_{dx}$, ${r}_{dy}$, $r$, ${k}_{11}$, ${k}_{21}$) as the independent parameters. Moreover, the system dynamics are also affected by the gyroscopic effects of the disc and shaft associated with the terms ${{\text{D}}}_{g}$ and ${{\text{S}}}_{g}$, respectively, and the rotary inertia of the disc and shaft associated with the terms ${{\text{D}}}_{r}$ and ${{\text{S}}}_{r}$, respectively.

A set of independent parameters listed in Table 1 are used in the forthcoming analysis. Most of these parameters are taken from the references [13,14,15, 23,24,25,26, 39, 43]. Independent parameters different from these values are specified at the caption of each figure. In most of the cases, the system dynamics are analyzed from the frequency response diagrams and phase angle plots. In frequency response diagrams, the amplitude of oscillation at the middle of the shaft (${U}_{m}={\Psi }_{1}\left(0.5\right){U}_{1}, {W}_{m}={\Psi }_{1}(0.5){W}_{1}$) is plotted with respect to the dimensionless frequency (${r}_{f}$). For the set of parameter values chosen for this work, the maximum deflection at the middle of the shaft is restricted below 0.1 times the length of the shaft. This is considered as the small deflection criterion for the present study. The maximum deflection can further be reduced by selecting the eccentricity ratio (${r}_{f}$) appropriately without compromising the qualitative results of the rotor system. Based on the small deflection criterion, the nonlinearities in the rotor system can be neglected.

Table 1 Independent parameters and its values

The analytical expressions derived for the horizontal and vertical displacements (Eqs. (16)) are verified by comparing the time-displacement and phase-plane plots obtained from Eqs. (16) with those obtained from the numerical simulation of the governing Eqs. (14). For both the horizontal and vertical oscillations, the analytical results match exactly with the numerical results. The horizontal direction results are presented shown in Fig. 3.

Fig. 3

Time response and phase plane plots in horizontal direction. Parameters: Table 1, ${c}_{i}=0.0000085$,and ${l}_{1}=0.2$

In most of the literatures on rotor dynamics, the damping along horizontal and vertical directions (${\mu }_{x}={\mu }_{z}= \mu$) are considered to be the same [22, 23, 28, 43]. Some researchers, though, analyzed the effect of different amount of damping (${\mu }_{x}\ne {\mu }_{z}$) on the vibrations of rotor system [39]. As the bearings are considered to be isotropic in this study, the only source of difference in damping is to consider two different values for external damping coefficients (${c}_{ex}\ne {c}_{ez}$). It is explained in the section "Exact Analytical Solution and Analysis of Free Vibrations" how in the special case of equal damping (${\mu }_{x}={\mu }_{z}= \mu$), the two equations along the horizontal and vertical directions (Eq. (12) with $\lambda =0$, $\nu =0$) are written as a single equation (Eq. (21)) in terms of a complex variable. This shows that the system responses along horizontal and vertical directions will differ only in case of different amount of damping (${\mu }_{x}\ne {\mu }_{z}$) along these two directions. For the choice of equal amount of damping (${\mu }_{x}={\mu }_{z}= \mu$), the system becomes isotropic and the system dynamics along these two directions become identical. This is verified from the frequency response diagrams and phase angle plots in Figs. 4.

Fig. 4

Frequency response and phase angle plots in horizontal and vertical direction. Parameters: a, b Table 1 and ${l}_{1}=0.3$, ${c}_{ez}=0.085$, ${{\text{c}}}_{2}=0.02$, c, d Table 1, ${c}_{ex}={c}_{ez}=0.0085$ and ${l}_{1}=0.3$

The two peaks in the frequency response diagram for different amount of damping along the horizontal and vertical directions (${\upmu }_{x}=0.00106$, ${\upmu }_{z}=0.0594$) are marked in Fig. 4a. These resonance frequencies are further verified from the Campbell diagram plotted in Fig. 5a. To plot this Campbell diagram, Eq. (20) is first solved for $\beta$ for different values of excitation frequency ${r}_{f}$. The imaginary part of $\beta$ is the damped natural frequency ${f}_{r}$, which is plotted in Fig. 5a with respect to ${r}_{f}$. The higher damping along vertical direction causes a noticeable reduction in peak amplitude of oscillations at second resonance frequency ${r}_{f}={\left({r}_{f}\right)}_{r2}=2.665$.

Fig. 5

Campbell diagrams a corresponding to the plots in Fig. 4a and b, b corresponding to the plots in Fig. 4c, d

The phase angle ${\phi }_{z}$ for horizontal oscillations changes suddenly from positive to negative near the first resonance frequency ${\left({r}_{f}\right)}_{r1}$ as shown in Fig. 4b. Contrary to that, the sudden change in phase angle ${\phi }_{x}$ for vertical oscillations is from negative to positive near ${\left({r}_{f}\right)}_{r1}$. The amplitude of oscillations and phase angles along horizontal and vertical directions become indistinguishable for same amount of damping (${\upmu }_{x}={\upmu }_{z}=0.0066$) as shown in Fig. 4c and d. Moreover, only one resonance peak is observed from the frequency response diagram. The presence of single resonance frequency is further verified from the Campbell diagram shown in Fig. 5b.

Equal amount of damping (${c}_{ex}={c}_{ez}$, ${c}_{1}={c}_{2}$) is considered for the forthcoming analysis wherein the effect of other system parameters on the dynamics of the rotor system is studied through frequency response and phase angle plots. As the vibration characteristics along horizontal and vertical directions become identical for equal amount of damping, only one set of results are plotted.

The values of the dependent parameters (${\omega }_{x}$, ${\omega }_{z}$, $G$, ${q}_{0}$, ${m}_{e}$, ${\upmu }_{x}$, ${\upmu }_{z}$, ${\mu }_{i}$) as well as the damped natural frequency (resonance frequency ${\left({r}_{f}\right)}_{r}$) associated with rest of the figures are listed in Table 2 for effective analysis of the results.

Table 2 Values of dependent parameters for different values of independent parameters

The amplitude-frequency and phase angle plots for different values of mass ratio ${r}_{m}$ (= $\rho AL/{M}_{d}$) are shown in Fig. 6. It is observed from Fig. 6 that the system resonant frequency increases with the increase of ${r}_{m}$. Also, the peak amplitude at resonance increases with the increase of ${r}_{m}$. It is noticed from the values of different parameters listed in Table 2 that the effective mass ${m}_{e}$ of the system is larger for higher values of ${r}_{m}.$ However, the magnitude of the gyroscopic coefficient $G$, the undamped natural frequency $\omega$ and amplitude of excitation ${q}_{0}$ increases with the increase of ${r}_{m}$, even though ${m}_{e}$ appears in the denominator of the expressions of $G$, $\omega$ and ${q}_{0}$ (Eqs. (13c) and (13d)). This results in higher values of the damped natural frequency ${\left({r}_{f}\right)}_{r}$ of the system as the value of ${r}_{m}$ is increased. The expression for $\upmu$ ($={\upmu }_{x}={\upmu }_{z}$) are inversely proportional to ${m}_{e}$ (Eqs. (13a) and (13b)) and consequently, their values decrease with the increase of ${r}_{m}$. This results in higher values of peak amplitude at resonance at higher values of ${r}_{m}$ and ${q}_{0}$ is increases with the increase of ${r}_{m}$. Physically, the higher values of ${r}_{m}$ causes the system stiffness to increase causing the damped natural frequency to increase and the peak amplitude at resonance increases due to reduction in damping factor $\upmu$. The asymptotic values of the phase angle ($\phi$) are ${0}^{^\circ }$ and ${180}^{^\circ }$ as ${r}_{f}\to 0$ and ${r}_{f}\to \infty$, respectively, with the sharp change in $\phi$ happening near the resonance frequency as shown in Fig. 6b. In all the forthcoming analysis, the nature of phase angle plots is similar to Fig. 6b. As, no new information is obtained from the phase angle plots, they are not included for the subsequent analysis.

Fig. 6

a Frequency response plots, and b Phase angle plots for different values of ${r}_{m}$. Parameters: Table 1, ${c}_{ex}={c}_{ez}=0.0085$, and ${l}_{1}=0.2$

The effect of the radius of gyration $r$ (dimensionless) of the shaft cross-section on the system response is shown in Fig. 7a. Exactly as in the case of mass ratio ${r}_{m}$, the values of the parameters $\left|G\right|$ (magnitude of $G$), $\omega$, ${q}_{0}$, and ${m}_{e}$ increase and the values of the parameters ${\upmu }_{x}$, and ${\upmu }_{z}$ decrease with the increase of $r$. The qualitative nature of the frequency–response curves for different values of $r$ shown in Fig. 7a which is similar to Fig. 6a plotted for different values of ${r}_{m}$; the resonance frequency and the peak amplitude at resonance increase as the value of $r$ is increased. The damping factors have more influence on the peak amplitude at resonance than the excitation amplitude ${q}_{0}$.

Fig. 7

Frequency response plots for different values of $r$ and ${{\text{r}}}_{dx}$. Parameters: Table 1, ${c}_{ex}={c}_{ez}=0.0085$, and ${l}_{1}=0.3$, a ${{\text{r}}}_{dx}=0.05$, b Table 1

The impact of the dimensionless mass moment of inertia of the disc about $x$-axis (${{\text{r}}}_{dx}={I}_{dx}/{\rho AL}^{3}$) on the frequency response curves is shown in Fig. 7b. The parameter ${{\text{r}}}_{dx}$ appear in the expression for ${m}_{e}$ given by Eq. (13c). With increasing ${{\text{r}}}_{dx}$, the value of the parameter ${m}_{e}$ increases which results in lower magnitudes of $G$, $\omega$, ${\upmu }_{x}$, ${\upmu }_{z}$ and ${q}_{o}$. As an outcome, the resonance frequency as well as the peak amplitude at resonance reduces for higher values of ${{\text{r}}}_{dx}$ as shown in Fig. 7b. The influence of ${{\text{r}}}_{dx}$ is contrary to the trend revealed by mass ratio ${r}_{m}$ and radius of gyration $r$ as shown in Figs. 6a and 7a.

The bearings at the end of the shaft are replaced by linear springs and damper (Kelvin–Voigt model) along horizontal and vertical directions. They directly influence the mode shape ${\Psi }_{1}$ shown in Fig. 2 as well as the natural frequency ${p}_{1}$. Other parameters of the rotor system governed by Eq. (14) are influenced through ${\Psi }_{1}$ and ${p}_{1}$. Figure 8a depicts the influence of the support spring stiffness ${k}_{21}$ on the frequency response plots. The stiffness of left-end bearing (bearing ${B}_{1}$) is kept constant at ${k}_{11}=500$ while obtaining the three frequency response curves for three different values of ${k}_{21}$ in Fig. 8a. The overall stiffness of the system decreases for higher values of ${k}_{21}$ resulting in lower resonant frequencies. The excitation amplitude ${q}_{0}$ and the damping factor $\upmu$ decrease with the increase of ${k}_{21}$ (Table 2) yielding the peak amplitude at resonance to increase as shown in Fig. 8a. It is to be mentioned here that the right-end bearing (bearing ${B}_{2}$) can be considered a rigid one for ${k}_{21}=6000$. When ${k}_{11}={k}_{21}=100$, the mode shape is symmetric about ${l}_{1}=0.5$ (refer Fig. 2). As the disc is installed at the middle of the shaft (${l}_{1}=0.5$), the gyroscopic parameter $G=-0.0089$ in Table 2 for ${k}_{11}={k}_{21}=500$ is entirely due to the gyroscopic effect of the shaft. As the stiffness of bearing ${B}_{2}$ is increased, the symmetry of the mode shape about ${l}_{1}=0.5$ is lost. The gyroscopic effect of the disc increases with the increase of ${k}_{21}$ which is manifested in the increasing value of $\left|G\right|$. Maximum value of $\left|G\right|$ is achieved for a rigid bearing at ${B}_{2}$.

Fig. 8

Frequency response plots for different values of ${k}_{21}$ and ${l}_{1}$. Parameters: ${c}_{ex}={c}_{ez}=0.0085$, a ${l}_{1}=0.5$, and b Table 1

Figure 8b depicts the effect of ${l}_{1}$ on the frequency response and phase angle plots. The parameter ${l}_{1}$ specifies the position of the disc from left-end of the support (from bearing ${B}_{1}$). If the disc is at the center of the shaft $({l}_{1}=0.5)$, the gyroscopic and rotary inertia effects of the disc associated with the terms ${D}_{g}$ and ${S}_{g}$, respectively, are zero (${D}_{g}{r}_{dy}{r}_{m} \left({t}_{5}- {t}_{6}\right)=0$, ${D}_{ri}{r}_{dx}{r}_{m} \left({t}_{5}- {t}_{6}\right)=0$). This leads to the largest effective mass ratio (${m}_{e}=2.042$) and smallest magnitude of gyroscopic coefficient ($\left|G\right|=0.008$) for ${l}_{1}=0.5$ as shown in Table 2. The value of the gyroscopic coefficient ($G=-0.008$) is entirely due to the gyroscopic effect of the shaft. The final consequence is the lowest resonance frequency for ${l}_{1}=0.5$ as shown in Fig. 8b. As the disc is moved away from the middle of the shaft and towards one of the bearing supports (${l}_{1}$ is either decreased or increased), the magnitude of $G$ is increased and ${m}_{e}$ is decreased leading to higher values of resonance frequencies. Because of the symmetry of the mode shape function ${\Psi }_{1}\left(y\right)$ about $y=0.5$, the frequency response curves would be identical for ${l}_{1}=0.3$ and ${l}_{1}=0.7$ (or ${l}_{1}=0.2$ and ${l}_{1}=0.8$). This can also be explained mathematically. In the expressions for ${m}_{e}$ and $G$ given by Eqs. (13c) and (13d), respectively, all the terms except ${t}_{5}- {t}_{6}=$ ${\left.{-\left(\frac{d{\Psi }_{1}}{dy}\right)}^{2}\right|}_{y={l}_{1}}$ and ${t}_{4}={\Psi }_{1}^{2}({l}_{1})$ remain the same while ${l}_{1}$ is varied. Now, because of the symmetry of the curve ${\Psi }_{1}\left(y\right)$ about $y=0.5$, ${\left.{\left(\frac{d{\Psi }_{1}}{dy}\right)}^{2}\right|}_{y=0.3}={\left.{\left(\frac{d{\Psi }_{1}}{dy}\right)}^{2}\right|}_{y=0.7}$, and ${\Psi }_{1}^{2}\left(0.3\right)={\Psi }_{1}^{2}(0.7)$. Consequently, the magnitudes of ${m}_{e}$ and $G$ will be the same leading to the identical frequency response curves for ${l}_{1}=0.3$ and ${l}_{1}=0.7$. As the disc approaches the support, the values of ${q}_{0}$, ${\upmu }_{x}$, ${\upmu }_{z}$, and ${\upmu }_{in}$ drop, which causes the amplitude peaks to decrease.

The influence of disc and shaft gyroscopic effects is illustrated in Fig. 9a. It is mentioned earlier that the terms associated with ${D}_{g}$ and ${S}_{g}$ are the gyroscopic effects of the disc and the shaft, respectively. The gyroscopic coefficient $G=0$ when both these effects are neglected (${D}_{g}={S}_{g}=0$). The consequence is the lowest resonance frequency as shown in Fig. 9a. On the other hand, the magnitude of $G$ ($=0.0530$) as well as the resonance frequency is the maximum for ${D}_{g}={S}_{g}=1$. The effective mass ${m}_{e}$ is independent of the gyroscopic terms. Consequently, the resonance frequency ${\left({r}_{f}\right)}_{r}$ and the amplitude of excitation ${q}_{0}$ remains unaltered. However, the damping factor $\upmu$ remains the same for all the values of ${D}_{g}$ and ${S}_{g}$. The outcome is the higher resonance frequency and the peak amplitude at resonance for higher values of the gyroscopic coefficient. The gyroscopic effect of the shaft appears to have a greater influence in increasing the resonance frequency and peak amplitude at resonance compared to the gyroscopic effect of the disc.

Fig. 9

Frequency response plots for different values of ${D}_{g}$, ${S}_{g}$, ${D}_{r}$ & ${S}_{r}$. Parameters: Table 1 and ${l}_{1}=0.3$. a ${D}_{r}={S}_{r}=1$, b ${D}_{g}={S}_{g}=1$

Figure 9b shows the effect of disc and shaft rotary inertia effects (${D}_{r}$ and ${S}_{r}$) on the rotor system responses (amplitude and phase angle). The rotary inertia terms associated with ${D}_{r}$ and ${S}_{r}$ appear in Eq. (13c) in the expression of effective mass ${m}_{e}$. It is to be noticed from Eq. (13) that the excitation amplitude ${q}_{0}$, gyroscopic coefficient $G$, and undamped natural frequency $\omega$ are all inversely proportional to ${m}_{e}$. In absence of the rotary inertia effects of the disc and shaft (${D}_{r}=$ ${S}_{r}=0$), the value of ${m}_{e}$ ($=1.401$) is the lowest and the magnitude of $G$ is the highest. This leads to the highest resonance frequency as shown in Fig. 9b. Furthermore, ${q}_{0}$ is found to be the highest ($=5.955$) resulting in highest peak amplitude at resonance for ${D}_{r}=$ ${S}_{r}=0$. On the other hand, highest value of ${m}_{e}$ and lowest magnitude of $G$ are obtained for ${D}_{r}={S}_{r}=1$. This leads to the lowest resonance frequency for ${D}_{r}={S}_{r}=1$. Lowest excitation amplitude ${q}_{0}$ results in the lowest peak amplitude of oscillation at resonance for ${D}_{r}={S}_{r}=1$. As in the case of gyroscopic effects, the shaft rotational inertia has greater influence in increasing the resonance frequency in comparison to the disc rotational inertia.

It is to be noted that all the aforementioned results are obtained without any internal damping (${c}_{i}=0$). It is shown in the section "Exact Analytical Solution and Analysis of Free Vibrations" that the response of the rotor system is always stable for ${c}_{i}=0$. However, a small amount of internal damping may cause instability of system response for frequency ratios beyond a critical value (${{r}_{f}\ge \left({r}_{f}\right)}_{c}$). This is verified in the forthcoming analysis.

The three frequency response curves shown in Fig. 10a are plotted for three difference values of internal damping coefficients. For effective analysis of the influence of internal damping on the system responses, the dependent parameters are listed in Table 3. It is observed from Table 3 that the gyroscopic parameter ($G$), undamped natural frequency ($\omega$), effective mass ratio (${m}_{e}$), amplitude of excitation (${q}_{0}$), and the resonance frequency (${\left({r}_{f}\right)}_{r}$) are all independent of ${c}_{i}$. However, the damping factor $\upmu$ ($={\upmu }_{x}={\upmu }_{z}$), and the internal damping factor ${\upmu }_{i}$ increases with the increase of ${c}_{i}$. This causes the peak amplitude at resonance to decrease with the increase of ${c}_{i}$ as shown in Fig. 10a. The range of frequencies corresponding to the stable solutions decreases with the increase of ${c}_{i}$. This is evident from the decreasing value of ${\left({r}_{f}\right)}_{c}$ with the increase of ${c}_{i}$. These critical values of ${r}_{f}$ separating the stable and unstable solutions for free vibrations are further verified by plotting the real part of the roots (${\beta }_{r}$) with respect to ${r}_{f}$. This plot is shown in Fig. 10b which depicts the change of sign of ${\beta }_{r}$ from negative to positive as the frequency ratio ${r}_{f}$ is increased beyond the critical value ${\left({r}_{f}\right)}_{c}$. Clearly, the homogeneous solution of Eq. (14) is stable for ${r}_{f}\le {\left({r}_{f}\right)}_{c}$ and unstable for ${r}_{f}>{\left({r}_{f}\right)}_{c}$.

Fig. 10

a Frequency response and b ${\beta }_{r}$ versus ${r}_{f}$ for different values of ${c}_{i}$. Parameters: Table 1, and ${l}_{1}=0.2$

Table 3 Parameter values for different values of internal damping coefficient

The responses of the rotor system (Eq. (14)) in the stable region (${r}_{f}<{\left({r}_{f}\right)}_{c}$), unstable region (${r}_{f}>{\left({r}_{f}\right)}_{c}$), and at the stability boundary (${r}_{f}={\left({r}_{f}\right)}_{c}$) are investigated in Fig. 11 for ${c}_{i}=0.000085$. The critical frequency ratio corresponding to ${c}_{i}=0.000085$ is ${\left({r}_{f}\right)}_{c}=3.806$. The time-displacement response of Eq. (14) for ${r}_{f}=2.5<{\left({r}_{f}\right)}_{c}$ is shown in Fig. 11a. This is a combination of homogeneous and particular solutions of Eq. (14). The frequencies of homogeneous and particular solutions superimpose causing the modulation at the initial phase as shown in Fig. 11b. As ${\beta }_{r}<0$, the homogeneous solution die out over time yielding a single periodic motion corresponding to the particular solution as shown in Fig. 11c. Since ${\beta }_{r}=0$ for ${r}_{f}=3.803={\left({r}_{f}\right)}_{c}$, the homogeneous solution never dies out. Consequently, the time-response of the system is always modulated as shown in Fig. 11d–f. However, the mean amplitude of oscillations will remain constant at steady state. On the other hand, the mean amplitude of oscillation increases unboundedly for ${r}_{f}=4>{\left({r}_{f}\right)}_{c}$ as shown in Fig. 11g–i. This homogeneous solution is unstable for ${r}_{f}=4$ because of positive value of ${\beta }_{r}$. This causes the unbounded time-displacement response of the rotor system depicted in Fig. 11g–i.

Fig. 11

Time responses for different values of ${r}_{f}$. Parameters: Table 1, ${\mu }_{i}=0.000085$, ${l}_{1}=0.2$, a–c ${r}_{f}=2.5$, d–f ${r}_{f}=3.806$ and g–i ${r}_{f}=4$

Conclusion

A systematic investigation of a continuous rotor model was performed in this paper to analyse the effect of different parameters on the natural frequency and stability of the system. The rotor system was modelled with the inclusion of several critical factors like the rotary inertia and gyroscopic effects of both shaft and disc, internal damping, large deformation of shaft, and restriction to shaft axial motion. The bearings on the two sides of the shaft were considered to be isotropic and were replaced by spring-dashpot systems along horizontal and vertical directions. The PDEs governing the system vibrations, derived from Hamilton's Principle, were reduced to a set of ODEs using the method of modal projection. As the paper is mainly focused in exploring the effect of different system parameters on the resonance frequency, only the linear system was analysed.

The effect of various independent parameters on the nature of vibrations of the linear rotor system were analyzed both numerically and analytically. These independent parameters are associated to the material and geometrical properties of the rotor system and connected to the governing ODEs through the effective mass ratio (${m}_{e}$) and gyroscopic coefficient ($G$). The dependent parameters, tabulated as functions of the independent parameters, were used for the effective analysis of the results. This methodical analysis, which connects the system dynamics to the material and geometric properties of the rotor system, could result in a suitable design.

The system becomes isotropic with identical responses along horizontal and vertical directions for equal amount of damping along these directions. The resonant frequency was observed to increase with the increase of mass ratio (${r}_{m}$), radius of gyration ($r$), and the end spring stiffness (${k}_{11}$, ${k}_{21}$). On the other hand, the resonance frequency decrease with the increase of the mass moment of inertia of the disc about x-axis (${r}_{dx}$). While the gyroscopic effects of the disc and shaft tend to increase the resonance frequency, the rotary inertia of the disc and shaft tend to decrease the resonance frequency.

The stability of the rotor system mainly depends upon the internal damping parameter (${\upmu }_{i}$). A strain rate dependent internal damping model was used in this paper. Analytical expression for a critical frequency ratio (${\left({r}_{f}\right)}_{c}$) corresponding to the stability boundary separating the stable and unstable regions was obtained. This critical value of ${r}_{f}$ was further verified by analysing the time responses of the rotor system for ${r}_{f}<{\left({r}_{f}\right)}_{c}$, ${r}_{f}={\left({r}_{f}\right)}_{c}$, and ${r}_{f}>{\left({r}_{f}\right)}_{c}$. For ${r}_{f}<{\left({r}_{f}\right)}_{c}$, the response was observed to reach a single periodic steady-state over time. A modulating time response was obtained for ${r}_{f}={\left({r}_{f}\right)}_{c}$. This is the consequence of superposition of homogeneous and particular solutions. For ${r}_{f}>{\left({r}_{f}\right)}_{c}$, the system is unstable and the time-response grows monotonically.

There is a lot of scope to extend the present work. The rotor system with nonlinearities arising from the large deformation of shaft, restriction to shaft axial motion, and nonlinear spring in place of bearings can be considered for future analysis. The feasibility of getting a same/different solution with nonlinear springs at the supports showing force–deflection relations similar to the Hertzian contact at ball bearings can be examined in future. One may try to derive a different mode shape function from a different set of boundary conditions obtained from the boundary terms which appear during the application of the Hamilton’s principle. Another scope for future work could be the use of hydrodynamic bearings instead of ball bearings.