Stability analysis of a rotor system with electromechanically coupled boundary conditions under periodic axial load

Abstract

The parametric instability of a rotor system with electromechanically coupled boundary conditions under periodic axial loads is studied. Based on the current flowing piezoelectric shunt damping technique, the detailed rotor model is established by the finite element (FE) method. In the matrix assembly procedure, a novel simple process is proposed to make the equations of shunt circuits more conveniently to be introduced into the global FE equations. The discrete state transition matrix method which is used for determining the influence of circuit parameters on instability regions in this paper has also been presented. The numerical simulation shows that only the combination instability regions exist when the shaft is rotating. The mechanical damping has different effect on the simple and combined instability regions. These two points are consistent with the previous references, which verifies the obtained FE model. In addition, the simulated results also reveal that the introduction of shunt circuits has little influence on the rotor’s original whirling frequencies. It gives rise to the appearance of new synchronous whirl modes. The new whirling frequencies are combined with the original ones to form the new combination instability regions. Furthermore, the resistance of shunt circuits has the same performance as the mechanical damping has. That is, moving up the start points of instability regions and expanding its width.

1 Introduction

The rotating machinery, such as gearboxes, motors, turbines and generators, is widely used in transportation like ship, airplane and automobile. Their stable operation plays a vital role in requirement of reliability and comfortability for such transportations. It is known that there are always more or less imbalance induced vibrations existing in rotor system, which will reduce the reliability and comfortability. To solve this problem, a novel ring-shaped piezoelectric damper [1] has been proposed. This damper, which uses shunted piezo stack as the fundamental damping element, has high stiffness and damping performance. It is installed between bearing and supporting structure. When the damper’s shunt circuits are closed, the whole system will become electromechanically coupled and the piezoelectric shunt damping will be generated, whereas when the circuits are opened or shorted, the whole system will become pure mechanical. In conclusion, this damper may be used to control the rotor vibrations [2]. The expectation is fine; however, there are some new problems may be encountered. One have known that when the rotor system subjected to time-dependent axial load, it may lead to parametric resonance or instability. In this case, a small parametric excitation may produce a large response when the frequency of the excitation is close to the combination of the natural frequencies of the system. Then the problem is: What is the influence of shunt circuits on the instability characteristics of such rotor system? About this, there have been very little study to be reported up to now. Thus, such problem is investigated in this paper. Before introducing this paper’s work, some relevant research activities must be reviewed.

As mentioned above, the rotor system will become pure mechanical if the shunt circuits are opened or shorted. In this case, actually, many research activities [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] about the dynamic stability analysis of the rotor system or the similar structure under periodic axial loads have been reported. When the shaft is not rotating, the whole system can be seen as a viscoelastic supported or simply supported column/beam. Iwatsubo et al. [3] studied the simple and combination resonances of a column under four typical cases of boundary conditions. In their research, they found that the damping has different effect on the simple and combination resonances. For the simple instability region, the external/internal damping moves up the generating points of the regions and reduces the regions’ width, whereas for the combination instability region, such damping moves up the generating points and expands its width. Saito et al. [4] investigated the stability of viscoelastic beams with an attached mass and viscoelastic end supports under axial and tangential periodic loads. Their research showed that when the beam is subjected to an axial periodic load, the combination resonance of difference type does not occur. Furthermore, In the case of combination resonance, the effect of damping is greater when the damping exists in the beam than when it is in the supports. Kang eta al. [5] examined the parametric instability of a Leipholz column under four boundary conditions. Their work aimed at providing a basic understanding of the disc brake pad instability. Huang et al. [6] presented a method for assessing the dynamic stability of simply supported columns with damping under arbitrary periodic axial loads. These works, which based on the nonrotating column/beam, have strong ties to the stability analysis of rotating structures.

To analyze the stability of rotating shaft under harmonic axial loads, Chen et al. [7] used the Timoshenko beam theory and FE method to build the rotor model, and then applied the Bolotin’s method to construct the instability regions. Their results showed that due to the Coriolis effect, the boundaries of the regions of dynamic instability were shifted out and the sizes of these regions were increased as the rotational speed increased. However, whether the Bolotin’s method is applicable to the rotating structure or not, there seems to have some disputes. Pei [10] found that using the Bolotin’s method may enlarge the instability region for the gyroscopic system, which may contradict the results based upon the Floquet’s method. Song et al. [13] presented a new method—discrete singular convolution. In their research, the external viscous damping and internal material damping were considered so as to analyze their influence on the stability of axial loaded rotating shaft. Qaderi et al. [14] investigated the dynamic responses of a rotating unbalanced shaft with geometrical nonlinearity under periodic axial loads. Therein the resonances, bifurcations, and stability of the response were analyzed. Phadatare et al. [16] studied the vibration and bifurcation analysis of a spinning rotor-disk-bearing system so as to reveal the effect of unbalance eccentricity and pulsating axial load on the dynamic stability. All of these papers are based on the rotor system. In addition, some research activities based on the rotating structures like cylindrical shell model also have great reference value. For instance, Han et al. [11] investigated the parametric instability of a rotating cylindrical shell under periodic axial loads. By using the multiple scale method, the analytical expressions of instability boundaries for various modes were obtained. Their theoretical analysis demonstrated that as long as rotation is considered, only combination instability regions exist for such rotating shell.

All of above-mentioned works have enlightened us and given us many inspiration. In this paper, the parametric stability of rotor system with electromechanically coupled boundary conditions under periodic axial load is further studied. The content of this paper can be listed as follows: In Sect. 2, the structure of proposed piezo damper and its shunt circuits are presented. Here, the current flowing shunt circuits [18] are used. In Sect. 3, FE model of the rotor system under periodic axial load at the end of the shaft has been derived. In this section, a novel simple process is proposed to make the equations of shunt circuits more conveniently to be assembled into the global FE equations. To be clear, the process is addressed in Appendix A. In Sect. 4, the free vibration and stability analysis are carried out so as to obtain the rotor’s whirling frequencies and instability regions. Specifically, Ref. [12] has shown that the DSTM method is very suitable for the stability analysis of rotor-bearing system under time-periodic base angular motions. In this paper, therefore, the DSTM method is also used. In Sect. 5, the numerical simulation is carried out and the discussion is given. Here, the rotor system with open-circuit condition is studied to verify the obtained FE model. Moreover, the influence of shunt circuits on the instability regions is stated. Finally, in Sect. 6, the conclusion is presented.

2 The vibration ring and shunt circuits

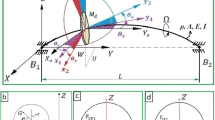
Before this study, a ring-shaped piezoelectric damper, called vibration ring, which may be used to control the rotor vibrations has been developed [1]. This damper uses the piezoelectric stack shunted with external shunt circuits as the fundamental element. As shown in Fig. 1a, the damper is installed between bearing house and supporting structure. When the shunt circuits are closed, the damper-bearing system becomes an electromechanical coupling system and its equivalent mechanical model is shown in Fig. 1b. Where η represents the mechanical damping, the mass m_b represents the equivalent mass of ball bearing and vibration ring, which can be easily derived from the kinetic energy of bearings and vibration rings, $\tilde{q} = q/\theta_{p}$ is generalized coordinate related to the electric charge q, k_eq is the stiffness related to damper’s mechanical structure and bearing house, k_eq1 is the stiffness related to piezoelectric stack, k_eq2 is the electromechanical coupling stiffness and ζ represents the shunt damping. Their expressions are given as

$$ k_{eq} = \frac{{2k_{1} k_{b} \cos^{2} \beta }}{{k_{b} + 2k_{1} \cos^{2} \beta }},k_{eq1} = 2k_{2} \cot^{2} \beta ,k_{eq2} = 2\cot^{2} \beta \frac{{\theta_{p}^{2} }}{{C_{p}^{S} }},\zeta = 2\cot^{2} \beta Z_{e} \theta_{p}^{2} $$

(1)

where k₁ is the stiffness of damper’s mechanical structure, k_b is the stiffness of isotropic bearing, k₂ is the compression stiffness of piezoelectric stack, β is a constant related to the damper’s mechanical configuration, θ_p is the generalized electromechanical coupling coefficient of piezo stack, $C_{p}^{S}$ is the piezo stack capacitor under constant strain and Z_e is the impedance of external shunt circuit. More detail about the parameters can be found in Ref. [1].

Fig. 1

Vibration ring: a the prototype and b equivalent mechanical model

From a general perspective, consider that each piezo stack in vibration ring is connected with multi-resonant shunts, as shown in Fig. 2. Each branch can be seen as if it were formed by an inductor L_fi (i = 1, 2,…, N) and a capacitor C_fi and by an inductor L_ti and a resistor R_ti connected in series. The inductor L_fi and capacitor C_fi produce a band-pass filtering effect with center frequency

$$ \omega_{fi} = \frac{1}{{\sqrt {L_{fi} C_{fi} } }} $$

(2)

Fig. 2

Current flowing shunt circuit

This effect is also called the current flowing effect [18, 19]. On the one hand, in this way, each branch works in a given narrow frequency band without interfering with the other branches. On the other hand, the inductor L_ti combines with the piezo stack capacitor ${\text{C}}_{{\text{p}}}^{{\text{T}}}$ (under constant stress) to produce the shunt vibration absorption effect at the tuning frequency

$$ \omega_{ti} = \frac{1}{{\sqrt {L_{ti} C_{p}^{T} } }} $$

(3)

The resistor R_ti is used to dissipate the vibration energy absorbed by the shunted piezo stack at frequencies close to the tuning frequency ω_ti. Since two inductors L_ti and L_fi are connected in series, they can be seen as a single inductor L_i = L_ti + L_fi. According to Ref. [18, 19], if the given center frequency ω_fi and tuning frequency ω_ti equal to the vibrating structure’s specific modal frequency ω_i, i.e., ω_fi = ω_ti = ω_i, the structure’s vibration at the modal frequency ω_i will be suppressed considerably. Once the filtering capacitance C_fi is given, the inductance value in each branch L_i can be calculated by [18].

$$L_{1}=\frac{C_{p}^{T}+C_{f1}}{\omega_{1}^{2}{C_{p}^{T}}C_{f1}}, L_{2}=\frac{C_{p}^{T}+C_{f2}}{\omega_{2}^{2}{C_{p}^{T}}C_{f2}}, ......,L_{N}=\frac{C_{p}^{T}+C_{fN}}{\omega_{N}^{2}{C_{p}^{T}}C_{fN}}$$

(4)

where ω₁, ω₂,…, ω_N are the modal frequencies of rotor system, i.e., the whirling frequencies of rotor system, respectively.

3 Finite element modelling of the rotor-vibration ring system

A rotor model with an offset rigid disk, which supported on ball bearings with vibration rings at two ends, is investigated. The finite element (FE) model is established as shown in Fig. 3, where the shaft is divided into n elements with n + 1 points and 4(n + 1) degrees of freedom (DOFs). Each shaft section is described by a Rayleigh beam element with 8 DOFs, and four of which are shared with the neighbor element. Assume that the disk locates at node i. Here, by using the Rayleigh beam theory, the disk is simplified as a lumped mass, and the polar moment of inertia and the radial moment of inertia can be taken into consideration. It is known that the FE model of rotor system can be divided into three parts, that is, the FE model of rotating shaft, the disk and the boundary conditions. Because there have been many studies [20] focused on FE modelling of rotor system, in this section, the equations of motion for the axial loaded rotating shaft and disk are given directly, whereas the equations of motion for the specific boundary conditions are derived in detail.

Fig. 3

The finite element model of the offset rotor with vibration rings

Assume that the homogeneous shaft’s internal damping is ignored. Then the governing equations of periodic axial loaded rotating shaft can be given as [5]:

$$ \begin{gathered} {\mathbf{M}}_{{\text{s}}} \ddot{\mathbf{{u}}}_{{{\text{vs}}}} + {\mathbf{G}}_{{\text{s}}} {\dot{\mathbf{u}}}_{{{\text{ws}}}} + \left[ {{\mathbf{K}}_{{\text{s}}} - P\left( t \right){\mathbf{S}}_{{\text{s}}} } \right]{\mathbf{u}}_{{{\text{vs}}}} = {\mathbf{0}} \hfill \\ {\mathbf{M}}_{{\text{s}}} \ddot{\mathbf{{u}}}_{{{\text{ws}}}} - {\mathbf{G}}_{{\text{s}}} {\dot{\mathbf{u}}}_{{{\text{vs}}}} + \left[ {{\mathbf{K}}_{{\text{s}}} - P\left( t \right){\mathbf{S}}_{{\text{s}}} } \right]{\mathbf{u}}_{{{\text{ws}}}} = {\mathbf{0}} \hfill \\ \end{gathered} $$

(5)

where M_s, G_s, K_s and S_s represent the global mass matrix, global gyroscopic matrix, global stiffness matrix and global axial stiffness matrix, respectively. u_vs and u_ws are the global displacement vectors, which have the form

$$ {\mathbf{u}}_{{{\text{vs}}}} = \left[ {v_{1} ,\theta_{w,1} ,v_{2} ,\theta_{w,2} , \ldots ,v_{n + 1} ,\theta_{w,n + 1} } \right]^{{\text{T}}} ,{\mathbf{u}}_{{{\text{ws}}}} = \left[ {w_{1} , - \theta_{v,1} ,w_{2} , - \theta_{v,2} , \ldots ,w_{n + 1} , - \theta_{v,n + 1} } \right]^{{\text{T}}} $$

Note that the first subscript ‘v’ or ‘w’ of all of displacement vectors in this paper represents Y or Z direction, respectively. P(t) is the periodic axial load which has the form

$$ P\left( t \right) = P_{cr} \left( {\alpha + \beta \cos \phi t} \right) $$

Here P_cr, α, β and ϕ are the fundamental static buckling load, static load coefficient, dynamic load coefficient and excitation frequency.

The governing equations for this eccentric disk are given as [20]:

$$ \begin{gathered} {\mathbf{M}}_{{\text{d}}} {\ddot{\mathbf{u}}}_{{{\text{vd}}}} + {\mathbf{G}}_{{\text{d}}} {\dot{\mathbf{u}}}_{{{\text{wd}}}} = {\mathbf{Q}}_{{{\text{vd}}}} \hfill \\ {\mathbf{M}}_{{\text{d}}} {\ddot{\mathbf{u}}}_{{{\text{wd}}}} - {\mathbf{G}}_{{\text{d}}} {\dot{\mathbf{u}}}_{{{\text{vd}}}} = {\mathbf{Q}}_{{{\text{wd}}}} \hfill \\ \end{gathered} $$

(6)

where u_vd = [v_i, θ_w,i]^T, u_wd = [w_i, − θ_v,i]^T are the nodal displacement vector of disk. In above expression

$$ \begin{aligned} & {\mathbf{M}}_{{\text{d}}} = \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & {J_{d} } \\ \end{array} } \right],{\mathbf{G}}_{{\text{d}}} = \Omega \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & {J_{p} } \\ \end{array} } \right] \\ & {\mathbf{Q}}_{{{\text{vd}}}} = m\Omega^{2} \left( {\left\{ {\begin{array}{*{20}c} {e\cos \gamma } \\ 0 \\ \end{array} } \right\}\cos \Omega t + \left\{ {\begin{array}{*{20}c} { - e\sin \gamma } \\ 0 \\ \end{array} } \right\}\sin \Omega t} \right) \\ & {\mathbf{Q}}_{{{\text{wd}}}} = m\Omega^{2} \left( {\left\{ {\begin{array}{*{20}c} {e\sin \gamma } \\ 0 \\ \end{array} } \right\}\cos \Omega t + \left\{ {\begin{array}{*{20}c} {e\cos \gamma } \\ 0 \\ \end{array} } \right\}\sin \Omega t} \right) \\ \end{aligned} $$

are the mass matrix, gyroscopic matrix and mass unbalance force of the eccentric disk. m, J_d and J_p are the mass, diametral and polar moment of inertia of disk, respectively. e and γ are the eccentricity and phase of eccentric mass.

3.1 Vibration ring and bearing support

In this subsection, the FE model of vibration ring and bearing support is derived. As shown in Fig. 3, the equations of motion for the boundary conditions can be easily derived by applying the Newton’s Second Law, which are given as

$$ \begin{aligned} & m_{b} \ddot{a}_{lz} + \eta \dot{a}_{lz} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{lz} - k_{eq2} \tilde{q}_{lz} = k_{eq} w_{1} + \eta \dot{w}_{1} \\ & k_{eq2} \left( {a_{lz} - \tilde{q}_{lz} } \right) = \zeta \dot{\tilde{q}}_{lz} \\ \end{aligned} $$

(7)

$$ \begin{gathered} m_{b} \ddot{a}_{rz} + \eta \dot{a}_{rz} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{rz} - k_{eq2} \tilde{q}_{rz} = k_{eq} w_{n + 1} + \eta \dot{w}_{n + 1} \hfill \\ k_{eq2} \left( {a_{rz} - \tilde{q}_{rz} } \right) = \zeta \dot{\tilde{q}}_{rz} \hfill \\ \end{gathered} $$

(8)

along z direction at x = 0 or L, and

$$ \begin{gathered} m_{b} \ddot{a}_{ly} + \eta \dot{a}_{ly} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{ly} - k_{eq2} \tilde{q}_{ly} = k_{eq} v_{1} + \eta \dot{v}_{1} \hfill \\ k_{eq2} \left( {a_{ly} - \tilde{q}_{ly} } \right) = \zeta \dot{\tilde{q}}_{ly} \hfill \\ \end{gathered} $$

(9)

$$ \begin{gathered} m_{b} \ddot{a}_{ry} + \eta \dot{a}_{ry} + \left( {k_{eq} + k_{eq1} + k_{eq2} } \right)a_{ry} - k_{eq2} \tilde{q}_{ry} = k_{eq} v_{n + 1} + \eta \dot{v}_{n + 1} \hfill \\ k_{eq2} \left( {a_{ry} - \tilde{q}_{ry} } \right) = \zeta \dot{\tilde{q}}_{ry} \hfill \\ \end{gathered} $$

(10)

along y direction at x = 0 or L, where v₁, w₁ represent the vertical and horizontal displacement of shaft at the left side and v_n+1, w_n+1 represent that at the right side, i.e., v₁ = v(0,t), w₁ = w(0,t), v_n+1 = v(L,t), w_n+1 = w(L,t). Here, the bearings are assumed to be isotropic, in which case the cross-coupling stiffness and damping are neglected.

When the piezo stack is shunted with two mode current flowing circuit, as shown in Fig. 4, the boundary conditions Eqs. (7)–(10) can be written in the following matrix form

$$ \begin{gathered} {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{lzc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{lzc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{lzc}}}} = {\mathbf{f}}_{{{\text{lzc}}}} \hfill \\ {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{rzc}}}} + {\mathbf{C}}_{{\text{c}}} \dot{{\mathbf{u}}}_{{{\text{rzc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{rzc}}}} = {\mathbf{f}}_{{{\text{rzc}}}} \hfill \\ {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{lyc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{lyc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{lyc}}}} = {\mathbf{f}}_{{{\text{lyc}}}} \hfill \\ {\mathbf{M}}_{{\text{c}}} {\ddot{\mathbf{u}}}_{{{\text{ryc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{ryc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{ryc}}}} = {\mathbf{f}}_{{{\text{ryc}}}} \hfill \\ \end{gathered} $$

(11)

where

$$ \begin{gathered} {\mathbf{M}}_{{\text{c}}} = \left[ {\begin{array}{*{20}c} {m_{b} } & 0 & 0 \\ 0 & {2\cot^{2} \beta \theta_{p}^{2} L_{1} } & 0 \\ 0 & 0 & {2\cot^{2} \beta \theta_{p}^{2} L_{2} } \\ \end{array} } \right],\;\;{\mathbf{C}}_{{\text{c}}} = \left[ {\begin{array}{*{20}c} \eta & 0 & 0 \\ 0 & {2\cot^{2} \beta \theta_{p}^{2} R_{t1} } & 0 \\ 0 & 0 & {2\cot^{2} \beta \theta_{p}^{2} R_{t2} } \\ \end{array} } \right] \hfill \\ {\mathbf{K}}_{{\text{c}}} = \left[ {\begin{array}{*{20}c} {k_{sum} } & { - k_{eq2} } & { - k_{eq2} } \\ { - k_{eq2} } & {\frac{{2\cot^{2} \beta \theta_{p}^{2} }}{{C_{f1} }} + k_{eq2} } & {k_{eq2} } \\ { - k_{eq2} } & {k_{eq2} } & {\frac{{2\cot^{2} \beta \theta_{p}^{2} }}{{C_{f2} }} + k_{eq2} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

and the displacement vectors u_lzc = [a_lz, ${\tilde{\text{q}}}_{{{\text{lz1}}}}$, ${\tilde{\text{q}}}_{{{\text{lz2}}}}$]^T, u_lyc = [a_ly, ${\tilde{\text{q}}}_{{{\text{ly1}}}}$, ${\tilde{\text{q}}}_{{{\text{ly2}}}}$]^T, u_rzc = [a_rz, ${\tilde{\text{q}}}_{{{\text{rz1}}}}$, ${\tilde{\text{q}}}_{{{\text{rz2}}}}$]^T, u_ryc = [a_ry, ${\tilde{\text{q}}}_{{{\text{ry1}}}}$, ${\tilde{\text{q}}}_{{{\text{ry2}}}}$]^T. The subscript 1 or 2 represents the generalized charge in the first or the second branch circuit. f_lzc = [$k_{eq} w_{1} + \eta \dot{w}_{1} , 0, 0$], f_lyc = [$k_{eq} v_{1} + \eta \dot{v}_{1} , 0, 0$], f_rzc = [$k_{eq} w_{n + 1} + \eta \dot{w}_{n + 1} , 0, 0$] and f_ryc = [$k_{eq} v_{n + 1} + \eta \dot{v}_{n + 1} , 0, 0$]. The readers can refer to Appendix A to see the procedure of constructing matrices M_c, C_c and K_c. Note that due to the introduction of these boundary conditions, the additional 12 DOFs are introduced. Therefore, the total DOFs for this rotor system are 4(n + 1) + 12.

Fig. 4

The two mode current flowing shunt circuit

3.2 Assembly of the finite element model of rotating shaft, disk, vibration ring and bearing

After assembling all the FE equations Eqs. 5, 6, and 11 for the rotating shaft, disk, vibration ring and bearing house, the final equations of motion for the whole system can be given as

$$ \begin{aligned} {\mathbf{M}}{\ddot{\mathbf{u}}}_{{\text{v}}} + {\mathbf{G}}{\dot{\mathbf{u}}}_{{\text{w}}} + \left[ {\mathbf{K}} - P\left( t \right){\mathbf{S}} \right]{\mathbf{u}}_{{\text{v}}}& = {\mathbf{Q}}_{{\text{v}}}\\ {\mathbf{M}}{\ddot{\mathbf{u}}}_{{\text{w}}} - {\mathbf{G}}{\dot{\mathbf{u}}}_{{\text{v}}} + \left[ {\mathbf{K}} - P\left( t \right){\mathbf{S}} \right]{\mathbf{u}}_{{\text{w}}} &= {\mathbf{Q}}_{{\text{w}}} \\ \end{aligned} $$

(12)

where M = M_s + M_d + diag(M_c, M_c, M_c, M_c), G = G_s + G_d + diag(C_c, C_c, C_c, C_c), K = K_s + diag(K_c, K_c, K_c, K_c), S = S_s, the displacement vectors u_v = [v₁, θ_w,1,…, v_n+1, θ_w,n+1, a_ly,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{ly}}{1}}$,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{ly}}{2}}$, a_ry,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{ry}}{1}}$,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{ry}}{2}}$]^T, u_w = [w₁, − θ_v,1, …, w_n+1, − θ_v,n+1, a_lz,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{lz}}{1}}$,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{lz}}{2}}$, a_rz,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{rz}}{1}}$,${\stackrel{\mathrm{\sim }}{\text{q}}}_{{\text{rz}}{2}}$]^T. It can be seen from Eq. (12) that the dimensions of all matrices appeared in that two equations are [2(n + 1) + 6] × [2(n + 1) + 6]. The generalized forces Q_v and Q_w have the form

$${\mathbf{Q}}_{{\text{v}}} = \left[ {0,\;0,\; \cdots ,\;\underbrace {{m\Omega^{2} e\left( {\cos \gamma \cos \Omega t - \sin \gamma \sin \Omega t} \right),\;0}}_{node\;i},\; \cdots ,\;0,\;0} \right]^{{\text{T}}} ,\;\;{\mathbf{Q}}_{{\text{w}}} = \left[ {0,\;0,\; \cdots ,\;\underbrace {{m\Omega^{2} e\left( {\cos \gamma \sin \Omega t + \sin \gamma \cos \Omega t} \right),\;0}}_{node\;i},\; \cdots ,\;0,\;0} \right]^{{\text{T}}}$$

.

In order to reduce the order of matrix equation and simplify it, note that

$$ \theta_{w,k} = \frac{{\partial v_{k} }}{\partial x},\;\;\theta_{v,k} = - \frac{{\partial w_{k} }}{\partial x}\;\;\;\;\left( {k = 1,2,\; \cdots ,\;n + 1} \right) $$

By introducing the following definition

$$ \begin{gathered} u_{k} = v_{k} + {\text{j}}w_{k} ,\;\;\theta_{k} = \theta_{w,k} - {\text{j}}\theta_{v,k} ,\;\;a_{l} = a_{ly} + {\text{j}}a_{lz} ,\;\;a_{r} = a_{ry} + {\text{j}}a_{rz} \hfill \\ \tilde{q}_{l1} = \tilde{q}_{ly1} + {\text{j}}\tilde{q}_{lz1} ,\;\;\tilde{q}_{l2} = \tilde{q}_{ly2} + {\text{j}}\tilde{q}_{lz2} ,\;\tilde{q}_{r1} = \tilde{q}_{ry1} + {\text{j}}\tilde{q}_{rz1} ,\;\;\tilde{q}_{r2} = \tilde{q}_{ry2} + {\text{j}}\tilde{q}_{rz2} \; \hfill \\ \end{gathered} $$

(13)

Then Eq. (12) can be simplified into the complex form

$$ {\mathbf{M}}\ddot{{\mathbf{u}}} + {\mathbf{G}}\dot{{\mathbf{u}}} + \left[ {{\mathbf{K}} - P\left( t \right){\mathbf{S}}} \right]{\mathbf{u}} = {\mathbf{Q}} $$

(14)

where u = u_v + ju_w, Q = Q_v + jQ_w and –jG is substituted by G for simplicity. Note that the simplification is only suitable to the system with isotropic boundary conditions.

4 Free vibration and stability analysis

In order to obtain the forward and backward whirling frequencies, the free vibration analysis is carried out. Note that the periodic axial force has the constant component which may affect the rotor’s dynamic characteristics. Hence, Eq. (14) should be reduced into the following homogenous time-invariant system

$$ {\mathbf{M}}\ddot{{\mathbf{u}}} + {\mathbf{G}}\dot{{\mathbf{u}}} + \left[ {{\mathbf{K}} - \alpha P_{cr} {\mathbf{S}}} \right]{\mathbf{u}} = {\mathbf{0}} $$

(15)

The solution of Eq. (15) has the form u(t) = φe^λt, where φ is a vector of complex numbers and the λ eigenvalue is also complex. Substituting this solution form into Eq. (15) gives the characteristic equation of form

$$ \left( {\lambda^{2} {\mathbf{M}} + \lambda {\mathbf{G}} + {\mathbf{K}} - \alpha P_{cr} {\mathbf{S}}} \right){{\varvec{\upvarphi}} } = 0 $$

(16)

Note that owing to the definition Eq. (13), all of matrices in Eq. (16) are Hermitian symmetry, in which case the right eigenvalues equal to left eigenvalue and the right-hand eigenvectors are same with the left-hand ones. If the mass matrix M is not singular, one can convert Eq. (16) into the linear eigenvalue problem

$$ {\mathbf{AV}} = \lambda {\mathbf{V}} $$

(17)

where

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} { - {\mathbf{M}}^{ - 1} {\mathbf{G}}} & { - {\mathbf{M}}^{ - 1} \left( {{\mathbf{K}} - \alpha P_{cr} {\mathbf{S}}} \right)} \\ {\mathbf{I}} & {\mathbf{O}} \\ \end{array} } \right],{\mathbf{V}} = \left\{ {\begin{array}{*{20}c} {{\varvec{\uppsi}}} \\ {\varvec{\upvarphi}} \\ \end{array} } \right\},{{\varvec{\uppsi}}} = \lambda {\varvec{\upvarphi} } $$

By solving Eq. (17), the forward and backward whirling frequencies and the complex form of amplitude of the shaft will be obtained. However, the mass matrix M is not always positive definite, for example, as the shunt circuits are shorted or opened (L₁ = L₂ = 0). Therefore, in this singular case, the spectral transformation method [21] should be used to solve this special quadratic eigenvalue problem. By introducing an appropriate eigenvalue shift as

$$ \mu = \lambda - \lambda_{0} $$

(18)

Equation (16) can be transformed into the following form

$$ \left[ {\begin{array}{*{20}c} { - {\mathbf{G}} - \lambda_{0} {\mathbf{M}}} & { - {\mathbf{K}} + \alpha P_{cr} {\mathbf{S}}} \\ {\mathbf{I}} & { - \lambda_{0} {\mathbf{I}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}} \\ {\mathbf{u}} \\ \end{array} } \right] = \mu \left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\mathbf{O}} \\ {\mathbf{O}} & {\mathbf{I}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}} \\ {\mathbf{u}} \\ \end{array} } \right] $$

(19)

Subsequently, through defining σ = 1/μ, Eq. (19) can be simplified as

$$ \left[ {\begin{array}{*{20}c} { - {\mathbf{G}} - \lambda_{0} {\mathbf{M}}} & { - {\mathbf{K}} + \alpha P_{cr} {\mathbf{S}}} \\ {\mathbf{I}} & { - \lambda_{0} {\mathbf{I}}} \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\mathbf{O}} \\ {\mathbf{O}} & {\mathbf{I}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}} \\ {\mathbf{u}} \\ \end{array} } \right] = \sigma \left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}} \\ {\mathbf{u}} \\ \end{array} } \right] $$

(20)

Equation (20) is namely the standard linear eigenvalue problem. Then solving Eq. (20) and note that

$$ \lambda = \frac{1}{\sigma } + \lambda_{0} $$

(21)

The eigenvalues and eigenvectors of this singular case will finally be determined.

For the purpose of determining the parametric instability regions of this rotor system, the discrete state transition matrix (DSTM) method which was developed by Friedmann et al. [22] is used. According to the characteristic of DSTM method, it is not appropriate to directly using the large FE matrices because there are so many matrix operations which may reduce the computational efficiency. To deal with this problem, the mode superposition method should be applied to reduce the order of matrices. Note that the above-mentioned vector φ is namely the mode shape. To obtain the mode shape of the nonrotating rotor model, the shaft’s rotating speed Ω should be set to 0 and the periodic axial force should be removed. Then by solving the eigenvalue problem, the mode shapes φ_m (m = 1, 2, …, M) will be derived, where M is the number of mode shapes. They can be combined to construct the modal matrix Φ = [φ₁, φ₂, …, φ_M]. Assume that the displacement response u(t) has the form

$$ {\mathbf{u}}\left( t \right) = {\mathbf{\Phi q}}\left( t \right) $$

(22)

Substituting Eq. (22) into Eq. (14) and premultiply each side by Φ^T, one can obtain

$$ {\tilde{\mathbf{M}}}{\ddot{\mathbf{q}}}\left( t \right) + {\tilde{\mathbf{G}}}{\dot{\mathbf{q}}}\left( t \right) + \left[ {\tilde{\mathbf{K}}} - P\left( t \right){\tilde{\mathbf{S}}} \right]{\mathbf{q}}\left( t \right) = {\tilde{\mathbf{Q}}} $$

(23)

where ${\tilde{\mathbf{M}}}{ = }{{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{M\Phi }}$, ${\tilde{\mathbf{G}}}{ = }{{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{G\Phi }}$, ${\tilde{\mathbf{K}}}{ = }{{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{K\Phi }}$, ${\tilde{\mathbf{S}}}{ = }{{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{S\Phi }}$ and ${\tilde{\mathbf{Q}}}{ = }{{\varvec{\Phi}}}^{{\text{T}}} {\mathbf{Q}}$. Note that Eq. (23) is a series of linear Mathieu equations, and therefore, it may be enough to determine the unstable regions only by using the DSTM method.

To apply the DSTM method, the homogenous form of Eq. (23) is considered. By converting it into the state-space form as

$$ {\dot{\mathbf{y}}}\left( t \right) = {\mathbf{B}}\left( t \right){\mathbf{y}}\left( t \right) $$

(24)

where the coefficient matrix B(t) is given as

$$ {\mathbf{B}}\left( t \right) = \left[ {\begin{array}{*{20}c} { - {\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{G}}}} & { - {\tilde{\mathbf{M}}}^{ - 1} \left( {{\tilde{\mathbf{K}}} - P\left( t \right){\tilde{\mathbf{S}}}} \right)} \\ {\mathbf{I}} & {\mathbf{O}} \\ \end{array} } \right] $$

(25)

and y(t) = [$\dot{\text{q}}$, q]. Here, O is an M × M zero matrix. In this method, the evaluation time should be divided into a series of small intervals and the following integration should be calculated

$$ {\mathbf{C}}_{k} = \frac{1}{{\Delta_{k} }}\int_{{t_{k - 1} }}^{{t_{k} }} {{\mathbf{B}}\left( t \right){\text{d}}t} \;k = 1,2, \ldots $$

(26)

where Δ_k = t_k – t_k-1. Then the approximate state transition matrix can be obtained as

$$ {{\varvec{\Xi}}} = \prod\limits_{k = 1}^{\infty } {\exp \left( {\Delta_{k} {\mathbf{C}}_{k} } \right)} $$

(27)

The eigenvalues of the matrix Ξ, which are often called the Floquet multipliers, can be used to determine the instability regions. When the absolute values of all the eigenvalues are smaller than 1, the system is stable, whereas if at least one of the absolute values of the Floquet multipliers is larger than 1, the system is unstable. Therefore, the instability criteria is given as

$$ \max \left( {\left| {\lambda_{i} } \right|} \right) > 1 $$

(28)

in which λ_i represents the ith eigenvalue of the matrix Ξ. It should be mentioned that due to the unavoidable roundoff errors in the numerical computations, the instability criteria are relaxed and chosen to be max(|λ_i|) > 1.0001.

5 Numerical results and discussion

In this section, the content is mainly divided into two parts. The first part is about verifying obtained rotor model. From Fig. 3 one can see that the obtained model can be reduced to a simpler one. For example, if the shunt circuits are opened, the electrical damping will tend to infinity and the boundary condition will be simplified as Fig. 5 shown.

Fig. 5

The simplified boundary condition of the obtained rotor model

In this case, if the shaft’s rotating speed Ω = 0, this rotor model can be seen as a column with an attached mass which is supported by the spring-mass-damping system under periodic axial load. A similar model has been studied in Refs. [8, 9]. Thus, to verify the obtained rotor model, the reduced model is investigated through comparison with the results reported in these references. In the numerical simulation, specifically, the shaft is divided into 64 elements, i.e., n = 64. Assume that the disk locates at a quarter of shaft length, then i = 17.

The second part is about analyzing the influence of circuit parameters on the instability regions. The FE model is remain unchanged except its boundary condition. In general, the circuit parameters, i.e., the inductance and capacitance, should be combined to form the electrical resonance and the resonant frequency should be tuned to the rotor system’s modal frequency. In this paper, however, the electrical resonant frequencies are set to the frequencies which distinguish from all of the rotor system’s modal frequency. This behavior will help the readers know more clearly about the effect of shunt circuits. Here, two mode current flowing shunt circuit is considered. If the electrical resonant frequencies of the first and second branch circuit are designated to be 900 rad/s and 2600 rad/s, respectively, assume that the filtering capacitance C_f1 and C_f2 equal to 5 × 10⁻⁶ F and 1 × 10⁻⁷ F, then the inductance value in each branch can be calculated by Eq. (4), which yields L₁ = 0.9328 H and L₂ = 1.5615 H.

Before carrying out the numerical simulation, the whirling frequencies under the conditions of open-circuit and closed-circuit should be analyzed firstly. The model parameters used in the numerical simulation are given in Table 1. According to Eq. (1), the values of k_eq, k_eq1, k_eq2 can be determined: k_eq = 2.635 × 10⁷ N/m, k_eq1 = 7.333 × 10⁷ N/m, k_eq2 = 2.444 × 10⁷ N/m. Section 4 has mentioned that the constant component of the periodic axial load may affect the rotor’s dynamic characteristics. Hence, the static load coefficient α used in this numerical simulation is equal to 0.5. The Campbell diagrams are shown in Fig. 6 and Fig. 7. By the way, it should be clarified that the specific values of static load coefficient α and rotating speed Ω which are used in the following analysis have no special meaning. The static load coefficient and rotating speed can affect the rotor’s whirling frequencies, and hence, the different values of α and Ω will lead to the different start points of instability regions. Thus, it is necessary to set their values before carrying out analysis so that the instability regions can be determined. The readers can refer to Refs. [7, 11, 15] to justify this description. It can be seen from Fig. 7 that there are four additional modes of forward/backward synchronous whirl existing due to the closed shunt circuit. This phenomenon can be explained by the transfer function method. Ref. [23] has shown that when a vibrating system has the piezoelectric shunts, for each single resonant RL shunt, it adds additional two poles to such system. Here, two resonant RL shunts are used and four poles are introduced for the rotor system. Each pole corresponding to the specific synchronous whirl and thus four additional synchronous whirl are introduced. To classify these additional synchronous whirl modes, the first two modes which are resulted from the first branch circuit are numbered by r₁ and r₂, whereas the last two modes which corresponding to the second branch circuit are numbered by s₁ and s₂. When the rotating speed Ω = 0 rad/s and 2000 rad/s, respectively, the first four forward/backward whirling frequencies under open-circuit condition are collected in Table 2, whereas when Ω = 2000 rad/s, the first eight forward/backward whirling frequencies under closed-circuit condition are collected in Table 3. Note that when the rotating speed Ω = 0 rad/s, the whirling frequencies, which are denoted by ω_n(·), are namely the natural frequencies of the nonrotating rotor system. These data will be used in the following analysis.

Table 1 Model parameters used in the numerical simulation

Fig. 6

The Campbell diagram of the rotor system for the open-circuit condition

Fig. 7

The Campbell diagram of the rotor system for the closed-circuit condition

Table 2 The whirling frequencies (rad/s) in the cases of rotating speed Ω = 0 rad/s and 2000 rad/s under open-circuit condition

Table 3 The whirling frequencies (rad/s) in the case of rotating speed 2000 rad/s under closed-circuit condition

5.1 Verification of obtained model

As mentioned before, the rotor system can be seen as a column with an attached mass when it is not rotating. In this case, if the column suffered from parametric instability, then according to the parametric instability theory [24], the starting points of instability regions on the frequency axis could be expressed as: (2/i)ω_p and (1/i)(ω_p + ω_q) (i = 1, 2, …), in which ω_p, ω_q are two different natural frequencies of the time-invariant system. The former groups of instability region are called the simple instability regions, and the latter groups are called the combination instability regions. The simple instability region with i = 1 is also called the primary instability region. By using four mode shapes to reduce the FE matrices, i.e., making M = 4, and then use the DSTM method, the stability diagram of the nonrotating case under the open-circuit condition is analyzed and plotted in Fig. 8. Here, shaded areas denote unstable regions. From this figure one can see that only the simple instability region and sum type combination instability region appear. This result is consistent with the conclusion which were obtained from Ref. [3, 5]. It can also be concluded that the external damping has different effect on the simple and combined instability region. For the simple instability region, the external damping degenerates the region as a whole, whereas for the combined one, it moves up the start points of instability region and expands the region’s width. In addition, such effect is more evident in high-order instability region, no matter for the simple or combined type. This phenomenon has been reported by the Ref. [3].

Fig. 8

The effect of external damping on the stability diagram of nonrotating case under the open-circuit condition: a η = 0 and b η = 200 and c η = 4000

The above analysis is about the nonrotating case. For the rotating case, the stability diagram under open-circuit condition is shown in Fig. 9. It can be seen from this figure that only the sum type combination instability region exists when the shaft is rotating. The similar phenomenon has also been reported in Ref. [11]. Therein a rotating cylindrical shell subjected to periodic axial loads was considered and the detailed theoretical analysis had been carried out. Although the rotating shell is different from the rotor system, the form of governing equations which were analyzed in Ref. [11] is same with Eq. (23) in this paper. Thus, it is easily to summarize that the rotating effect remove the simple instability region, no matter it is a rotating shell or a rotor system.

Fig. 9

The effect of rotating speed on the instability regions under the open-circuit condition. The mechanical damping and resistance value are all set to zero

Furthermore, to verify the DSTM method, the time responses of modal displacement are calculated. One can transform Eq. (24) into state space form as

$$ {\dot{\mathbf{y}}}\left( t \right) = {\mathbf{B}}\left( t \right){\mathbf{y}}\left( t \right) + {\mathbf{R}}\left( t \right),\;{\mathbf{R}}\left( t \right) = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{Q}}}} \\ {\mathbf{0}} \\ \end{array} } \right] $$

(29)

Note that the expression of B(t) has been given in Eq. (25) and the real and imaginary part of column vector y(t), respectively, represent the modal displacement response along vertical and horizontal direction. Here, the case of β = 0.25 is studied. The top view of stability chart is marked in Fig. 9, as the red rectangle highlighted. The front view of that is shown in Fig. 10 and four points, Γ₁, Γ₂, Γ₃, Γ₄ are selected for verification. Wherein ‘NaN’ in the coordinates of these points represents that the maximum absolute value of all of eigenvalues is smaller than 1.0001 at the specific excitation frequency. Specifically, the time responses for the first variable q₁ of y(t) in Eq. (29) are plotted. It can be seen from Fig. 10 that the time responses are stable for points Γ₁, Γ₄ which are outside the unstable regions and they are divergent for points Γ₂, Γ₃ which are inside unstable regions. Then the DSTM is verified. Overall, this rotor model is effective.

Fig. 10

The stability chart at the case of β = 0.25 and the modal displacement responses of q₁. Here, NaN represents that the maximum absolute value of all the eigenvalues is smaller than 1.0001 at the specific excitation frequency

5.2 The effects of circuit parameters upon parametric instability

Note that when the shunt circuits are closed, the whirling frequencies of r₁ and r₂ mode or that of s₁ and s₂ mode are very close to each other. Thus, the first and second additional groups of whirling frequencies are, respectively, denoted by r and s for simplicity. In this subsection, the mechanical damping η is eliminated. If the rotating speed Ω is still equal to 2000 rad/s, the readers can find from Tables 2 and 3 that there is little difference between the whirling frequencies under open-circuit condition and that under closed-circuit condition. To demonstrate the influence of circuit parameters on the instability regions, the stability diagrams under these two conditions are plotted together for comparison, as shown in Fig. 11. In this figure, all of resistance values are all set to zero, i.e., R_t1 = R_t2 = 0 ohms. Here, eight modes are included in this case, i.e., M = 8. The 3D plots of Fig. 11 are also plotted for distinguishing the instability regions more clearly, as shown in Fig. 12. It can be found from Fig. 9, 10, Fig. 11 that apart from the original instability regions under open-circuit condition, when the shunt circuits are closed, the additional whirling frequencies are combined with the original whirling frequencies under open-circuit condition to form the new combination instability regions (The pure red region in Fig. 11). This phenomenon further demonstrates that there is no primary instability region as long as the rotation is considered for this rotor system. Now, the readers may understand why the electrical resonant frequencies are set to 900 rad/s and 2600 rad/s, which distinguish from all of the rotor system’s whirling frequencies. This behavior is aimed at separating the new instability regions from the original regions more clearly.

Fig. 11

The influence of circuit condition on the instability regions under open-circuit condition and closed-circuit condition, where R_t1 = R_t2 = 0 ohms. The blue regions represent the case of open-circuit condition and the red ones represent that of closed-circuit condition

Fig. 12

The 3D plots of Fig. 11. Wherein the z coordinate represents the amplitude growth rate of the unstable responses

In Sect. 2, we have introduced that the resistors of shunt circuits are used to dissipate the vibration energy. It just like playing the role of mechanical damping. Therefore, to understand the influence of resistance on the instability regions, the cases of R_t1 = R_t2 = 10 and 50 ohms are investigated. For comparison, the stability diagrams are also plotted in the same figure, as shown in Fig. 13. It can be observed from Figs. 11, 12, 13 that when the shunt circuit is closed, the performance of resistance is similar with that of mechanical damping, as subsection 5.1 discussed. In addition, one can see that the resistance only has the similar effect on the new combination instability regions. This means that we can enlarge or regulate the stability regions by tuning the parameters of the shunt circuits.

Fig. 13

The influence of resistance on the instability region. Herein the resistances used in the first and second branch circuit R_t1 and R_t2 are all varying from 10 to 50 ohms: a R_t1 = R_t2 = 10 ohms and b R_t1 = R_t2 = 50 ohms

6 Conclusion

Based on the piezoelectric shunt damping technology, the effects of circuit parameters on the parametric instability of an electromechanical coupled rotor system under periodic axial load are studied using the DSTM method. After the two mode current flowing shunt circuits are connected, the rotor model is established by the FE method. Herein a novel simple process is proposed to help us more conveniently to put the equations of electric circuits into the global FE equations. This process is not only suitable for the current flowing circuit but also for the other kinds of circuits. One can directly use the circuit theory to derive the shunt circuits’ equations and assemble them into FE equations. To verify the obtained model, the special cases under open-circuit condition are investigated for comparison with the former references.

The numerical simulation shows that the rotation effect erases the primary instability region. As long as the shaft starts to rotate, only the combination instability region which is located by the combined whirling frequencies can be observed. The external shunt circuits introduce the additional synchronous whirl modes. These additional whirling frequencies ω_ej (j = 1, 2,…) are combined with the original frequencies ω_fi/ω_bi (i = 1, 2,…) to form the new combination instability regions. Their start points can be written as: ω_fi + ω_ej and ω_bi + ω_ej. Furthermore, the resistance plays the same role of mechanical damping, that is, moving up the start points of new instability regions and expanding its width.

Appendix

Note that the second equation in Eq. (7)–(10) are similar and compact. What their final forms like depends on what shunted circuit the vibration ring connected. Hence, it is necessary to derive their specific forms in the case of using current flowing shunt circuits. Before giving the general FE model using N branch shunt circuits, the case of using single branch is discussed as follows. In which case, the second equation in Eq. (7) is analyzed here.

For a shunted piezo stack, it is equivalent to an ideal voltage source U_p in series with a capacitor $C_{p}^{S}$ or an ideal current source in parallel with such capacitor. When the stack is shunted with a single resonant circuit, its circuit diagram is shown in Fig. 

Fig. 14

The circuit diagram for a piezo stack shunted with a single resonant circuit

14. In this case, the electrical impedance Z_e is equal to 1/sC_f1 + sL₁ + R_t1, where s is the Laplace transform variable. According to Eq. (1), the second equation in Eq. (7) can be written as

$$ 2\cot^{2} \beta \frac{{\theta_{p}^{2} }}{{C_{p}^{S} }}\left( {a_{lz} - \frac{{q_{lz} }}{{\theta_{p} }}} \right) = 2\theta_{p}^{2} \cot^{2} \beta \left( {\frac{1}{{sC_{f1} }} + sL_{1} + R_{t1} } \right)\frac{{\dot{q}_{lz} }}{{\theta_{p} }} $$

(A1)

Equation (A1) can be straightforwardly transformed into the following time domain expression:

$$ L_{1} \ddot{q}_{lz} + R_{t1} \dot{q}_{lz} + \left( {\frac{1}{{C_{p}^{S} }} + \frac{1}{{C_{f1} }}} \right)q_{lz} - \frac{{\theta_{p} }}{{C_{p}^{S} }}a_{lz} = 0 $$

(A2)

Actually Eq. (A2) can be directly derived using Kirchhoff’s Voltage Law (KVL) through Fig. 14. It is obvious that the voltage generated by the piezo stack due to the electromechanical effect is equal to $(\theta_{p} /C_{p}^{S} )a_{lz}$. This inspired us that for the multi-resonant shunts, its circuit diagram can be drawn as Fig. 

Fig. 15

The circuit diagram of multi-resonant shunt circuit

15. From Fig. 15 the following equations can be obtained using KVL

$$ \left\{ \begin{gathered} \dot{\tilde{q}}_{lz} = \dot{\tilde{q}}_{lz1} + \dot{\tilde{q}}_{lz2} + \cdots + \dot{\tilde{q}}_{lzN} \Rightarrow \tilde{q}_{lz} = \tilde{q}_{lz1} + \tilde{q}_{lz2} + \cdots + \tilde{q}_{lzN} \hfill \\ L_{1} \ddot{\tilde{q}}_{lz1} + R_{t1} \dot{\tilde{q}}_{lz1} + \frac{{\tilde{q}_{lz1} }}{{C_{f1} }} + \frac{{\tilde{q}_{lz} }}{{C_{p}^{S} }} - \frac{{a_{lz} }}{{C_{p}^{S} }} = 0 \hfill \\ L_{2} \ddot{\tilde{q}}_{lz2} + R_{t2} \dot{\tilde{q}}_{lz2} + \frac{{\tilde{q}_{lz2} }}{{C_{f2} }} + \frac{{\tilde{q}_{lz} }}{{C_{p}^{S} }} - \frac{{a_{lz} }}{{C_{p}^{S} }} = 0 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ L_{N} \ddot{\tilde{q}}_{lzN} + R_{tN} \dot{\tilde{q}}_{lzN} + \frac{{\tilde{q}_{lzN} }}{{C_{fN} }} + \frac{{\tilde{q}_{lz} }}{{C_{p}^{S} }} - \frac{{a_{lz} }}{{C_{p}^{S} }} = 0 \hfill \\ \end{gathered} \right. $$

(A3)

where the charge in each branch shunt has been transformed into generalized charge through dividing it by the generalized electromechanical coupling factor θ_p. Note that the first equation of Eq. (A3) is only valid under the zero initial condition. Combining Eq. (A3) and the first equation in Eq. (7), the following matrix equation can be obtained

$$ {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{lzc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{lzc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{lzc}}}} = {\mathbf{f}}_{{{\text{lzc}}}} $$

(A4)

where

$$ \begin{gathered} {\mathbf{M}}_{{\text{c}}} = {\text{diag}}\left[ {m_{b} ,\;L_{1} ,\;L_{2} ,\; \cdots ,\;L_{N} } \right],\;\;{\mathbf{C}}_{{\text{c}}} = {\text{diag}}\left[ {\eta ,\;R_{t1} ,\;R_{t2} ,\; \cdots ,\;R_{tN} } \right] \hfill \\ {\mathbf{K}}_{{\text{c}}} = \left[ {\begin{array}{*{20}c} {k_{sum} } & { - k_{eq2} } & { - k_{eq2} } & \cdots & { - k_{eq2} } \\ { - \frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{f1} }} + \frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{p}^{S} }}} & \cdots & {\frac{1}{{C_{p}^{S} }}} \\ { - \frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{f2} }} + \frac{1}{{C_{p}^{S} }}} & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & {\frac{1}{{C_{p}^{S} }}} \\ { - \frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{p}^{S} }}} & \cdots & {\frac{1}{{C_{p}^{S} }}} & {\frac{1}{{C_{fN} }} + \frac{1}{{C_{p}^{S} }}} \\ \end{array} } \right] \hfill \\ {\mathbf{f}}_{{{\text{lzc}}}} = \left[ {k_{eq} w\left( {0,t} \right) + \eta \dot{w}\left( {0,t} \right),\;0,\; \cdots ,\;0} \right]^{{\text{T}}} = \left[ {k_{eq} w_{1} + \eta \dot{w}_{1} ,\;0,\; \cdots ,\;0} \right]^{{\text{T}}} \hfill \\ {\mathbf{u}}_{{{\text{lzc}}}} = \left[ {a_{lz} ,\;\tilde{q}_{lz1} ,\;\tilde{q}_{lz2} ,\; \cdots ,\;\tilde{q}_{lzN} } \right]^{{\text{T}}} \hfill \\ \end{gathered} $$

(A5)

In the same manner, the matrix equation of Eq. (8)–(10) for the other boundary conditions can be derived, which are given as

$$ \begin{gathered} {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{rzc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{rzc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{rzc}}}} = {\mathbf{f}}_{{{\text{rzc}}}} \hfill \\ {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{lyc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{lyc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{lyc}}}} = {\mathbf{f}}_{{{\text{lyc}}}} \hfill \\ {\mathbf{M}}_{{\text{c}}} \ddot{\mathbf{{u}}}_{{{\text{ryc}}}} + {\mathbf{C}}_{{\text{c}}} {\dot{\mathbf{u}}}_{{{\text{ryc}}}} + {\mathbf{K}}_{{\text{c}}} {\mathbf{u}}_{{{\text{ryc}}}} = {\mathbf{f}}_{{{\text{ryc}}}} \hfill \\ \end{gathered} $$

(A6)

where

$$\begin{aligned} & {\mathbf{f}}_{{{\text{rzc}}}} = \left[ {k_{{eq}} w\left( {L,t} \right) + \eta \dot{w}\left( {L,t} \right),0, \ldots ,0} \right]^{{\text{T}}} = \left[ {k_{{eq}} w_{{n + 1}} + \eta \dot{w}_{{n + 1}} ,0, \ldots ,0} \right]^{{\text{T}}} \\ & {\mathbf{f}}_{{{\text{lyc}}}} = \left[ {k_{{eq}} v\left( {0,t} \right) + \eta \dot{v}\left( {0,t} \right),0, \ldots ,0} \right]^{{\text{T}}} = \left[ {k_{{eq}} v_{1} + \eta \dot{v}_{1} ,0, \ldots ,0} \right]^{{\text{T}}} \\ & {\mathbf{f}}_{{{\text{ryc}}}} = \left[ {k_{{eq}} v\left( {L,t} \right) + \eta \dot{v}\left( {L,t} \right),0, \ldots ,0} \right]^{{\text{T}}} = \left[ {k_{{eq}} v_{{n + 1}} + \eta \dot{v}_{{n + 1}} ,0, \ldots ,0} \right]^{{\text{T}}} \\ & {\mathbf{u}}_{{{\text{rzc}}}} = \left[ {a_{{rz}} ,\tilde{q}_{{rz1}} ,\tilde{q}_{{rz2}} , \ldots ,\tilde{q}_{{rzN}} } \right]^{{\text{T}}} \\ & {\mathbf{u}}_{{{\text{lyc}}}} = \left[ {a_{{ly}} ,\tilde{q}_{{ly1}} ,\tilde{q}_{{ly2}} , \ldots ,\tilde{q}_{{lyN}} } \right]^{{\text{T}}} \\ & {\mathbf{u}}_{{{\text{ryc}}}} = \left[ {a_{{ry}} ,\tilde{q}_{{ry1}} ,\tilde{q}_{{ry2}} , \ldots ,\tilde{q}_{{ryN}} } \right]^{{\text{T}}} \\ \end{aligned}$$

(A7)

Note that the stiffness matrix K_c in Eq. (A5) is asymmetric. To symmetrize it, enlightened by the designation: k_eq2 = 2cot²β ·$\theta_{p}^{2} /C_{p}^{S}$, multiply each row which corresponding to the generalized charge $\tilde{q}_{lzi}$ by 2cot²β ·$\theta_{p}^{2}$, one can obtain the following symmetric expression:

$$ \begin{gathered} M_{c} = diag\left[ {m_{b} ,\;2\cot^{2} \beta \theta_{p}^{2} L_{1} ,\;2\cot^{2} \beta \theta_{p}^{2} L_{2} ,\; \cdots ,\;2\cot^{2} \beta \theta_{p}^{2} L_{N} } \right] \hfill \\ C_{c} = diag\left[ {\eta ,\;2\cot^{2} \beta \theta_{p}^{2} R_{t1} ,\;2\cot^{2} \beta \theta_{p}^{2} R_{t2} ,\; \cdots ,\;2\cot^{2} \beta \theta_{p}^{2} R_{tN} } \right] \hfill \\ K_{c} = \left[ {\begin{array}{*{20}c} {k_{sum} } & { - k_{eq2} } & { - k_{eq2} } & \cdots & { - k_{eq2} } \\ { - k_{eq2} } & {\frac{{2\cot^{2} \beta \theta_{p}^{2} }}{{C_{f1} }} + k_{eq2} } & {k_{eq2} } & \cdots & {k_{eq2} } \\ { - k_{eq2} } & {k_{eq2} } & {\frac{{2\cot^{2} \beta \theta_{p}^{2} }}{{C_{f2} }} + k_{eq2} } & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & {k_{eq2} } \\ { - k_{eq2} } & {k_{eq2} } & \cdots & {k_{eq2} } & {\frac{{2\cot^{2} \beta \theta_{p}^{2} }}{{C_{fN} }} + k_{eq2} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A8)

From above description, one can see that this process is not only applicable to the current flowing shunt circuits, but also for the other kinds of shunt circuits. One can directly use the circuit theory to derive the shunt circuits’ governing equations and assemble them into the global FE equations. The key point is that substituting the voltage source which generated from the piezo stack by the term $(\theta_{p} /C_{p}^{S} )a_{lz}$. This is namely the representative of electromechanical coupling.