1 Introduction

Parametric instability problem of rotating systems subjected to periodic axial forces has been an active research issue and has been investigated by many researchers. Chen and Ku used finite element method to study dynamic stability of a rotating Timoshenko shaft [1], a rotating shaft embedded in an isotropic Winkler-type foundation [2] and a rotating Timoshenko shaft-disk system [3], respectively. Lee analyzed dynamic stability of spinning pre-twisted cantilever beams subjected to axial pulsating loads [4] and axial base excitations [5] by assumed mode method, respectively. Chen and Peng [6] studied dynamic stability of a rotating composite shaft under axial periodic forces by finite element method. Sheu and Chen [7] proposed a lumped mass model to study parametric instability of a cantilever shaft-disk system subjected to axial and follower loads. Lin and Chen [8] investigated dynamic stability of spinning pre-twisted sandwich beams with a constrained damping layer subjected to periodic axial loads. Other researchers [9–23] have also investigated vibration and dynamic stability of rotating systems.

Generally, when parametric instability problems are dealt with, the governing differential equations are reduced to a Mathieu–Hill equation, And the Mathieu–Hill equation determines boundaries of instability regions by using existing theoretical methods such as Bolotin [24], Floquet [18], and multiple scale method [10–12, 25] etc. In the most cases, results obtained by using Bolotin, Floquet and multiple scales method are coincident with each other except for some small errors. However, recently, Bolotin’s method is considered to lead to enlargement of instability regions for gyroscopic systems, and may contradict the results by using Floquet’s method [18], which is worthy of being focused on. To the authors’ knowledge, up till now, study on this problem has not been reported except the work of Pei [18]. In addition, it should be noted that when these theoretical methods are applied, parametric instability regions are determined by Mathieu–Hill equation. Whether another way to solve this problem exists or not is worth considering. Fortunately, another way [26] has been applied to analyze parametric instability problem, in which instability regions are determined by a direct simulation method, rather than the previously mentioned way. In the authors’ previous work [27–29], a direct simulation technique—discrete singular convolution (DSC) [30], has been successfully applied to analyze dynamic instability of beams. In the present work, this direct simulation technique is applied to parametric instability analysis of a rotating shaft under a periodic axial force. And dynamic instability regions obtained by this direct way are compared to those by using theoretical methods of Bolotin and Floquet, which will further illustrate the contradiction between Bolotin and Floquet. Especially, to the authors’ knowledge, experimental reports on this problem have not been published. Therefore, the present numerical study appears especially important.

Discrete singular convolution (DSC) method proposed by Wei [31] has emerged as a new highly efficient technique for numerically solving differential equations. Although DSC method is considered as a local method, it has spectral level accuracy [32, 33]. Compared to other conventional numerical methods, this method has the global methods’ high level accuracy and the local methods’ flexibility for handling complex geometries and boundary conditions [34]. Like generalized differential quadrature (GDQ) method [35], DSC method can provide accurate solutions with relatively much fewer grid points. But DSC has some advantages over GDQ for solving higher-order vibration problems [34]. Compared to finite element method (FEM) [36], DSC method just need spatial discretization, and there are no real elements like the elements in FEM, which is quite different from FEM. Moreover, DSC method also can give extremely accurate and stable results for high-frequency vibration analysis of beams and plates [37, 38]. For more advantages of DSC for numerical solutions, readers may refer to published works of Wei et al. [30–34, 37–47]. DSC method has been successfully applied in vibration analysis of structures. Wei et al. [39–41] applied DSC method to vibration analysis of beams and plates with different boundary and internal support conditions [42–47], analysis and prediction of high-frequency vibrations [37, 38], and also explored matched interface boundary (MIB) method to treat free edges of plates [48]. Civalek used DSC method to solve vibration problems of thick rectangular plates [49], isotropic and orthotropic rectangular plates [50], laminated composite plates [51], rotating truncated conical shells [52], rotating laminated cylindrical shells [53] and laminated composite conical and cylindrical shells [54, 55]. Wang et al. [56] applied DSC method to vibration analysis of beams and rectangular plates with free edges, Timoshenko beams [57], thin isotropic and anisotropic rectangular plates [58], stepped beams [59] and plates [60]. To extend the scope of DSC method, DSC-Ritz [61, 62] and DSC-element [63] method were explored for vibration analysis of thick plates, shallow shells, rectangular Mindlin plates. These studies indicate that DSC method works very well for vibration analysis of beams, plates and shells etc.

In vibration analysis of beams, plates and shells, DSC method is used to discretize the spatial derivatives and reduce the given partial differential equations into an eigenvalue problem [39–47]. However, for solutions of dynamic responses of beams or rotating shafts in time domain, the governing differential equations should be directly solved by DSC procedure [23, 27–29]. In the authors’ previous work [23], the governing differential equations of a rotating ship shaft under axial force have been solved by using DSC method. In that work, effects of number of blades in the propeller on parametric instability are focused on, and the exciting frequency of axial force is related to spinning speed, which is a very special case. For the most common cases, the exciting frequency of periodic axial force has no any relation with spinning speed such as those forces in the works of [1–4, 6–9, 12, 13]. Moreover, only external viscous damping is considered in the authors’ previous work [23] briefly. In fact, damping of rotating shafts includes external damping and internal material damping. Considering effects of internal material damping, the corresponding term relating to internal material damping is added to the governing differential equations of shafts, which complicate the equations. And DSC procedure for solving the problem considered here will be more complex than ever before.

This study extends the previous effort of the authors further to investigate parametric instability of rotating shafts under periodically varying axial forces by using DSC method which is completely different from theoretical methods of Floquet and Bolotin. A DSC procedure is given to solve the governing differential equations of a rotating Euler shaft under a periodic axial force. Influence of external viscous damping and internal material damping is also considered, and Voigt–Kelvin model [16] is used to describe the behavior of internal material damping. Parametric instability regions are presented to demonstrate the effects of spinning speed on rotating shafts without damping and with damping, respectively. Numerical results obtained by using DSC procedure are compared to those by using theoretical methods.

2 Theoretical modal and algorithm

2.1 Equations of motion for rotating shafts

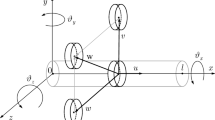
Figure 1 illustrates a uniform simply supported Euler shaft rotating about its longitudinal axis with a constant spinning speed Ω, subjected to a periodic axial force P(t) = P D cos(θt), and (XYZ) is the fixed coordinate system while (xyz) is the coordinate system attached to the shaft with the x-axis aligned with the X-axis. Using Euler–Bernoulli beam theory, effect of rotatory inertia is neglected. The equations [9, 16] of motion can be written as

$$\begin{aligned} & m\frac{{\partial^{2} u_{y} }}{{\partial t^{2} }} - 2m\varOmega \frac{{\partial u_{z} }}{\partial t} - m\varOmega^{2} u_{y} + C\frac{{\partial u_{y} }}{\partial t} + EI\alpha_{i} \frac{{\partial^{5} u_{y} }}{{\partial t\partial x^{4} }} + EI\frac{{\partial^{4} u_{y} }}{{\partial x^{4} }} + P(t)\frac{{\partial^{2} u_{y} }}{{\partial x^{2} }} = 0 \\ & m\frac{{\partial^{2} u_{z} }}{{\partial t^{2} }} + 2m\varOmega \frac{{\partial u_{y} }}{\partial t} - m\varOmega^{2} u_{z} + C\frac{{\partial u_{z} }}{\partial t} + EI\alpha_{i} \frac{{\partial^{5} u_{z} }}{{\partial t\partial x^{4} }} + EI\frac{{\partial^{4} u_{z} }}{{\partial x^{4} }} + P(t)\frac{{\partial^{2} u_{z} }}{{\partial x^{2} }} = 0 \\ \end{aligned}$$
(1)

where u v , u z are the transverse displacements in the y- and z-direction, m, C, E, I, α i and t are the mass per unit length, the viscous damping coefficient, Young’s modulus, the area moment of inertia, retardation time [16] and time, respectively. P D and θ are the amplitude and circular frequency of the periodic axial force.

Fig. 1
figure 1

The rotating shaft and coordinate systems

Full size image

For simplicity, introducing following dimensionless quantities:

$$X = \frac{x}{l}\quad U_{Y} = \frac{{u_{y} }}{l}\quad U_{Z} = \frac{{u_{z} }}{l}\quad \alpha = \frac{{P_{D} }}{{P_{cr} }}\quad \overline{\varOmega } = \frac{\varOmega }{\omega }\quad \varTheta = \frac{\theta }{\omega }\quad \zeta_{e} = \frac{C}{2m\omega }\quad \zeta_{i} = \frac{{\alpha_{i} }}{2\omega }\quad \tau = \omega t\quad U = \sqrt {U_{Y}^{2} + U_{Y}^{2} }$$

where l is the length, P cr  = π 2 EI/l 2 is the buckling force of a non-spinning simply supported shaft, \(\omega =\uppi^{2} \sqrt {EI/ml^{4} }\) is the natural bending frequency of non-spinning shaft for the first mode, \(\overline{\varOmega }\) is dimensionless spinning speed, \(\varTheta\) is dimensionless exciting frequency, \(\zeta_{e}\) is viscous damping ratio, \(\zeta_{i}\) is reduced retardation time, U is the composition of U Y and U Z .

Then, Eq. (1) can be written as

$$\begin{aligned} & \frac{{\partial^{2} U_{Y} }}{{\partial \tau^{2} }} - 2\overline{\varOmega } \frac{{\partial U_{Z} }}{\partial \tau } - \overline{\varOmega }^{2} U_{Y} + 2\zeta_{e} \frac{{\partial U_{Y} }}{\partial \tau } + \frac{{2\zeta_{i} }}{{\uppi^{4} }}\frac{{\partial^{5} U_{Y} }}{{\partial \tau \partial X^{4} }} + \frac{1}{{\uppi^{4} }}\frac{{\partial^{4} U_{Y} }}{{\partial X^{4} }} + \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\uppi^{2} }}\frac{{\partial^{2} U_{Y} }}{{\partial \tau^{2} }} = 0 \\ & \frac{{\partial^{2} U_{Z} }}{{\partial \tau^{2} }} + 2\overline{\varOmega } \frac{{\partial U_{Y} }}{\partial \tau } - \overline{\varOmega }^{2} U_{Z} + 2\zeta_{e} \frac{{\partial U_{Z} }}{\partial \tau } + \frac{{2\zeta_{i} }}{{\uppi^{4} }}\frac{{\partial^{5} U_{Z} }}{{\partial \tau \partial X^{4} }} + \frac{1}{{\uppi^{4} }}\frac{{\partial^{4} U_{Z} }}{{\partial X^{4} }} + \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\uppi^{2} }}\frac{{\partial^{2} U_{Z} }}{{\partial \tau^{2} }} = 0 \\ \end{aligned}$$
(2)

And Eq. (2) can be changed into

$$\begin{aligned} & \frac{{\partial^{2} U_{Y} }}{{\partial \tau^{2} }} = 2\overline{\varOmega } \frac{{\partial U_{Z} }}{\partial \tau } + \overline{\varOmega }^{2} U_{Y} - 2\mathop \zeta \nolimits_{e} \frac{{\partial U_{Y} }}{\partial \tau } - \frac{{2\zeta_{i} }}{{\uppi^{4} }}\frac{{\partial^{5} U_{Y} }}{{\partial \tau \partial X^{4} }} - \frac{1}{{\uppi^{4} }}\frac{{\partial^{4} U_{Y} }}{{\partial X^{4} }} - \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\uppi^{2} }}\frac{{\partial^{2} U_{Y} }}{{\partial \tau^{2} }} \\ & \frac{{\partial^{2} U_{Z} }}{{\partial \tau^{2} }} = - 2\overline{\varOmega } \frac{{\partial U_{Y} }}{\partial \tau } + \overline{\varOmega }^{2} U_{Z} - 2\zeta_{e} \frac{{\partial U_{Z} }}{\partial \tau } - \frac{{2\zeta_{i} }}{{\uppi^{4} }}\frac{{\partial^{5} U_{Z} }}{{\partial \tau \partial X^{4} }} - \frac{1}{{\uppi^{4} }}\frac{{\partial^{4} U_{Z} }}{{\partial X^{4} }} - \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\uppi^{2} }}\frac{{\partial^{2} U_{Z} }}{{\partial \tau^{2} }} \\ \end{aligned}$$
(3)

The boundary conditions are

$$U(0,\tau ) = U(1,\tau ) = 0,\quad \frac{{\partial^{2} U(0,\tau )}}{{\partial X^{2} }} = \frac{{\partial^{2} U(1,\tau )}}{{\partial X^{2} }} = 0$$
(4)

2.2 Discrete singular convolution and procedure

In the DSC algorithm originally introduced by Wei [30], the function f(x) and its derivatives with respect to the x coordinate at a grid point x i are approximated by a linear sum of discrete values f(x k ) in a narrow bandwidth [x − x W , x + x W ]. This expression can be written as follows [40, 53]

$$\left. {\frac{{d^{n} f(x)}}{{dx^{n} }}} \right|_{{x = x_{i} }} = f^{(n)} (x) \approx \sum\limits_{k = - W}^{W} {\delta_{{\Delta ,{\kern 1pt} \sigma }}^{(n)} } (x_{i} - x_{k} )f(x_{k} )\quad \left( {n = 0,1,2, \ldots } \right)$$
(5)

where superscript(n) denotes the nth-order derivative with respect to x and 2 W + 1 is the computational bandwidth which is centered around x and is usually smaller than the whole computational domain. δ is a singular kernel. The DSC algorithm can be realized by using many approximation kernels [45, 46]. Recently, an efficient kernel—regularized Shannon kernel (RSK) [37–40, 42, 43] was proposed to solve applied mechanic problems. The RSK is given as [39]

$$\delta_{{\Delta ,{\kern 1pt} \sigma }} (x - x_{k} ) = \frac{{\sin [(\uppi/\Delta )(x - x_{k} )]}}{{(\uppi/\Delta )(x - x_{k} )}}\exp \left[ { - \frac{{(x - x_{k} )^{2} }}{{2\sigma^{2} }}} \right],\quad \sigma > 0$$
(6)

where Δ is the grid spacing. The parameter σ determines the width of the Gaussian envelope and often varies in association with the grid spacing, σ = rΔ. Here r is a parameter chosen in computation. It is also known that the truncation error is very small due to the use of the Gaussian regularizer. When the regularized Shannon’s kernel is used, the detailed expressions for \(\delta_{\Delta ,\sigma }^{(n)}\) can be easily obtained. Readers may refer to some published references [40, 42, 44].

In solution procedure for governing differential equations of rotating shafts, the DSC discrete scheme Eq. (5) is utilized for the spatial discretization and the fourth-order Runge–Kutta (RK4) scheme is used for the time discretization [23, 27–29, 64]. The computational domain of coordinate X is [0,1], and the coordinate X is equally spaced, the grid sizes are denoted by ΔX = (1 − 0)/N (N is the total number of partition grid on the computational domain [0,1]), the grid points are denoted by X j  = (j − 1)ΔX (j = 1, 2,…, N + 1). So X j  − X j+k = −kΔX. The approximate values of U Y and U Z at the grid point X j are expressed as U Y,i and U Z,i . Then, Eq. (2) can be expressed as

$$\left\{ {\begin{array}{*{20}l} {\frac{\partial }{\partial \tau }\left[ {\begin{array}{*{20}l} {U_{Y,j} } \hfill \\ {U_{Z,J} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {V_{Y,j} } \hfill \\ {V_{Z,j} } \hfill \\ \end{array} } \right]} \hfill \\ {\frac{\partial }{\partial \tau }\left[ {\begin{array}{*{20}l} {V_{Y,j} } \hfill \\ {V_{Z,J} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } {\kern 1pt} - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {V_{Y,j} } \hfill \\ {V_{Z,j} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{\pi^{4} }}\frac{\partial }{{\partial X^{4} }}\left[ {\begin{array}{*{20}l} {V_{Y,j} } \hfill \\ {V_{Z,j} } \hfill \\ \end{array} } \right] + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {U_{Y,j} } \hfill \\ {U_{Z,j} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{\pi^{4} }}\frac{{\partial^{4} }}{{\partial X^{4} }} + \left. {\frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\pi^{2} }}\frac{{\partial^{2} }}{{\partial X^{2} }}} \right)\left[ {\begin{array}{*{20}l} {U_{Y,j} } \hfill \\ {U_{Z,j} } \hfill \\ \end{array} } \right]} \right.\quad \left( {j = 1,2, \ldots ,N + 1} \right)} \hfill \\ \end{array} } \right.$$
(7)

Let

$$\begin{aligned} \{ Y_{1,j} \} & = \{ Y_{1,1} ,{\kern 1pt} Y_{1,2} , \ldots ,Y_{1,2N + 2} \} = \{ U_{{Y,1{\kern 1pt} ,}} U_{Y,2} , \ldots ,U_{Y,N + 1} ,{\kern 1pt} V_{Y,1} {\kern 1pt} ,V_{Y,2} , \ldots {\kern 1pt} ,V_{Y,N + 1} \} \\ \{ Y_{2,j} \} & = \{ Y_{2,1} ,{\kern 1pt} Y_{2,2} ,{\kern 1pt} \ldots ,Y_{2,2N + 2} \} = \{ U_{Z,1,} U_{Z,2} , \ldots ,U_{Z,N + 1} ,V_{Z,1} ,V_{Z,2} , \ldots ,V_{Z,N + 1} {\kern 1pt} {\kern 1pt} \} \quad (j = 1,2, \ldots ,2N + 2) \\ \end{aligned}$$

When j = 1, 2,…, N + 1

$$F_{i,j} = Y_{i,j + N + 1} \quad (i = 1,2)$$
(8)

and when j = N + 2, N + 3,…, 2 N + 2

$$\left\{ {\left[ {\begin{array}{*{20}l} {F_{1,j} } \hfill \\ {F_{2,j} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {Y_{1,j} } \hfill \\ {Y_{2,j} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{\uppi^{4} }}\frac{\partial }{{\partial X^{4} }}\left[ {\begin{array}{*{20}l} {Y_{1,j} } \hfill \\ {Y_{2,j} } \hfill \\ \end{array} } \right] + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1} } \hfill \\ {Y_{2,j - N - 1} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{\uppi^{4} }}\frac{{\partial^{4} }}{{\partial X^{4} }} + \left. {\frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{\uppi^{2} }}\frac{{\partial^{2} }}{{\partial X^{2} }}} \right)} \right.\left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1} } \hfill \\ {Y_{2,j - N - 1} } \hfill \\ \end{array} } \right]} \right.$$
(9)

Then, we have a unified semi-discretized equation.

$$\frac{{\partial Y_{i,j} }}{\partial \tau } = F_{i,j} \quad (i = 1,2,\;j = 1,2, \ldots ,2N + 2)$$
(10)

The temporal discretization expressions of Eq. (10) by using fourth-order Runge–Kutta method are given as

$$Y_{i,j}^{n + 1} = Y_{i,j}^{n} + \Delta \tau Y_{i,j + N + 1}^{n} + \frac{{\Delta \tau^{2} }}{6}(L_{i,j + N + 1,1} + L_{i,j + N + 1,2} + L_{i,j + N + 1,3} )\quad (i = 1,2,\;j = 1,2, \ldots ,N + 1)$$
(11)
$$Y_{i,j}^{n + 1} = Y_{i,j}^{n} + \frac{\Delta \tau }{6}(L_{i,j,1} + 2L_{i,j,2} + 2L_{i,j,3} + L_{i,j,4} )\quad (i = 1,2,\;j = N + 2,N + 3, \ldots ,2N + 2)$$
(12)

where \(L_{i,j,1} = F_{i,j,1}^{n}\), \(L_{i,j,2} = F_{i,j,2}^{n}\), \(L_{i,j,3} = F_{i,j,3}^{n}\), \(L_{i,j,4} = F_{i,j,4}^{n}\)(i = 1,2, j = N + 2, N + 3, …, 2 N + 2), and here superscript n denotes time level, ∆τ is the time step, so τ = n∆τ. Using DSC discrete scheme Eq. (5), the discretization expressions for \(F_{i,j,1}^{n}\), \(F_{i,j,2}^{n}\), \(F_{i,j,3}^{n}\), \(F_{i,j,4}^{n}\) are

$$\begin{aligned} & \left\{ {\left[ {\begin{array}{*{20}l} {L_{1,j,1} } \hfill \\ {L_{2,j,1} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F_{1,j,1}^{n} } \hfill \\ {F_{2,j,1}^{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {Y_{1,j}^{n} } \hfill \\ {Y_{2,j}^{n} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)} \left[ {\begin{array}{*{20}l} {Y_{1,j + k}^{n}} \hfill \\ {Y_{2,j + k}^{n}} \hfill \\ \end{array} } \right] + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1}^{n} } \hfill \\ {Y_{2,j - N - 1}^{n} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\left. {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X) + \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{{{\pi }}^{2} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(2)} ( - k\Delta X)} } \right)\left[ {\begin{array}{*{20}l} {Y_{1,j + k - N - 1}^{n} } \hfill \\ {Y_{2,j + k - N - 1}^{n} } \hfill \\ \end{array} } \right]} } \right.} \right. \\ & \left\{ {\left[ {\begin{array}{*{20}l} {L_{1,j,2} } \hfill \\ {L_{2,j,2} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F_{1,j,2}^{n} } \hfill \\ {F_{2,j,2}^{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {Y_{1,j}^{n} + (\Delta \tau /2)L_{1,j,1} } \hfill \\ {Y_{2,j}^{n} + (\Delta \tau /2)L_{2,j,1} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)\left[ {\begin{array}{*{20}l} {Y_{1,j + k}^{n} + (\Delta \tau /2)L_{1,j + k,1} } \hfill \\ {Y_{2,j + k}^{n} + (\Delta \tau /2)L_{2,j + k,1} } \hfill \\ \end{array} } \right]} + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1}^{n} + (\Delta \tau /2)Y_{1,j}^{n} } \hfill \\ {Y_{2,j - N - 1}^{n} + (\Delta \tau /2)Y_{2,j}^{n} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)} + \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{{{\pi }}^{2} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(2)} ( - k\Delta X)} } \right)\left[ {\begin{array}{*{20}l} {Y_{1,j + k - N - 1}^{n} + (\Delta \tau /2)Y_{1,j + k}^{n} } \hfill \\ {Y_{2,j + k - N - 1}^{n} + (\Delta \tau /2)Y_{2,j + k}^{n} } \hfill \\ \end{array} } \right]} \right. \\ & \left\{ {\left[ {\begin{array}{*{20}l} {L_{1,j,3} } \hfill \\ {L_{2,j,3} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F_{1,j,3}^{n} } \hfill \\ {F_{2,j,3}^{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {Y_{1,j}^{n} + (\Delta \tau /2)L_{1,j,2} } \hfill \\ {Y_{2,j}^{n} + (\Delta \tau /2)L_{2,j,2} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)\left[ {\begin{array}{*{20}l} {Y_{1,j + k}^{n} + (\Delta \tau /2)L_{1,j + k,2} } \hfill \\ {Y_{2,j + k}^{n} + (\Delta \tau /2)L_{2,j + k,2} } \hfill \\ \end{array} } \right]} + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1}^{n} + (\Delta \tau /2)Y_{1,j}^{n} + (\Delta \tau^{2} /4)L_{1,j,1} } \hfill \\ {Y_{2,j - N - 1}^{n} + (\Delta \tau /2)Y_{2,j}^{n} + (\Delta \tau^{2} /4)L_{2,j,1} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)} + \frac{{\alpha \cos (\varTheta {\kern 1pt} \tau )}}{{{{\pi }}^{2} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(2)} ( - k\Delta X)} } \right)\left[ {\begin{array}{*{20}l} {Y_{1,j + k - N - 1}^{n} + (\Delta \tau /2)Y_{1,j + k}^{n} + (\Delta \tau^{2} /4)L_{1,j + k,1} } \hfill \\ {Y_{2,j + k - N - 1}^{n} + (\Delta \tau /2)Y_{2,j + k}^{n} + (\Delta \tau^{2} /4)L_{2,j + k,1} } \hfill \\ \end{array} } \right]} \right. \\ & \left\{ {\left[ {\begin{array}{*{20}l} {L_{1,j,4} } \hfill \\ {L_{2,j,4} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {F_{1,j,4}^{n} } \hfill \\ {F_{2,j,4}^{n} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - 2\zeta_{e} 2\overline{\varOmega } } \hfill \\ { - 2\overline{\varOmega } {\kern 1pt} - 2\zeta_{e} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {Y_{1,j}^{n} + \Delta \tau {\kern 1pt} L_{1,j,3} } \hfill \\ {Y_{2,j}^{n} + \Delta \tau {\kern 1pt} L_{2,j,3} } \hfill \\ \end{array} } \right] - \frac{{2\zeta_{i} }}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)\left[ {\begin{array}{*{20}l} {Y_{1,j + k}^{n} + \Delta \tau {\kern 1pt} L_{1,j + k,3} } \hfill \\ {Y_{2,j + k}^{n} + \Delta \tau {\kern 1pt} L_{2,j + k,3} } \hfill \\ \end{array} } \right]} + \overline{\varOmega }^{2} \left[ {\begin{array}{*{20}l} {Y_{1,j - N - 1}^{n} + \Delta \tau {\kern 1pt} Y_{1,j}^{n} + (\Delta \tau^{2} /2)L_{1,j,2} } \hfill \\ {Y_{2,j - N - 1}^{n} + \Delta \tau {\kern 1pt} Y_{2,j}^{n} + (\Delta \tau^{2} /2)L_{2,j,2} } \hfill \\ \end{array} } \right] - \left( {\frac{1}{{{{\pi }}^{4} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(4)} ( - k\Delta X)} + \frac{{\alpha {\text{cos(}}\varTheta {\kern 1pt} \tau )}}{{{{\pi }}^{ 2} }}\sum\limits_{k = - W}^{ + W} {\delta_{\Delta ,\sigma }^{(2)} ( - k\Delta X)} } \right)\left[ {\begin{array}{*{20}l} {Y_{1,j + k - N - 1}^{n} + \Delta \tau {\kern 1pt} Y_{1,j + k}^{n} + (\Delta \tau^{2} /2)L_{1,j + k,2} } \hfill \\ {Y_{2,j + k - N - 1}^{n} + \Delta \tau {\kern 1pt} Y_{2,j + k}^{n} + (\Delta \tau^{2} /2)L_{2,j + k,2} } \hfill \\ \end{array} } \right]\quad (j = N + 2,N + 3, \ldots ,2N + 2)} \right. \\ \end{aligned}$$
(13)

where [−W, +W] is the computational bandwidth. Kernels \(\delta_{\Delta ,\sigma }^{(2)}\) and \(\delta_{\Delta ,\sigma }^{(4)}\) can be easily obtained [40, 42, 44]. All of these coefficients are only dependent on grid size. When the grid point distribution is given, the coefficients can be computed once and stored for use during the computation.

The overall calculation procedure can be summarized as follows [23, 27–29]:

  1. (a)

    with the initial values for \(Y_{i,j}^{0}\) or the values of \(Y_{i,j}^{n}\) (i = 1, 2, j = 1, 2, …, 2N + 2) at previous time level n. And the values beyond the computational domain can be obtained by anti-symmetric extension according to simply supported boundary [45];

  2. (b)

    values of \(F_{i,j,1}^{n} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} F_{i,j,2}^{n} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} F_{i,j,3}^{n} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} F_{i,j,4}^{n} {\kern 1pt} {\kern 1pt}\) (i = 1, 2, j = N + 2, N + 3, …, 2N + 2) at the time level n can be obtained from Eq. (13);

  3. (c)

    substituting the values in Eq. (13) into Eqs. (11) and (12), values of \(Y_{i,j}^{n + 1}\) (i = 1,2, j = 1, 2, …,2N + 2) at new time level n + 1 can be calculated;

  4. (d)

    the computational time is advanced (i.e. τ = τ + Δτ, n = n + 1), and the whole procedure above is repeated, until calculation precision is reached.

3 Numerical results and discussions

In this section, parametric instability regions for the first mode of a rotating shaft with different spinning speeds under a periodic axial force are presented. Effects of spinning speed on instability regions of rotating shaft without damping and with external viscous and internal material damping are also discussed, respectively.

3.1 Parametric instability regions for shafts with no damping

In order to discuss effects of spinning speed on parametric instability regions for shafts with no damping, values of different spinning speeds \(\overline{\varOmega }\) are chosen as 0.3, 0.5, 0.7. The initial conditions and parameters in DSC algorithm are set: \(U_{Y} (i\Delta X,0) = 0.001\sin (i\Delta X\uppi)\), \(U_{Z} (i\Delta X,0) = 0\), \(\partial U_{Y} (i\varLambda X,0)/\partial \tau = \partial U_{Z} (i\varLambda X,0)/\partial \tau = 0\) (i = 0,1,2,…,N), N = 16, W = 15, r = 2.5, \(\Delta \tau\) = 3.0 × 10−6. For the choice of N, W and r, readers may refer to the works of [40, 42, 65].

Figure 2 shows dynamic responses of dimensionless displacements at midpoint for a rotating shaft with no damping and spinning speed \(\overline{\varOmega }\) = 0.3. It is observed that the dynamic responses for θ/2ω = 1.0 α = 0.05, θ/2ω = 0.9 α = 0.40 and θ/2ω = 1.1 α = 0.42 in Fig. 2a, c, e, are dynamically unstable; while the dynamic responses for θ/2ω = 0.9 α = 0.38 and θ/2ω = 1.1 α = 0.40 in Fig. 2b, d, are dynamically stable. The whole procedure above is repeated, then the principal parametric instability region for the first mode shown as Fig. 3 is plotted. It is found that the parametric instability region determined by DSC algorithm is coincident with that determined by Floquet’s method [18] very well. The parametric instability region is ‘V’ shape, and when the exciting frequency is twice of the natural bending frequency of non-spinning shaft (θ/2ω = 1.0), the parametric instability is the most serious.

Fig. 2
figure 2

Dynamic responses of dimensionless displacements for a rotating shaft with no damping and spinning speed \(\overline{\varOmega }\) = 0.3. a θ/2ω = 1.0 α = 0.05, b θ/2ω = 0.9 α = 0.38, c θ/2ω = 0.9 α = 0.40, d θ/2ω = 1.1 α = 0.40, e θ/2ω = 1.1 α = 0.42

Full size image
Fig. 3
figure 3

Parametric instability region for a rotating shaft with no damping and spinning speed \(\overline{\varOmega }\) = 0.3

Full size image

Similarly, parametric instability regions with different spinning speeds \(\overline{\varOmega }\) = 0.5 and 0.7 for a rotating shaft with no damping are plotted in Figs. 4 and 5. It is observed from these figures that parametric instability regions determined by DSC algorithm are in good agreement with those determined by Floquet’s method, respectively, which verifies applicability of DSC algorithm to parametric instability analysis of rotating shafts. And all the parametric instability regions are ‘V’ shapes. It is also seen that there are some errors in these figures, especially when the value of α is very large. The reasons for obvious errors are that the first approximation [18] of Floquet’s method and assumed mode method are applied to determine the boundaries of instability regions. Due to neglecting the second and higher-order terms, when the value of the axial force (α) is very large, the application of the first approximation will result in obvious error. Moreover, the assumed mode is not the real mode of the shaft subjected to a periodic axial force. The difference of assumed mode and real mode gets very obvious with large value of α, which also lead to obvious error.

Fig. 4
figure 4

As Fig. 3, but \(\overline{\varOmega }\) = 0.5, Key as for Fig. 3

Full size image
Fig. 5
figure 5

As Fig. 3, but \(\overline{\varOmega }\) = 0.7, Key as for Fig. 3

Full size image

A comparison of parametric instability regions with different spinning speeds for a rotating shaft with no damping is shown in Fig. 6, and instability regions determined by Floquet’s and Bolotin’s methods are also plotted. It is observed from Fig. 6a that parametric instability regions determined by DSC and Floquet’s methods are ‘V’ shapes, and do not vary obviously with spinning speed increasing, which means spinning speed has no significant influence on parametric instability regions of rotating shafts without damping. While seen from Fig. 6b, parametric instability regions determined by Bolotin’s method expand with spinning speed increasing [1–3, 6, 7], which contradict the present numerical results by DSC and those by Floquet’s method. From the above comparison and contrast, it may be considered that the present numerical results obtained by DSC support Floquet’s method, but disagree with Bolotin’s method. In the work of Pei [18], Bolotin’s method is considered to result in the enlargement of instability regions for rotating systems, and may be considered to be not adapted to parametric instability analysis of rotating systems. The present study further validates the viewpoint in the work of Pei by using a direct numerical simulation method, rather than a theoretical method. Especially, to the authors’ knowledge, there are no experimental reports on this problem. Therefore, this numerical study appears especially important to enhance understanding parametric instability of rotating systems.

Fig. 6
figure 6

Effects of spinning speed on parametric instability regions for a rotating shaft with no damping. a Parametric instability regions by DSC and Floquet’s methods, b parametric instability regions by DSC, Floquet’s and Bolotin’s methods

Full size image

Figure 7 shows dimensionless displacements of midpoint on the shaft under different spinning speeds with θ/2ω = 0.9 α = 0.38. It is found that the amplitudes of displacements increase with spinning speed increasing. Therefore, it may be considered that the increase of spinning speed does not affect the size of parametric instability regions of rotating shafts with no damping obviously, while results in the increase of the amplitude of displacement.

Fig. 7
figure 7

Dynamic responses of transverse displacements under different speeds with θ/2ω = 0.9 α = 0.38

Full size image

3.2 Parametric instability regions for shafts with damping

In this sub-section, effects of spinning speed on parametric instability regions of rotating shafts with external viscous damping and internal material damping are discussed. And influence of increase of damping on parametric instability regions is also analyzed.

Figure 8 shows dynamic responses of dimensionless displacements at midpoint for a rotating shaft with spinning speed \(\overline{\varOmega }\) = 0.3 and external damping \(\zeta_{e}\) = 0.05. It is seen that the dynamic responses for θ/2ω = 1.0 α = 0.20, and θ/2ω = 0.9 α = 0.42 from Figs. 8b, d, are dynamically unstable; while the dynamic responses for θ/2ω = 1.0 α = 0.18 and θ/2ω = 0.9 α = 0.40 from Fig. 8a, c, reduce with time increasing, and are dynamically stable. The whole procedure above is repeated, then the parametric instability region with \(\overline{\varOmega }\) = 0.3, \(\zeta_{e}\) = 0.05 shown as Fig. 9 is plotted. Similarly, the parametric instability regions with different spinning speeds \(\overline{\varOmega }\) = 0.5 and 0.7 for rotating shafts with damping \(\zeta_{e}\) = 0.05 are presented in Figs. 10 and 11. In order to analyze damping effects, the instability regions for rotating shafts with no damping are also plotted in Figs. 9, 10 and 11.

Fig. 8
figure 8

Dynamic responses of transverse dimensionless displacements for a rotating shaft with external damping \(\zeta_{e}\) = 0.05 and spinning speed \(\overline{\varOmega }\) = 0.3. a θ/2ω = 1.0 α = 0.18, b θ/2ω = 1.0 α = 0.20, c θ/2ω = 0.9 α = 0.40, d θ/2ω = 0.9 α = 0.42

Full size image
Fig. 9
figure 9

Dynamic instability region of a rotating shaft with \(\overline{\varOmega }\) = 0.3 \(\zeta_{e}\) = 0.05

Full size image
Fig. 10
figure 10

As Fig. 9, but \(\overline{\varOmega }\) = 0.5, Key as for Fig. 9

Full size image
Fig. 11
figure 11

As Fig. 9, but \(\overline{\varOmega }\) = 0.7, Key as for Fig. 9

Full size image

In Figs. 9, 10 and 11, it is found that the parametric instability regions determined by DSC algorithm agree well with those determined by Floquet’s method, respectively, although there are some errors. It is also observed from Figs. 9, 10 and 11 that the boundaries of parametric instability regions for a rotating shaft with external damping intersect with those for a rotating shaft with no damping in certain cases, respectively. Furthermore, this phenomenon gets more obvious with spinning speed increasing, and is quite different from that for non-spinning beams. According to conclusions in the book of Bolotin [24], the boundaries of parametric instability regions for beans with external damping are included in those for beams with no damping, and these two kinds of boundaries cannot intersect each other. To the authors’ knowledge, this phenomenon for rotating shafts has not been reported in the published works [1–3, 6, 7]. Therefore, this phenomenon is a new found, which can enhance more understanding to parametric instability of rotating systems. However, on the cause of this phenomenon, further investigation on this problem is needed.

A comparison of parametric instability regions with different spinning speeds for rotating shafts with external damping \(\zeta_{e}\) = 0.05 is shown in Fig. 12. It is found that the instability regions for rotating shafts with damping determined by DSC and Floquet’s method are enlarged as spinning speed increases, which means that the increase of spinning speed leads to enlargement of instability regions for rotating shafts with damping, but has little influence on instability regions for rotating shafts without damping seen from Fig. 6. Therefore, due to the existence of damping, spinning speed has a significant influence on parametric instability regions of rotating shafts. In addition, effect of the increase of damping on parametric instability regions is demonstrated in Fig. 13. It is seen that the increase of damping results in the reduction of parametric instability region, which improves dynamic stability of systems. And the effect is very obvious when the exciting frequency is near twice of the natural frequency.

Fig. 12
figure 12

Effects of spinning speed on parametric instability regions for a rotating shaft with external damping \(\zeta_{e}\) = 0.05

Full size image
Fig. 13
figure 13

Effects of the increase of damping on parametric instability regions with \(\overline{\varOmega }\) = 0.5

Full size image

Parametric instability regions of rotating shafts with internal material damping under different spinning speeds are plotted in Figs. 14, 15 and 16. Similarly to Figs. 9, 10 and 11, it is observed from Figs. 14, 15 and 16 that the boundaries of parametric instability regions for rotating shafts with internal damping intersect with those for rotating shafts with no damping, respectively. Moreover, this phenomenon gets more obvious as spinning speed increases. Figure 17 shows the comparison of parametric instability regions with different spinning speeds for rotating shafts with internal damping \(\zeta_{i}\) = 0.05. It is found that the instability regions are enlarged as spinning speed increases, that is to say the increase of spinning speed leads to enlargement of instability regions for rotating shafts with internal material damping. These above conclusions are similar to those for rotating shafts with external damping, which means internal material damping has the same influence on parametric instability regions of rotating shafts as external viscous damping.

Fig. 14
figure 14

Dynamic instability region of a rotating shaft with \(\overline{\varOmega }\) = 0.3 \(\zeta_{i}\) = 0.05

Full size image
Fig. 15
figure 15

As Fig. 14, but \(\overline{\varOmega }\) = 0.5, Key as for Fig. 14

Full size image
Fig. 16
figure 16

As Fig. 14, but \(\overline{\varOmega }\) = 0.7, Key as for Fig. 14

Full size image
Fig. 17
figure 17

Effects of spinning speed on parametric instability regions for a rotating shaft with internal damping \(\zeta_{i}\) = 0.05

Full size image

4 Conclusions

Parametric instability of a rotating shaft with different spinning speeds subjected to a periodic axial force has been studied by using DSC method. External viscous damping and internal material damping (Voigt–Kelvin model) are considered. Effects of spinning speed and damping on parametric instability regions for rotating shafts also have been investigated. The following conclusions may have been drawn.

  1. 1.

    For rotating shafts with no damping, parametric instability regions with different spinning speeds determined by DSC method are ‘V’ shapes, and do not vary obviously with spinning speed increasing, which agree well with those determined by Floquet’s method, but are quite different from those determined by Bolotin’s method. It may be considered that the numerical results obtained by DSC method support Floquet’s method, disagree with Bolotin’s method, and further validate the viewpoint in the work of Pei [18]. Therefore, it is strongly recommended that Bolotin’s method should not be applied to parametric instability analysis for rotating systems. Moreover, considering that experimental reports on this problem have not been published, this present numerical study appears especially important to help us to better understand parametric instability of rotating systems.

  2. 2.

    For rotating shafts with damping, the effects of external viscous damping and internal material damping on parametric instability regions are similar. Parametric instability regions under different spinning speeds determined by DSC method are enlarged significantly as spinning speed increases, that is to say the increase of spinning speed results in the enlargement of instability region, which are in good agreement with those obtained by Floquet’s method. The present results further support Floquet’s method. In addition, the increase of damping results in reduction of parametric instability region, which is helpful to improve dynamic stability of rotating systems, especially when the exciting frequency is near twice of the natural frequency.

  3. 3.

    The boundaries of parametric instability regions for a rotating shaft with damping (external and internal damping) intersect with those for a rotating shaft with no damping in certain cases, respectively. Moreover, this phenomenon gets more obvious with spinning speed increasing, which is quite different from that for non-spinning beams. This phenomenon has not been studied in the published works, which can enhance more understanding to parametric instability of rotating systems.

  4. 4.

    The effects of spinning speed on parametric instability regions are different from those in some published works. It may be considered that spinning speed has no significant influence on parametric instability regions for rotating shafts with no damping, while has a great effect on parametric instability regions for rotating shafts with damping including external and internal damping. The parametric instability regions for rotating shafts with damping are enlarged significantly as spinning speed increases. Of course, the spinning speed considered here is lower to the critical spinning speed.

  5. 5.

    Parametric instability regions are determined by judging stability of displacement responses obtained by using DSC procedure to directly solve governing differential equations of rotating shafts, which is quite different from the way by using theoretical methods. The present study further validates the viewpoint in the work of Pei by using a direct simulation method–DSC, rather than a theoretical method.

  6. 6.

    This study extends the application field of DSC method from vibration and buckling analysis of beams (boundary-value problem) to dynamic response solution and parametric instability analysis of rotating shafts (initial-value problem). The calculation procedure for solving governing differential equations of rotating shafts can also be used to solve other problems.