Estimation of Ship Heave and Pitch Under Wave Loads Using Kalman Filtering

Abstract

Ships or any marine vessels experience loads in form of dynamic wave and wind forces. These affect the motion of ships in both transverse and longitudinal direction. The motions of ship are an important parameter to be controlled as well as to be known in order to prevent any failures like capsizing or structural instability. Therefore, it is of utmost importance to predict the ship motions. This paper attempts to study the ship motions using Kalman filter (KF) considering a regular sea state. Initially, the dynamic longitudinal loads are obtained by the long-term prediction method on basis of ship motion calculations using strip theory. The measurements are then corrupted via noise to simulate practical observations. The unknown parameters like sectional wave exciting force and sectional hydro-mechanic force are then estimated using KF by analysing the problem as a 2D problem using linear Airy wave theory under assumption that the body is a rectangular floating frame. The problem can then be extended to actual load conditions and sea states.

1 Introduction

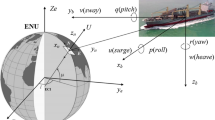
Marine vessels are subjected to various forces due to waves, winds and currents. Such extraneous forces affect the motion of ship. Ship motions play a crucial role in understanding the dynamic loading on the ship structures and components. In case of aircraft carriers and similar vessels, unstable ship motions can hamper the process of recovery and deployment of aircraft or vessel. Unstable ship motions also have an adverse effect on the passengers as well as crew of the vessel like motion sickness. The design of ships is also heavily dependent on the motions of the ship. For example, it would be difficult to have loose machinery at parts of the ship which experience the most movement. Hence, it is of utmost importance to have an estimate of ship motions in order to avoid similar circumstances. A ship model can be represented through six degrees of motions (DoF). Figure 1 shows the brief explanation of motion direction, and the other axis details are reported in Table 1.

Fig. 1

Degrees of freedom of a ship

Table 1 Notations for ship motions and descriptions

The previous works have been reported by Triantafyllou [1] in estimating the real-time ship motions using Kalman filter in order to land aircraft on a ship. Through this paper, an attempt is to effectively use the Kalman filter (KF) estimation algorithm to obtain these ship motions so as to find the forces acting on the structure of the ship. Assuming only head waves are being encountered by the ship, herein only the wave loads are considered and the wind loads are ignored. Lewis [2] had contributed towards obtaining the equations of motion. Using the strip theory, which was developed by [3] based on slender body assumption, the ship body is divided into many sections and wave loads will be found at each section of the ship. It will subsequently be integrated to find it on the structure as a whole. Strip theory has introduced coefficients of ship motions like added mass coefficients and damping coefficients. The added mass coefficients can be found out through the recent work by [4].

In this paper, attempt is made to estimate the ship motions using the extended Kalman filter [5, 6]. For this study, the sea conditions are assumed to be defined by Airy wave theory (also known as linear wave theory) and the vessel to be a slender rectangular frame. The equation of motion is obtained by using simple free-body diagrams and then modelled into a state-space equation as given in [7] as to create the foundation for KF algorithm which requires the description of states of the system. The parameters to be estimated are the ship motion, its velocity and the damping factor.

Hence, the first part of this paper will deal with forming the equations of motions for uncoupled heave and pitch when subjected to head waves. Next, the equations will be modelled as state-space equations, and the later part will be the implementation of KF to these equations so as to get the estimate of required parameters. The problem can also be extended to regular sea state in order to solve for coupled ship motions under nonlinear waves using Stokes wave theory. This data can be used to estimate the forces acting on the structure of the ship and hence giving the required feedback to the system in order to ensure that the integrity of the structure is not compromised.

2 Problem Formulation

Off late knowing apriori the structural health of the ships is important for the safety of the vessels. Ship motions play a huge roll in load carrying capacity and hence it is crucial to know these motions. In this paper, we will attempt to estimate the ship motions when the ship structure is subjected to wave loading. The estimation will be done by using Kalman filtering [8]. The problem will be handled in framework of linear wave theory and keeping parameters other than those to be estimated as constant. The damping factor is considered to be an unknown parameter, which will be estimated.

3 Equations of Ship Motion and Modelling

For obtaining the equation of motion for the ship, we will be taking 2D cross sections and analysing them section by section to obtain the equation of motion for the complete body. As we have assumed a slender cuboidal shape, each longitudinal cross section will be similar and the same applies to each transverse cross section as well. The forces acting on the each section and consequently, the whole body will be its weight, buoyant force and wave loads.

3.1 Wave Loading Under Linear Waves

Wave motion will result in loading on the body. Here, we will be assuming that wave motion follows small amplitude wave theory (or Airy wave theory). Waves will exhibit a local fluid particle acceleration [9] which will exert force on each “strip” of the body in both horizontal and vertical directions. The formula for the local fluid particle acceleration (a_z) in vertical direction is

$$ a_{z} = - agk\frac{{\sinh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\cos \left( {kx - \omega t} \right) $$

(1)

where a is the wave amplitude, g is the acceleration due to gravity, k is the wave number, ω is the wave frequency and d is the depth of water. The local fluid particle acceleration (a_x) in the horizontal direction is

$$ a_{z} = - agk\frac{{\cosh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\sin \left( {kx - \omega t} \right) $$

(2)

3.2 Uncoupled Heave Motion

Given that it is an uncoupled heave motion, we will be considering only the vertical forces in this case. The free-body diagram of the body is as below (see Fig. 2).

Fig. 2

Vertical forces on the body, (here, L, B, H and D_s are the length, breadth, height and draft of the ship, respectively)

The total vertical force F_z on the body will be

$$ F_{z} = \mathop \int \limits_{ - L/2}^{L/2} \rho_{{\text{m}}} {\text{BH}}\left( {agk} \right)\frac{{\sinh \left( {k\left( {d + D_{{\text{s}}} } \right)} \right)}}{{\cosh \left( {kd} \right)}}\cos \left( {kx - \omega t} \right){\text{d}}x $$

(3)

Hence, the exciting force term after solving Eq. (3) is

$$ F_{z} = \rho_{{\text{m}}} {\text{BH}}\left( {agk} \right)\frac{{\sinh \left( {k\left( {d + D_{{\text{s}}} } \right)} \right)}}{{\cosh \left( {kd} \right)}}*2\sin \left( \frac{kL}{2} \right)\cos \left( {\omega t} \right) $$

According to (Fig. 2), the equation of motion for uncoupled heave motion will be

$$ \begin{aligned} \left( {M + A_{33} } \right)\ddot{z} + B_{33} \dot{z} + K_{33} z & = \rho_{{\text{m}}} {\text{BH}}\left( {agk} \right) \\ & \quad \frac{{\sinh \left( {k\left( {d + D_{s} } \right)} \right)}}{{\cosh \left( {kd} \right)}}\cos \left( {kx - \omega t} \right){\text{d}}x \\ \end{aligned} $$

(4)

where $M = {\rho }_{\mathrm{m}}(\mathrm{LBH})$ is the mass of the ship, ${A}_{ij}$ is the added mass, ${B}_{ij}$ is the damping coefficient, ${K}_{ij}$ is the restoring factor where the subscript $ij$ refers to the effect of parameter on the body in $i$ direction due to motion of body in $j$ direction. For the sake of ease in calculations, the following are assumed.

$$ \begin{aligned} \rho_{{\text{m}}} {\text{BH}}\left( {agk} \right)\frac{{\sinh \left( {k\left( {d + D_{{\text{s}}} } \right)} \right)}}{{\cosh \left( {kd} \right)}} \times 2*\sin \left( \frac{kL}{2} \right) & = F_{z} \left( {M + A_{33} } \right)\ddot{z} \\ & \quad + B_{33} \dot{z} + K_{33} z \\ & = F_{3} \cos \left( {\omega t} \right) \\ \end{aligned} $$

which is reformulated after dividing Eq. (4) by $(M+{A}_{33})$

$$ \ddot{z} + C_{z} \dot{z} + K_{z} z = {\text{F}}_{{\text{z}}} \cos \left( {\omega t} \right) $$

(5)

3.3 Uncoupled Pitch Motion

Similarly, the pitch equations can be written based on the notations as explained in the Fig. 3.

Fig. 3

Forces acting in pitch motion

From Eq. (2), the moment due to vertical force can be calculated as

$$ \begin{aligned} M_{z} & = \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} \left[ {\rho_{m} B\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right)} \right] \\ & \quad \left[ {\left( {agk} \right)\frac{{\sinh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\cos \left( {kx - \omega t} \right)} \right]x \end{aligned} $$

(6)

From Eq. (1), the moment due to horizontal force can be calculated as

$$ \begin{aligned} M_{x} & = \mathop \int \limits_{x = - L/2}^{x = L/2} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} \left[ {\rho_{m} B\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right)} \right] \\ & \quad \left[ {\left( {agk} \right)\frac{{\cosh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\sin \left( {kx - \omega t} \right)} \right]z \end{aligned} $$

(7)

The equation for the pitch motion is

$$ \left( {I_{y} + A_{55} } \right)\ddot{\theta } + B_{55} \dot{\theta } + K_{55} \theta = M_{x} + M_{z} $$

Equation (8) is derived and reformulated from Eqs. (6), (7) and Appendix B

$$ \begin{aligned} \ddot{\theta} + C_{\theta} \dot{\theta} + K_{\theta} \theta & = C_{1}\theta^{2} \sin \left( {\omega t} \right) \\ & \quad + C_{2}\theta \cos \left( {\omega t} \right) + C_{3}\sin \left( {\omega t} \right) \\ \end{aligned} $$

(8)

where $C_{\theta } = \frac{{B_{55} }}{{I_{y} + A_{55} }}$ and $K_{\theta } = \frac{{K_{55} }}{{I_{y} + A_{55} }}$. The values of ${C}_{1},{C}_{2}$ and ${C}_{3}$ are given in Appendix A.

3.4 State-Space Modelling

State-space modelling is a representation of a system as a mathematical model for first-order differential equations. The state variables are the parameters whose value (or state) keeps changing with respect to time. The variables can be dependant or independent of each other, and the state-space model is the one with least number of parameters involved. The state-space representation and general equation are shown below [see Fig. 4 and Eq. (9)].

Fig. 4

State-space representation

$$ \begin{aligned} \dot{x}\left( t \right) & = A\left( t \right)x\left( t \right) + B\left( t \right)u\left( t \right) \\ y\left( t \right) & = C\left( t \right)x\left( t \right) + D\left( t \right)u\left( t \right) \\ \end{aligned} $$

(9)

Here, x is state vector, y is output vector, u is control or input vector, A is state transition matrix, B is input matrix, C is output matrix, and D is feed-forward matrix (zero if the system does not have direct feed-through). The discrete form of the same can be taken at different states being, state k + 1 at time t + ∆t and state k at time t leading to the following relation

$$ x_{k + 1} = \left[ {I + \Delta t A_{k} } \right]x_{k} + B_{k} u_{k} \Delta t $$

4 Kalman Filter

Kalman filtering is an algorithm used to estimate the state of a system at a given time based on the past measurements. KF, being an optimal filter, is a linear one and does an excellent job in minimizing the mean square estimation error. It is a recursive algorithm which obtains the estimate from a very noisy data but what makes it even more useful is that it gives an even better estimate than other filtering techniques because it also takes state estimates into account while calculating the estimate.

The algorithm involves two recursive steps, prediction and updating. The prediction step involves rough estimates which are produced by KF, with the initial prediction given by the user. In the next stage, the actual state is measured by sensors on the system. The measurement contains some amount of error and is accompanied by random noise. The next step involves updating these estimates. The concept of weighted average will be used here in which the measurement values hold more importance. After this, the state is changed and a new prediction is made for that state. This algorithm runs recursively. The KF algorithm is represented in a discrete form [10], based upon the assumption that the state of system ($k$) at a particular time t is related to its prior state $(k - 1)$ at time $t - \Delta t$ using

$$ x_{k} = A_{k} x_{k - 1} + B_{k} u_{k} + w_{k - 1} $$

Here, ${x}_{k}$ is state vector which has the information about the state of system at a given point of time t, ${A}_{k}$ is state transition matrix which gives the dependence of the next state, k, parameter on the parameters in the previous state, $k-1$. ${B}_{k}$ is input matrix which gives the relation of given inputs on the state vector, ${u}_{k}$ is input vector, which contains the inputs given to the system, and ${w}_{k}$ is process noise term

$$ z_{k} = H_{k} x_{k} + v_{k} $$

Again, ${z}_{k}$ is measurement vector which contains the measurements of quantities measured, ${H}_{k}$ is transformation matrix which relates the measured quantities to the state parameters, and ${v}_{k}$ is measurement noise, which is the random noise obtained due to errors in measuring the required quantities. As mentioned earlier, the KF works in two steps: predict and update [11]. The probability distribution functions (pdf) of the state variables play the most important role in the prediction and estimation of variables. The expected value and the variances as well as co-variances at a given state of a variables quantify the state parameters. This information is stored in the co-variance matrix ${P}_{k}$ where the diagonal elements are the variances of the state variables and the remaining elements of the matrix are the co-variances between the corresponding terms of the state vector.

$$ P_{k|k - 1} = {\varvec{E}}\left[ {\left( {x_{k} - \hat{x}_{k|k - 1} } \right)\left( {x_{k} - \hat{x}_{k|k - 1} } \right)^{{\text{T}}} } \right] $$

The KF equations for predictions constitute of the following

$$ \begin{aligned} \hat{x}_{k|k - 1} & = A_{k} \hat{x}_{k - 1|k - 1} + B_{k} u_{k} \\ P_{k|k - 1} & = A_{k} P_{k - 1|k - 1} A_{k}^{T} + Q_{k} \\ \end{aligned} $$

where $\hat{x}_{k}$ is the predicted state vector and $Q_{k}$ is the process noise co-variance matrix due to the noise from control inputs.

$$ Q_{k} = {\varvec{E}}\left[ {w_{k} w_{k}^{T} } \right] $$

The equations for the measurement update are:

$$ \begin{aligned} K_{k} & = P_{k|k - 1} H_{k}^{T} \left( {H_{k} P_{k|k - 1} H_{k}^{T} + R_{k} } \right)^{ - 1} \\ \hat{x}_{k|k - 1} & = \hat{x}_{k|k - 1} + K_{k} \left( {z_{k} - H_{k} \hat{x}_{k|k - 1} } \right) \\ P_{k|k} & = \left( {I - K_{k} H_{k} } \right)P_{k|k - 1} \\ \end{aligned} $$

where K is the Kalman gain and R is the measurement noise co-variance matrix given as

$$ R_{k} = {\varvec{E}}\left[ {v_{k} v_{k}^{T} } \right] $$

Once the measurement update is done, the state is updated as well from (k − 1) → k recursively and the prediction step is carried out.

4.1 Extended Kalman Filter

The above-mentioned algorithm is for a linear system. In our case, the Eqs. (5) and (8) are continuous and nonlinear. The nonlinearity is handled by an extension of the KF algorithm called as the extended Kalman filter (EKF). The algorithm for continuous time EKF involves the steps as shown below [12]

$$ \begin{aligned} \dot{x}\left( t \right) & = f\left( {x\left( t \right),u\left( t \right)} \right) + w\left( t \right) \\ z\left( t \right) & = h\left( {x\left( t \right)} \right) + v\left( t \right) \\ \end{aligned} $$

$f(\cdot )$ being nonlinear is expanded using Taylor series and then linearized about $\widehat{x}(t)$ as:

$$ f\left( {x\left( t \right),u\left( t \right)} \right) = f\left( {\hat{x}\left( t \right),u\left( t \right)} \right) + \frac{\partial f}{{\partial x}}\left. \right|_{{\hat{x}\left( t \right),u\left( t \right)}} \left[ {x\left( t \right) - \hat{x}\left( t \right)} \right] $$

$$ A\left( t \right) = \frac{\partial f}{{\partial x}}\left. \right|_{{\hat{x}\left( t \right),u\left( t \right)}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial f_{1} }}{{\partial x_{1} }}} & \cdots & {\frac{{\partial f_{1} }}{{\partial x_{n} }}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial f_{n} }}{{\partial x_{1} }}} & \cdots & {\frac{{\partial f_{n} }}{{\partial x_{n} }}} \\ \end{array} } \right] $$

where A(t) is known as the Jacobian matrix of $f\left( \cdot \right)$. Similarly, one may write for the measurement transformation matrix $H\left( t \right) = \frac{\partial h}{{\partial x}}\left. \right|_{{\hat{x}\left( t \right)}}$. The equations for Kalman gain are

$$ \begin{aligned} K\left( t \right) & = P\left( t \right)H^{T} \left( t \right)R^{ - 1} \left( t \right) \\ \dot{P}\left( t \right) & = F\left( t \right)P\left( t \right) + P\left( t \right)F^{T} \left( t \right) \\ & \quad + G\left( t \right)Q\left( t \right)G^{T} \left( t \right) - K\left( t \right)R\left( t \right)K^{T} \left( t \right) \\ \end{aligned} $$

This again just like KF goes on recursively and one obtain the estimated states of the system. In order to get an even more optimized solution, another extension of KF, i.e. the ensemble Kalman filter (EnKF), is used in which one run the whole KF algorithm for a given number of times to get a mean of the estimate at any given point of time and the covariance matrices are generated through the ensemble equations [13]. This helps in optimizing the algorithm when noisy quantities may result in singular matrices which may give very large estimates by producing singular matrices which do not have defined inverse matrices. Hence, EnKF proves to be a very useful tool in getting better estimates.

5 Implementing the Kalman Filter

With reference to the equation of motion we derived [see Eq. (5)], our parameters to be estimated are heave position $z$, heave velocity $\dot{z}$ and damping coefficient $C_{z}$. The equation is a continuous nonlinear equation which results in the following state space.

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}l} z \\ {\dot{z} } \\ {C_{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\dot{z} } \\ { - C_{z} \dot{z} - K_{z} z + F_{z} \cos \left( {\omega t} \right)} \\ 0 \\ \end{array} } \right] + w\left( t \right) $$

(10)

We have taken the initial values and prediction of position and velocity to be zero for both heave and pitch motions.

Fig. 5

Results for heave position, velocity and damping factor

Similarly, the state space for pitch motion [Eq. (8)] is

Fig. 6

Results for pitch angle, velocity and damping factor

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}l} \theta \\ {\dot{\theta } } \\ {C_{\theta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\dot{\theta } } \\ { - C_{\theta } \dot{\theta } - K_{\theta } \theta + C_{1} \theta^{2} \sin \left( {\omega t} \right) + C_{2} \theta \cos \left( {\omega t} \right) + C_{3} \sin \left( {\omega t} \right)} \\ 0 \\ \end{array} } \right] $$

(11)

The results obtained after implementing the EKF on the above equations (Eqs. 10 and 11) are depicted in Fig. 5 for heave motion and Fig. 6 for pitch motion.

As it can be seen in the results, the measurement follows the equation of motion which varies with some random noise. The estimated values try to converge with the true state. The convergence is dependent on Q and R matrices. A higher value of Q and a lesser value of R are highly suitable for a better convergence of the estimate. The results clearly show that the ensemble version of Kalman filter can be used as a tool to estimate the motions (translational and rotational) along with estimation of damping parameter for the ship motions.

6 Conclusion

The motion and control of ships are important for carrying out marine operations successfully. Since there are various forces acting on the ship in all directions, it becomes really necessary to have an accurate estimate of ship motions in order to have an idea about the movement of ship and forces acting on the structure of the ship. Once the time series of position and velocity is known, acceleration can be found out which can give us an estimate of forces acting on the ship. It becomes an integral part of structural health monitoring. Kalman filter does an excellent job in estimating the required quantities with respect to the noisy measurements.

In this paper, an attempt is made to estimate the position, velocity and the damping factor for the heave and pitch directions of a ship. Initially, the forces are calculated on the ship by dividing it into small cross sections throughout its length and derived from their respective equations of motion. The equations of motions were written into state-space representation as to aid the KF algorithm. Since these equations are nonlinear, one had to use the extended Kalman filter form. Thus, this paper provides a basic formulation and tutorial on how ship motion can be modelled under wave loads and estimated by Kalman filtering techniques.

7 Appendix

7.1 Appendix A

The adjoining table gives the values of quantities taken for this problem (Table 2).

Table 2 Notations and assumed values for ship dimensions and obtained values of coefficients

7.2 Appendix B

$$ \begin{aligned} M_{z} & = \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} \left[ {\rho_{{\text{m}}} B\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right)} \right] \\ & \quad \left[ {\left( {agk} \right)\frac{{\sinh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\cos \left( {kx - \omega t} \right)} \right]x \\ & = C_{p} \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} x\frac{{\sinh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}} \cos \left( {kx - \omega t} \right)\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right) \\ & = C_{p} \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} e^{kz} x\cos \left( {kx - \omega t} \right)\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right) \\ & = \frac{{C_{p} }}{k}\mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} x\cos \left( {kx - \omega t} \right)\left( {e^{{k\left( {D_{{\text{s}}} + x\theta } \right)}} - 1} \right){\text{d}}x \\ M_{x} & = \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} \left[ {\rho_{{\text{m}}} B\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right)} \right] \\ & \quad \left[ {\left( {agk} \right)\frac{{\cosh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}}\sin \left( {kx - \omega t} \right)} \right]z \\ & = C_{p} \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} z\frac{{\sinh \left( {k\left( {d + z} \right)} \right)}}{{\cosh \left( {kd} \right)}} \\ & \quad \cos \left( {kx - \omega t} \right)\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right) \\ & = C_{p} \mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \mathop \int \limits_{z = 0}^{{z = D_{{\text{s}}} + x\theta }} e^{kz} z\cos \left( {kx - \omega t} \right)\left( {{\text{d}}z} \right)\left( {{\text{d}}x} \right) \\ & = \frac{{C_{p} }}{k}\mathop \int \limits_{{x = - \frac{L}{2}}}^{{x = \frac{L}{2}}} \sin \left( {kx - \omega t} \right) \\ & \quad \left[ {1 + \left[ {k\left( {D_{{\text{s}}} + x\theta } \right) - 1} \right]e^{{k\left( {D_{{\text{s}}} + x\theta } \right)}} } \right]{\text{d}}x \\ \end{aligned} $$

Both the equations are further integrated using symbolic integration in MATLAB and then added together to give

$$ M_{{{\text{total}}}} = C_{1} \theta^{2} \sin \left( {\omega t} \right) + C_{2} \theta \cos \left( {\omega t} \right) + C_{3} {\sin}\left( {\omega t} \right) $$