1 Introduction

Ship navigation at sea is considerably dependent on the positioning signals of the global navigation satellite system (GNSS) used for ship positioning. The stability of the GNSS signal will affect the usual operation of the gyrocompass, automatic identification system, autopilot, and other equipment, influencing ship control. Although merchant ships are generally equipped with two or more sets of GNSSs, various situations, such as lightning strikes, shielding, and interference, may arise, causing a GNSS signal outage. A strapdown inertial navigation system (SINS) can provide navigation information for a vessel without using external sensors and is unbiased by external factors [1]. However, the navigation information provided by the SINS maintains high precision for only a short period of time [2]. Therefore, the SINS navigation error will accumulate over time [3]. This error can be mitigated by periodically or continuously updating the inertial system using external measurements, which can considerably improve the navigation accuracy. Thus, ship navigation researches are currently focused on algorithms of SINS/GNSS approaches and other multi-sensor-integrated navigation frame technologies.

The implementation of multi-sensor navigation is dependent on effective data fusion algorithms to manage large amounts of raw sensor measurements and achieve reasonably accurate navigational information. The Kalman filter (KF) is a popular algorithm applied to the data fusion algorithms as an optimal estimator for a linear stochastic system based on the initial values, dynamic system, measurement models, and a priori knowledge regarding noise [4]. In a recent study, a simplified integrated navigation algorithm has been designed for a carrier with low dynamic motion [5]. However, the KF is only suitable for systems that can be linearized, which is not possible in case of vessel navigation systems. Therefore, other approaches, such as EKF [6], which has been primarily applied to situations with simple principles and a low computational burden, have been widely investigated. The EKF algorithm can be optimized for various applications [7, 8]. In case of unknown noise distribution, the algorithm can be optimized using adaption algorithms in measurement and progress covariance matrices. From this viewpoint, numerous filtering algorithms, such as the Huber-based EKF and the optimal estimation theory based on maximum likelihood, have been derived [9, 10]. The EKF algorithm was implemented by linearizing a nonlinear system, and the observation model with respect to the current state is obtained using a first-order Taylor series expansion. Clearly, this approximation introduces substantial errors into EKF when the posterior mean and covariance of the transformed random variables are calculated, resulting in suboptimal performance or even the divergence of the filter [11].

The UKF algorithm was proposed in a previously conducted study [12]. The UKF algorithm tracks the states using a series of sigma points; this tracking is accomplished via the usage of novel deterministic sampling approaches to approximate the optimal gain and prediction terms in the KF framework, which is considerably easier than simulating an arbitrary nonlinear function. According to Merwe and Wan, an unscented transform can be used to approximate the nonlinear systems, achieving an error reduction of approximately 30% when compared with EKF [13]. Various scholars have investigated adaptive filtering algorithms based on UKF. For example, a refined strong tracking UKF was developed to enhance the robustness against kinematic model errors by adapting the influence of prior information [14]. Further [15], an adaptive fading UKF based on Mahalanobis distance (M-distance) was developed to improve the adaptability and robustness of the local state estimations against the process modeling errors. UKF algorithms have been applied to integrated navigation in various scenarios [16,17,18,19] and are constantly applied and improved by scholars. A previous study has [20] refrained from using the covariance upper bound to eliminate the correlation of the local states. However, UKF is prone to numerical instability, resulting in dimensional errors or divergence and limiting their applications in complex systems, including situations involving rapid dynamics or strong nonlinearity.

In a previous study [21], a nonlinear filtering method has been proposed based on cubature transformation, termed as the cubature KF (CKF). CKF can be considered as a second-order approximation to a nonlinear system. Unlike UKF, CKF uses 2n cubature points to propagate the state and a covariance matrix, resulting in a lower computation burden compared with that associated with UKF [22]. CKF and its extensions have been extensively applied in integrated navigation [4, 23, 24]. Although CKF exhibits excellent theoretical performance and is widely used in practice, inaccurate mathematical models or noise statistics will result in large state estimation errors or even divergence. Numerous scholars have improved CKF to resolve this issue. For example, a square-root-adaptive CKF has been applied in space attitude estimation [25] and an improved fifth-degree CKF algorithm has been proposed, which includes an adaptive error covariance matrix scaling algorithm to improve the accuracy under large-misalignment angles [26]. A new algorithm, termed the improved strong tracking seventh-degree spherical simple-radial CKF, was proposed [27] to address the uncertainty associated with the prior state estimate covariance.

Numerous studies have investigated the SINS/GNSS-integrated vessel navigation. Some previous studies [1, 28,29,30] have focused on the large model errors that can be attributed to the measurement and system noise, and several adaptive approaches have been designed to improve the robustness and adaptability of the ship-integrated navigation algorithms. Previous studies [31, 32] have verified the effectiveness of the KF and UKF algorithms in case of the SINS/GNSS-integrated navigation of a merchant ship, and their application to an unmanned surface vehicle was verified using an experimental ship test. These studies intended to evaluate the applicability of considerably robust algorithms to real-time problems. They considered the accuracy of the estimates and the processing time of the measurements, which should be considered during real-time estimations.

However, these studies focused on optimizing a single algorithm and neglected the effect of applying multiple filtering algorithms to vessels exhibiting varying movements in the ocean. Furthermore, these studies have generalized the integrated navigation problem for a vessel as an optimal estimation problem for a strongly nonlinear system. This study makes the following contributions to determine whether this assumption is suitable in all conditions. (1) In an artificial marine environment, the trajectory cannot be simply characterized as a straight or curved line. We design a sensor data generator based on a dynamic ship model to generate considerably realistic data to simulate various the motion and marine conditions of a ship at sea. (2) The performances of EKF, UKF, and CKF under various motion conditions, marine environments, and sensor working conditions are compared. This is performed in a more comprehensive manner when compared with previous studies.

This study is organized as follows. Section 2 presents the vessel movement model, the simulation of the sensor data, and the error model of the vessel-integrated navigation, respectively. Section 3 demonstrates the manner in which the conventional EKF, UKF, and CKF can improve the accuracy of the raw sensor simulation data. Section 4 validates the algorithms based on some simulations by considering various motion states in a marine environment. The final section presents the conclusions of this study and proposals for future work.

2 Methods

2.1 Ship separation model with sensors

2.1.1 Coordinate frames and rigid body model

Before applying filters to the vessel SINS/GNSS, appropriate systems must be established to assess the vessel’s movement for generating virtual data mimicking the motion of a real vessel. Maneuvering model group (MMG) separation modeling [33] is adopted to analyze the movement of a system having six degrees of freedom; this approach has been extensively used to study ship motion control and state estimation. The ship is generally considered to be a rigid body to determine the motion of the vessel, and the shape and internal mass distribution do not change with the movement of the vessel. After assuming an infinite water depth, we consider Newton’s laws of motion and the MMG model and ignore the mutual coupling between the heave and the remaining four degrees of freedom. The dynamic equations used for transforming one body-fixed reference to another can be given as follows:

$$\begin{gathered} \left( {m + m_{x} } \right)\left( {\dot{u} - vr + wq} \right) = X_{H} + X_{P} + X_{R} \hfill \\ \left( {m + m_{y} } \right)\left( {\dot{v} + ur - pw} \right) = Y_{H} + Y_{P} + Y_{R} \hfill \\ \left( {m + m_{z} } \right)\left( {\dot{w} - qu + vp} \right) = Z_{H} \hfill \\ \left( {I_{xx} + J_{xx} } \right)\dot{p} + \left( {I_{zz} - I_{yy} } \right)qr = K_{H} + K_{P} + K_{R} \hfill \\ \left( {I_{yy} + J_{yy} } \right)\dot{q} + \left( {I_{zz} - I_{yy} } \right)pr = M_{H} + M_{P} + M_{R} \hfill \\ \left( {I_{zz} + J_{zz} } \right)\dot{r} + \left( {I_{yy} - I_{xx} } \right)qp = N_{H} + N_{P} + N_{R} \hfill \\ \end{gathered}$$
(1)

where m is the mass of the vessel and mx, my, and mz denote the additional values observed when the vessel is sailing. Ixx, Iyy and Izz are the moments of inertia about the xb, yb, zb axes, respectively, whereas Jxx, Jyy and Jzz are the additional moments of inertia about the xb, yb and zb axes. The subscripts H, P, R represent the force experienced by the hull, the thrust of the propeller, and the hydrodynamic force of the rudder acting on the vessel, respectively. u, v, w, p, q, r represent the linear and angular velocities, expressed with respect to the body-fixed frame. We applied the previously proposed formulas for obtaining hydrodynamic parameters [33, 34] to obtain specific algorithms with respect to these parameters.

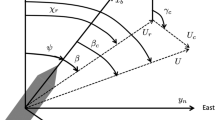
Two coordinate frames are introduced, i.e., the moving coordinate frame fixed on the vessel, denoted as the body-fixed reference, and the tangent plane on the surface of the Earth, denoted as the ENU (N-frame; East North Up) frame, where the xn axis points toward the geographic east, the yn axis points toward the north, and the zn axis points toward the terrestrial surface. Based on the rotation of two reference frames of rigid bodies, \(T_{b}^{n}\) and \(R_{b}^{n}\) are the transformation matrices of the angular velocity and linear velocity between the body-fixed and ENU frames.

$$\begin{gathered} T_{b}^{n} = \left[ {\begin{array}{*{20}c} {{\text{c}} (\varphi )} & {0} & {{\text{s}} (\varphi )} \\ {{\text{t}} \left( \theta \right){\text{s}} \left( \varphi \right)} & {1} & { - {\text{t}} (\theta ){\text{c}} (\varphi )} \\ { - {\text{s}} (\varphi ){\text{c}} \left( \theta \right)^{ - 1} } & {0} & {{\text{c}} \left( \varphi \right){\text{c}} \left( \theta \right)^{ - 1} } \\ \end{array} } \right] \hfill \\ R_{b}^{n} = \left[ \begin{gathered} {\text{c}} \left( \psi \right){\text{c}} \left( \varphi \right) - {\text{s}} \left( \theta \right){\text{s}} \left( \varphi \right){\text{s}} \left( \psi \right), \\ {\text{s}} \left( \psi \right){\text{c}} \left( \varphi \right) + {\text{s}} \left( \theta \right){\text{c}} \left( \psi \right){\text{s}} \left( \varphi \right), \\ - {\text{c}} \left( \theta \right){\text{s}} \left( \varphi \right), \\ \end{gathered} \right. \hfill \\ \left. \begin{gathered} - {\text{s}} \left( \psi \right){\text{c}} \left( \theta \right),{\text{s}} \left( \varphi \right){\text{c}} \left( \psi \right) + {\text{s}} \left( \theta \right){\text{c}} \left( \varphi \right){\text{s}} \left( \psi \right) \hfill \\ \, {\text{c}} \left( \theta \right){\text{s}} \left( \psi \right),{\text{s}} \left( \varphi \right){\text{s}} \left( \psi \right) - {\text{s}} \left( \theta \right){\text{c}} \left( \psi \right){\text{c}} \left( \varphi \right) \hfill \\ \, {\text{s}} \left( \theta \right), \, {\text{c}} \left( \theta \right){\text{s}} \left( \varphi \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(2)

Here, s(*) = sin(*), c(*) = cos(*), and t(*) = tan(*). The notation for the vessel’s kinetic and reference frames implies the kinematic relation between the linear and angular displacement frames, as shown in Fig. 1.

Fig. 1
figure 1

Reference frames and notation variables for the vessel

Full size image

2.1.2 Simulation of the vessel sensor models

Gyroscopes and accelerometers are the primary inertial sensors of SINS, and the vessel’s navigation information is obtained from the inertial measurement unit (IMU) calculations. In case of the SINS equations, i denotes the Earth-centered frame, n denotes the ENU frame, e denotes the Earth-centered fixed frame, and b denotes a body-fixed frame. fb denotes the accelerometer output, \(\omega_{ib}^{b}\) denotes the angular velocity measured by the gyroscope, \(\omega_{{x_{a} y_{a} }}^{{z_{a} }}\) (xa = i, e, n; ya = e, n, b; za = n, b) denotes the rotational rate along za with respect to xa and ya. qnb denotes the rotating quaternion between b and n. In actual applications, the vessel’s velocity, attitude, and position can be obtained by integrating the angular rate and acceleration obtained from the IMU calculations, as shown in (3). The attitude and position of the vessel in the ENU frame are obtained from the inverse trigonometric operation of qnb and \(R_{e}^{n(t)}\).

$$\left\{ {\begin{array}{*{20}l} {\dot{q}_{nb} = qw_{nb}^{b} /2, w_{nb}^{b} = w_{ib}^{b} - R_{n}^{b} \left( {w_{ie}^{n} + w_{en}^{n} } \right)} \hfill \\ {\begin{array}{*{20}l} {\dot{v}_{nb} = R_{b}^{n} f^{b} - \left( {2w_{ie}^{n} + w_{en}^{n} } \right) \times v^{n} + g^{n} } \hfill \\ {R_{en}^{t} = \left\{ {\left[ {I - \left( {x_{t} \times } \right)} \right]R_{en}^{t - 1} } \right\}, x_{t} = Fv_{nb}^{t} T } \hfill \\ \end{array} } \hfill \\ \end{array} } \right.$$
(3)

where F is the transformation matrix associated with the Earth’s radius and curvature as well as the vessel’s latitude and altitude. T is the sampling period in case of SINS.

Until now, the complete solution process has been introduced in case of SINS. The attitude, velocity, and displacement of the vehicle model calculation are substituted into the inverse calculation model for SINS to obtain the SINS simulation data generated using MMG. Finally, errors are added to the generated SINS data. This process is equivalent to the installation of a mathematical sensor on a mathematical vessel model.

The GNSS model can be simulated as:

$$\left\{ {\begin{array}{*{20}l} {pos^{\prime}_{gnss} = pos^{n} + pos_{error} } \hfill \\ {v^{\prime}_{gnss} = v^{n} + v_{error} } \hfill \\ \end{array} } \right.$$
(4)

where poserror and verror are the position and velocity errors of the GNSS, respectively. The specific schematic sensors are based on MMG.

2.2 Dynamic SINS error model

The SINS error model is an important feature that should be considered. The obtained error terms lead to the divergence of the SINS’s state after integration and must be rectified in a timely manner. Figure 2 shows that the solution equation of SINS is nonlinear; thus, the error propagation model of SINS is nonlinear. The error models can be primarily categorized as small-misalignment-angle models and large-misalignment-angle models. In a small-misalignment model, the error equation of the position is linear and can be expressed as follows:

$$\delta \dot{\Omega } = \left[ {\delta \Omega \times } \right]\left( {\omega_{ie}^{n} + \omega_{en}^{n} } \right) + \left( {\delta \omega_{ie}^{n} + \delta \omega_{en}^{n} } \right) - R_{b}^{n} \omega_{ib}^{b}$$
(5)

where δ specifies the error and Ω denotes the attitude of the vessel. The error equations with respect to velocity and position are identical in case of the small- and large-misalignment-angle models and will be introduced below.

Fig. 2
figure 2

The principle of the mathematical sensor model based on the dynamic vessel model

Full size image

For the error model of SINS with a large misalignment angle, the conversion matrix \(C_{n}^{{n^{\prime}}}\) must be introduced between the ideal navigation coordinate system n and the actual navigation coordinate system n'. This matrix is generated by the SINS error source during the rotation of the coordinate system and is expressed as follows:

$$\begin{gathered} C_{n}^{{n^{\prime}}} = \left[ \begin{gathered} {\text{c}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \psi } \right) - {\text{s}}\left( {\delta \varphi } \right){\text{s}}\left( {\delta \theta } \right){\text{s}}\left( {\delta \psi } \right), \\ - {\text{c}}\left( {\delta \theta } \right){\text{s}}\left( {\delta \psi } \right), \\ {\text{s}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \psi } \right){\text{ } + \text{ c}}\left( {\delta \varphi } \right){\text{s}}\left( {\delta \theta } \right){\text{s}}\left( {\delta \psi } \right), \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \left. \begin{gathered} {\text{c}}\left( {\delta \varphi } \right){\text{s}}\left( {\delta \psi } \right){\text{ } + \text{ s}}\left( {\delta \varphi } \right){\text{s}}\left( {\delta \theta } \right){\text{c}}\left( {\delta \psi } \right), - {\text{s}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \theta } \right) \hfill \\ {\text{ c}}\left( {\delta \theta } \right){\text{c}}\left( {\delta \psi } \right),{\text{ s}}\left( {\delta \theta } \right) \hfill \\ {\text{s}}\left( {\delta \varphi } \right){\text{s}}\left( {\delta \psi } \right) - {\text{c}} \left( {\delta \varphi } \right)s\left( {\delta \theta } \right)c\left( {\delta \psi } \right),{\text{ c}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \theta } \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(6)

By assuming that \(\omega_{{nn^{\prime}}}^{{n^{\prime}}}\) is the angular velocity of n’ relative to the n frame, the relation between \(\omega_{{nn^{\prime}}}^{{n^{\prime}}}\) and the error of the rotational angular velocity \(\delta \dot{\Omega }\) can be given as follows in (7).

$$\left\{ \begin{gathered} \omega_{{nn^{\prime}}}^{{n^{\prime}}} { = }C_{w}^{ - 1} \delta \dot{\Omega } \hfill \\ C_{w} { = }\left[ {\begin{array}{*{20}c} {{\text{c}}\left( {\delta \varphi } \right)} & {0} & {{\text{ } - \text{ s}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \theta } \right)} \\ {0} & {1} & {{\text{s}}\left( {\delta \theta } \right)} \\ {{\text{s}}\left( {\delta \varphi } \right)} & {0} & {{\text{c}}\left( {\delta \varphi } \right){\text{c}}\left( {\delta \theta } \right)} \\ \end{array} } \right] \hfill \\ \end{gathered} \right.$$
(7)

Further, the error dynamic function in ENU frame can be given as follows in (8).

$$\left\{ {\begin{array}{*{20}l} {\delta \dot{\Omega }^{n} = C_{w}^{ - 1} \left[ {\left( {I - C_{n}^{{n^{\prime}}} } \right)\hat{\omega }_{in}^{n} } \right.{\kern 1pt} + \left. {C_{n}^{{n^{\prime}}} \delta \omega_{in}^{n} - R_{b}^{{n^{\prime}}} \delta \omega_{ib}^{b} } \right]} \hfill \\ \begin{gathered} \delta \dot{V}^{n} = \left[ {I - \left( {C_{n}^{{n^{\prime}}} } \right)^{T} } \right]R_{b}^{n} \hat{f}^{b} + \left( {C_{n}^{{n^{\prime}}} } \right)^{T} R_{b}^{{n^{\prime}}} \delta f^{b} \hfill \\ \, - \left( {2\delta \omega_{ie}^{n} + \delta \omega_{en}^{n} } \right) \times \left( {\hat{V}^{n} - \delta V^{n} } \right) \hfill \\ \, - \left( {2\hat{\omega }_{ie}^{n} + \hat{\omega }_{en}^{n} } \right) \times \delta V^{n} + \delta g^{n} \hfill \\ \end{gathered} \hfill \\ \begin{gathered} \delta \dot{L} = \delta v_{N}^{n} /\left( {R_{m} + h} \right) \hfill \\ \delta \dot{\lambda } = \delta v_{E}^{n} sec\left( L \right)/\left( {R_{n} + h} \right) \hfill \\ \, + \delta Lv_{E}^{n} tan\left( L \right)sec\left( L \right)/\left( {R_{n} + h} \right) \hfill \\ \end{gathered} \hfill \\ {\delta \dot{h} = \delta v_{U}^{n} } \hfill \\ \end{array} } \right.$$
(8)

The error dynamics in ENU frame with respect to the attitude \(\delta \Omega^{n}\), velocity \(\delta V^{n}\), and position \([\delta L\delta \lambda \delta h]\) (L, λ, and h denote the latitude, longitude, and height of the vessel) are obtained in (8), where ^ specifies the estimated values, which is the sum of the error δ and the true value. Rm and Rn are the Earth’s radius for a meridian circle and the prime vertical.

Above the water surface, the latitude errors δL and δh are small in magnitude. It satisfied \(\delta h \le \hat{R}_{m} + \hat{h}\) and \(\delta h \le \hat{R}_{n} + \hat{h}\). Thus, the parameter error in (8) can be linearized as (9):

$$\left\{ {\begin{array}{*{20}l} {\delta \omega_{ie}^{n} = \left[ {\begin{array}{*{20}c} 0 \\ { - \omega_{ie} \sin \hat{L}\delta L} \\ {\omega_{ie} \cos \hat{L}\delta L} \\ \end{array} } \right]} \hfill \\ {\delta \omega_{en}^{n} = \left[ {\begin{array}{*{20}c} { - \delta v_{N}^{n} /(\hat{R}_{m} + \hat{h})} \\ {\delta \dot{\lambda }\cos \hat{L} - \lambda \cos \hat{L}\delta L} \\ {\delta \dot{\lambda }\sin \hat{L} + \lambda \cos \hat{L}\delta L} \\ \end{array} } \right]} \hfill \\ \end{array} } \right.$$
(9)

3 Nonlinear Kalman Filters

In this section, we present the nonlinear KF algorithms, including EKF, UKF, and CKF, which will be applied to estimate the states of the vessel. Then, the nonlinear filtering algorithm most suitable for the SINS/GNSS of the ship is selected by comparing the data fusion results obtained for the ship sensors.

For this problem, consider the general equations of the state and the measurement of the discrete-time nonlinear dynamical system.

$$\left\{ {\begin{array}{*{20}l} {X_{k} = \Phi_{k,k - 1} X_{k - 1} + \Gamma_{k - 1} W_{k - 1} } \hfill \\ {Z_{k} = H_{k} X_{k} + V_{k} } \hfill \\ \end{array} } \right.$$
(10)

where \(X = [\delta \dot{\Omega }^{n} ,\delta \dot{V}^{n} ,\delta L,\delta \lambda ,\delta h]\), Φk,k-1 is a nonlinear vector function determined by (8), and Γk-1 is the noise matrix of the nonlinear system. Zk = [Lgnss, λgnss, hgnss, VEgnss, VNgnss, VUgnss]. Zk, Wk and Vk are the random system and measurement noise at k steps, respectively, satisfying Wk-1 ∈ N (0, Q) and Vk-1 ∈ N (0, R).

3.1 Extended Kalman filter

EKF is one of most commonly employed nonlinear filtering approaches. In estimation theory, EKF is a nonlinear version of the KF linearized based on an estimate of the current mean and covariance. In this case, the state transition and observation models should be linear functions of the state, which is a differential function of the Jacobian matrix in the state prediction equation. The EKF applied in case of SINS/GNSS for a vessel is applied via two primary steps.

In the process of time update, the propagated state \(\hat{X}_{k,k - 1}\) and covariance matrix Pk,k−1 for instant are calculated. Moreover, the Kalman gain Kk, update state \(\hat{X}_{k}\), and covariance matrix Pk are updated in the measurement update process. Here, H() is the Jacobian matrix of the observation parameter matrix, which is determined using Xk, Zk. And Fk−1 is the Jacobian matrix of Φ(Xk −1). As shown in Fig. 3, the errors with respect to the position and velocity can be estimated and rectified. Although EKF can be easily implemented and is computationally efficient, this filter is not suitable for highly nonlinear models, particularly in case of large-misalignment-angle models and when there is excessive interference noise.

Fig. 3
figure 3

Framework of the SINS/GNSS data fusion algorithm based on EKF

Full size image

3.2 Unscented Kalman filter

EKF is renowned as the state-of-the-art tool for fusion with SINS/GNSS, which is realized by linearizing the nonlinear system using a Taylor series expansion. However, the trajectory of a ship is complex and cannot be simply described by straight lines or curves. Additionally, the dynamic model errors, abnormal errors induced by multi-sensor integration, and environmental disturbances may increase the nonlinearity of the system, which is beyond the capability of the weakly nonlinear Kalman estimation.

UKF is a modification of the conventional KF, applied to address nonlinear processes. The UKF process is fundamentally identical to the EKF process and involves two steps of time and measurement updates. The UKF applied in case of SINS/GNSS for a vessel can be presented as follows.

Here, \(\left( {\chi_{i} ,\omega_{i} } \right) \leftarrow {\text{UT}}\left( {\hat{X}_{k - 1} ,\kappa ,n,P_{{\text{k } - \text{ 1}}} } \right)\) denotes the generation of 2n + 1 sigma sampling points, n denotes the number of state variables in X, and the constant weights ωi (including variables related to ωi, such as α, β and κ) have been described in a previously conducted study [11]. After optimal estimation is performed, the system will update its cross covariance matrix \(\hat{P}_{xz|k}\) to iterate the system and the error covariance of the system will be reduced, which can be explained in Fig. 4 similar to Fig. 3 with the frame. The UKF reduces the linearization errors of EKF using a deterministic sampling approach, increasing the computational burden.

Fig. 4
figure 4

Framework of the SINS/GNSS data fusion algorithm based on UKF

Full size image

3.3 Cubature Kalman filter

CKF uses the spherical–radial cubature rule to compute the multivariate moment integrals observed in the nonlinear Bayesian filter. CKF is similar to UKF; however, its mathematical theory is more rigorous. CKF avoids the problem of high computational complexity in high-dimensional nonlinear systems, alleviates dimensional problems, and avoids the need to estimate α, β and κ with empirical values, similar to that performed in case of UKF.

The schematic of the CKF principle applied for achieving SINS/GNSS-integrated navigation in this study is presented below.

As shown in Figs. 4 and 5, the differences between CKF and UKF are primarily reflected in the following aspects. The sample points in the time update are not generated as sigma points but as cubature points denoted by Cb() in Fig. 5. These points associate with the vectors Sk-1 and Xk-1 and the length n of Xk-1. Sk-1 and Pk-1 are related as \(P_{k - 1} { = }S_{k - 1} S^{T}_{k - 1}\), \(\omega_{i} \equiv {1/2}n\), and \(\varepsilon_{i} { = }\sqrt n S_{k - 1} + X_{k - 1}\). Similarly, for achieving measurement update, \(P_{x|k,k - 1} { = }S^{\prime}_{k - 1} \left( {S^{T}_{k - 1} } \right)\) and \(\chi^{\prime}_{i} { = }\sqrt n S^{\prime}_{k,k - 1} + \hat{X}_{k,k - 1}\). In addition to the generation of the sampling points, the estimations of the error covariance and innovation covariance differ from those in case of UKF.

Fig. 5
figure 5

Framework of the SINS/GNSS data fusion algorithm based on CKF

Full size image

4 Simulations and Results

In this section, we compare the results obtained using the EKF, UKF, and CKF filters when the algorithms are applied to the SINS/GNSS-integrated vessel navigation problem. In Sect. 2.1, a SINS and GPS data generation model was proposed. Different errors, including Gaussian model errors and random bias, are induced to accurately represent a low-cost IMU system. The sensor error characteristics are presented in Table 1.

Table 1 Characteristics of the simulated sensors
Full size table

The following three simulations were performed in the test system to comprehensively assess the integrated navigation performance of different algorithms under different conditions at sea. In each case, the simulation was performed 20 times and the results were averaged. Moreover, there are no obvious deviation differences between each time. It also conforms to the knowledge of ship maneuvering model [33]. Thus, the simulated ship sensor data obtained using the dynamic large surface vessel model are available.

4.1 Cyclic motion (Case 1)

Generally, cyclic motion experiments are conducted to measure the area required for turning and the velocity of turning with a large rudder angle. Here, we simulate cyclic motion without considering external disturbances, such as wind flows, to determine the optimal filtering algorithm in cases, during which frequent changes can be observed with respect to the vessel heading. The initial velocity and heading of the ship are 15.5 knots and 0°, respectively, and the model parameters are presented in Table 2.

Table 2 Parameters of the simulation ship
Full size table

The algorithms are initialized by selecting the parameters that optimally adjust the behavior of the estimators with respect to their convergence. The parameters selected to initialize the algorithms are given below.

The state vector and covariance matrix of the state are as follows: \(\hat{X}_{0} = [0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0]^{{\text{T}}}\), \(P_{0} {\text{ } = \text{ diag}}[0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0 \, 0]^{{\text{T}}}\).

The covariance matrices of the process and measurement noise are as follows:

$$Q_{k} {\text{ } = \text{ diag}}[(10^{ \circ } /{\text{h}})^{2} \, (10^{ \circ } /{\text{h}})^{2} \, (10^{ \circ } /{\text{h}})^{2} (15{{ \upmu {\rm g}}})^{2} \, (15{{ \upmu {\rm g}}})^{2} \, (15{{ \upmu {\rm g}}})^{2} \, ]^{{\text{T}}}$$
$$R_{k} {\text{ } = \text{ diag}}[(\sqrt {20{\text{ m}}} )^{2} \, (\sqrt {20{\text{ m}}} )^{2} \, (\sqrt {20{\text{ m}}} )^{2} (0.4{\text{ m}}/{\text{s}})^{2} \, (0.4{\text{ m}}/{\text{s}})^{2} \, (0.4{\text{ m}}/{\text{s}})^{2} ]^{{\text{T}}} .$$

Because pitching and heave are not important for surface vessels, our comparative analysis of the filtering algorithms excludes these states.

Figure 6 shows the performance of three filtering algorithms in case of normal cyclic motion and boxplots of the residuals. The trajectories show that the algorithms behave similarly. During the initial stage of cyclic motion, the ship inclines and is displaced in the direction opposite to the rotation. Further, UKF and CKF deviate with respect to the position estimation. However, in the steady stage, the performances of the three algorithms are almost identical, although the UKF and CKF trajectories are closer to the actual trajectory (red). With respect to the attitude, UKF and CKF perform better during rolling estimation. At 406 s, there was an obvious error in UKF estimation, corresponding to a change in the heading from − 180° to 180° at 460 s. This result indicates that UKF is sensitive to the angle changes in integrated navigation, similar to that demonstrated in the following simulation. In case of velocity estimation, EKF is obviously inferior to the remaining two filtering algorithms, exhibiting a large oscillation.

Fig. 6
figure 6

The performances of the three filtering algorithms in cyclic motion and boxplots of the residuals

Full size image

The boxplots present our statistical analyses of the data. For example, the median is represented by a central tendency line, and the quartiles (bottom and top lines of the boxes) show the data dispersion, data distribution, and presence of outliers (atypical values). The interquartile interval, containing 50% of the residual values estimated using UKF, becomes narrow in the presence of few outliers, indicating the higher accuracy of UKF and CKF compared with EKF.

The results are quantitatively presented in Table 3, where the outliers beyond 3σ are excluded. Notably, the dispersion center of the heading for all estimators is approximately zero (ideal for residues), except for the displacement; however, the mean values of 3.95, 2.843, and 2.971 m for the EKF, UKF, and UKF displacement errors are small, indicating that the three filtering algorithms can restrain the divergence of SINS under cyclic motion. However, the standard deviation associated with EKF displacement is large at 10.734 and 8.9756 m, which is not ideal. UKF and CKF are superior to EKF when estimating the position, velocity, and attitude, demonstrating that the system is strongly nonlinear when the ship turns. When estimating the heading, the CKF value of − 0.005° ± 0.088° is better than the UKF value of 0.0302° ± 0.075°.

Table 3 Mean and standard deviation for integrated navigation based on three filtering algorithms under cyclic motion
Full size table

Figure 7 shows the efficiency of the three algorithms when subjected to inaccurate initial conditions or in case of a GPS outage. Further, results are presented for a case in which errors of 2° and 2 m/s are introduced into the initial attitude angles and velocities, respectively; EKF converges more slowly and produces more errors during attitude estimation. In case of a GPS outage, the following results are observed from 200 to 210 s. We used the \(\hat{X}_{k}\) estimated at 199 s to rectify the SINS within 10 s of the GPS signal outage and obtained the integrated navigation results shown in Fig. 7. EKF diverges during this 10 s period, demonstrating that integrated navigation based on EKF under frequent vessel course changes is strongly dependent on the GPS signal; thus, the estimated error is unreliable in case of a GPS outage. In this situation, UKF and CKF perform better than EKF, and UKF exhibits the optimal performance during heading estimation.

Fig. 7
figure 7

Results in case of inaccurate initial conditions and a GPS outage

Full size image

Figure 8 presents the influence of the estimated gyroscope and accelerometer noise on the three filtering algorithms. Here, we increased the compass and accelerometer noise terms by five times, maintaining Qk and Rk constant.

Fig. 8
figure 8

Integrated navigation results obtained when the gyroscope and accelerometer noise terms are increased by five times during cyclic motion

Full size image

The results obtained when the gyroscope noise is increased by five times are shown in Fig. 8. During the early stages of cyclic motion, the positioning accuracy of the integrated navigation based on EKF is considerably affected, and the convergence is slower than those of UKF and CKF. During the steady stage, particularly toward the end of the trajectory, the accuracy improves. However, with regard to the heading estimation, CKF exhibits the worst performance among the three methods. Further, the UKF results are sensitive to the gyroscope noise during heading and velocity estimation, as expected because the sampling weights of the sigma points are different, whereas the weights of the CKF sampling points remain identical; thus, UKF is more sensitive to the state of the sampling points.

The results obtained when the accelerometer noise is increased by five times are shown in Fig. 8. The accelerometer noise influences the integrated navigation of the three filtering methods but only slightly impacts EKF. However, in case of attitude estimation, particularly heading estimation, and velocity estimation, CKF shows strong adaptability, better than those of EKF and UKF.

4.2 Linear motion (Case 2)

Here, we verify the integrated navigation results obtained using the three filtering methods under linear motion. Without considering the influence of wind, waves, or currents, if a ship moves in a straight line, its motion is equivalent to the motion on land (not affected by the binding force of the water surface), which has been frequently reported [9, 13, 14]. Thus, we have not discussed this case here. We use the same ship model and filtering parameters employed in case 1 and apply a constant wind interference of 5 m/s at 90° and a constant current interference of 1 m/s at 180°. Further, we refer the reader to a previous study [30] for calculating the force and moment of the wind and flow. In addition, a simple course-keeping proportion–integral–derivative (PID) controller with a propeller and rudder as the input is designed for this simulation to ensure that the ship can sail along the given course under the interference of wind and current. The initial vessel parameters are VN = 9.3 knot, VE = 13 knots, and an initial heading of 43.5°.

Figure 9 shows that the results of the three filtering algorithms are similar with respect to their displacement. In case of the attitude, CKF performs slightly better than UKF, whereas UKF and CKF perform significantly better than EKF. With respect to the velocity during integrated navigation, there is no obvious difference between CKF and UKF, both of which are superior to EKF.

Fig. 9
figure 9

Performances of three filtering algorithms for linear motion and boxplots of the residuals

Full size image

Within the interquartile interval, the residuals estimated by UKF and CKF are fairly similar. With respect to displacement estimation, UKF and CKF are similar; with respect to velocity estimation, UKF and CKF show less dispersion than EKF. Notably, EKF shows a substantial zero-bias error with respect to attitude estimation, which is inferior to the UKF and CKF results.

Quantitative results are presented in Table 4, in which the outliers beyond 3σ are excluded. The dispersion center of the heading for all the three estimators is approximately zero, and better results are obtained when compared with those obtained during cyclic motion. UKF and CKF show accurate attitude estimates, with mean residuals of 0.0372° and 0.0408°, respectively. In addition, the velocity residuals are convergent, with standard deviations of 0.1030 and 0.1014 m/s toward east and 0.1399 and 0.1405 m/s toward north. Thus, the results obtained using the three filtering algorithms are similar, and the displacement residual is smaller than that for cyclic motion, with standard deviations of 2.5–3.5 m.

Table 4 Mean and standard deviation in case of integrated navigation based on three filtering algorithms under linear motion
Full size table

The results for the three filtering algorithms are divergent when initial errors of 2°/s and 2 m/s are applied with respect to the initial state in linear motion; hence, we applied initial errors of 0.5° in terms of attitude and 0.5 m/s in terms of velocity to study the filtering algorithms. As shown in Fig. 10, there is no obvious difference between the three filtering algorithms with respect to position estimation. In case of rolling estimation, UKF and CKF are less affected by the error during initial alignment, whereas all the three filtering algorithms are affected in case of heading estimation. Moreover, the velocity estimation results show that UKF and CKF are more accurate than EKF and are less affected by the errors.

Fig. 10
figure 10

Influence of inaccurate initial conditions with initial errors of 0.5° and 0.5 m/s

Full size image

In case of a GPS outage, the integrated navigation results for all the three filtering algorithms are divergent. This result can be observed when an excessive initial error is input to the SINS, and the SINS position error is strongly coupled with the attitude and velocity errors; moreover, the integrated navigation results diverge if the attitude excitation signal is insufficient to obtain an accurate SINS position solution. Similar results with errors in SINS have been reported [31].

Figure 11 shows the results obtained when the gyroscope and accelerometer noise are amplified by five times and Qk is maintained constant. When the gyroscope noise is increased, the trajectories of the three filtering algorithms are not considerably affected; EKF is closer to the real trajectory (red) in this case. UKF and CKF obtain superior attitude estimations. The three filtering algorithms are affected by the gyroscope noise during velocity estimation, resulting in errors. The results obtained with respect to the increased accelerometer noise are similar to those for the gyroscope noise. However, during velocity estimation, the three filtering algorithms exhibit error convergence, and superior results are obtained in case of UKF and CKF.

Fig. 11
figure 11

Integrated navigation results obtained when the gyroscope and accelerometer noise are increased by five times during linear motion

Full size image

The gyroscope noise has a greater effect on the integrated navigation results than the accelerometer noise. Therefore, the gyroscope noise should be accurately estimated for obtaining accurate integrated navigation results.

4.3 Wind and Current with Poor Maneuvering (Case 3)

The simulations were performed under natural conditions in this case. Because of the complexity of the model, this case was used to simulate a situation in which the ship loses control or exhibits poor maneuverability. Neither the propeller nor the rudder force can act on the ship in this case. Further, the three filtering algorithms were compared.

As shown in Fig. 12, for the position estimates, the UKF and CKF errors are significantly greater than the EKF error. Further, the interquartile intervals, containing 50% and 75% of the residual values with respect to the narrow interquartile range of the box plot, are more divergent in case of UKF and CKF. During attitude estimation, EKF performs better than UKF and CKF; however, the advantage of EKF in case of rolling estimation is not obvious according to the upper and lower quartiles. Moreover, during velocity estimation, EKF exhibits substantial variation and the velocity residual is larger than those of UKF and CKF.

Fig. 12
figure 12

Integrated navigation results demonstrating that the ship is affected by wind and current with poor maneuvering and its boxplots of the residuals

Full size image

As shown in Fig. 13, we increased the gyroscope and accelerometer noises by five times to evaluate the influence of noise on the three filtering algorithms. The position and velocity estimations of UKF and CKF exhibit substantial errors when the gyroscope error is increased. The gyroscope noise exhibits more influence when compared with that of the accelerometer noise. However, the three filtering algorithms are observed to vary only slightly in case of attitude estimation.

Fig. 13
figure 13

Integrated navigation results obtained when the gyroscope and accelerometer noise are increased by a factor of five for the condition of poor maneuvering

Full size image

In case of initial alignment errors and a GPS signal outage, the correction excitation signal is insufficient, resulting in a large simulation error. Further, integrated navigation based on the usage of three filtering algorithms failed.

To demonstrate the conclusion more evidently, we provide a comparison table between the three cases (Table 5). The accuracy of velocity estimation with EKF is poor. Hence, it is not reflected in the table. Moreover, we use A > B to indicate that the estimation accuracy of A is higher than that of B.

Table 5 Comparison between the three cases
Full size table

5 Conclusion

Compared with previous studies, the data generator used in this paper simulates ship movements under various conditions, based on which the analysis and conclusion of SINS/GNSS-integrated navigation with various disturbances and noises are more persuasive. Further, we observe that all three standard Kalman filtering methods investigated in this study limit the SINS divergence. By studying EKF in three cases, we found that EKF is more suitable in the SINS/GNSS-integrated navigation of a large surface vessel when the nonlinearity of the ship is not strong. Furthermore, it is strongly dependent on the accuracy of the external sensors. UKF and CKF exhibit the opposite performance and are more robust. In addition, UKF can better adapt to gyroscope noise when estimating the heading under both cyclic and linear motions, whereas CKF can better adapt to accelerometer noise. However, both these methods have higher requirements with respect to the intensity of the excitation signal needed for correction. Therefore, UKF and CKF are recommended for cases in which the angle and velocity are large and change frequently.