Parametric Identification of Ship’s Maneuvering Motion Based on Kalman Filter Algorithm

Abstract

In order to solve the identification problem for ship response model parameters, the method using Kalman filter algorithm was developed. Firstly, the first order linear, first order nonlinear and second order linear models were established. Then they were dispersed, and the parameters of the models were identified using Kalman filter algorithm. At last, simulation experiment was carried out. The simulation results show that the algorithm is able to identify the ship motion parameters online accurately and efficiently, and it is feasible and effective.

1 Introduction

Ship maneuverability is one of the important ship hydrodynamic performances, and is closely related to the security of the ship’s navigation. With the development of modern shipbuilding industry and shipping business, as well as people improve safety awareness,ship maneuverability is taken seriously more and more [1]. Especially the IMO (International Maritime Organization, IMO) has issued provisional standards and formal standards for ship maneuverability in 1993 and 2002 [2]. It puts forward the specific requirements to the maneuvering forecast and the maneuverability index which ships should meet during the ship design phase. And it greatly promotes the ship maneuverability prediction research.

Simulation using ship maneuvering motion mathematical model on the computer is the most practical and effective method for the prediction and assessment of maneuverability in ship design phase [3, 4]. The premise of this method is modeling the ship in mathematic, and determine the hydrodynamic derivatives of mathematical model is the key step. At present, there are two major kinds of mathematical models of ship maneuvering [5]: one is hydrodynamic model, including the integrated model and separate model; and the other is responding model, including maneuverability index K, T which may be obtained by linear hydrodynamic parameters. The hydrodynamic parameters of ship maneuvering motion equations can be obtained using system identification. This method is simple and effective, and can be directly used in the analysis of the test results of the real ship [6]. This can avoid ‘the scale effect’ brought by the different Reynolds number between model and real ship [7].

Kalman filtering theory has been widely used in many fields, and has become one of the basic methods of state estimation [8, 9]. It is not only used for dynamic system state estimation, but also can be used for dynamic system parameters estimated online. Under certain assumptions, the results got by the Kalman filter algorithm are optimal.

In this paper, motion parameters of Ship response model are identified using Kalman filter algorithm online. The simulation results show that this algorithm can identify the ship motion parameters online effectively, and it has an important signification for the ship parameters identification.

2 Establishment of the Ship Motion Equations

In this paper, the classical KT equations are used as the ship mathematical model for the ship maneuverability identification research.

First-order linear response model is

$$ T\dot{r}+r=K\delta $$

(1)

First-order nonlinear response model is

$$ T\dot{r}+r+\alpha {r^3}=K\delta $$

(2)

Second-order linear response model is

$$ {T_1}{T_2}\ddot{r}+({T_1}+{T_2})\dot{r}+r=K\delta +K{T_3}\dot{\delta} $$

(3)

In the formulas, r is the angular velocity of the turn bow, $\delta$ is rudder angle, $K,T,{T_1},{T_2}$ and ${T_3}$ are maneuverability index, α is nonlinear coefficient.

Forward difference discrimination equations of formulas (1) and (2) are

$$ r(k+1)=\left(1-\frac{{\Delta t}}{T}\right)r(k)+\frac{{K\Delta t}}{T}\delta (k) $$

(4)

$$ r(k+1)=\left(1-\frac{{\Delta t}}{T}\right)r(k)+\frac{{K\Delta t}}{T}\delta (k)-\frac{{\alpha \Delta t}}{T}{r^3}(k) $$

(5)

Where, $\Delta t$ is the sampling interval.

When T ₁ T ₂   = h, T ₁   + T ₂   = g, forward difference discrimination equation of formulas (3) is

$$ r(k+1)={a_1}r(k)+{a_2}r(k-1)+{b_1}\delta (k)+{b_2}\delta (k-1) $$

(6)

In the formulas, a ₁ , a ₂ , b ₁ , and b ₂ are identification parameters. The relationship between them and ship maneuverability parameters are as follows:

$$ \left\{ \begin{array}{lll} \begin{array}{lll} h=\frac{{\Delta {t^2}}}{{1-{a_1}-{a_2}}}, & g=\frac{{(2-{a_1})\Delta t}}{{1-{a_1}-{a_2}}} \\ K= \frac{{{b_1}+{b_2}}}{{1-{a_1}-{a_2}}}, & {T_1}= \frac{{g+\sqrt{{{{g^2}-4h}}}}{2}}{} \\ \qquad{T_2}=g-{T_1}, & {T_3}= \frac{{{b_1}\Delta t}}{{b_1}+{b_2}} \end{array} \end{array} \right. $$

(7)

From Eqs. 4, 5, 6, and 7, first-order linear response model of training samples are

$$ \left\{ {\begin{array}{l} {x(k)={{{[r(k),\delta (k)]}}^T}} \\{y(k)=r(k+1)} \\\end{array}} \right.. $$

(8)

First-order nonlinear response model of training samples are

$$ \left\{ {\begin{array}{l} {x(k)={{{[r(k),\delta (k),{r^3}(k)]}}^T}} \\{y(k)=r(k+1)} \\\end{array}} \right.. $$

(9)

Second-order nonlinear response model of training samples are

$$ \left\{ {\begin{array}{l} {x(k)={{{[r(k),r(k-1),\delta (k),\delta (k-1)]}}^T}} \\{y(k)=r(k+1)} \\\end{array}} \right.. $$

(10)

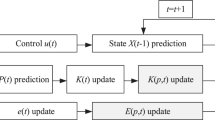
3 Parameter Identification Based on Kalman Filter Method

Assuming that the system can be identified with the following difference equation:

$$ \begin{array}{l} y(k)+{a_1}y(k-1)+\cdots +{a_n}y(k-n) \hfill \\ ={b_1}u(k-1)+\cdots +{b_m}u(k-m)+v(k) \end{array}$$

(11)

Where u(k) and y(k) are the system inputs, and the output sequence. a _i (i = 1,2,…,n) and b _j (j = 1,2,…,m) are the unknown parameters of the system. {v(k)} are zero-mean Gaussian white noise sequence, and

$$ E\{v(k){v^T}(j)\}={R_k}{\delta_k}_j $$

(12)

When using Kalman filter algorithm to estimate system parameters, first the unknown parameters of the system should be seen as unknown states, and then the system dynamic differential equation 8 is transformed into the state-space equations. Therefore,

$$ \left\{ {\begin{array}{c} {{x_1}(k)={a_1}(k)} \\ \cdots \\{{x_n}(k)={a_n}(k)} \\{{x_{n+1 }}(k)={b_1}(k)} \\ \cdots \\{{x_{n+m }}(k)={b_m}(k)} \\\end{array}} \right. $$

(13)

$$ \left\{ {\begin{array}{c} {{x_1}(k+1)={a_1}(k)+{w_1}(k)} \\\cdots \\{{x_n}(k+1)={a_n}(k)+{w_n}(k)} \\{{x_{n+1 }}(k+1)={b_1}(k)+{w_{n+1 }}(k)} \\\cdots \\{{x_{n+m }}(k+1)={b_m}(k)+{w_{n+m }}(k)} \\\end{array}} \right. $$

(14)

Where in Eq. 11, {w _i (k)} (i = 1,2,…,n + m) are the noise component of the parameters, assuming that they are zero-mean Gaussian white noise sequence, and independent with {v(k)}. The system state equation can be got:

$$ X(k+1)=\phi (k+1,k)X(k)+\Gamma (k)W(k) $$

(15)

Wherein: $\phi (k+1,k)=I$, $\Gamma (k)=I$, $W(k)$ are vector s consisting of {w _i (k)} (i = 1,2,…,n + m), and $E\{W(k){W^T}(j)\}={Q_k}{\delta_k}_j$.

When let:

$$ C(k)=[-y(k-1),\cdots -y(k-n),u(k-1)\cdots u(k-m)] $$

(16)

We can get the observation equation from the system state equation:

$$ y(k)=C(k)X(k)+v(k) $$

(17)

Getting the state space equation

$$ \left\{ \begin{array}{l} {X(k)=\phi (k,k-1)X(k-1)+\Gamma (k-1)W(k-1)} \\ {y(k)=C(k)X(k)+v(k)} \end{array} \right. $$

(18)

If the coefficient matrixes $\phi (k,k-1),\Gamma (k),C(k)$ are determined, we can directly estimate parameter by using the Kalman filter equations.

Kalman filter’s recursive algorithm is as follows:

Basing on the previous filtered value $\hat{X}(k-1|k-1)$ calculate state one-step prediction

$$ \hat{X}(k|k-1)=\phi (k,k-1)\hat{X}(k-1|k-1) $$

(19)

State estimation equation is:

$$ \hat{X}(k|k)=\hat{X}(k|k-1)+K(k)[y(k)-C(k)\hat{X}(k|k-1)] $$

(20)

Then calculating the forecast error variance matrix:

$$ \begin{array}{l} P(k|k-1) =\phi (k|k-1)P(k-1|k-1){\phi^T}(k|k-1) \\ \qquad \qquad \qquad +\Gamma (k-1)Q(k-1){\Gamma^T}(k-1) \end{array}$$

(21)

Calculating the Kalman gain:

$$ K(k)=P(k|k-1){C^T}(k){{[C(k)P(k|k-1){C^T}(k)+R(k)]}^{-1 }} $$

(22)

Calculating filtering error matrix:

$$ P(k|k)=[I-K(k)C(k)]P(k|k-1) $$

(23)

4 Simulation Experiment

The simulation is a numerical simulation of a certain type of ship, including the first-order linear, first-order nonlinear and second-order linear model. In the simulation experiments, the ship response model integrates using the 4-order Runge–Kutta method, and sampling interval is 1. The initial values of the first-order linear response model are K = 0, T = 1. The initial value of the first-order nonlinear response model is K = 0, T = 0, α = 0. The initial values of the second order linear model are K = 1, T ₁   = 100, T ₂   = 0.5, T ₃   = 0.7.

The comparison results in simulation are shown in Tables 1, 2, and 3, the courses of the individual identification parameters curve are shown in Figs. 1, 2, and 3.

Table 1 First-order linear simulation data table

Table 2 First-order nonlinear simulation data table

Table 3 Second-order nonlinear simulation data table

Fig. 1

Curves of first-order linear simulation (a) the error curve of K, (b) the error curve of T

Fig. 2

Curves of first-order nonlinear simulation (a) the error curve of K, (b) the error curve of T, (c) the error curve of α

Fig. 3

Curves of second-order linear simulation (a) the error curve of K, (b) the error curve of T1, (c) the error curve of T_2, (d) the error curve of T₃

• (a) Comparison of first-order linear simulation

• (b) Comparison of first-order nonlinear simulation

• (c) Comparison of second-order linear simulation

Figures 1, 2, and 3 show that the various parameters reach the true value in about 40 steps. When choose a suitable initial value, the algorithms has a greater converge speed. It is known that the maximum error of parameters using Kalman filter algorithm is less than 0.5 % from Tables 1, 2, and 3. And it proves that the algorithm can identify the parameters of ship response model online fast and accurately.

5 Conclusion

The method is reached to identify the parameters of ship response model online using Kalman fitter algorithm beginning in the ship response model in this paper. The simulation results show that the method can identify the parameters of ship response model fast and accurately online. And it has great significance on the simulation of ship maneuverability.