Immersed Boundary Method for High Reynolds Number Compressible Flows Around an Aircraft Configuration

Abstract

This study focuses on the immersed boundary method (IBM) for high Reynolds number compressible flow. Using the hierarchical Cartesian grid makes it difficult to resolve the thin boundary layer of high Reynolds number flow around an object because the grid is refined equally in every direction. To alleviate the requirement for the grid size of the wall, the development of a wall boundary condition using a turbulent wall function is necessary. The IBM development is based on a hierarchical Cartesian grid generator and compressible flow solver called the University of Tokyo Cartesian-grid-based automatic flow solver (UTCart). The flow solver is validated through subsonic flow over a 2D bump. The skin friction distribution is reproduced accurately by the proposed IBM. A flow around NASA common research model is solved. A flux-based method is developed based on the balance of the numerical fluxes and used for the evaluation of the aerodynamic forces. The results exhibit favorable agreement with the existing experimental data and numerical results from the body-fitted grid.

1 Introduction

The boundary layer on the surface of a transport aircraft at the cruise condition is almost fully turbulent. The Reynolds number (Re) of the flow based on the main wing chord length is on the order of 10⁷ (Wahls 2001; Green and Quest 2011). In addition, modern aircraft have high-aspect-ratio wings and long fuselages that increase their surface area. Thus, the computational costs of a direct numerical simulation or a large eddy simulation (LES) for an external flow around an aircraft are still too high for engineering purposes. Choi and Moin (2012) reported that more than 10⁸ cells are required to spatially resolve the flow around a wing whose aspect ratio is 4, even when a wall-modeled LES is used. The simulation also requires many time steps because the time scale of the unsteady turbulent vortices is several orders of magnitude smaller than that of the mean flow. Therefore, the Reynolds-averaged Navier–Stokes (RANS) simulation is widely used for external flows around an aircraft, especially for industrial application. In the derivation of the RANS equation, the temporal fluctuation component and the mean component are decomposed. The computation is carried out only through the mean component, and a steady-state solution is obtained unless strong instabilities (e.g., separated flows behind a bluff body or artificial oscillating motion) exist in the flow field. Under the cruise condition, the flow is mostly attached to the surface; thus, RANS simulations are fairly accurate. For example, in the Drag Prediction Workshops (DPWs) (2017), the RANS simulation capability for an aircraft aerodynamic prediction was widely investigated. These studies (Sclafani et al. 2010, 2013; Lee-Rausch et al. 2014; and Hashimoto et al. 2014) validated the results on body-fitted grids. The computational grids for RANS simulations are designed to resolve the viscous sublayer of the turbulent boundary layer, using high-aspect-ratio cells that conform to the wall surface. Using the immersed boundary method (IBM) on Cartesian grids for the wall boundary condition, the grids are not aligned to the wall surface (non-body-fitted grids). The cells’ aspect ratio near the wall is fixed to unity when Cartesian grid is used which is not suitable for high Reynolds number flow simulations. To resolve the viscous sublayer, many cells are required as compared with that of the typical body-fitted grid. In simple 2D problems, research (Takahashi and Imamura 2014; de Tullio et al. 2007) has proved that turbulent boundary layers can be reproduced when the viscous sublayer is sufficiently resolved. However, simulating 3D turbulent flows using such a fine grid is not realistic. Simulations of flows around high-aspect-ratio wings are quite difficult to perform owing to the uniform cell size requirement in the span-wise direction.

This chapter presents a methodology for simulating a high Reynolds number flow using RANS equation on hierarchical Cartesian grids in combination with IBM. We propose a new approach which applies the modified wall function to IBM. Additionally, a flux-based method is developed based on the balance of the numerical fluxes in order to evaluate the aerodynamic forces.

The remainder of this chapter is organized as follows. Section 2 describes the baseline flow solver using Cartesian grids and the IBM for turbulent flow simulation. A method to calculate the aerodynamic force acting on the immersed bodies is also explained. Section 3 provides numerical results, e.g., turbulent flow over a 2D bump and around an aircraft configuration. Finally, Sect. 4 summarizes the chapter.

2 Numerical Methods

2.1 The Baseline Grid Generator and Flow Solver (UTCart)

The specification of the baseline flow solver the University of Tokyo Cartesian-grid-based automatic flow solver (UTCart) is described. UTCart consists of two parts: the grid generation and the flow solver. First, the hierarchical Cartesian grid is automatically generated using tree data structures, i.e., the quadtree (2D) or oct-tree (3D). The shapes of input objects are defined by sets of line segments in 2D or by Standard Triangulated Language files (i.e., sets of triangular facet segments) in 3D. Then, binary tree structures and bounding boxes are constructed for each object to search the nearest segments. The cells intersecting the input object are treated as wall cells. In addition, the cells inside the object are classified as body cells, whereas those outside the object are classified as fluid cells. The grid distribution around the object is controlled by the following two options. The first option is to control the numbers of cells in the layers of the same cell size. Figure 16.1 illustrates the case where the minimum number of cells in each layer is set to 4. The minimum cell size near the wall (the first layer) is doubled after at least four cells of the same size, and this continues to the far-field boundary. The number of cells in each layer is controlled as necessary. The second option is the refinement box which is used to refine uniformly a certain area of the computational domain. The refinement box is specified by the minimum/maximum coordinates of the rectangular (2D) or cuboid (3D) and the uniform cell size inside. After the generation of the hierarchical Cartesian grid, the grid is partitioned using the METIS library (2019) for a parallel computation based on the message passing interface. In each divided grid domain, sleeve cells are specified for the communication between the domains.

Fig. 16.1

Layers and the refinement box of the generated grid

In the second step, a flow calculation is performed. The numerical methods in the solver are summarized in Table 16.1. The flow simulation by UTCart is based on the compressible Euler/Navier–Stokes equations in a conservation form. For high Reynolds number flows, RANS simulations are carried out using a turbulence model. The governing equations are as follows:

Table 16.1 Numerical methods for UTCart

$$\frac{{\partial \user2{Q}~}}{{\partial t}} + \frac{{\partial \left( {\user2{F}_{j} - \user2{F}_{{V,j}} } \right)}}{{\partial x_{j} }} = 0,$$

(16.1)

where $\varvec{Q} = \left[ {\rho , \rho u_{i} , \rho E} \right]^{\text{T}}$ is the vector of conservative variables. $\varvec{F}_{j} = \left[ {\rho u_{j} , \rho u_{i} u_{j} + p\delta_{ij} ,\left( {\rho E + p} \right)u_{j} } \right]^{\text{T}}$ is inviscid flux, and $\varvec{F}_{V,j} = \left[ {0,\tau_{ij} ,\tau_{jk} u_{k} - q_{j} } \right]$ denotes viscous flux (i, j, k = 1, 2 for 2D, and i, j, k = 1, 2, 3 for 3D). Here, ρ is the density, $u_{i}$ is the velocity, E is the total energy per unit mass, $\tau_{ij}$ is the viscous stress tensor, and $q_{j}$ is the heat flux. The ideal gas law for relating the thermal quantities is

$$p = \rho RT,E = \frac{p}{{\rho \left( {\gamma - 1} \right)}} + \frac{1}{2}u_{k} u_{k} ,$$

(16.2)

where T is the temperature, R is the gas constant, and γ = 1.4 is the ratio of the specific heat. The viscous stress tensor and the heat flux are approximated as

$$\tau_{ij} = 2\left( {\mu + \mu_{t} } \right)\left[ {S_{ij} - \frac{1}{3}S_{kk} \delta_{ij} } \right],\;q_{j} = - c_{p} \left( {\frac{\mu }{Pr} + \frac{{\mu_{t} }}{{Pr_{t} }}} \right)\frac{\partial T}{{\partial x_{j} }},$$

where μ is the molecular viscosity, $\mu_{t}$ is the eddy viscosity, $S_{ij} = 1/2\left( {\partial u_{j} /\partial x_{i} + \partial u_{i} /\partial x_{j} } \right)$, and $c_{p} = \gamma /\left( {\gamma - 1} \right)R$ is the specific heat at constant pressure. Prandtl number Pr is set to 0.72, and turbulent Prandtl number ${ \Pr }_{t}$ is set to 0.9. When the eddy viscosity $\mu_{t}$ is set to 0, Eq. (16.1) becomes the Navier–Stokes equations. In Euler calculations, the molecular viscosity μ is additionally set to 0. Spalart–Allmaras one-equation turbulence model (SA) (Spalart and Allmaras 1992) calculates the eddy viscosity. The version of SA used in this research is an SA-noft2 model (Turbulence Modeling Resource 2019), which neglects the $f_{t2}$ term. The equations of SA-noft2 are as follows:

$$\begin{aligned} \frac{\partial }{\partial t }\left( {\widetilde{\nu }} \right) + u_{i} \frac{\partial }{{ \partial x_{i} }}\left( {\widetilde{\nu }} \right) & = \frac{1}{ \sigma }\left[ {\frac{\partial }{{ \partial x_{i} }}\left( {\left( {\nu + \widetilde{\nu }} \right)\frac{{\partial \widetilde{\nu }}}{{ \partial x_{i} }}} \right) + c_{b2} \frac{{\partial \widetilde{\nu }}}{{ \partial x_{i} }}\frac{{\partial \widetilde{\nu }}}{{ \partial x_{i} }}} \right] + c_{b1} \widetilde{S}\widetilde{\nu } \\ & \quad - {\text{c}}_{{{\text{w}}1}} f_{w} \left( {\frac{{\widetilde{\nu }}}{ d }} \right)^{2} , \\ \end{aligned}$$

(16.3)

$$\mu_{t} = \rho \widetilde{\nu }f_{v1} ,f_{v1} = \frac{{\chi^{3} }}{{ \chi^{3} + c_{v1}^{ 3} }},\chi = \frac{{\widetilde{\nu }}}{ \nu },\widetilde{S} =\Omega + \frac{{\widetilde{\nu }}}{{ \kappa^{2} d^{2} }},\Omega = \sqrt {2W_{ij} W_{ij} } ,$$

$$W_{ij} = \frac{1}{ 2 }\left( {\frac{{\partial u_{i} }}{{ \partial x_{j} }} - \frac{{\partial u_{j} }}{{ \partial x_{i} }}} \right),f_{v2} = 1 - \frac{\chi }{{ 1 + \chi f_{v1} }},f_{w} = g\left[ {\frac{{1 + c_{w3}^{ 6} }}{{ g^{6} + c_{w3}^{ 6} }}} \right]^{{\frac{1}{6}}} ,$$

$$g = r + c_{w2} \left( {r^{6} - r} \right),r = {\min} \left[ {\frac{{\widetilde{\nu }}}{{\widetilde{S}\kappa^{2} d^{2} }},10} \right],$$

where d denotes the distance from the local point $x_{i}$ to the nearest point on the wall surface. The closure constants are

$$c_{b1} = 0.1355,\sigma = 2/3,c_{b2} = 0.622,\kappa = 0.41,$$

$$c_{w1} = c_{b1} /\kappa^{2} + \left( {1 + c_{b2} } \right)/\sigma ,c_{w2} = 0.3,c_{w3} = 2,\;{\text{and}}\;c_{v1} = 7.1.$$

The governing equations are discretized by the cell-centered finite volume method. The hierarchical Cartesian grids are treated as unstructured data structure. The inviscid flux is evaluated using the simple low-dissipation advection upstream splitting method (AUSM) scheme (Shima and Kitamura 2011). The third-order monotonic upwind scheme for conservation laws (MUSCL) is used to increase the spatial accuracy. The viscous flux is calculated using a modified second-order central difference (Wang et al. 2010). The accuracy of the convective and diffusive flux of the SA model is second order. Gradients of the primitive variables are calculated using the weighted least square method (WLSQ) (Shima et al. 2013). The matrix-free Gauss–Seidel, which is an implicit time integration method, is used for the time integration (Shima 1997). All the numerical computations are steady; thus, a local time-stepping method is introduced to accelerate convergence. The subsonic far-field boundary conditions are determined based on the method proposed by Chakravarthy and Osher (1983).

2.2 Immersed Boundary Method for UTCart

Figure 16.2 is the schematic of the grid near the wall boundary. The cells intersecting the body surface are the wall cell, and the cell completely inside the fluid domain is the fluid cell. UTCart imposes the wall boundary condition at the center between fluid cell and the wall cell [point face center (FC)]. A discrete-forcing IBM is used to determine the boundary conditions. Here, the IBM for inviscid and low Reynolds number viscous flows is explained. The IBM for high Reynolds number flow is described in the next subsection.

Fig. 16.2

Schematic of the wall boundary condition of the immersed surface

To determine the physical quantities of FC, an image point (IP) is set on the wall-normal line through FC, assuming one-dimensional variable profiles between the IP and the wall. The distance between the IP and the wall is $d_{\text{IP}}$ related to the size of the ambient cells $\Delta x$ by

$$d_{\text{IP}} = r_{\text{IP}} \Delta x,$$

(16.4)

where $r_{\text{IP}}$ is the ratio of the IP distance to the cell size on the wall, which is a constant value. The minimum value for $r_{\text{IP}}$ is $\sqrt 2$ in 2D and $\sqrt 3$ in 3D for the IPs to be located in the fluid cells. Typically, the $r_{\text{IP}}$ value is set to 2–3. An exception may occur where two walls are located close to each other. If IP is located in the wall, the wall boundary is considered to be a step-wise face, and the value at FC is determined using the value at the fluid cell including the FC to avoid a numerical problem.

In the explanation below, the quantities at the IP and FC are represented by subscripts IP and FC, respectively. The primitive variables q at the IP is linearly interpolated locally inside the cell as

$$\varvec{q}_{\text{IP}} = \varvec{q}_{P} + \left. {\frac{{\partial \varvec{q}}}{{\partial x_{j} }}} \right|_{P} \left( {x_{{j,{\text{IP}}}} - x_{j,P} } \right),$$

(16.5)

where the subscript P denotes the value at the center of the cell including the IP. Then, the primitive variables at FC are calculated using the quantities at the IP. For example, the pressure is assumed to satisfy the zero-gradient condition on the wall. The wall-normal velocity must satisfy the non-penetration condition, where the normal velocity is zero on the wall. Thus, a linear profile between the IP and the wall is assumed. The boundary condition for the tangential velocity $u_{t}$ depends on whether the wall is slip or non-slip. The numerical flux at FC is calculated using the primitive variables at FC. An upwind scheme calculates the inviscid flux. The viscous flux is calculated using only the quantities at FC assuming the adiabatic wall boundary condition for the heat flux.

During the grid partitioning for the parallel flow computation, a modification is applied to the list of sleeve cells when IBM is used (Imamura et al. 2017). As illustrated in Fig. 16.2, physical quantities at the IP are used to define the wall boundary condition at the FC which is an interface between the fluid cell and wall cell. Extra communication is required if IP and FC are located in different domains.

2.3 Wall Function for RANS

A wall boundary condition for UTCart to simulate turbulent flows is presented. The SA wall model developed by Allmaras et al. (2012) is used to evaluate the effect of the neglected molecular viscosity and construct a universal law of the wall. This wall velocity model is derived under the assumption for the law of the wall analysis: incompressible, zero pressure gradient, constant outer edge velocity, ignore advection terms, and gradient terms parallel to the wall. The shape of this function is presented in Fig. 16.3.

Fig. 16.3

SA wall model developed by Allmaras et al. (2012)

$$u^{ + } = f_{\text{SA}} \left( {y^{ + } } \right),$$

(16.6)

where $u^{ + }$ and $y^{ + }$ are the normalized tangential velocity using wall friction velocity $u_{\tau }$ and distance in the wall unit, respectively. By substituting the tangential velocity at IP in Eq. (16.6), Newton’s iteration is performed to obtain $u_{\tau }$. Then, the tangential velocity at FC is calculated as

$$u_{{t,{\text{FC}}}} = u_{\tau } f_{\text{SA}} \left( {y_{\text{FC}}^{ + } } \right).$$

(16.7)

Furthermore, the temperature at FC is calculated by the Crocco–Busemann relationship (White 2006):

$$T_{FC} = T_{\text{IP}} + \frac{{{ \Pr }^{1/3} }}{{2c_{p} }}\left( {u_{{t,{\text{IP}}}}^{2} - u_{{t,{\text{FC}}}}^{2} } \right).$$

(16.8)

Then, the density at FC is calculated as:

$$\rho_{\text{FC}} = \frac{{p_{\text{FC}} }}{{RT_{\text{FC}} }}.$$

(16.9)

The velocity profile defined by the wall function in Eq. (16.6) is a nonlinear function. However, a spatial scheme with second-order accuracy reconstructs a linear (first-order polynomial) profile within a cell. As a result, the velocity profile assumed by the wall function cannot be reproduced in the cell. To overcome this problem, the velocity profile and related flow variables should be modified. This idea originates from Capizzano (2011). The tangential velocity profile is modified using the first derivative of the SA wall model:

$$f_{\text{SA,mod}} \left( {y^{ + } } \right) = u_{\text{IP}}^{ + } + \left. {\frac{{{\text{d}}f_{\text{SA}} }}{{{\text{d}}y^{ + } }}} \right|_{\text{IP}} \left( {y_{\text{IP}}^{ + } - y^{ + } } \right).$$

(16.10)

The inviscid flux on the face is calculated using the tangential velocity $u^{ + } \left( {y_{\text{FC}}^{ + } } \right)$ obtained by Eq. (16.10). In this velocity profile (Fig. 16.4), the tangential velocity at $y^{ + } = 0$ is nonzero; thus, a virtual slip velocity is imposed on the wall. Note that the viscous flux on the face is directly calculated as $\uptau_{\text{FC}} = \rho_{\text{FC}} u_{\tau }^{2}$.

Fig. 16.4

Modification of the velocity profile

Along with the velocity profile modification, it is important to maintain the balance of the shear stress,

$$\left( {\nu + \nu_{t} } \right)\frac{{{\text{d}}u}}{{{\text{d}}y}} = \frac{{\tau_{w} }}{\rho },$$

(16.11)

where $\tau_{w}$ is the wall shear stress. Note that Eq. (16.11) is an approximate relationship in the inner layer of the boundary layer, where the convection and pressure gradients are negligible. Thus, a modification is required on the eddy viscosity profile corresponding to the modification of the velocity profile. In the modified velocity profile of Eq. (16.10), the velocity gradient $({\text{d}}u/{\text{d}}y)$ is constant. Accordingly, $\nu_{t}$ must be constant in the region between the IP and the wall to maintain the constant shear stress implied by Eq. (16.11). Here, the near-wall solution of $\widetilde{\nu }$ is retained, and only the wall-damping function $f_{v1}$ in Eq. (16.3) is modified to avoid additional complexity. To realize the constant profile of the eddy viscosity, the wall-damping function must be

$$f_{v1} \sim\frac{1}{d},$$

(16.12)

because of the near-wall solution of $\widetilde{\nu }$ is proportional to the wall distance d. For the implementation, the profile of $f_{v1}$ must be continuous. Thus, the wall-damping function is redefined as

$$f_{v1} = \left\{ {\begin{array}{*{20}c} {f_{{v1,{\text{original}}}} \left( {d \ge d_{\text{cutoff}} } \right)} \\ {f_{{v1,{\text{near{-}wall}}}} \left( {d < d_{\text{cutoff}} } \right)} \\ \end{array} } \right..$$

(16.13)

Cutoff distance $d_{\text{cutoff}}$ is equal to the distance between the IP and the wall, $d_{\text{IP}}$. The original damping function $f_{v1}$ is

$$f_{{v1,{\text{original}}}} = \frac{{\chi^{3} }}{{\chi^{3} + c_{v1}^{3} }},$$

(16.14)

and $f_{{v1,{\text{near{-}wall}}}}$ is a modified damping function near the wall defined as

$$f_{{v1,{\text{near{-}wall}}}} = r_{d} \frac{{\left( {\chi r_{d} } \right)^{3} }}{{\left( {\chi r_{d} } \right)^{3} + c_{v1}^{3} }},$$

(16.16)

where $r_{d} = d_{\text{cutoff}} /d$. Note that $f_{{v1,{\text{near{-}wall}}}}$ is a product of $r_{d}$ and the original $f_{v1}$ at $d = d_{\text{cutoff}}$. When the IP is located in the log layer of the turbulent boundary layer, $f_{{v1,{\text{near{-}wall}}}}$ is approximately equal to $r_{d}$. This function depends on the relative position of the IP in the boundary layer. For example, the shape of the function with $y_{\text{IP}}^{ + } = 50$ is illustrated in Fig. 16.5. The modified eddy viscosity profile has a kink at the cutoff point. The following technique is used to calculate the viscous fluxes on the faces. Here, face lr is considered, which is the face between cells l and r. The eddy viscosity on the face is required to calculate the viscous flux on faces l, r, and $\nu_{t,lr}$. However, the simple average of $\nu_{t,l}$ and $\nu_{t,r}$ is different from the true value of the profile if the kink exists between cells l and r. This may cause numerical errors. Thus, the following procedure is adopted to eliminate the effect of the kink. The averages of left and right cells for $\widetilde{\nu }$, $\nu$ and d are calculated as follows:

Fig. 16.5

Modification of the eddy viscosity profile

$$\begin{aligned} & \widetilde{\nu }_{lr} = r_{lr} \widetilde{\nu }_{l} + \left( {1 - r_{lr} } \right)\widetilde{\nu }_{r} , \\ & \nu_{lr} = r_{lr} \nu_{l} + \left( {1 - r_{lr} } \right)\nu_{r} , \\ & d_{lr} = r_{lr} d_{l} + \left( {1 - r_{lr} } \right)d_{r} , \\ \end{aligned}$$

(16.17)

where $r_{lr}$ is the ratio of the cell sizes:

$$r_{lr} = \frac{{\Delta x_{r} }}{{\Delta x_{l} + \Delta x_{r} }}.$$

(16.18)

The eddy viscosity is calculated by those quantities:

$$\left. {\nu_{t} } \right|_{lr} = \widetilde{\nu }_{lr} f_{v1} \left( {\chi_{lr} ,d_{lr} } \right),$$

(16.19)

where $\chi_{lr} = \widetilde{\nu }_{lr} /\nu_{lr}$. The $\nu$ profile is nearly linear near the wall, and the numerical error is smaller than the simple average of $\nu_{t}$.

Corresponding to the modification of the velocity and eddy viscosity profiles, the thermal boundary condition has now been reconsidered. The Crocco–Busemann relationship in Eq. (16.8) is differentiated in terms of wall-normal coordinate yields:

$$\frac{{{\text{d}}T}}{{{\text{d}}y}} = \frac{{{ \Pr }^{1/3} }}{{c_{p} }}u_{t} \frac{{{\text{d}}u_{t} }}{{{\text{d}}y}}.$$

(16.20)

In the modified velocity profile in Eq. (16.10), the normal gradient of the tangent velocity is constant below the IP. Here, $u_{\tau }$ is assumed to be nearly constant because the velocity gradient in the log layer is small. Thus, the temperature gradient is nearly constant below the IP, and the temperature profile becomes a linear profile:

$$T_{\text{FC}} = T_{\text{IP}} - \frac{{{\text{d}}T}}{{{\text{d}}y}}_{\text{IP}} \left( {y_{\text{IP}} - y_{\text{FC}} } \right),$$

(16.21)

where the temperature gradient at IP is calculated in Eq. (16.20).

The proposed method is thoroughly tested through the simulations of the flat-plate turbulent boundary layer. Further details are discussed by Tamaki et al. (2017) and Tamaki (2018).

2.4 Force Calculation Method

To compute the aerodynamic force, the polygon-based method (Nonomura and Onishi 2017) which integrates over the input CAD surface is often used. In this method, the physical quantities (e.g., pressure) on the Cartesian grid are interpolated and/or extrapolated onto the CAD surface before the integration. This method is the same as the force integration method of conventional body-fitted grids, except for the interpolation and/or extrapolation. However, arbitrariness exists in the interpolation and/or extrapolation formula; thus, the computed forces may contain additional numerical errors. In addition, the integration accuracy depends on the resolution of the CAD surface. Therefore, the calculation of force acting on the immersed body based on the flow solution needs to be explored.

To remove the uncertainties related to the previous discussion, new force integration is developed based on the balance of the numerical flux. This idea is similar to the far-field methods (van Dam 1999; Kusunose and Crowder 2002); however, the integration surface is the step-wise cell boundary between the fluid cell and the wall cell. Unlike the far-field method, the pressure and viscous component of the force are calculated using this new method because the integration surface is near the object surface. The force can also be decomposed when multiple objects exist in the computational domain.

As illustrated in Fig. 16.6, an immersed body $\varGamma_{S}$ in Cartesian grids is considered. The step-wise cell boundary near the wall and the far-field boundary are named $\varGamma_{G}$ and $\varGamma_{F}$, respectively. Note that the normal vectors of $\varGamma_{G}$ and $\varGamma_{F}$ are pointing outside the computational domain. Furthermore, the domain between $\varGamma_{G}$ and $\varGamma_{F}$ and that between $\varGamma_{G}$ and $\varGamma_{S}$ are named $V_{1}$ and $V_{2}$, respectively. To perform component-wise integration of the aerodynamic force, the integral over $\varGamma_{F}$ is replaced by that over $\varGamma_{G}$. The momentum equation is integrated over domain $V_{1}$ assuming neither mass source nor body force exists in the domain. The near-field integration formula for the aerodynamic force is described as follows:

Fig. 16.6

Description of the computational domain and the boundaries

$$F_{i} = \int_{{\varGamma_{G} }} {\left\{ {\rho \left( {u_{i} - U_{\infty ,i} } \right)u_{j} + \left( {p - p_{\infty } } \right)\delta_{ij} - \tau_{ij} } \right\}} n_{j} {\text{d}}S.$$

(16.22)

Equation (16.22) is discretized on the faces that compose $\varGamma_{G}$:

$$F_{i} = \sum\limits_{{{\text{face}} \in \varGamma_{G} }} {\left[ {\left\langle {\left( {\rho u_{i} u_{j} + p\delta_{ij} } \right)\hat{n}_{j} } \right\rangle - \left\langle {\rho u_{j} \hat{n}_{j} } \right\rangle U_{\infty ,i} - p_{\infty } \delta_{ij} \hat{n}_{j} - \left\langle {\tau_{ij} \hat{n}_{j} } \right\rangle } \right]_{\text{face}} } ,$$

(16.23)

where $\left\langle {\left( {\rho u_{i} u_{j} + p\delta_{ij} } \right)\hat{n}_{j} } \right\rangle$ are the momentum components of the inviscid flux, $\left\langle {\rho u_{j} \hat{n}_{j} } \right\rangle$ is the mass component of inviscid flux, and $\left\langle {\tau_{ij} \hat{n}_{j} } \right\rangle$ is the momentum components of the viscous flux. Note that $\hat{n}_{j}$ is the normal vector component of the faces on $\varGamma_{G}$. Here, the integral of the viscous flux is considered to be the viscous component of the aerodynamic force, and the remainder is considered to be pressure component. The aerodynamic forces acting on each part of the immersed body (or each object) can be decomposed when the faces are classified with respect to the nearest part or object. Thus, it is suggested that one uses the same inviscid and viscous numerical fluxes as those in the flow calculation of the flux components in Eq. (16.23). The evaluated force directly reflects the accuracy of the flux used in the flow calculation, and no additional numerical error is produced.

3 Numerical Results

3.1 Subsonic Flow Over a 2D Bump

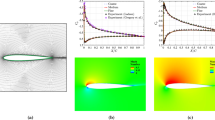
The first test case is the subsonic flow over a 2D bump defined in the NASA Turbulence Model Resource (TMR) (2019). The effect of the stream-wise pressure gradient is small compared to that of viscous force, except for the location close to a separation point (Tennekes and Lumley 1972). In this problem, the validity of the proposed IBM is investigated in a flow with a mild pressure gradient. This is because the effect of the stream-wise pressure gradient is neglected in the baseline, which is an approximated governing equation for the proposed IBM. The Reynolds number based on reference length L, and the free-stream Mach number of 0.2 is 3 × 10⁶, and the free-stream temperature is 300 K. The overview of the grid and the boundary conditions are illustrated in Fig. 16.7. Five grids with different grid resolutions are prepared to check the trend of grid convergence as tabulated in Table 16.2. In addition, $r_{\text{IP}}$ is fixed to 3 for this problem. CFL3D (2019) computes the reference result on the 1409 × 641 grid. These reference computational results are also provided in the TMR. The $y_{\text{IP}}^{ + }$ in Table 16.2 is estimated by $c_{f}$ of this reference result. The results of the original IBM and modified IBM are compared to clarify the importance of the modification proposed in Sect. 2.3. The specification of these methods is summarized in Table 16.3.

Fig. 16.7

Computational grid over the bump

Table 16.2 Setting of computational grids over the 2D bump

Table 16.3 Specification of the original and modified IBMs

The distributions of the pressure and skin friction coefficients on the bump are illustrated in Figs. 16.8 and 16.9, respectively. The reference result by CFL3D is also illustrated in the same figures. On one hand, a large oscillation is observed on the pressure coefficient $C_{p}$ in the original IBM results, and the skin friction deviates from the reference result. This trend is obvious in the fine grids; the result in grid 5 predicts the peak of $c_{f}$ at a different location, and the magnitude of $c_{f}$ is approximately 30% smaller than the reference result. As a result, no trend of grid convergence is observed in the original IBM results. However, the modified IBM reproduces the distribution of $c_{f}$ more accurately. The oscillation of $C_{p}$ is smaller than the original IBM result, and the magnitude of $C_{p}$ is also more accurate. In addition, the skin friction on the finer grids has better agreement with the reference result; thus, a correct grid convergence trend toward the reference result is confirmed. Therefore, the modified IBM can reproduce this flow with a certain degree of accuracy.

Fig. 16.8

Distribution of the pressure coefficient on the bump

Fig. 16.9

Distribution of the skin friction coefficient on the bump

3.2 Flow Analysis Around the NASA Common Research Model

To investigate the capability of the proposed framework for aerodynamic prediction on a civil transport aircraft, transonic flows around the NASA common research model (CRM) (Vassberg et al. 2008) are simulated (Tamaki 2018; Tamaki and Imamura 2018). The NASA CRM was developed as a benchmark in the DPWs (2017). This geometry is widely tested in wind tunnel experiments (Rivers and Dittberner 2014; Ueno et al. 2014) and in numerical simulations (Sclafani et al. 2010, 2013; Lee-Rausch et al. 2014; Hashimoto et al. 2014; Yamamoto et al. 2012; Vassberg et al. 2014; and Tinoco et al. 2017). Using CFD simulations, a domestic workshop in Japan, the Aerodynamic Prediction Challenge (APC) (2019) workshop, was held recently to investigate the accuracy of the aerodynamic prediction of the NASA CRM. The geometry tested in this workshop consists of a fuselage, main wings, and horizontal tails with the incident angle of attack of i_H = 0°. The calculation setting in this section is adjusted to the condition of the experiment (Ueno et al. 2014) in Japan Aerospace Exploration Agency (JAXA) transonic wind tunnel, using a 2.16% scale model (the mean aerodynamic chord $c_{\text{ref}} = 151.31\,{\text{mm}})$. The free-stream Mach number is 0.847; the free-stream temperature is 284 K; and the Reynolds number based on the mean aerodynamic chord is 2.26 × 10⁶. The angles of attack are from −1.79° to 5.72°. In the wind tunnel experiment, the wing is deformed by the aerodynamic force acting on it (Tinoco et al. 2017). The geometry used in this simulation is also deformed based on the experimental data. The deformation (twist and bend) of the wing was measured (Ueno et al. 2014), and the data were provided in the workshop (2019).

The grid is shown in Fig. 16.10. Here, a symmetric boundary condition is assigned on the y = 0 plane, and a half-span model is simulated. To reduce the computational cost, two different cell sizes are specified on the wall. The wing upper surface and the tail are covered by the finest level of the cell because the flow features in those regions are important in terms of accurate aerodynamic force simulation. The other parts (the fuselage and wing lower surface) are covered with the second next level of the cell to reduce the computational cost. The ratio of the IP distance to the cell size, $r_{\text{IP}}$, is set to 3. Coarse, medium, and fine grids are prepared to check the grid sensitivity. In addition, a “medium-b” grid is created by changing the number of cells in the second layer (refer to Fig. 16.1). Table 16.4 describes the specification of these grids. The lengths in the table are based on the actual scale of the NASA CRM $(c_{\text{ref}} = 275.8\,{\text{inch}})$. The cell number slightly changes when the wing is deformed, and the numbers presented in the table are α = 2.94°.

Fig. 16.10

Computational grid for UTCart (medium grid, except for the overview)

Table 16.4 Settings of the computational grid around the NASA CRM for UTCart

The UTCart computational cases are as follows. First, the grid sensitivity is examined at α = 2.94° on the coarse, medium, medium-b, and fine grids. Then, the flows at α = −1.79, 0.62, 2.47, 2.94, 3.55, 4.65, and 5.72° are simulated on the medium grid. Furthermore, reference calculations are conducted by a flow solver FaSTAR, developed by JAXA (Hashimoto et al. 2012), on body-fitted grids. The computational grids are provided in the APC workshop (Third Aerodynamic Prediction Challenge (APC-III) 2019).

Figure 16.11 compares the surface pressure coefficient distributions of the two flow solvers. The qualitative features (e.g., the position of the shock on the wing upper surface) have good agreement with each other. Figure 16.12 presents the surface pressure coefficient distributions on the section of the wing. As illustrated in Fig. 16.13, the definition of the sections follows that of the APC workshop. These sections are identical to the positions of the pressure taps of the experiment. At the inboard sections, the surface pressure coefficient in the UTCart result has good agreement with the FaSTAR result and the experimental data. The pressure distributions at the outboard sections are slightly different from the FaSTAR result. The UTCart grid size on the upper surface of the wing is uniform. Accordingly, the number of cells in the local chord is smaller than that of the outboard sections, indicating that the grid resolution relative to the local chord length is low in the outboard sections and is assumed to be one of the causes of the inaccuracy. Furthermore, the shock thickness of the UTCart result is thinner than that in the FaSTAR result at Section I. This indicates that the UTCart computational grid has a higher grid resolution in the chord-wise direction than the grid for FaSTAR.

Fig. 16.11

Surface pressure coefficient calculated by UTCart, medium grid (α = 2.94°)

Fig. 16.12

Surface pressure coefficient on the wing sections (α = 2.94°)

Fig. 16.13

Definition of the wing sections of the NASA CRM

Figure 16.14 presents the component-wise aerodynamic coefficients. The pressure drag computed by UTCart is overestimated, especially on the coarse grid. The pressure drag in the medium-b grid result is 3 drag counts (1 drag count is 10⁻⁴) larger than the value of the medium grid result. This indicates that the pressure drag is dependent on the grid resolution in the region away from the wall, revealing that a proper grid refinement is required. Furthermore, the viscous drag is overestimated by 7 drag counts even on the fine grid. This difference is caused by the wing and the body. Simultaneously, the lift coefficient in the UTCart result is overestimated as compared to the FaSTAR result, whereas the pitching moment coefficient is underestimated. For these two coefficients, the trend of grid convergence is observed toward the FaSTAR result. The main cause of these discrepancies is the main wing. It may also be due to the grid resolutions that capture the curvature of the leading edge and the thickness of the trailing edges.

Fig. 16.14

Comparison of the aerodynamic coefficients of the NASA CRM (α = 2.94°)

Figure 16.15 shows the computed and measured drag polar (drag coefficient vs. lift coefficient) of this aircraft configuration. The basic trend of each coefficient indicates fair agreement between the UTCart and FaSTAR results and between the UTCart results and the experimental data.

Fig. 16.15

Drag polar of NASA CRM

4 Summary

We explored the methodology for high Reynolds number flow simulations using hierarchical Cartesian grids in combination with IBM. To reduce the computational cost, the wall function, i.e., the model of the near-wall part of the turbulent boundary layer, was combined with IBM. The velocity of the wall model was modified to linear profile to avoid numerical problems. We also demonstrated that the modification of the eddy viscosity is essential to retain the balance of the shear stress near the wall. The temperature profile is also modified accordingly. The object surface was immersed in the Cartesian grid, and uncertainty was thus remarked in the evaluation of the aerodynamic force. We clarified the relation between the aerodynamic force and the numerical flux in the flow calculation. In the 2D bump problem, modified IBM, the new approach introduced in this study, achieved higher accuracy than that of the original IBM in predicting the skin friction and pressure coefficients. Consistent grid convergence toward the converged solution was observed. In the flow simulations in the NASA CRM configuration under the cruise condition, the flow patterns showed fair agreement with those of FaSTAR and experimental data. Also, the basic trend of aerodynamic coefficients was predicted correctly using the UTCart.

The proposed framework can be used to estimate the basic flow feature around a complex geometry within a short time. Although the accuracy of the conventional CFD simulation may be higher once a well-tailored body-fitted grid is prepared, the proposed framework can also predict the flow with a certain degree of accuracy. The grid generation is fully automatic; thus, the total workload for the flow simulations is reduced compared to that of the conventional simulation on body-fitted grids. In addition, shape optimization problems are conducted without a manual procedure in the sequence of calculations. Thus, the proposed framework will be beneficial as a tool for aerodynamic design.