An Immersed Boundary Method on Cartesian Adaptive Grids for the Simulation of Compressible Flows

Abstract

In this article, we present an immersed boundary method (IBM) for the simulation of compressible flows encountered in aerodynamics. The immersed boundary methods allow the mesh not to conform to obstacles, whose influence is taken into account by modifying the governing equations locally (either by a source term within the equation or by imposing the flow variables or fluxes locally, similarly to a boundary condition).

A main feature of the approach we propose is that it relies on structured Cartesian grids in combination with a dedicated HPC Cartesian solver, taking advantage of not only their low memory and CPU time requirements but also the automation of the mesh generation and adaptation. Turbulent flow simulations are performed with Reynolds-Averaged Navier–Stokes equations or with Large-Eddy Simulation approach, in combination with a wall function at high Reynolds number, in order to mitigate the cell count resulting from the isotropic nature of Cartesian cells.

The objective of this paper is to demonstrate the capability of the present immersed boundary method on Cartesian adaptive grids to capture compressible flow features. Results obtained are in good agreement with classical body-fitted approaches but with a significant reduction of the time of the whole process, that is, a day for RANS simulations, including the mesh generation.

1 Introduction

The rise of Computational Fluid Dynamics (CFD) in aerospace sciences in the past decades is due to the growth of the computational power in combination with the increase of robustness and accuracy of CFD solvers. Today, Reynolds-Averaged Navier–Stokes (RANS) simulations on body-fitted meshes are commonly performed by the aeronautical industry in the design phase. The geometrical complexity of the configurations has increased too, taking into account for more details, such as track fairings on an aircraft or rotor head components for a helicopter. Consequently, the mesh generation, which requires usually manual interaction and expertise, has become a major bottleneck of the CFD workflow. This means that efficient tools are required to perform parametric studies and evaluate quickly the impact of a modification of a shape or some details onto the performances of an aircraft. High-fidelity CFD tools are generally not necessary at this stage; lifting-line tools can be used to get trends quickly, but models are often limited to certain flow assumptions. Low-fidelity CFD (e.g., Euler solutions) could be appropriate, but automatic mesh generation is the barrier to override. The immersed boundary methods (IBMs) can be seen as a good compromise between the quality of the solution and how quickly it can be obtained. This concept refers initially to the work of Peskin [32, 33], which employed a novel approach many decades ago to simulate biological flows onto Cartesian grids which did not conform to the geometry. The obstacles lying in the flow are taken into account by introducing a forcing term into the momentum equations. Since then, many variants of this approach have been developed, as quoted by Mittal and Iaccarino [25]. A first approach consists in introducing a continuous source term and is well suited for flows with immersed elastic boundaries [6, 32]. In this context, the source term represents the exchange of momentum between the fluid and solid through a law based on the theory of elasticity. However, in the limit of rigid boundaries, this problem is stiff, leading to a lack of stability and accuracy. Several discrete forcing methods have been developed for flow simulations around solid bodies, among which the ghost-cell direct forcing approach, as developed by Mittal et al. [26], Fadlun et al. [16], and Tseng et al. [41]. The IBM can be used on the whole geometry [29, 41] or locally [27, 43] to capture the potential effects of geometrical details. A similar approach consists in cutting cells that intersect the geometry, which has proven efficient and robust for inviscid flow simulations and low Reynolds flows around complex geometries (see Coirier and Powell [12] and Berger and Aftosmis [4]).

The use of Cartesian grids with local grid refinement in combination with embedded obstacles (either with immersed boundary or with cut-cell methods) seems to be well suited for a high level of automation and computational efficiency [4, 8, 29]. Although the use of adaptive Cartesian grids around arbitrary immersed obstacles is conceptually attractive, the resolution of high Reynolds number flows requires wall models [5, 9] to restrict the number of points within the boundary layer.

This paper proposes an efficient, fast, and robust immersed boundary method on adaptive structured Cartesian grids to perform CFD simulations of compressible flows. The method relies on a second-order accurate finite-volume HPC solver dedicated to Cartesian grids, enabling to deal with a wide range of flow regimes, from subsonic to supersonic flows, for steady RANS simulations or Large-Eddy Simulations (LES). Musker’s algebraic wall function [28] is applied within the IBM approach on Cartesian grids in order to solve high Reynolds number flows.

This paper is organized as follows: in Sect. 2, the ghost-cell direct forcing IBM approach used here is described. The way the different immersed boundary conditions are reconstructed at each iteration is detailed. Section 3 describes how this approach is meaningful when applied on Cartesian adaptive grids: an automatic workflow starting from input surfaces describing immersed boundaries has been developed, in combination with a dedicated HPC Cartesian solver, providing results within a short timeline. Section 4 presents two IBM simulations: the first test-case that is considered is the supersonic flow around a blunt body, which is a geometrically simple obstacle but demonstrates the capability of the present method to adapt the mesh during the simulation without any effort while increasing the accuracy of the simulation. The second simulation is a Large-Eddy Simulation of the flow around a three-dimensional high-lift airfoil. Results are compared to experimental data and a reference body-fitted solution.

2 Description of the Immersed Boundary Method

2.1 Governing Equations

The Navier–Stokes equations for a compressible flow can be expressed as follows:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \frac{\partial \rho}{\partial t} + \frac{\partial }{\partial x_j}\left( \rho u_j \right) &=& 0 \\ \displaystyle \frac{\partial \rho u_i}{\partial t} + \frac{\partial }{\partial x_j}\left( \rho u_i u_j \right) &=& \displaystyle -\frac{\partial p}{\partial x_i} + \frac{\partial }{\partial x_j}\left( \sigma_{ij} \right) {~~~~~~~~~~}i=1,2,3 {}\\ \displaystyle \frac{\partial \rho E}{\partial t} + \frac{\partial }{\partial x_j}\left( \left( \rho E+p \right)u_j \right) &=& \displaystyle -\frac{\partial }{\partial x_j}\left( Q_j \right) + \frac{\partial }{\partial x_j}\left( \sigma_{ij}u_i \right), \\ \end{array} \right. \end{aligned} $$

(1)

where ρ denotes the fluid density, u the velocity vector, p the pressure, ρE the total energy per unit mass, σ the viscous stress tensor, and Q the heat flux vector. In our approach, the system (1) is solved for interior cells using a cell-centered finite-volume method of second order of accuracy. W will denote the conservative variables W = (ρ, ρu, ρv, ρw, ρE) in the following. The Reynolds-Averaged Navier–Stokes (RANS) equations are solved with the Spalart–Allmaras turbulence model [39].

2.2 The Immersed Boundary Method

The immersed boundary method described in this paper relies on a ghost-cell direct forcing formulation, derived from the approaches of Fadlun et al. [16] and Tseng and Ferziger [41]. This approach consists in imposing the flow variables W at some particular points, which will be called IB or target points, close to the obstacles to mimic a boundary condition.

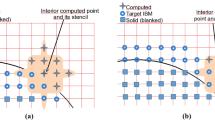
First, solid and fluid regions are identified geometrically, by a hole-cutting algorithm [3, 24]. Solid points are marked by squares in Fig. 1. At the fringe of solid region, two layers of IB target points are marked, to be compliant with the numerical scheme, relying on two ghost cells. The solution W is reconstructed at these IB target points using information in the fluid close enough to the wall, at image points. Figure 2 displays the case where target IB point A (green dot) is inside the obstacle S. For a sake of simplicity, the image point B (in red dot) can be represented as the symmetrical point of target IB point A with respect to the solid boundary. For that purpose, the distance to the obstacles and also the gradient of the distance to get the normals n are required. As depicted in Fig. 2, the image points do not usually match fluid points; thus, the solution W at point B is obtained by a second-order interpolation using donor points D ₁, D ₂, D ₃, and D ₄. Point N is the resulting point on the obstacle for which the physical boundary condition shall be recovered implicitly. This point N is obtained by a projection following the normals n.

Fig. 1

Spatial stencil involving IB target points for a viscous simulation: with interior (a) and exterior (b) IB target points. Note that target points can be located either inside or outside the obstacle

Fig. 2

Sketch describing the present direct forcing IBM approach. Solution W at IB target point A is built up using the corresponding interpolated value of W at its image point B

The update of the solution W at time iteration n + 1 using an explicit time integration scheme can be summarized as follows:

• Computation of the flow primitive variables W = (ρ, u, v, w, T) (where ρ is the fluid density, u, v, and w are the velocity vector components in the Cartesian frame, and T is the temperature) for fluid points: $W^{n+1}_{i,j}=f(W^n_{k,l})$, (k, l) being the indices of the points in the spatial stencil centered on point of index (i, j)

• Computation of $\hat {W}^{n+1}$ by interpolation of its neighboring values W ⁿ⁺¹ (superscript $\hat {.}$ denotes an interpolated value)

• Reconstruction of the flow variables at IB target points $\tilde {W}^{n+1}$, according to the interpolated value $\hat {W}^{n+1}$.

• Update of ghost cell values at the borders of abutting grids.

2.3 Types of Immersed Boundary Conditions

The reconstruction at IB target points depends on the type of the immersed boundary condition (IBC) defined locally by the input surface.

2.3.1 Wall Slip and No-Slip IBCs

As displayed in Fig. 2, the image point is not necessarily the mirror point of the IB target point with respect to the wall. Thus, slip and no-slip boundary conditions can be implicitly recovered at the wall by a linear reconstruction of the normal component of the velocity, u _n = 0 and u = 0, respectively.

In the case of a no-slip boundary condition where ∥u∥=0 at the wall, a one-dimensional linear interpolation is applied given u(B) as follows:

$$\displaystyle \begin{aligned} \displaystyle \mathbf{u}(A)=\frac{\Delta_{A,N}}{\Delta_{B,N}}~\mathbf{u}(B)\,, \end{aligned}$$

where Δ_A,N and Δ_B,N are the signed distance of IB target point A and IB image point B to the wall point N, respectively.

In the case of a slip boundary condition, the velocity vector u can be decomposed in a normal vector and a tangential vector as

$$\displaystyle \begin{aligned}\mathbf{u}={\mathbf{u}}_t+{\mathbf{u}}_n\,.\end{aligned}$$

The normal velocity vector is obtained by a linear reconstruction, similar to the one applied on u for the no-slip boundary condition. The tangential velocity vector is then obtained by u _t(A) = u(B) −∥u _n(B)∥n, where ∥u _n(B)∥ is the magnitude of the normal velocity at IB image point B and n is the normal vector to the wall defined at point A.

Pressure and density gradients are assumed equal to zero in the normal direction to the wall in the close vicinity to the wall, and hence p(A)=p(B) and ρ(A)=ρ(B). The pseudo-viscosity $\tilde {\nu }$ of Spalart–Allmaras one-equation turbulence model is recovered by the same linear interpolation such that $\tilde {\nu }$ is implicitly zero at the wall.

2.3.2 Wall Function for High Reynolds Flow Simulations

Our approach relies on an IBM approach on adaptive Cartesian grids, leading to prohibitive cell counts to resolve the viscous stress in the boundary layer until the wall. Moreover, this method is devoted to aeronautical configurations where high Reynolds numbers are often considered. This issue is a key point addressed by many researchers in the field of IBMs, using a wall function to represent the wall shear stress in the case of viscous flow simulations at high Reynolds numbers [5, 9, 10]. In our approach, Musker’s algebraic wall function [28] is used to reconstruct the velocity at IB target points, enabling to place first Cartesian cells near the walls at y ⁺ ≈ 100. Details on the wall function are provided in [31]. Figure 3 displays the IB target point A and its image point B, for which the variables W _B are interpolated from the computed cells. Instead of a linear reconstruction to recover u = 0 at the wall, a wall function is applied between the image point B and the wall. Similarly to the slip boundary condition, the velocity vector is decomposed into a tangential vector and a normal vector. The tangential velocity vector at point A is obtained as follows:

$$\displaystyle \begin{aligned}\displaystyle {\mathbf{u}}_t(A) = \frac{U_A}{U_B} {\mathbf{u}}_t(B) \,,\end{aligned} $$

where U _P = ∥u _t(P)∥ denotes the magnitude of the tangential velocity at any point P.

Fig. 3

Wall function for IBM: IB target point is A and corresponding image point is B. In red dots are IB target points around the obstacle; in blue dots, their image points

The velocity vector at point B is obtained by interpolation from its neighboring points. Knowing the modulus of the tangential velocity at image point B, the friction velocity u _τ is obtained by a Newton–Raphson’s method on Musker’s algebraic wall function. Then, y ⁺ at point A is computed by $\displaystyle y^+=\frac {\Delta _{A,N} u_{\tau }}{\nu }$. The algebraic function (2) provides the modulus of the tangential velocity vector at point A.

$$\displaystyle \begin{aligned} \displaystyle u^{+}=5.424 \arctan\left[\frac{2y^{+}-8.15}{16.7}\right]+\log~\left[ \frac{ \left( y^{+}+10.6 \right)^{9.6} }{\left( y^{+2}-8.15~y^{+}+86 \right)^2} \right]-3.52\,. {} \end{aligned} $$

(2)

The normal velocity at image point B is obtained by a simple projection:

$$\displaystyle \begin{aligned}{\mathbf{u}}_n(B)= (\mathbf{u} (B) \boldsymbol{\cdot} \mathbf n) \mathbf n\,,\end{aligned}$$

where n denotes the unit normal vector at the wall passing through points A and B.

The tangential velocity at IB image point B can be expressed by

$$\displaystyle \begin{aligned} {\mathbf{u}}_t(B)= (\mathbf{u}(B) \boldsymbol{\cdot} \mathbf{t}) \mathbf{t}\,. \end{aligned}$$

We could have imposed the flow to be locally parallel to the wall, which means u _n = 0, but this tends in practice to delay the separation on massively separated flows. Thus, a 1D linear interpolation is performed to compute the normal velocity:

$$\displaystyle \begin{aligned} \displaystyle {\mathbf{u}}_n(A)=\frac{\Delta_{A,N}}{\Delta_{B,N}} {\mathbf{u}}_n(B)\,. \end{aligned}$$

The resulting three components of the velocity vector u at point A are then obtained by summing the corresponding normal and tangential vector components. In the case of a RANS modeling using Spalart–Allmaras model [39], the pseudo-viscosity $\tilde {\nu }$ must also be estimated at IB target point A. Under the assumption of an equilibrium boundary layer, ${ \tilde \nu }$ can be defined as

$$\displaystyle \begin{aligned}{\tilde \nu}=\frac{1}{f_{v1}}\kappa~u_{\tau}y\,,\end{aligned}$$

where f _v1 is the damping function of Spalart–Allmaras model, which is a nonlinear function of ${\tilde \nu }$, and thus $\tilde \nu$ is also obtained by finding explicitly the root of the resulting quartic equation.

2.3.3 Use of Several Types of Immersed Boundary Conditions for a Given Configuration

Several types of immersed boundary conditions can be defined in a single computation, typically to perform a simulation around a model set in a wind tunnel. In that case, a wall function is applied at the boundary of the model, a slip boundary condition at wind tunnel walls, and an inflow and an outflow boundary conditions at inlet and outlet, respectively. The nature of the immersed boundary condition to be applied is determined by the nature of the input surface on which the IB target point A is projected. If the projection point N lies on a surface tagged as an injection immersed boundary, then the injection immersed boundary condition is flagged for IB point A.

3 IBM on Adaptive Cartesian Grids

3.1 Motivation

Most immersed boundary methods available in the literature rely on adaptive Cartesian grids: Cartesian embedded methods remove the bottleneck of the mesh generation, since the adaptive Cartesian mesh generation can be easily automated even for arbitrary complex geometries. In order to preserve the simplicity of a pure Cartesian approach, the Cartesian mesh is defined down to the wall, relying on the IBM approach to take into account for obstacles. Cartesian cells cannot be refined down to the wall in general (except those cases where the wall is aligned with an axis), so a wall function is mandatory to compute high Reynolds number flows with a reasonable cell count. The strength of the IBM approach on adaptive Cartesian grids used in combination with a Cartesian CFD solver provides an automated and efficient tool for the simulation of flows around complex geometries, provided the IBM preprocessing is robust and fast.

3.2 Automatic IBM Preprocessing for Complex Geometries

3.2.1 Description of the Workflow

The IBM preprocessing can be separated into the following steps:

• The automatic Cartesian mesh generation from a discretized CAD.

• The computation of information required for the IBC reconstruction at each time step of the flow simulation.

First, a Cartesian mesh is generated automatically. This mesh is made of a set of structured uniform grids. The different refinement levels are managed thanks to an octree structure in 3D and quadtree in 2D [30], enabling to prescribe the mesh resolution near each boundary and within the fluid, in order to avoid coarsening in the wake for instance. Ghost cells are explicitly built, such that an overlapping exists between neighboring grids, with a minimum overlap. An example of a Cartesian mesh generated around a 2D profile is displayed in Fig. 4. To generate that case, the input data are a 1D discretization of the profile and the cell size required in its vicinity (equal to 0.1% of the chord length here). The Cartesian mesh skeleton is a quadtree (i.e., an octree in 2D) mesh, as displayed in Fig. 4a. Each element of the quadtree is then filled with a Cartesian grid of a constant number of cells per direction (specified by the user), resulting in an adaptive Cartesian mesh displayed in Fig. 4b. As shown in this figure, some grids that are entirely inside the solid are removed, to reduce memory requirements. The IBM preprocessing is then achieved, based on several geometrical algorithms initially developed for overset grids [3]. Some of the steps are illustrated by the IBM preprocessing of the previous NACA0012 configuration.

• Interior cells are marked using a blanking technique, either using the X-ray technique introduced by Meakin[24] or using a line-of-sight algorithm [3]. Figure 4b and c represents the same mesh, but blanked-out points are not displayed on the latter.

  Fig. 4

  

  Example of a mesh around a NACA0012 profile, profile in green. (a) Quadtree skeleton mesh in blue around the NACA0012 profile. (b) Resulting Cartesian mesh (Cartesian patches fully inside the solid are removed). (c) Same Cartesian mesh after blanking of interior cells

• The signed distance field is then computed in the whole computational domain (as it is required for the turbulence model later).

• IB target points are marked at the fringe of blanked points (green dots in Fig. 2).

• Normal vectors at IB target points are computed as the local gradient of the signed distance.

• IB target points are then projected onto the immersed boundaries following the normal vectors, resulting in boundary points (yellow dots in Fig. 2).

• The location of image points is determined inside the fluid region (red dots in Fig. 2).

• The interpolation data for image points are computed (donor cell indices and weights, with donor points marked in blue dots in Fig. 2).

More details can be found in [31], especially on the location of image points, for which a special care is required to ensure the robustness of the preprocessing and the simulation.

3.2.2 Evaluation of Performance of the Preprocessing

A performance study has been achieved in [31] that demonstrates the capability of the method to generate a mesh and prepare a CFD simulations within less than 20 min even for a 1.5 billion point resulting mesh around a landing gear geometry. This is depicted in Fig. 5, which represents the execution time versus the number of cores with a fixed number of points per core (five million points). Another fact is that the distance field computation on the whole domain represents a large part of the execution time. Future work will consist in improving this, using a Fast Marching Method [38] for instance, as the distance field must be accurate in the vicinity of the obstacles. As the current distance field computation relies on an orthogonal projection on the triangular surfaces, preconditioned with a k-d tree, further points are the most time-consuming as the number of candidate triangles for the projection is bigger than for close points to the obstacles.

Fig. 5

Weak scaling study: five million nodes distributed per core

IBM preprocessing is achieved by an assembly of Cassiopee functions available in several modules (see reference [3] for a general description of Cassiopee or the website [1]).

3.3 IBM Simulations Using a Dedicated Cartesian CFD Solver

3.3.1 FastS HPC Solver

The ONERA HPC FastS solver [2, 22] is used to solve the compressible Navier–Stokes equations using a finite-volume method. It contains a structured multiblock solver that can solve RANS, LES, DNS, steady, and unsteady simulations. Its main feature is its efficiency in dealing with unsteady simulations (see [13]) as it enables to update ten million cells per second per core on a single Intel Broadwell core; in other words, 300 million cells can be updated per second on a 28-core node. FastS contains a solver dedicated to Cartesian grids that is used to perform IBM simulations on Cartesian grids. Despite the relatively high cell count obtained by the block-structured Cartesian mesh generation in comparison with a classical body-fitted unstructured approach, a dedicated Cartesian solver requires much less memory and CPU time than a structured curvilinear solver and also an unstructured solver. Here, the Cartesian solver is 2.5 times more efficient in terms of CPU time and memory than the structured curvilinear solver using the same numerical methods.

FastS solver relies on a hybrid MPI/OpenMP framework, where the memory is distributed (by distributing CFD grids) on the processors at high level, i.e., between nodes, whereas multithreading is managed via OpenMP within a given node. For our purpose, where Cartesian grids are uniform and containing few cells in comparison with grids resolving boundary layers accurately, the N Cartesian grids are distributed between the NT cores using OpenMP.

3.3.2 Numerical Methods

For RANS computations, two spatial schemes are considered, depending on the flow regime: the Roe–MUSCL scheme [36] or an AUSM scheme [23], which is based on a modification of the AUSM+(P) scheme (see Edwards and Liou [15]), which is second-order accurate. Jacobian approximations are those proposed by Jameson and Yoon [18] and Coakley [11], whereas the linear system is solved by the LU-SGS method [18]. The steady and unsteady RANS equations are solved using Spalart–Allmaras one-equation turbulence model [39].

For LES computations, a hybrid centered/upwind scheme [23] is retained to manage a good compromise between robustness and accurate simulation of the turbulent small eddies [19], whereas the temporal integration is achieved by a three-step Runge–Kutta explicit scheme, or by a second-order implicit Gear scheme with local Newton sub-iterations [14].

For Large-Eddy Simulations (LES), the filtered equations are obtained using the formalism developed by Vreman [42]. A Monotone Integrated LES approach (or MILES [7, 17]) is performed, that is, no subgrid-scale model is used as the numerical dissipation of the scheme acts as a subgrid scale model.

3.3.3 Update of IBM Points During the CFD Simulation

The IBM target points must be updated at each sub-step of the time integration. FastS solver updates first fluid cells on each Cartesian grid at time sub-step n, then IB target cells are updated, and finally, transfers between neighboring grids are performed to update the ghost cells. For RANS and LES IBM simulations, Musker’s wall model is currently applied at IB target cells only.

MPI transfers between nodes are achieved in a single step: a global transfer to update all the target points and the ghost cells. This is possible because the IBM preprocessing prevents from IB image points to be interpolated by ghost cells (which are explicitly defined in the Cartesian mesh).

In practice, only fluid points are computed by FastS CFD solver, and transfers between abutting grids and IBM updates are performed by a library of Connector module of Cassiopee package [3]. Both FastS and Cassiopee modules handle the same CGNS/Python tree in memory [34, 37]; in other words, arrays defining the CFD simulation (metrics, flow fields) are shared in memory without copy. This is made possible by the fact that ghost cells are explicitly built during the mesh generation, justifying the use of an overset Cartesian mesh, with minimum overlapping.

3.4 Adaptation of the Mesh During the IBM Simulation

The Cartesian mesh adaptation developed for IBM simulations derives from the one developed within an overset grid framework [30], where the near-body regions are defined by a set of structured body-fitted grids close to the obstacles. Similarly, an octree is generated, representing the skeleton of the Cartesian mesh. Finest refinement levels are first defined close to the obstacles, depending on the mesh spacing imposed in the vicinity of them. Similarly to the original approach, where bodies are represented by overset body-fitted grids, the adaptation consists in adapting the skeleton octree according to a refinement indicator, and the set of Cartesian grids is then regenerated. The algorithm is the following:

Step 1:

Building of the skeleton octree $\mathcal {O}_i$ and generation of the Cartesian set of overlapping grids $\mathcal {M}_i$, where i denotes the adaptation cycle (i = 0 initially).

Step 2:

IBM preprocessing.

Step 3:

N iterations of a CFD simulation (N being big enough to pass the transient phase and to stabilize a mean flow (for unsteady computations) or to converge the solution (for steady computations)).

Step 4:

Computation of the physical sensor for adaptation and stored at cell centers. This sensor depends on the physical problem (it can be the vorticity for the wake capture); for unsteady simulations, the maximum value of the sensor during the period is registered, whereas the last value of the sensor is registered for steady simulations.

Step 5:

The sensor is then used to compute the indicator on the skeleton octree $\mathcal {O}_i$ used to generate the Cartesian mesh $\mathcal {O}_{i+1}$ that has been computed. As explained in [30], the number of points after adaptation is controlled (e.g., the increase of the number of points must not exceed 20% of the previous mesh), which provides an automatic values of thresholds of the sensor above and under which octree elements have to be refined or coarsened.

Step 6:

Once this indicator is computed, the octree skeleton mesh is adapted, denoted $\mathcal {O}_{i+1}$. A new set of Cartesian grids, denoted $\mathcal {M}_{i+1}$, is then automatically generated.

Step 7:

Interpolation of the previous solution defined on mesh $\mathcal {M}_{i}$ onto the new mesh $\mathcal {M}_{i+1}$.

Step 8:

i = i + 1, then restart to Step 2 until the criterion that finalizes the adaptation is satisfied. For steady-state simulations, the solution is then converged on the final mesh

For steady flow simulations, the sensor is computed once at convergence and several convergence cycles are performed, whereas for unsteady flows with a stable mean flow, we assume that the mean flow does not vary much during a given period and that the maximum of the sensor for each point is used for the adaptation.

The whole process is automatic, and several adaptations are required to adapt the mesh to the flow features as the number of cells is controlled at each remeshing step and does not exceed 20% more in terms of cell count than the previous mesh. In our approach, the number of adaptation cycles does not exceed generally 5, and no specific criteria based on error estimator for instance are computed to stop the adaptation: as the number of points is increased by 20% at each adaptation (roughly), then 5 adaptations would multiply the number of points by 2.5, which means that during a simulation, one should expect having 2.5 times more computational resources than expected at the first cycle.

Note that the refinement level imposed near each obstacle can be set unchanged during the adaptations even if new refinement levels are created elsewhere.

Adaptation of the octree mesh can also be performed a priori: refinement zones can be prescribed in addition to the triangular surfaces describing the obstacles. These refinement zones are closed surfaces. The initial skeleton octree $\mathcal {O}_0$ is then adapted before generating the Cartesian mesh: in that case, the indicator consists in marking octree leaves for refinement if they intersect or lie within the refinement zone and if the cell spacing prescribed for that refinement zone is not reached yet. This approach has been performed on the second test-case in Section 4.2.

4 Numerical Results

A wide range of validations and applications can be found in [35], from Euler to LES simulations, from subsonic to supersonic flows either for two-dimensional academic configurations or for geometrically complex configurations.

Here, we focus on two applications: the first application consists of a simulation of a supersonic flow around a blunt body, in order to demonstrate the capability of the present immersed boundary method to be combined with Cartesian mesh adaptation that occurs periodically during the simulation.

The second test-case is an unsteady three-dimensional simulation around a three-element airfoil, for which the physics is complex. Our objectives are not only to assess first that aerodynamics features on such a case can be captured by a Cartesian method (despite some improvements to be done and further work to be achieved to obtain satisfactory results for aeroacoustics) but also to enhance the HPC capabilities of the whole workflow and especially of the flow solver.

4.1 Validation of the Adaptive Cartesian IBM on a Two-Dimensional Supersonic Case

The bow shock test-case is one of the cases of the International Workshop on High-Order CFD Methods. In this workshop, this case is designed to isolate testing of the shock-capturing properties of schemes using the detached bow shock upstream of a two-dimensional blunt body in supersonic flow. This case is computationally expedient, being steady, two-dimensional, and inviscid, with well-defined boundary conditions. In [21], the author shows that high-order schemes on unstructured grids are able to capture the shock location with very low pressure and enthalpy errors.

The geometry is a flat center section, with two constant radius sections, top and bottom. The flat section is one unit length, and each radius is half the unit length. While the flow is symmetric top and bottom, a full domain is computed to support potentially spurious behavior. The aft section of the body is not included to avoid developing an unsteady wake. The Mach number is M _∞ = 4.

Here, our first objective is to validate the IBM approach for supersonic flows. The Cartesian grid is automatically generated around the obstacle. The finest refinement level is imposed not only in the vicinity of the obstacle but also within a refinement zone, which is prescribed prior to the preprocessing. This zone is defined by a circle of radius 3.5 L, where L is the unit length around the blunt body, with a uniform cell size of 0.01 L.

In order to capture the detached shock accurately, an adaptation of the Cartesian mesh is performed periodically during the CFD simulation, as described in Sect. 3.4. The sensor is computed after N iterations (where N is 1000), and it is chosen here as the maximum difference of the Mach number for all the directions of the mesh between the current cell and its direct neighboring cells.

The whole process is automatic and three adaptations are required to adapt the mesh to the shock as the number of cells is controlled at each remeshing step. Figure 6 represents the initial mesh with the refinement zone located at 3.5 times the radius to the center of the blunt body. It is made by 730,000 points over 47 Cartesian grids. The final adapted mesh is made by 1.27 million points over 190 grids, obtained after the three adaptation cycles. In the present adaptation method, new refinement levels can be added; here, the finest refinement level located in the vicinity of the detached shock is equal to 5.10⁻⁴L. It can be noticed that some regions have been coarsened, but the initial spacing near the wall is preserved here.

Fig. 6

Bow shock test-case: Cartesian mesh. (a) Initial mesh. (b) Adapted mesh

The CFD simulation has been performed using second-order accurate Roe scheme (with minmod limiter). Figure 7 displays the flow field characteristics through the isocontours of the Mach number: it can be noticed that the shock is better captured after adaptation, which is located around it. Some small oscillations can be noticed near the shock, due to the spatial scheme. A slip immersed boundary condition is applied to model the blunt body.

Fig. 7

Bow shock test-case: isocontours of Mach number. (a) Initial mesh. (b) Adapted mesh

For a steady inviscid flow, the total enthalpy, $\displaystyle H=\frac {\rho E + p}{\rho }$, is constant, where ρE is the total energy, ρ the density, and p the total pressure. The error in this quantity provides a first quantifiable measure of the quality of the computed solution of the general Euler equations (as opposed to schemes that specifically optimize for steady, inviscid flow and enforce H to a constant value). Along the stagnation streamline, the stagnation pressure on the cylinder surface is predicted by the Rayleigh–Pitot formula,

$$\displaystyle \begin{aligned} \displaystyle \frac{p_{02}}{p_1}=\frac{1-\gamma+2\gamma Ma_1^2}{\gamma+1}~\left( \frac{(\gamma+1)^2 Ma_1^2}{4\gamma Ma_1^2-2(\gamma-1) }\right)^{\frac{\gamma}{\gamma-1}}, \end{aligned}$$

where p ₀₂ is the total pressure at stagnation point, p ₁ is the static pressure upstream of the shock, Ma is the Mach number, and γ is the specific heat ratio. Subscript ₁ refers to conditions upstream of the shock and ₂ to the stagnation point. Table 1 provides a comparison of the wall pressure ratio, showing that the adapted mesh improves this value, by dividing by 10 the relative error with respect to the theory.

Table 1 Comparison of pressure ratios

4.2 Unsteady Flow Simulation Around a High-Lift Airfoil

The test-case is an extruded three-element high-lift airfoil with deployed slat and flap. This kind of configuration is of major interest for acoustics since high-lift devices deployed on aircraft to increase lift at low speed are responsible for a significant part for the airframe noise during the approach phase. An experimental campaign has been conducted in the framework of the joint ONERA/DLR LEISA2 project; experimental data are also provided within the AIAA BANC workshops to validate the numerical methods applied for aerodynamics and acoustics analyses. A reference study is the LES simulation of Terracol and Manoha [40] on a 2.6 billion body-fitted meshes. Six million hours of CPU were required on 4096 processors to perform this simulation. This simulation has also been performed by LBM solvers using an IBM approach on Cartesian grids [20].

The aim of the simulation presented here is to focus only on the aerodynamics phenomena and not on the acoustics, since the way the information is transferred from a grid of a level l to a grid of a different level (twice as coarse) leads to small perturbations that are a major issue for a far-field acoustics analysis.

4.2.1 Description of the Test-Case

The reduced geometry configuration is used here (F16). The retracted wing chord length c is 300 mm. The slat and flap are deployed, respectively, of 27.834^∘ and 35, 011^∘. The flow conditions are M _∞ = 0.178, α = 6.15^∘ and a Reynolds number of Re = 1.23 million, based on the chord. The wing span is chosen the same as the reference CFD study, that is, 0.25 c.

An IBM simulation with FastS solver is performed on a set of Cartesian grids using Musker’s wall function applied at IB target points. The mesh is composed by 660 million points, with an adapted spatial resolution in the vicinity of the flap and the slat and in their cavity and wake regions, with a smallest cell size equal to 1.5 10⁻⁴c. The external border of the computational domain is located at 50 c. The mesh is represented on different views displayed in Fig. 8.

Fig. 8

Views of the IBM Cartesian mesh around the high-lift airfoil. (a) General view around the three-element airfoil. (b) Close-up view near the slat cove. (c) Close-up view near the trailing edge of the main element. (d) Close-up view near the trailing edge of the flap

The LES simulation has been initialized by a RANS simulation in order to get rid of transient phenomena. The spatial scheme is the modified AUSM scheme [23], to manage a good compromise between robustness and accurate simulation of the turbulent small eddies [19], whereas the temporal integration is an explicit three-step Runge–Kutta scheme, with a global time step, Δt = 0, 16 μs. The simulation has been performed on 224 Intel Broadwell cores of ONERA SATOR cluster, for a CPU cost of 0.4 μs per point per iteration. The flow quantities have been averaged on a period of 80 ms.

4.2.2 Results

Figure 9 displays the density gradient resulting from the LES simulation using the wall-modeled IBM. The comparison with the reference simulation of Terracol and Manoha shows that the IBM approach enables to capture the main features of this flow: recirculation bubble in slat and flap cavities, turbulent boundary layers, and wakes. This is also assessed by the comparison of the averaged velocity between the reference LES and the IBM simulation and experimental data, displayed in Fig. 10. The location of recirculation bubble in cavities is well captured. Besides, the simulated flows in the vicinity of the suction side of the flap differ from the experiments, where a strong separation occurs unlike the LES simulations. Other wind tunnel tests did not reveal that separation, and Terracol [40] demonstrated that this difference was due to the influence of the wind tunnel walls.

Fig. 9

Instant views of the flow represented by the density gradient: comparison between the wall-resolved LES (a) and the IBM simulations (b, c, and d)

Fig. 10

Views of the averaged flow: isocontours of the velocity amplitude and streamlines; comparison between experiments (left-hand side), the reference wall-resolved LES simulation (center), and the IBM LES simulation (right-hand side). (a) Experiments: slat cove. (b) Body-fitted LES: slat cove. (c) Wall-modeled IBM: slat cove. (d) Experiments: main element trailing edge. (e) Body-fitted LES: main element trailing edge. (f) Wall-modeled IBM: main element trailing edge. (g) Experiments: flap. (h) Body-fitted LES: flap. (i) Wall-modeled IBM: flap

Two rakes of probes are defined in the fluid, as displayed in Fig. 11. At these locations, the velocity and velocity fluctuation profiles are compared against the experiment and the reference LES body-fitted simulation, as displayed in Fig. 12, showing a good agreement between both simulations and also with the experimental results.

Fig. 11

Probe locations: (a) 04-2 in the slat cove and (b) 18-3 in the trailing edge cove of the main wing

Fig. 12

Comparison of velocity profiles at probe 04-2 (a) and at probe 18-3 (b); velocity fluctuations at probe 04-2 (c) and 18-3 (d). IBM simulation is compared against the reference LES simulation, PIV, and LDV data

5 Conclusions

In this chapter, we have presented an immersed boundary method (IBM) on adaptive Cartesian grids for the simulation of compressible flows. As the IBM enables the mesh not to conform to the obstacles, Cartesian meshes are attractive for that purpose as their generation and adaptation are usually fast and easy to perform. Using both approaches together enables to get rid of the mesh generation, which is a tedious task for engineers as the configurations that are simulated become more and more complex geometrically. CFD simulations are then performed by a dedicated HPC Cartesian solver, taking advantage of the low memory and CPU time requirements for Cartesian grids (since metrics do not need to be stored, flux balances are simplified).

The approach that has been developed relies on a workflow that needs to be automatic, robust, and fast, starting from a triangulation of the immersed obstacles only. For that purpose, an automatic preprocessing has been developed, which enables to generate the Cartesian mesh and compute the data required for the reconstruction of the solution in the vicinity of the immersed boundaries. As an example, it is possible to prepare a CFD simulation of an IBM Cartesian mesh of 1.5 billion points around a landing gear within less than 20 min, requiring less than 360 GBytes of memory.

Several types of immersed boundaries have been developed such that not only inviscid or viscous wall boundaries can be reconstructed but also injection and outlet boundaries can be defined as immersed boundaries, provided the corresponding triangulated surface is defined as input. Turbulent flow simulations are performed with Reynolds-Averaged Navier–Stokes equations using Spalart–Allmaras model or with a Large-Eddy Simulation approach, in combination with an algebraic wall function in order to mitigate the cell count resulting from the isotropic nature of Cartesian cells.

Initially, the mesh is refined in the vicinity of the obstacles, with different refinement levels possible for different parts of the obstacles (a leading or trailing edge of a wing can be better resolved than the rest of the wing). It is possible to prescribe refinement zones a priori if the flow physics is known; otherwise, Cartesian mesh adaptation can be performed during the simulation to capture the main features of the flow. The adaptation is performed periodically, after passing the transient phase, and is valid for steady flows or for unsteady flows but with a stable mean flow.

To validate that approach, the first test-case has been considered, which is the simulation of the inviscid and supersonic flow around a blunt body. This test-case demonstrates the capability of the present approach to perform automatically immersed boundary simulations in combination with Cartesian mesh adaptation, performed periodically during the simulation to improve the capture of the flow characteristics without knowing it a priori.

The second application is an unsteady simulation of the flow around a high-lift airfoil. For that case, refinement zones are prescribed in regions where the wakes are developed. Aerodynamics results are evaluated here and compared with experiments and a reference LES simulation on a structured body-fitted mesh by Terracol [40]. Some works have to be achieved to be able to evaluate the acoustics, as no specific treatment is achieved yet when crossing an interface from a fine grid to a coarser grid (twice as coarse here), leading to reflections of unsupported structures back into the finer grid. This is one topic on which we will focus in the future.

Future work will also concern the improvement of the wall modeling using wall functions, especially to improve the skin friction, which is a major concern for compressible aerodynamics applications, especially for aircrafts. Adaptation of the mesh within the boundary layer is a topic of interest, as the cell spacing close to the wall is currently determined by the user, usually considering the Reynolds number and a y ⁺ value of 100 roughly computed for a flat plate, which is not really relevant for any configuration.

Adapted wall models for Large-Eddy Simulations will also be considered. Another topic is to extend the method to bodies in relative motion, aiming at simulating flows around configurations such as control surfaces on wings or VTOLs.