Keywords

1 Introduction

The investigation of magnetohydrodynamics flow with heat transfer phenomenon in non-Newtonian liquids has substantial usages in technology and science, like construction of heat exchangers, installation of nuclear accelerators, design for cooling of nuclear reactors, turbo machinery, blood flow measurement techniques. Ahmed et al. [1] investigated impact of MHD on Jeffrey liquid flow along an extended surface using power law temperature. Analytical solutions of non-linear PDEs using slip conditions are instigated flow of non-Newtonian MHD liquid in a pipe towards a porous medium was analyzed by Zeeshan and Ellahi [2]. Nejad et al. [3] reported MHD stream of electrically conducting power law liquids towards an isothermal vertical wavy sheet. 3-Dimensional MHD Jeffrey nanoliquid flow along thermally radiative surface under heat generation phenomenon was examined by Shehzad et al. [4]. Das et al. [5] reported behavior of melting phenomenon on MHD stagnant point Jeffrey liquid stream towards an extended surface with slip conditions. Venkateswarlu and Satya Narayana [6] scrutinized behavior of chemical reactant on viscoelastic liquid stream along a vertical plate with MHD. Rashidi et al. [7] explored impact of magnetohydrodynamic and heat phenomena on two dimensional liquid flows along a porous medium. Sheikholeslami et al. [8] obtained the simulation of problem of CuO-water nanoliquid stream with convective heat phenomenon. Ellahi et al. [9] reported simultaneous impacts of magnetohydrodynamic and partial slip on peristaltic stream of Jeffery liquid in a rectangular duct. Significance of Joule heating phenomenon in third-grade liquid stream towards a radiative plate was studied by Hayat et al. [10].

Both homogeneous and heterogeneous reactants are involved in numerous chemically reacting schemes. Some of them have capability to proceed slow or not, excluding catalyst. The homogeneous and heterogeneous reactants interplay is very compound including consumption and production of reactant species at different rates both within liquid and on catalytic exterior like reactions occurring in production of polymer and ceramics, hydrometallurgical industry, crops damage via freezing, dispersion and fog formation, food processing, equipment design for chemical processing, cooling towers and temperature fields and moisture over agricultural fields and groves of fruit trees. Merkin [11] considered homogeneous-heterogeneous reactions model in stream of viscous liquid towards a flat plate. He noted that outer reaction is superior mechanism near leading edge of surface. Significance of homogenous-heterogeneous reactants in stream of viscous liquid was numerically investigated by Chaudhary and Merkin [12]. Stagnant-point stream along an extended plate using homogeneous/heterogeneous reactants was analyzed by Bachok et al. [13]. Khan and Pop [14] reported significance of homogeneous-heterogeneous reactants of viscoelastic liquid stream along an extended surface. Homogeneous heterogeneous reactants in micropolar liquid flow along a permeable extended/shrinking plate was examined by Shaw et al. [15]. Khan and Pop’s [14] work was extended by Kameswaran et al. [16] for nanoliquid along a porous extended plate. Importance of homogeneous-heterogeneous reactants in stagnant point carbon nanotubes flow with Newtonian heating was reported by Hayat et al. [17]. Behaviour of nanoliquid MHD flow with homogeneous heterogeneous reactants and condition for velocity slip was also examined by Hayat et al. [18]. Hayat et al. [19] reported significance of homogeneous-heterogeneous reactants in Powell-Eyring liquid flow. Hayat et al. [20] examined Oldroyd-B MHD liquid flow using homogeneous heterogeneous reactions with Cattaneo-Christov model. Significance of MHD in bi-directional stream of nanoliquid with homogeneous heterogeneous reactants and second-order velocity slip was analyzed by Hayat et al. [21].

Newtonian heating (or cooling process) is process where internal resistance is supposed to be neglected in comparing with its surface resistance. Currently this phenomenon has been used by various researchers because of its practical usages like to configuration heat exchanger, conjugate warmth exchange around fins and furthermore in convective streams setup where bounding edges absorb heat by solar radiations. The Von Kármán stream and heat phenomenon of an electrically conducting liquid was given by Sahoo [22]. Salleh et al. [23] examined heat transfer flow along an extended surface using Newtonian heating. Significance of Newtonian heating in second grade liquid flow along an extended surface was considered in [24]. Unsteady viscous liquid MHD flow towards a flat surface using Navier slip and Newtonian heating effects was reported Makinde [25]. Uddin et al. [26] is analyzed MHD flow of nanoliquid towards a flat vertical surface with Newtonian heating. Sarif et al. [27] numerically studied viscous flow induced by extended plate using Newtonian heating through Keller Box technique. 3-Dimensional couple stress magnetohydrodynamic liquid flow with Newtonian heating is studied in [28]. Impact of viscous dissipation and Newtonian heating on nanoliquids flow towards a flat surface was investigated by Makinde [29]. The flow of Walters B liquid with Newtonian heating was reported in [30].

The heterogeneous homogeneous reactants and Newtonian heating phenomenon in flow of Walters B liquid along a stretched plate is investigated. Inclined MHD, Stagnant flow and Joule heating is also considered. The non-linear ODEs are solved by OHAM [31, 32]. Statistical approach is used to check the statistical significance of physical parameters and the drag forces/local Nusselt number. Significance of various sundry parameters on velocity, temperature and concentration fields, skin friction and Nusselt numbers are examined very carefully.

2 Formulation

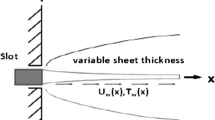
Walters B stagnation-point liquid flow with homogeneous and heterogeneous reactions over a stretched plate is considered here. The flow is confined to \(y\ge 0\). Applied magnetic field in such a way thats its making angle \(\psi \) with axis. Surface is also subjected to Newtonian heating. Contribution due to viscous-dissipation and Joule heating is present.

Simple homogeneous heterogeneous reactant model is [20]

$$\begin{aligned} \mathbf {A}+2\mathbf {B}\rightarrow 3\mathbf {B},\qquad \text {rate}=ab^{2}k_{1}. \end{aligned}$$
(1)

with

$$\begin{aligned} \mathbf {A}\rightarrow \mathbf {B},\qquad \text {rate}=ak_{2}\text {,} \end{aligned}$$
(2)

where (a, b) are concentrations of chemical species (\(\mathbf {A}, \mathbf {B}\)) on the other side, rate constants are presented as (\(k_{1},k_{2}\)). These reactants equations tells us that in external stream and at outer boundary layer edge, reaction rate is zero. The governing equations are [14, 15]

$$\begin{aligned} \frac{\partial \bar{v}}{\partial y}+\frac{\partial \bar{u}}{\partial x}=0, \end{aligned}$$
(3)
$$\begin{aligned}&\bar{u}\frac{\partial \bar{u}}{\partial x}+\bar{v}\frac{\partial \bar{u}}{\partial y} -\nu \frac{\partial ^{2} \bar{u}}{\partial y^{2}}+\frac{k_{0}}{\rho } \left[ \bar{u}\frac{\partial ^{3} \bar{u}}{\partial x\partial y^{2}}+\frac{\partial \bar{u}}{\partial x}\frac{\partial ^{2} \bar{u}}{\partial y^{2}}\right. \nonumber \\&\ \ \qquad \left. +\bar{v}\frac{\partial ^{3}u }{\partial y^{3}}-\frac{\partial \bar{u}}{\partial y}\frac{\partial ^{2} \bar{u}}{\partial x\partial y}\right] -U_{e}\frac{ dU_{e}}{dx} +\frac{\sigma B_{0}^{2}}{\rho }\sin ^{2}\psi \left( \bar{u}-U_{e}\right) = 0, \end{aligned}$$
(4)
$$\begin{aligned} \bar{u}\frac{\partial \bar{T}}{\partial x}+ \bar{v}\frac{\partial \bar{T}}{\partial y}-\frac{K}{\rho c_{p}}\frac{\partial ^{2} \bar{T}}{\partial y^{2}}-\frac{\sigma B_{0}^{2}}{\rho c_{p}}\sin ^{2}\psi \left( \bar{u}-U_{e}\right) ^{2}=0, \end{aligned}$$
(5)
$$\begin{aligned} \bar{u}\frac{\partial \bar{a}}{\partial x}+\bar{v}\frac{\partial \bar{a}}{\partial y}+k_{1}\bar{a} \bar{b}^{2}-D_{A}\frac{ \partial ^{2} \bar{a}}{\partial y^{2}}=0, \end{aligned}$$
(6)
$$\begin{aligned} \bar{u}\frac{\partial \bar{b}}{\partial x}+\bar{v}\frac{\partial \bar{b}}{\partial y}-k_{1}\bar{a}\bar{b}^{2}-D_{B}\frac{ \partial ^{2} \bar{b}}{\partial y^{2}}=0, \end{aligned}$$
(7)

with

$$\begin{aligned}&\bar{u}\left( x,0\right) =cx,\text { }\bar{v}(x,0)=0,\text { }\left. \frac{\partial \bar{T}}{\partial y}\right| _{y=0}=-h_{s}\bar{T}, \nonumber \\&D_{B}\left. \frac{\partial \bar{b}}{\partial y}\right| _{y=0}+k_{s}\bar{a}=0, D_{A}\left. \frac{\partial \bar{a}}{\partial y}\right| _{y=0}-k_{2}\bar{a} =0, \end{aligned}$$
(8)
$$\begin{aligned} \bar{u}\rightarrow U_{e}(x)=dx,\text { }\bar{T}\rightarrow \bar{T}_{\infty }\ \bar{a}\rightarrow \bar{a}_{0},\text { }\bar{b}\rightarrow 0\ \text {as}\ y\rightarrow \infty . \end{aligned}$$
(9)

\(\sigma \) electrical conductivity, \(B_{0}\) magnetic field, \(k_{0}\) liquid material parameters, \(U_{w}\) stretching velocity, T temperature, \(\nu \) kinematic viscosity, \(U_{e}\) free stream velocity, thermal conductivity denoted by K, \(\rho \) density of liquid, \(c_{p}\) specific heat, \(D_{B}\) and \(D_{A}\) diffusion species coefficients of B and A, \(T_{\infty }\) ambient liquid temperature, \(a_{0}\) positive dimensional constant, \(h_{s}\) denotes heat transfer coefficient and c represents stretching rate.

Introducing dimensionless variables

$$\begin{aligned}&\left. \bar{v}\left( x,y\right) =-\sqrt{c\nu }f\left( \eta \right) ,\text { } \bar{u}\left( x,y\right) =cxf^{\prime }\left( \eta \right) ,\right. \nonumber \\&\theta =\frac{\bar{T}-\bar{T}_{\infty }}{\bar{T}_{\infty }}, \text { }h(\eta )=\frac{\bar{b}}{\bar{a}_{0}},\text { }g(\eta )=\frac{\bar{a}}{\bar{a}_{0}},\text { }\eta =\sqrt{\frac{c}{\nu }}y. \end{aligned}$$
(10)

Thus

$$\begin{aligned} \begin{aligned}&f^{\prime \prime \prime }-\left( f^{\prime }\right) ^{2}-We\left[ 2f^{\prime }f^{\prime \prime \prime }-\left( f^{\prime \prime }\right) ^{2}-ff^{\left( iv\right) }\right] +ff^{\prime \prime }+A^{2}\\&\ \,\,\quad -M^{2}\sin ^{2}\psi \left( -A+ f^{\prime }\right) =0, \end{aligned} \end{aligned}$$
$$\begin{aligned} \text { }f^{\prime }\left( 0\right) =1,f^{\prime }\left( \infty \right) =A,\text { }f\left( 0\right) =0,\text { } \end{aligned}$$
(11)
$$\begin{aligned} \theta ^{\prime \prime }+\Pr f\text { }\theta ^{\prime }+M^{2}\Pr Ec\sin ^{2}\psi \left( f^{\prime }-A\right) ^{2}=0, \end{aligned}$$
$$\begin{aligned} \theta ^{\prime }(0)= -\gamma -\gamma \theta \left( 0\right) ,\text { }\theta (\infty )=0, \end{aligned}$$
(12)
$$\begin{aligned} \frac{1}{Sc}g^{\prime \prime }-Kgh^{2}+fg^{\prime }=0, \end{aligned}$$
$$\begin{aligned} g^{\prime }\left( 0\right) =K_{2}g(0),\text { }g\left( \infty \right) \rightarrow 1, \end{aligned}$$
(13)
$$\begin{aligned} \frac{\delta _{1}}{Sc}h^{\prime \prime }+Kgh^{2}+fh^{\prime }=0, \end{aligned}$$
$$\begin{aligned} \delta _{1}h^{\prime }\left( 0\right) =-K_{2}g(0),\text { }h\left( \infty \right) \rightarrow 0. \end{aligned}$$
(14)

Hartman number is denoted by M, ratio parameter is given by A, Weissenberg number denoted by We, Prandtl number is given by \(\Pr \), Eckert number is denoted by Ec and conjugate parameter is given by \(\gamma \), strength of homogeneous reactant parameter is denoted by K, \(\delta _{1}\) the ratio of mass diffusion coefficient, \(K_{2}\) the strength of heterogeneous reaction parameter and Sc the Schmidt number and defined as

$$\begin{aligned} M= & {} \sqrt{\frac{\sigma B_{0}^{2}}{\rho c}},\text { }\ \ \text { }A=\frac{a}{c },\text { }We=\frac{k_{0}c}{\mu _{0}},\text { }\Pr =\frac{\mu _{0}c_{p} }{K}, \nonumber \\ Ec= & {} \frac{U_{m}^{2}}{c_{p}T_{\infty }},\text { }\gamma =h_{s}\sqrt{ \frac{\nu }{a}},\text { }K=\frac{k_{1}a_{0}^{2}}{c}, \nonumber \\ K_{2}= & {} \frac{k_{2}l\mathop {\mathrm {Re}}_{x}^{-1/2}}{D},\text { }\delta _{1}=\frac{ D_{B}}{D_{A}},\ Sc=\frac{\nu }{D_{A}}. \end{aligned}$$
(15)

Where coefficients of diffusion of chemical species (\(\mathbf {B},\mathbf {A}\)) are of comparable size. This argument provides us to make further supposition that diffusion coefficients (\(D_{B},D_{A}\)) are equal i.e. \(\delta _{1}=1\) and therefore [12]:

$$\begin{aligned} h\left( \eta \right) +g\left( \eta \right) -1=0. \end{aligned}$$
(16)

Now Eqs. (13) and (14) yield

$$\begin{aligned} \frac{1}{Sc}g^{\prime \prime }-Kg\left( g-1\right) ^{2}+fg^{\prime }=0, \end{aligned}$$
(17)

with

$$\begin{aligned} g^{\prime }\left( 0\right) -K_{2}g\left( 0\right) =0 ,\text { }g\left( \eta \right) \rightarrow 1\text { as }\eta \rightarrow \infty \text {. } \end{aligned}$$
(18)

The expression of \(C_{fx}\) and \(Nu_{x}\) are

$$\begin{aligned} C_{fx}=\frac{\tau _{w}}{\rho U_{w}^{2}},\text { }Nu_{x}=\frac{ xq_{w}}{K\left( T-T_{\infty }\right) }, \end{aligned}$$
(19)

where

$$\begin{aligned} q_{w}=-K\left( \frac{\partial \bar{T}}{\partial y}\right) _{y=0}, \tau _{w}=\left[ \mu _{0}\frac{\partial \bar{u}}{\partial y}-k_{0}\left( \bar{v}\frac{\partial ^{2} \bar{u}}{\partial y^{2}} +\bar{u}\frac{\partial ^{2} \bar{u}}{\partial x\partial y} +2\frac{\partial \bar{u}}{\partial x}\frac{\partial \bar{u}}{\partial y}\right) \right] _{y=0}. \end{aligned}$$
(20)

Thus

$$\begin{aligned} \left( \mathop {\mathrm {Re}}_{x}\right) ^{1/2}C_{f}= f^{\prime \prime }\left( 0\right) -3We f^{\prime \prime }\left( 0\right) , \end{aligned}$$
(21)
$$\begin{aligned} \left( \mathop {\mathrm {Re}}_{x}\right) ^{-1/2}Nu_{x}=\gamma \left( 1+\frac{1}{\theta \left( 0\right) }\right) , \end{aligned}$$
(22)

where \(\mathop {\mathrm {Re}}_{x}=cx^{2}/\nu \) denotes local Reynolds parameter.

3 OHAM

The governing system of nonlinear ODEs are solved analytically by invoking reliable methodology called optimal homotopy analysis method. Average squared residual errors (ASRE) and corresponding optimal convergence control parameters are computed. Initial guesses and linear operators \(\left( f_{0},\theta _{0},L_{f},L_{\theta }\right) \) are

$$\begin{aligned} f_{0}\left( \eta \right) =A\eta -\left( A-1\right) \left( 1-\exp \left( -\eta \right) \right) ,\text { }\theta _{0}\left( \eta \right) =\frac{ \gamma \exp \left( -\eta \right) }{1-\gamma },\text { }g_{0}\left( \eta \right) =1-\frac{1}{2}\exp \left( -K_{2}\eta \right) , \end{aligned}$$
(23)
$$\begin{aligned} L_{f}\left[ f\left( \eta \right) \right] =\frac{d^{3}f}{d\eta ^{3}}-\frac{df }{d\eta },\text { }L_{\theta }\left[ \theta \left( \eta \right) \right] = \frac{d^{2}\theta }{d\eta ^{2}}-\theta ,\text { }L_{g}\left[ g\left( \eta \right) \right] =\frac{d^{2}g}{d\eta ^{2}}-g, \end{aligned}$$
(24)

satisfying the following properties

$$\begin{aligned} L_{f}\left[ \bar{C}_{1}+ \bar{C}_{2}e ^{\eta } + \bar{C}_{3}e ^{-\eta }\right] =0, \end{aligned}$$
(25)
$$\begin{aligned} L_{\theta }\left[ \bar{C}_{4} e^ {\eta } + \bar{C}_{5}e ^{-\eta } \right] =0, \end{aligned}$$
(26)
$$\begin{aligned} L_{g}\left[ \bar{C}_{6}e^ {\eta } + \bar{C}_{7}e ^{-\eta } \right] =0, \end{aligned}$$
(27)

in which \(\bar{C}_{i}\left( i=1,\ldots ,7\right) \) are constants.

4 Optimal Convergence Control Parameters

Convergence control parameters (\(\hslash _{f}\), \(\hslash _{\theta }\), \(\hslash _{g}\)) are calculated by BVPh2.0 package. These values can be obtained by minimizing total error. The average square residual error (ASRE) are used for minimizing the CPU time, at mth-order of approximation as follows

$$\begin{aligned} \varepsilon _{m}^{f}\left( \hslash _{f},\hslash _{\theta }\right) =\frac{1}{ 1+N_1}\sum _{j=0}^{N_1}\left[ \sum _{i=0}^{k}\left( f_{i}\right) _{\eta =j\pi } \right] ^{2}, \end{aligned}$$
$$\begin{aligned} \varepsilon _{m}^{\theta }\left( \hslash _{f},\hslash _{\theta }\right) = \frac{1}{1+N_1}\sum _{j=0}^{N_1}\left[ \sum _{i=0}^{k}\left( f_{i}\right) _{\eta =j\pi },\sum _{i=0}^{k}\left( \theta _{i}\right) _{\eta =j\pi }\right] ^{2}, \end{aligned}$$

and

$$\begin{aligned} \varepsilon _{m}^{g}\left( \hslash _{f},\hslash _{g}\right) =\frac{1}{1+N_1} \sum _{j=0}^{N_1}\left[ \sum _{i=0}^{k}\left( f_{i}\right) _{\eta =j\pi },\sum _{i=0}^{k}\left( g_{i}\right) _{\eta =j\pi }\right] ^{2}. \end{aligned}$$

The optimal values of \(\left( \hslash _{f},\hslash _{\theta },\hslash _{g}\right) \) are \(\hslash _{f}=-0.427635, \hslash _{\theta }=-0.8078\) and \(\hslash _{g}=-0.93495\). when \(A=0.1, We=0.2, \psi =\pi /3, \delta =0.2, K_{1}=1.5, \Pr =0.7, K_{2}=0.2, Ec=0.4\) and \(Sc=0.4\). In Fig. 1, corresponding total residual error is plotted. Optimal convergence control parameters are given in Table 1. Table 1 shows individual averaged squared residual errors of momentum, energy equations at various order of approximation. By increasing order of approximation, squared residual error decreases.

Fig. 1
figure 1

Total error versus order of approximations

Full size image
Table 1 ASREs at various order of approximations when \(\psi =\pi /3\), \(A=0.1\), \(We=0.2\), \(K_{2}=0.2\), \(\delta =0.2\), \(\Pr =0.7\), \(K_{1}=1.5\), \(Sc=0.4\) and \(Ec=0.4\) by means of optimal control parameters \(\hbar _{f}=-0.427635\), \(\hbar _{\theta }=-0.8078, \hbar _{g}=-0.93495\)
Full size table
Fig. 2
figure 2

a Impact of We on \(f^{\prime }\left( \eta \right) \). b Impact of M on \(f^{\prime }\left( \eta \right) \)

Full size image

5 Discussion

In this section, physical interpretation of the results for velocity, temperature and concentration fields are discussed.

Change in velocity field with an increment in We is plotted in Fig. 2a. When velocity of extending plate is larger than free stream velocity i.e. \(\left( A<1\right) \), velocity field reduces for larger values of We. However for \(A>1\), velocity profile rises. Irrespective of A, corresponding boundary layer thins with enhancement in We. Physically, larger values of We rises tensile stresses as a result oppose momentum transport. Consequently, boundary layer width reduces. Significance of M on \(f^{\prime }\) for both \(A>1\) and \(A<1\) cases are drawn in Fig. 2b. Enhancement in magnetic number corresponds the reduction in velocity field when \(A<1\) and reverse effect is observed on velocity field for \(A>1\). Since, applied transverse magnetic field creates a retardant force. It has ability to resist liquid motion and because of this reason, corresponding boundary layer width reduces for increment in magnetic field.

\(f^{\prime }\) is mounting function of A is reported in Fig. 3a. Boundary layer width rises with enhancement in A with \(A<1\), while thinner boundary layer becomes for case of enhancement in A provided \(A>1\). Additionally, no boundary layer is noted for \(A=1\).

Figure 3b is elucidated behavior of inclination angle \(\psi \) on \(f^{\prime }\left( \eta \right) \) for cases \(A<1\) and \(A>1\). It is noticed that velocity field is decreasing for \(\psi \) when \(A<1\) and reverse behavior is observed for \(A>1\). In fact, with augmented \(\psi \), significance of magnetic field on liquid particles rises because of rise in Lorentz force. Therefore, velocity field reduces. It is also examined that for \(\psi =0\), magnetic field impact on velocity profile is zero while for \(\psi =\pi /2\), maximum resistance is observed.

Fig. 3
figure 3

a Impact of A on \(f^{\prime }\left( \eta \right) \). b Impact of \(\Pr \) on \(\theta \left( \eta \right) \)

Full size image
Fig. 4
figure 4

a Impact of \(\Pr \) on \(\theta \left( \eta \right) \). b Impact of Ec on \(\theta \left( \eta \right) \)

Full size image
Fig. 5
figure 5

a Impact of \(\gamma \) on \(\theta \left( \eta \right) .\) b Impact of \(\psi \) on \(\theta \left( \eta \right) \)

Full size image

The ratio of momentum to thermal diffusivity is defined as Prandtl parameter which enhances pure convection but reduces conduction. Therefore, thermal boundary layer thins and heat transfer rate at surface rises for increment \(\Pr \) (see Fig. 4a).

Higher values of Eckert number, heat up liquid near vicinity of bounding surface and therefore, corresponding boundary layer width rises (Fig. 4b).

Effect of \(\gamma \), characterizing Newtonian heating strength on temperature field is sketched in Fig. 5a. It is examined that stronger convective heating permits thermal impact to penetrate deeper into quiescent liquid. Hence, corresponding thermal boundary layer width for larger \(\gamma \) surface heat flux, being proportional to \(\gamma \) is mounting function of \(\gamma \).

Figure 5b is drawn \(\psi \) on temperature distribution. Temperature field is increased for high values of \(\psi \). Because, higher \(\psi \) corresponds to increase magnetic field which opposes liquid flow. Therefore, rise in temperature field occur.

Fig. 6
figure 6

a Impact of \(K_{1}\) on \(g\left( \eta \right) \). b Impact of \(K_{2}\) on \(g\left( \eta \right) \). c Impact of Sc on \( g\left( \eta \right) \)

Full size image

Influence of \(K_1\) on concentration profile is investigated in Fig. 6a. Concentration field reduces. Additionally boundary layer width increases for higher strength of homogeneous reaction number.

Significance of \(K_{2}\) on concentration field is analyzed in Fig. 6b. Concentration field reduces near surface of plate and it rises away from surface for larger \(K_{2}\).

Effect of Sc on concentration field is illustrated in Fig. 6c. Concentration field decreases for higher Schmidt parameter. Additionally, solutal boundary layer width reduces. As Schmidt parameter is ratio of diffusivity of momentum to mass, so larger Schmidt parameter corresponds to little mass diffusivity. Consequently, concentration profile reduces.

Friction and local Nusselt numbers for different values of sundry parameters are provided in Tables 2 and 3. Friction coefficient is enhanced by increasing M, We, \(\psi \) and A. On other side, local Nusselt parameter rises for increment in \(M, A, We, \gamma \) and \(\Pr \) while it reduces for large \(\psi \) and Ec.

Table 2 Variation of skin friction coefficient for various values of physical parameter
Full size table
Table 3 Numerical values of Nusselt number
Full size table

6 Statistical Paradigm

We lengthen our examination for different out-turn of significant parameters on the inspected issue. Arranged by need to comprehend correlation between different sundry parameter and friction coefficient (F.C.) and furthermore for Nusselt number. We revealed estimations of F.C. in Table 2 and Nusselt number in Table 3. The estimations of correlation coefficients (c.c) are examined and recorded in Tables 4 and 5 concerning F.C. and Nusselt number. It is evident that estimation of c.c is limited between (\(-1,1\)). Moreover absolute value is limited somewhere in range of 0 and 1. The c.c is not just investigate the connection between two variates yet in addition uncovers the opposite and direct correspondence between them.

The c.c has accompanying interpretations:

  • Positive perfect linear relationship of variables occurs if \(r=1\).

  • Negative perfect linear relationship of variables occurs if \(r=-1\).

  • Strong +ve linear relationship of variables occurs if \(0.7\le r\le 1\).

  • Strong −ve linear relationship of variables occurs if \(-1\le r\le -0.7\).

  • No linear relationship of variables holds if \(r=0\). It is noted from Table 4, that strongly positive correlation is hold for friction coefficient according to all physical attributes under study. Whereas for the Nusselt number, we have found positive and negative correlation for all the parameters in Table 5.

Table 4 Correlation coefficient for skin friction coefficient
Full size table
Table 5 Correlation coefficient for Nusselt number
Full size table

7 Probable Error (P.E.)

The P.E. of c.r. can be computed by invoking following formula

$$\begin{aligned} P.E.\left( r\right) =0.6745\frac{\left( 1-r^{2}\right) }{\sqrt{n}}, \end{aligned}$$

where c.c. is denoted by r and number of observations is denoted by n. The c.c. is insignificant if r is less than P.E. This shows that no correlation between variables exists. The correlation is said to be certain when value of r is 6 times more than the P.E. and insignificant when r is less than \(P.E.\left( r\right) \). This reveals that r is significant. Thus P.E. is computed to see reliability of value of c.c. Probable error of friction and local Nusselt number are given in Tables 6 and 7. It is noted that for insignificant correlation \(r<P.E.\left( r\right) \), and for significant correlation \(r>6P.E.\left( r\right) \).

Table 6 P.E. for skin friction coefficient
Full size table
Table 7 P.E. for Nusselt number
Full size table

7.1 Statistical Proclamation

Tables 8 and 9 are made for values of \(\frac{r}{P.E.\left( r\right) }\). From these tables, it is noted that all values are satisfied abovementioned relation (see Table 8). Also, for \(\psi \) and \(Ec, r < P.E.\left( r\right) \) which tells us the statistically insignificance of correlation coefficient. For \(r=1\), we obtain perfect significant correlation. Consequently, here correlation coefficients are remarkable and parameters are greatly interconnected to physical attributes (see Tables 8 and 9).

Table 8 Values of \(\frac{r}{P.E.\left( r\right) }\) for skin friction coefficient
Full size table
Table 9 Values of \(\frac{r}{P.E.\left( r\right) }\) for Nusselt number
Full size table

8 Conclusions

Here we studied significance of homogeneous/heterogeneous reactants and inclined MHD in stagnant point flow of Walters’ B liquid. Heat transfer phenomenon using Newtonian heating is carried out. The key points are mentioned below.

  • \(f^{\prime }(\eta )\) is decaying function of M and We for \(A<1\), while it is mounting function of M and We according to \(A>1\).

  • Increment in M and We corresponds to a thinner momentum boundary layer.

  • Significance rise is noted in temperature profile for higher conjugate parameter.

  • Strongly positive correlation exists for friction coefficient according to all the physical attributes on the contrary the negative relation is observed for \(\psi \) and Ec with the Nusselt number.