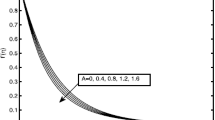1 Introduction

An impressive consideration has been given to heat conduction [1,2,3] because of its ample applications in several fields. The traditional one-dimensional (1D) fundamental model to characterize heat conduction is analyzed through Fourier’s relation [4]. This yields an approach to analyze heat conduction and develops the foundation to investigate the thermal process of heat transfer in recent years. However, an ambiguity of Fourier’s model [5,6,7] is that the whole structure is affected directly by the original disruption. Such behavior disprove the causality principle [8, 9] through heat conduction paradox. Cattaneo [10] recommended a generalized model which yields the relaxation factor into account. The Cattaneo basic expression only comprises partial time derivatives whereas larger spatial gradients might be needed [11] for the entire process. Hence, modifying the “time derivative” by “Oldroyds’ upper-convected derivative,” Christov [12] recommended the frame-indifferent modification of the Cattaneo expression:

$$ \mathbf{q}+\lambda \left(\frac{\partial \mathbf{q}}{\partial t}+\mathbf{v}.\mathbf{\nabla}\mathbf{q}-\mathbf{q}.\mathbf{\nabla}\mathbf{v}+\left(\mathbf{\nabla}.\mathbf{v}\right)\mathbf{q}\right)=- k\operatorname{grad} T. $$

Here (q, λ, v, k, T) indicate heat flux, thermal relaxation parameter, velocity, thermal conductivity, and temperature, respectively. The aforementioned expression justifies objectivity principle and fascinates the attention of recent investigators [13,14,15,16,17,18,19,20,21,22,23,24,25].

Fluid flow and heat transport characteristics over a flat or stretched surface have turned to be the ground of great importance due to their numerous applications in plastic and rubber sheet manufacturing, filaments and polymer sheets, glass blowing, etc. Stretching flow towards a flat surface is firstly explored by Crane [26]. Moreover, plates in usage with variable thickness are utilized in marine and aeronautical configurations and mechanical and civil engineering. For reliable and effective design, it is essential to consider buckling loads for these plates. No doubt the usage of variable thickness supports to decrease the load of mechanical elements and develop the effectiveness of materials [27]. Few studies comprising the simultaneous characteristics of variable thickness and heat transfer can be found in the attempts [28,29,30,31,32].

Although required in definite utilizations, thermal stratification influences the performance of the condenser and could be destructive for structural reliability of the pool walls prepared through concrete. Analysis on rigidly stratified medium demonstrates that stationary regions are energetic at the boundary of cold and hot water, which minimizes the service lifetime of plants and several demanding components [33]. For instance, the blight heat elimination process in fast devices encounters the phenomenon of stratification at relatively high temperature producing exhaustion in nuclear mechanisms. Thus, from the structural security opinion as well, stratified coolant aspects are significant [34]. Representative studies on thermal stratification are given in [35,36,37]. Moreover, the ability of a substance to control heat is recognized as thermal conductivity. It is either constant or differs with temperature linearly for liquid metals from 0 to 400 °F [38]. Representative investigations regarding this topic can be mentioned through [39,40,41,42] and several studies therein.

The current investigation intends to analyze the non-Fourier flux characteristics in flow of Walter-B material over the surface with variable thickness. Stagnation velocity is considered nonlinear. Heat transfer in the presence of thermal stratification and temperature-dependent thermal conductivity is analyzed. A homotopic algorithm [43,44,45,46,47,48,49,50] is utilized to obtain convergent expressions. Graphical trends for several significant variables versus velocity and temperature fields are discussed in detail.

2 Formulation

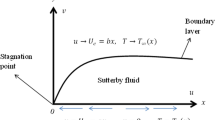
Here steady two-dimensional stagnation point flow of Walter-B material towards a surface moving with nonlinear velocity is modeled. A stretching surface of variable thickness generates the flow. Heat transfer via non-Fourier flux theory is investigated. Thermal stratification along with temperature-dependent thermal conductivity is retained. Viscous dissipation effects are not accounted. The governing equations are

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, $$
(1)
$$ u\frac{\partial u}{\partial x}+ v\frac{\partial u}{\partial y}={U}_e\frac{dU_e}{dx}+\frac{\mu_0}{\rho}\left(\frac{\partial^2 u}{\partial {y}^2}\right)-\frac{k_0}{\rho}\left(\begin{array}{c}\hfill u\frac{\partial^3 u}{\partial x\partial {y}^2}+ v\frac{\partial^3 u}{\partial {y}^3}\hfill \\ {}\hfill -\frac{\partial u}{\partial y}\frac{\partial^2 u}{\partial x\partial y}+\frac{\partial v}{\partial y}\frac{\partial^2 u}{\partial {y}^2}\hfill \end{array}\right), $$
(2)
$$ u\frac{\partial T}{\partial x}+ v\frac{\partial T}{\partial y}+\lambda \left(\begin{array}{c}\hfill u\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}+ v\frac{\partial v}{\partial y}\frac{\partial T}{\partial y}+ u\frac{\partial v}{\partial x}\frac{\partial T}{\partial y}+ v\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}\hfill \\ {}\hfill +2 uv\frac{\partial^2 T}{\partial x\partial y}+{u}^2\frac{\partial^2 T}{\partial {x}^2}+{v}^2\frac{\partial^2 T}{\partial {y}^2}\hfill \end{array}\right)=\frac{1}{\rho {c}_p}\frac{\partial }{\partial y}\left( k(T)\frac{\partial T}{\partial y}\right), $$
(3)
$$ u={U}_w( x)={U}_0{\left( x+ b\right)}^n, v=0, T={T}_w={T}_0+ c\left( x+ b\right)\ \mathrm{at}\ y={A}_1{\left( x+ b\right)}^{\frac{1- n}{2}}, $$
(4)
$$ u\to {U}_e(x)={U}_{\infty }{\left( x+ b\right)}^n, T\to {T}_{\infty }={T}_0+ d\left( x+ b\right)\ \mathrm{when}\ y\to \infty . $$
(5)

Here (u, v) specify the liquid velocities parallel to horizontal and vertical directions, \( \nu =\left(\frac{\mu}{\rho}\right) \) the kinematic viscosity, ρ the fluid density, (k0, μ0) the short memory coefficient and restricting viscosity at low shear rate, (Uw(x), Ue(x)) the stretching and free stream velocities, (T, T∞) the fluid and ambient fluid temperature, (U0) the reference velocity, (b, c, d) the dimensional constants, A1 the small variable with respect to the surface is adequately thin, and k(T) the temperature-dependent thermal conductivity, which is given as [20]

$$ k(T)={k}_{\infty}\left(1+\varepsilon \frac{T-{T}_{\infty }}{\nabla T}\right). $$
(6)

Here, ambient fluid thermal conductivity is denoted by k∞, ε is the small parameter which characterizes the behavior of temperature on thermal conductivity and ∇T = T − T0. Also, the type of motion, surface shape and characteristics of the boundary layer can be controlled through the parameter n. It is worth pointing that the present analysis reduced to a surface with growing thickness and convex outer shape, whereas the analysis converted to a surface with growing thickness and convex outer shape when n < 1. Also, for n = 0, the motion is reduced to a linear case with constant velocity. Considering [16],

$$ \begin{array}{c}\psi =\sqrt{\frac{2}{n+1}\nu {U}_0{\left( x+ b\right)}^{n+1}} F\left(\xi \right),\xi =\sqrt{\frac{n+1}{2}\frac{U_0}{\nu}{\left( x+ b\right)}^{n-1}} y, u={U}_0{\left( x+ b\right)}^n{F}^{\prime}\left(\xi \right),\\ {} v=-\sqrt{\frac{n+1}{2}\nu {U}_0{\left( x+ b\right)}^{n-1}}\left( F\left(\xi \right)+\eta \frac{n-1}{n+1}{F}^{\prime}\left(\xi \right)\right),\Theta \left(\xi \right)=\frac{T-{T}_{\infty }}{T_w-{T}_0},\end{array} $$
(7)

the continuity equation ((1)) is fulfilled automatically and the emerging nonlinear problems in F and Θ are

$$ {F}^{\hbox{'}\hbox{'}\hbox{'}}-\frac{2 n}{n+1}{F}^{\prime 2}+{ F F}^{\hbox{'}\hbox{'}}+\beta \left(\frac{3 n-1}{2}{F}^{\prime \prime 2}-\left(3 n-1\right){F}^{\hbox{'}}{F}^{\hbox{'}\hbox{'}\hbox{'}}+\frac{n+1}{2}{F F}^{iv}\right)+\frac{2 n}{n+1}{A}^2=0, $$
(8)
$$ \left(1+\varepsilon \Theta \right)\;{\Theta}^{{\prime\prime} }+\varepsilon {\Theta}^{\prime 2}+ \Pr F{\Theta}^{\prime }+ \Pr \gamma \left(\begin{array}{c}\hfill \frac{n-3}{2} F{F}^{\prime }{\Theta}^{\prime}\hfill \\ {}\hfill -\frac{n+1}{2}{F}^2{\Theta}^{{\prime\prime}}\hfill \end{array}\right)+ \Pr \left( S+\Theta \right)\;\left(\begin{array}{c}\hfill \gamma F{F}^{{\prime\prime}}\hfill \\ {}\hfill -\frac{2 n}{n+1}\gamma {F}^{\prime 2}-\frac{2}{n+1}{F}^{\prime}\hfill \end{array}\right)=0, $$
(9)
$$ F\left(\alpha \right)=\alpha \frac{1- n}{1+ n},{F}^{\prime}\left(\alpha \right)=1,{F}^{\prime}\left(\infty \right)= A, $$
(10)
$$ \Theta \left(\alpha \right)=1- S,\Theta \left(\infty \right)=0. $$
(11)

Here, prime signifies differentiation with respect to ξ and \( \alpha ={A}_1\sqrt{\frac{n+1}{2}\frac{U_0}{v}}. \) Letting F(ξ) = f(ξ − α) = f(η) and Θ(ξ) = θ(ξ − α) = θ(η), Eqs. (8)–(11) yield

$$ {f}^{\hbox{'}\hbox{'}\hbox{'}}-\frac{2 n}{n+1}{f}^{\prime 2}+{ f f}^{\hbox{'}\hbox{'}}+\beta \left(\frac{3 n-1}{2}{f}^{\prime \prime 2}-\left(3 n-1\right){f}^{\hbox{'}}{f}^{\hbox{'}\hbox{'}\hbox{'}}+\frac{n+1}{2}{f f}^{iv}\right)+\frac{2 n}{n+1}{A}^2=0, $$
(12)
$$ \left(1+\varepsilon \theta \right)\;{\theta}^{{\prime\prime} }+{\varepsilon \theta}^{\prime 2}+ \Pr f{\theta}^{\prime }+ \Pr \gamma \left(\begin{array}{c}\hfill \frac{n-3}{2} f{f}^{\prime }{\theta}^{\prime}\hfill \\ {}\hfill -\frac{n+1}{2}{f}^2{\theta}^{{\prime\prime}}\hfill \end{array}\right)+ \Pr \left( S+\theta \right)\;\left(\begin{array}{c}\hfill \gamma f{f}^{{\prime\prime}}\hfill \\ {}\hfill -\frac{2 n}{n+1}\gamma {f}^{\prime 2}-\frac{2}{n+1}{f}^{\prime}\hfill \end{array}\right)=0, $$
(13)
$$ f(0)=\alpha \frac{1- n}{1+ n},\kern0.75em {f}^{\prime }(0)=1,{f}^{\prime}\left(\infty \right)= A, $$
(14)
$$ \theta (0)=1- S,\theta \left(\infty \right)=0, $$
(15)

where A\( \left(=\frac{U_{\infty }}{U_0}\right) \) represents the ratio of velocities, Pr\( \left(=\frac{\mu {c}_p}{k}\right) \) the Prandtl number, \( \beta \left(=\frac{k_0{U}_0{\left( x+ b\right)}^{n-1}}{\mu_0}\right) \) the local Weissenberg number, S\( \left(=\frac{d}{c}\right) \) the thermal stratification parameter, and γ(=λU0(x + b)n − 1) the relaxation factor.

Our analysis reduces to Fourier’s situation when γ = 0 in Eq. (13).

The skin friction coefficient is defined as

$$ {C}_f=\frac{\tau_w}{\frac{1}{2}\rho {u}_w^2}, $$
(16)

with

$$ {\tau}_w={\mu}_0{\left(\frac{\partial u}{\partial y}\right)}_{y={A}_1{\left( x+ b\right)}^{\frac{1- n}{2}}}-{k}_0{\left( u\frac{\partial^2 u}{\partial x\partial y}-2\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}\right)}_{y={A}_1{\left( x+ b\right)}^{\frac{1- n}{2}}}. $$
(17)

Utilizing Eq. (17) in Eq. (16), the dimensionless form of the skin friction coefficient is given below:

$$ \sqrt{\mathrm{R}{\mathrm{e}}_x}{C}_f=\sqrt{\frac{n+1}{2}}{\left(\left[1-\beta \left(\frac{7 n-1}{2}{f}^{\prime }-2\eta \frac{n-1}{2}{f}^{\prime \prime}\right)\right]\kern.2em {f}^{\prime \prime }+\beta \eta \frac{n-1}{2}{f}^{\prime }{f}^{\prime \prime \prime}\right)}_{\eta =0}, $$
(18)

with Rex = uw(x)(x + b)/ν showing the local Reynolds number.

3 Series solutions via homotopic procedure

Our intention here is to compute the convergent solution expressions for Eqs. (12) and (13) along with conditions (14) and (15). For this purpose, the initial approximations and linear operators are considered as

$$ {f}_0\left(\eta \right)= A\eta +\left(1- A\right)\kern.2em \left(1-{e}^{-\eta}\right)+\alpha \frac{1- n}{1+ n},{\theta}_0\left(\eta \right)=(1- S){e}^{-\eta}, $$
(19)
$$ {L}_f={f}^{{\prime\prime\prime} }-{f}^{\prime },{L}_{\theta}={\theta}^{{\prime\prime} }-\theta, $$
(20)

with

$$ {L}_f\left({C}_1+{C}_2{e}^{\eta}+{C}_3{e}^{-\eta}\right)=0,{L}_{\theta}\left({C}_4{e}^{\eta}+{C}_5{e}^{-\eta}\right)=0, $$
(21)

in which Ci(i = 1 − 5) signify the arbitrary constants.

Convergence of secured obtained solutions is verified through the homotopy analysis method (HAM). Auxiliary variables (ℏf,  ℏθ) involved in formulated series solutions are significant for such motivation. Thus, Figs. 1 and 2 highlight the plots for 12th order of approximations. The values verifying the convergence are in the ranges −1.40 ≤ ℏf ≤  − 0.20 and −1.65 ≤ ℏθ ≤  − 0.90.

Fig. 1
figure 1

ℏ-curve for f'

Full size image
Fig. 2
figure 2

ℏ-curve for θ

Full size image

4 Discussion

This section highlights the salient characteristics of the ratio of velocities (A), Prandtl number (Pr), local Weissenberg number (β), thermal stratification parameter (S), thermal relaxation factor (γ), and power index (n) on velocity f′(η) and temperature θ(η) through Figs. 3, 4, 5, 6, 7, 8, 9, and 10.

Fig. 3
figure 3

A variation on f'

Full size image
Fig. 4
figure 4

β variation on f'

Full size image
Fig. 5
figure 5

n variation on f'

Full size image
Fig. 6
figure 6

n variation on θ

Full size image
Fig. 7
figure 7

ε variation on θ

Full size image
Fig. 8
figure 8

γ variation on θ

Full size image
Fig. 9
figure 9

Pr variation on θ

Full size image
Fig. 10
figure 10

S variation on θ

Full size image

Figure 3 communicates the behavior of A on f′(η). It is remarked that f′(η) boosts via larger A. Impact of β on f′(η) is reported through Fig. 4. Larger β reduces f′(η), which relates to a thinner momentum layer. Physically, viscoelasticity yields tensile stress which diminishes the boundary layer and thus f′(η) reduces. Figure 5 characterizes the features of n on f′(η). Clearly f′(η) shows increasing behavior for larger n. Actually, stretching velocity rises for larger n and consequently more deformation in the fluid is generated. Thus, f′(η) rises.

Characteristics of n on θ(η) are disclosed through Fig. 6. It is explored that both θ(η) and thermal layer thickness boost for larger n. Effect of ε on θ(η) is portrayed via Fig. 7. Here, θ(η) augments when ε is increased. In fact, thermal conductivity rises through larger ε, due to which a considerable amount of heat moves from the sheet to the material. Therefore, θ(η) augments. Figure 8 highlights the influence of γ on θ(η). Here, θ(η) decays for higher γ. From the physical point of view, elements of the material need more time to transport heat to its adjacent elements, due to which θ(η) decays. Salient features of S on θ(η) is depicted in Fig. 9. It is noticed that θ(η) and the associated layer thickness decay for higher S. Physically, temperature difference reduces between the surface of the sheet and liquid, which generates the reduction in θ(η). Figure 10 explores the impact of Pr on θ(η). As expected, θ(η) and the corresponding layer thickness reduce when Pr is enhanced. An enhancement in Pr corresponds to a slow rate of thermal diffusion.

Convergence of series solution is verified numerically through Table 1. It is noticed that the 25th order of deformations are acceptable regarding convergent expressions of velocity and temperature. Characteristics of β and A on surface drag force \( \left({C}_f\mathrm{R}{\mathrm{e}}_x^{1/2}\right) \) is disclosed through Table 2. Here, \( {C}_f\mathrm{R}{\mathrm{e}}_x^{1/2} \) decays via larger β and A. Table 3 delivers the comparative analysis of skin friction coefficient (i.e., when β = 0 and n = 1) with the work of Mahapatra and Gupta [51]. Reasonable agreement is observed.

Table 1 Convergence of HAM expression for various orders of deformations when  n = 1.5, A = γ = K2 = 0.2,K1 = 0.1,S = 0.3, α=ε = 0.5, Pr = 1.2, and ℏf = ℏθ =  − 0.9
Full size table
Table 2 Skin friction \( \left({C}_f\mathrm{R}{\mathrm{e}}_x^{1/2}\right) \) for distinct values of parameters β and A when n = 1.5, γ=0.2,S = 0.3, ε = 0.5,α = 0.2, and Pr = 1.2
Full size table
Table 3 Comparative analysis of obtained results of f″(0) with [51] when n = 1 and β = 0
Full size table

5 Final remarks

Here non-Fourier heat flux in stagnation point flow towards nonlinear stretching flow of Walter’s B material is addressed. The main findings are summarized below.

  • There is reverse behavior of A and β on f′(η) qualitatively.

  • Temperature (θ(η)) via γ and Pr is less when compared with ε.

  • Fourier’s expression has high temperature in comparison to non-Fourier expression.

  • Surface drag force decays for larger A and β.

  • Viscous material results can be achieved by putting β = 0.