Theoretical and analytical analysis of shear rheology of Oldroyd-B fluid with homogeneous–heterogeneous reactions

Abstract

This research article communicates an analytical investigation for the three-dimensional steady incompressible flow of Oldroyd-B fluid subject to stretchable surface. The flow of material induced through stretchable surface with Darcy-Forchheimer medium. Homogeneous–heterogeneous reactions is considered. Convective boundary conditions and heat source/sink effects are considered for the heat transport. Boundary layer concept is used in the development of flow problem. Series solutions are obtained of the nonlinear system through homotopy technique. Physical significance of pertinent parameters are discussed and plotted graphically. Heat transfer rate is discussed numerically.

Introduction

Non Newtonian materials play an imperative role in frequent mechanical and industrial engineering and branches of applied science. The non-Newtonian materials are divided into three different categories, namely integral, differential and rate types. There are numerous non-Newtonian material models like Jeffrey model, Eyring model, Prandtl Eyring model, Casson model, second grade, Sisko model, Oldroyd-B model, Carreaue model and so on. Here we have considered Oldroyd-B model which is a rate material that exhibits properties of retardation and relaxation times. Zhang et al. (2016) discussed heat transport characteristics in flow of Oldroyd-B nanoliquid subject to time-dependent thin-film stretchable sheet. Shivakumara et al. (2015) scrutinized thermal convective instability in nanoliquid flow of Oldroyd-B fluid over a porous medium. Forced convective nanomaterial flow of Oldroyd-B fluid between two isothermal stretchable disks with magnetic field is examined by Hashmi et al. (2017). Zhang et al. (2018) explored thin-flim flow of Oldroyd-B nanoliquid with Cattaneo-Christov double diffusion. They also considered chemical reaction and dissipation effects. Shehzad et al. (2014) scrutinized 3D-forced convective Oldroyd-B fluid flow with thermophoresis and Brownian diffusions. Kumar et al. (2018) worked on the nanomaterial flow of Oldroyd-B fluid subject to radiative flux and dissipation. Electrical conducting nanomaterial flow of non-Newtonian liquid subject to porous stretchable sheet is investigated by Das et al. (2018). Gireesha et al. (2018) discussed heat and mass transport in nanoliquid flow of Oldroyd-B material with heat source/sink by a stretchable surface. Khan and Mahmood (2016) discussed combined effects of heat source/sink and thermophoretic diffusion in nanoliquid flow of non-Newtonian fluid inside stretchable disks. Flow of Oldroyd-B nanomaterial with heat source/sink and radiative flux is explored by Waqas et al. (2017a). Refs. Shehzad (2018), Hayat et al. (2016a, b, 2017a, b, c, d, e, 2018a, b), Khan et al. (2016, 2017a, b, c, d, e, f, 2018a, b), Muhammad et al. (2017), Ellahi et al. (2014a, b, 2016), Meraj et al. (2017), Alamri et al. (2019), Akbarzadeh et al. (2018), Hassan et al. 2018), Rashidi et al. (2018), Tamoor et al. (2017), Waqas et al. (2017b) represent various fluid models subject to different flow assumptions.

Keeping such effectiveness in mind, we have considered 3D cubic chemical reactive flow of Oldroyd-B material subject to Darcy-Forchheimer porous medium. Series solutions are developed through homotopy technique (Shirkhani et al. 2018; Hayat et al. 2017f; Fagbade et al. 2018; Khan et al. 2017g, h, 2018c; Skoneczny and Skoneczny 2018; Khan et al. 2019; Naghshband and Araghi 2018; Hayat et al. 2018c, d, e; Raftari and Vajravelu 2012; Xinhui et al. 2012; Han et al. 2014; Turkyilmazoglu 2010a, b, 2014; Ahmad et al. 2018; Abbasi et al. 2019). Heat transfer rate is deliberated in tabular form.

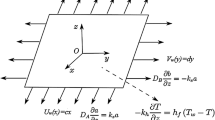
Modeling

The cubic autocatalysis at the surface is defined as follows:

$$A^{ * } + 2B^{ * } \to 3B^{ * } ,\,{\text{ rate}} = k_{\text{c}} a^{ * * } b^{2} ,\,$$

(1)

and

$$A^{ * } \to B^{ * } ,\,{\text{ rate}} = k_{\text{s}} a^{ * * } ,\,$$

(2)

where $a^{ * * }$ and $b$, respectively, indicate the concentrations of species $A^{ * }$ and $B^{ * }$ and $k_{\text{c}}$ and $k_{\text{s}}$ are the rate constants.

In component form, the flow equations are as defined by Shehzad et al. (2014):

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0,\,$$

(3)

$$\left. \begin{aligned} u\frac{\partial u}{\partial x} & + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} + \lambda_{1} \left( {\begin{array}{*{20}c} {u^{2} \tfrac{{\partial^{2} u}}{{\partial x^{2} }} + v^{2} \tfrac{{\partial^{2} u}}{{\partial y^{2} }} + w^{2} \tfrac{{\partial^{2} u}}{{\partial z^{2} }} + 2uv\tfrac{{\partial^{2} u}}{\partial x\partial y}} \\ { + 2vw\tfrac{{\partial^{2} u}}{\partial y\partial z} + 2uw\tfrac{{\partial^{2} u}}{\partial x\partial z}} \\ \end{array} } \right) \\ & \;\; - \nu \left[ {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \lambda_{2} \left( {\begin{array}{*{20}c} {u\tfrac{{\partial^{3} u}}{{\partial x\partial z^{2} }} + v\tfrac{{\partial^{3} u}}{{\partial y\partial z^{2} }} + w\tfrac{{\partial^{3} u}}{{\partial z^{3} }}} \\ { - \tfrac{\partial u}{\partial x}\tfrac{{\partial^{2} u}}{{\partial z^{2} }} - \tfrac{\partial u}{\partial y}\tfrac{{\partial^{2} v}}{{\partial z^{2} }} - \tfrac{\partial u}{\partial z}\tfrac{{\partial^{2} w}}{{\partial z^{2} }}} \\ \end{array} } \right)} \right] - \frac{\nu }{K}u - Fu^{2} = 0 \\ \end{aligned} \right\},$$

(4)

$$\left. \begin{aligned} u\frac{\partial v}{\partial x} & + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} + \lambda_{1} \left( {\begin{array}{*{20}c} {u^{2} \tfrac{{\partial^{2} v}}{{\partial x^{2} }} + v^{2} \tfrac{{\partial^{2} v}}{{\partial y^{2} }} + w^{2} \tfrac{{\partial^{2} v}}{{\partial z^{2} }}} \\ { + 2uv\tfrac{{\partial^{2} v}}{\partial x\partial y} + 2vw\tfrac{{\partial^{2} v}}{\partial y\partial z} + 2uw\tfrac{{\partial^{2} v}}{\partial x\partial z}} \\ \end{array} } \right) \\ & \;\; - \nu \left[ {\frac{{\partial^{2} v}}{{\partial z^{2} }} + \lambda_{2} \left( {\begin{array}{*{20}c} {u\tfrac{{\partial^{3} v}}{{\partial x\partial z^{2} }} + v\tfrac{{\partial^{3} v}}{{\partial y\partial z^{2} }} + w\tfrac{{\partial^{3} v}}{{\partial z^{3} }}} \\ { - \tfrac{\partial v}{\partial x}\tfrac{{\partial^{2} u}}{{\partial z^{2} }} - \tfrac{\partial v}{\partial y}\tfrac{{\partial^{2} v}}{{\partial z^{2} }} - \tfrac{\partial v}{\partial z}\tfrac{{\partial^{2} w}}{{\partial z^{2} }}} \\ \end{array} } \right)} \right] - \frac{\nu }{K}v - Fv^{2} \\ \end{aligned} \right\},$$

(5)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = \frac{k}{{\rho c_{\text{p}} }}\frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{{Q_{0} }}{{\rho c_{\text{p}} }}\left( {T - T_{\infty } } \right),$$

(6)

$$u\frac{{\partial a^{ * * } }}{\partial x} + v\frac{{\partial a^{ * * } }}{\partial y} + w\frac{{\partial a^{ * * } }}{\partial z} = D_{\text{A}} \frac{{\partial^{2} a^{ * * } }}{{\partial z^{2} }} - k_{\text{c}} a^{ * * } b^{2} ,$$

(7)

$$u\frac{\partial b}{\partial x} + v\frac{\partial b}{\partial y} + w\frac{\partial b}{\partial z} = D_{\text{B}} \frac{{\partial^{2} a}}{{\partial z^{2} }} + k_{\text{c}} a^{ * * } b^{2} ,$$

(8)

With

$$\left. \begin{aligned} u = & u_{w} \left( x \right) = ax,\, \, v = 0,\, \, w = 0,\, \, - k\frac{\partial T}{\partial z} = h_{\text{f}} \left( {T_{\text{f}} - T} \right)\,{\text{ at}}z = 0 \\ D_{\text{A}} \frac{{\partial a^{ * * } }}{\partial z} = & k_{s} a^{ * * } ,\, \, D_{\text{B}} \frac{\partial b}{\partial z}{\mathbf{ = - }}k_{\text{s}} a^{ * * } {\text{ at }}z = 0 \\ u \to & 0,\, \, v \to 0,\, \,\, \, T \to T_{\infty } ,\, \, a^{ * * } \to a_{0} ,\, \, b \to 0{\text{ at }}z = \infty \\ \end{aligned} \right\},$$

(9)

where $x,y,z$ denote the Cartesian coordinates, $u,v,w$ velocity components, $\rho$ the density, $\nu$ the kinematic viscosity, $\lambda_{1}$ and $\lambda_{2}$ represent the relaxation and retardation time, $F\left( { = \tfrac{{C_{b} }}{{K^{1/2} }}} \right)$ the coefficient of non-uniform inertia, $\nu = \left( {\frac{\mu }{\rho }} \right)$ the kinematic viscosity, $K$ the permeability of porous medium, $C_{\text{b}}$ the drag coefficient, $T$ is constant surface temperature, $k$ the thermal conductivity, $c_{\text{p}}$ the specific heat, $T_{\infty }$ the ambient temperature, $Q_{0}$ the heat source/sink coefficient, $D_{\text{A}}$ and $D_{\text{B}}$ the diffusion coefficients, $a_{0}$ the positive constant and $T_{\text{f}} ,\;h_{\text{f}}$ the fluid temperature and heat transfer coefficient.

Considering

$$\left. \begin{aligned} \zeta = & \sqrt {\frac{a}{v}} z, \, u{\mathbf{ = }}axf^{\prime}(\zeta ),\, \, v = ayg(\zeta ),\, \, w = - \left( {av} \right)^{{\tfrac{1}{2}}} f(\zeta ),\,\; \\ \theta (\zeta ) = & \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\;\;a^{**} = a_{0} \phi (\zeta ),\;\;b = a_{0} h(\zeta )\;\ \\ \end{aligned} \right\}.$$

(10)

we have

$$f^{\prime\prime\prime} + \varLambda f^{\prime} + \beta_{1} \left( {2ff^{\prime}f^{\prime\prime} - f^{2} f^{\prime\prime\prime}} \right)\, + ff^{\prime\prime} + \beta_{2} \left( {f^{\prime \prime 2} - f^{\prime}f^{(4)} } \right) - \left( {1 + F_{\text{r}} } \right)\,f^{\prime 2} = 0,$$

(11)

$$g^{\prime\prime} - \varLambda g + fg^{\prime} - f^{\prime}g + \beta_{1} \left( {2ff^{\prime}g^{\prime} - f^{2} g^{\prime\prime}} \right)\, + \beta_{2} \left( {f^{\prime}g^{\prime\prime} - fg^{\prime\prime\prime} - gf^{\prime\prime\prime} + g^{\prime}f^{\prime\prime}} \right) - F_{\text{r}} g^{2} = 0,$$

(12)

$$\theta^{\prime\prime} + \mathop {\Pr }\limits \left( {f\theta^{\prime} + S\theta } \right) = 0,\,$$

(13)

$$\frac{1}{Sc}\phi '' + f\phi ' - k_{1} h^{2} \phi = 0,\,$$

(14)

$$\frac{1}{Sc}h^{\prime\prime} + fh^{\prime} + k_{1} h^{2} \phi = 0,\,$$

(15)

$$\left. \begin{aligned} & f = 0 = g , { }f^{\prime} = 1 , { }\theta^{\prime}\left( 0 \right) = - \gamma \left( {1 - \theta \left( 0 \right)} \right)\, , { }\phi '\left( 0 \right) = k_{2} \phi \left( 0 \right),\, \\ & \delta h^{\prime}\left( 0 \right) = - k_{2} \phi \left( 0 \right)\,, \\ & f^{\prime}\left( \infty \right) \to 0 , { }g\left( \infty \right) \to 0 , { }\theta \left( \infty \right) \to 0, \, \phi \left( \infty \right){\mathbf{ \to }}1 , { }h\left( \infty \right){\mathbf{ \to }}0 \\ \end{aligned} \right\},$$

(16)

where $\varLambda \left( { = \tfrac{\nu }{Ka}} \right)$ denotes porosity parameter, $Fr\left( { = \tfrac{{C_{b} }}{{K^{{\tfrac{1}{2}}} }}} \right)$ the inertial coefficient variable, $\beta_{1} \left( { = \lambda_{1} a} \right)$ the fluid relaxation, $\beta_{2} \left( { = \lambda_{2} a} \right)$ the fluid retardation, $Pr\left( { = \tfrac{\nu }{\alpha }} \right)$ the Prandtl number, $\gamma \left( { = \tfrac{{h_{\text{f}} }}{k}\sqrt {\tfrac{v}{a}} } \right)$ the Biot number, $S\left( { = \tfrac{{Q_{0} }}{{a\rho c_{\text{p}} }}} \right)$ the heat source/sink parameter, $Sc\left( { = \tfrac{\nu }{{D_{\text{A}} }}} \right)$ the Schmidt number, $k_{1} \left( { = \frac{{k_{\text{c}} a_{0}^{2} }}{{a }}} \right)$ the homogeneous strength variable, $k_{2} \left( { = \tfrac{{k_{\text{s}} }}{{D_{\text{A}} }}\sqrt {\tfrac{v}{a}} } \right)$ the heterogeneous strength variable, $\delta \left( { = \tfrac{{D_{\text{B}} }}{{D_{\text{A}} }}} \right)$ the diffusion parameter.

For comparable mass diffusions we put $D_{\text{A}}$ and $D_{\text{B}}$ as equal; we have

$$\phi \left( \zeta \right) + h\left( \zeta \right) = 1;\,$$

(17)

one has

$$\frac{1}{Sc}\phi^{\prime\prime} + f\phi^{\prime} - k_{1} \left( {1 - \phi } \right)^{2} \phi = 0,$$

(18)

with

$$\phi^{\prime}\left( 0 \right) = k_{2} \phi \left( 0 \right),\, \, \phi \left( \infty \right)\, \to 1.$$

(19)

The heat transfer rate is mathematically defined as

$$Nu_{x} = \frac{{xq_{\text{w}} }}{{k\left( {Tw - T_{\infty } } \right)}},$$

(20)

where hall flux is defined as

$$q_{\text{w}} = - k\frac{\partial T}{\partial z}\;|_{z = o} ,$$

(21)

Finally, one has

$$Nu_{x} Re_{x}^{ - 0.5} = -\theta^{\prime}\left( 0 \right),$$

(22)

where $Re_{x} \left( { = \tfrac{{u_{\text{w}} x}}{\nu }} \right)$ symbolizes the local Reynolds number.

Solution procedure

We have

$$\left. \begin{aligned} f_{0} \left( \zeta \right) = 1 - e^{ - \zeta } , \hfill \\ \, \, g_{0} \left( \zeta \right) = 0,\, \, \hfill \\ \theta_{0} \left( \zeta \right) = \frac{\gamma }{1 + \gamma }e^{ - \zeta } ,\, \hfill \\ \, \phi_{0} \left( \zeta \right) = 1 - \frac{1}{2}e^{{ - k_{2} \zeta }} ,\, \hfill \\ \end{aligned} \right\},$$

(23)

$$\left. \begin{aligned} L_{\text{f}} \left( \zeta \right) = & f^{\prime\prime\prime} - f^{\prime},\;L_{\text{g}} = g^{\prime\prime} - g,\, \\ L_{\theta } \left( \zeta \right) = & \theta^{\prime\prime} - \theta ,\;L_{\phi } = \phi '' - \phi ,\, \\ \end{aligned} \right\},$$

(24)

with the following characteristics:

$$\left. \begin{aligned} L_{f} \left[ {A_{{_{ * } 1}} + A_{{_{ * } 2}} e^{ - \zeta } + A_{{_{ * } 3}} e^{\zeta } } \right] & = 0, \\ L_{g} \left[ {A_{{_{ * } 5}} e^{ - \zeta } + A_{{_{ * } 5}} e^{\zeta } } \right] & = 0, \\ L_{\theta } \left[ {A_{{_{ * } 6}} e^{ - \zeta } + A_{{_{ * } 7}} e^{\zeta } } \right] & = 0, \\ L_{\phi } \left[ {A_{{_{ * } 8}} e^{ - \zeta } + A_{{_{ * } 9}} e^{\zeta } } \right] & = 0, \\ \end{aligned} \right\},$$

(25)

where $A_{*i} \left( {i = 1 - 9} \right)$ designates are arbitrary constants

$$\left. \begin{aligned} A_{{_{ * } 2}} = & A_{{_{ * } 4}} = A_{{_{ * } 6}} = A_{{_{ * } 8}} = 0,\, \\ \, A_{{_{ * } 1}} = & - A_{{_{ * } 3}} - f_{\text{m}}^{ *} (0),\, \, A_{{_{ * } 3}} = \frac{{\partial f_{\text{m}}^{ *} \left( \zeta \right)}}{\partial \zeta }\;|_{\zeta = 0} ,\, \, A_{{_{ * } 5}} = - \frac{{\partial g_{\text{m}}^{ *} \left( \zeta \right)}}{\partial \zeta }\;|_{\zeta = 0} ,\, \\ A_{{_{ * } 7}} = & \frac{1}{1 + \gamma }\left[ {\frac{{\partial \theta_{m}^{*} \left( \zeta \right)}}{\partial \zeta }\;|_{\zeta = 0} - \gamma \left( {\theta_{\text{m}}^{ *} \left( 0 \right)} \right)} \right],\, \\ \, A_{{_{ * } 9}} = & \frac{1}{{1 + k_{2} }}\left[ {\frac{{\partial \phi_{\text{m}}^{ *} \left( \zeta \right)}}{\partial \zeta }\;|_{\zeta = 0} - k_{2} \left( {\phi_{\text{m}}^{ *} \left( 0 \right)} \right)} \right] \\ \end{aligned} \right\}.$$

(26)

Convergence analysis

In series solutions auxiliary variables $h_{\text{f}} ,h_{\text{g}} ,h_{\theta } ,h_{\phi }$ play an important role to adjust the convergence portion. Therefore, we have plotted $h{\text{ - curves}}$ for such analysis in Figs. 1 and 2. From these plots the valuable ranges are $- \;1.8\; \le \;h_{\text{f}} \; \le \; - \;0.1,\;\; - \;1.6\, \le \;h_{\text{g}} \; \le \; - \;0.1,$$- \;2.1 \le h_{\theta } \le 0.1$ and $- \;2.1 \le h_{\varphi } \le 0.1.$ Table 1 is sketched for the numerical iterations of convergence analysis.

Fig. 1

$h{\text{ - curves for }}f^{\prime\prime}\left( 0 \right) {\text{and}} g^{\prime}\left( 0 \right)$

Fig. 2

$h{\text{ - curves for}} \theta^{\prime}\left( 0 \right) {\text{and}} \phi^{\prime}\left( 0 \right)$

Table 1 Different iterations for series solutions when $\varLambda = 0.1,$ $\beta_{1} = 0.1,$ $\beta_{2} = 0.1,$ $Fr = 0.3,$ $Pr = 1,\;\,\gamma = 0.1,$ $k_{1} = 0.2,$ $k_{2} = 0.1$ and $Sc = 1$

Discussion

This section is established to explore the impacts of interesting variables on velocity, temperature and concentration fields. For this purpose we have plotted Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18. Porosity variable behavior on velocity $f^{\prime}\left( \xi \right)$ is presented in Fig. 3. Velocity diminishes versus larger porosity variable. Physically, due to porous media, more resistance occurred to the flow particles which make the velocity of fluid weaker. In Fig. 4, we have plotted the impact of fluid relaxation variable on velocity field. Here we observed that the velocity of material particles enhances versus larger relaxation variable. Furthermore, boundary layer shows an increasing impact against larger relaxation variable. Figure 5 is outlined to show the velocity field against retardation variable. Here we noticed that velocity field declines via higher retardation parameter. Inertia variable impact on velocity field is highlighted in Fig. 6. Here velocity curves slowly increase when the inertia variable takes the maximum range. Also layer thickness upsurges versus larger inertia variable. Inspiration of porosity variable on $g\left( \xi \right)$ is depicted in Fig. 7. Here initially velocity of liquid particles increases and then shows decreasing impact when the porosity variable take the maximum values. Salient aspects of relaxation and retardation variable on $g\left( \xi \right)$ is outlined in Figs. 8 and 9. From these sketches we can see that velocity field monotonically decays initially near the stretchable surface and then monotonically upsurges against larger relaxation and retardation variables. Figure 10 is revealed for the impact of Forchheimer number or inertia coefficient variable on $g\left( \xi \right)$. Here we noticed that velocity component in y-direction upsurges versus larger Forchheimer number. It is also noticed that layer thickness enhances against larger Forchheimer number.

Fig. 3

$f^{\prime} {\text{versus }}\varLambda$

Fig. 4

$f^{\prime}\; {\text{versus}} \ \beta_{1}$

Fig. 5

$f^{\prime}\; {\text{versus}}\; \beta_{2}$

Fig. 6

$f^{\prime}\; {\text{versus}}\; Fr$

Fig. 7

$g\; {\text{versus}}\; \varLambda$

Fig. 8

$g\; {\text{versus}}\; \beta_{1}$

Fig. 9

$g\, {\text{versus}}\; \beta_{2}$

Fig. 10

$g\; {\text{versus}}\; Fr$

Fig. 11

$\theta \; {\text{versus}}\; Pr$

Fig. 12

$\theta \;{\text{versus}}\; \gamma$

Fig. 13

$\theta \;{\text{versus }}\;S$

Fig. 14

$\phi \; {\text{versus}}\; Sc$

Fig. 15

$\phi \;{\text{versus}}\; k_{1}$

Fig. 16

$\phi \;{\text{versus}}\; k_{2}$

Fig. 17

Nusselt number versus $\varLambda {\text{and}} \gamma$

Fig. 18

Nusselt number versus $\gamma {\text{and}} Pr$

Behavior of Prandtl number on thermal field is recorded in Fig. 11. Lesser thermal field is noticed against higher Prandtl number. Characteristics of Biot number on thermal field is shown in Fig. 12. Here temperature is an increasing function of larger Biot number. Physically, larger Biot number increases the convection process at the stretchable surface which leads to upsurges the temperature field. Figure 13 predicts the salient attributes of heat generation/absorption or heat source/sink variable on the thermal field. In this study, $S > 0$ highlights the heat generation or heat source and $S < 0$ signifies the absorption or sink and $S = 0$ signposts there is no heat generation/absorption or heat source/sink. But here we have only presented the effect of heat generation on the thermal field. Thermal field is an increasing behavior against heat generation variable.

Figure 14 highlights the salient attributes of Schmidt number on mass concentration field. Physically, Schmidt number is the combination of momentum and mass diffusivity. Here mass concentration increases against higher Schmidt number. Also concentration layer thickness upsurges versus rising estimations of Schmidt number. Attributes of homogeneous reactive variable on mass concentration is sketched in 15. Here we have examined reduction in solutal layer and as well as in mass concentration via higher homogeneous reactive variable. Behavior of heterogeneous reactive variable on mass concentration is revealed in Fig. 16. From this sketch, we have examined that concentration of reaction species at the surface upsurges against higher estimation of heterogeneous reactive variable.

Graphical sketch of heat transfer rate against various flow variables like porosity parameter, Biot number and Prandtl number is highlighted in Figs. 17 and 18. From these sketches, we have noticed that magnitude of heat transfer decays versus higher estimations of porosity parameter and Biot number.

Concluding remarks

The valuable results of the presented problem are recorded below:

• Velocity of material particles in x direction decays against higher porosity variable.

• Velocity shows contrast impact against relaxation and retardation variables.

• Thermal declines versus Prandtl number.

• Higher heat generation variable upsurge the temperature of material particles.

• Concentration presents contrast impact against homogeneous and heterogeneous reactive parameters.

• Magnitude of heat transfer rate decays against larger porosity parameter and Biot number.