Keywords

1 Introduction

The multiple players pursuit–evasion differential games of simple motion with geometric or integral constraints are widely studied in many works (see eg. [1–12]). For the case of many pursuers against one evader, the game is described by the following differential equations:

$$\begin{aligned}&\dot{x}_i=u_i,\ \ x_i(0)=x_{i0},\ \ |u_i|\le \rho _i,\ \ i=1,\ldots ,m,\\&\dot{y}=v,\ \ y(0)=y_0,\ \ |v|\le \sigma , \end{aligned}$$

where \(x_i, y, u_i, v\in \mathbb {R}^n\), \(\rho _i\ge 0\), \(\sigma >0\), \(x_{i0}\ne y_0\), and \(i=1,\ldots ,m\). Here, pursuit is said to be completed if \(x_i(\tau )=y(\tau )\) for some \(i\in \{1,\ldots ,m\}\) and \(\tau \ge 0\), and evasion is said to be possible if \(x_i(t)\ne y(t)\) for all \(i=1,\ldots ,m\), and \(t\ge 0\).

One of the earliest work of evasion differential game in the case of many pursuers versus one evader was by Pshenichnii [11]. In his work, the maximum speed of each player is equal to 1. The necessary and sufficient condition of evasion was obtained where evasion is possible if and only if \(y_0\notin intconv \{x_{10},\ldots ,x_{m0}\}\).

The current paper is closely related to the following work by Chernous’ko [3]. The author examined the evasion differential game of one evader versus many pursuers which is described by the following simple differential equations:

$$\begin{aligned}&\dot{x}_i=u_i, \ \ |u_i|\le kv, \ \ 0<k<1,\\&\dot{y}=v, \ \ |v|\le v. \end{aligned}$$
Fig. 1
figure 1

Trajectory of Evader

Full size image

Trajectory of one evader against each pursuer is pictured in the following diagram in Fig. 1 where Q is the position of point P at time \(t_A\); \(\alpha \) is the angle between the ray x and segment \({ {AQ}}\) where \(0\le \alpha \le \pi \); R is the current distance QE; \(\varphi \) is the current angle between the segments QE and QA, and s is the arc length of curve AE. The author’s strategy is to ensure \(EP\ge L\) for all \(t\ge t_0\) before the evader moving back to the horizontal line and continue to move away from pursuer horizontally. By the strategy, he proved that evasion is possible.

Also, the work by Ibragimov et al. [5] was devoted on differential game of evasion. The work deals with the evasion differential game of m pursuers \(x_1,\ldots ,x_m\) and one evader y described by the equations

$$\begin{aligned}&\qquad \qquad \dot{x}_i = u_i,\ \ x_i(0)=x_{i0}, \\&\dot{y} = v,\ \ y(0)=y_0,\ \ x_{i0}\ne y_0,\ \ i=1,\ldots ,m. \end{aligned}$$

The game occurs in the plane and the following conditions:

$$\begin{aligned} \int _{0}^{\infty }|u_i(s)|^2ds\le \rho ^2_i,\ \ i=1,\ldots ,m,\ \ \int _{0}^{\infty }|v(s)|^2ds\le \sigma ^2, \end{aligned}$$

were imposed on control functions of the players. The main result of the paper is as follows: if the total resource of pursuers does not exceed that of evader, that is \(\rho ^2_1+\rho ^2_2+\ldots \rho ^2_m\le \sigma ^2\), then evasion is possible.

We are to construct a different approach and strategy for evasion problem which is similar to Chernous’ko’s [3], for the case of one evader against one pursuer. Like Chernous’ko’s problem, evader is moving on a straight line as pursuer is approaching the evader. When the distance between them reaches a particular distance which is greater than zero, the evader will maneuver to avoid the pursuer. The strategy of the maneuver is different from Chernous’ko’s where the control set of the evader in our problem is a sector. We also assume the maximal speed of the pursuer is equal to 1 and the maximal speed of the evader is \(\alpha \) where \(\alpha >1\). We find a sufficient condition for the evader to escape from the pursuer.

2 Statement of the Problem

We study an evasion differential game of one pursuer P and one evader E with geometric constraints on controls of players described by equations:

$$\begin{aligned} P: & {} \dot{x}=u,\ x(0)=x_0,\ |u|\le 1,\end{aligned}$$
(1)
$$\begin{aligned} E: & {} \dot{y}=v,\ y(0)=y_0,\ v\in \mathbf {S}, \end{aligned}$$
(2)

where \(x, x_{0}, u, y, y_0, v \in \mathbb {R}^2\), \(x_{0}\ne y_0\), u is the control parameter of the pursuer P, v is that of the evader E,

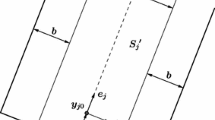
$$\mathbf {S}=\{(v_1,v_2)|\ v_1^2+v_2^2\le \alpha ^2,\ |v_1|\le v_2\tan \varphi ,\ v_2\ge 0\},$$

\(\alpha >1\) and \(\varphi \), \(0<\varphi <\frac{\pi }{2}\), is a given angle. Note that \(\mathbf {S}\) is a sector with the radius \(\alpha \) and central angle \(2\varphi \) (Fig. 2).

Fig. 2
figure 2

Sector \(\mathbf {S}\)

Full size image

Definition 1

A Borel measurable function \(u(t)=(u_{1}(t),u_{2}(t))\), \(|u(t)|\le 1\), \(t\ge 0\), is called admissible control of the pursuer x.

Definition 2

A Borel measurable function \(v(t)=(v_1(t),v_2(t))\), \(v(t)\in \mathbf {S}\), \(t\ge 0\), is called admissible control of the evader y.

Definition 3

A function

$$V(t,y,x,u), \ V:[0,\infty )\times R^2\times H(0,\rho )\rightarrow \mathbf {S},$$

is called strategy of the evader, if for any admissible control u(t) the following initial value problem

$$\begin{aligned} \dot{x}=u(t), \ x(0)=x_{0},\nonumber \end{aligned}$$
$$\begin{aligned} \dot{y}=V(t,y,x,u(t)), \ y(0)=y_0,\nonumber \end{aligned}$$

has a unique solution (x(t), y(t)), \(t\ge 0\), with absolutely continuous components x(t) and y(t).

Definition 4

We say that evasion is possible in the game (1)–(2) if there exists a strategy V of the evader E such that for any admissible control of the pursuer \(x(t)\ne y(t)\) for all \(t\ge 0\).

Problem

Find sufficient conditions of evasion in the game (1)–(2).

The condition \(v(t)\in \mathbf {S}\), \(t\ge 0\), implies that state of the evader y(t) belongs to the sector \(\mathbf {S}_1=\{y_0+ta \ | \ a\in \mathbf {S},t\ge 0\}\). Initial position of the pursuer may be in \(\mathbf {S}_1\) as well as outside \(\mathbf {S}_1\). In process of pursuit, the pursuer can move throughout the plane. In this regard, the pursuer have advantage. However, the evader has advantage in speed, since \(\alpha >1\).

3 Main Result

The main result of the paper is the following statement.

Theorem 1

If \(\alpha \cos \varphi _0\ge 1\) and \(\alpha \sin \varphi _0>1\) at some \(0<\varphi _0\le \varphi \), then evasion is possible in the game (1)–(2).

Proof

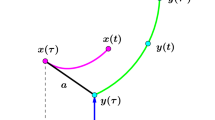
Choose any number a, \(0<a<\min |x_{0}-y_0|\). We construct a strategy for the evader as follows:

$$\begin{aligned} v(t)=\left\{ \begin{array}{l l} \left( 0,\alpha \right) , \ if \ 0\le t<\tau , \\ \left( \pm (c+|u_{1}(t)|), \sqrt{\alpha ^2-\left( c+|u_{1}(t)|\right) ^2}\right) , \\ \qquad \qquad \qquad \qquad \,\,\, if \ \tau \le t\le t_1,\\ \left( 0,\alpha \right) , \ if \ t>t_1, \end{array} \right. \end{aligned}$$
(3)

where \(\tau \) is the first time when \(|y(\tau )-x(\tau )|=a\),

$$t_1=\tau +\frac{a}{\sqrt{\left( \alpha -1\right) ^2-c^2}}, \ \ \ c=\alpha \sin \varphi _0-1.$$

Note that such a time \(\tau \) may not exist. If so, then we let \(v(t)=(0,\alpha )\) for all \(t\ge 0\). In (3), \(\pm \) means \(v_1(t)=c+|u_{1}(t)|\), if \(x_{1}(\tau )\le y_1(\tau )\) and \(v_1(t)=-(c+|u_{1}(t)|)\), if \(x_{1}(\tau )\ge y_1(\tau )\), where \(x(t)=(x_{1}(t),x_{2}(t))\), \(y(t)=(y_1(t),y_2(t))\).

Estimate \(|y(t)-x(t)|, \tau \le t\le t_1\). We have

$$\begin{aligned} |y(t)-x(t)|= & {} \left| y(\tau )+\int _{\tau }^{t}v(s)ds-\left( x(\tau )+\int _{\tau }^{t}u(s)ds\right) \right| \\\ge & {} |y(\tau )-x(\tau )|-\left| \int _{\tau }^{t}v(s)ds\right| -\left| \int _{\tau }^{t}u(s)ds\right| \\\ge & {} a-(t-\tau )(\alpha +1). \end{aligned}$$

Without loss of generality, we assume that \(y_1(\tau )\ge x_{1}(\tau )\), and hence \(v_1(t)=c+|u_{1}(t)|\), \(\tau \le t\le t_1\). Then, on the other hand, for the points x(t) and y(t) we have

$$\begin{aligned} |y(t)-x(t)|\ge & {} y_{1}(t)-x_{1}(t)\\= & {} y_{1}(\tau )+\int _{\tau }^{t}v_{1}(s)ds-\left( x_{1}(\tau )+\int _{\tau }^{t}u_{1}(s)ds\right) \\= & {} y_{1}(\tau )-x_{1}(\tau )+\int _{\tau }^{t}\left( v_{1}(s)-u_{1}(s)\right) ds\\= & {} y_{1}(\tau )-x_{1}(\tau )+\int _{\tau }^{t}\left( c+|u_{1}(s)|-u_{1}(s)\right) ds\\\ge & {} c\cdot (t-\tau ) \end{aligned}$$

Thus, \(|y(t)-x(t)|\ge f(t)\), where

$$f(t)=\max \{a-(t-\tau )(\alpha +1),\ c(t-\tau )\}.$$

Note that the function f(t) has only one minimum on \([\tau ,t_1]\), since the first function in the \(\max \) decreases, whereas the second function increases. The function f(t) takes its minimum at

$$\begin{aligned} t_*=\tau +\frac{a}{\alpha (1+\sin \varphi _0)}\in \left[ \tau ,t_1\right] . \end{aligned}$$

We have

$$\begin{aligned} |y(t)-x(t)|\ge & {} c\cdot (t_*-\tau )\\= & {} c\cdot \dfrac{a}{\alpha (1+\sin \varphi _0)}\nonumber \\\ge & {} \dfrac{c}{2\alpha }\cdot a, \ \ \ \ \ \ \tau \le t\le t_{1}. \end{aligned}$$

In particular, at the time \(t_{1}\)

$$\begin{aligned} |y(t_{1})-x(t_{1})|\ge \dfrac{c}{2\alpha }\cdot a. \end{aligned}$$
(4)

Moreover, at the time \(t=t_1\) the pursuer cannot be above the horizontal line \(y=y_2(t_1)\) of the xy-plane. Indeed,

$$\begin{aligned} y_{2}(t_{1})-x_{2}(t_{1})= & {} y_{2}(\tau )+\int _{\tau }^{t_{1}}v_{2}(t)dt-\left( x_{2}(\tau )+\int _{\tau }^{t_{1}}u_{2}(t)dt\right) \nonumber \\= & {} y_{2}(\tau )-x_{2}(\tau )+\int _{\tau }^{t_{1}}\left( v_2(t)-u_{2}(t)\right) dt\nonumber \\\ge & {} -a+\int _{\tau }^{t_{1}}\left( \sqrt{\alpha ^{2}-\left( c+|u_{1}(t)|\right) ^{2}}-\sqrt{1-\left| u_{1}(t)\right| ^{2}}\right) dt \end{aligned}$$
(5)

It is not difficult to show that

$$\sqrt{\alpha ^{2}-\left( c+|u_{1}(t)|\right) ^{2}}-\sqrt{1-\left| u_{1}(t)\right| ^{2}}\ge \sqrt{\left( \alpha -1\right) ^{2}-c^{2}}.$$

Then right-hand side of (5) can be estimated from below by

$$\begin{aligned} -a+\int _{\tau }^{t_{1}}\sqrt{\left( \alpha -1\right) ^{2}-c^{2}}dt=-a+\left( t_{1}-\tau \right) \sqrt{\left( \alpha -1\right) ^{2}-c^{2}}=0 \end{aligned}$$

Thus, \(y_2(t_1)\ge x_{2}(t_1)\).

Next, according to (3) \(v(t)=(0,\alpha )\), \(t>t_1\). We estimate \(|x(t)-y(t)|\) at \(t>t_1\). Since

$$\displaystyle y_1(t)-x_{1}(t)=y_{1}(t_1)-x_{1}(t_1)-\int _{t_1}^{t}u_{1}(s)ds$$

and

$$\displaystyle y_2(t)-x_{2}(t)\ge y_2(t_1)-x_{2}(t_1)+\alpha (t-t_1)-\int _{t_1}^{t}|u_{2}(s)|ds\ge 0.$$

Last inequality because of \(y_2(t_1)\ge x_{2}(t_1)\) and \(|u_{2}(t)|\le 1\).

Therefore

$$\begin{aligned} |x(t)-y(t)|&\ge \left( \left( y_{1}(t_1)-x_{1}(t_1)-\int _{t_1}^{t}u_{1}(s)ds\right) ^2\right. \\&\qquad +\left. \left( y_2(t_1)-x_{2}(t_1)+\alpha (t-t_1)-\int _{t_1}^{t}|u_{2}(s)|ds\right) ^2\right) ^{1/2}. \end{aligned}$$

Using the triangle inequality, we can estimate right-hand side of this inequality from below by

$$\begin{aligned}&\sqrt{\left| y_{1}(t_1)-x_{1}(t_1)\right| ^2+\left( y_2(t_1)-x_{2}(t_1)+\alpha (t-t_1)\right) ^2} \\&\quad - \sqrt{\left( \int _{t_1}^{t}u_{1}(s)ds\right) ^2+\left( \int _{t_1}^{t}|u_{2}(s)|ds\right) ^2}. \end{aligned}$$

By the Cauchy–Schwarz inequality we obtain

$$\begin{aligned} \left( \int _{t_{1}}^{t}u_{1}(s)ds\right) ^{2}+\left( \int _{t_{1}}^{t}|u_{2}(s)|ds\right) ^{2}\le & {} \left( \int _{t_{1}}^{t}1\cdot |u_{1}(s)|ds\right) ^{2}+\left( \int _{t_{1}}^{t}1\cdot |u_{2}(s)|ds\right) ^{2}\\\le & {} \int _{t_{1}}^{t}1^{2}ds\int _{t_{1}}^{t}u_{1}^{2}(s)ds+\int _{t_{1}}^{t}1^{2}ds\int _{t_{1}}^{t}u_{2}^{2}(s)ds\\= & {} (t-t_{1})\int _{t_{1}}^{t}\left( u_{1}^{2}(s)+u_{2}^{2}(s)\right) ds\\\le & {} (t-t_1)^2. \end{aligned}$$

Therefore,

$$\begin{aligned} |x(t)-y(t)|\ge & {} \left( \left( y_{1}(t_1)-x_{1}(t_1)\right) ^2+\left( y_2(t_1)-x_{2}(t_1)\right) ^2+\left( \alpha (t-t_1)\right) ^2\right) ^{1/2}-(t-t_1)\nonumber \\\ge & {} \sqrt{\left( \frac{ac}{2\alpha }\right) ^2+\alpha ^2(t-t_1)^2}-(t-t_1) \end{aligned}$$
(6)

since \(|y(t_1)-x(t_1)|^2\ge (\frac{ac}{2\alpha })^2\).

To estimate the expression (6) from below, we let \(\dfrac{ac}{2\alpha }=b\), \((t-t_1)=x\) and consider the function

$$g(x)=\sqrt{b^2+\alpha ^2x^2}-x, \ \ \ x\ge 0.$$

This function takes its minimum at \(x=x_*=\dfrac{b}{\alpha \sqrt{\alpha ^2-1}}\). Thus

$$\begin{aligned} |x(t)-y(t)|\ge & {} g(x_*)\\= & {} \dfrac{\sqrt{\alpha ^2-1}}{\alpha }b=\dfrac{\sqrt{\alpha ^2-1}}{2\alpha ^2}ac, \ \ \ \ t\ge t_1. \end{aligned}$$

Next, we estimate \(y_2(t)-x_{2}(t)\) for \(t\ge \tau '=\tau +ra\) where

$$r=\dfrac{1}{\sqrt{\left( \alpha -1\right) ^2-c^2}}+\dfrac{c}{2\alpha ^2\sqrt{\alpha ^2-1}}.$$

Since \(y_2(t_1)\ge x_{2}(t_1)\),

$$\begin{aligned} y_{2}(t)-x_{2}(t)= & {} y_{2}(t_{1})+\int _{t_{1}}^{t}v_2(s)ds-x_{2}(t_1)-\int _{t_{1}}^{t}u_{2}(s)ds\\\ge & {} y_{2}(t_{1})-x_{2}(t_1)+\int _{t_{1}}^{t}\alpha \ ds-\int _{t_{1}}^{t}1 \ ds\\\ge & {} (\alpha -1)(t-t_{1})\\\ge & {} (\alpha -1)(\tau '-t_{1})\\= & {} \dfrac{(\alpha -1)c}{2\alpha ^{2}\sqrt{\alpha ^{2}-1}}\cdot a \\= & {} ap, \end{aligned}$$

where \(p=\dfrac{(\alpha -1)c}{2\alpha ^{2}\sqrt{\alpha ^{2}-1}}\).    \(\square \)

Thus, we can conclude that

  1. (1)

    \(|x(t)-y(t)|\ge a\) for \(0\le t\le \tau \),

  2. (2)

    \(|x(t)-y(t)|\ge \frac{c}{2\alpha }\cdot a\) for \(\tau \le t\le t_1\),

  3. (3)

    \(y_2(t)>x_{2}(t)\), for \(t\ge t_1\),

  4. (4)

    \(|x(t)-y(t)|\ge \dfrac{\sqrt{\alpha ^2-1}}{2\alpha ^2}ac\) for \(t\ge t_1\),

  5. (5)

    \(y_2(t)-x_{2}(t)\ge ap\) for \(t\ge \tau '\).

In particular, \(y(t)\ne x(t), \ t>0\).

Hence, at the time \(t_1\) the evader will be above the horizontal line where is the pursuer x. Thus, at the time \(t_1\) the pursuer x became “behind” the evader. Since \(v_2(t)\ge \alpha \cos \varphi _0\ge 1\ge u_{2}(t)\), then \(y_2(t)>x_{2}(t)\), for all \(t\ge t_1\).

If a-approach occurs with the pursuer x at a time \(\tau \), then the evader uses maneuver on \([\tau ,t_1]\) which ensures the inequality \(y_2(t_1)\ge x_{2}(t_1)\). Further, the strategy of the evader guarantees him the inequality \(y_2(t)>x_{2}(t)\) for all \(t\ge t_1\).

4 Conclusion

A simple motion evasion differential game of one pursuer and one evader whose control set is a sector has been considered in the plane. If \(\alpha \cos \varphi _0\ge 1\) and \(\alpha \sin \varphi _0>1\), then evasion from one pursuer has been presented. The strategy for the evader was constructed as well. Moreover, distances between the pursuer and evader have been estimated.