Evasion Differential Game of One Evader and Many Slow Pursuers

Abstract

We study a simple motion evasion differential game of m pursuers and one evader. The maximum speed of pursuers is 1, and that of evader is $\sigma > 1$. If for all time the state of the evader doesn’t coincide with the state of any pursuer, then evasion is said to be possible. The evader strives to avoid capture. This problem was studied by F.L. Chernous’ko in 1976. We propose a new evasion strategy, which guarantees evasion from any initial positions of players and enables us to estimate the number of approach times from the above by $m(m+1)/2$. Also, it is established that all approach times of each pursuer to the evader may occur only on the time interval associated with the first approach time of the pursuer to the evader.

1 Introduction

The field of differential games was pioneered by Isaacs [17]. Evasion problem on the infinite time interval $[t_0, \infty )$ was introduced and studied by Pontryagin and Mischenko [24]. Mishchenko et al. [23] proposed a new maneuver for evasion in the game of many pursuers.

A substantial part of the researches study simple motion pursuit or evasion differential games with many players. Chernous’ko [9] studied an evasion game of one faster evader and several pursuers with a state constraint for the evader. The evader must remain in a neighborhood of a given ray during the game. It was proved that the faster evader can escape from the pursuers. This result later on was extended by Chernous’ko and Zak [10, 27,28,29] to more general differential game problems. Related problems of evasion from a group of pursuers were studied in [7] and [11].

Blagodatskikh and Petrov [6] obtained necessary and sufficient condition of evasion in a simple motion differential game of a group of pursuers and a group of evaders in ${\mathbb {R}}^n$ where all evaders use the same control. By definition, pursuit is considered completed if the state of a pursuer coincides with the state of at least one evader. Also, the works [5, 26] related to such games.

In [25], a pursuit-evasion game involving one pursuer and multiple evaders motivated by the seminal “selfish herd” model of Hamilton was considered. The pursuer can freely move in any direction with bounded speed, and evaders move with bounded speed and bounded turning speed. Using Isaacs’ heuristic argument, an optimal strategy for the pursuer was constructed and it was concluded that the optimal strategy for the pursuer is to focus on a single evader that can be captured in minimum time. Moreover, “non-targeted” evaders are always able to escape.

The paper of Lee and Bakolas [22] studies a differential game of a heterogeneous group of pursuers and one evader. Pursuers individually attempt to capture the evader, that is, the strategy of the group of pursuers is not cooperative. The evader tries to delay or avoid capture.

Ramana and Mangal [30] studied pursuit-evasion games of multiple pursuers and a high-speed single evader with holonomic constraints in an open domain. Using the idea of Apollonius circle, an escape strategy was developed for the high speed evader. Jin and Qu [18] also apply the Apollonius circles for the evader and each pursuer to study how the evader can form a better strategy to avoid or prolong the capture time provided a successful escape impossible. The work of Awheda and Schwartz [4] also relates to a multi-pursuer pursuit-evasion differential game. Chen at al. [8] studied a simple motion pursuit differential game of many identical pursuers and one faster evader. The evader is captured if the evader becomes in $d_c$ distance from a pursuer. Sufficient conditions of completion of game were obtained. We refer to work [21] for a detailed survey of results on differential games of many players where the controls of players are under geometric constraints.

In the case of integral constraints, evasion differential games of many players were studied in the papers [2, 14,15,16]. The work [15] is devoted to the differential game of many pursuers and many evaders where the total energy of evaders greater or equal to that of pursuers. Evasion strategies are constructed to avoid from any initial positions of players.

There are few papers on multi pursuer differential games with state constraints. For example, interesting results were obtained by Alexander et al. [1] for a discrete time simple motion differential game in an unbounded region. Kuchkarov et al [20] studied a differential game of many pursuers and one evader on a cylinder, where all the players have equal dynamic capabilities. The paper of Kuchkarov et al [19] is devoted to pursuit and evasion differential games on manifolds with Euclidean metric where necessary and sufficient conditions of evasion are obtained. The optimal number of pursuers in the differential games on the 1-skeleton of orthoplex was found [3] to capture a single faster evader by many pursuers.

In the present paper, we study a simple motion evasion differential game of m pursuers and one evader. The maximum speed of pursuers is 1 and that of evader is $\sigma > 1$. This problem of evasion was studied in [9]. In the present paper, we propose a new evasion strategy and prove that the evader can avoid from pursuers moving in any $\varepsilon$-vicinity of any straight line passing through the initial state of evader. Also, we show that the number of approach times doesn’t exceed $m(m+1)/2$, whereas this number was estimated by $2^m-1$ in [9]. Another an important point to note is the fact that the approach times of each pursuer $x_i$ to the evader may occur only on the time interval $[\tau _i, \tau _i')$ associated with the first approach time $\tau _i$ of the pursuer $x_i$ to the evader.

It should be noted that the results of the current paper can be applied to multiple objective adversarial games such as Reach-avoid (RA) [12, 31] and Capture-the-flag [13] games. For example, for the RA games, there are not only the attacker (evader) and the defender (the team of pursuers), but there is also a target area. The attacker’s goal is to reach the target area without being captured, while the defender team attempts to delay or prevent the attacker from entering the target area by capturing attacker. The results of the current paper allow us to conclude that a high-speed attacker can reach the target area without being captured.

2 Statement of Problem

Consider a simple motion differential game of m pursuers $x_1,..., x_m$ and one evader y in ${\mathbb {R}}^d$, $d \ge 2$, whose dynamics are described by the following equations

$$\begin{aligned} \begin{aligned}&\dot{x}_i=u_i,&x(0)=x_{i0},&\quad ||u_i|| \le 1,\\&\dot{y}=v,&y(0)=0,&\quad ||v|| \le \sigma , \end{aligned} \end{aligned}$$

(1)

where $x_i, x_{i0}, y, y_0, u_i, v \in {\mathbb {R}}^n$, $x_{i0} \ne y_0$, $i=1, 2, \dots , m$, and $\sigma$, $\sigma >1$, is a given number, $u_i$ is control parameter of pursuer $x_i$, and v is that of evader y.

Definition 1

Measurable functions $u_i(t)$, $||u_i(t)|| \le 1$, and v(t), $||v(t)|| \le \sigma$, $t \ge 0$, are called controls of the pursuer $x_i$ and the evader y, respectively.

Definition 2

The strategy of evader is defined as a function $V: {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}^{(2\,m+1)d} \rightarrow {\mathbb {R}}^d$,

$$\begin{aligned} (t, \theta _1, \theta _2, y, x_1,\dots , x_m, u_1, \dots u_m) \rightarrow V(t, \theta _1, \theta _2, y, x_1,\dots , x_m, u_1, \dots u_m) \end{aligned}$$

for which initial value problem (1) with $v=V(t, \theta _1, \theta _2, y, x_1,\dots , x_m, u_1, \dots u_m)$ has a unique solution $(y(t), x_1(t), \dots , x_m(t))$ for $\theta _1=\theta _1(t)$, $\theta _2=\theta _2(t)$, and arbitrary controls $u_1=u_1(t)$,..., $u_m=u_m(t)$ of pursuers, where $\theta _1(t)$ and $\theta _2(t)$, $t \ge 0$, are given functions.

The behaviors of the pursuers are arbitrary, that is, the pursuers apply any controls and the evader applies a strategy.

Definition 3

We say that evasion is possible in the game (1) if there exists a strategy V of evader such that, for any controls of pursuers, $x_i(t) \ne y(t)$ for all $t \ge 0$ and $i=1,...,m$.

Problem 1

Construct a strategy V for the evader, for which evasion is possible in game (1).

It is sufficient to consider the case where $d=2$. We therefore study the evasion of one evader from many slow pursuers in the plane.

3 Evasion from One Pursuer

In this section, we consider an evasion differential game of one pursuer and one evader in ${\mathbb {R}}^2$. We use the temporary notation $x=(x_1, x_2)$ for the pursuer and $u=(u_1, u_2)$ for its control parameter only in this section. The dynamics of pursuer x and evader y are described by the equations

$$\begin{aligned} \begin{array}{ll} \dot{x} =u, &{} x(0)=x_0, \\ \dot{y}=v, &{} y(0)=y_0, \end{array} \end{aligned}$$

(2)

where $x_0 \ne y_0$, $y=(y_1, y_2)$, and $v=(v_1, v_2)$ is control parameter of evader. The controls of players satisfy the inequalities

$$\begin{aligned} ||u(t)|| \le 1 \quad \text {and}\quad ||v(t)|| \le \sigma , \ \ t \ge 0. \end{aligned}$$

(3)

We fix the numbers $\alpha$ and a

$$\begin{aligned} 0< \alpha< \frac{1}{2}(\sigma -1), \ \ 0< a <||x_0-y_0||. \end{aligned}$$

(4)

The pursuer x applies an arbitrary control $u(t)=(u_1(t), u_2(t))$, $t \ge 0$, and let $x(t)=(x_1(t), x_2(t))$ be the corresponding trajectory of the pursuer.

We now construct a strategy for the evader. Fist, the evader starting from the initial time $t=0$ moves with the velocity

$$\begin{aligned} V_0 = (0, \sigma ), \ \ t \in [0, \tau ), \end{aligned}$$

(5)

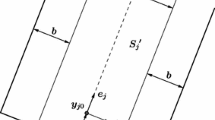
i.e., $v_1(t)=0$, $v_2(t)=\sigma$, parallel to the Oy-axis, where $\tau$ is the first time when $||x(t)-y(t)||=a$. We call $\tau$ the a-approach time of pursuer to the evader. The segment between the points $y_0$ and $y(\tau )$ in Fig.  is the trajectory of the evader corresponding to (5).

Fig. 1

Trajectory of the evader when $x_1(\tau ) \le y_1(\tau )$

Note that time $\tau$ may not occur. In this case, we have $||x(t)-y(t)|| > a$ for all $t \ge 0$ and, clearly, $x(t) \ne y(t)$ for all $t \ge 0$. Therefore, we assume that the time $\tau$ occurs. Also, we define $\tau '=\tau + \frac{4a}{\sigma -1}$.

Also, we use temporarily the notation $V(t) = (V_1(t), V_2(t))$ only in section, where

$$\begin{aligned} V_1(t)=\left\{ \begin{array}{cl} |u_1(t)| + \alpha , &{} x_1(\tau ) \le y_1(\tau )\\ -(|u_1(t)| + \alpha ), &{} x_1(\tau ) > y_1(\tau ) \end{array} \right. , \ \ V_2(t)=\sqrt{\sigma ^2-V_1^2(t)}. \end{aligned}$$

(6)

Clearly, $|V_1(t)| \le |u_1(t)| + \frac{1}{2}(\sigma -1) \le \sigma$, and so $V_2(t)$ is defined. The evader applies the following strategy on $[\tau , \tau ')$:

$$\begin{aligned} V(t)=(V_1(t), V_2(t)), \ \ t \in [\tau , \tau '). \end{aligned}$$

(7)

We call V(t) defined by (7) a maneuver of the evader y against the pursuer x. For the final part of evader’s strategy, we let

$$\begin{aligned} V_0 = (0, \sigma ), \ \ t \ge \tau '. \end{aligned}$$

(8)

The main result of this section is the following statement which will be used to prove the main result of the paper in Sect. 4.

Lemma 1

Let the evader use the strategy (5), (7), and (8), where $\tau$ is the a-approach time of the pursuer x to the evader y. Then,

$$\begin{aligned}{} & {} ||y(t)-x(t)|| \ge a, \ \ 0 \le t \le \tau ,\nonumber \\{} & {} ||y(t)- x(t)|| > \frac{\alpha a}{2\sigma }, \ \ \tau \le t \le \tau ', \end{aligned}$$

(9)

$$\begin{aligned}{} & {} y_2(t)- x_2(t) > a, \ \ t \ge \tau '. \end{aligned}$$

(10)

Proof

We will prove this lemma by considering the three parts of evader’s strategy defined by formulas (5), (7), (8), respectively. First, the evader moves with the velocity $v(t)=(0, \sigma )$, $0 \le t < \tau$, along the vertical line. The corresponding trajectory of the evader is a segment with the endpoints $y_0$ and $y(\tau )$ (see Fig. 1). By definition of $\tau$, we have $||x(t)-y(t)||\ge a$ for $0 \le t \le \tau$.

To prove (9), we consider the case $x_1(\tau ) \le y_1(\tau )$, hence, by (6) $V_1(t)=|u_1(s)|+\alpha$. The argument when $x_1(\tau ) > y_1(\tau )$ is completely analogous. The curve between the points $y(\tau )$ and $y(\tau ')$ in Fig. 1  is the trajectory of the evader corresponding to the maneuver (7). We have, for $\tau \le t \le \tau '$,

$$\begin{aligned} \begin{aligned} ||y(t)-x(t)||&\ge y_1(t)-x_1(t)=y_1(\tau )-x_1(\tau )+\int \limits _\tau ^t V_1(s)ds-\int \limits _\tau ^t u_1(s)ds\\&=y_1(\tau )-x_1(\tau )+\int \limits _\tau ^t(|u_1(s)|+\alpha )ds-\int \limits _\tau ^t u_1(s)ds\\&\ge \alpha (t-\tau ). \end{aligned} \end{aligned}$$

On the other hand,

$$\begin{aligned} \begin{aligned} {||y(t)-x(t)||}&{\ge ||y(\tau )-x(\tau )||-\left\| \int \limits _\tau ^t V(s)ds\right\| -\left\| \int \limits _\tau ^t u(s)ds\right\| }\\&\ge a-\int \limits _\tau ^t||V(s)||ds-\int \limits _\tau ^t||u(s)||ds\\&\ge a-(\sigma +1)(t-\tau ). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} ||y(t)-x(t)||\ge h(t) = \max \{\alpha (t-\tau ), a-(\sigma +1)(t-\tau )\}. \end{aligned}$$

Fig. 2

Graph of the function h(t)

Since the function $h_1(t)=\alpha (t-\tau )$, $t \ge \tau$, is increasing, and the function $h_2(t)=a-(\sigma +1)(t-\tau )$, $t \ge \tau$, is decreasing, therefore the function h(t), $t \ge \tau$, achieves its minimum at $t=t^*$ where $h_1(t)= h_2(t)$ (see Fig. ). We can see that $t^*=\tau +\frac{a}{\alpha +\sigma +1} \in [\tau , \tau ']$. Hence, for any $t \in [\tau , \tau ']$, by (4) we have

$$\begin{aligned} ||y(t)-x(t)||\ge h(t^*)=\alpha (t^*-\tau ) ={\frac{\alpha a}{\sigma +1+\alpha } > \frac{\alpha a}{2\sigma },} \end{aligned}$$

which proves (9).

Next, to prove (10), first we show that

$$\begin{aligned} y_2(\tau ')-x_2(\tau ') > a. \end{aligned}$$

(11)

Indeed, for $\tau \le t \le \tau '$, due to the obvious inequality $y_2(\tau )-x_2(\tau ) \ge -||y(\tau )-x(\tau )|| = -a$ we have

$$\begin{aligned} y_2(t)-x_2(t)= & {} y_2(\tau )-x_2(\tau )+\int \limits _\tau ^t V_2(s)ds-\int \limits _\tau ^t u_2(s)ds \nonumber \\\ge & {} -a+\int \limits _\tau ^t\left( \sqrt{\sigma ^2-(|u_1(s)|+\alpha )^2}-\sqrt{1-u_1^2(s)}\right) ds. \end{aligned}$$

(12)

Noting that the function

$$\begin{aligned} f(\xi )=\sqrt{\sigma ^2-(\xi +\alpha )^2}-\sqrt{1-\xi ^2}, \ \ \xi \in [0, 1], \end{aligned}$$

achieves its minimum at $\xi _0=\frac{\alpha }{\sigma -1}$, it follows from (12) that

$$\begin{aligned} \begin{aligned} y_2(t)- x_2(t)&\ge -a+(t-\tau )\left( \sqrt{\sigma ^2-(\xi _0+\alpha )^2}-\sqrt{1-\xi _0^2}\right) \\&=-a+(t-\tau )\sqrt{(\sigma -1)^2-\alpha ^2}. \end{aligned} \end{aligned}$$

In particular, for $t=\tau '$ we obtain

$$\begin{aligned} y_2(\tau ')- x_2(\tau ')\ge -a + \frac{4a}{\sigma -1}\sqrt{(\sigma -1)^2-\alpha ^2} > a. \end{aligned}$$

(13)

Hence, (8) implies that, for $t \ge \tau '$,

$$\begin{aligned} \begin{aligned} y_2(t)- x_2(t)&= y_2(\tau ')- x_2(\tau ') + \int \limits _{\tau '}^t v_2(s)ds - \int \limits _\tau ^t u_2(s)ds \\&> a+(t-\tau ')(\sigma -1) > a. \end{aligned} \end{aligned}$$

The proof of the lemma is complete. $\square$

In particular, Lemma 1 implies that even though the pursuer is on the vertical line and above the evader, the evader can avoid from capturing using the maneuver.

4 Evasion from Many Pursuers

We prove the following statement.

Theorem 4.1

For any initial positions of players, evasion is possible in game (1).

We have divided the proof into subsections.

4.1 Definitions of Parameters

Let $\alpha$, $a_1$ and $\beta$ be any fixed numbers that satisfy the following relations

$$\begin{aligned} 0< \alpha< \min \left\{ 1, \frac{1}{2}(\sigma -1)\right\} , \ \ 0< a_1 < \min _{i=1, \dots , m}||y_0 - x_{i0}||, \ \ \beta = \frac{(\sigma -1)\alpha }{64\sigma ^2}. \end{aligned}$$

We define a decreasing geometric sequence $\{a_k\}_{k=1}^\infty$ by the equation $a_{k+1}=\beta a_k$, $k=1,2,...$.

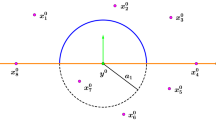
Next, we assume that the evader is moving under some strategy. We say that $t=\tau _1 > 0$ is the $a_1$-approach time of a pursuer $x_{i_0}$ to the evader if $||x_{i_0}(\tau _1)-y(\tau _1)||=a_1$ and $||x_i(t)-y(t)|| > a_1$ for all $0 \le t < \tau _1$ and $i=1,2,..., m$. In general, if $\tau _{k-1}$, $k \ge 2$, is the $a_{k-1}$-approach time, then we define the time $t=\tau _k > \tau _{k-1}$ to be the $a_k$-approach time if for a pursuer $x_{i_1}$ $||x_{i_1}(\tau _k)-y(\tau _k)||=a_k$ and $||x_i(t)-y(t)|| > a_k$ for all $0 \le t < \tau _k$ and $i=1,2,..., m$.

Fig. 3

$\tau _k$ is the $a_k$-approach time of the pursuers $x_i$, $x_j$ and $x_k$ to the evader y

Thus, we have defined a monotone increasing sequence $\tau _1< \tau _2 <...$ of the approach times. Notice that the same time $\tau _k$ can be the $a_k$-approach time of several pursuers to the evader. For example, in Fig.  $\tau _k$ is an $a_k$-approach time of the pursuers $x_i$, $x_j$ and $x_k$ to the evader. If there are more than one pursuers, for which $\tau _k$ is the $a_k$-approach time, we choose any of these pursuers and, without restriction of generality, label it by $x_k$. Hence, by the definition of $\tau _k$ we have

$$\begin{aligned} ||y(t)-x_i(t)|| > a_k, \ \ i=1,2,...,m, \ \ 0 \le t < \tau _k, \ \ ||y(\tau _k)-x_k(\tau _k)|| = a_k. \end{aligned}$$

(14)

It should be noted that the same pursuer $x_k$ can have several other approach times $\tau _{k'}$, $\tau _{k''}$,...., beyond the approach time $\tau _k$.

Let

$$\begin{aligned} \tau _k'=\tau _k+\frac{4a_k}{\sigma -1}, \ k=1, 2,..., \ \tau _0=0, \ \tau _0'=\infty . \end{aligned}$$

Notice that the sequence $\tau _1', \ \tau _2', \ \tau _3', \ldots$ is not necessarily monotone.

4.2 Strategy for the Evader

Without loss of generality, we assume that $y_0=(0,0)$, that is, the evader is at the origin at the initial time. For $k=1, 2, \dots$, we define the maneuvers $V_k(t)=(V_{k1}(t), V_{k2}(t))$, as follows

$$\begin{aligned} V_{k1}(t)=\left\{ \begin{array}{cl} |u_{k1}(t)|+\alpha , &{} x_{k1}(\tau _k)\le y_1(\tau _k),\\ -(|u_{k1}(t)|+\alpha ),&{} x_{k1}(\tau _k)>y_1(\tau _k), \end{array}\right. \ \ \ V_{k2}(t)=\sqrt{\sigma ^2-V_{k1}^2(t)}. \end{aligned}$$

(15)

First, the evader moves starting from the time $\tau _0=0$ along the y-axis with the velocity $v(t)=V_0 =(0, \sigma )$. If the $a_1$-approach time $\tau _1 > 0$ doesn’t occur, that is, $||y(t)-x_i(t)|| > a_1$ for all $i=1,2,..., m$ and $t \ge 0$, then, clearly, $x_i(t) \ne y(t)$, $t \ge 0$, $i=1,2,..., m$, and so evasion is possible in the game.

Let the $a_1$-approach time $\tau _1 > 0$ occur. In general, the evader constructs its strategy as follows. Let the time $\tau _k$, $k \ge 1$, occur.

(i) if the time $\tau _{k+1}$ occurs in the interval $[\tau _k, \tau _k')$, then $v(t)=V_k(t)$ on $[\tau _k, \tau _{k+1})$.

(ii) if the time $\tau _{k+1}$ doesn’t occur in $[\tau _k, \tau _k')$, then $v(t)=V_k(t)$ on $[\tau _k, \tau _k')$.

(iii) if the time $\tau _{k+1}$ occurs in $[\tau _k', \infty )$, then $v(t)=V_0$ on $[\tau _k', \tau _{k+1})$.

(iv) if the time $\tau _{k+1}$ never occurs, then $v(t)=V_0$ on $[\tau _k', \infty )$.

Fig. 4

Group attacks of $x_1$, $x_2$, $x_3$ on $[\tau _1, \tau _3')$ and $x_4$, $x_5$ on $[\tau _4, \tau _5')$

For the times in Fig. , $\tau _2$ occurs in $[\tau _1, \tau _1')$; therefore, by item (i) $v(t)=V_1(t)$ on $[\tau _1, \tau _2)$. Similarly, $\tau _3 < \tau _2'$; therefore, $v(t)=V_2(t)$ on $[\tau _2, \tau _3)$. However, $\tau _4$ is not in $[\tau _3, \tau _3')$; therefore, by item (ii) $v(t)=V_3(t)$ on $[\tau _3, \tau _3')$, and by item (iii) $v(t)=V_0$ on $[\tau _3', \tau _4)$. Finally, since there is no an approach time on $[\tau _5', \infty )$, therefore by item (iv) $v(t)=V_0$ on this interval.

The functions $\theta _1(t)$ and $\theta _2(t)$ in Definition 2 are defined as follows. Let $\theta _1(t)=\max _{\tau _k \le t}\tau _k=\tau _K$ for some $K \ge 1$. In other words, $\tau _K$ is the greatest of the values $\tau _k$ defined by the current time t. Then, we define $\theta _2(t)= \tau _K'$. For example, if $\tau _0 \le t < \tau _1$, then $K=0$; if $\tau _1 \le t < \tau _2$, then $K=1$. The strategy of the evader described by steps (i)-(iv) means that at the current time t (recall $t \ge \tau _K$) $v(t)=V_K(t)$ if $t < \tau _K'$, and $v(t)=V_0(t)$ if $t \ge \tau _K'$.

According to the description of evader’s strategies (i)-(iv), there are two possible cases.

Case A. The finite approach times $\tau _1$, $\tau _2$,..., $\tau _{k_1}$ with $\tau _1< \tau _2<... < \tau _{k_1}$, occur so that $\tau _2 < \tau _1'$, $\tau _3 < \tau _2'$,..., $\tau _{k_1} < \tau _{k_1-1}'$, and there is no an approach time in $[\tau _{k_1}, \tau _{k_1}')$ for some $k_1 \ge 1$. Then, we say that the evader is under a group attack of the pursuers $x_1$, $x_2$,..., $x_{k_1}$ on the time interval $[\tau _1, \tau _{k_1}')$. Thus, the first group attack of pursuers ends at $\tau _{k_1}'$.

By items (i)-(iv), the strategy of the evader on the interval $[\tau _0, \tau _{k_1}')$ can be written as follows:

$$\begin{aligned} v(t)=\left\{ \begin{array}{ll} V_0,&{} \tau _0 \le t< \tau _1,\\ V_k(t),&{} \tau _k \le t< \tau _{k+1}, \ \ k=1,2,..., k_1-1, \\ V_{k_1}(t),&{} \tau _{k_1} \le t < \tau _{k_1}'. \end{array}\right. \end{aligned}$$

(16)

By item (iii) starting $\tau _{k_1}'$, the evader starts to apply $v(t)=V_0$ and after some time the evader may undergo another group attack of pursuers.

Figure 4 illustrates two group attacks of pursuers. The evader is under a group attack of the pursuers $x_1$, $x_2$, $x_3$ on $[\tau _1, \tau _3')$, and it is under a group attack of the pursuers $x_4$, $x_5$ on $[\tau _4, \tau _5')$.

Fig. 5

Trajectory of the evader

Figure  illustrates the three sections of the evader’s trajectory between the points $y(\tau _1)$, $y(\tau _2)$, $y(\tau _3)$, and $y(\tau _3')$ corresponding to some maneuvers $v(t)=V_1(t)$, $v(t)=V_2(t)$, and $v(t)=V_3(t)$ where $\tau _2 < \tau _1'$, $\tau _3 < \tau _2'$ and there is no an approach time in $[\tau _3, \tau _3')$.

Since by the definition of approach times we have $\tau _k < \tau _{k+1}$, $k \ge 1$, therefore, in view of the conditions $\tau _{k+1} < \tau _k'$, $k=1,..., k_1-1$, we get in Case A the following inclusion

$$\begin{aligned} {[}\tau _1, \tau _{k_1}') = \cup _{k=1}^{k_1-1} [\tau _k, \tau _{k+1}) \cup [\tau _{k_1}, \tau _{k_1}') \subset \cup _{k=1}^{k_1} [\tau _k, \tau _k'), \end{aligned}$$

(17)

For example, for the interval $[\tau _1, \tau _3')$ in Fig. 4, we have $[\tau _1, \tau _3') \subset \cup _{k=1}^3 [\tau _k, \tau _k')$.

It is natural to ask questions: Can the same pursuer participate several times in the same group attack? Can the number of approach times in a group attack be finite? Description (i)-(iv) doesn’t exclude the case where the number of pursuers in a group attack is infinite.

Case B. Let infinitely many successive approach times $\tau _1$, $\tau _2$,... of pursuers $x_1$, $x_2$,... to the evader occur satisfying the conditions $\tau _k< \tau _{k+1} < \tau _k'$ for all $k=1,2,...$. Then, $[\tau _k, \tau _{k+1}) \subset [\tau _k, \tau _k')$ and so, for any $n \ge 1$, we have

$$\begin{aligned} {[}\tau _1, \tau _n) = \cup _{k=1}^{n-1} [\tau _k, \tau _{k+1}) \subset \cup _{k=1}^{n-1} [\tau _k, \tau _k'), \end{aligned}$$

(18)

Clearly,

$$\begin{aligned} \tau _{n}-\tau _1 = \sum _{k=1}^{n-1} (\tau _{k+1}-\tau _k)< \sum _{k=1}^{n-1} (\tau _k'-\tau _k)< \sum _{k=1}^\infty \frac{4a_k}{\sigma -1} = \frac{4a_1}{(\sigma -1)(1-\beta )} < \infty . \end{aligned}$$

This means that the increasing sequence $\tau _n$ is bounded. Then, the limit $\tau _\infty = \lim _{n \rightarrow \infty } \tau _n$ exists. Note that in Case B inclusion (18) holds for any $n \ge 1$, and passing to limit as $n \rightarrow \infty$ in (18) we obtain

$$\begin{aligned}{}[\tau _1, \tau _\infty ) \subset \cup _{k=1}^\infty [\tau _k, \tau _k'). \end{aligned}$$

(19)

By items (i)-(iv), the evader’s strategy on the interval $[\tau _1, \tau _{\infty })$ is

$$\begin{aligned} v(t)= V_k(t), \ \ t \in [\tau _k, \tau _{k+1}), \ \ \tau _k < \tau _{k-1}', \ \ k=1, 2, \ldots . \end{aligned}$$

(20)

From now on, we use ${\bar{\tau }}$ to denote $\tau _{k_1}'$ in Case A, and to denote $\tau _\infty$ in Case B. We’ll discuss in detail the first group attack, which starts at the time $\tau _1$ and ends at ${\bar{\tau }}$. Another group attack may occur after the time ${\bar{\tau }}$ as well, which can be studied in a similar fashion.

The results of Sect. 4.4 show that Case B will not happen. Also, in the following subsections, we’ll answer the questions: Can the same pursuer participate in several group attacks as well? Is the number of group attacks finite?

4.3 Estimation of Distance Between Evader and FE

Take any $a_p$-approach time $\tau _p$ of the pursuer $x_p$ to the evader y, where $p \in \{1, 2, \dots , k_1\}$ in Case A, and p is any positive integer in Case B, and we will estimate the distance between $x_p(t)$ and y(t) for $t \ge \tau _p$. In order to obtain the desired estimate, we introduce for $t \in [\tau _p, \tau _p']$ a fictitious evader (FE) $z_p$ whose motion is described by the equation

$$\begin{aligned} \dot{z}_p= w_p, \ z_p(\tau _p)=y(\tau _p), \end{aligned}$$

where $w_p$ is control parameter of FE $z_p$. We let

$$\begin{aligned} w_p(t)=V_p(t)=(V_{p1}(t), V_{p2}(t)), \ \ t \in [\tau _p, \tau _p'). \end{aligned}$$

(21)

Fig. 6

Evader y and fictitious evader $z_p$

Then, by (9) we have

$$\begin{aligned} ||z_p(t)-x_p(t)|| > \frac{\alpha a_p}{2\sigma } \quad \text {for} \quad \tau _p \le t \le \tau _p'. \end{aligned}$$

(22)

Moreover, by (10)

$$\begin{aligned} z_{p2}(\tau _p') - x_{p2}(\tau _p') > a_p. \end{aligned}$$

(23)

Note that FE $z_p$ moves only on the time interval $[\tau _p, \tau _p')$ and its initial state $z(\tau _p)$ coincides with the initial state $y(\tau _p)$ of the real evader.

In Case A, by (16) the strategy of evader on the interval $[\tau _p, \tau _{k_1}')$, $k_1 \ge p$, is

$$\begin{aligned} v(t)=\left\{ \begin{array}{ll} V_k(t), &{} t \in [\tau _k, \tau _{k+1}), \ \ k=p, p+1, \ldots , k_1-1,\\ V_{k_1}(t), &{} t \in [\tau _{k_1}, \tau _{k_1}'), \end{array}\right. \end{aligned}$$

(24)

where

$$\begin{aligned} \tau _k < \tau _{k-1}', \ \ k=p+1, p+2,..., k_1; \end{aligned}$$

(25)

and in Case B, by the description (i)-(iv) the evader’s strategy on the interval $[\tau _p, \tau _{\infty })$ is

$$\begin{aligned} v(t)= V_k(t), \ \ t \in [\tau _k, \tau _{k+1}), \ \ \tau _k < \tau _{k-1}', \ \ k=p,p+1, \ldots . \end{aligned}$$

(26)

For the distance between the points y(t) and $z_p(t)$ on $[\tau _p, \tau _*]$, $\tau _*= \min \{\tau _p', {\bar{\tau }}\}$, where ${\bar{\tau }}= \tau _{k_1}'$ in Case A, and ${\bar{\tau }}= \tau _{\infty }$ in Case B, we prove the following lemma, where we use the inclusion

$$\begin{aligned}{}[\tau _p', t) \subset [\tau _{p+1}, t) \subset \cup _{k \ge p+1, \ \tau _k \le t}[\tau _k, \tau _k'), \ \ \tau _{p+1} \le t \le {\bar{\tau }}, \end{aligned}$$

(27)

following from (17) and (19) for both Case A and Case B.

Lemma 2

Let the evader use strategy (24) in Case A and (26) in Case B. Then,

$$\begin{aligned} ||y(t)-z_p(t)|| \le \frac{16\sigma }{\sigma -1}a_{p+1} \quad \text {for}\quad \tau _p \le t \le \tau _*. \end{aligned}$$

(28)

This lemma says that if $\tau _p' \le {\bar{\tau }}$, then $\tau _*= \tau _p'$ and estimate (28) is true on $\tau _p \le t \le \tau _p'$, and that if $\tau _p' > {\bar{\tau }}$, then $\tau _*= {\bar{\tau }}$ and estimate (28) is true on $\tau _p \le t \le {\bar{\tau }}$.

Proof

Note that $y(\tau _p)=z(\tau _p)$ and there is no an approach time in the interval $[\tau _p, \tau _p')$, then by (21) and (24) $v(t)=w_p(t)=V_p(t)$, $t \in [\tau _p, \tau _p')$, and so (28) is satisfied.

We let now one or several approach times $\tau _{p+1}$, $\tau _{p+2}$,... occur in the interval $[\tau _p, \tau _p')$. In Fig. , the sections of the trajectory of evader correspond to distinct maneuvers.

Since by (21) and (24) $v(t)=w_p(t)=V_p(t)$, $t \in [\tau _p, \tau _{p+1})$, therefore, $y(t) = z_p(t)$, $t \in [\tau _p, \tau _{p+1})$, and so (28) is satisfied.

For $t \in [\tau _{p+1}, \tau _*)$, we obtain

$$\begin{aligned} ||y(t)-z_p(t)||= & {} \left\| y(\tau _p)+\int \limits _{\tau _p}^{\tau _{p+1}}V_p(s)ds+\int \limits _{\tau _{p+1}}^t v(s)ds\right. \left. - z(\tau _p) - \int \limits _{\tau _p}^{\tau _{p+1}}V_p(s)ds - \int \limits _{\tau _{p+1}}^tV_p(s)ds\right\| \nonumber \\= & {} \left\| \int \limits _{\tau _{p+1}}^t(v(s)-V_p(s))ds\right\| \le \int \limits _{\tau _{p+1}}^t\Vert v(s) -V_p(s)\Vert ds \le \int \limits _{\tau _{p+1}}^t 2\sigma ds, \end{aligned}$$

(29)

where we used the inequality $\Vert v(s)-V_p(s)\Vert \le \Vert v(s)\Vert +\Vert V_p(s)\Vert \le 2\sigma$. Since due to the condition $t \le \tau _* \le {\bar{\tau }}$ we have inclusion (27), and $\beta \le 1/2$ implies that $\sum _{k= p+1}^\infty a_k = \frac{a_{p+1}}{1-\beta } \le 2a_{p+1}$, therefore we obtain from (29) that

$$\begin{aligned} \Vert y(t)-z_p(t)\Vert\le & {} 2\sigma (t-\tau _{p+1}) \le 2\sigma \sum _{k \ge p+1, \ \tau _k \le t}(\tau _k'-\tau _k) = 2\sigma \sum _{k \ge p+1, \ \tau _k \le t} \frac{4a_k}{\sigma -1}\nonumber \\< & {} \frac{8\sigma }{\sigma -1} \sum _{k = p+1}^\infty a_k = \frac{8\sigma }{\sigma -1}\cdot \frac{a_{p+1}}{1-\beta } \le \frac{16\sigma }{\sigma -1}a_{p+1}. \end{aligned}$$

(30)

The proof of the lemma is complete. $\square$

4.4 Estimation of Distance Between Evader and Pursuer

We estimate now the distance between the evader y and pursuer $x_p$.

Lemma 3

Let the evader use strategy (24) in Case A or (26) in Case B. Then,

$$\begin{aligned} \Vert y(t)-x_p(t)\Vert > a_{p+1}, \ \ \tau _p \le t \le \tau _*, \end{aligned}$$

(31)

and if for the pursuer $x_p$ the inequality $\tau _p' \le {\bar{\tau }}$ holds, then

$$\begin{aligned} y_2(t)-x_{p2}(t) > a_{p+1}, \ \ t \ge \tau _p'. \end{aligned}$$

(32)

Proof

To prove (31), we observe that both inequalities (22) and (28) are true on $\tau _p \le t \le \tau _*$, and therefore,

$$\begin{aligned} \begin{aligned} \Vert y(t)-x_p(t)\Vert&\ge \Vert x_p(t)-z_p(t)\Vert -\Vert z_p(t)-y(t)\Vert \\&> \frac{\alpha }{2\sigma }a_p-\frac{16\sigma }{\sigma -1}a_{p+1} = \frac{\alpha }{4\sigma }a_p. \end{aligned} \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert y(t)-x_p(t)\Vert > \frac{\alpha }{4\sigma }a_p \ge \beta a_p = a_{p+1}, \ \ \tau _p \le t \le \tau _*, \end{aligned}$$

and (31) is proved.

Next, to prove (32), we let $\tau _p' \le {\bar{\tau }}$. Since $z_{p2}(\tau _p')-x_{p2}(\tau _p') > a_p$ by (23) and

$$\begin{aligned} \Vert y(\tau _p')- z_p(\tau _p')\Vert \le \frac{16\sigma }{\sigma -1}a_{p+1} \end{aligned}$$

by (28), therefore we have

$$\begin{aligned} \begin{aligned} y_2(\tau _p')-x_{p2}(\tau _p')&=(z_{p2}(\tau _p')-x_{p2}(\tau _p')) + (y_2(\tau _p')-z_{p2}(\tau _p'))\\&\ge a_p-\Vert y(\tau _p')- z_p(\tau _p')\Vert> a_p-\frac{16\sigma }{\sigma -1}a_{p+1} > \frac{1}{2} a_p. \end{aligned} \end{aligned}$$

(33)

For $t \ge \tau _p'$, using (33) and the fact that $u_{p2}(s) \le 1$ we have

$$\begin{aligned} y_2(t)-x_{p2}(t)= & {} y_2(\tau _p')-x_{p2}(\tau _p')+\int _{\tau _p'}^tv_2(s)ds-\int _{\tau _p'}^tu_{p2}(s)ds\nonumber \\> & {} \frac{1}{2}a_p + \int _{\tau _p'}^tv_2(s)ds - (t-\tau _p'). \end{aligned}$$

(34)

First, we prove (32) for $\tau _p' \le t \le {\bar{\tau }}$. Indeed, since $v_2(t) > 0$ for all $t \ge 0$, therefore $\int _{\tau _p'}^tv_2(s)ds \ge 0$. Also, by (27)

$$\begin{aligned} t-\tau _p'= & {} mes([\tau _p',t)) \le mes\left( \cup _{p+1 \le k, \ \tau _k \le t}[\tau _k, \tau _k')\right) \le \sum _{k \ge p+1, \ \tau _k \le t}(\tau _k'-\tau _k) \nonumber \\= & {} \sum _{k \ge p+1, \ \tau _k \le t}\frac{4a_k}{\sigma -1} \le \frac{4 }{\sigma -1}\sum \limits _{k = p+1}^\infty a_k \le \frac{8 }{\sigma -1}a_{p+1}. \end{aligned}$$

(35)

Therefore, it follows from (34) that

$$\begin{aligned} y_2(t)-x_{p2}(t)> \frac{1}{2}a_p-\frac{8\sigma }{\sigma -1} a_{p+1}> \frac{1}{2}a_p-\frac{\alpha }{8\sigma } a_p> \frac{1}{4}a_p > a_{p+1}, \ \ \tau _p' \le t \le {\bar{\tau }}, \end{aligned}$$

(36)

and (32) is proved for $\tau _p' \le t \le {\bar{\tau }}$.

We conclude that, if $\tau _p' > {\bar{\tau }}$ for the pursuer $x_p$, then (31) implies that

$$\begin{aligned} \Vert y(t)-x_p(t)\Vert > a_{p+1}, \ \ \tau _p \le t \le {\bar{\tau }}, \end{aligned}$$

(37)

and if $\tau _p' \le {\bar{\tau }}$, then combining the inequalities (31) and (36) we obtain (37). Hence, (37) is true for each pursuer $x_p$ in the group attack in both Case A and Case B.

An important conclusion to draw from the inequality (37) is that, for $k \ge p+1$, there is no an $a_k$-approach time $\tau _k$ of the pursuer $x_p$ to the evader on the time interval $\tau _p < t \le {\bar{\tau }}$. Indeed, if there was an $a_k$-approach time $\tau _k$ with $\tau _p < \tau _k \le {\bar{\tau }}$ and $k \ge p+1$, then we would have had $\Vert y(\tau _k)-x_p(\tau _k)\Vert = a_k$. However, this is impossible since $a_k \le a_{p+1}$ and by (37) $\Vert y(\tau _k)-x_p(\tau _k)\Vert > a_{p+1}$.

Consequently, each pursuer $x_p$ in the group attack has only one approach time $\tau _p$ on the time interval $\tau _p \le t \le {\bar{\tau }}$. Therefore, all the pursuers in the group attack are distinct. Moreover, the number of pursuers in the group attack $\le m$ since there are at most m approach times in the group attack. Thus, Case B is excluded. There are only finite number of pursuers $x_1$, $x_2$,..., $x_{k_1}$ with $k_1 \le m$ in the (first) group attack. Hence, we deal with only Case A where ${\bar{\tau }} = \tau _{k_1}'$ and the group attack ends at $\tau _{k_1}'$.

Next, we proceed to prove (32) for $t \ge \tau _{k_1}'$ assuming that $\tau _p' \le \tau _{k_1}'$. Clearly, the inequality $\tau _p' \le \tau _{k_1}'$ is satisfied at least for $p=k_1$, that is, for the pursuer $x_{k_1}$. We estimate now the right-hand side of (34) for $t \ge \tau _{k_1}'$. Note that if several group attacks occur on the time interval $[\tau _{k_1}', t)$, by the description of evader’s strategy (i)-(iv) the evader moves with the velocity $v(t)=V_0$ between the group attacks and after the last group attack as well.

Fig. 7

Evader is under a group attack on the intervals $[\tau _1, \tau _{k_1}')$, $[\tau _{k_1+1}, \tau _{k_2}')$, $[\tau _{k_2+1}, \tau _{k_3}')$

Figure   illustrates three group attacks on the intervals $[\tau _{k_j+1}, \tau _{k_{j+1}}')$, $j=0, 1,2$, where $k_0=0$.

To estimate the integral $\int _{\tau _p'}^t v_2(s)ds$ in (34), we use the representation $[\tau _p', t) = I \cup J$, $I \cap J = {\emptyset }$, where the evader undergoes a group attack of some pursuers on I, and the evader moves with the velocity $v(t)=V_0$ on J. For example, for the interval $[\tau _p', t)$ in Fig. 7, we have

$$\begin{aligned} I = [\tau _p', \tau _{k_1}')\cup [\tau _{k_1+1}, \tau _{k_2}')\cup [\tau _{k_2+1}, \tau _{k_3}'), \ \ J = [\tau _{k_1}', \tau _{k_1+1})\cup [\tau _{k_2}', \tau _{k_2+1}) \cup [\tau _{k_3}', t). \end{aligned}$$

In general, for $t \ge \tau _{k_1}'$, let $j_0 \ge 0$ be the greatest integer such that $\tau _{k_{j_0}+1} \le t$. We then have

$$\begin{aligned} I= & {} [\tau _p', \tau _{k_1}') \cup \left( \cup _{1\le j \le j_0} \ [\tau _{k_j+1}, \tau _{k_{j+1}}')\right) \text { if } \ t \notin [\tau _{k_{j_0}+1}, \tau _{k_{j_0+1}}'),\\ I= & {} [\tau _p', \tau _{k_1}') \cup \left( \cup _{1\le j \le j_0-1} \ [\tau _{k_j+1}, \tau _{k_{j+1}}')\right) \cup [\tau _{k_{j_0}+1}, t) \text { if } \ t \in [\tau _{k_{j_0}+1}, \tau _{k_{j_0+1}}'). \end{aligned}$$

Next, by (27)

$$\begin{aligned}{}[\tau _p', \tau _{k_1}') \subset [\tau _{p+1}, \tau _{k_1}') \subset \cup _{p+1 \le k \le k_1}[\tau _k, \tau _k') \end{aligned}$$

and, for the a group attack on $[\tau _{k_j+1}, \tau _{k_{j+1}}')$, we have $\tau _{k+1} < \tau _k'$, $k=k_j+2,...,k_{j+1}$, and so similar to (17) we can write

$$\begin{aligned}{}[\tau _{k_j+1}, \tau _{k_{j+1}}') \subset \cup _{k=k_j+1}^{k_{j+1}} [\tau _k, \tau _k'), \end{aligned}$$

(38)

therefore $I \subset \cup _{k \ge p+1, \ \tau _k \le t} \ [\tau _k, \tau _k')$, and the length |I| of I can be estimated as follows

$$\begin{aligned} |I| \le \sum _{k \ge p+1, \ \tau _k \le t}(\tau _k'-\tau _k) = \sum _{k \ge p+1, \ \tau _k \le t}\frac{4a_k}{\sigma -1} \le \frac{4 }{\sigma -1}\sum \limits _{k = p+1}^\infty a_k \le \frac{8 }{\sigma -1}a_{p+1}. \end{aligned}$$

(39)

Since $v_2(t) > 0$ for all $t \in I$, therefore $\int _I v_2(s) ds \ge 0$. Using this and (39) we obtain

$$\begin{aligned} \int _{\tau _p'}^tv_2(s)ds&= \int _{I\cup J}v_2(s)ds = \int _I v_2(s) ds + \int _J\sigma ds \ge \int _J\sigma ds = \sigma |J|\\&= \sigma |[\tau _p', t]\setminus I| \ge \sigma (t-\tau _p'-|I|) \ge \sigma \left( t-\tau _p'-\frac{8}{\sigma -1} a_{p+1}\right) . \end{aligned}$$

Thus, it follows from (34) that if $\tau _p' \le \tau _{k_1}'$, then for any $t \ge \tau _{k_1}'$,

$$\begin{aligned} y_2(t)-x_{p2}(t)> & {} \frac{1}{2}a_p-\frac{8\sigma }{\sigma -1} a_{p+1} + (\sigma -1)(t-\tau _p') \\> & {} \frac{1}{2}a_p-\frac{\alpha }{8\sigma } a_p> \frac{1}{4}a_p > a_{p+1}, \end{aligned}$$

which is the desired conclusion. The proof of the lemma is complete. $\square$

We are now in a position to prove Theorem 4.1.

Proof

Let $\tau _p' \le \tau _{k_1}'$ for a pursuer $x_p$ in the first group attack of pursuers. Note that this condition is satisfied at least for $p=k_1$. Combining the inequality in (14) with $k=p$, inequality (31) where $\tau _* = \tau _p'$, and inequality (32) we obtain that $\Vert y(t)-x_p(t)\Vert > a_{p+1}$ for all $t \ge 0$. Therefore, the pursuer $x_p$, for which $\tau _p' \le \tau _{k_1}'$, can never reach the $a_{p+1}$-vicinity of the evader y. Hence, $x_p$ will not participate in the further group attacks starting from the second one satisfying the inequality $y_2(t)-x_{p2}(t) > a_{p+1} \ge a_{k_1+1}$, $t \ge \tau _p'$ ($p \le k$).

If the time $\tau _{k_1+1}$ occurs, then the evader undergoes the second group attack of some pursuers on an interval $[\tau _{k_1+1}, \tau _{k_2}')$ for some $k_2 \ge k_1+1$. We can use similar arguments to obtain $\Vert y(t)-x_q(t)\Vert > a_{q+1}$ for all $t \ge 0$ and for some $q \in \{k_1+1,..., k_2\}$ for which $\tau _q' \le \tau _{k_2}'$. The pursuer $x_q$ will not participate in further group attacks starting from the third one staying "behind" the evader satisfying the inequality $y_2(t)-x_{q2}(t) > a_{q+1} \ge a_{k_2+1}$, $t \ge \tau _q'$, and so on.

Thus, after the first group attack of pursuers $x_1, x_2,..., x_{k_1}$ we can ignore at least one pursuer, for example, $x_{k_1}$, after the second group attack of pursuers $x_{k_1+1}, x_{k_1+2},..., x_{k_2}$ we can ignore at least one pursuer from this group of pursuers, for example, $x_{k_2}$, and so on. Since the total number of pursuers is m, therefore after at most m group attacks of pursuers all the pursuers remain "behind" the evader. The proof of Theorem 4.1 is complete. $\square$

We can now estimate from above the total number of approach times. Since there are at most m approach times in the first group attack of pursuers, there are at most $m-1$ approach times in the second group attack of pursuers and so on, therefore the total number of the approach times is at most $m+(m-1)+...+1=m(m+1)/2$. If $\tau _{k_{j_0}}$ is the last approach time, then $k_{j_0} \le m(m+1)/2$ and

$$\begin{aligned} \Vert x_i(t)-y(t)\Vert > r = a_{k_{j_0}+1}, \ \ t \ge 0, \ \ i=1,2,...,m. \end{aligned}$$

(40)

This means that the evader can avoid from all pursuers moving at the distance not less than r from them.

5 Discussion

5.1 The Evader Moves in $\varepsilon$-Vicinity of the Oy-axis

For any given positive number $\varepsilon$, we can choose the number $a_1$ so that the trajectory of evader is always in the $\varepsilon$-vicinity of the Oy-axis (Fig. ). Indeed, since $v(t) = V_0=(0, \sigma )$, (hence, $v_1(t) = 0$) if $t \notin I_1= \bigcup \limits _{k \ge 1} [\tau _k, \tau _k')$, therefore if $a_1 \le \frac{\sigma -1}{8\sigma }\varepsilon$, then

$$\begin{aligned} |y_1(t)|&=\left| \int \limits _0^t v_1(s)ds\right| = \int \limits _0^t |v_1(s)|ds = \int \limits _{I_1\cap [0,t]} |v_1(s)|ds \\&\le \int \limits _{I_1} |v_1(s)|ds \le \sum \limits _{k \ge 1}\int \limits _{\tau _k}^{\tau _k'} |v_1(s)|ds \le \sum \limits _{k \ge 1}\sigma (\tau _k' - \tau _k)\\&\le \sum \limits _{k = 1}^\infty \frac{4\sigma a_k}{\sigma -1} \le \frac{8\sigma }{\sigma -1}a_1 \le \varepsilon . \end{aligned}$$

Fig. 8

Evader can avoid moving only in an $\varepsilon$-neighborhood of the Oy-axis

Hence, $|y_1(t)| \le \varepsilon$ for all $t \ge 0$, meaning that the state of the evader is in the $\varepsilon$-vicinity of the Oy-axis for all $t \ge 0$.

For simplicity of the proof of Theorem 4.1, the evader moved around the Oy-axis. In fact, we could take any ray l with the beginning at $y_0$ and construct a strategy for the evader to escape from pursuers in the $\varepsilon$-vicinity of the ray l as well.

Next, it follows from $|I_1| \le \frac{8 }{\sigma -1}a_1 = \frac{\varepsilon }{\sigma } < \varepsilon$ that the measure of the set $I_1$ can be made smaller than any given positive number $\varepsilon$ by choosing $a_1$. Thus, the evader moves under a group attack of some pursuers only on a subset of the set $I_1$ of measure less than $\varepsilon$, and outside the set $I_1$ the evader moves with velocity $v(t) = V_0=(0, \sigma )$.

5.2 Informativeness

The estimate (40) allows the evader to weaken the condition to informativeness. We show that it suffices for the evader to use only information about $x_1(t),..., x_m(t), y(t)$, $u_1(t-\delta ), u_2(t-\delta ),..., u_m(t-\delta )$ at the current time to avoid from capturing, where $\delta$ is a positive number.

Indeed, let

$$\begin{aligned} {\hat{u}}_i(t)=\left\{ \begin{array}{ll} 0, &{} 0 \le t \le \delta \\ u_i(t-\delta ), &{} t > \delta \end{array}\right. , \ \ \ i=1,2,..., m. \end{aligned}$$

(41)

Clearly, $\Vert {\hat{u}}_i(t)\Vert \le 1$. We consider auxiliary objects (AO) ${\hat{x}}_i(t)$, $i=1,2,..., m$, whose dynamics are given by the equations

$$\begin{aligned} \dot{{\hat{x}}}_i = {\hat{u}}_i, \ \ i=1,2,..., m, \end{aligned}$$

and their trajectories are defined as follows. AO ${\hat{x}}_i$ moves with the trajectory ${\hat{x}}_i(t) = x_{i0} + \int _0^t {\hat{u}}_i(s)ds$, $t \ge 0$, if there is no an $a_k$-approach time of the pursuer $x_i$ to the evader y. If the first $a_i$-approach time $\tau _i$ occurs, then AO ${\hat{x}}_i$ moves with the trajectory ${\hat{x}}_i(t) = x_{i}(\tau _k) + \int _{\tau _k}^t {\hat{u}}_i(s)ds$ for $t \ge \tau _i$.

In general, whenever the $a_{i_l}$-approach time $\tau _{i_l}$, $l=1,2,...$, of the pursuer $x_i$ to the evader y occurs, ${\hat{x}}_i$ moves with the trajectory ${\hat{x}}_i(t) = x_{i}(\tau _{i_l}) + \int _{\tau _{i_l}}^t {\hat{u}}_i(s)ds$ until the next approach time $\tau _{i_{l+1}}$. Clearly, the trajectory of AO ${\hat{x}}_i$ is, in general, discontinuous at the approach times $\tau _{i_l}$.

For $0 \le t \le \delta$, by (41), we have

$$\begin{aligned} \Vert x_i(t)-{\hat{x}}_i(t)\Vert= & {} \left\| x_{i0} + \int \limits _0^{t}u_i(s)ds - x_{i0} - \int \limits _0^{t}{\hat{u}}_i(s)ds \right\| \\= & {} \left\| \int \limits _0^{t}u_i(s)ds \right\| \le \int \limits _{0}^{t}\Vert u_i(s)\Vert ds \le t \le \delta , \end{aligned}$$

and, for $t > \delta$ and $\tau _{i_l} \le t < \tau _{i_{l+1}}$, we have

$$\begin{aligned} \Vert x_i(t)-{\hat{x}}_i(t)\Vert= & {} \left\| x_i(\tau _{i_l}) + \int \limits _{\tau _{i_l}}^{t}u_i(s)ds - x_i(\tau _{i_l}) - \int \limits _{\tau _{i_l}}^{t}u_i(s-\delta )ds \right\| \nonumber \\\le & {} \int \limits _{\tau _{i_l}-\delta }^{\tau _{i_l}}\Vert u_i(s)\Vert ds + \int \limits _{t-\delta }^{t}\Vert u_i(s)\Vert ds \le \int \limits _{\tau _{i_l}-\delta }^{\tau _{i_l}}1ds + \int \limits _{t-\delta }^{t}1ds \le 2\delta , \end{aligned}$$

(42)

and so $\Vert x_i(t)-{\hat{x}}_i(t)\Vert \le 2\delta$ for all $t \ge 0$.

The evader knows now information about $x_1(t),..., x_m(t), y(t)$, ${\hat{u}}_1(t), {\hat{u}}_2(t),..., {\hat{u}}_m(t)$ at the current time t. We let the evader use strategy (16) with $u_i(t)$ replaced by ${\hat{u}}_i(t)$ in (15). By Theorem 4.1, we have then $\Vert y(t)- {\hat{x}}_i(t)\Vert > r_0$ for some $r_0 > 0$. Consequently, if we choose $\delta < r_0/4$, then by (42)

$$\begin{aligned} \Vert y(t)-x_i(t)\Vert \ge \Vert y(t)- {\hat{x}}_i(t)\Vert - \Vert {\hat{x}}_i(t) -x_i(t)\Vert> r_0-2\delta > r_0/2, \end{aligned}$$

that is the evader can avoid from capturing moving from each pursuer at least $r_0/2$ distance away.

5.3 The Case Where $\tau _{k_1}' < \tau _p'$ for the Pursuer $x_p$

Figure  illustrates this case. It is important to note that if $\tau _{k_1}' < \tau _p'$ (see Fig. 4 where $\tau _{k_1}'=\tau _3' < \tau _2' = \tau _p'$), then the inequality $\Vert y(t)-x_p(t)\Vert > a_{p+1}$ in (31) may not be true for $\tau _{k_1}' \le t \le \tau _p'$. Since (31) was proved based on (28), and in its turn (28) was proved using the fact that the interval $[\tau _{p+1}, t)$ is a subset of the set $A=\cup _{k \ge p+1, \ \tau _k \le t} \ [\tau _k, \tau _k')$. However, if $\tau _{k_1}' < \tau _p'$, then the interval $[\tau _{k_1}', t)$ is not, in general, a subset of A. For example, if $\max \limits _{p+1 \le k \le k_1}\tau _k' < \min \{\tau _p', \tau _{k_1+1}\}$ and $\max \limits _{p+1 \le k \le k_1}\tau _k'< t < \min \{\tau _p', \tau _{k_1+1}\}$, then, clearly, the interval $[\max \limits _{p+1 \le k \le k_1}\tau _k', t)$ is not a subset of the set A.

Fig. 9

For the pursuer $x_p$, $\tau _{k_1}' < \tau _p'$

Also, note that if $\tau _{k_1}' < \tau _p'$, then the pursuer $x_p$, in general, can approach to an $a_k$ distance of the evader for some $k \ge p+1$ on the time interval $[\tau _{k_1}', \tau _p')$, but it is important to note that after the time $\tau _p'$ there is no an $a_k$-approach time to the evader for $k \ge p+1$. Indeed, by (23) we have

$$\begin{aligned} y_2(\tau _p') - x_{p2}(\tau _p')= & {} y_2(\tau _p') - z_{p2}(\tau _p') + z_{p2}(\tau _p') - x_{p2}(\tau _p') > y_2(\tau _p') - z_{p2}(\tau _p') + a_p\nonumber \\= & {} a_p + y_2(\tau _{k_1}') + \int \limits _{\tau _{k_1}'}^{\tau _p'}v_2(s)ds - z_{p2}(\tau _{k_1}') - \int \limits _{\tau _{k_1}'}^{\tau _p'}V_{p2}(s)ds. \end{aligned}$$

(43)

Since, for the set $I_2= \bigcup \limits _{\tau _k \ge \tau _{k_1}'} [\tau _k, \tau _k')=\bigcup \limits _{k \ge k_1+1} [\tau _k, \tau _k')$, similar to (39) we have $|I_2| \le \frac{8}{\sigma -1}a_{k_1+1} \le \frac{8}{\sigma -1}a_{p+1}$, and by (28)

$$\begin{aligned} y_2(\tau _{k_1}')- z_{p2}(\tau _{k_1}') \ge -\Vert y(\tau _{k_1}')- z(\tau _{k_1}')\Vert \ge -\frac{16\sigma }{\sigma -1}a_{p+1}, \end{aligned}$$

therefore using the obvious inequality $V_{p2}(s) \le \sqrt{\sigma ^2-\alpha ^2}$ we obtain from (43) that

$$\begin{aligned} y_2(\tau _p') - x_{p2}(\tau _p')\ge & {} a_p -\frac{16\sigma }{\sigma -1}a_{p+1} + \int \limits _{[\tau _{k_1}', \tau _p')\backslash I_2}\sigma ds - \int \limits _{\tau _{k_1}'}^{\tau _p'}\sqrt{\sigma ^2-\alpha ^2}ds\\\ge & {} a_p -\frac{16\sigma }{\sigma -1}a_{p+1} + \left( \tau _p' - \tau _{k_1}'- \frac{8}{\sigma -1}a_{p+1}\right) \sigma - (\tau _p' - \tau _{k_1}')\sqrt{\sigma ^2-\alpha ^2}\\= & {} a_p -\frac{24\sigma }{\sigma -1}a_{p+1} + (\tau _p' - \tau _{k_1}')(\sigma - \sqrt{\sigma ^2-\alpha ^2}) \ge a_p -\frac{24\sigma }{\sigma -1}a_{p+1} \ge \frac{a_p}{2}. \end{aligned}$$

Then, for $t \ge \tau _p'$, using the fact that $v_2(s)=\sigma$, $s \in [\tau _p',t)\backslash I_2$ and $v_2(s) > 0$, $s \in I_2$, we have

$$\begin{aligned} y_2(t) - x_{p2}(t)= & {} y_2(\tau _p') + \int \limits _{\tau _p'}^t v_2(s)ds - x_{p2}(\tau _p') - \int \limits _{\tau _p'}^t u_{p2}(s)ds \\= & {} y_2(\tau _p') - x_{p2}(\tau _p') + \int \limits _{[\tau _p',t)\backslash I_2}\sigma ds + \int \limits _{I} v_2(s) ds - \int \limits _{\tau _p'}^t 1ds \\\ge & {} \frac{a_p}{2} + \left( t-\tau _p' - \frac{8}{\sigma -1}a_{p+1}\right) \sigma - (t-\tau _p')\\= & {} \frac{a_p}{2} - \frac{8\sigma }{\sigma -1}a_{p+1} + (\sigma -1)(t-\tau _p') > a_{p+1}. \end{aligned}$$

Hence, for the pursuer $x_p$, there is no an $a_k$, $k \ge p+1$, approach time to the evader on the interval $t \ge \tau _p'$. This fact shows that the number of pursuers participating in the group attacks decreases more faster.

6 Conclusion

We have studied a simple motion evasion differential game of many pursuers and one faster evader and proposed a new strategy for the evader.

In in the paper of Chernous’ko [9], the evader first moves along a straight line l. Then, as the $a_1$-approach time $\tau _1$ occurs, the evader starting from this time moves along some spiral curves and at most $2^{m-1}$ approach times may occur until the evader reaches the straight line l again. The same pursuer can have several approach times during this period. As the evader reaches the straight line l, it moves again along l until the another approach time occurs. Then, the evader moves again along some spirals and at most $2^{m-2}$ approach times may occur until the evader reaches the straight line l again and so on. Therefore, the total number of approach times in that paper is $\le 2^{m-1}+2^{m-2}+\cdots +1 = 2^m-1$.

In the present paper, in the first group attack at most m approach times may occur and the evader, in general, doesn’t reach again the Oy-axis after the first group attack, but moves parallel to the Oy-axis with the speed $\sigma$ until the second group attack of pursuers occurs. Any pursuer participated in a group attack cannot have another approach time in the same group attack.

Also, we can specify at least one pursuer from each group attack, which will not participate in the following group attacks. This is namely the last pursuer joined the group attack. Therefore, the total number of approach times $\tau _k$ of m pursuers during the game doesn’t exceed $m(m+1)/2$ in the present paper.

The proof of Theorem 4.1 strongly depended on the inequality that $\tau _p' \le \tau _{k_1}'$. If $\tau _p' > \tau _{k_1}'$ for a pursuer $x_p$, then this pursuer can have an $a_k$-approach time to the evader for some $k > k_1$. In other words, this pursuer can participate in the next group attack of pursuers. However, good news is that this pursuer will not have any $a_k$-approach time to the evader for $k \ge p+1$ on the interval $[\tau _p', \infty )$. Hence, this pursuer will not participate in further group attacks after the time $\tau _p'$.