1 Introduction

Differential games have been an object of research since the 1960 (see, for example, Isaacs [18], Friedman [12], Hajek [14], Pontryagin [27], Krasovskii and Subbotin [21], Petrosyan [26]). A great number of works were devoted to simple motion pursuit and evasion differential games of many players. Mainly, controls of players are subjected to either geometric or integral constraints. In the case of geometric constraints, Croft [11] showed that in the n-dimensional Euclidean ball n lions can catch the man while the man can escape from \(n-1\) lions. A similar game problem was studied by Ivanov [19] on any convex compact set and an estimate from above was obtained for guaranteed pursuit time. In the case of an unbounded region, interesting results were obtained by Alexander et al. [1].

A new evasion maneuver was proposed by Mishchenko et al. [25] in the game of many pursuers. Chernous’ko [7] studied an evasion game of one evader and several pursuers where the evader was faster than the pursuers. It was proved that evader can avoid pursuers by remaining in a neighborhood of a given ray. Later on, the result of this paper was extended by Zak to more general differential game problems (see, for example, [33]). Also, evasion from a group of pursuers were studied by Borowko et al. [6] and Chernous’ko [9].

A simple motion differential game of many pursuers and one evader, when all players have the same dynamic possibilities, was studied in \({\mathbb {R}}^n\) by Pshenichnii [28]. Namely, it was proved that if the initial state of the evader belongs to the convex hull of pursuers’ initial states, then pursuit can be completed; otherwise, evasion is possible. Based on this work, Pshenichnii et al. [29] developed the method of resolving functions for solving linear pursuit problems with many pursuers. In the case of integral constraints, the method of resolving functions was developed by Belousov [4]. Later on, the results of the paper [28] were extended by many researchers. For example, when control sets of players are convex compact sets, Grigorenko [13] obtained the necessary and sufficient conditions of evasion of one evader from several pursuers. The papers [8, 23] are also extensions of [28]. In the work [22], the game problem of many pursuers and one evader was studied on a cylinder. In the recent work of Kuchkarov et al. [24], the results of [28] were extended to differential games on manifolds with Euclidean metric.

Petrov [5] obtained necessary and sufficient condition of evasion in a simple motion differential games of a group of pursuers and a group of evaders in \({\mathbb {R}}^n\) where all evaders use the same control. By definition, pursuit is considered completed if the state of a pursuer coincides with the state of at least one evader. Also, the works [3, 32] relate to such games.

The present paper is devoted to the evasion differential game of K pursuers and M evaders described by equations

$$\begin{aligned}&\dot{x}_i=u_i,\quad x_i(0)=x_{i0},\quad i=1,\ldots ,K, \end{aligned}$$
(1.1)
$$\begin{aligned}&\dot{y}_j=v_j,\quad y_j(0)=y_{j0},\quad j=1,\ldots ,M, \end{aligned}$$
(1.2)

with integral constraints

$$\begin{aligned}&\int \limits _{0}^{\infty }|u_i(s)|^2\mathrm{d}s\le \rho _i^2, \quad i=1,\ldots ,K, \end{aligned}$$
(1.3)
$$\begin{aligned}&\int \limits _{0}^{\infty }|v_j(s)|^2\mathrm{d}s\le \sigma _j^2,\quad j=1,\ldots ,M, \end{aligned}$$
(1.4)

where \(x_i, y_j, u_i, v_j\in {\mathbb {R}}^n\), \(n \ge 2\), and \(\rho _i, \sigma _j\) are given positive numbers, \(x_{i0} \ne y_{j0}\) for all \(i=1,\ldots ,K,\) and \(j=1,\ldots ,M\). Control systems with integral constraints on the control functions arise in problems, where the control resource is exhausted by consumption, such as energy, finance, food (see, e.g.,[10, 15, 20]).

A linear differential game of many pursuers and one evader (\(M = 1\)) when the control functions of players are subjected to integral constraints was first studied by Satimov et al. [30]. For the game (1.1)–(1.4), the result of that paper can be formulated as follows: if \(\rho _1^2+\cdots +\rho _K^2 > \sigma _1^2\), then pursuit can be completed. In the paper of Satimov et al. [31], it was shown that if

$$\begin{aligned} \rho _1^2 + \cdots + \rho _K^2 \le \sigma _1^2, \end{aligned}$$
(1.5)

then evasion is possible from some initial positions of players. In general, an evasion game of K pursuers and \(M=1\) evader was studied in the work of Ibragimov et al. [17], and it was proven that if (1.5) holds, then for any initial positions of players evasion is possible. Later on, Ibragimov and Satimov [16] studied a pursuit game problem of K pursuers and M evaders described by Eqs. (1.1)–(1.4) in a closed convex subset of \({\mathbb {R}}^n\). It was established that if

$$\begin{aligned} \rho _1^2 + \cdots + \rho _K^2 > \sigma _1^2 + \cdots + \sigma _M^2, \end{aligned}$$

then pursuit can be completed. In the evasion game problem studied by Idham et al. [2] in \(\ell _2\), strategies of evaders were constructed based on the fact that the space \(\ell _2\) is infinite dimensional.

In the present paper, we study the game (1.1)–(1.4) in \({\mathbb {R}}^n\) in the case where

$$\begin{aligned} \rho _1^2 + \cdots + \rho _K^2 \le \sigma _1^2 + \cdots + \sigma _M^2. \end{aligned}$$

If this is the case, we show that evasion is possible from any initial positions of players. In addition, we construct explicit strategies for the evaders.

We use the following notations.

  • \(\zeta _0 = (x_{10}, \ldots , x_{K0}, y_{10}, \ldots , y_{M0})\) is initial position of players.

  • \(V_j\) is the strategy of j-th evader,

  • \(p_i(t) = \rho _i^2 - \int \limits _0^t|u_i(s)|^2\mathrm{d}s\), \(q_j(t) = \sigma _j^2 - \int \limits _0^t|v_j(s)|^2\mathrm{d}s\),

  • \(\sigma = \left( \sigma _1^2 + \cdots + \sigma _M^2\right) ^{1/2}\), \(\rho = \left( \rho _1^2 + \cdots + \rho _K^2\right) ^{1/2}\), \(d = \min \limits _{i=1,\ldots ,K,\ j=1, \ldots , M}|x_{i0}-y_{j0}|\),

  • \(e_j = \frac{y_{j0}-z_0}{|y_{j0}-z_0|}\), and \(e'_j\) is a unit vector orthogonal to the vector \(e_j\) to be obtained from \(e_j\) by rotating it to the angle \(-\frac{\pi }{2}\),

  • \(S_j=\{\xi \in {\mathbb {R}}^2 \ | \ |(\xi -y_{j0},e_j')|\le a+b, (\xi -y_{j0},e_j) \ge -b\}\), and

    \(S_j' = \{\xi \in {\mathbb {R}}^2 \ | \ |(\xi -y_{j0}, e_j')| \le a, \ (\xi -y_{j0}, e_j) \ge -b \}\) are strips,

  • \(I_j(t)=\{s\in \{1,\ldots ,K\} \ | \ x_s(t)\in S_j\}\),

  • \(d_0=\min \{|y_{i0}-y_{j0}| \ \mid \ y_{i0} \ne y_{j0}, i,j=1,\ldots ,M\}\),

  • \(a_{j1}, a_{j2}, \ldots \) are given numbers that satisfy \(a_{j,i+1} = \kappa \cdot a_{j,i}^4\) where \(\kappa \in (0,1)\),

  • \(\tau _{ji}\) is the \(a_{ji}\)-approach time of the evader \(y_j\) with some pursuers; \(x_{ji}\) is the pursuer that is chosen to apply maneuver at \(\tau _{ji}\); \(\tau '_{ji} = \tau _{ji} + \frac{a_{ji}}{\alpha }\) (later they are used without j),

  • Continuous attack of a group of the pursuers \( x_{{\omega }_{k-1}+1}, \ldots , x_{{\omega }_k}\), is started at \(\tau _{{\omega }_{k-1}+1}\) and is completed at \(\tau ^*_{{\omega }_k}= \max \{\tau '_{{\omega }_{k-1}+1}, \ldots , \quad \tau '_{{\omega }_k}\}\), \({\omega }_0=0, \ \tau ^*_0 = 0\), \(\tau '_0=\tau '_1\),

  • \(J_{i+1}=\cup _{j = i+1}^{{\omega }_k}[\tau _j, \tau '_j), \ {\omega }_{k-1}+1 \le i < {\omega }_k; \ J_{{\omega }_k+1}=\emptyset \),

  • \(z_i\) is i-th fictitious evader, and \(w_i\) is its control parameter.

2 Statement of Problem

We consider a differential game described by Eqs. (1.1)–(1.4) where \(K \ge 1, \ M \ge 1\). First, we give definitions for control functions of players and strategies of evaders.

Definition 2.1

Borel measurable functions \(u_i(t)\), \(t \ge 0\), and \(v_j(t)\), \(t \ge 0\), that satisfy the constraints (1.3) and (1.4), respectively, are called controls of the pursuer \(x_i\), \(i\in \{1,\ldots , K\}\) and evader \(y_j\), \(j \in \{1, \ldots , M\}\), respectively.

Definition 2.2

If \(y_j(t_j) = x_i(t_j)\) at some \(j \in \{1, \ldots ,M\}\), \(i \in \{1, \ldots , K\}\) and \(t_j > 0\), then we say that the evader \(y_j\) is captured by the pursuer \(x_i\) at the time \(t_j\).

To define the strategies of evaders, we introduce new scalar parameters \(q_j = q_j(t)\), \(t \ge 0\), by equations

$$\begin{aligned} \dot{q}_j = -|v_j(t)|^2, \ q_j(0) = \sigma _j^2, \quad j=1,2, \ldots ,M. \end{aligned}$$

Clearly, \(q_j(t) = \sigma _j^2 - \int \limits _0^t|v_j(s)|^2\mathrm{d}s\), and \(q_j(t)\) expresses the amount of energy of evader \(y_j\) remained at the time t. Let \(\zeta _0 = (x_{10}, \ldots , x_{K0}, y_{10}, \ldots , y_{M0})\).

Definition 2.3

A function \(V_j(\zeta _0, t, y_j, q_j, x_1,\ldots , x_K, u_1, \ldots , u_K)\), \(j \in \{1, \ldots ,M\}\), is called strategy of the evader \(y_j\) if

  1. (i)

    for any controls of the pursuers \(u_i=u_i(t)\), \(i=1, \ldots , K\), the initial value problem

    $$\begin{aligned} \left\{ \begin{array}{l l} \dot{x}_1=u_1(t), &{}\quad x_1(0)=x_{10},\\ \vdots &{}\quad \vdots \\ \dot{x}_K =u_K(t), &{}\quad x_K(0)=x_{K0},\\ \dot{y}_j =V_j(\zeta _0, t, y_j, q_j, x_1, \ldots , x_K, u_1(t), \ldots , u_K(t)), &{}\quad y_j(0)=y_{j0},\\ \dot{q_j} = -|V_j(\zeta _0, t, y_j, q_j, x_1, \ldots , x_K, u_1(t), \ldots , u_K(t))|^2, &{}\quad q_j(0) = \sigma _j^2, \end{array} \right. \end{aligned}$$
    (2.1)

    has a unique solution \((x_1(t), \ldots , x_K(t), y_j(t), q_j(t))\), \(t\ge 0\),

  2. (ii)

    along this solution

    $$\begin{aligned} \int \limits _0^{\infty }|V_j(\zeta _0, t, y_j(t), q_j(t), x_1(t), \ldots , x_K(t), u_1(t), \ldots , u_K(t))|^2\mathrm{d}t \le \sigma _j^2. \end{aligned}$$
    (2.2)

By a solution of the initial value problem (2.1), we mean \((K+2)\)-tuple \((x_1(t), \ldots , x_K(t)\), \(y_j(t)\), \(q_j(t))\), \(t\ge 0\), with absolutely continuous components \(x_i(t)\), \(i = 1, \ldots ,K\), \(y_j(t)\), and \(q_j(t)\) that satisfy initial conditions in (2.1), differential equations in (2.1) almost everywhere on \([0, \infty )\) and \(q_j(t) \ge 0\).

Definition 2.4

We say that evasion is possible in the game (1.1)–(1.4) if there are strategies of evaders such that, for any controls of the pursuers, for all \(t > 0\) and \(i = 1, \ldots , K\), there exists \(j_0 \in \{1,2, \ldots ,M\}\) such that \(x_i(t) \ne y_{j_0}(t)\).

Thus, evaders apply strategies, whereas the pursuers use any controls. In other words, behaviors of pursuers are any. Pursuers try to capture each evader, and evaders try to avoid. If at least one evader is not captured by pursuers for all \(t \ge 0\), then by Definition 2.4 evasion is possible. It should be noted that we will not study the existence and uniqueness of solution for the system of Eq. (2.1). We construct strategies \(V_j\), \(j = 1, \ldots , M\), for evaders such that the initial value problem (2.1) has a unique solution and (2.2) is satisfied as well.

Now, formulate the problem.

Problem 1

Find a condition of evasion in terms of \(\rho _1, \ldots , \rho _K\) and \(\sigma _1,\ldots , \sigma _M\).

3 Main Result

Let \(\sigma = \left( \sigma _1^2 + \cdots + \sigma _M^2\right) ^{1/2}, \ \rho = \left( \rho _1^2 + \cdots + \rho _K^2\right) ^{1/2}\). The main result of the paper is the following statement.

Theorem 3.1

If \(\sigma \ge \rho \), then for any initial position of players \(\zeta _0\), evasion is possible in the game (1.1)–(1.4).

First, we give the structure of proof. In constructing the strategies for evaders the fact that \(\sigma > \rho \) is crucial. Therefore, the case \(\sigma = \rho \) is reduced to the case \(\sigma > \rho \) (Sect. 3.1). Then disjoint strips corresponding to evaders are constructed and each evader further moves only in his own strip (Sect. 3.2). Next, strategies for evaders are constructed (Sect. 3.3).

If for a pursuer \(x_i \in S\), the inequalities \((y(t),e ) \ge (x_i(t),e)\) and \(y(t) \ne x_i(t)\) hold at some time \(t=\theta \ge 0 \), then they hold for all \(t \ge \theta \) while the pursuer moves in the strip S and the evader’s energy is positive (Sect. 3.4). In particular, this is true for all pursuers \(x_i\) for which \(x_{i0} \in S\) and \((y_0,e ) \ge (x_{i0},e)\), where \(\theta =0\). In other words, such pursuers moving in S can never capture the evader while its energy q(t) is positive.

To estimate the distance between any pursuer \(x_p\) moving in S and the evader y on the time interval \([\tau _p, \tau '_p]\), where \(\tau _p\) is \(a_p\)-approach time, we introduce fictitious evaders (FE) \(z_i\) (Sect. 3.5) and estimate their energies. Then, we estimate the distance \(|z_p(t)-x_p(t)|\) on \([\tau _p, \tau '_p]\) from below (Sect. 3.6). Next, we estimate \(|z_p(t)-y(t)|\) from above (Sect. 3.7). Use these estimates to estimate \(|y(t)-x_p(t)|\) on \([\tau _p, \tau '_p]\) from below, which allows to conclude that \(x_p(t) \ne y(t)\), and moreover, \(a_{p+1}\)-approach will not occur with the pursuer \(x_p\) on \([\tau _p, \tau '_p]\) (Sect. 3.8). In addition, we show that \((y(\tau '_p),e ) \ge (x_p(\tau '_p),e)\) and \(y(\tau '_p) \ne x_p(\tau '_p)\). As mentioned above, pursuer \(x_p\) moving in S cannot capture the evader on \(t \ge \tau '_p\) as long as \(q(t)>0\).

Further, we estimate the evaders’ energies to prove that \(q_j(t) > 0\), \(t \ge 0\), for some \(j \in \{1, \ldots ,M\}\) and then prove that evasion is possible on any interval [0, T] providing that the number of approach times in [0, T] is finite (Sect. 3.9). Then finiteness of the number of approach times in any interval [0, T] is established (Sect. 3.10).

Finally, we choose parameters to satisfy all imposed conditions throughout the paper (Sect. 3.11), show that evader moves by remaining in the set \(S'\) whose width 2a can be made as small as we wish, give a method of reduction of the game in \({\mathbb {R}}^n\) to the game in \({\mathbb {R}}^2\), and then discuss the strategies of evaders (Sect. 4).

Proof The fact that evasion is possible in \({\mathbb {R}}^2\) implies that evasion is possible in \({\mathbb {R}}^n\) (see Sect. 4.2). Therefore, we prove the theorem for \({\mathbb {R}}^2\). \(\square \)

3.1 Reduction to the Case \(\sigma > \rho \)

Show that the case \(\sigma = \rho \) can be reduced to the case \(\sigma > \rho \). Indeed, let \(\sigma = \rho \). Set

$$\begin{aligned} v_j(t)=0, \quad 0 \le t \le \tau ^0, \quad j=1, \ldots , M, \end{aligned}$$
(3.1)

where \(t = \tau ^0\) is the first time at which

$$\begin{aligned} |x_i(t)-x_{i0}| = \frac{d}{4}, \text { where } \ d = \min _{i=1,\ldots ,K, \ j=1, \ldots , M}|x_{i0}-y_{j0}| \end{aligned}$$
(3.2)

for at least one of the numbers \(i \in \{1, \ldots , K\}\). Such a time \(\tau ^0\) may not exist meaning that \(|x_i(t)-x_{i0}| < d/4\) for all \(i \in \{1, \ldots , K\}\) and \(t \ge 0\). In this case, we let \(\tau ^0 = \infty \), and evasion is possible since

$$\begin{aligned} |x_i(t)- y_j(t)|= & {} |x_i(t)-x_{i0} + x_{i0}-y_{j0}|\\\ge & {} |x_{i0}- y_{j0}|-|x_{i}(t)-x_{i0}|\\> & {} d - \frac{d}{4} = \frac{3d}{4} \end{aligned}$$

for all i and j, and, hence, \(x_i(t)\ne y_j(t)\), \(t\ge 0\). Let \(\tau ^0\) be finite. Say \(|x_s(t)-x_{s0}| = d/4\) at some \(t=\tau ^0\) and \(s \in \{1, \ldots , K\}\). Then in view of (3.1) at the time \(t=\tau ^0\) the total resource of the evaders is still \(\sigma _1^2 + \cdots + \sigma _M^2\) since they have not moved on \([0, \tau ^0]\). The total resource of the pursuers remained at the time \(\tau ^0\) is

$$\begin{aligned} p(\tau ^0) = \sum _{i=1}^{K}p_i(\tau ^0), \quad p_i(t) = \rho _i^2-\int \limits _{0}^{t}|u_i(s)|^2\mathrm{d}s. \end{aligned}$$

We have

$$\begin{aligned} p(\tau ^0)= & {} \sum _{i=1}^{K}\rho _i^2 - \sum _{i=1}^{K}\int \limits _{0}^{\tau ^0}|u_i(t)|^2\mathrm{d}t \le \rho ^2 - \int \limits _{0}^{\tau ^0}|u_s(t)|^2\mathrm{d}t. \end{aligned}$$
(3.3)

Since

$$\begin{aligned} \frac{d}{4} = |x_s(\tau ^0)- x_{s0}| = \left| \int \limits _{0}^{\tau ^0}u_s(t)\mathrm{d}t\right| \le \left( \tau ^0 \int \limits _{0}^{\tau ^0}|u_s(t)|^2\mathrm{d}t\right) ^{1/2}, \end{aligned}$$

the pursuer \(x_s\) has spent a positive resource \(\int \limits _{0}^{\tau ^0}|u_s(t)|^2\mathrm{d}s \ge \frac{d^2}{16\tau ^0}\), and so by (3.3) \(p(\tau ^0) < \rho ^2\). Thus, at the time \(t=\tau ^0\), we have [see (3.1)]

$$\begin{aligned} \sum _{j=1}^{M}q_j(\tau ^0) = \sigma ^2 > \rho ^2-\frac{d^2}{16\tau ^0}\ge p(\tau ^0) \end{aligned}$$

meaning that the total energy of evaders is greater than that of pursuers at the time \(\tau ^0\). Moreover, \(x_i(\tau ^0)\ne y_j(\tau ^0)\) for all i and j. Thus, without loss of generality, we can assume that \(\sigma > \rho \).

Remark 3.2

According to Definition 2.3, evaders are not allowed to know information about \(p_i(\tau ^0)\). Hence, evaders do not know the value \(p(\tau ^0)\). However, evaders know the fact that \(p(\tau ^0) \le \rho ^2 - \frac{d^2}{16\tau ^0} < \sigma ^2\) at the time \(\tau ^0\). Therefore, if \(\sigma = \rho \), then at the time \(\tau ^0\) evaders use \(\bar{\rho } = \sqrt{\rho ^2 - \frac{d^2}{16\tau ^0}}\) instead of \(\rho \) to construct their strategies at \(t \ge \tau ^0\). At the time \(\tau ^0\) evaders exactly know that \(\sigma > \bar{\rho }\).

3.2 Disjoint Strips

To construct disjoint strips, consider two cases.

Case 1 \(y_{i0} \ne y_{j0}\), for all \(i \ne j\), \(i,j=1,\ldots ,M\). Let \(z_0\) be any point that doesn’t coincide with \(y_{10}\) if \(M=1\); and any point that doesn’t lie on any straight line passing through the points \(y_{i0}\) and \(y_{j0}\) for all \(i,j = 1, \ldots , M\), \(i\ne j\), if \(M \ge 2\). Hence, \(z_0 \ne y_{j0}, \ j = 1,\ldots , M\).

Fig. 1
figure 1

Sets \(S_j\) and \(S'_j\)

Full size image

Let

$$\begin{aligned} e_j = \frac{y_{j0}-z_0}{|y_{j0}-z_0|}, \quad j=1, \ldots , M, \end{aligned}$$

and let \(e'_j\) be a unit vector orthogonal to the vector \(e_j\) to be obtained from \(e_j\) by rotating it to the angle \(-\frac{\pi }{2}\), that is, by rotating clockwise to the angle \(\frac{\pi }{2}\).

We define a strip \(S_j\) associated with each point \(y_{j0}\) as follows:

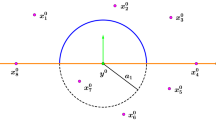
$$\begin{aligned} S_j=\{\xi \in {\mathbb {R}}^2 \ | \ |(\xi -y_{j0},e_j')|\le a+b, (\xi -y_{j0},e_j) \ge -b\}, \end{aligned}$$

where the positive numbers a and b are any if \(M=1\), and if \(M \ge 2\), they are chosen so that \(S_i\cap S_j = \varnothing \) if \(i\ne j\), and \(z_0\notin S_j\) for all \(i,j=1,\ldots ,M\) (see Fig. 1). If \(M \ge 2\), we can choose such numbers a and b, since the rays \(\zeta _j(t) = z_0 + e_jt, \ t >0, \ j=1,\ldots ,M\), have no common point. Let

$$\begin{aligned} I_j(t)=\{s\in \{1,\ldots ,K\} \ | \ x_s(t)\in S_j\}, \quad j=1,\ldots , M, \ t \ge 0. \end{aligned}$$

In other words, \(I_j(t)\) is the set of numbers of pursuers in the strip \(S_j\) at the current time t. In the case \(M \ge 2\), because of \(S_i\cap S_j = \varnothing \), we have \(I_i(t)\cap I_j(t)=\varnothing \) for all \(i\ne j\).

Case 2 There exist initial states \(y_{i0}, y_{j0}\), \(i \ne j\) with \(y_{i0} = y_{j0}\). Let \(y'_{i0}=y_{i0}+ \varepsilon v_{i0}, \ i=1,\ldots , M\), where unit vectors

$$\begin{aligned} v_{i0}=\left( \cos \frac{2\pi (i-1)}{M}, \ \sin \frac{2\pi (i-1)}{M}\right) , \quad i=1, \ldots , M, \end{aligned}$$
(3.4)

are the vertices of regular M-gon with the center at the origin, \(\varepsilon \) is a positive number that satisfies the following condition

$$\begin{aligned} \varepsilon < \min \left\{ \frac{\sigma ^2-\rho ^2}{M}, \frac{d^2}{64\rho ^2}, \rho ^2, \frac{d_0}{2}\right\} , \end{aligned}$$
(3.5)

where

$$\begin{aligned} d_0=\min \{|y_{i0}-y_{j0}| \ \mid \ y_{i0} \ne y_{j0}, \quad i,j=1,\ldots ,M\}, \end{aligned}$$

and d is defined by (3.2). Since \(\varepsilon < d_0/2\), we have \(y'_{i0} \ne y'_{j0}\) for all \(i \ne j\), \(i,j=1,\ldots ,M\). We now use the procedure of construction of strips in Case 1, with \(y_{i0}\) replaced by \(y'_{i0}\) for all \(i=1,\ldots ,M\).

In Case 2, first we bring all the evaders to points \(y'_{i0}, \quad i=1, \ldots ,M\). To this end, we let

$$\begin{aligned} v_i(t) = v_{i0}, \ j=1,\ldots , M, \quad 0 \le t \le \varepsilon . \end{aligned}$$

Then, clearly, at the time \(t=\varepsilon \), we have \(y_i(\varepsilon )= y'_{i0}\) for all \(i=1, \ldots ,M\), and

$$\begin{aligned} \sum _{j=1}^{M}q_j(\varepsilon ) = \sum _{j=1}^{M}\sigma _j^2 - M\varepsilon > \sum _{i=1}^{K}\rho _i^2 \ge \sum _{i=1}^{K}p_i(\varepsilon ), \end{aligned}$$

showing that the total energy of the evaders at the time \(t=\varepsilon \) is still greater than that of the pursuers. Moreover,

$$\begin{aligned} y_j(t) \ne x_i(t), \quad 0 \le t \le \varepsilon , \quad j=1, \ldots ,l, \quad i=1, \ldots , K, \end{aligned}$$

because by (3.5)

$$\begin{aligned} |y_j(t) - x_i(t)|\ge & {} |y_0 - x_{i0}| - \left| \int \limits _0^{\varepsilon }v_{j0}\mathrm{d}s\right| - \left| \int \limits _0^{\varepsilon }u_i(s)\mathrm{d}s\right| \nonumber \\> & {} \frac{3d}{4} - \varepsilon - \sqrt{\varepsilon }\rho \ge \frac{3d}{4} - 2\sqrt{\varepsilon }\rho \ge \frac{d}{2} >0. \end{aligned}$$
(3.6)

Thus, Case 2 can be reduced to Case 1. Therefore, we can assume at the beginning that \(y_{i0} \ne y_{j0}\) for all \(i \ne j\), \(i,j = 1,\ldots , M\).

3.3 The Construction of Strategies for Evaders

We construct a strategy for each evader \(y_j\) to move in the strip (Fig. 1)

$$\begin{aligned} S'_j = \{\xi \in {\mathbb {R}}^2 \ | \quad |(\xi -y_{j0}, e_j')| \le a, \quad (\xi -y_{j0}, e_j) \ge -b \}. \end{aligned}$$

Let us choose a number \(a_{j1}\) that satisfies the condition

$$\begin{aligned} 0< a_{j1} < \min \left\{ \frac{1}{2}, \frac{a}{2}, b, \frac{d}{2}\right\} , \end{aligned}$$
(3.7)

where d is defined by (3.2), and let \(a_{j,i+1} = \kappa \cdot a_{ji}^4\), \(i=1, 2, \ldots \). The number \(\kappa \in (0,1)\) will be specified later.

Then, clearly, terms of the sequence \(a_{j1}, a_{j2}, \ldots \) satisfy the following inequalities

$$\begin{aligned} a_{j,i+1} < a_{j,i}^4, \quad i = 1, 2, \ldots , \end{aligned}$$
(3.8)

and, therefore, by the inequality \(a_{j1} < 1/2\), we obtain

$$\begin{aligned}&a_{j,i+1} + a_{j,i+2} + \cdots< a_{j,i+1} + a_{j,i+1}^4 + a_{j,i+1}^{16}+ \cdots \nonumber \\&\quad< a_{j,i+1} + a_{j,i+1}^2 + \cdots < 2a_{j,i+1}, \quad i=0,1,2, \ldots , \end{aligned}$$
(3.9)

and

$$\begin{aligned} \sum _{i=0}^{\infty }\sqrt{a_{j,i+1}}< \sqrt{a_{j1}} + a^2_{j1} + a_{j1}^8 + \cdots < 2\sqrt{a_{j1}}. \end{aligned}$$
(3.10)

We say that a pursuer \(x_s\) is j-active at the time \(t \ge 0\) if \(x_s(t) \in S_j\) and \((e_j, x_s(t)) > (e_j, y_j(t))\), otherwise \(x_s\) is called j-passive at the time t. We say that \(t = \tau _{ji} \ge 0\) is \(a_{ji}\)-approach time of a pursuer \(x_s\) to the evader \(y_j\) if this pursuer is j-active at \(\tau _{ji}\) and the equation \(|x_s(\tau _{ji})-y_j(\tau _{ji})|=a_{ji}\) is first satisfied at the time \(\tau _{ji}\). Thus, for the specified sequence of numbers \(a_{j1}, a_{j2}, \ldots \), first we define \(\tau _{j1}\) as the \(a_{j1}\)-approach time, then we define \(\tau _{j2}\) as the \(a_{j2}\)-approach time and so on. Therefore, \(\tau _{j1}< \tau _{j2} < \cdots \).

It should be noted that the same \(\tau _{ji}\) can be \(a_{ji}\)-approach time for several pursuers to the evader \(y_j\). If there are more than one of such pursuers, then we take any of these pursuers and, for convenience, we denote this pursuer by \(x_{ji}\). Starting from the time \(\tau _{ji}\) on some time interval, the evader \(y_j\) uses a maneuver to be defined against the specified pursuer \(x_{ji}\). While a pursuer \(x_s\) is j-passive, for \(x_s\), neither approach time is defined nor maneuver is applied against. Note that j-passive pursuer at some \(t'\) might be able to be j-active at some \(t'' \ge t'\). Therefore, one pursuer can have several approach times to the same evader.

We make the following convention: If a pursuer makes \(a_{ji}\)- and \(a_{jl}\)- approaches at times \(\tau _{ji}\) and \(\tau _{jl}\), respectively, then this pursuer is labeled by \(x_{ji}\) and \(x_{jl}\) respectively at these times. Also, for convenience, we’ll write \(x_{ji}, y_j, y_{j0}, q_j, \tau _{ji}, a_{ji}, I_j(t), e_j, e_j', S_j, S_j', v_j\) without j as \(x_i, y, y_0, q, \tau _i, a_i, I(t), e, e', S, S', v\).

Define numbers

$$\begin{aligned} \tau _i' = \tau _i + \frac{a_i}{\alpha }, \quad i=1, 2, \ldots , \end{aligned}$$

where \(\alpha \) is a positive number, which will be specified later. Note that, in general, the sequence \(\tau '_1, \tau '_2, \ldots \) is neither increasing nor decreasing. Throughout the paper we impose conditions on parameters \(\alpha , a_1, a_2, \ldots \) and we choose the parameters in Sect. 3.11.

Describe the idea of construction of evader’s strategy. On the time interval \([0, \tau _1)\), the evader y moves parallel to the vector e. Note that \(\tau _1\), the first time of \(a_1\)-approach with a pursuer may not occur. In this case, either \(|y(t)-x_i(t)| > a_1\) or \((y(t),e) \ge (x_i(t),e)\) and \(y(t) \ne x_i(t)\) for all \(\ t \ge 0\) and \(i = 1, \ldots , K\). The latter case will be discussed in Sect. 3.4. In both cases, we let \(\tau _1 = \infty \), and because of \(y(t) \ne x_i(t), \ t \ge 0\), evasion is possible.

Let \(a_i\)-approaches occur at finite times \(\tau _i\), \(i=1,2, \ldots \). On the set \([\tau _i, \tau '_i)\backslash \cup _{j\ge i+ 1} [\tau _j, \tau '_j)\), the evader y uses a maneuver against the pursuer \(x_i\), \(i=1,2, \ldots \). Also we say that the evader is under the attack of pursuer \(x_i\) on this set.

Note that \(a_2\)-approach may occur before the time \(\tau _1'\), that is, \(\tau _2 < \tau _1'\), and then \(a_3\)-approach may occur before the time \(\max \{\tau '_1, \tau '_2\}\), that is, \(\tau _3 < \mathrm{max}\{\tau '_1, \tau '_2\}\) and so on. If this process is broken off at some first time \(\tau _p^* \doteq \max \{\tau '_1, \ldots , \tau '_p \}\) with \(p \ge 1\), that is, \(\tau _j < \max \{\tau '_1, \ldots , \tau '_{j-1}\}\) (\(\tau '_0 \doteq \tau '_1\)) for all \(j=1, \ldots ,p\) and \(\tau _{p+1} > \tau _p^*\), then we say that the evader undergo the continuous attack of the pursuers \( x_1, \ldots , x_p \) on the time interval \([\tau _1, \tau ^*_p)\). In other words,

  1. (i)

    \([\tau _1, \tau ^*_p) = \cup _{i=1}^p[\tau _i, \tau '_i)\), that is, at each \(t \in [\tau _1, \tau ^*_p)\), the evader is under the attack of a pursuer \(x_j\), \(j \in \{1, \ldots ,p\}\),

  2. (ii)

    all pursuers \(x_i, \ i = 1, \ldots ,p\), participate in attack on \([\tau _1, \tau ^*_p]\),

  3. (iii)

    \(\tau _{p+1} > \tau ^*_p\) and on the interval \([\tau ^*_p, \ \tau _{p+1})\) the evader is not under the attack of any pursuer.

It should be noted that one pursuer can attend several times in the sequence \( x_1, \ldots , x_p \) with different labels.

At the time \(\tau ^*_p\), a continuous attack of the group of pursuers \( x_1, \ldots , x_p\) is stopped. The evader y moves again parallel to the vector e on \([\tau ^*_p, \tau _{p+1})\). In general, on the set \({\mathbb {R}}\backslash \cup _{i\ge 1}[\tau _i, \tau _i')\), the evader is not under attack of any pursuer. Starting from \(\tau _{p+1}\) the evader may undergo a continuous attack of another group of pursuers. It should be noted that one pursuer can participate in several continuous group attacks too.

Let \([\tau _{{\omega }_{k-1}+1}, \tau ^*_{{\omega }_k}), \ k=1,2, \ldots , ({\omega }_0 = 0)\), be time intervals where the evader undergoes a continuous attack of a group of pursuers \(x_{{\omega }_{k-1}+1}, \ldots , x_{{\omega }_k}\), where \(\tau ^*_{{\omega }_k} = \max \{\tau '_{{\omega }_{k-1}+1}, \ldots , \tau '_{{\omega }_k}\}\). Hence, on the time intervals \([\tau ^*_{{\omega }_k}, \tau _{{\omega }_k+1}), \ k=1,2, \ldots \), the evader is not under attack of any pursuer. For convenience, let \(\tau ^*_0 = 0\). If for some \({\omega }_k\) there is no approach time greater than \(\tau ^*_{{\omega }_k}\), then we put \(\tau _{{\omega }_k+1} = \infty \).

Define a natural-valued function \(r=r(t), \ \tau _{{\omega }_{k-1}+1} \le t < \tau ^*_{{\omega }_k}\), which may change its value only at points \(\tau _i, \ \tau '_i, \ i= {\omega }_{k-1}+1, \dots , {\omega }_k\), as follows:

$$\begin{aligned} r(t)=\max \{j \in \{{\omega }_{k-1}+1, \dots , {\omega }_k\}| \ \tau _j \le t < \tau '_j\} \quad \text {if } \ t \in [\tau _{{\omega }_{k-1}+1}, \tau ^*_{{\omega }_k}). \end{aligned}$$
(3.11)

Here some properties of the function r(t).

Property 3.3

Let \(i \in \{{\omega }_{k-1}+1, \ldots {\omega }_k\}\) be any number. Then

$$\begin{aligned} \mathrm{(i)} \,\,r(t) = i,\quad \text { if } \ t \in [\tau _i, \tau '_i)\backslash J_{i+1}, \quad \hbox {where } J_{i+1}=\cup _{j = i+1}^{{\omega }_k}[\tau _j, \tau '_j), \ i < \omega _k;\quad \ J_{{\omega }_k+1}=\emptyset , \end{aligned}$$
(3.12)

(ii) if \(\tau _{i+1} < \tau '_i\),   then \(r(t)=i\) on \([\tau _i, \tau _{i+1})\),

(iii) if \(\tau _{i+1} \ge \tau '_i\),   then \(r(t)=i\) on \([\tau _i, \tau '_i)\).

Proof

(i) Indeed, let \(t \in [\tau _p, \tau '_p)\backslash J_{p+1}\). Then \(t \in [\tau _p, \tau '_p)\), and so by (3.11) \(r(t) \ge p\). However, because of \(t \notin J_{p+1}\), we get \(r(t) < p+1\). Hence, \(r(t) = p\).

(ii) Let \(\tau _{i+1} < \tau '_i\). Then \([\tau _i, \tau _{i+1}) \subset [\tau _i, \tau '_i)\backslash J_{i+1}\), and therefore by (3.12) \(r(t)= i\).

(iii) Let now \(\tau _{i+1} \ge \tau '_i\). Then \([\tau _i, \tau '_i)\backslash J_{i+1} = [\tau _i, \tau '_i)\), and so therefore by (3.12) we get \(r(t)= i, \ t \in [\tau _i, \tau '_i)\). \(\square \)

Thus, r(t) is a step function.

Fig. 2
figure 2

Continuous attack of the pursuers \(x_1, \ x_2, \ x_3\), and \(x_4\) is completed at \(\tau '_2\)

Full size image

Give an example (see Fig. 2). On the interval \([0, \tau _1)\) the evader is not under attack of any pursuer; \(r(t) = 1\) if \(t \in [\tau _1, \tau _2)\); \(r(t) = 2\) if \(t \in [\tau _2, \tau _3)\cup [\tau '_3, \tau _4)\cup [\tau '_4, \tau '_2)\); \(r(t) = 3\) if \(t \in [\tau _3,\tau '_3)\); \(r(t) = 4\) if \(t \in [\tau _4,\tau '_4)\) and the evader uses (3.14). At the time \( \tau ^*_4 = \tau '_2\), continuous attack of the pursuers \(x_1\), \(x_2\), \(x_3\) and \(x_4\) is completed. Then on the interval \([\tau '_2, \tau _5)\), the evader is not under attack of any pursuer. Starting from the time \(\tau _5\) the evader undergoes an attack of another group of pursuers.

We now start constructing a strategy for the evader y. Set \(v(t) = 0\) if \(I(t) = \emptyset \), else

$$\begin{aligned} v(t) = \left\{ \begin{array}{ll} \left( \sum \nolimits _{k \in I(t)}|u_k(t)|^2\right) ^{1/2}e, &{}\quad q(t)>0,\\ 0, &{}\quad q(t)=0, \end{array}\right. , \ \ t \in [\tau ^*_{{\omega }_k}, \tau _{{\omega }_k+1}), \quad k=0,1,2, \ldots \end{aligned}$$
(3.13)

For \(k=0\), we have \([\tau ^*_{{\omega }_0}, \tau _{{\omega }_0+1}) = [0, \tau _1)\), therefore, the evader uses (3.13) on \([0, \tau _1)\) as well. Thus, by (3.13) the evader moves parallel to the vector e on the intervals \([\tau ^*_{{\omega }_k}, \tau _{{\omega }_k+1}), \ k=0,1,2, \ldots \).

For \(i=1,2, \ldots \), let

$$\begin{aligned} V_{1i}(t)= & {} \left\{ \begin{array}{ll} \alpha + |(u_i(t), e')|, &{}\quad (y(\tau _i),e') \ge (x_i(\tau _i),e'),\\ -(\alpha + |(u_i(t), e')|), &{}\quad (y(\tau _i),e') < (x_i(\tau _i),e'),\\ \end{array} \right. \\ V_{2i}(t)= & {} \alpha +\left( \sum _{k \in I(t)\backslash \{i\}}|u_k(t)|^2+(u_i(t),e)^2\right) ^{1/2}. \end{aligned}$$

For \(t \in [\tau _{{\omega }_{k-1}+1}, \tau ^*_{{\omega }_k}), \ k=1,2, \ldots \), the maneuver of the evader against the pursuer \(x_r\) is defined as follows:

$$\begin{aligned} v(t) = \left\{ \begin{array}{ll} V_{1r}(t)e' + V_{2r}(t)e, &{}\quad q(t) > 0,\\ 0 &{}\quad q(t) = 0, \end{array} \right. \end{aligned}$$
(3.14)

where \(r=r(t)\) defined by (3.11).

3.4 Evasion from the Pursuer \( x_i \) for which \((y(\theta ),e) \ge (x_i(\theta ),e)\)

Let \((y(\theta ),e ) \ge (x_i(\theta ),e)\) and \(y(\theta ) \ne x_i(\theta )\) for a pursuer \(x_i\) at some time \(\theta \ge 0 \). We show that if \(x_i(s) \in S\), \(\theta \le s \le t\), then \(x_i(t) \ne y(t)\) for any behavior of the pursuer \(x_i\), as long as \(q(t)>0\). Let \(x_i(s) \in S\), \(\theta \le s \le t\).

Consider two cases 1) \(\theta \in [\tau ^*_{{\omega }_p}, \tau _{{\omega }_p+1})\), and 2) \( \theta \in [\tau _{{\omega }_p+1},\tau ^*_{{\omega }_{p+1}})\) at some \(p \in \{0,1, \ldots \}\), where \(\tau ^*_{{\omega }_p}\) is the time when continuous attack of a group of the pursuers \( x_{{\omega }_{p-1}+1},\ldots , x_{{\omega }_p}\) is completed, and the attack of another group of pursuers \(x_{{\omega }_p+1}, \ldots ,x_{{\omega }_{p+1}}\) is started at the time \(\tau _{{\omega }_p+1}\) and completed at the time \(\tau ^*_{{\omega }_{p+1}}\).

Case 1 Let \(\theta \in [\tau ^*_{{\omega }_p},\tau _{{\omega }_p+1}), \ p \in \{0,1, \ldots \}\).

A. Let \(\theta \le t < \tau _{{\omega }_p+1}\). Since \((y(\theta )-x_i(\theta ),e) \ge 0\), then by (3.13) we have \((y(\theta )-x_i(\theta ), \int \limits ^t_\theta v(s)\mathrm{d}s) \ge 0\), and hence

$$\begin{aligned} |y(t)-x_i(\theta )|^2\ge & {} |y(\theta )-x_i(\theta )|^2 + \left( y(\theta )-x_i(\theta ), \int \limits ^t_\theta v(s)\mathrm{d}s\right) + \left| \int \limits ^t_\theta v(s)\mathrm{d}s\right| ^2\\\ge & {} |y(\theta )-x_i(\theta )|^2 + \left( \int \limits ^t_\theta \left( \sum _{k \in I(t)}|u_k(s)|^2\right) ^{1/2}\mathrm{d}s\right) ^2\\\ge & {} |y(\theta ) - x_i(\theta )|^2 + \left( \int \limits _{\theta }^{t}|u_i(s)|\mathrm{d}s\right) ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} |y(t)-x_i(t)|\ge & {} |y(t)-x_i(\theta )|- \left| \int \limits ^t_\theta u_i(s)\mathrm{d}s\right| \\\ge & {} \left( |y(\theta ) - x_i(\theta )|^2 + \left( \int \limits _{\theta }^{t}|u_i(s)|\mathrm{d}s\right) ^2\right) ^{1/2} - \int _{\theta }^{t}|u_i(s)|\mathrm{d}s. \end{aligned}$$

Since the right-hand side of this inequality is positive, and so \( y(t)\ne x_i(t) \). Moreover, in the view of (3.13), \((y(t)-x_i(t),e) \ge 0, \ \theta \le t \le \tau _{{\omega }_p+1}.\)

B. Let now \(\tau _{{\omega }_{p}+1} \le t < \tau ^*_{{\omega }_{p+1}}\). We get

$$\begin{aligned} (y(t),e)-(x_i(t),e)= & {} (y(\theta ),e)-(x_i(\theta ),e)+\int \limits _{\theta }^{t}(v(s),e)\mathrm{d}s-\int \limits _{\theta }^{t}(u_i(s),e)\mathrm{d}s\\\ge & {} \int \limits _{\theta }^{\tau _{{\omega }_p+1}}(v(s),e)\mathrm{d}s + \int \limits _{\tau _{{\omega }_p+1}}^{t}(v(s),e)\mathrm{d}s\\&\quad - \int \limits _{\theta }^{\tau _{{\omega }_p+1}}(u_i(s),e)\mathrm{d}s - \int \limits _{\tau _{{\omega }_p+1}}^{t}(u_i(s),e)\mathrm{d}s. \end{aligned}$$

In view of (3.14), we then have

$$\begin{aligned}&(y(t),e)-(x_i(t),e) \ge \int \limits _{\theta }^{\tau _{{\omega }_p+1}}\left( (v(s),e) -(u_i(s),e)\right) \mathrm{d}s \nonumber \\&\quad + \int \limits _{\tau _{{\omega }_p+1}}^{t}\left[ \alpha + \left( \sum _{k \in I(t)\setminus \{r\}}|u_k(s)|^2 + (u_r(s),e)^2\right) ^{1/2}-(u_i(s),e)\right] \mathrm{d}s > 0, \end{aligned}$$
(3.15)

where \(r=r(t)\). The first integral is not negative since by (3.13), \((v(s),e) \ge (u_i(s),e), \ \theta \le t \le \tau _{{\omega }_{p}+1}\), and the second integral is clearly positive. Hence, \( y(t) \ne x_i(t), \ \tau _{{\omega }_{p}+1} \le t < \tau ^*_{{\omega }_{p+1}}\).

C. Let now \(t \ge \tau ^*_{{\omega }_{p+1}}\). Then it can be shown that inequalities (3.15) and \((v(t),e) \ge (u_i(t),e)\) [see (3.13) and (3.14)], imply that \((y(t),e)-(x_i(t),e) > 0\) for all \(t \ge \tau ^*_{{\omega }_{p+1}}\). Hence, \(x_i(t) \ne y(t)\) for all \(t \ge \theta \).

Case 2 Let \(\theta \in [\tau _{{\omega }_p+1}, \tau ^*_{{\omega }_{p+1}})\). Then according to (3.14)

$$\begin{aligned} (v(t),e) \ge \alpha + |u_i(t)| > (u_i(t),e), \quad \theta \le t < \tau ^*_{{\omega }_p}, \end{aligned}$$

and therefore for any \( t > \theta ,\) we obtain \((y(t),e) > (x_i(t),e)\), provided \(x_i(s) \in S\), \(s \in [\theta , t]\).

Thus, in both cases, if \((y(\theta ),e) \ge (x_i(\theta ), e)\), \(y(\theta ) \ne x_i(\theta )\) and \(x_i(s) \in S\), \(\theta \le s \le t\), for a pursuer \(x_i\) and some time \(\theta \), then \((y(t),e) \ge (x_i(t), e)\) and \(y(t) \ne x_i(t)\). What if this pursuer goes out of the set S and moves outside S till some time \( \tau \) for which \( (x_i(\tau ), e) > (y(\tau ), e) \) and gets again into the set S to make some \(a_j\)-approach? We will discuss this question in Sect. 3.10.

3.5 Fictitious Evaders

To estimate distances between pursuers and evaders, we define fictitious evaders (FEs) \( z_i, \ i= {\omega }_{k-1}, \ldots , {\omega }_k\), by the equations

$$\begin{aligned} \dot{z}_i=w_i, \quad z_i(\tau _i)=y(\tau _i), \quad \tau _i \le t < \tau '_i, \end{aligned}$$
(3.16)

where \( w_i \) is the control parameter of the FE \( z_i \). According to (3.16), the initial position of FE \( z_i \) at \( \tau _i \) coincides with the position of the evader at the same time \( \tau _i\), and FE \( z_i \) is defined only on the time interval \( [\tau _i,\tau '_i) \). We define the strategy of FE \( z_i \) as follows:

$$\begin{aligned} w_i(t)=V_{1i}(t)e' + V_{2r}(t)e, \quad \tau _i \le t < \tau '_i, \end{aligned}$$
(3.17)

where \(V_{2r}(t)\) is the same as in (3.14). Note that \((w_i(t),e) = (v(t),e)=V_{2r}(t), \ \tau _i \le t < \tau '_i\), that is speeds of the FE \( z_i \) and the evader y along the direction e are the same. Also combining (3.14) and (3.17), we observe that \(z_r(t) = y(t), \ \tau _r \le t\le \tau '_r\).

Next, show that

$$\begin{aligned} \int \limits _{\tau _i}^{\tau '_i}|w_i(s)|^2\mathrm{d}s \le 2\sigma ^2. \end{aligned}$$
(3.18)

Indeed, introducing the following vector functions

$$\begin{aligned} f(s) = (\alpha , \alpha ) \hbox { and } g(s) = \left( |(u_i(s),e')|, \left( \sum _{k \in I(t)\setminus \{r\}}|u_k(s)|^2+(u_r(s),e)^2\right) ^{1/2}\right) , \end{aligned}$$

we obtain

$$\begin{aligned}&V_{1i}^2(s)+V_{2r}^2(s)\\&\qquad = (\alpha + |(u_i(s),e')|)^2 + \left( \alpha + \left( \sum _{k \in I(s)\setminus \{r\}}|u_k(s)|^2+(u_r(s),e)^2\right) ^{1/2}\right) ^2\\&\qquad =|f(s) + g(s)|^2. \end{aligned}$$

Then by the Minkowskii inequality

$$\begin{aligned}&\left( \int \limits _{\tau _i}^{\tau '_i}|w_i(s)|^2\mathrm{d}s\right) ^{1/2} = \left( \int \limits _{\tau _i}^{\tau '_i}\left( V_{1i}^2(s)+V_{2r}^2(s)\right) \mathrm{d}s\right) ^{1/2} \nonumber \\&\qquad =\left( \int \limits _{\tau _i}^{\tau '_i}|f(s) + g(s)|^2\mathrm{d}s\right) ^{1/2} \le \left( \int \limits _{\tau _i}^{\tau '_i}|f(s)|^2\mathrm{d}s\right) ^{1/2} + \left( \int \limits _{\tau _i}^{\tau '_i}|g(s)|^2\mathrm{d}s\right) ^{1/2}\nonumber \\&\qquad = \left( \int \limits _{\tau _i}^{\tau '_i}2\alpha ^2\mathrm{d}s\right) ^{1/2} + \left( \int \limits _{\tau _i}^{\tau '_i}\left( (u_i(s),e')^2 + \sum _{k \in I(s)\setminus \{r\}}|u_k(s)|^2+(u_r(s),e)^2 \right) \mathrm{d}s\right) ^{1/2}\nonumber \\ \end{aligned}$$
(3.19)

Since

$$\begin{aligned} \int \limits _{\tau _i}^{\tau '_i}(u_i(s),e')^2\mathrm{d}s \le \int \limits _{\tau _i}^{\tau '_i}|u_i(s)|^2\mathrm{d}s \le \rho _i^2, \end{aligned}$$

and

$$\begin{aligned} \int \limits _{\tau _i}^{\tau '_i}\left( \sum _{k \in I(s)\setminus \{r\}}|u_k(s)|^2+(u_r(s),e)^2 \right) \mathrm{d}s \le \rho ^2. \end{aligned}$$

then requiring that

$$\begin{aligned} \alpha a_1 \le (\sigma - \rho )^2 \end{aligned}$$
(3.20)

and using definition of \(\tau '_i\), we obtain from (3.19)

$$\begin{aligned} \left( \int \limits _{\tau _i}^{\tau '_i}|w_i(s)|^2\mathrm{d}s\right) ^{1/2}\le & {} \sqrt{2\alpha a_i} + \sqrt{\rho _i^2 + \rho ^2}\\\le & {} \sqrt{2\alpha a_1} + \rho \sqrt{2} \le \sigma \sqrt{2} \end{aligned}$$

which is the desired conclusion.

3.6 Estimation of the Distance Between FE and Pursuer

Let us estimate the distance \(|x_p(t)-z_p(t)|\), \( t\in [\tau _p,\tau '_p)\), between the FE \(z_p\) and pursuer \(x_p\) for any \(p \in \{{\omega }_{k-1}+1, \ldots , {\omega }_k\}\). To this end, estimate \(|x_p(t)-z_p(t)|\) in two ways. Since \(|x_p(\tau _p)-z_p(\tau _p)|=a_p\), then by the Cauchy–Schwartz inequality and inequality (3.18), we have

$$\begin{aligned} |x_p(t)-z_p(t)|\ge & {} |x_p(\tau _p)-z_p(\tau _p)|-\bigg |\int \limits _{\tau _p}^{t}w_p(s)\mathrm{d}s\bigg |-\bigg |\int \limits _{\tau _p}^{t}u_p(s)\mathrm{d}s\bigg |\nonumber \\\ge & {} a_p - (\sqrt{2}+1) \sqrt{t-\tau _p}\cdot \sigma \end{aligned}$$
(3.21)

provided

$$\begin{aligned} \int \limits _{\tau _p}^{t}|u_p(s)|^2\mathrm{d}s \le \rho _p^2. \end{aligned}$$

On the other hand by (3.14), signs of

$$\begin{aligned} (z_p(\tau _p),e')-(x_p(\tau _p),e') = (y(\tau _p),e')-(x_p(\tau _p),e') \end{aligned}$$

and \(\pm (\alpha +|(u_p(s),e')|)\) are the same, and therefore

$$\begin{aligned} |z_p(t)-x_p(t)|\ge & {} |(z_p(t)-x_p(t),e')| \ge |(z_p(\tau _p),e')-(x_p(\tau _p),e')|\nonumber \\&\quad + \int \limits _{\tau _p}^{t}(\alpha +|(u_p(s),e')|)\mathrm{d}s - \int \limits _{\tau _p}^{t}|(u_p(s),e')|\mathrm{d}s\nonumber \\\ge & {} \alpha (t-\tau _p). \end{aligned}$$
(3.22)

From (3.21) and (3.22), we conclude that

$$\begin{aligned} |z_p(t)-x_p(t)|\ge h(t), \quad h(t)=\max \{a_p- (\sqrt{2}+1)\sigma \sqrt{t-\tau _p}, \quad \alpha (t-\tau _p)\}. \end{aligned}$$

Since the function \( h_1(t)=a_p-(\sqrt{2}+1)\sigma \sqrt{t-\tau _p}\) decreases on \( [\tau _p,\tau '_p]\) from \(a_p\) to \(a_p-(\sqrt{2}+1)\sigma \sqrt{\frac{a_p}{\alpha }}\), and \(h_2(t)=\alpha (t-\tau _p)\) increases on \( [\tau _p, \tau '_p]\) from 0 to \(a_p\), and therefore the function h(t) has the only minimum point \(t_* \in (\tau _p,\tau '_p)\), which is the only root of the equation \(h_1(t) = h_2(t)\). We can see that

$$\begin{aligned} t_* = \tau _p + \frac{4a_p^2}{\left( (\sqrt{2}+1)\sigma + \sqrt{(3+2\sqrt{2})\sigma ^2 + 4\alpha a_p}\right) ^2}. \end{aligned}$$

Then, \(h_2(t_*) > \frac{\alpha a^2_p}{6\sigma ^2}\), provided \(\alpha \) and \(a_p\) are required to satisfy the inequalities

$$\begin{aligned} 0< \alpha< 1,\ 12\alpha a_p < \sigma ^2. \end{aligned}$$
(3.23)

Then we obtain the following estimate for the distance between FE \(z_p\) and pursuer \(x_p\)

$$\begin{aligned} |z_p(t)-x_p(t)| > \frac{\alpha a^2_p}{6\sigma ^2}, \quad \tau _p \le t \le \tau '_p. \end{aligned}$$
(3.24)

In addition,

$$\begin{aligned} (z_p(\tau '_p) - x_p(\tau '_p),e)= & {} (z_p(\tau _p) - x_p(\tau _p),e) + \int \limits _{\tau _p}^{\tau '_p}((v(s),e) - (u_p(s),e))\mathrm{d}s\\\ge & {} -a_p + \int \limits _{\tau _p}^{\tau '_p}(\alpha + |(u_p(s),e)| - (u_p(s),e))\mathrm{d}s \\\ge & {} -a_p + \alpha (\tau '_p-\tau _p) = 0, \end{aligned}$$

then according to (3.16) and (3.17), we obtain

$$\begin{aligned} (y(\tau '_p), e)= & {} (y(\tau _p), e) + \int \limits _{\tau _p}^{\tau '_p}(v(s),e)\mathrm{d}s\nonumber \\= & {} (z_p(\tau _p),e) + \int \limits _{\tau _p}^{\tau '_p}(w_p(s),e)\mathrm{d}s\nonumber \\= & {} (z_p(\tau '_p),e) \ge (x_p(\tau '_p), e). \end{aligned}$$
(3.25)

The inequality (3.25) shows that at the time \(\tau '_p\) the pursuer \(x_p\) becomes passive.

Fig. 3
figure 3

Evader y and FE \(z_p\)

Full size image

3.7 Estimation of the Distance Between Evader and FE

To estimate the distance \(|x_p(t)-y(t)|\) between the evader y and pursuer \(x_p\) for \(t\in [\tau _p, \tau '_p)\), we first estimate the distance \(|y(t)-z_p(t)|\) between the evader y and FE \(z_p\) on the time interval \([\tau _p, \tau '_p)\) assuming that \(q(t) > 0\).

If \(a_{p+1}\)-approach time \(\tau _{p+1} > \tau '_p\), then by Property 3.3 (iii) \(r=r(t)= p\) for all \(t \in [\tau _p, \tau '_p)\). Hence, comparing (3.14) with (3.17) we get \(w_p(t)=v(t), \ \ \tau _p \le t < \tau '_p\). Consequently \(y(t)=z_p(t)\), \(t \in [\tau _p, \tau '_p]\), and so \(|y(t)-z_p(t)|=0\), \(t \in [\tau _p, \tau '_p]\).

Let now \(\tau _{p+1} \in (\tau _p, \tau '_p)\). Then by Property 3.3 (ii) \(r=r(t)= p\) for \(t \in [\tau _p, \tau _{p+1})\), and comparing (3.14) with (3.17) we get \(w_p(t)=v(t), \ \tau _p \le t < \tau _{p+1}\).

Then (see Fig. 3)

$$\begin{aligned} \begin{array}{ll} y(\tau _{p+1}) &{}=y(\tau _p)+\int \limits _{\tau _p}^{\tau _{p+1}}v(t)\mathrm{d}t\\ &{}= z_p(\tau _p)+\int \limits _{\tau _p}^{\tau _{p+1}}w_p(t)\mathrm{d}t=z_p(\tau _{p+1}). \end{array} \end{aligned}$$

Therefore, for \(\tau _{p+1}\le t < \tau '_p\), we get

$$\begin{aligned} |y(t)-z_p(t)|= & {} \left| y(\tau _{p+1})+\int \limits _{\tau _{p+1}}^{t}v(s)\mathrm{d}s-z_p(\tau _{p+1})-\int \limits _{\tau _{p+1}}^{t}w_p(s)\mathrm{d}s\right| \nonumber \\\le & {} \int \limits _{\tau _{p+1}}^{t}|v(s)-w_p(s)|\mathrm{d}s \end{aligned}$$
(3.26)

Since \(w_p(t) = v(t)\) on \([\tau _{p+1}, t]\backslash J_{p+1}\), where \(J_{p+1}\) is defined in (3.12), then combining (3.14) and (3.17) with (3.26), yields

$$\begin{aligned} |y(t)-z_p(t)|\le & {} \int \limits _{[\tau _{p+1}, t)\cap J_{p+1}}|v(s)-w_p(s)|\mathrm{d}s\nonumber \\\le & {} \int \limits _{J_{p+1}}(2\alpha + |(u_r(s), e')|)+|(u_p(s),e')|)\mathrm{d}s, \end{aligned}$$
(3.27)

where \(r = r(s)\). As

$$\begin{aligned} |(u_r(s), e')| \le |u_r(s)| \le \sqrt{\sum _{i=1}^{K}|u_i(s)|^2}\mathrm{d}s \end{aligned}$$

then from (3.27) by using the Cauchy–Schwartz inequality we get

$$\begin{aligned} |y(t)-z_p(t)|\le & {} 2\alpha \ \mathrm{mes}(J_{p+1}) + 2\int \limits _{J_{p+1}}\sqrt{\sum _{i=1}^{K}|u_i(s)|^2}\mathrm{d}s\nonumber \\\le & {} 2\alpha \ \mathrm{mes}(J_{p+1}) + 2\rho \sqrt{\mathrm{mes}(J_{p+1})}, \end{aligned}$$
(3.28)

where \(\mathrm{mes}(J_{p+1})\) denotes the Lebesgue measure of the set \(J_{p+1}\). Since \(J_{p+1} \subset \cup _{i \ge p+1}[\tau _p, \tau '_p)\), then (3.9) implies that

$$\begin{aligned} \mathrm{mes}(J_{p+1}) \le \sum _{i \ge p+1}(\tau '_i-\tau _i) \le \sum _{i=p+1}^{\infty }\frac{a_i}{\alpha } \le \frac{2a_{p+1}}{\alpha }, \end{aligned}$$

Thus, the last inequality and (3.28) yield that

$$\begin{aligned} |y(t)-z_p(t)| \le 4a_{p+1}+ 2\rho \sqrt{\frac{2a_{p+1}}{\alpha }} < 4\rho \sqrt{\frac{2a_{p+1}}{\alpha }} \end{aligned}$$
(3.29)

provided that the parameters \(a_{p+1}\) and \(\alpha \) satisfy the condition

$$\begin{aligned} 2a_{p+1}\alpha < \rho ^2. \end{aligned}$$
(3.30)

Thus, we have obtained an estimate for \(|y(t)-z_p(t)|\) which is given by (3.29).

3.8 Estimation of Distance Between Pursuer and Evader

Finally, estimate the distance between the pursuer \(x_p\) and evader on the time interval \([\tau _p, \tau '_p)\) when evader’s energy is positive. It follows from (3.24) and (3.29) that

$$\begin{aligned} |x_p(t)-y(t)|\ge & {} |x_p(t)-z_p(t)|-|z_p(t)-y(t)|\nonumber \\> & {} \frac{\alpha a_p^2}{6\sigma ^2} - 4\rho \sqrt{\frac{2a_{p+1}}{\alpha }}\ge \frac{\alpha a_p^2}{12\sigma ^2} \end{aligned}$$
(3.31)

provided that \(\frac{\alpha a_p^2}{12 \sigma ^2} \ge 4\rho \sqrt{\frac{2a_{p+1}}{\alpha }}\). Solve this inequality for \(a_{p+1}\) to obtain a new requirement for parameters \(a_{p+1}, \ a_p,\) and \(\alpha \)

$$\begin{aligned} a_{p+1} \le \frac{\alpha ^3}{144\cdot 32\cdot \rho ^2\cdot \sigma ^4}a_p^4. \end{aligned}$$
(3.32)

Thus, for any \(t \in [\tau _p, \tau '_p)\),

$$\begin{aligned} |x_p(t) - y(t)| > \frac{\alpha a_p^2}{12\sigma ^2}. \end{aligned}$$
(3.33)

Also, require that

$$\begin{aligned} \frac{\alpha a_p^2}{12\sigma ^2} \ge a_{p+1}. \end{aligned}$$
(3.34)

Then (3.33) implies that \(|x_p(t)-y(t)| > a_{p+1}\). Therefore, for any \(j \ge p+1\), \(a_j\)-approach doesn’t occur on \([\tau _p, \tau '_p]\) with the pursuer \(x_p\). According to (3.25) \((y(\tau '_p), e) \ge (x_p(\tau '_p), e)\). As it was proved earlier in Sect. 3.4, the inequalities \(x_p(\tau '_p) \ne y(\tau '_p)\) [which follows from (3.33)] and \((y(\tau '_p),e) \ge (x_p(\tau '_p),e)\) imply that \((y(t), e) \ge (x_p(t), e)\) and \(y(t) \ne x_p(t)\) for all \(t > \tau '_p\), while \(x_p(s) \in S\) for all \(\tau '_p \le s \le t\), and \(q(t)>0\). That is this pursuer becomes passive while \(x_p(t) \in S\), \(t > \tau '_p\).

3.9 Estimation of Evaders Energy and Possibility of Evasion

Let T be any positive number, and \(\tau ^*_{{\omega }_l} \ \ ({\omega }_0 = 0, \ \tau ^*_0 = 0), \ l = 0, 1, \ldots \), be the times when continuous attack of a group of pursuers is completed, and \(\tau _{{\omega }_l+1}, \ l = 0, 1, \ldots \), be the times when continuous attack of a group of pursuers is started. The time T can be either in an interval \([\tau ^*_{{\omega }_p}, \tau _{{\omega }_p+1})\) or in an interval \([\tau _{{\omega }_{p-1}+1}, \tau ^*_{{\omega }_p})\) for some p. First, estimate the energy of the evader spent on the time interval [0, T]. Since on the intervals \([\tau ^*_{{\omega }_l}, \tau _{{\omega }_l+1}), \ l = 0,1, \ldots ,\) the evader uses (3.13), and on the intervals \([\tau _{{\omega }_{l-1}+1}, \tau ^*_{{\omega }_l}), \ l =1,2, \ldots ,\) the evader is under the attack of pursuers and uses (3.14). Consequently, the evader spends the following amount of energy

$$\begin{aligned} \int \limits _{0}^{T}|v(t)|^2\mathrm{d}t \le A_1 + A_2 + A_3, \end{aligned}$$
(3.35)

where

$$\begin{aligned} A_1= & {} \sum \limits _{l=0}^{p-1}\int \limits _{\tau _{{\omega }_l}^*}^{\tau _{{\omega }_l+1}}\left( \sum _{i\in I(t)}|u_i(t)|^2\right) \mathrm{d}t,\\ A_2= & {} \sum \limits _{l=1}^{p-1}\int \limits _{\tau _{{\omega }_{l-1}+1}}^{\tau ^*_{{\omega }_l}}\left( V_{1r}^2(t) + V_{2r}^2(t)\right) \mathrm{d}t,\\ A_3= & {} \left\{ \begin{array}{ll} \int \limits _{\tau _{{\omega }_p}^*}^T\left( \sum \nolimits _{i\in I(t)}|u_i(t)|^2\right) \mathrm{d}t, &{} \quad \hbox {if} \quad T \in [\tau _{{\omega }_p}^*, \tau _{{\omega }_p+1}),\\ \int \limits _{\tau _{{\omega }_{p-1}+1}}^{T}\left( V_{1r}^2(t) + V_{2r}^2(t)\right) \mathrm{d}t, &{}\quad \hbox {if} \quad T \in [\tau _{{\omega }_{p-1}+1}, \tau _{{\omega }_p}^*), \end{array}\right. \end{aligned}$$

where \(r=r(t)\).

Since \((u_r(t),e')^2 + (u_r(t),e)^2 = |u_r(t)|^2\), then similar to (3.19), with i replaced by r, we obtain for any \(\lambda , \mu \in [\tau _{{\omega }_{p-1}+1}, \tau _{{\omega }_p}^*)\) and \(\lambda \le \mu \) that

$$\begin{aligned}&\left( \int \limits _{\lambda }^{\mu }\left( V_{1r}^2(s)+V_{2r}^2(s)\right) \mathrm{d}s\right) ^{1/2} \nonumber \\&\quad = \left( \int \limits _{\lambda }^{\mu }2\alpha ^2\mathrm{d}s\right) ^{1/2} + \left( \int \limits _{\lambda }^{\mu }\left( (u_r(s),e')^2 + \sum _{i \in I(s)\setminus \{r\}}|u_i(s)|^2+(u_r(s),e)^2 \right) \mathrm{d}s\right) ^{1/2}\nonumber \\&\quad = \sqrt{2\alpha ^2(\mu - \lambda )} + \left( \int \limits _{\lambda }^{\mu }\left( \sum _{i \in I(s)}|u_i(s)|^2\right) \mathrm{d}s\right) ^{1/2}. \end{aligned}$$
(3.36)

Then, by the inequality \(\int \limits _{\lambda }^{\mu }\left( \sum _{i \in I(s)}|u_i(s)|^2\right) \mathrm{d}s \le \rho ^2\), we can see that

$$\begin{aligned}&\int \limits _{\lambda }^{\mu }\left( V_{1r}^2(s)+V_{2r}^2(s)\right) \mathrm{d}s \nonumber \\&\quad = 2\alpha ^2(\mu - \lambda ) + 2\sqrt{2\alpha ^2(\mu - \lambda )}\rho + \int \limits _{\lambda }^{\mu }\left( \sum _{i \in I(s)}|u_i(s)|^2\right) \mathrm{d}s. \end{aligned}$$

Therefore, (3.35) can be rewritten as follows:

$$\begin{aligned} \int \limits _{0}^{T}|v(t)|^2\mathrm{d}t \le \int \limits _{0}^{T}\sum _{i\in I(t)}|u_i(t)|^2\mathrm{d}t + B_1+ B_1' + B_2 + B_2', \end{aligned}$$
(3.37)

where

$$\begin{aligned} B_1= & {} \sum \limits _{l=1}^{p-1} 2\alpha ^2 (\tau ^*_{{\omega }_l}- \tau _{{\omega }_{l-1}+1}), \quad B_2 = \sum \limits _{l=1}^{p-1} 2\sqrt{2\alpha ^2 (\tau ^*_{{\omega }_l}- \tau _{{\omega }_{l-1}+1})}\rho ,\nonumber \\ B_1'= & {} \left\{ \begin{array}{ll} 0,&{}\quad T \in [\tau _{{\omega }_p}^*, \tau _{{\omega }_p+1}),\\ 2\alpha ^2 (T - \tau _{{\omega }_{p-1}+1}),&{}\quad T \in [{\tau _{{\omega }_{p-1}+1}}, \tau _{{\omega }_p}^*), \end{array} \right. \end{aligned}$$
(3.38)
$$\begin{aligned} B_2'= & {} \left\{ \begin{array}{ll} 0,&{}\quad T \in [\tau _{{\omega }_p}^*, \tau _{{\omega }_p+1}),\\ 2\rho \sqrt{2\alpha ^2 (T - \tau _{{\omega }_{p-1}+1})},&{}\quad T \in [{\tau _{{\omega }_{p-1}+1}}, \tau _{{\omega }_p}^*). \end{array}\right. \end{aligned}$$
(3.39)

Next, estimate \(B_1, B_1', B_2, B_2'\). Using (3.9) yields for \(l=1,\ldots , p-1\),

$$\begin{aligned} \alpha ^2(\tau _{{\omega }_l}^*-\tau _{{\omega }_{l-1}+1})\le & {} \alpha ^2\sum _{\tau _j\in [\tau _{{\omega }_{l-1}+1},\tau ^*_{{\omega }_l})}(\tau '_j-\tau _j) =\alpha ^2\sum _{\tau _j\in [\tau _{{\omega }_{l-1}+1},\tau ^*_{{\omega }_l})}\frac{a_j}{\alpha }\nonumber \\\le & {} \alpha (a_{{\omega }_{l-1}+1}+a_{{\omega }_{l-1}+2}+\ldots )\le 2\alpha a_{{\omega }_{l-1}+1}, \end{aligned}$$
(3.40)

Similarly, for \(T \in [{\tau _{{\omega }_{p-1}+1}}, \tau _{{\omega }_p}^*)\),

$$\begin{aligned} \alpha ^2 (T - \tau _{{\omega }_{p-1}+1}) \le \alpha ^2(\tau _{{\omega }_p}^*-\tau _{{\omega }_{p-1}+1}) \le 2\alpha a_{{\omega }_{p-1}+1}. \end{aligned}$$
(3.41)

Then, combining the inequalities (3.40) and (3.41) with (3.38) and then using (3.9), we get

$$\begin{aligned} B_1 + B_1'\le & {} 2\sum \limits _{l=1}^{p-1}\alpha ^2(\tau _{{\omega }_l}^* - \tau _{{\omega }_{l-1}+1}) + 2\alpha ^2(T - \tau _{{\omega }_{p-1}+1})\nonumber \\\le & {} 4\alpha \sum _{i=1}^{p-1}a_{{\omega }_{l-1}+1} + 4\alpha a_{{\omega }_{p-1}+1} \le 4\alpha \sum _{i=1}^{\infty }a_{i} \le 8\alpha a_1. \end{aligned}$$
(3.42)

Combining (3.40) and (3.41) with (3.39), and then using (3.10), we obtain

$$\begin{aligned} B_2 + B_2'\le & {} 2\rho \sum \limits _{l=1}^{p-1}\sqrt{2\alpha ^2(\tau _{{\omega }_l}^* - \tau _{{\omega }_{l-1}+1})} + 2\rho \sqrt{2\alpha ^2(T - \tau _{{\omega }_{p-1}+1})}\nonumber \\\le & {} 4\rho \sum _{i=1}^{p-1}\sqrt{\alpha a_{{\omega }_{l-1}+1}} + 4\rho \sqrt{\alpha a_{{\omega }_{p-1}+1}} \le 4\rho \sum _{i=1}^{\infty }\sqrt{\alpha a_{i}} \le 8\rho \sqrt{\alpha a_1}. \end{aligned}$$
(3.43)

Therefore, using (3.42) and (3.43), we obtain from (3.37)

$$\begin{aligned} \int \limits _{0}^{T}|v(t)|^2\mathrm{d}t \le 4\alpha a_1 + 8\rho \sqrt{\alpha a_1} + \int \limits _{0}^{T}\sum _{i\in I(t)}|u_i(t)|^2\mathrm{d}t. \end{aligned}$$
(3.44)

Let \( \alpha \), \( a_1 \) satisfy the following inequality

$$\begin{aligned} 4\alpha a_1 + 8\rho \sqrt{\alpha a_1} < \frac{\sigma ^2 - \rho ^2}{2M}. \end{aligned}$$
(3.45)

Then it follows from (3.44) that

$$\begin{aligned} \int \limits _{0}^{T}|v(t)|^2\mathrm{d}t < \frac{\sigma ^2-\rho ^2}{2M}+\int \limits _{0}^{T}\sum _{i\in I(t)}|u_i(t)|^2\mathrm{d}t. \end{aligned}$$
(3.46)

We again think of all evaders moving in the sets \(S_j, \ j=1, \ldots ,M\), and proceed to show that evasion is possible in the game (1.1)–(1.4). For the evader \(y_j, \ j \in \{1, \ldots , M\}\), the inequality (3.46) can be written as follows:

$$\begin{aligned} \int \limits _{0}^{T}|v_j(t)|^2\mathrm{d}t < \frac{\sigma ^2-\rho ^2}{2M} + \int \limits _{0}^{T}\sum _{i\in I_j(t)}|u_i(t)|^2\mathrm{d}t. \end{aligned}$$
(3.47)

Clearly, the evader \(y_j\) can move using strategies (3.13) and (3.14) not being captured on [0, T] providing that \(q_j(t) > 0\) and the number of approach times in [0, T] for this evader is finite. We claim that for any \(T>0\), the inequality \(q_i(t) > 0\), \(0 \le t \le T\), holds for at least one \(i \in \{1, \ldots , M\}\). Finiteness of approach times will be shown in the next subsection. This means that at least one of the evaders is not captured on [0, T]. Assume the contrary, that is

$$\begin{aligned} \int \limits _{0}^{T}|v_j(t)|^2\mathrm{d}t \ge \sigma _j^2\quad \hbox { for all } j = 1, \ldots , M, \end{aligned}$$

at some \(T > 0\). Since \(I_{j_1}(t) \cap I_{j_2}(t) = \emptyset \) for every \(j_1 \ne j_2\), and \(I_j (t) \subset {1, 2, \ldots , M}\), then from (3.47), we obtain

$$\begin{aligned} \sigma ^2= & {} \sigma ^2_1 + \cdots +\sigma ^2_M \le \sum \limits _{j=1}^{M}\int \limits _{0}^{T}|v_j(t)|^2\mathrm{d}t \\< & {} \frac{\sigma ^2-\rho ^2}{2}+\sum \limits _{j=1}^{M}\int \limits _{0}^{T}\sum _{i\in I_j(t)}|u_i(t)|^2\mathrm{d}s\\\le & {} \frac{\sigma ^2-\rho ^2}{2} + \rho ^2 = \frac{\sigma ^2+\rho ^2}{2} < \sigma ^2. \end{aligned}$$

A contradiction. Thus, for any time \(T > 0\), at least one of the evaders is not captured on [0, T]. Note that strategies of evaders do not depend on T.

3.10 Finiteness of the Number of Approaches

Is the number of approach times \(\tau _1, \tau _2, \ldots \) in any time interval [0, T] finite? or are there infinitely many approach times \(\tau _1, \tau _2, \ldots \) on an interval [0, T]? We show that for any finite time interval [0, T], the number of approach times \(\tau _1, \tau _2, \ldots \) is finite. To see this, we take any pursuer \(x_i\) and show that the number of approach times of \(x_i\) in [0, T] is finite.

Let \(\tau _i\) be the first an \(a_i\)-approach time of the pursuer \(x_i\) with the evader. On the interval \([\tau _i, \tau _i')\), as shown in Sect. 3.9 that a new \(a_j\)-approach (\(j \ge i+1\)) will not occur with this pursuer. According to (3.33), at the time \(\tau '_i\) the inequality \((y(\tau '_i), e) \ge (x_i(\tau '_i), e)\) holds. It was shown in Sect. 3.9 that, if \(x_i(s) \in S\) for all \(\tau _i' \le s \le t\), then \((y(t),e) \ge (x_{i}(t),e)\) and \(y(t) \ne x_i(t)\), and therefore, starting from \(\tau '_i\), this pursuer is passive, and because of the inequality \((y(t),e) \ge (x_{i}(t),e)\), \(t \ge \tau _i'\), further approach times are not defined while \(x_i(t) \in S\).

There is only one way for the pursuer \(x_i\) to make a new \(a_j\)- approach with the evader: The pursuer \(x_i\) has to go out of the set S, and move outside S for some time to get \((x_{i}(t),e) > (y(t),e)\), then get into the set S again to make a new approach with the evader.

Show that at any approach time \(\tau _k\) the pursuer \(x_i\) will be in \(S'\). Indeed, by the definition of the approach time \(\tau _k\), we have \(|y(\tau _k)-x_i(\tau _k)|=a_k\) and therefore

$$\begin{aligned} |(x_k(\tau _k)-y_0,e')|\le & {} |(x_k(\tau _k) - y(\tau _k),e')|+ |(y(\tau _k)-y_0,e')|\\\le & {} a_k + \frac{a}{2} < a, \end{aligned}$$

meaning that \(x_i(\tau _k) \in S'\). Here, the inequality \(|(y(\tau _k)-y_0, e')| < \frac{a}{2}\), which will be proved in Sect. 4.2, and assumption

$$\begin{aligned} a_k < \frac{a}{2} \ \hbox { for all } i=1, 2, \ldots , \end{aligned}$$
(3.48)

are used.

We now estimate the number of approach times on the interval [0, T]. Let \(t'\) be an approach time. Then by the reasoning above we have \(x_i(t') \in S'\). Let \(x_i(t'') \notin S\) at some time \(t''\). That is, at the time \(t'\) the pursuer is in \(S'\), and at the time \(t''\) the pursuer \(x_i\) is outside S. Then

$$\begin{aligned} b \le |x_i(t'') - x_i(t')| = \left| \int \limits _{t'}^{t''}u_i(s)\mathrm{d}s\right| \le \int \limits ^{t''}_{t'}|u_i(s)|\mathrm{d}s. \end{aligned}$$
(3.49)

If there are N approach times in \((\tau _i, T]\), then the pursuer \(x_i\) must have gone out of S at least N times. Note that at each approach time the pursuer is in \(S'\). Let \(x_i(t_j') \in S'\) and \(x_i(t''_j) \notin S, \ j=1, \ldots ,N\). According to (3.49),

$$\begin{aligned} b \le \int \limits _{t'_j}^{t''_j}|u_i(s)|\mathrm{d}s,\quad j=1, \ldots , N. \end{aligned}$$
(3.50)

Clearly, \(t'_j< t''_j<t'_{j+1}, \ j=1, 2, \ldots ,N\), and so intervals \([t'_j, t''_j], \ j=1, 2, \ldots , N\), are disjoint. Then, we obtain from (3.50)

$$\begin{aligned} Nb \le \sum _{j=1}^{N} \int \limits _{t'_j}^{t''_j}|u_i(s)|\mathrm{d}s \le \int \limits _{0}^{T}|u_i(s)|\mathrm{d}s \le \sqrt{T}\cdot \rho _i \le \rho \sqrt{T}. \end{aligned}$$

Hence, \(N \le \frac{\rho \sqrt{T}}{b}\). Thus, the number of approach times with the pursuer \(x_i\) on [0, T] is finite and does not exceed \(\left[ \frac{\rho \sqrt{T}}{b}\right] +1\).

Therefore, the total number of approaches with all pursuers on [0, T] does not exceed \(K\left( \left[ \frac{\rho \sqrt{T}}{b}\right] +1\right) \). Thus, we can conclude that the number of approach times \(\tau _1, \ \tau _2, \ldots \), is finite on any interval [0, T] and hence they have no limit point on [0, T].

3.11 Estimate of Parameters

We imposed the following conditions on the parameters \(\kappa , \, \alpha ,\, a_i,\,\quad i=1, 2, \ldots \):

  1. A.

    \(0< \kappa<1, \ \ 0< a_1 < \min \left\{ \frac{1}{2}, \frac{a}{2}, b, d\right\} \) [see (3.7)];

  2. B.

    \(0< \alpha< 1, \ 12\alpha a_i < \sigma ^2\) [see (3.23)];

  3. C.

    \(\frac{\alpha a_i^2}{12\sigma ^2} > a_{i+1}\) [see (3.34)];

  4. D.

    \(a_{i+1} < a_i^4\) [see (3.8)];

  5. E.

    \(4\alpha a_1 + 8\rho \sqrt{\alpha a_1} < \frac{\sigma ^2-\rho ^2}{2M}\) [see (3.45)];

  6. F.

    \(a_i<\frac{a}{2}\) [see (3.48)];

  7. G.

    \(2\alpha a_{i+1} < \rho ^2\) [see (3.30)];

  8. H.

    \(a_{i+1} \le \frac{\alpha ^3}{144\cdot 32\cdot \rho ^2 \sigma ^4}a_i^4\) [see (3.32)];

  9. I.

    \(2\alpha a_1 \le (\sigma -\rho )^2\) [see (3.20)];

To satisfy all these inequalities, we choose parameters. Let

$$\begin{aligned} a_1 = \frac{a^2\alpha }{16\sigma ^2}, \end{aligned}$$

where a is the number in definition of \(S'\). Next, choose the number \(\alpha , \ 0< \alpha < \min \{1,\sigma ^2\}\), to satisfy the inequalities

$$\begin{aligned} 12\alpha a_1< (\sigma -\rho )^2, \quad \alpha a_1< \frac{(\sigma ^2-\rho ^2)^2}{64M^2(2\rho +1)^2}, \quad a_1 < \min \left\{ \frac{1}{2}, \frac{\rho ^2}{2}, \frac{a}{2}, b, d \right\} . \end{aligned}$$
(3.51)

Then choose \(\kappa \) by the formula

$$\begin{aligned} \kappa = \frac{\alpha ^3}{144\cdot 32\sigma ^6}. \end{aligned}$$
(3.52)

Observe that \(\kappa < 1\). After that choose numbers \(a_2, a_3, \ldots \) by the formula

$$\begin{aligned} a_{i+1} = \kappa a_i^4, \quad i=1,2, \ldots . \end{aligned}$$
(3.53)

Note that by the third inequality of (3.51) and (3.53) the inequalities \(1/2 \ge a_1> a_2 > \ldots \) hold. Then, we show that all the above inequalities A–I are satisfied.

Indeed, A follows from (3.51) and (3.52). B is satisfied since by the first inequality of (3.51)

$$\begin{aligned} 12\alpha a_i \le 12\alpha a_1< (\sigma -\rho )^2 < \sigma ^2. \end{aligned}$$
(3.54)

Next, show the inequality in C. Indeed, to show

$$\begin{aligned} \frac{\alpha a_i^2}{12\sigma ^2} > a_{i+1} = \frac{\alpha ^3 a_i^4}{144\cdot 32\sigma ^6}, \end{aligned}$$

it is sufficient to show that

$$\begin{aligned} a_i^2 \alpha ^2 < 12\cdot 32\sigma ^4. \end{aligned}$$

This inequality is valid since by (3.54)

$$\begin{aligned} (a_i \alpha )^2 \le (a_1 \alpha )^2< \sigma ^4/144 < 12\cdot 32\sigma ^4. \end{aligned}$$

Since \(\kappa < 1\), then (3.53) implies D. Since \(\alpha \in (0, 1)\), \(0< a_{i+1} < a_1\) and \(a_1 < \rho ^2/2\), then we obtain

$$\begin{aligned} 2\alpha a_{i+1}< 2a_{i+1}< 2a_1 < \rho ^2, \end{aligned}$$

which gives us the validity of option G.

We now think of E. The numbers \(\alpha \) and \(a_1\) are less than 1, and therefore \(\alpha a_1 < \sqrt{\alpha a_1}\). Then according to the second inequality of (3.51) we have

$$\begin{aligned} 4\alpha a_1 + 8\rho \sqrt{\alpha a_1}< 4\sqrt{\alpha a_1} + 8\rho \sqrt{\alpha a_1} = 4(1+2\rho )\sqrt{\alpha a_1} < \frac{\sigma ^2-\rho ^2}{2M}, \end{aligned}$$

and so E is satisfied. Next, F follows from the inequalities \(a_1 < \min \{\frac{1}{2}, \frac{a}{2}\}\) and \(a_i > a_{i+1}, \ i=1,2, \ldots \). Since \(\sigma \ge \rho \), H follows from (3.52) and (3.53). I also follows from the first inequality in (3.51).

Now, we turn to the game with the evaders \(y_1, \ldots , y_M\). We choose the parameters \(\alpha _i,\, \ a_{j1}, \ a_{j2}, \ldots \) as follows. Let \(a_{j1} = a_1\) for all \(j=1,\, \ldots ,\, M\). We choose \(\alpha _i = \alpha \). We define the numbers \(a_{j2}, \ a_{j3}, \ldots \) by formula

$$\begin{aligned} a_{j, i+1} = \kappa a_{j i}^4,\quad i=1, 2, \ldots , \quad j=1, \ldots ,\, M. \end{aligned}$$

Note that by the choice of the numbers \(a_{j1}\) we obtain \(a_{1i} = \ldots = a_{Mi}\), \(i=1, 2, \ldots \). Therefore, inequalities \(a_{ji} < \frac{a}{2}\) are satisfied. Proof of Theorem 3.1 is complete.

4 Discussion

4.1 The Evader Moves in a Corridor of width a

If parameters are chosen as in Sect. 3.11, then we show that the evader moves in a corridor of width a. More precisely, we show that \(|(y(t) - y_0, e')| \le a/2\). Indeed,

$$\begin{aligned} |(y(t) - y_0, e')|= & {} \left| \int \limits _{0}^{t}(v(s), e')\mathrm{d}s\right| \le \int \limits _{0}^{t}|(v(s),e')|\mathrm{d}s\\\le & {} \left( \int \limits _{E}+\int \limits _{[0, t]\backslash E}\right) |(v(s),e')|\mathrm{d}s \end{aligned}$$

where

$$\begin{aligned} E=\bigcup _{\{i|\tau _i\in [0, t]\}} [\tau _i, \tau '_i]. \end{aligned}$$

Note that by (3.13), \((v(t),e') = 0, \ t \in [0, t]\backslash E\). Therefore,

$$\begin{aligned} |(y(t) - y_0, e')|\le & {} \int \limits _{E}|(v(s),e')|\mathrm{d}s\\\le & {} \sum _{i=1}^{\infty } \int \limits _{\tau _i}^{\tau '_i}|(v(s),e')|\mathrm{d}s \le \sum _{i=1}^{\infty }\sqrt{(\tau '_i-\tau _i)\int \limits _{\tau _i}^{\tau '_i}(v(s),e')^2\mathrm{d}s}\\\le & {} \sigma \cdot \sum _{i=1}^{\infty }\sqrt{(\tau '_i-\tau _i)} \le \sigma \cdot \sum _{i=1}^{\infty }\sqrt{\frac{a_i}{\alpha }}. \end{aligned}$$

From this using (3.10) and the formula \(a_1=\frac{a^2\alpha }{16\sigma ^2}\), we get

$$\begin{aligned} |(y(t) - y_0, e')| < 2\sigma \sqrt{\frac{a_1}{\alpha }}=\frac{a}{2}. \end{aligned}$$

This means the evader always moves in the set

$$\begin{aligned} S'=\{\xi | \ \ |(\xi - y_{0},e')| \le \frac{a}{2}, \ \ \ (\xi - y_{0},e) \ge -b\}. \end{aligned}$$

We have shown that the evader moves in a / 2 neighborhood of the ray \(\zeta (t) = y_0 + et, \ t \ge 0\).

4.2 Reduction to the Game in \({\mathbb {R}}^2\)

Give a procedure of reduction of the game in \({\mathbb {R}}^n, \ n \ge 3\), to the game in \({\mathbb {R}}^2\). Given \(x_{i0}-y_{j0} \ne 0, \ i=1, \ldots , K; \ j=1, \ldots , M\), we choose a unit vector \(e_1\) different from the vectors \(\pm (x_{i0}-y_{j0})/|x_{i0}-y_{j0}|, \ i=1, \ldots , K; \ j=1, \ldots , M\). Let \(\bar{x} \) stand for \(x-(x, e_1)e_1\), the projection of x on the subspace \(L_1 = \{x \in {\mathbb {R}}^n| \ (x,e_1)=0\}\). One can verify that \(x_{i0} \ne y_{j0}\) implies that \(\bar{x}_{i0} \ne \bar{y}_{j0}\). For the projections of the pursuers on \(L_1\), we obtain from (1.1) the following equations

$$\begin{aligned} \dot{\bar{x}}_i = \bar{u}_i, \ \bar{x}_i(0) =\bar{x}_{i0}, \end{aligned}$$

where

$$\begin{aligned} \int \limits _0^{\infty }|\bar{u}_i(s)|^2\mathrm{d}s= \int \limits _0^{\infty }\left( |u_i(s)|^2 - (u_i(s), e_1)^2\right) \mathrm{d}s \le \int \limits _0^{\infty }|u_i(s)|^2\mathrm{d}s \le \rho _i^2. \end{aligned}$$

Consider the evader’s projection \({\bar{y}}_j \in L_1\) whose motion is described by the equation

$$\begin{aligned} \dot{\bar{y}}_j = v_j, \ \bar{y}_j(0) = \bar{y}_{j0}, \ \int \limits _0^{\infty }|v_j(s)|^2\mathrm{d}\le \sigma _j^2, \end{aligned}$$

where \(v_j(t) \in L_1, \ t \ge 0\). Since \(\bar{x}_i(t) \ne \bar{y}_j(t)\) implies \(x_i(t) \ne y_j(t)\), therefore if evasion is possible in the game in \(L_1\), then evasion is possible in the game (1.1)–(1.2). Note that the evader \(y_j(t)\) uses the same control function \(v_j(t)\) as its projection \(\bar{y}_j(t)\). Thus, evasion problem in \({\mathbb {R}}^n\) is reduced to an evasion problem in \((n-1)\)-dimensional space \(L_1\). We can proceed analogously to reduce the problem in \(L_1\) to evasion problem in an \((n-2)\)-dimensional space and so on. After some finite steps, we obtain a two-dimensional space.

4.3 Important Points of the Solution

According to the constructed strategies of the evaders, the total energy of the evaders spent by a time t might be greater than that of pursuers. Indeed, it can be seen from (3.14) and (3.13) that if any pursuer is in one of the sets \(S_j\), the total energy of the evaders can be estimated from below as follows. When the evader \(y_j\) is moving on the time interval \([0, \tau _{1j}]\), by (3.13)

$$\begin{aligned} \int \limits _0^t|v_j(t)|^2\mathrm{d}t = \int \limits _0^t\sum _{i \in I_j(t)} |u_i(t)|^2\mathrm{d}t, \end{aligned}$$

meaning that the evader \(y_j\) spends energy same as all the pursuers in the strip \(S_j\). When the evader \(y_j\) moves on a time interval \([\tau _{{\omega }_{l-1}+1}, \tau _{{\omega }_l}^*]\), by (3.14) we have

$$\begin{aligned} \int \limits _{\tau _{{\omega }_{l-1}+1}}^{\tau _{{\omega }_l}^*}|v_j(t)|^2\mathrm{d}t \ge \int \limits _{\tau _{{\omega }_{l-1}+1}}^{\tau _{{\omega }_l}^*}\sum _{i \in I_j(t)}(2\alpha ^2 + |u_i(t)|^2)\mathrm{d}t > \int \limits _{\tau _{{\omega }_{l-1}+1}}^{\tau _{{\omega }_l}^*} \sum _{i \in I_j(t)}|u_i(t)|^2\mathrm{d}t. \end{aligned}$$

Hence, on the interval \([\tau _{{\omega }_{l-1}+1}, \tau _{{\omega }_l}^*]\), the evader \(y_j\) spends energy more than that of all pursuers in \(S_j\). In a similar fashion, we can verify that if the evader \(y_j\) moves on the interval \([\tau ^*_j, \tau _{j+1}]\) according to (3.13), then the evader \(y_j\) spends energy same as all the pursuers in the strip \(S_j\) on the time interval \([\tau ^*_j, \tau _{j+1}]\), where \(\tau ^*_j\) is time group pursuit is completed at and at \(\tau _{j+1}\) another group pursuit is started.

Therefore, we can conclude that the total energy spent by evaders at any time t greater than or equal to that of all the pursuers. By this reason, we first reduced the case \(\sigma _1^2 + \cdots + \sigma _M^2 = \rho _1^2 + \ldots + \rho _K^2\) to the case \(\sigma _1^2 + \cdots + \sigma _M^2 > \rho _1^2 + \cdots + \rho _K^2\). Then we constructed strategies for the evaders, which depend on some parameters. We have chosen the parameters so that the total energy of the evaders be less than \(\sigma _1^2 + \cdots + \sigma _M^2\).

Next, the movement of the evaders in the disjoint strips \(S_j, \ j=1, \ldots , M\), is crucial. Because of disjointness of the strips, the control parameter of any pursuer cannot appear in the strategies of two different evaders \(y_i\) and \(y_j\) with \(i \ne j\). This condition is important for admissibility of the strategies of evaders.

The fact that approach times \(\tau _i\) have no finite limit point is another key point in the proof of the main result since if the approach times have a finite limit point, the evader can be captured before his energy is exhausted. In fact, one pursuer, say \(x_i\), can make infinitely many \(a_{{\omega }_1}\)-, \(\ a_{{\omega }_2}\)-, ..., -approaches at some times \(\tau _{{\omega }_1}, \ \tau _{{\omega }_2},... \rightarrow \infty \) respectively.

4.4 Realization of Evaders’ Strategies

By Definition 2.3, to construct the strategy \(V_j\), the evader \(y_j\) knows information about parameters \(t, y_j, q_j\), \(x_1,\ldots \), \(x_K\), \(u_1, \ldots \), \(u_K\) at each time \(t \ge 0\).

The initial position \(\zeta _0\), which is known to evaders, is used to find the numbers d, \(d_0\) and \(\varepsilon \). Also, the evaders employ only \(\zeta _0\) to construct the points \(y'_{j0}\) and vectors \(v_{j0}\), \(e_j, e'_j\), and, hence, strips \(S_j, \ S'_j\), \(j=1, \ldots ,M\).

Step 1 Check the equation \(\sigma = \rho \). If it is so, using techniques of Sect. 3.1, we obtain \(q(\tau ^0) > p(\tau ^0)\) where \(\tau ^0\) is the time for which \(|x_s(\tau ^0)-x_{i0}|=d/4\) at some \(1 \le s \le K\) then we go to Step 2. Here, the evader \(y_j\) needs the information about \(x_i(t), \ i=1, \ldots ,K\), and time t to check the condition \(|x_i(t)-x_{i0}|= d/4\). To this end, the evaders employ the following controls

$$\begin{aligned} v_j(t) = 0,\quad j=1, \ldots ,M, \quad 0 \le t \le \tau ^0. \end{aligned}$$

As mentioned in Remark 3.2 that the evaders do not know \(p(\tau ^0)\), but they know \(\bar{\rho }\) and the fact that \(p(\tau ^0) \le \bar{\rho }\). From now on the evaders use \(\bar{\rho }\) instead of \(\rho \). If \(\sigma > \rho \), then we put \(\tau ^0 = 0\) and go to Step 2.

Step 2 Let \(q(\tau ^0) > p(\tau ^0)\). We check whether \(y_{i0} = y_{j0}\) for some \(i \ne j\), \(i,j \in \{1, \ldots ,M\}\). If so the evaders move to the points \(y'_{j0}\) by using the following controls

$$\begin{aligned} v_j(t) = v_{j0},\quad j=1, \ldots ,M, \quad \tau ^0 \le t \le \tau ^0 + \varepsilon . \end{aligned}$$

This control is constructed based on \(\zeta _0\). To choose the parameter \(a_{j1}\) [see (3.7)], we use d which depends also on \(\zeta _0\). Note that \(a_{j1} < d/2\) and by (3.6) \(|x_i(t)-y_j(t)|> d/2\) for all \(i=1, \ldots ,K; \ j=1, \ldots ,M\), and therefore there is no \(a_{j1}\)-approach time in the time interval \(\tau ^0 \le t \le \tau ^0 + \varepsilon \).

If \(y_{i0} \ne y_{j0}\) for all \(i\ne j\), \(i,j \in \{1, \ldots ,M\}\), then we put \(\varepsilon = 0\) and go to Step 3.

Step 3 Let \(q(\tau ^0 + \varepsilon ) > p(\tau ^0 + \varepsilon )\) and \(y'_{i0} \ne y'_{j0}\) for all \(i\ne j\), \(i,j \in \{1, \ldots ,M\}\). Then evaders use strategies (3.13) and (3.14) where we have to put \(\tau ^*_0 = \tau ^0 + \varepsilon \). In this step, the strategies of evaders are constructed based on the information about \(t, y_j, q_j\), \(x_1,\ldots \), \(x_K\), \(u_1, \ldots \), \(u_K\) at each time \(t \ge 0\). While \(q_j(t)>0\) the evader \(y_j\) is not captured by any pursuer. If \(q_j(t)=0\), the energy of the evader \(y_j\) is exhausted, \(y_j\) is not able further to move, and then it can be captured by a pursuer.

Importantly, the number of summands in the definition of \(V_{2i}(t)\) depends on t, therefore the measurability of \(V_{2i}(t)\) needs to be explained. This follows from the fact that any pursuer \(x_i\) can stay in the strip S only on a closed time interval since \(x_i(t)\) is continuous and S is closed.

5 Conclusion

In the present paper, we have solved completely the simple motion evasion differential game of many evaders from many pursuers when control functions of the players are subject to integral constraints. We have shown that if

$$\begin{aligned} \rho _1^2 + \cdots + \rho _K^2 \le \sigma _1^2 + \cdots + \sigma _M^2, \end{aligned}$$

then evasion is possible from any initial position \(\zeta _0\) of players. In addition, we have constructed explicit strategies for the evaders. Note that this inequality is a necessary condition of evasion as well since if it does not hold, then pursuit can be completed from any initial position of players [16]. Thus, the result of the present paper fills the long standing gap in the simple motion differential game of many players with integral constraints. In future, this result can be extended to differential games described by more general linear differential equations.