Keywords

1 Introduction

Data envelopment analysis (DEA) [1] is a nonparametric and linear programming-based technique which evaluates the relative efficiency of homogeneous DMUs on the basis of multiple inputs and multiple outputs. Since the time DEA was proposed, it has got comprehensive attention both in theory and in applications. The beauty of DEA is its ability to measure relative efficiencies of DMUs without assuming prior weights on the inputs and outputs. The first model in DEA is the CCR model [1] which deals with proportional changes in inputs and outputs. The CCR efficiency score reflects the proportional maximum input reduction (or output augmentation) rate which is common to all inputs (outputs). But it neglects the slacks corresponding to inputs and outputs. To overcome this shortcoming of CCR model, Tone presented Slack-based Measure (SBM) model [15] in DEA, which puts aside the assumption of proportionate changes in inputs and outputs, and deals with slacks directly. The primal part of the SBM model directly deals with input excesses and output shortfalls of the concerned DMUs. On the other hand, the dual part of the SBM model can be interpreted as profit maximization model and it aims to calculate the optimal virtual costs and prices (also known as weights) of inputs and outputs for the concerned DMUs. Other theoretical extensions of SBM model can be seen in [4, 13].

The conventional DEA models are limited to only crisp input/output data and also their weights take only crisp values. However, in real-world problems, two situations can be possible: (1) Input/output data may have imprecision or fuzziness and (2) the weights of data may have fuzzy essence. To deal with imprecise data, the notion of fuzziness has been introduced in DEA. The DEA is extended to fuzzy DEA (FDEA) in which the imprecision is represented by fuzzy sets or FNs [7, 14]. The SBM efficiency in DEA is extended to fuzzy settings in [6, 11, 12]. Several approaches have been developed to deal with fuzzy data in FDEA. These approaches are as follows: (1) tolerance approach [14], (2) \(\alpha \)-cut approach [7], (3) fuzzy ranking approach [5], and (4) possibility approach [8]. However, very less emphasis has been given to FDEA models with fuzzy weights. Mansourirad et al. [10] are the first who introduced fuzzy weights in fuzzy CCR model and proposed a method based on \(\alpha \)-cut approach to evaluate weights for outputs in terms of TFNs. In this paper, we propose a dual SBM model with fuzzy weights corresponding to crisp input and output data. We reduce the proposed model into crisp linear programming problem (LPP) by using ranking function of an FN. The proposed model gives the fuzzy efficiencies and the fuzzy weights corresponding to inputs and outputs of the concerned DMUs as TFNs.

The paper is organized as follows: Section 2 presents preliminaries which include basic definitions. Section 3 presents the description of primal and dual parts of the SBM model. Section 4 presents the dual SBM model with fuzzy weights and its reduction to a crisp LPP. Section 5 presents the results and discussion of a numerical example to illustrate the proposed model. The last Section 6 concludes the findings of our study.

2 Preliminaries

The basic definitions in the fuzzy set theory can be seen from [16]. This section includes the definition of TFN and arithmetic operations on TFNs [2]. It also includes ranking function which maps FN to the real line [9].

2.1 Triangular Fuzzy Number

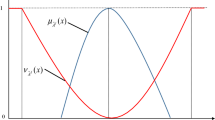
A TFN \(\tilde{A},\) denoted by \((a_1 ,a_2 ,a_3 ),\) is defined by the membership function \(\mu _{\tilde{A}} \) given by

$$\begin{aligned} \mu _{\tilde{A}} (x)=\left\{ {{\begin{array}{ll} {\dfrac{x-a_1 }{a_2 -a_1 },} &{} {a_1 <x\le a_2 ,} \\ {1,} &{} {x=a_2 ,} \\ {\dfrac{x-a_3 }{a_2 -a_3 },} &{} {a_2 \le x<a_3 ,} \\ {0,} &{} {\hbox {otherwise,}} \\ \end{array} }} \right. \end{aligned}$$

\(\forall x\in R.\) In the present study, \(\tilde{0}=(0,0,0), \tilde{1}=(1,1,1)\) and \(\tilde{a}=(a,a,a)\) where \(a\in R.\)

2.2 Arithmetic Operations on TFNs

Let \(\tilde{A}= (a_1 ,a_2 ,a_3 )\) and \(\tilde{B}= (b_1 ,b_2 ,b_3 )\) be two TFNs. Then,

Addition: \(\tilde{A}\oplus \tilde{B}= (a_1 +b_1 ,a_2 +b_2 ,a_3 +b_3 ).\)

Subtraction: \(\tilde{A}\;\Theta \;\tilde{B}= (a_1 -b_3 ,a_2 -b_2 ,a_3 -b_1 ). \)

Scalar multiplication: \(k\tilde{A}= \left\{ {\begin{array}{ll} (ka_1 ,ka_2 ,ka_3 ), &{} k\ge 0, \\ (ka_3 ,ka_2 ,ka_1 ), &{} k<0. \\ \end{array}} \right. \)

Multiplication: \(\tilde{A}\otimes \tilde{B}= (\min (a_1 b_1 ,a_1 b_3 ,a_3 b_1 ,a_3 b_3 ), a_2 b_2 , \max (a_1 b_1 ,a_1 b_3 ,a_3 b_1 ,a_3 b_3 )).\)

2.3 Ranking Function

Let \(F(R)\) be the set of all FNs. A ranking function [9] \(\mathfrak {R}\) is a mapping from \(F(R)\) to the real line. The FNs can easily be compared by using ranking functions. The rank of TFN \(\tilde{A}= (a_1 ,a_2 ,a_3 ),\) represented by \(\mathfrak {R}(\tilde{A}),\) is defined by \(\mathfrak {R}(\tilde{A}) = (a_1\,+\,2a_2\,+\,a_3 )/4.\)

Let \(\tilde{A}= (a_1 ,a_2 ,a_3 )\) and \(\tilde{B}= (b_1 ,b_2 ,b_3 )\) be two TFNs in \(F(R)\). Then,

  1. 1.

    \(\tilde{A}\) is said to be equal to \(\tilde{B}\) based on ranking function \(\mathfrak {R},\) written as \(\tilde{A}\mathop =\limits _\mathfrak {R}\tilde{B},\) iff \(\mathfrak {R}(\tilde{A})=\mathfrak {R}(\tilde{B}).\)

  2. 2.

    \(\tilde{A}\) is said to be less than or equal to \(\tilde{B}\) based on ranking function \(\mathfrak {R},\) written as \(\tilde{A}\mathop \le \limits _\mathfrak {R}\tilde{B},\) iff \(\mathfrak {R}(\tilde{A})\le \mathfrak {R}(\tilde{B}).\)

  3. 3.

    \(\tilde{A}\) is said to be greater than or equal to \(\tilde{B}\) based on ranking function \(\mathfrak {R},\) written as \(\tilde{A}\mathop \ge \limits _\mathfrak {R}\tilde{B},\) iff \(\mathfrak {R}(\tilde{A})\ge \mathfrak {R}(\tilde{B}).\)

  4. 4.

    \(\tilde{A}\) is said to be less than or equal to \(\tilde{0}\) based on ranking function \(\mathfrak {R},\) written as \(\tilde{A}\mathop \le \limits _\mathfrak {R}\tilde{0},\) iff \(\mathfrak {R}(\tilde{A})\le \mathfrak {R}(\tilde{0}).\)

Theorem: \( \mathfrak {R}(c\tilde{A}+\tilde{B})= c \mathfrak {R}(\tilde{A})+\mathfrak {R}(\tilde{B}), c\) is any constant. (Linearity property [11]).

3 Slack-based Measure Model

Assume that the performance of a set of \(n\) homogeneous DMUs (\( \text {DMU}_{j}\); \(j = 1,{\ldots }, n\)) is to be measured. The performance of \(\text {DMU}_{j}\) is characterized by a production process of \(m\) inputs (\(x_{ij}\); \(i = 1,{\ldots }, m\)) to yield \(s\) outputs (\(y_{rj}\); \(r = 1,{\ldots }, s\)). Let \(y_{rk} \) be the amount of the \(r\text {th}\) output produced by the \(k\text {th}\) DMU and \(x_{ik} \) be the amount of the \(i\text {th}\) input used by the \(k\text {th}\) DMU. Assume that input and output data are positive. The primal of SBM model [15] of the \(k\)th DMU, represented by \(\text {SBM-P}_{k }\), is defined as

$$\begin{aligned} \begin{array}{l} \hbox {SBM-P}_k \quad \quad \rho _k =\text {min} \dfrac{1-(1/m)\sum _{i=1}^m {s_{ik}^- /x_{ik} } }{1+(1/s)\sum _{r=1}^s {s_{rk}^+ /y_{rk} } } \\ \quad \quad \text {subject}\, \text {to}\, x_{ik} =\sum \nolimits _{j=1}^n {x_{ij} \lambda _{jk} +s_{ik}^- }\ \forall i, \\ \quad \quad y_{rk} =\sum \nolimits _{j=1}^n {y_{rj} \lambda _{jk} -s_{rk}^+ }\ \forall r, \\ \quad \quad \lambda _{jk} \ge 0\ \forall j, s_{ik}^- \ge 0\ \forall i, s_{rk}^+ \ge 0\ \forall r, \\ \end{array} \end{aligned}$$

where \(s_{rk}^+ \) is the slack in the \(r\text {th}\) output of the \(k\text {th}\) DMU; \(s_{ik}^- \) is the slack in the \(i\text {th}\) input of the \(k\text {th}\) DMU; \(\lambda _{jk} \)’s, i.e., \((\lambda _{j1} , \lambda _{j2} , \ldots ,\lambda _{jn} )\) are non-negative variables for \(j=1, 2, \ldots , n.\) The \(k\text {th}\) DMU is SBM efficient if \(\rho _k =1\) and all \(s_{ik}^- =0, s_{rk}^+ =0,\) i.e., no input excesses and no output shortfalls in any optimal solution.

\(\text {SBM-P}_{k }\) can be transformed into LPP using Charnes–Cooper transformation given in [1]. Multiply a scalar \(t_k >0\) to both the denominator and the numerator of \(\text {SBM-P}_{k}\). This causes no change in the value of \(\rho _k \). The value of \(t_k \) can be adjusted in such a way that the denominator becomes 1. The \(\text {SBM-P}_{k}\) model in LPP form becomes

$$\begin{aligned} \text {LPP-SBM-P}_k \quad \tau _k&= \text {min}\ t_k -\frac{1}{m}\sum \limits _{i=1}^m {S_{ik}^- /x_{ik} } \\ \quad \quad \text {subject}\, \text {to}\, 1&=t_k +\frac{1}{s}\sum \limits _{r=1}^s {S_{rk}^+ /y_{rk} } , \\ \quad \quad t_k x_{ik}&=\sum \limits _{j=1}^n {x_{ij} \Lambda _{jk} +S_{ik}^- } \forall i,\\ t_k y_{rk}&=\sum _{j=1}^n {y_{rj} \Lambda _{jk} -S_{rk}^+ } \forall r, \end{aligned}$$
$$\begin{aligned} \Lambda _{jk} \ge 0\ \forall j, S_{ik}^- \ge 0\ \forall i, S_{rk}^+ \ge 0\ \forall r, t_k >0, \end{aligned}$$

where \(\rho _k = \tau _k , \lambda _{jk} = \Lambda _{jk} /t_k \forall j, s_{ik}^- =S_{ik}^- /t_k \forall i \) and \(s_{rk}^+ =S_{rk}^+ /t_k \forall r.\)

The dual of \(\text {LPP-SBM-P}_{k}\) , represented by \(\text {SBM-D}_{k}\) , can be expressed as follows:

$$\begin{aligned} \begin{array}{l} \text {SBM-D}_k \quad \quad E_k =\max \xi _k \\ \quad \quad \text {subject}\, \text {to}\, \xi _k + \sum \nolimits _{i=1}^m {x_{ik} v_{ik} } -\sum _{r=1}^s {y_{rk} u_{rk} } =1, \\ \quad \quad \sum \nolimits _{r=1}^s {y_{rj} u_{rk} } -\sum \nolimits _{i=1}^m {x_{ij} v_{ik} } \le 0\ \forall j, \\ \quad \quad v_{ik} \ge \frac{1}{mx_{ik} }\ \forall i, u_{rk} \ge \frac{\xi _k }{sy_{rk} }\ \forall r. \\ \end{array} \end{aligned}$$

where \(\xi _k \in R, v_{ik}\ \forall i\), and \(u_{rk}\ \forall r\) are the dual variables corresponding to \(\text {LPP-SBM-P}_{k }\). The dual variables \(v_{ik}\) and \(u_{rk} \) are the weights associated with the \(i\text {th}\) input and the \(r\text {th}\) output, respectively. The \(E_{k}\) is the SBM efficiency of the \(k\text {th}\) DMU.

4 Dual SBM Model with Fuzzy Weights

In conventional \(\text {SBM-D}_{k}\) model, the weights of inputs and outputs are found as crisp quantities. However, in real-world problems, the weights may have fuzzy essence. Therefore, in this paper, weights of inputs and outputs are taken as TFNs, and thus, the \(\text {SBM-D}_{k}\) model becomes fuzzy \(\text {SBM-D}_{k}\) (\(\text {FSBM-D}_{k})\) model given by

$$\begin{aligned} \text {FSBM-D}_k \quad \quad \tilde{E}_k \mathop =\limits _\mathfrak {R}\max \tilde{\xi }^{k} \end{aligned}$$
$$\begin{aligned} \begin{array}{l} \text {subject}\; \text {to}\,\; \tilde{\xi }^{k} \oplus \sum \nolimits _{i=1}^m {x_{ik} \tilde{v}^{ik}} \;\Theta \sum \nolimits _{r=1}^s {y_{rk} \tilde{u}^{rk}} \mathop =\limits _\mathfrak {R}\tilde{1}, \\ \sum \nolimits _{r=1}^s {y_{rj} \tilde{u}^{rk}} \Theta \sum \nolimits _{i=1}^m {x_{ij} \tilde{v}^{ik}} \mathop \le \limits _\mathfrak {R}\tilde{0}\ \forall j, \\ \tilde{v}^{ik} \mathop \ge \limits _\mathfrak {R}\frac{1}{mx_{ik} } \tilde{1}\ \forall i, \tilde{u}^{rk} \mathop \ge \limits _\mathfrak {R}\frac{1}{sy_{rk} }\tilde{\xi }^{k}\ \forall r, \\ v_1^{ik} \le v_2^{ik} \le v_3^{ik}\ \forall i, u_1^{rk} \le u_2^{rk} \le u_3^{rk}\ \forall r, \xi _1^k \le \xi _2^k \le \xi _3^k . \end{array} \end{aligned}$$

where \(\tilde{v}^{ik}\)and \(\tilde{u}^{rk}\) are the triangular fuzzy weights associated with the \(i\text {th}\) input and the \(r\text {th}\) output, respectively. The \(\tilde{E}_k \) is the fuzzy SBM efficiency of the \(k\text {th}\) DMU which is also found as a TFN. By using the ranking function of TFN, \(\text {FSBM-D}_{k}\) model reduces to Model 1, which is as follows:

$$\begin{aligned} \begin{array}{l} \text {Model-1}\quad \mathfrak {R}(\tilde{E}_k )=\max \mathfrak {R}(\tilde{\xi }^{k})\\ \text {subject}\, \text {to}\, \mathfrak {R}(\tilde{\xi }^{k}) +\sum \nolimits _{i=1}^m {x_{ik} \mathfrak {R}(\tilde{v}^{ik})} -\sum \nolimits _{r=1}^s {y_{rk} \mathfrak {R}(\tilde{u}^{rk})} =\mathfrak {R}(\tilde{1}),\\ \sum \nolimits _{r=1}^s {y_{rj} \mathfrak {R}(\tilde{u}^{rk})} -\sum \nolimits _{i=1}^m {x_{ij} \mathfrak {R}(\tilde{v}^{ik})} \le \mathfrak {R}(\tilde{0})\ \forall j,\\ \mathfrak {R}(\tilde{v}^{ik})\ge \frac{1}{mx_{ik} } \mathfrak {R}(\tilde{1})\ \forall i, \mathfrak {R}(\tilde{u}^{rk})\ge \frac{1}{sy_{rk} }\mathfrak {R}(\tilde{\xi }^{k})\ \forall r,\\ v_1^{ik} \le v_2^{ik} \le v_3^{ik}\ \forall i, u_1^{rk} \le u_2^{rk} \le u_3^{rk}\ \forall r, \xi _1^k \le \xi _2^k \le \xi _3^k . \end{array} \end{aligned}$$

By putting the values of \(\mathfrak {R}(\tilde{\xi }^{k}), \mathfrak {R}(\tilde{v}^{ik}) \ \forall i \), and \(\mathfrak {R}(\tilde{u}^{rk})\ \forall r,\) the Model-1 reduces to Model-2, which is crisp LPP.

$$\begin{aligned} \begin{array}{l} \text {Model-2}\quad E_k =\max (\xi _1^k +2\xi _2^k +\xi _3^k )/4 \\ \text {subject}\, \text {to}\, (\xi _1^k +2\xi _2^k +\xi _3^k )+ \sum \nolimits _{i=1}^m {x_{ik} } (v_1^{ik} +2v_2^{ik} +v_3^{ik} )\\ \quad \quad \quad -\sum \nolimits _{r=1}^s {y_{rk} } (u_1^{rk} +2u_2^{rk} +u_3^{rk} )=4, \\ \quad \sum \nolimits _{r=1}^s {y_{rj} } (u_1^{rk} +2u_2^{rk} +u_3^{rk} )-\sum \nolimits _{i=1}^m {x_{ij} } (v_1^{ik} +2v_2^{ik} +v_3^{ik} )\le 0\ \forall j, \\ \end{array} \end{aligned}$$
$$\begin{aligned} \begin{array}{l} \quad \frac{v_1^{ik} +2v_2^{ik} +v_3^{ik} }{4}\ge \frac{1}{mx_{ik} }\ \forall i, u_1^{rk} +2u_2^{rk} +u_3^{rk} \ge \frac{\xi _1^k +2\xi _2^k +\xi _3^k }{sy_{rk} }\ \forall r, \\ \quad v_1^{ik} \le v_2^{ik} \le v_3^{ik}\ \forall i, u_1^{rk} \le u_2^{rk} \le u_3^{rk}\ \forall r, \xi _1^k \le \xi _2^k \le \xi _3^k . \\ \end{array} \end{aligned}$$

5 Results and Discussion of a Numerical Example

In this section, we provide a numerical example to illustrate the proposed dual SBM model with fuzzy weights. Table 1 presents the performance evaluation problem of six DMUs with two inputs I\(_{1}\) and I\(_{2}\), and two outputs O\(_{1}\) and O\(_{2}\).

Table 1 Input and output data of six DMUs
Full size table
Table 2 Fuzzy efficiencies \(\tilde{\xi }^{k}=(\xi _1^k ,\xi _2^k ,\xi _3^k )\) and \(\mathfrak {R}(\tilde{\xi }^{k})\)
Full size table
Table 3 Fuzzy weights corresponding to inputs
Full size table
Table 4 Fuzzy weights corresponding to outputs
Full size table

The fuzzy efficiencies of all DMUs are evaluated from Model-2, which are shown in Table 2. The results reveal that the rank of each fuzzy efficiency score lies between 0 and 1, i.e., \(0<\mathfrak {R}(\tilde{\xi }^{k})\le 1.\) The fuzzy weights corresponding to inputs and outputs of the concerned DMU are also evaluated by using Model-2, which are shown in Tables 3 and 4, respectively. These fuzzy weights provide additional information to the decision maker, which is not provided by crisp weights in crisp dual SBM model.

6 Conclusion

In this paper, we proposed a dual SBM model with fuzzy weights (\(\text {FSBM-D}_{k})\) for crisp inputs and outputs. The \(\text {FSBM-D}_{k}\) model is then reduced to crisp LPP by using ranking function. The proposed model evaluates the components of fuzzy efficiencies and fuzzy weights corresponding to inputs and outputs as TFNs. These fuzzy efficiencies and fuzzy weights provide additional information to the decision maker, which helps to deal with uncertainty in real-life problems.