Keywords

1 Introduction

DEA is non-parametric linear programing (LP) based technique to determine the relative efficiency of homogeneous DMUs when the production process consists of multiple inputs and multiple outputs (Ramanathan 2003). There exist some mathematical programs in DEA such as: Fractional, Input minimization (Output oriented) and Output maximization (Input oriented) etc. (Cooper et al. 2007). DEA calculates maximal performance measure for each DMU relative to other DMUs. CCR model (Charnes et al. 1978) find the constant returns to scale (CRS) and BCC model (Banker et al. 1984) find the variable returns to scale (VRS), they neglects the slacks in the evaluation of efficiencies. To solve this neglection can be computed using the slack based measure (SBM) model non-radial and non-oriented DEA model (Tone 2001).

Conventional DEA deals with crisp input and crisp output data. But in real world applications, some input and/or output data possess some degree of fluctuation or imprecision or uncertainties such in health sector as quality of input resources, quality of treatment, the satisfaction level of patients, quality of medicines etc. The fluctuation can take the form of intervals, ordinal relations and fuzzy numbers etc. Therefore, to deal with such type of real life situations, we plan to extend crisp DEA to FDEA by making use of fuzzy numbers in DEA. FDEA models represent real world applications more realistically than the conventional DEA models.

The rest of the paper is organized as follows: Sect. 2 presents the literature review. Section 3 presents preliminaries required to develop the model of which include basic definitions performance efficiency, fuzzy number, triangular fuzzy number and expected values. Section 4 presents the background of primal and dual parts of the fuzzy SBM model. Section 5 presents an application to health sector to illustrate the proposed model. Section 6 concludes the finding of our work.

2 Literature Review

This section reviews some DEA based studies on health care sector around all over the world. Over the last 50 years India has built a sound health sector infrastructure (Agarwal et al. 2006). According to the literature, in the present time, the role of the health care sector has been expanding than the public health care sector in India. Determining the health care performance efficiency has an important role in developed as well as developing countries. There are some studies to determine the performance efficiencies of health care using DEA in Indian context (Mogha et al. 2014(a), (b)). The most important role in the economy of any developed as well as developing countries is health care of urban and rural areas. Sengupta (1992) was the first author to introduce the fuzzy measure, regression, entropy and fuzzy mathematical programming approach in DEA. Afsharinia et al. (2013) determined the performance efficiency of clinical units using fuzzy essence. Tsai et al. (2010) proposed the fuzzy analytic hierarchy process (FAHP) and fuzzy sensitive analysis based approach to measure the policy of Taiwan hospitals in DEA. Dotoli et al. (2015) developed a novel cross-efficiency fuzzy DEA model for evaluating different elements under uncertainty with application to the health care system. Mansourirad et al. (2010) were the first to introduce fuzzy weights in fuzzy CCR (FCCR) model and proposed a model using \(\alpha \)-cut approach to evaluate weights for outputs in terms of TFNs. The SBM performance efficiency in DEA is extended to fuzzy forms (Jahanshahloo et al. 2004 and Saati et al. 2009). Puri and Yadav (2013) proposed a slack based measure model with fuzzy weights corresponding to fuzzy inputs and fuzzy outputs using \(\alpha -\) cut approach.

3 Preliminary

This section includes some basic definitions and notions of fuzzy set theory (Zimmermann 1996), fuzzy number (FN), triangular fuzzy number (TFN), arithmetic operations on TFNs (Chen 1994) and expected values (Ghasemi 2015).

3.1 Performance Efficiency (Charnes 1978)

The performance efficiency of a DMU is defined as the ratio of the weighted sum of outputs (virtual output) to the weighted sum of inputs (virtual input). Thus, Performance efficiency \(=\frac{virtual\,\, output}{virtual\,\, input}\).

DEA evaluates the relative performance efficiency of a DMU in a set of homogeneous DMUs. The relative performance efficiency of a DMU lies in the range (0, 1].

3.2 Fuzzy Number (FN) (Zimmermann 1996)

An FN \(\tilde{M}\) is defined as a convex normalized fuzzy set \(\tilde{M}\) of the real line such that

  1. (1)

    there exists exactly one with \(\mu _{\tilde{M}}(x_0)=1\). \(x_0\) is called the mean value of \(\tilde{M}\),

  2. (2)

    \(\mu _{\tilde{M}}\) is a piecewise continuous function, called the membership function of \(\tilde{M}\).

3.3 Triangular Fuzzy Number (TFN) (Zimmermann 1996)

The TFN \(\tilde{M}\) is an FN denoted by \(\tilde{M} =(a,b,c)\) and is defined by the membership function \(\mu _{\tilde{M}}\) given by

$$\begin{aligned} \mu _{\tilde{M}}(x)=\left\{ \begin{array}{ll} \frac{x-a}{b-a},\, a< x\le b,\\ \frac{c-x}{c-b},\, b\le x < c, \\ 0, \, elsewhere, \end{array} \right. \end{aligned}$$

for all .

This TFN can be said to be “approximately equal to b”, where b is called the modal value, and (a,c) is called support of the TFN (a,b,c).

3.4 Arithmetic Operations on TFNs (Chen 1994)

Let \(\tilde{M1}= (a_1,b_1,c_1)\) and \(\tilde{M2}= (a_2,b_2,c_2)\) be two TFNs. Then, the arithmetic operations on TFNs are given as follows:

  • Addition: \(\tilde{M1}\oplus \tilde{M2}= (a_1+a_2,b_1+b_2,c_1+c_2)\).

  • Subtraction: \(\tilde{M1}\ominus \tilde{M2}= (a_1-c_2,b_1-b_2,c_1-a_2)\).

  • Multiplication: \(\tilde{M1} \otimes \tilde{M2}= (min (a_1a_2,a_1c_2,c_1a_2, c_1c_2),b_1b_2, max(a_1a_2,a_1c_2,c_1a_2, c_1c_2))\)

  • Scalar multiplication:

    $$\begin{aligned} \lambda {\tilde{M}_I}=\left\{ \begin{array}{ll} (\lambda a_1,\lambda b_1,\lambda c_1),\, for \,\lambda \ge 0\\ (\lambda c_1,\lambda b_1,\lambda a_1),\, for \,\lambda <0 \\ \end{array} \right. \end{aligned}$$

3.5 The Expected Values of FNs (Ghasemi 2015)

The expected interval (EI) of a TFN \(\tilde{M}=(a,b,c)\) defined as follows: \(EI(\tilde{M})=[E^L(\tilde{M}),E^U(\tilde{M})]\), where

\(E^L(\tilde{M})=\frac{a+b}{2}\) and

\(E^R(\tilde{M})=\frac{b+{c}}{2}\).

And expected value (EV) of a TFN \(\tilde{M}=(a,b,c)\) defined as follows:

\(EV(\tilde{M})= \frac{1}{2}(E^L(\tilde{M})+E^U(\tilde{M}))=\frac{a+2b+c}{4}.\)

4 Background

This paper measures the fuzzy input weights, fuzzy output weights and fuzzy efficiency of 12 community health cares of Meerut district of Uttar Pradesh (UP) State.

4.1 SBM DEA Model

Let the performance of a set of n homogeneous DMUs (\(DMU_j=1,2,3,...,n\)) be determined. The performance efficiency of \(DMU_j\) is characterized by a production process of m inputs \(x_{ij} (\mathrm{i}=1,2,3,...,\mathrm{m})\) to produce s outputs \(y_{rj} (\mathrm{r}=1,2,3,...,\mathrm{s})\). Assume \(x_{ij_o}\) be the amount of the ith input used and \(y_{rj_o}\) be the amount of the rth output produced by the \({DMU_{j_o}}\). Let input data and output data be positive. The primal SBM model (Tone 2001) for \({DMU_{j_o}}\) is given by the following model:

Model 1: (Primal SBM model)

$$\begin{aligned} \begin{array}{c} \rho _{j_o}= \min {\frac{1-(1/m)\sum _{i=1}^{m}{s^{-}_{ij_o}}/x_{ij_o}}{{1+(1/s)}\sum _{r=1}^{s}{s^{+}_{rj_o}}/y_{rj_o}}}\\ subject\,\, to \end{array} \end{aligned}$$
(1)
$$\begin{aligned}&{x_{ij_o}}=\sum \nolimits _{j=1}^{n}{ x_{ij}{\mu _{jj_o}}}+s^{-}_{ij_o},\,\,\forall i&\end{aligned}$$
(2)
$$\begin{aligned}&{y_{rj_o}}=\sum \nolimits _{j=1}^{n}{ y_{rj}{\mu _{jj_o}}}-s^{+}_{rj_o},\,\,\forall r&\end{aligned}$$
(3)
$$\begin{aligned}&\mu _{jj_o}\ge 0,\,\,\forall j,\,\, s^{-}_{ij_o} \ge 0,\,\,\forall i\,\,,s^{+}_{rj_o}\ge 0,\,\,\forall r&\end{aligned}$$
(4)

where \(s^{-}_{ij_o}\) and \(s^{+}_{rj_o}\) are the slack variables in the ith input of the \(DMU_{j_o}\) and rth output of the \(DMU_{j_o}\) respectively.

Definition 1

(Tone 2001) \(\rho _{j_o} \) is called SBM efficiency (SBME) of \(DMU_{j_o}\). \(DMU_{j_o}\) is SBM efficient if \(\rho _{j_o}^* = 1\).

This condition is equivalent to \(s^{-*}_{ij_o} =0\) and \(s^{+*}_{rj_o} =0\), i.e., no output shortfalls and no input excesses in optimal solution, otherwise inefficient.

Model 1 can be transformed into linear programming (LP) using normalization method (Charnes et al. 1978). In Model 1, multiply by a scalar \(p_{j_o} > 0\) to both the numerator and denominator. The value of \(p_{j_o}\) can be adjusted in such a way that the numerator becomes 1. Thus Model 1 is reduced to the following model (Model 2):

Model 2:

$$\begin{aligned} \begin{array}{c} E_{j_o} =\max p_{j_o}+\frac{1}{s}{\sum \nolimits _{r=1}^{s}{{S^{+}_{rj_o}}/y_{rj_o}}},\\ subject\,\, to \end{array} \end{aligned}$$
(5)
$$\begin{aligned}&p_{j_o}-\frac{1}{m}\sum \nolimits _{i=1}^{m}{S^{-}_{ij_o}}/x_{ij_o}=1,&\end{aligned}$$
(6)
$$\begin{aligned}&p_{j_o}x_{ij_o}=\sum \nolimits _{j=1}^{n}{x_{ij}\lambda _{jj_o}}+S^{-}_{ij_o}\,\,\forall i,&\end{aligned}$$
(7)
$$\begin{aligned}&p_{j_o}y_{rj_o}=\sum \nolimits _{j=1}^{n}{y_{rj}\lambda _{jj_o}}-S^{+}_{rj_o}\,\,\forall r,&\end{aligned}$$
(8)
$$\begin{aligned}&\lambda _{jj_o}\ge 0\,\forall j, S^{-}_{ij_o} \ge 0,\,\,\forall r, S^{+}_{rj_o}\ge 0,\,\,\forall i,\,p_{j_o}>0,&\\ {w here}&p_{j_o} {\mu _{jj_o}}=\lambda _{jj_o},\,\forall j, {p_{j_o}}s^{-}_{ij_o}=S^{-}_{ij_o},\,\forall i \,\,{a nd}\,\, {p_{j_o}}s^{+}_{rj_o}=S^{+}_{rj_o},\,\forall r \nonumber&\end{aligned}$$
(9)

Let \(\theta _{j_o},\,\,u_{ij_o}\) and \(v_{rj_o}\) be the dual variables corresponding to (6), (7) and (8) respectively. Then the Dual problem LPP in Model 2 is given by:

Model 3: (Dual SBM model)

$$\begin{aligned} \begin{array}{c} E^{D}_{j_o} =\min \theta _{j_o}, \\ subject\,\, to \end{array} \end{aligned}$$
(10)
$$\begin{aligned}&\sum \nolimits _{r=1}^{s}{y_{rj}v_{rj_o}}+\sum \nolimits _{i=1}^{m}{x_{ij}u_{ij_o}}\le 0,\,\, \forall j,&\end{aligned}$$
(11)
$$\begin{aligned}&\theta _{j_o}+\sum \nolimits _{i=1}^{m}{x_{ij_o}u_{ij_o}}+\sum \nolimits _{r=1}^{s}{y_{rj_o}v_{rj_o}}\ge 1,&\end{aligned}$$
(12)
$$\begin{aligned}&u_{ij_o}+ \frac{\theta _{j_o}}{mx_{ij_o}}\le 0 \forall i,&\end{aligned}$$
(13)
(14)

All the variables \(\theta _{j_o}\), \(u_{ij_o}\) and \(v_{rj_o}\) are unrestricted in sign.

4.2 Proposed Fuzzy Dual SBM Model

In conventional SBM model the input-output data and input-output weights are in crisp form. But in real world application, these weights and data may have fuzzy values. Thus, in this paper, input-output data and input-output weights are taken as TFNs. Model 3 is reduced to the following model:

Model 4:

$$\begin{aligned} \begin{array}{ccc} &{} \tilde{E}^{D}_{j_o} =\min \tilde{\theta }_{j_o},\nonumber &{} \\ &{} subject\,\, to \nonumber &{}\\ &{}\sum \nolimits _{r=1}^{s}{\tilde{y}_{rj}\otimes \tilde{v}_{rj_o}}+\sum \nolimits _{i=1}^{m}{\tilde{x}_{ij}\otimes \tilde{u}_{ij_o}}\le \tilde{0},\,\, \forall j, \nonumber &{}\\ &{} \tilde{\theta }_{j_o}+\sum \nolimits _{i=1}^{m}{\tilde{x}_{ij_o}\otimes \tilde{u}_{ij_o}}+\sum \nolimits _{r=1}^{s}{\tilde{y}_{rj_o}\otimes \tilde{v}_{rj_o}}\ge \tilde{1}, \nonumber &{} \\ &{} m\,\, \tilde{u}_{ij_o} \otimes \tilde{x}_{ij_o}+\tilde{\theta }_{j_o}\le \tilde{0} \,\,\forall \, i,\,\,s\,\, \tilde{v}_{rj_o} \otimes \tilde{y}_{rj_o}\ge \tilde{1} \,\,\forall \, r,\nonumber &{} \end{array} \end{aligned}$$

where \(\tilde{x}_{ij}\) and \(\tilde{y}_{rj}\) are the triangular fuzzy inputs and outputs respectively; \(\tilde{u}_{ij_o}\) is the triangular fuzzy weight corresponding to the ith input and \(\tilde{v}_{rj_o}\) is the triangular fuzzy weight corresponding to the rth output. By using expected values of TFN, Model 4 reduces to the following model:

Model 5:

$$\begin{aligned} \begin{array}{ccc} &{} EV(\tilde{E}^{D}_{j_o}) =\min EV( \theta ^{1}_{j_o}, \theta ^{2}_{j_o}, \theta ^{3}_{j_o}),\nonumber &{} \\[1mm] &{} subject\,\, to \nonumber &{} \\[1mm] &{}{EV(\sum \nolimits _{r=1}^{s}{y^{1}_{rj}{v^{1}_{rj_o}}},\sum \nolimits _{r=1}^{s}{y^{2}_{rj}{v^{2}_{rj_o}}},\sum \nolimits _{r=1}^{s}{y^{3}_{rj}{v^{3}_{rj_o}}})}+{EV(\sum \nolimits _{i=1}^{m}{x^{1}_{ij}{u^{1}_{ij_o}}},\sum \nolimits _{i=1}^{m}{x^{2}_{ij}{u^{2}_{ij_o}}}}, \nonumber &{}\\[1mm] &{}{\sum \nolimits _{i=1}^{m}{x^{3}_{ij}{u^{3}_{ij_o}}})}\le EV(0,0,0),\,\, \forall j,\nonumber &{} \\[1mm] &{} EV(\theta ^{1}_{j_o}, \theta ^{2}_{j_o}, \theta ^{3}_{j_o})+{EV( \sum \nolimits _{i=1}^{m}{x^{1}_{ij_o}u^{1}_{ij_o}},\sum \nolimits _{i=1}^{m}{x^{2}_{ij_o}u^{2}_{ij_o}},\sum \nolimits _{i=1}^{m}{x^{3}_{ij_o}u^{3}_{ij_o}})}+ \nonumber &{} \\[1mm] &{} {EV(\sum \nolimits _{r=1}^{s}{ y^{1}_{rj_o}v^{1}_{rj_o}},\sum \nolimits _{r=1}^{s}{y^{2}_{rj_o}v^{2}_{rj_o}},\sum \nolimits _{r=1}^{s}{y^{3}_{rj_o}v^{3}_{rj_o}})} \ge EV(1,1,1), \nonumber &{} \\[1mm] &{} m\,\,{EV( x^{1}_{ij_o} u^{1}_{ij_o} ,x^{2}_{ij_o} u^{2}_{ij_o} ,x^{3}_{ij_o} u^{3}_{ij_o} )}+EV(\theta ^{1}_{j_o}, \theta ^{2}_{j_o}, \theta ^{3}_{j_o})\le EV( 0,0,0) ,\,\,\forall i, \nonumber &{} \\[1mm] &{} s\,\,{ EV(y^{1}_{rj_o} v^{1}_{rj_o} ,y^{2}_{rj_o} v^{2}_{rj_o} ,y^{3}_{rj_o} v^{3}_{rj_o} )}\ge EV( 1,1,1),\,\, \forall r,\nonumber &{} \end{array} \end{aligned}$$

Using expected values in Model 5, we get Model 6.

Model 6:

$$\begin{aligned} \begin{array}{ccc} &{} E^{D1}_{j_o} =\min \frac{1}{4} {(\theta ^{1}_{j_o}+2 \theta ^{2}_{j_o}+ \theta ^{3}_{j_o})},\nonumber &{} \\[1mm] &{} subject\,\, to \nonumber &{}\\[1mm] &{}{ \sum \nolimits _{r=1}^{s}{(y^{1}_{rj}v^{1}_{rj_o}+2{y^{2}_{rj}v^{2}_{rj_o}}+{y^{3}_{rj}v^{3}_{rj_o}})}}-\sum \nolimits _{i=1}^{m}{({x^{1}_{ij}u^{1}_{ij_o}}+2{x^{2}_{ij}u^{2}_{ij_o}}+{x^{3}_{ij}u^{3}_{ij_o}})}\le 0,\,\, \forall j, \nonumber &{}\\[1mm] &{} (\theta ^{1}_{j_o}+2 \theta ^{2}_{j_o}+\theta ^{3}_{j_o})+{ \sum \nolimits _{i=1}^{m}{(x^{1}_{ij_o}u^{1}_{ij_o}+2{x^{2}_{ij_o}u^{2}_{ij_o}}+{x^{3}_{ij_o}u^{3}_{ij_o} })}}+\nonumber &{} \\[1mm] &{} {\sum \nolimits _{r=1}^{s}{( {y^{1}_{rj_o}v^{1}_{rj_o}}+2{y^{2}_{rj_o}v^{2}_{rj_o}}+{y^{3}_{rj_o}v^{3}_{rj_o}})}}\ge 4, \nonumber &{} \\[1mm] &{}m\,\, (x^{1}_{ij_o} u^{1}_{ij_o}+2 x^{2}_{ij_o} u^{2}_{ij_o}+ x^{3}_{ij_o} u^{3}_{ij_o})+(\theta ^{1}_{j_o}+2 \theta ^{2}_{j_o}+\theta ^{3}_{j_o})\le 0 \,\, \forall \, i,\nonumber &{} \\[1mm] &{} s\,\,(y^{1}_{rj_o} v^{1}_{rj_o}+2 y^{2}_{rj_o} v^{2}_{rj_o}+y^{3}_{rj_o} v^{3}_{rj_o})\ge 4, \,\,\forall \, r,\nonumber &{}\\[1mm] &{} u^{1}_{ij_o}\le u^{2}_{ij_o}\le u^{3}_{ij_o} \,\,\forall i,\,\,v^{1}_{rj_o}\le v^{2}_{rj_o}\le v^{3}_{rj_o} \,\,\forall r,\,\,\theta ^{1}_{j_o}\le \theta ^{2}_{j_o} \le \theta ^{3}_{j_o}.\nonumber \end{array} \end{aligned}$$

SBME of \(DMU_{j_o}\) is written as \(SBME_{j_o}\) and is given by \(SBME_{j_o}=(E_{j_o}^{DI})^{-1}\).

Table 1. Fuzzy input and fuzzy output data
Full size table
Table 2. Efficiencies and fuzzy Input weights of 12 hospitals
Full size table

5 Application to the Health Sector

In this section, we present an application to illustrate the proposed fuzzy dual SBM model. In this paper, DMUs are CHCs in Meerut district of Uttar Pradesh, India. The performance of each CHC is determined based on two fuzzy inputs and two fuzzy outputs. The input-output data in fuzzy form are given in Table 1.

For \(DMU_j, \,\,j=1,2,3,...,12\)  

\(1^{st}\) :

Input (\(x_{1j}\)) = Sum of number of doctors and number of staff nurses

\(2^{nd}\) :

Input (\(x_{2j}\)) = Number of pharmacists

\(1^{st}\) :

Output (\(y_{1j}\)) = Number of inpatients

\(2^{nd}\) :

Output (\(y_{2j}\)) = Number of outpatients

 

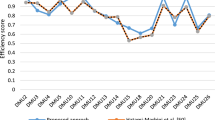
The fuzzy efficiencies of all CHCs are determined from Model 6, which are given in Table 2. The fuzzy efficiency scores lie between zero and 1. The fuzzy weights corresponding to fuzzy inputs and fuzzy outputs of the concerned CHCs are also determined by using Model 6, which are given in Tables 2 and 3. The fuzzy efficiencies and weights for every CHC are obtained by executing a MATLAB program of Model 6. In this application H11 is SBM inefficient hospital, other hospitals are SBM efficient.

Table 3. Fuzzy output weights of 12 hospitals
Full size table

6 Conclusion

In this piece of work, we proposed a fuzzy dual SBM model (Model 4) with fuzzy weights in fuzzy DEA. Model 4 is then reduced to crisp LP SBM model (Model 6) by using expected values of FNs. Model 6 determines the fuzzy efficiencies and components of fuzzy weights corresponding to fuzzy inputs and fuzzy outputs as TFNs. Model 6 also determines the SBM efficient and SBM inefficient DMUs. These fuzzy efficiencies and fuzzy weights provided extra information to the decision maker, which is not provided by crisp dual SBM model.