Development of intuitionistic fuzzy data envelopment analysis models and intuitionistic fuzzy input–output targets

Abstract

In this paper, we develop intuitionistic fuzzy data envelopment analysis (IFDEA) and dual IFDEA (DIFDEA) models based on $\alpha$- and $\beta$-cuts. We determine intuitionistic fuzzy (IF) efficiencies based on $\alpha$- and $\beta$-cuts. We develop an IF correlation coefficient (IFCC) between IF variables to validate the DIFDEA models. We propose an index ranking approach to rank the decision making units (DMUs). Also, we propose an approach to find the IF input–output targets which help to make inefficient DMUs as efficient DMUs in IF environment. Finally, an example and a health sector application are presented to illustrate and compare the proposed methods.

1 Introduction

Data envelopment analysis (DEA) is a linear programming based nonparametric technique for measuring the relative efficiencies of decision making units (DMUs) which utilize multiple inputs to produce multiple outputs. Charnes et al. (1978) proposed the CCR DEA model which determines the performance efficiencies of DMUs. DMUs can be any governmental agencies and nonprofitable organizations like hospitals, educational institutions, banks, transportation etc. The relative performance efficiency of a DMU is defined as the ratio of its performance efficiency to the largest performance efficiency. The relative performance efficiency of a DMU lies in the range (0, 1]. There are some studies of crisp DEA in different areas (Banker et al. 1984; Barnum et al. 2011; Charnes et al. 1978; Hollingsworth et al. 1999; Mogha et al. 2014; Ramanathan and Ramanathan 2010).

The conventional DEA is limited to crisp input and crisp output data. But real world applications have some input and/or output data which possess some degree of fluctuation or imprecision or uncertainties. The fluctuation can take the form of intervals, ordinal relations and fuzzy numbers. Fuzzy set theory (Zadeh 1965) is an important tool to handle fluctuations/uncertainties in real world problems. There are some studies of fuzzy DEA (FDEA) in different areas (Moheb-Alizadeh et al. 2011; Dotoli et al. 2015; Jahanshahloo et al. 2009; Kao and Liu 2000; Tsai et al. 2010). In fuzzy set theory, sum of the degree of membership (acceptance) and degree of non-membership (rejection) of an element is equal to one, i.e. the rejection value is equal to one minus the acceptance value (Zou et al. 2016). But in real world problems, there is possibility that the sum of the acceptance and rejection values of an element may come out to be less than one. Thus, there remains some degree of hesitation. Fuzzy set theory (Zimmermann 2011) is not appropriate to deal with such problems; rather intuitionistic fuzzy set (IFS) theory is more suitable.

IFS theory, proposed by Atanassov (1986), is an extension of fuzzy set theory and has been found to be more useful to deal with vagueness/uncertainty. The IFS considers both the acceptance value and rejection value of an element such that the sum of both values is less than one, i.e. it may have hesitation. Since its invention/inception, the IFS theory has received more and more attention and has been used in a wide range of applications, such as reliability (Shu et al. 2006), logic programming (Atanassov and Gargov 1998), decision making (Li 2005), medical diagnosis (De et al. 2001), and pattern recognition (Dengfeng and Chuntian 2002). Puri and Yadav (2015) proposed an intuitionistic fuzzy optimistic and pessimistic DEA models. Otay et al. (2017) proposed a new multi-expert IFDEA and IF analytic hierarchy process (IF-AHP) to determine the performance evaluation of healthcare institutions. Hajiagha et al. (2013) proposed IFDEA model with IF inputs and IF outputs using the aggregation operator.

Beauty of IFS theory over fuzzy set theory is that IFS theory separates the degree of membership (acceptance) and the degree of non-membership (rejection) of an element in the set. With the help of IFS theory, we can decide about the degree of acceptance, degree of rejection and degree of hesitation for some quantity. For example, in health sector, there exist two inputs: (i) number of beds and (ii) sum of number of pathologists and laboratory technicians and two outputs: (i) number of pathology operations and (ii) sum of number of plaster and tubal ligation which possess some degree of hesitation due to the difference in thought at the management level and the hospital level. Moreover, under the mentioned reasons, hospital management would be more interested in running a hospital with less number of beds, pathologist and doctors (employees) in order to reduce the cost on beds, pathologist and doctors, whereas the hospital manager may be interested in having more beds, pathologist and doctors at the disposal of the hospital in order to accommodate more patients, handle day-to-day increased workload and overcome the profit reductions due to the inefficiency of some existing beds, pathologist and doctors, i.e. the number of beds, pathologist and doctors is likely to be an undesirable attribute for the hospital management, however a desirable attribute for the hospital manager. So, the difference of thought at management level and hospital level may lead to the existence of hesitation in the patients, and availability of beds, pathologist and doctors at hospital level. This hesitation is responsible for both the membership and non-membership degrees of the data for the number of beds and doctors of a hospital. Hence, the number of beds, pathologist and doctors possesses IF behaviour at hospital level and thus can be taken as IF input in DEA. The inputs and outputs possess some degree of hesitation due to the difference in thought at the management level and the actual hospital level. So, uncertainty in inputs and outputs can be well taken as IFN.

In this paper, we develop DIFDEA models using $\alpha -,\,\beta$-cut to determine the IF efficiency and IF correlation coefficient (IFCC) between IF variables and propose a ranking approach to rank the DMUs. Also, this study determines the IF input target and IF output target for inefficient DMUs.

The rest of the paper is organized as follows: Section 2 presents the preliminaries. Section 3 presents the extension of DEA to DIFDEA. Section 4 presents the proposed IFCC to validate the proposed DIFDEA models. Section 5 presents the proposed IF ranking approach. Section 6 presents the illustrative example and a health sector application. Last section of the paper concludes the findings of this paper.

2 Preliminaries

This section includes some basic definitions and notions.

Definition 1

(Arya and Yadav (2017)) The performance efficiency of a DMU is defined as the ratio of the weighted sum of outputs (called virtual output) to the weighted sum of inputs (called virtual input). Thus,

$$\begin{aligned} \hbox {Performance efficiency} =\dfrac{virtual\,\, \text{ output }}{virtual\,\, \text{ input }}. \end{aligned}$$

The relative performance efficiency of a DMU is defined as the ratio of its performance efficiency to the largest performance efficiency. The relative performance efficiency of a DMU lies in the range (0, 1]. DEA evaluates the relative performance efficiency of a set of homogeneous DMUs (Arya and Yadav 2017).

Definition 2

(Zimmermann 2011) A fuzzy number (FN) $\tilde{A}$ is defined as a convex normalized fuzzy set $\tilde{A}$ of the real line $\mathbb R$ with membership function $\mu _{\tilde{A}}$ such that

• there exists exactly one $x_0\in \mathbb R$ with $\mu _{\tilde{A}}(x_0)=1$. $x_0$ is called the mean value of $\tilde{A}$,

• $\mu _{\tilde{A}}$ is a piecewise continuous function on $\mathbb R$.

Definition 3

(Arya and Yadav 2017) The triangular FN (TFN) $\tilde{A}$ is a FN denoted by $\tilde{A} =(a^l,a^m,a^u)$ and is defined by the membership function $\mu _{\tilde{A}}$ given by

$$\begin{aligned} \mu _{\tilde{A}}(x)=\left\{ \begin{array}{ll} \dfrac{x-a^l}{a^m-a^l},&{}\quad a^l< x\le a^m,\\ \dfrac{a^u-x}{a^u-a^m},&{}\quad a^m\le x < a^u, \\ 0, &{}\quad {\text{ elsewhere }}, \end{array} \right. \end{aligned}$$

for all $x \in \mathbb {R}$, where $a^m$ is called the modal value and $(a^l,a^u)$ is called support of the TFN $(a^l,a^m,a^u)$.

Definition 4

(Arithmetic operations on TFN)  (Arya and Yadav 2017) Let $\tilde{A_1}= ({a_1}^l,{a_1}^{m},{a_1}^u)$ and $\tilde{A_2}= ({a_2}^{l},{a_2}^{m},{a_2}^{u})$ be two TFNs. Then, the arithmetic operations on TFNs are given as follows:

• Adition: $\tilde{A_1}\oplus \tilde{A_2}= ({a_1}^l+{a_2}^{l},{a_1}^{m}+{a_2}^m,{a_1}^u+{a_2}^{u})$.

• Subtraction: $\tilde{A_1}\ominus \tilde{A_2}= ({a_1}^l-{a_2}^{u},{a_1}^{m}-{a_2}^m,{a_1}^u-{a_2}^{l})$.

• Multiplication: $\tilde{A_1} \otimes \tilde{A_2}\approx (min ({a_1}^l{a_2}^{l},{a_1}^{l}{a_2}^{u},{a_1}^u{a_2}^{l}, {a_1}^u{a_2}^{u}),{a_1}^{m}{a_2}^m,max ({a_1}^l{a_2}^{l},{a_1}^{l}{a_2}^{u},{a_1}^u{a_2}^{l}, {a_1}^u{a_2}^{u}))$.

• Scalar multiplication:

  $$\begin{aligned} \lambda {\tilde{A_1}}=\left\{ \begin{array}{ll} (\lambda {a_1}^l,\lambda {a_1}^m,\lambda {a_1}^u),&{}\quad {\text{ for }} \quad \lambda \ge 0,\\ (\lambda {a_1}^u,\lambda {a_1}^m,\lambda {a_1}^l),&{}\quad {\text{ for }} \quad \lambda <0. \\ \end{array} \right. \end{aligned}$$

Definition 5

(Intuitionistic fuzzy set (IFS))  (Arya and Yadav 2018) Let us suppose that X is a universe of discourse. Then, an IFS in X is denoted by $\tilde{A}^I$ and is defined by $\tilde{A}^I= \{(x,{\mu _{\tilde{A}^I}(x)},{\nu _{\tilde{A}^I}(x)})\,\forall x \in X \}$, where $\mu _{\tilde{A}^I}: X \rightarrow [0,1]$ and $\nu _{\tilde{A}^I}: X \rightarrow [0,1]$ represent the membership and non-membership functions, respectively, of an element x in $\tilde{A}^I$. The values $\mu _{\tilde{A}^I}(x)$ and $\nu _{\tilde{A}^I}(x)$ represent the membership and non-membership values of x being in $\tilde{A}^I$ with the condition that $0 \le \mu _{\tilde{A}^I}(x)+\nu _{\tilde{A}^I}(x) \le 1$. The hesitation (indeterminacy) degree of an element x being in $\tilde{A}^I$ is defined as $\pi _{\tilde{A}^I}(x)=1-\mu _{\tilde{A}^I}(x)-\nu _{\tilde{A}^I}(x)$$\forall x\in X$. Obviously $0\le \pi _{\tilde{A}^I}(x)\le 1$. If $\pi _{\tilde{A}^I}(x)=0$, then $\tilde{A}^I$ is reduced to a fuzzy set.

Definition 6

(Normal IFS)  (Arya and Yadav 2018) Let $\tilde{A}^I=\{(x,{\mu _{\tilde{A}^I}(x)},{\nu _{\tilde{A}^I}(x)}):x \in X\}$ be an IFS. Then, $\tilde{A}^I$ is called the normal IFS if $\exists$ an $x\in X$ such that $\mu _{\tilde{A}^I}(x)=1$ and $\nu _{\tilde{A}^I}(x)=0$.

Definition 7

(Convex IFS)  (Arya and Yadav 2018) Let $\tilde{A}^I=\{(x,{\mu _{\tilde{A}^I}(x)},{\nu _{\tilde{A}^I}(x)}):x \in X\}$ be an IFS. Then, $\tilde{A}^I$ is called the Convex IFS if

• (i) min $(\mu _{\tilde{A}^I}(x),\mu _{\tilde{A}^I}(y)) \le \mu _{\tilde{A}^I}(\lambda x+(1-\lambda )y)$, $\forall x,y \in X$ and $\lambda \in [0,1]$, i.e., $\mu _{\tilde{A}^I}$ is quasi-concave function over X.

• (ii) max $(\nu _{\tilde{A}^I}(x),\nu _{\tilde{A}^I}(y)) \!\ge \! \nu _{\tilde{A}^I}(\lambda x+(1\!-\!\lambda )y)$, $\forall x,y \!\in \! X$ and $\lambda \!\in \! [0,1]$, i.e., $\nu _{\tilde{A}^I}$ is quasi-convex function over X.

Definition 8

($\alpha$-cut)  The $\alpha$-cut of an IFS $\tilde{A}^I$ is denoted by $A^I_{\alpha }$ and defined as $A^I_{\alpha }=\{x:\mu _{\tilde{A}^I}(x) \ge \alpha \};\,\,\alpha \in [0,1]$.

Definition 9

($\beta$-cut)  The $\beta$-cut of an IFS $\tilde{A}^I$ is denoted by $B^I_{\beta }$ and defined as $B^I_{\beta }=\{x:\nu _{\tilde{A}^I}(x) \le \beta \};\,\,\beta \in [0,1]$.

Definition 10

(Intuitionistic fuzzy number (IFN))  (Arya and Yadav 2018) The IFN is an extension of a FN (Zimmermann 2011) in IF environment. This is defined as follows:

Let $\tilde{A}^I=\{(x,\mu _{\tilde{A}^I}(x),\nu _{\tilde{A}^I}(x)):x \in \mathbb {R}\}$ be an IFS, where $\mathbb R$ is the set of all real numbers. Then, $\tilde{A}^I$ is called the IFN if the following conditions hold:

• (i) There exists a unique $x_0 \in \mathbb R$ such that $\mu _{\tilde{A}^I}(x_0)=1$ and $\nu _{\tilde{A}^I}(x_0)=0,$

• (ii) $\tilde{A}^I$ is convex IFS,

• (iii) $\mu _{\tilde{A}^I}$ and $\nu _{\tilde{A}^I}$ are piecewise continuous functions on $\mathbb {R}$.

Mathematically, an IFS $\tilde{A}^I=\{(x,\mu _{\tilde{A}^I}(x),\nu _{\tilde{A}^I}(x)):x \in \mathbb {R}\}$ is an IFN if $\mu _{\tilde{A}^I}$ and $\nu _{\tilde{A}^I}$ are piecewise continuous functions from $\mathbb {R}$ to [0, 1] and $0\le \mu _{\tilde{A}^I}(x)+\nu _{\tilde{A}^I}(x)\le 1,\,\,\forall x \in \mathbb {R}$ given by

$$\begin{aligned} \mu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} g_1(x),&{}\quad a^l \le x< a^{m},\\ 1,&{}\quad x = a^m, \\ h_1(x), &{}\quad a^{m}< x \le a^u ,\\ 0,&{}\quad {\hbox {elsewhere}}, \end{array} \right. \\\ \nu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} g_2(x),&{}\quad a^{'l} \le x< a^{m},\\ 0,&{}\quad x= a^{m}, \\ h_2(x), &{}\quad a^{m} < x \le a^{'u}, \\ 1,&{}\quad {\hbox {elsewhere}}, \end{array} \right. \end{aligned}$$

where $a^{m}$ is called the mean value of $\tilde{A}^I;\, a^m-a^l$ and $a^u-a^m$ are called the left and right hand spreads of membership function $\mu _{\tilde{A}^I}$, respectively; $a^m-a^{'l}$ and $a^{'u}-a^m$ are called the left and right hand spreads of hesitation function $\pi _{\tilde{A}^I}$, respectively; $g_1$ and $h_1$ are called piecewise continuous, increasing and decreasing functions in $[a^l,a^m)$ and $(a^m,a^u]$, respectively; and $g_2$ and $h_2$ are called piecewise continuous, strictly increasing and strictly decreasing functions in $[a^{'l},a^m)$ and $(a^m,a^{'u}]$, respectively. The IFN $\tilde{A}^I$ is represented by $\tilde{A}^I=(a^l,a^m,a^u;a^{'l},a^m,a^{'u})$, where $a^{'l}\le a^l \le a^m \le a^u \le a^{'u}$. Its graphical representation is given in Figure 1.

Fig. 1

Membership and non-membership functions of IFN $\tilde{A}^I$

Remark 1

For an IFN $\tilde{A}^I$, the $\alpha$- and $\beta$-cuts are closed intervals as follows:

• $A^I_{\alpha }=\{x:\mu _{\tilde{A}^I}(x) \ge \alpha \}=[a(\alpha ),b(\alpha )];\,\,\alpha \in (0,1]$,

• $B^I_{\beta }=\{x:\nu _{\tilde{A}^I}(x) \le \beta \}=[a'(\beta ),b'(\beta )];\,\,\beta \in [0,1)$,

where $a(\alpha ),\,\,b'(\beta )$ are increasing functions of $\alpha$ and $\beta$, respectively, and $b(\alpha ),\,\,a'(\beta )$ are decreasing functions of $\alpha$ and $\beta$, respectively.

Definition 11

(Triangular intuitionistic fuzzy number (TIFN))  (Arya and Yadav 2018) The TIFN $\tilde{A}^I=(a^l,a^{m},a^u;a^{'l},a^{m},a^{'u})$ is an IFN with the membership function $\mu _{\tilde{A}^I}$ and non-membership function $\nu _{\tilde{A}^I}$ given by

$$\begin{aligned} \mu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} \dfrac{x-a^l}{a^{m}-a^l},&{}\quad a^l< x \le a^{m},\\ \dfrac{a^u-x}{a^u-a^{m}}, &{}\quad a^{m} \le x< a^u, \\ 0, &{}\quad {\hbox {elsewhere}}, \end{array} \right. \\ \nu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} \dfrac{x-a^{m}}{a^{'l}-a^{m}},&{}\quad a^{'l}< x \le a^{m},\\ \dfrac{a^{m}-x}{a^{m}-a^{'u}}, &{}\quad a^{m} \le x <a^{'u}, \\ 1,&{}\quad {\hbox {elsewhere}}, \end{array} \right. \end{aligned}$$

where $a^l,a^{m},a^u,a^{'l},a^{'u} \in \mathbb R$ such that $a^{'l} \le a^l \le a^{m} \le a^u \le a^{'u}$. Its graphical representation is given in Figure 2.

Fig. 2

TIFN $\tilde{A}^I= (a^l,a^m,a^u;a'^l,a^m,a'^u)$

Definition 12

(Positive IFN)  Let $\tilde{A}^I= (a^l,a^{m},a^u;{a'}^l,a^{m},{a'}^u)$ be an IFN. Then, $\tilde{A}^I$ is called a positive IFN if $a'^l >0$.

Definition 13

(Arithmetic operations on TIFN)  (Arya and Yadav 2018) Let $\tilde{A_1}^I= ({a_1}^l,{a_1}^{m},{a_1}^u;{a_1}^{'l},{a_1}^{m},{a_1}^{'u})$ and $\tilde{A_2}^I= ({a_2}^l,{a_2}^{m},{a_2}^u;{a_2}^{'l},{a_2}^{m},{a_2}^{'u})$ be two TIFNs. Then, the arithmetic operations on TIFNs are given as follows:

• (i) Addition: $\tilde{A_1}^I\oplus \tilde{A_2}^I= ({a_1}^l+{a_2}^l,{a_1}^{m}+{a_2}^m,{a_1}^u+{a_2}^u;{a_1}^{'l}+{a_2}^{'l},{a_1}^{m}+{a_2}^m,{a_1}^{'u}+{a_2}^{'u})$.

• (ii) Multiplication: $\tilde{A_1}^I \otimes \tilde{A_2}^I\approx ({a_1}^l{a_2}^l,{a_1}^{m}{a_2}^m,{a_1}^u{a_2}^u; {a_1}^{'l}{a_2}^{'l},{a_1}^{m}{a_2}^m, {a_1}^{'u}{a_2}^{'u})$, where $\tilde{A_1}^I,\,\tilde{A_2}^I >0$.

• (iii) Scalar multiplication: If $\lambda \in \mathbb R$, then

  $$\begin{aligned} \lambda {\tilde{A_1}^I}=\left\{ \begin{array}{ll} (\lambda {a_1}^l,\lambda {a_1}^m,\lambda {a_1}^u;\lambda {a_1}^{'l},\lambda {a_1}^m, \lambda {a_1}^{'u}),\, \,\lambda \ge 0,\\ (\lambda {a_1}^u,\lambda {a_1}^m,\lambda {a_1}^l;\lambda {a_1}^{'u},\lambda {a_1}^m, \lambda {a_1}^{'l}),\, \,\lambda \le 0. \\ \end{array} \right. \end{aligned}$$

3 Extension of DEA to DIFDEA models

DEA is a linear programming based methodology to measure the relative efficiencies of DMUs when the production process consists of multiple inputs and outputs. Assume that the performance of a set of n homogeneous DMUs (DMUj; $j = 1,2,3,\ldots ,n$) is to be measured (Arya and Yadav 2017). Let us suppose that each DMU utilizes m inputs to produce s outputs. Consider the jth DMU: $\mathrm{{DMU}}_{j}, \,j=1,2,3,...,n$. Let $x_{ij}$ be the amount (value) of the ith input utilized and $y_{rj}$ be the amount (value) of the rth output produced by the jth DMU, $j = 1,2,3,\ldots ,n, \ i = 1,2,3,\ldots ,m, \ r = 1,2,3,\ldots ,s$.

Then, the efficiency of $\mathrm{{DMU}}_{j}$ is given by Charnes et al. (1978)

$$\begin{aligned} E_j=\dfrac{\sum \limits _{r=1}^{s}{{v_{rj}}{y_{rj}}}}{\sum \limits _{i=1}^{m}{{u_{ij}}{x_{ij}}}}, \quad j=1,2,\ldots ,n, \end{aligned}$$

where $u_{ij}$ and $v_{rj}$ are the weights corresponding to ith input and rth output of $\mathrm{{DMU}}_j$, respectively.

In the CCR fractional program (FP) (Charnes et al. 1978), the efficiency of the $\mathrm{{DMU}}_{jo}$ is to be maximized subject to the condition that the ratio of the virtual output to the virtual input of every DMU should be less than or equal to unity. The CCR (ratio) fractional DEA program and the corresponding linear program (LP) for $\mathrm{{DMU}}_{j_o}$ are given in Table 1. In these models, the efficiency of $\mathrm{{DMU}}_{jo}$ is denoted by $E_{j_o}$ and $\varepsilon > 0$ is a non-Archimedean infinitesimal constant.

Table 1 Crisp DEA Models: Fractional and LP forms

If DMUs have IF input and IF output data, then we develop intuitionistic fuzzy DEA (IFDEA) models to determine the efficiencies of DMUs. Assume that the performance of $\mathrm{{DMU}}_j$ ($j=1,2,\ldots ,n$) is characterized by a production process of m IF inputs $\tilde{x}_{ij}^I; i = 1, 2, 3, \ldots , m$ to yield s IF outputs $\tilde{y}_{rj}^I; r = 1, 2, 3, \ldots ,s$. Let IF efficiency of $\mathrm{{DMU}}_{j_o}$ be represented by $\tilde{E}_{j_o}^I$. Then, IFDEA model (Model 1) is given as follows:

Model 1 :

(IFDEA)

$$\begin{aligned}&\max \tilde{E}_{j_o}^I=\sum _{r=1}^{s}{v_{rj_o}}{\tilde{y}_{rj_o}^I}\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}}{\tilde{x}_{ij_o}^I}=\tilde{1}^I,\\&\sum _{r=1}^{s}{v_{rj_o}}{\tilde{y}_{rj}^I}-\sum _{i=1}^{m}{u_{ij_o}}{\tilde{x}_{ij}^I}\le \tilde{0}^I, \,\,j=1,2,3,\ldots ,n, \\&u_{ij_o},v_{rj_o}{\ge }\varepsilon , \ \forall {i{=}1,2,3,\ldots ,m;} \ \forall {r{=}1,2,3,\ldots ,s;}\,\,\varepsilon \\&\quad >0 \text{ is } \text{ a } \text{ non-Archimedean } \text{ infinitesimal } \text{ constant }, \end{aligned}$$

where $u_{ij_o}$ and $v_{rj_o}$ are the weights corresponding to the ith IF input and rth IF output, respectively.

3.1 Methodology for solving IFDEA model

Assume that IF input ${\tilde{x}_{ij}}^I$ and IF output ${\tilde{y}_{rj}}^I$ are TIFNs. Let $\tilde{x}_{ij}^I={(x_{ij}^L,x_{ij}^{M},x_{ij}^U;x_{ij}'^L,x_{ij}^{M},x_{ij}'^U)}$ and $\tilde{y}_{rj}^I=(y_{rj}^L,y_{rj}^{M},y_{rj}^U;y_{rj}'^L,y_{rj}^{M},y_{rj}'^U)$. Then, Model 1 is transformed to the following model (Model 2):

Model 2 :

$$\begin{aligned}&\max \tilde{E}_{j_o}^I=\sum _{r=1}^{s}{v_{rj_o}}{ {\left( y_{rj_o}^L,y_{rj_o}^{M},y_{rj_o}^U;y_{rj_o}'^L,y_{rj_o}^{M},y_{rj_o}'^U\right) }}\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}}{ {\left( x_{ij_o}^L,x_{ij_o}^{M},x_{ij_o}^U;x_{ij_o}'^L,x_{ij_o}^{M},x_{ij_o}'^U\right) }}=(1,1,1;1,1,1),\\&\sum _{r=1}^{s}{v_{rj_o}}{{\left( y_{rj}^L,y_{rj}^{M},y_{rj}^U;y_{rj}'^L,y_{rj}^{M},y_{rj}'^U\right) }}\\&\qquad -\sum _{i=1}^{m}{u_{ij_o}}{{\left( x_{ij}^L,x_{ij}^{M},x_{ij}^U;x_{ij}'^L,x_{ij}^{M},x_{ij}'^U\right) }}\\&\quad \le (0,0,0;0,0,0),\, j=1,2,3,\ldots ,n, \\&u_{ij_o},v_{rj_o}\ge \varepsilon , \,\forall {i,r}. \end{aligned}$$

3.2 Models based on $\alpha$-cut

Replacing IF input $\tilde{x}_{ij}^I$ and IF output $\tilde{y}_{rj}^I$ by their $\alpha$-cuts $[\alpha x_{ij}^M+(1-\alpha )x_{ij}^L,\alpha x_{ij}^M+(1-\alpha )x_{ij}^U]$ and $[\alpha y_{rj}^M+(1-\alpha )y_{rj}^L,\alpha y_{rj}^M+(1-\alpha )y_{rj}^U]$, respectively. Let the $\alpha$-cut of $\tilde{E}_{j_o}^I$ be $[E_{j_o,\alpha }^L,E_{j_o,\alpha }^U]$. Then, Model 2 is reduced to the following model (Model 3):

Model 3 :

$$\begin{aligned}&\max \left[ E_{j_o,\alpha }^L,E_{j_o,\alpha }^U\right] =\sum _{r=1}^{s}{v_{rj_o}}\left[ \alpha y_{rj_o}^M \right. \\&\quad \left. +(1-\alpha )y_{rj_o}^L, \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^U\right] \\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}}{\left[ \alpha x_{ij_0}^M{+}(1-\alpha )x_{ij_o}^L,\alpha x_{ij_o}^M{+}(1-\alpha )x_{ij_o}^U\right] }{=}[1,1],\\&\sum _{r=1}^{s}{v_{rj_o}}{\left[ \alpha y_{rj}^M+(1-\alpha )y_{rj}^L,\alpha y_{rj}^M+(1-\alpha )y_{rj}^U\right] }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}}{\left[ \alpha x_{ij}^M+(1-\alpha )x_{ij}^L,\alpha x_{ij}^M+(1-\alpha )x_{ij}^U\right] } \\&\le [0,0], \,\,j=1,2,3,\ldots ,n, \\&u_{ij_o},v_{rj_o}\ge \varepsilon , \,\forall {i,r}. \end{aligned}$$

Model 3 is given in lower and upper bound model. The lower bound model of Model 3 is given as below:

Model 4 :

$$\begin{aligned}&\max E_{j_o,\alpha }^L=\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^L\right) }\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^U\right) }=1,\\&\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^L\right) }\\&\qquad -\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^U\right) }\le 0,\\&\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj}^M+(1-\alpha )y_{rj}^U\right) }\\&\qquad -\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij}^M+(1-\alpha )x_{ij}^L\right) } \\&\quad \le 0, \,\,j=1,2,3,\ldots ,n,\ j\ne j_o, \\&u_{ij_o},v_{rj_o}\ge \varepsilon , \,\forall {i,r}. \end{aligned}$$

Model 4 is a DEA model, and the levels of inputs and outputs are now adjusted unfavourably to the evaluated $\mathrm{{DMU}}_{j_o}$ and in favour of the other DMUs. For $\mathrm{{DMU}}_{j_o}$, the outputs are adjusted at their lower bounds and the inputs are adjusted at their upper bounds. For other DMUs, the outputs are adjusted at their upper bounds and the inputs are favourably adjusted at their lower bounds. Thus, the $\mathrm{{DMU}}_{j_o}$ comes to the worst possible position compared with other DMUs based on $\alpha$-cut.

The upper bound model of Model 3 is given as below:

Model 5 :

$$\begin{aligned}&\max E_{j_o,\alpha }^U=\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^U\right) }\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^L\right) }=1,\\&\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^U\right) }\\&\qquad -\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^L\right) }\le 0, \\&\sum _{r=1}^{s}{v_{rj_o}}{\left( \alpha y_{rj}^M+(1-\alpha )y_{rj}^L\right) }\\&\qquad -\sum _{i=1}^{m}{u_{ij_o}}{\left( \alpha x_{ij}^M+(1-\alpha )x_{ij}^U\right) } \\&\quad \le 0, \,\,j=1,2,3,\ldots ,n, \ j\ne j_o, \\&u_{ij_o},v_{rj_o}\ge \varepsilon , \, \forall {i,r} . \end{aligned}$$

Model 5 is also a DEA model, where the levels of inputs and outputs are adjusted in favour of the evaluated $\mathrm{{DMU}}_{j_o}$ and in unfavour of other DMUs. For the evaluated DMU, the outputs are adjusted at their upper bounds and the inputs are adjusted at their lower bounds. Unfavourably for the other DMUs, the outputs are adjusted at their lower bounds and the inputs are adjusted at their upper bounds. Thus, the $\mathrm{{DMU}}_{j_o}$ comes to the best possible position compared with the other DMUs based on $\alpha$-cut.

The dual of Model 4 is written as follows:

Model 6 :

$$\begin{aligned}&\min \xi _{j_o,\alpha }^L=\theta _{j_o}^L-\epsilon \left( \sum _{r=1}^{s}{S_{rj_o,\alpha }^{+}}+\sum _{i=1}^{m}{S_{ij_o,\alpha }^{-}}\right) \\&\text{ subject } \text{ to } \\&\theta _{j_o}^L \left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^U\right) -\lambda _ {j_o}^L\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^U\right) \\&\quad -\sum _{j=1,\ne j_o}^{n}{\lambda _j^L\left( \alpha x_{ij}^M+(1-\alpha )x_{ij}^L\right) }-S_{ij_o,\alpha }^{-}= 0,\,\forall i\\&\lambda _{j_o}^L\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^L\right) +\sum _{j=1,\ne j_o}^{n}{{\lambda _{j}^L}{\left( \alpha y_{rj}^M+(1-\alpha )y_{rj}^U\right) }}\\&\quad -S_{rj_o,\alpha }^{+}= \left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^L\right) ,\,\forall r\\&\lambda _{j}^L,\,S_{ij_o,\alpha }^{-},\,S_{rj_o,\alpha }^{+}\ge 0, \,\forall j=1,2,3,\ldots ,n, \\&\quad j\ne j_o, \, \theta _{j_o}^L \text{ is } \text{ unrestricted } \text{ in } \text{ sign }. \end{aligned}$$

In Model 6, $S_{ij_o,\alpha }^{-}$ and $S_{rj_o,\alpha }^{+}$ are the slack variables, $\lambda _{j}^L$ is the non-negative dual variable corresponding to the jth primal (Model 4) constraints, =1,2,3,...,n and $\theta _{j_o}^L$ is unrestricted dual variable corresponding to the equation constraint in the primal problem (Model 4).

The dual of Model 5 is written as follows:

Model 7 :

$$\begin{aligned}&\min \xi _{j_o,\alpha }^U=\theta _{j_o}^U-\varepsilon \left( \sum _{r=1}^{s}{S_{rj_o,\alpha }^{+}}+\sum _{i=1}^{m}{S_{ij_o,\alpha }^{-}}\right) \\&\text{ subject } \text{ to } \\&\theta _{j_o}^U\left( \alpha x_{ij_o}^M+(1-\alpha )x_{ij_o}^L\right) -\lambda _{j_o}^U\left( \alpha x_{ij_0}^M+(1-\alpha )x_{ij_o}^L\right) \\&\quad -\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^U\left( \alpha x_{ij}^M+(1-\alpha )x_{ij}^U\right) }-S_{ij_o,\alpha }^{-}= 0,\,\forall i\\&\lambda _{j_o}^U\left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^U\right) +\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^U{\left( \alpha y_{rj}^M+(1-\alpha )y_{rj}^L\right) }}\\&\quad -S_{rj_o,\alpha }^{+}= \left( \alpha y_{rj_o}^M+(1-\alpha )y_{rj_o}^U\right) ,\,\forall r\\&\lambda _{j}^U,\,S_{ij_o,\alpha }^{-} ,\,S_{rj_o,\alpha }^{+}\ge 0, \,\forall j,\, \, \theta _{j_o}^U \text{ is } \text{ unrestricted } \text{ in } \text{ sign }, \end{aligned}$$

where $\lambda _{j}^U$ is the non-negative dual variable corresponding to the jth primal (Model 5) constraints, j=1,2,3,...,n and $\theta _{j_o}^U$ is unrestricted dual variable corresponding to the equation constraint in the primal problem (Model 5). Models 6 and 7 are the proposed DIFDEA models based on $\alpha$-cut and will be denoted as $PDIFDEA_{j_o,\alpha }$.

Definition 14

Efficient and inefficient DMUs based on $\alpha$-cut,

• $\mathrm{{DMU}}_{j_o}$ is fully efficient if $\xi _{j_o,\alpha }^{L*}=1$ for any $\alpha \in (0,1]$.

• $\mathrm{{DMU}}_{j_o}$ is efficient if $\xi _{j_o,\alpha }^{U*}=1$ and $\xi _{j_o,\alpha }^{L*}<1$ for any $\alpha \in (0,1]$.

• $\mathrm{{DMU}}_{j_o}$ is inefficient if $\xi _{j_o,\alpha }^{U*}<1$ for any $\alpha \in (0,1]$.

Axiom 3.1

The lower bound efficiency is less than or equal to upper bound efficiency of $\mathrm{{DMU}}_{j_o}$, i.e. $\xi _{j_o,\alpha }^{L*}\le \xi _{j_o,\alpha }^{U*} \forall \alpha \in (0,1]$.

3.3 Models based on $\beta$-cut

Replacing IF input $\tilde{x}_{ij}^I$ and IF output $\tilde{y}_{rj}^I$ by their $\beta$-cuts ${\tilde{x}_{ij}}^I={[\beta {x_{ij}'^L}+ (1-\beta ){x_{ij}^M}, \beta {x_{ij}'^U}+ (1-\beta ){x_{ij}^M}]}$ and ${\tilde{y}_{rj}}^I = {[ \beta {y_{rj}'^L}+(1-\beta ){y_{rj}^M}, \beta {y_{rj}'^U}+(1-\beta ){y_{rj}^M}]}$, respectively, Model 2 is reduced to the following model:

Model 8 :

$$\begin{aligned}&\max \left[ E_{j_o,\beta }^L,E_{j_o,\beta }^U\right] =\sum _{r=1}^{s}{v_{rj_o}'}\left[ \beta {y_{rj_o}'^L}\right. \\&\quad \left. +(1-\beta ){y_{rj_o}^M}, \beta {y_{rj_o}'^U}+(1-\beta ){y_{rj_o}^M}\right] \\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}'}{\left[ \beta {x_{ij_o}'^L}+ (1-\beta ){x_{ij_o}^M}, \beta {x_{ij_o}'^U}+ (1-\beta ){x_{ij_o}^M}\right] }=[1,1],\\&\sum _{r=1}^{s}{v_{rj_o}'}{\left[ \beta {y_{rj}'^L}+(1-\beta ){y_{rj}^M}, \beta {y_{rj}'^U}+(1-\beta ){y_{rj}^M}\right] }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}'}{\left[ \beta {x_{ij}'^L}+ (1-\beta ){x_{ij}^M}, \beta {x_{ij}'^U}+ (1-\beta ){x_{ij}^M}\right] }\\&\le [0,0], \,\, j=1,2,3,\ldots ,n, \ j\ne j_o, \\&u_{ij_o}',v_{rj_o}'\ge \varepsilon , \,\forall {i,r}. \end{aligned}$$

Model 8 is given in lower and upper bound model. The lower bound model of Model 8 is given as below:

Model 9 :

$$\begin{aligned}&\max E_{j_o,\beta }^L=\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj_o}'^L}+(1-\beta ){y_{rj_o}^M}\right) }\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij_o}'^U}+ (1-\beta ){x_{ij_o}^M}\right) }=1,\\&\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj_o}'^L}+(1-\beta ){y_{rj_o}^M}\right) }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij_o}'^U}+ (1-\beta ){x_{ij_o}^M}\right) }\le 0,\\&\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj}'^U}+(1-\beta ){y_{rj}^M}\right) }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij}'^L}+ (1-\beta ){x_{ij}^M}\right) } \le 0, \\&\quad j=1,2,3,\ldots ,n, \ j\ne j_o, \ u_{ij_o}',v_{rj_o}'\ge \varepsilon , \,\forall {i,r} . \end{aligned}$$

Model 9 is a DEA model, the levels of inputs and outputs are now adjusted unfavourably to the evaluated $\mathrm{{DMU}}_{j_o}$ and in favour of the other DMUs. For $\mathrm{{DMU}}_{j_o}$, the outputs are adjusted at their lower bounds and the inputs are adjusted at their upper bounds. For other DMUs, the outputs are adjusted at their upper bounds and the inputs are favourably adjusted at their lower bounds. Thus, the $\mathrm{{DMU}}_{j_o}$ comes to the worst possible position compared to other DMUs based on $\beta$-cut.

The upper bound model of Model 8 is given as below:

Model 10 :

$$\begin{aligned}&\max E_{j_o,\beta }^U=\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj_o}'^U}+(1-\beta ){y_{rj_o}^M}\right) }\\&\text{ subject } \text{ to } \\&\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij_o}'^L}+ (1-\beta ){x_{ij_o}^M}\right) }=1,\\&\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj_o}'^U}+(1-\beta ){y_{rj_o}^M}\right) }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij_o}'^L}+ (1-\beta ){x_{ij_o}^M}\right) }\le 0,\\&\sum _{r=1}^{s}{v_{rj_o}'}{\left( \beta {y_{rj}'^L}+(1-\beta ){y_{rj}^M}\right) }\\&\quad -\sum _{i=1}^{m}{u_{ij_o}'}{\left( \beta {x_{ij}'^U}+ (1-\beta ){x_{ij}^M}\right) }\le 0, \\&\quad j=1,2,\ldots ,n, \ j\ne j_o, \ u_{ij_o}',v_{rj_o}'\ge \varepsilon , \,\forall {i,r} . \end{aligned}$$

Model 10 is also a DEA model, where the levels of inputs and outputs are adjusted in favour of the evaluated $\mathrm{{DMU}}_{j_o}$ and in unfavour of other DMUs. For the evaluated $\mathrm{{DMU}}_{j_o}$, the outputs are adjusted at their upper bounds and the inputs are adjusted at their lower bounds. Unfavourably for the other DMUs, the outputs are adjusted at their lower bounds and the inputs are adjusted at their upper bounds. Thus, the $\mathrm{{DMU}}_{j_o}$ comes to the best possible position compared to other DMUs based on $\beta$-cut.

The dual of Model 9 is written as follows:

Model 11 :

$$\begin{aligned}&\min \xi _{j_o,\beta }^{'L}=\theta _{j_o}^{'L}-\epsilon \left( \sum _{r=1}^{s}{S_{rj_o}^{+}}+\sum _{i=1}^{M}{S_{ij_o}^{-}}\right) \\&\text{ subject } \text{ to } \\&\theta _{j_o}^{'L}\left( \beta {x_{ij_o}'^U}+ (1-\beta ){x_{ij_o}^M}\right) - \lambda _{j_o}^{'L}\left( \beta {x_{ij_o}'^U}- (1-\beta ){x_{ij_o}^M}\right) \\&\quad -\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^{'L}\left( \beta {x_{ij}'^L}+ (1-\beta ){x_{ij}^M}\right) }-S_{ij_o,\beta }^{-}= 0,\,\forall i\\&\lambda _{j_o}^{'L}\left( \beta {y_{rj_o}'^L}+(1-\beta ){y_{rj_o}^M}\right) +\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^{'L}{\left( \beta {y_{rj}'^U}+(1-\beta ){y_{rj}^M}\right) }}\\&\quad -S_{rj_o,\beta }^{+}= \left( \beta {y_{rj_o}'^L}+(1-\beta ){y_{rj_o}^M}\right) ,\,\forall r\\&\lambda _{j}^{'L}\ge 0 \,\,\forall j;\,S_{ij_o}^{-},\,S_{rj_o}^{+}\ge 0, \forall i, r;\,\, \, \theta _{j_o}^{'L} \,\,\text{ is } \text{ unrestricted } \text{ in } \text{ sign }. \end{aligned}$$

The dual of Model 10 is written as follows:

Model 12 :

$$\begin{aligned}&\min \xi _{j_o,\beta }^{'U}=\theta _{j_o}^{'U}-\epsilon \left( \sum _{r=1}^{s}{S_{rj_o}^{+}}+\sum _{i=1}^{m}{S_{ij_o}^{-}}\right) \\&\text{ subject } \text{ to } \\&\theta _{j_o}^{'U} \left( \beta {x_{ij_o}'^L}+ (1-\beta ){x_{ij_o}^M}\right) -\lambda _{j_o}^{'U}\left( \beta {x_{ij_o}'^L}+ (1-\beta ){x_{ij_o}^M}\right) \\&\quad -\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^{'U}\left( \beta {x_{ij}'^U}+(1-\beta ){x_{ij}^M}\right) }-S_{ij_o}^{-}= 0,\,\forall i,\\&\lambda _{j}^{'U}\left( \beta {y_{rj_o}'^U}+(1-\beta ){y_{rj_o}^M}\right) +\sum _{j=1,\ne j_o}^{n}{\lambda _{j}^{'U}{\left( \beta {y_{rj}'^L}+(1-\beta ){y_{rj}^M}\right) }}\\&\quad -S_{rj_o}^{+}= \left( \beta {y_{rj_o}'^U}+(1-\beta ){y_{rj_o}^M}\right) ,\,\forall r,\\&\lambda _{j}^{'U}\ge 0\,\, \forall j; S_{ij_o}^{-},\,S_{rj_o}^{+},\,\ge 0 \,\forall i,r;\, \, \theta _{j_o}^{'U} \,\,\text{ is } \text{ unrestricted } \text{ in } \text{ sign }. \end{aligned}$$

Models 11 and 12 are the proposed dual IFDEA (DIFDEA) models based on $\beta$-cut and will be denoted as $PDIFDEA_{j_o,\beta }$.

Definition 15

Efficient and inefficient DMUs based on $\beta$-cut,

• $\mathrm{{DMU}}_{j_o}$ is fully efficient if $\xi _{j_o,\beta }^{'L*}=1$ for any $\beta \in [0,1)$.

• $\mathrm{{DMU}}_{j_o}$ is efficient if $\xi _{j_o,\beta }^{'U*}=1$ and $\xi _{j_o,\beta }^{'L*}<1$ for any $\beta \in [0,1)$.

• $\mathrm{{DMU}}_{j_o}$ is inefficient if $\xi _{j_o,\beta }^{'U*}<1$ for any $\beta \in [0,1)$.

Axiom 3.2

The lower bound efficiency is less than or equal to upper bound efficiency of $\mathrm{{DMU}}_{j_o}$, i.e. $\xi _{j_o,\beta }^{'L*}\le \xi _{j_o,\beta }^{'U*}\,\, \forall \beta \in [0,1)$.

3.4 IF input targets and IF output targets

The main objective of DEA models is to identify the efficient and inefficient DMUs and to suggest to make the inefficient DMUs as efficient DMUs. An inefficient DMU can become efficient using adjusting inputs (called input targets) and/or adjusting outputs (called output targets). The ith input target and rth output target for $\mathrm{{DMU}}_{j_0}$ are denoted by $\bar{x}_{ij_0}$ and $\bar{y}_{rj_0}$, respectively, and are defined by Agarwal (2014)

$$\begin{aligned} \bar{x}_{ij_0}=\theta _{ij_0}^*x_{ij_0}-S_{ij_0}^-,\,\,\,\bar{y}_{rj_0}=y_{rj_0}+S_{rj_0}^+ \end{aligned}$$

If inputs and outputs are IFNs, then the adjusting IF inputs (called IF input target) and/or adjusting IF outputs (called IF output target) for $\mathrm{{DMU}}_{j_0}$ are denoted by $\bar{\tilde{x_{ij_0}}}^I$ and $\bar{\tilde{y_{rj_0}}}$, respectively, and are defined by

$$\begin{aligned} {\bar{\tilde{x}}}_{ij_0}^I=\tilde{\theta }_{j_0}^{I*}\tilde{x}_{ij_0}^I-S_{ij_0}^-, \,\,\,\bar{\tilde{y_{rj_0}}}^I={\bar{\tilde{y}}}_{rj_0}^I+S_{rj_0}^+. \end{aligned}$$

4 Proposed IF correlation coefficients (IFCCs) to validate the proposed DIFDEA models

Definition 16

(Isotonicity test)  If positive correlation coefficients between input–output data are found (Avkiran et al. 2008), the selection of inputs and outputs is justified.

Avkiran et al. (2008) and Tsai et al. (2006) proposed the isotonicity test to validate the conventional DEA models. Puri and Yadav (2013) proposed the fuzzy correlation coefficients between fuzzy input–output data. In this paper, we are concerned with the evaluation of $\xi _{j_o,\alpha }^L,\xi _{j_o,\alpha }^U,\xi _{j_o,\beta }^{'L}\,and\,\,\xi _{j_o,\beta }^{'U}$ on the basis of the IF input–output data. To ensure the validity of the proposed DIFDEA models, we find the IFCCs between IF variables. To the best of our knowledge, in the literature, nobody has proposed the IFCCs. Therefore, in this paper, we propose the IFCCs between IF variables using expected values (Hung and Wu 2001).

4.1 Expected interval and expected value of an IFN

Let $\tilde{A}^I=(a^m;a^m-a^l,a^u-a^m;a^m-b^l,b^u-a^m)$ be an IFN with membership and non-membership functions $\mu _{\tilde{A}^I}(x)$ and $\nu _{\tilde{A}^I}(x)$, respectively, given by

$$\begin{aligned} \mu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} g_1(x),&{}\quad a^l \le x< a^{m},\\ 1,&{}\quad x = a^m, \\ h_1(x), &{}\quad a^{m}< x \le a^u ,\\ 0,&{}\quad \mathrm{{elsewhere}}. \end{array} \right. \\ \nu _{\tilde{A}^I}(x)= & {} \left\{ \begin{array}{ll} g_2(x),&{}\quad b^l \le x< a^{m},\\ 0,&{}\quad x= a^{m}, \\ h_2(x), &{}\quad a^{m} < x \le b^u, \\ 1,&{}\quad \mathrm{{elsewhere}}. \end{array} \right. \end{aligned}$$

The expected interval (Grzegorzewski 2003) of $\tilde{A}^I$ is the crisp interval $EI(\tilde{A}^I)$ given by $EI(\tilde{A}^I)=[E^{*L}(\tilde{A}^I),E^{*U}(\tilde{A}^I)]$, where

$$\begin{aligned} E^{*L}(\tilde{A}^I)&={\dfrac{b^l+a^m}{2}}+{\dfrac{1}{2}{\int _{b^l}^{a^m} {g_2(x)\mathrm{{d}}x}}-{\dfrac{1}{2}\int _{a^l}^{a^m}{g_1(x) \mathrm{{d}}x}}}, \end{aligned}$$

(4.1)

$$\begin{aligned} E^{*U}(\tilde{A}^I)&={\dfrac{a^m+b^u}{2}}+{\dfrac{1}{2}{\int _{a^m}^{a^u} {h_1(x)\mathrm{{d}}x}}-{\dfrac{1}{2}\int _{a^m}^{b^u}{h_2(x) \mathrm{{d}}x}}}. \end{aligned}$$

(4.2)

The expected value of an IFN is given by

$$\begin{aligned} EV(\tilde{A}^I)=\dfrac{E^{*L}(\tilde{A}^I)+E^{*U}(\tilde{A}^I)}{2}. \end{aligned}$$

(4.3)

Theorem 1

Let $\tilde{A}^I=(a^l,a^m,a^u;b^l,a^m,b^u)$ be a TIFN. Then, $EV(\tilde{A}^I)= \frac{a^l+b^l+4 a^m+a^u+b^u}{8}.$

Proof

Using (4.1), we have $E^{*L}(\tilde{A}^I)=\frac{a^l+2 a^m+b^l}{4}$.

Using (4.2), we have $E^{*U}(\tilde{A}^I)=\frac{a^u+2 a^m+b^u}{4}$.

Therefore, $EV(\tilde{A}^I)= \frac{a^l+b^l+4 a^m+a^u+b^u}{8}.$$\square$

4.2 Proposed IFCC between IF variables

Definition 17

(correlation coefficients between variables)  Let x and y be two crisp variables and (x, y) assume the values $(x_i,y_i),\,i=1,2,3,\ldots ,n$. Then, the correlation coefficient between x and y is denoted by C(x, y) and is defined by

$$\begin{aligned} C(x,y)=\dfrac{n\sum \limits _{i=1}^{n}{x_i y_i}-\sum \limits _{i=1}^{n}{x_i}\sum \limits _{i=1}^{n}{y_i}}{\sqrt{n\sum \limits _{i=1}^{n}{{x_i}^2}-\left( \sum \limits _{i=1}^{n}{x_i}\right) ^2}.\sqrt{n\sum \limits _{i=1}^{n}{{y_i}^2}-\left( \sum \limits _{i=1}^{n}{y_i}\right) ^2}}.\nonumber \\ \end{aligned}$$

(4.4)

Let $\tilde{x}^I$ and $\tilde{y}^I$ be two IF variables and $(\tilde{x}^I,\tilde{y}^I)$ assume the values $(\tilde{x}_i^I,\tilde{y}_i^I),\,i=1,2,3,\ldots ,n$. Then, the IFCC between $\tilde{x}^I$ and $\tilde{y}^I$ is denoted by $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ and is defined by

$$\begin{aligned}&\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)\nonumber \\&\quad =\frac{n\sum \limits _{i=1}^{n} {{\tilde{x_i}^I}{\tilde{y_i}^I}}-{\sum \limits _{i=1}^{n}{\tilde{x_i}^I}} {\sum \limits _{i=1}^{n}{\tilde{y_i}^I}}}{\sqrt{n\sum \limits _{i=1}^{n} {\left( \tilde{x_i}^I\right) ^2}-\left( \sum \limits _{i=1}^{n}{\tilde{x_i}^I}\right) ^2}. {\sqrt{n\sum \limits _{i=1}^{n}{\left( \tilde{y_i}^I\right) ^2}-\left( \sum \limits _{i=1}^{n} {\tilde{y_i}^I}\right) ^2}}}.\nonumber \\ \end{aligned}$$

(4.5)

The square of a positive TIFN $\tilde{A}^I$ is given by

$$\begin{aligned}&(\tilde{A}^I)^2=\tilde{A}^I.\tilde{A}^I\nonumber \\&\quad =(a^l,a^m,a^u;a'^l,a^m,a'^u).(a^l,a^m,a^u;a'^l,a^m,a'^u)\nonumber \\&\quad =((a^l)^2,(a^m)^2,(a^u)^2;(a'^l)^2,(a^m)^2,(a'^u)^2). \end{aligned}$$

(4.6)

It is difficult to apply (4.5) if data are large. To obtain the IFCC between the IF variables, we propose a new method using the expected value approach as described below:

Let $\tilde{x}_i^I=(x_i^l,x_i^m,x_i^u;x_i^{'l},x_i^m,x_i^{'u})$ and $\tilde{y}_i^I=(y_i^l,y_i^m,y_i^u;y_i^{'l},y_i^m,y_i^{'u})$ be TIFNs. Then, the $\alpha$-cut of $\tilde{x}_i^I$ is the interval $[x_{i,\alpha }^L,x_{i,\alpha }^U]$, where $x_{i,\alpha }^L=\alpha x_{i}^m+(1-\alpha ) x_{i}^l$, and $x_{i,\alpha }^U=\alpha x_{i}^m+(1-\alpha ) x_{i}^u$, $\alpha \in (0,1]$.

Similarly, the $\alpha$-cut of $\tilde{y}_i^I$ is the interval $[y_{i,\alpha }^L,y_{i,\alpha }^U]$, where $y_{i,\alpha }^L=\alpha y_{i}^m+(1-\alpha ) y_{i}^l$, and $y_{i,\alpha }^U=\alpha y_{i}^m+(1-\alpha ) y_{i}^u$, $\alpha \in (0,1]$.

The expected interval (EI) of the IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I )$ based on $\alpha$-cuts of $\tilde{x}_i^I$ and $\tilde{y}_i^I$ is defined as the interval $C_{\alpha }^{EI}(\tilde{x}^I,\tilde{y}^I)=[C_{\alpha }^L(\tilde{x}^I,\tilde{y}^I),C_{\alpha }^U(\tilde{x}^I,\tilde{y}^I)]$, where

$$\begin{aligned}&C_{\alpha }^L\left( \tilde{x}^I,\tilde{y}^I\right) \nonumber \\&\quad =\frac{n\sum \limits _{i=1}^{n}{{x_{i,\alpha }^L}{y_{i,\alpha }^L}}-{\sum \limits _{i=1}^{n}{x_{i,\alpha }^L}}{\sum \limits _{i=1}^{n}{y_{i,\alpha }^L}}}{\sqrt{n\sum \limits _{i=1}^{n}{\left( x_{i,\alpha }^L\right) ^2}-\left( \sum \limits _{i=1}^{n}{x_{i,\alpha }^L}\right) ^2}.{\sqrt{n\sum \limits _{i=1}^{n}{\left( y_{i,\alpha }^L\right) ^2}-\left( \sum \limits _{i=1}^{n}{y_{i,\alpha }^L}\right) ^2}}}. \,\,\end{aligned}$$

(4.7)

$$\begin{aligned}&C_{\alpha }^U\left( \tilde{x}^I,\tilde{y}^I\right) \nonumber \\&\quad =\frac{n\sum \limits _{i=1}^{n}{{x_{i,\alpha }^U}{y_{i,\alpha }^U}}-{\sum \limits _{i=1}^{n}{x_{i,\alpha }^U}}{\sum \limits _{i=1}^{n}{y_{i,\alpha }^U}}}{\sqrt{n\sum \limits _{i=1}^{n}{\left( x_{i,\alpha }^U\right) ^2}-\left( \sum \limits _{i=1}^{n}{x_{i,\alpha }^U}\right) ^2}.{\sqrt{n\sum \limits _{i=1}^{n}{\left( y_{i,\alpha }^U\right) ^2}-\left( \sum \limits _{i=1}^{n}{y_{i,\alpha }^U}\right) ^2}}}.\nonumber \\ \end{aligned}$$

(4.8)

Observe that $C_{\alpha }^L(\tilde{x}^I,\tilde{y}^I)$ and $C_{\alpha }^U(\tilde{x}^I,\tilde{y}^I)$ are the correlation coefficients based on the data $(x_{i,\alpha }^L,y_{i,\alpha }^L)$ and $(x_{i,\alpha }^U,y_{i,\alpha }^U)$, respectively, $i=1,2,3,\ldots ,n$. These correlation coefficients satisfy the following properties:

• 1. $C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)\in [-1,1]$ and $C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)\in [-1,1]$$\forall \alpha \in (0,1]$.

• 2. $C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)=1$ and $C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)=1$ if $\tilde{x}^I=\tilde{y}^I$$\forall \alpha \in (0,1]$.

• 3. $C_\alpha ^L(\tilde{x}^I,\tilde{y}^I){=}C_\alpha ^L(\tilde{y}^I,\tilde{x}^I)$ and $C_\alpha ^U(\tilde{x}^I,\tilde{y}^I){=}C_\alpha ^U(\tilde{y}^I,\tilde{x}^I)$$\forall \alpha \in (0,1]$.

The expected value (EV) of IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ based on $\alpha$-cut is denoted by $C_\alpha ^{EV}(\tilde{x}^I,\tilde{y}^I)$ and is defined by

$$\begin{aligned} C_\alpha ^{EV}(\tilde{x}^I,\tilde{y}^I)=\dfrac{1}{2}{\left[ C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)+C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)\right] },\,\,\alpha \in (0,1]. \end{aligned}$$

(4.9)

The $\beta$-cut of $\tilde{x}_i^I$ is the interval $[x_{i,\beta }^{'L},x_{i,\beta }^{'U}]$, where $x_{i,\beta }^{'L}=\beta x_{i}^{'l}+(1-\beta ) x_{i}^m$, and $x_{i,\beta }^{'U}=\beta x_{i}^{'u}+(1-\beta ) x_{i}^m \,\,\forall \beta \in [0,1)$. Similarly, the $\beta$-cut of $\tilde{y}_i^I$ is the interval $[y_{i,\beta }^{'L},y_{i,\beta }^{'U}]$, where $y_{i,\beta }^{'L}=\beta y_{i}^{'l}+(1-\beta ) y_{i}^m$, and $y_{i,\beta }^{'U}=\beta y_{i}^{'u}+(1-\beta ) y_{i}^m\,\,\forall \beta \in [0,1)$.

The EI of IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ based on $\beta$-cuts of $\tilde{x}_i^I$ and $\tilde{y}_i^I$ is defined as the interval $C_{\beta }^{'EI}(\tilde{x}^I,\tilde{y}^I)=[C_{\beta }^{'L}(\tilde{x}^I,\tilde{y}^I),C_{\beta }^{'U}(\tilde{x}^I,\tilde{y}^I)]$, where

$$\begin{aligned}&C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)\nonumber \\&\quad =\frac{n\sum \limits _{i=1}^{n}{{x_{i,\beta }^{'L}}{y_{i,\beta }^{'L}}}-{\sum \limits _{i=1}^{n}{x_{i,\beta }^{'L}}}{\sum \limits _{i=1}^{n}{y_{i,\beta }^{'L}}}}{\sqrt{n\sum \limits _{i=1}^{n}{\left( x_{i,\beta }^{'L}\right) ^2}-\left( \sum \limits _{i=1}^{n}{x_{i,\beta }^{'L}}\right) ^2}.{\sqrt{n\sum \limits _{i=1}^{n}{\left( y_{i,\beta }^{'L}\right) ^2}-\left( \sum \limits _{i=1}^{n}{y_{i,\beta }^{'L}}\right) ^2}}}. \end{aligned}$$

(4.10)

$$\begin{aligned}&C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)\nonumber \\&\quad =\frac{n\sum \limits _{i=1}^{n}{{x_{i,\beta }^{'U}}{y_{i,\beta }^{'U}}}-{\sum \limits _{i=1}^{n}{x_{i,\beta }^{'U}}}{\sum \limits _{i=1}^{n}{y_{i,\beta }^{'U}}}}{\sqrt{n\sum \limits _{i=1}^{n}{\left( x_{i,\beta }^{'U}\right) ^2}-\left( \sum \limits _{i=1}^{n}{x_{i,\beta }^{'U}}\right) ^2}.{\sqrt{n\sum \limits _{i=1}^{n}{\left( y_{i,\beta }^{'U}\right) ^2}-\left( \sum \limits _{i=1}^{n}{y_{i,\beta }^{'U}}\right) ^2}}}.\nonumber \\ \end{aligned}$$

(4.11)

Observe that $C_{\beta }^{'L}(\tilde{x}^I,\tilde{y}^I)$ and $C_{\beta }^{'U}(\tilde{x}^I,\tilde{y}^I)$ are the correlation coefficients based on the data $(x_{i,\beta }^{'L},y_{i,\beta }^{'L})$ and $(x_{i,\beta }^{'U},y_{i,\beta }^{'U})$, respectively, $i=1,2,3,\ldots ,n$. These correlation coefficients satisfy the following properties:

• 1. $C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)\in [-1,1]$ and $C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)\in [-1,1]\forall \beta {\in } [0,1)$.

• 2. $C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)=1$ and $C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)=1$ if $\tilde{x}^I=\tilde{y}^I\,\,\forall \beta \in [0,1)$.

• 3. $C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)=C_\beta ^{'L}(\tilde{y}^I,\tilde{x}^I)$ and $C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)=C_\beta ^{'U}(\tilde{y}^I,\tilde{x}^I)\,\,\forall \beta \in [0,1)$.

The EV of IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ based on $\beta$-cut is denoted by $C_\beta ^{'EV}(\tilde{x}^I,\tilde{y}^I)$ and is defined by

$$\begin{aligned} C_\beta ^{'EV}(\tilde{x}^I,\tilde{y}^I)= & {} \dfrac{1}{2}\left[ C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)\right. \nonumber \\&\left. +C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)\right] ,\,\beta \in [0,1). \end{aligned}$$

(4.12)

The EV of IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ based on $\alpha$- and $\beta$-cuts is denoted by $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)$ and is defined by

$$\begin{aligned} C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)=\dfrac{C_{\alpha }^{EV} (\tilde{x}^I,\tilde{y}^I)+C_{\beta }^{'EV}(\tilde{x}^I,\tilde{y}^I)}{2} \end{aligned}$$

(4.13)

Theorem 2

Let $[C_\alpha ^L(\tilde{x}^I,\tilde{y}^I),C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)]$ and $[C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I),C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)]$ be the EIs of the IFCC $\tilde{C}(\tilde{x}^I,\tilde{y}^I)$ based on $\alpha$- and $\beta$-cuts, respectively. Then, $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)=\dfrac{C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)+C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)+C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)+C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)}{4}.$

Proof

The EV of IFCC $\tilde{C}^I(\tilde{x}^I,\tilde{y}^I)$ based on $\alpha$- and $\beta$-cuts is given by

$$\begin{aligned} \,\,\,C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)= & {} \dfrac{C_{\alpha }^{EV}(\tilde{x}^I,\tilde{y}^I)+C_{\beta }^{'EV}(\tilde{x}^I,\tilde{y}^I)}{2} \end{aligned}$$

Using (5.9) and (5.12), we get

$$\begin{aligned}&C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)=\dfrac{1}{2}\left[ \dfrac{C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)+C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)}{2}\right. \nonumber \\&\qquad \left. +\dfrac{C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)+C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)}{2}\right] \\&\quad =\dfrac{C_\alpha ^L(\tilde{x}^I,\tilde{y}^I)+C_\alpha ^U(\tilde{x}^I,\tilde{y}^I)+C_\beta ^{'L}(\tilde{x}^I,\tilde{y}^I)+C_\beta ^{'U}(\tilde{x}^I,\tilde{y}^I)}{4} \end{aligned}$$

$\square$

$C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)$ satisfies the following properties:

• 1. $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)\in [-1,1]$.

• 2. $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)=1$ if $\tilde{x}^I=\tilde{y}^I$.

• 3. $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)=C_{\alpha ,\beta }^{EV}(\tilde{y}^I,\tilde{x}^I)$.

Remark If the value of $C_{\alpha ,\beta }^{EV}(\tilde{x}^I,\tilde{y}^I)$ for each $\tilde{x}^I\,\,and\,\,\tilde{y}^I$ is positive, then the proposed DIFDEA models are consistent and inclusion of IF variables is justified.

5 Proposed intuitionistic fuzzy ranking approach

Ranking has an important role in DEA. Some definitions are as follows:

Definition 18

In DEA, the ranking index (Chen and Klein 1997) for the jth DMU is:

$$\begin{aligned} R_{j}= \dfrac{\sum _{i=0}^{n}{\left( (E_j)_{\alpha _i}^U-c\right) }}{\sum _{ i=0}^{n}{\left( (E_j)_{\alpha _i}^U-c\right) }-\sum _{i=0}^{n}{\left( (E_j)_{\alpha _i}^L-d\right) }};\,\,n\rightarrow \infty , \end{aligned}$$

where $(E_j)_{\alpha _i}^L$ and $(E_j)_{\alpha _i}^U$ are the lower bound and upper bound efficiencies of the jth DMU, respectively, for $\alpha _i\in (0,1]$; $c=\min \limits _{\alpha _i} \,(E_j)_{\alpha _i}^L$ and $d=\max \limits _{\alpha _i} \,(E_j)_{\alpha _i}^U$.

Definition 19

Let $A=[a,b]$ and $B=[c,d]$ be two intervals. Then, the difference $A-B$ of A and B is defined as $A-B=[a-d,b-c]$.

5.1 Methodology

The proposed index ranking (PIR) method evaluates the efficiencies of DMUs.

To the best of our knowledge, in the DEA literature, there is no ranking approach for IFNs.

The proposed method uses $\alpha$- and $\beta$-cuts to rank the DMUs.

(i) Index based on $\alpha$-cut

Suppose $a_{\alpha _i}=\min \limits _{j}{\xi _{j,\alpha _i}^L}$ and $b_{\alpha _i}=\max \limits _{j}{\xi _{j,\alpha _i}^U}$ for $\alpha \in (0,1]$. Obviously, $\xi _{j,\alpha _i}^U-a_{\alpha _i}$ is positive for all j for any $\alpha \in (0,1]$ and $(\xi _{j,\alpha _i}^L-b_{\alpha _i})$ is negative for all j for any $\alpha _i\in (0,1]$. Thus, the index value is defined by

$$\begin{aligned} I_{j}=\dfrac{\sum _{i=0}^{n}{(\xi _{j,\alpha _i}^U-a_{\alpha _i})}}{\sum _{i=0}^{n}{(\xi _{j,\alpha _i}^U-a_{\alpha _i})}-\sum _{i=0}^{n}{(\xi _{j,\alpha _i}^L-b_{\alpha _i})}}. \end{aligned}$$

(5.1)

(ii) Index based on $\beta$-cut

Suppose $c_{\beta _i}=\min \limits _{j}{\xi _{j,\beta _i}^{'L}}$ and $d_{\beta _i}=\max \limits _{j}{\xi _{j,\beta _i}^{'U}}$.

Obviously, $\xi _{j,\beta _i}^{'U}-d_{\beta _i}$ is negative and $\xi _{j,\beta _i}^{'L}-c_{\beta _i}$ is positive for all j for any $\beta _i \in [0,1)$. Thus, the index value is defined by

$$\begin{aligned} I_{j}^{'}=\dfrac{\sum _{i=0}^{n}{(\xi _{j,\beta _i}^{'U}-d_{\beta _i})}}{\sum _{i=0}^{n}{(\xi _{j,\beta _i}^{'U}-d_{\beta _i})}-\sum _{i=0}^{n}{(\xi _{j,\beta _i}^{'L}-c_{\beta _i})}}. \end{aligned}$$

(5.2)

(iii) Now, we construct the composite index of IF efficiencies based on $I_{j}$ and $I_{j}^{'}$ for the jth DMU is given by

$$\begin{aligned} IC_{j}=\eta \,\,I_{j}+(1-\eta ) \,\,I_{j}^{'} \end{aligned}$$

(5.3)

where $\eta \in (0, 1)$ is a parameter depending on the decision- maker’s intention. Generally, $\eta$ is taken as 0.5.

5.1.1 Algorithm for the PIR approach

Based on the above analysis, we suggest the following algorithm for ranking:

Step 1:

Determine both $\xi _{j_o,\alpha }^L$ and $\xi _{j_o,\alpha }^U$ given by Model 6 and Model 7, respectively, for each $\mathrm{{DMU}}_{j_o}$, $j_o=1,2,3,\ldots ,n$.

Step 2:

Determine both $\xi _{j_o,\beta }^{'L}$ and $\xi _{j_o,\beta }^{'U}$ given by Model 11 and Model 12, respectively, for each $\mathrm{{DMU}}_{j_o}$, $j_o=1,2,3,\ldots ,n$.

Step 3:

Determine both $I_{j_o}$ and $I_{j_o}^{'}$ given by (5.1) and (5.2), respectively for each $\mathrm{{DMU}}_{j_o}$, $j_o=1,2,3,\ldots ,n$.

Step 4:

Determine $IC_{j_o}$ given by (5.3) for each $\mathrm{{DMU}}_{j_o}$, $j_o=1,2,3,\ldots ,n$.

Step 5:

Rank the DMUs according to the decreasing values of $IC_{j_o}$.

This PIR method is suitable for the IFN efficiencies because it is based on $\alpha$- and $\beta$-cut and it can handle the large quantity of IFNs.

The flowchart showing the overview of the proposed methods is given in Figure 3.

Fig. 3

Overview of the proposed method

5.2 Merits of the proposed methods over existing methods

The proposed method determines the efficiencies of DMUs in interval form based on $\alpha$-cut and $\beta$-cut. The proposed IFCC is used to validate the proposed models based on IF variables. But, the fuzzy DEA (FDEA) models determine the efficiencies of DMUs based on $\alpha$-cut only. The proposed method uses $\alpha$-cut and $\beta$-cut to rank the DMUs. The proposed ranking method gives the aggregate rank for all $\alpha$-cuts and $\beta$-cuts. But, the existing ranking methods in FDEA (Arya and Yadav (2017, 2018)) of DMUs based on $\alpha$-cut only and existing ranking methods in IFDEA (Puri and Yadav (2015), Daneshvar Rouyendegh (2011)) do not use $\alpha$-cut and $\beta$-cut.

6 Numerical examples

In this section, to ensure the validity of the proposed models, we consider an illustrative example and a health sector application. The efficiencies obtained by the proposed models will be termed as proposed efficiencies (PEs).

6.1 An illustrative example:

Let there be 5 DMUs having two IF inputs and two IF outputs which are represented as TIFNs. The IF input and IF output data are listed in Table 2.

Table 2 IF inputs and IF outputs for 5 DMUs

6.1.1 Determining efficiencies of DMUs

The IFCC between IF variables (IF inputs–outputs) are determined using (4.13) and are shown in Table 3. Table 3 shows the lower and upper bounds of each expected interval based on $\alpha$- and $\beta$-cuts. Also, the corresponding expected values come out to be positive. Therefore, the inclusion of the IF input and IF output data are justified, and the DIFDEA models are consistent.

Table 3 IFCCs between IF inputs–outputs

The $\xi _{j,\alpha }^L, \xi _{j,\alpha }^U,\,\xi _{j,\beta }^{'L}\,\,and\,\,\,\xi _{j,\beta }^{'U}$ for each $\mathrm{{DMU}}_{j}$ are calculated using Models 6, 7, 11 and 12 for different $\alpha \,and\,\,\beta \in [0,1]$, respectively. The results are shown in Table 4. By using the software Lingo, the values of the $\xi _{j,\alpha }^L, \xi _{j,\alpha }^U,\,\xi _{j,\beta }^{'L}\,\,and\,\,\,\xi _{j,\beta }^{'U}$ for $\alpha ,\,\, \beta =0(0.25)1.0$ are calculated (see Table 4) for each DMU.

Table 4 The IF efficiencies for $\alpha ,\,\, \beta =0(0.25)1.0$

The composite index values for 5 DMUs are $IC(\mathrm{{DMU}}1) = 0.3569; IC(\mathrm{{DMU}}2) = 0.38; IC(\mathrm{{DMU}}3) = 0.3587; IC(\mathrm{{DMU}}4) = 0.455; IC(\mathrm{{DMU}}5) = 0.3435$. The DMUs are ranked by using PIR discussed in Sect. 5 as $\mathrm{{DMU}} 4>\mathrm{{DMU}} 2>\mathrm{{DMU}} 3>\mathrm{{DMU}} 1>\mathrm{{DMU}} 5$.

6.1.2 Comparison of proposed efficiencies and crisp efficiencies

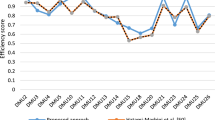
To validate the proposed efficiencies through PDIFDEA, the proposed efficiencies are compared with the efficiencies of crisp DEA (crisp efficiencies) and are given in Table 5. In Table 5, the efficiencies of DMUs are found to be smaller by PDIFDEA compared to crisp DEA. In Table 5, DMUs 2, 4 and 5 are efficient in crisp DEA, but these are inefficient with efficiency scores 0.38, 0.455 and 0.3435 using PDIFDEA, respectively. Therefore, PDIFDEA is more realistic rather than crisp DEA. Crisp DEA and PDIFDEA may give the same efficiencies for certain data. Crisp DEA does not deal with the uncertainty/vagueness, but PDIFDEA deals with the uncertainty/vagueness. Therefore, PDIFDEA is more efficient rather than crisp DEA.

6.1.3 Determining IF input–output targets of DMUs

Finally, we obtain the IF input targets and IF output targets discussed in Sect. 3.4 which are shown in Table 6.

From input targets, we conclude that

• (i) for DMU 1, the IF inputs have to be decreased from (3.5, 4, 4.5; 3.2, 4.0, 4.7) and $(1.9,2.1,2.3;1.7,2.1,2.5)$ to (2.18, 3.4, 4.5; 1.57, 3.4, 4.7) and $(1.18,1.8,2.3;0.93,1.8,2.5)$, respectively, to become efficient,

• (ii) for DMU 2, the IF inputs have to be decreased from (2.9, 2.9, 2.9; 2.9, 2.9, 2.9) and $(1.4,1.5,1.6;1.3,1.5,1.8)$ to (2.4, 2.9, 2.9; 1.89, 2.9, 2.9) and $(1.17,1.5,1.6;0.84,1.5,1.8)$, respectively, to become efficient,

• (iii) for DMU 3, the IF inputs have to be decreased from (4.4, 4.9, 5.4; 4.2, 4.9, 5.6) and $(2.2,2.6,3;2.1,2.6,3.2)$ to (2.5, 4.21, 5.4; 1.84, 4.21, 5.6) and $(1.25,2.24,3.0,0.94,2.24,3.2)$, respectively, to become efficient,

• (iv) for DMU 4, the IF inputs have to be decreased from (3.4, 4.1, 4.8; 3.1, 4.1, 4.9) and $(2.2,2.3,2.4;2.1,2.3,2.6)$ to (2.89, 4.1, 4.8; 2.11, 4.1, 4.9) and $(1.87,2.3,2.4;1.43,2.3,2.6)$, respectively, to become efficient,

• (v) for DMU 5, the IF inputs have to be decreased from (5.9, 6.5, 7.1; 5.6, 6.5, 7.2) and $(3.6,4.1,4.6;3.5,4.1,4.7)$ to (3.77, 6.5, 7.1; 3.38, 6.5, 7.2) and $(2.3,4.1,4.6;1.82,4.1,4.7)$, respectively, to become efficient.

Table 5 Comparison of proposed efficiencies and crisp efficiencies

Table 6 IF input target and IF output target for 5 DMUs

Table 7 Hospital notations

Table 8 IF input and IF output data for 16 hospitals. Source: Administrative Office, Meerut district, Uttar Pradesh, India.

Table 9 IFCCs between IF variables

Table 10 The IF efficiencies based on $\alpha , \beta =0(0.25)0.5$ of 16 hospitals

Table 11 The IF efficiencies based on $\alpha , \beta =0.75(0.25)1.0$ of 16 hospitals

Table 12 Comparison of proposed efficiencies and crisp efficiencies

Table 13 IF input target and IF output target data for 16 hospitals

6.2 Health sector application

This is a real life application in health sector. The most important role in the economy of any country is health care of rural and urban areas. Health care is of three types: primary (in which individuals and families are directly connected to health system), secondary (in which patients from primary health care are referred to specialists in higher hospitals for treatment) and tertiary health care (in which specialized consultative care is provided usually on referral from primary and secondary medical care). The performance of hospitals has become a major concern of planners and policy-makers in India. The Uttar Pradesh (U.P) state is one of the largest states of India. It has 18 divisions. Meerut is one of them which has 6 districts named as Baghpat, Bulandshahr, Ghaziabad, GB Nagar, Meerut and Hapur. Each district has some public hospitals. Total number of public hospitals in Meerut division is 16. In this paper, we discuss the performance efficiency of public hospitals which are in Meerut division. Table 7 gives the public hospitals in Meerut division.

6.2.1 Variables and data selection

In this study, we have taken two inputs: (i) total number of beds (say $\tilde{x_1}^I$) and (ii) sum of number of pathologists and number of laboratory technicians (say $\tilde{x_2}^I$) and two outputs: (i) number of pathology operations (say $\tilde{y_1}^I$) and (ii) sum of number of plaster and number of tubal ligation (say $\tilde{y_2}^I$) of 16 hospitals which possess some degree of hesitation due to the difference in thought at the management level and the actual hospital level. So, uncertainty in input data and output data at hospital level can be well taken as TIFN. The IF input and IF output data are provided by the administrative office, Meerut district, Uttar Pradesh, India, for the calender year 2013–2014, and it is shown in Table 8.

6.2.2 Determining efficiencies of hospitals

The IFCCs between IF variables (IF inputs–outputs) are determined using (4.13) and are shown in Table 9. Table 9 shows the lower and upper bounds of each expected interval based on $\alpha$- and $\beta$-cuts. Also, the corresponding expected values come out to be positive. Therefore, the inclusion of the IF input and IF output data is justified and the DIFDEA models are consistent.

The IF efficiencies of all hospitals are evaluated using Models 6, 7, 11 and 12 for different $\alpha \,\, and\,\,\beta -$ values, which are shown in Tables 10 and 11. The composite index $IC_j$ of IF efficiencies $\xi _{j,\alpha }^L, \xi _{j,\alpha }^U,\,\xi _{j,\beta }^{'L}\,\,and\,\,\,\xi _{j,\beta }^{'U}$ for each $\mathrm{{DMU}}_{j}$ is calculated and shown in Tables 10 and 11. The ranks of the hospitals using the PIR approach are obtained as $\mathrm{{GC}}>\mathrm{{MC}}>\mathrm{{GS}}>\mathrm{{MFD}}>\mathrm{{BLC}}>\mathrm{{BC}}>\mathrm{{MD}}>\mathrm{{GBC}}>\mathrm{{GD}}>\mathrm{{GBD}}>\mathrm{{GFD}}>\mathrm{{BD}}>\mathrm{{BLK}}>\mathrm{{BLD}}>\mathrm{{HCM}} >\mathrm{{BLFD}}$. Thus, GC is the best performer hospital and BLFD is the worst performer hospital.

6.2.3 Comparison of proposed efficiencies and crisp efficiencies

To validate the proposed efficiencies of hospitals through PDIFDEA, the proposed efficiencies are compared with the efficiencies of crisp DEA (crisp efficiencies) and are given in Table 12. Table 12 shows that the efficiencies of hospitals are smaller by PDIFDEA compared to crisp DEA. In Table 12, hospitals BD, BLD, GFD, GBD and HCM are efficient in crisp DEA, but these hospitals are inefficient with efficiency scores 0.3963, 0.3259, 0.4017, 0.4167 and 0.2979 using PDIFDEA, respectively. Therefore, PDIFDEA is more realistic rather than crisp DEA. Crisp DEA and PDIFDEA may give same efficiencies for certain data. Crisp DEA does not deal with the uncertainty/vagueness, but PDIFDEA deals with the uncertainty/vagueness. Therefore, PDIFDEA is more efficient rather than crisp DEA. Hence, we preferred PDIFDEA rather than crisp DEA.

6.2.4 Determining IF input–output targets of hospitals

Finally, we obtain the IF input target and IF output target data which are shown in Table 13. Using these IF input target and IF output target, we make the inefficient hospitals as efficient hospitals. For the inefficient hospital BC, the IF inputs have to be decreased from (140, 144, 150; 135, 144, 155) and (2, 2, 8; 1, 2, 15) to $(13.16,48.96,148.5;11.61,48.96,153.45)$ and (0.18, 0.68, 7.92; 0.07, 0.68, 14.85), respectively, to become efficient. Similarly, we find the IF inputs decreased values for other inefficient hospitals and are shown in Table 13.

7 Conclusion

In this paper, we have determined the performance efficiencies of DMUs. The real world applications data have some degree of uncertainties. To deal with such data, we have considered them as TIFNs. We have developed IFDEA models based on $\alpha -,\,\beta$-cuts. Four DIFDEA models (Models 6, 7, 11 and 12) have been developed to determine the performance efficiencies of the DMUs. Next, we have developed IF index ranking approach for DIFDEA models. This ranking approach is efficient and effective for the large number of IF input–output data. We have also proposed the targets for the DMUs with IF inputs–outputs. Finally, an example and a health sector application are presented to illustrate the proposed models. To ensure the validity of the proposed models, we have considered the performance of 16 hospitals in the Meerut zone of India with two IF inputs: total number of beds, sum of number of pathologists and number of laboratory technicians, and two IF outputs: number of pathology operations, sum of number of plaster and number of tubal ligation. GC is determined as the best performer hospital with high level of efficiencies, and BLFD is the worst performer hospital with low level of efficiencies. We also determined the IF input–output targets data for inefficient DMUs by which it is found that how an inefficient hospital is made efficient hospital. PDIFDEA has realistic point of view better representing inefficient performance efficiencies, but crisp DEA has an optimistic point of view to the same problem. By extending to IF environment, the DEA method is more effective for real world applications in the sense that it covers hesitation also.

8 Limitations and Future Research Plan

This paper has some limitations. The proposed models are studied under the constant returns to scale (CRS). We plan to extend these models to the variable returns to scale (VRS). The uncertainty in this paper is limited to TIFNs. We plan to use the trapezoidal IFNs and interval valued intuitionistic fuzzy sets to determine the efficiencies of real world applications.