Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Determination of electromagnetic parameters of dielectric bodies that have complicated geometry or structure is an urgent problem arising e.g. when nanocomposite or artificial materials and media are used as elements of various devices. However, as a rule, these parameters cannot be directly measured (because of composite character of the material and small size of samples), which leads to the necessity of applying methods of mathematical modeling and numerical solution of the corresponding forward and inverse electromagnetic problems [21]. It is especially important to develop the solution techniques when the inverse problem for bodies of complicated shape are considered in the resonance frequency range, which is the case when permittivity of nanocomposite materials must be reconstructed [19, 20].

One of possible applications of composites is the creation of radio absorbing materials that can be used in systems that provide electromagnetic compatibility of modern electronic devices and in ‘Stealth’-type systems aimed at damping and decreasing reflectivity of microwave electromagnetic radiation from objects to be detected [7, 17]. When calculating reflection and absorption characteristics of electromagnetic microwave radiation of radio absorbing materials, researchers use models employing the data on the material constants (permittivity, permeability, conductivity) of these materials in the microwave range. Such composites often contain carbon particles, short carbon fibers, carbon nanofibers, and multilayer carbon nanotubes as fillers for polymer dielectric matrices [7, 13, 17]. The use of carbon nanotubes enables one to achieve a significant (up to 10 dB) absorption of microwave electromagnetic radiation at relatively thin composite layers and low volume fractions of nanotubes and hence a small weight, in a broad frequency range (up to 5 GHz). Such characteristics are caused by both the geometrical sizes of individual nanotubes and their electrophysical properties; among the most important parameters here are permittivity and electric conductivity (which can vary over very wide ranges).

It is important to determine permittivity and conductivity not only of a composite as a solid body (as in [7, 17]), but also of its components, e.g., nanotubes, whose physical characteristics can vary substantially in the process of composite formation.

The forward scattering problem for a diaphragm in a parallel-plane waveguide was considered in [14]. In papers [1, 3, 8, 9, 16, 23–25] the inverse problem of reconstructing complex permittivity was analyzed from the measurements of the transmission coefficient; in [8, 9, 15] the artificial neural networks method was applied.

Several techniques for the permittivity determination of homogeneous materials loaded in a waveguide are reported [1, 3, 6]. The permittivity reconstruction of inhomogeneous structures are not as widely investigated and only a few studies exist for multilayered materials [2, 10]. Note a recently developed advanced approach [5] that can be also applied to numerical solution of this inverse problem.

However, the solution in closed form to the inverse problem of permittivity determination of materials loaded in a waveguide is not available in the literature, to the best of our knowledge, even for the simplest configuration of a parallel-plane dielectric insert in a guide of rectangular cross section. This fact dictates the aim of this work: to develop a method of solution to the inverse problem of reconstructing effective permittivity of layered dielectrics in the form of diaphragms in a waveguide of rectangular cross section that would enable both obtaining solution in a closed form for benchmark problems and efficient numerical implementation. We note that the corresponding forward problem for a one-sectional diaphragm is considered in [11] and [22].

2 Statement of the Problem

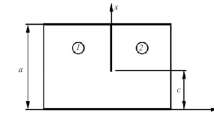
Assume that a waveguide \(P = \left\{ {x:0 < x_1 < a,0 < x_2 < b, - \infty < x_3 < \infty } \right\} \) with the perfectly conducting boundary surface \(\partial P\) is given in Cartesian coordinate system. A three-dimensional body \(Q\) \(\left( {Q \subset P} \right) \)

$$ \quad Q = \left\{ {x:0 < x_1 < a,0 < x_2 < b,0 < x_3 < l} \right\} $$

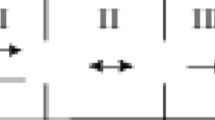
is placed in the waveguide; the body has the form of a diaphragm (an insert), namely, a parallelepiped separated into \(n\) sections adjacent to the waveguide walls. Domain \(P\backslash \bar{Q}\) is filled with an isotropic and homogeneous layered medium having constant permeability \( \left( {\mu _0 > 0} \right) \) in whole waveguide \(P\), the sections of the diaphragm

$$\begin{aligned} Q_0&= \left\{ x: 0 < x_1 < a, 0 < x_2 < b, -\infty < x_3 < 0\right\} \\ Q_j&= \left\{ x: 0 < x_1 < a, 0 < x_2 < b, l_{j - 1} < x_3 < l_{j}\right\} ,\,j = 1, \ldots , n\\ Q_{n + 1}&= \left\{ x: 0 < x_1 < a, 0 < x_2 < b, l < x_3 < +\infty \right\} \end{aligned}$$

are filled each with a medium having constant permittivity \( {\varepsilon _j > 0}\); \(l_0:=0\), \(l_n : = l\).

The electromagnetic field inside and outside of the object in the waveguide is governed by Maxwell’s equation:

$$\begin{aligned} \begin{array}{l} \mathrm{rot}\;{\mathbf {H}} = - i\omega \varepsilon {\mathbf {E}} + {\mathbf {j}}_E^0 \\ \mathrm{rot}\;{\mathbf {E}} = i\omega \mu _0 {\mathbf {H}}, \\ \end{array} \end{aligned}$$
(1)

where \({\mathbf {E}}\) and \({\mathbf {H}}\) are the vectors of the electric and magnetic field intensity, \({\mathbf {j}}\) is the electric polarization current, and \(\omega \) is the circular frequency.

Assume that \(\pi /a < k_0 < \pi /b\), where \(k_0 \) is the wavenumber, \(k_0^2 = \omega ^2 \varepsilon _0 \mu _0\) [12]. In this case, only one wave \(H_{10}\) propagates in the waveguide without attenuation (we have a single-mode waveguide [12]).

The incident electrical field is

$$\begin{aligned} {\mathbf {E}}^0 = {\mathbf {e}}_2 A\sin \left( \frac{\pi x_1}{a}\right) e^{-i\gamma _0 x_3} \end{aligned}$$
(2)

with a known \(A\) and \(\gamma _0 = \sqrt{k_0^2 - \pi ^2/a^2}\).

Solving the forward problem for Maxwell’s equations with the aid of (1) and the propagation scheme in Fig. 1, we obtain explicit expressions for the field inside every section of diaphragm \(Q\) and outside the diaphragm:

$$\begin{aligned} E_{(0)}&= \sin \left( \frac{\pi x_1}{a}\right) (Ae^{-i\gamma _0 x_3}+ Be^{i\gamma _0 x_3}), \quad x \in Q_0,\end{aligned}$$
(3)
$$\begin{aligned} E_{(j)}&= \sin \left( \frac{\pi x_1}{a}\right) (C_{j} e^{-i\gamma _j x_3 } + D_j e^{i\gamma _j x_3}),\\ j&= 1, \dots , n + 1; \qquad D_{n + 1} = 0, \quad x \in Q_j,\nonumber \end{aligned}$$
(4)

where \(\gamma _j = \sqrt{k_j^2 - \pi ^2/a^2}\) and \(k_j^2 = \omega ^2\varepsilon _j \mu _0\).

Fig. 1
figure 1

Multilayered diaphragms in a waveguide

Full size image

From the transmission conditions on the boundary surfaces of the diaphragm sections

$$\begin{aligned}{}[E_{(j)}] = [E_{(j + 1)} ] = 0; \quad \frac{\partial [E_{(j)}]}{\partial x_3} = \frac{\partial [E_{(j + 1)}]}{\partial x_3} = 0, \;j = 0, \dots , n + 1. \end{aligned}$$
(5)

applied to (3) and (4) we obtain using conditions (5) a system of equations for the unknown coefficients

$$\begin{aligned} \left\{ \begin{array}{l} A + B = C_1 + D_1 \\ \gamma _0 \left( {B - A} \right) = \gamma _1 \left( {D_1 - C_1 } \right) \\ C_j e^{ - i\gamma _j l_j } + D_j e^{i\gamma _j l_j } = C_{j + 1} e^{ - i\gamma _{j + 1} l_j } + D_{j + 1} e^{i\gamma _{j + 1} l_j } \\ \gamma _j (D_j e^{i\gamma _j l_j } - C_j e^{ - i\gamma _j l_j }) = \,\gamma _{j + 1} (D_{j + 1} e^{i\gamma _{j + 1} l_j } - C_{j + 1} e^{ - i\gamma _{j + 1} l_j }), \;\; j = 1, \dots , n.\\ \end{array}\right. \end{aligned}$$
(6)

where \(C_{n + 1} = F,\;D_{n + 1} = 0\). In system (6) coefficients \(A\), \(B\), \(C_j\), \(D_j\), \(\varepsilon _j\), \((j = 1, \dots , n)\) are supposed to be complex.

We can express \(C_j\), \(D_j\) from \(C_{j + 1}\), \(D_{j + 1}\) in order to obtain a recurrent formula that couples amplitudes \(A\) and \(F\).

We prove that this recurrent formula has the form

$$\begin{aligned} A = \frac{1}{2\prod \limits _{j = 0}^n {\gamma _j } }\left( {\gamma _n p_{n + 1} } \right. + \gamma _0 q_{n + 1} )Fe^{ - i\gamma _0 l_n }, \end{aligned}$$
(7)

where

$$\begin{aligned} p_{j + 1} = \gamma _{j - 1} p_j \cos \alpha _j + \gamma _j q_j i\sin \alpha _j ; \quad p_1 : = 1, \end{aligned}$$
(8)
$$\begin{aligned} q_{j + 1} = \gamma _{j - 1} p_j i\sin \alpha _j + \gamma _j q_j \cos \alpha _j ; \quad q_1 : = 1. \end{aligned}$$
(9)

Here \(\alpha _j = \gamma _j (l_j - l_{j - 1} )\), \(j = 2, \dots , n\). Note that similar formulas are obtained in classical monographs dealing with wave propagation in layered media, e.g, in [4].

3 Inverse Problem for Multisectional Diaphragm

Formulate the inverse problem for a multisectional diaphragm that will be addressed in this work.

Inverse problem P: find (complex) permittivity \(\varepsilon _j \) of each section from the known amplitude \(A\) of the incident wave and amplitude \(F\) of the transmitted wave at different frequencies.

It is reasonable to consider the right-hand side of (7) as a complex-valued function with respect to \(n\) variables \(\varepsilon _j \). For \(n \) sections we must know amplitudes \(A\) and \(F\) for each of \(n\) frequency values to have a consistent system of \(n\) equations with respect to \(n\) unknown permittivity values \(\varepsilon _j\). This system is then solved to obtain the sought-for permittivity values.

Let us rewrite Eq. (7) in the form

$$\begin{aligned} G(h)= H, \quad H:= \frac{2A\gamma _0 e^{ i\gamma _0 l_n }}{F}, \end{aligned}$$
(10)

where

$$\begin{aligned} G(h):=\frac{1}{\prod \limits _{j = 1}^n {\gamma _j } }\left( {\gamma _n p_{n + 1} } \right. + \gamma _0 q_{n + 1} ), \end{aligned}$$
(11)

and \( h:=(\varepsilon _1, \dots , \varepsilon _n). \)

We will consider (11) as a complex function of \(n\) complex variables. It follows from (8) and (9) that

$$\begin{aligned} \begin{pmatrix} p_{j+1}\\ q_{j+1}\\ \end{pmatrix} = \begin{pmatrix} \cos \alpha _{j}&{} i\sin \alpha _{j}\\ i\sin \alpha _{j} &{} \cos \alpha _{j}\\ \end{pmatrix} \begin{pmatrix} \gamma _{j-1}&{} 0\\ 0 &{} \gamma _{j}\\ \end{pmatrix} \begin{pmatrix} p_{j}\\ q_{j}\\ \end{pmatrix} \end{aligned}$$
(12)

\((j=1,\dots ,n)\). Thus we can represent \(p_{n+1}\), \(q_{n+1}\) via finite multiplication of matrices by formula (12). From representation (12) we select, for every fixed \(j\), only the matrices depending on \(\gamma _j\). Finally we obtain

$$\begin{aligned} \begin{pmatrix} \gamma _{j}&{} 0\\ 0 &{} \gamma _{j+1}\\ \end{pmatrix} \begin{pmatrix} \cos \alpha _{j}&{} i\sin \alpha _{j}\\ i\sin \alpha _{j} &{} \cos \alpha _{j}\\ \end{pmatrix} \begin{pmatrix} \gamma _{j-1}&{} 0\\ 0 &{} \gamma _{j}\\ \end{pmatrix} = \begin{pmatrix} \gamma _{j}\gamma _{j-1}\cos \alpha _{j} &{} i\gamma _{j}^{2}\sin \alpha _{j}\\ i\gamma _{j+1}\gamma _{j-1}\sin \alpha _{j} &{} \gamma _{j}\gamma _{j+1}\cos \alpha _{j} \end{pmatrix}. \end{aligned}$$
(13)

Dividing matrix (13) by \(\gamma _j\) we have

$$\begin{aligned} \begin{pmatrix} \gamma _{j-1}\cos \alpha _{j} &{} i\gamma _{j}\sin \alpha _{j}\\ i\gamma _{j+1}\gamma _{j-1}\sin \alpha _{j}/\gamma _j &{} \gamma _{j+1}\cos \alpha _{j} \end{pmatrix}. \end{aligned}$$
(14)

Taking into account Taylor series for functions \(\sin \alpha _{j}\) and \(\cos \alpha _{j}\) and that \(\alpha _j = \gamma _j (l_j - l_{j - 1} )\) (14) we see that each coefficient of this matrix depends on \(\gamma _j^2\). Since \(\gamma _j^2 = \varepsilon _j \mu _0 \omega ^2 - {\pi ^2}/{a^2}\) we have that each coefficient of matrix (14) is an analytical function w.r.t. \(\varepsilon _j\). Hence function \(G(h)\) depends on \(\varepsilon _j\) analytically for every \(j\), \((j=1,\dots ,n)\).

Using Hartogs’ theorem [18] we obtain the following statement

Theorem 3.1

\(G(h)\) is holomorphic on \(\mathbf{C}^{n}\) as a function of \(n\) complex variables.

Let us formulate inverse problem P for \(n\)-sectional diaphragm in the following form. Consider \(n\) different frequencies \(\varOmega =(\omega _1, \dots , \omega _n)\) and functions \(G_j(h):=G(h,\omega _j)\), \(j=1,\dots ,n\). It is necessary find a solution to the (nonlinear) system of \(n\) equations w.r.t. \(n\) variables \(\varepsilon _1, \dots , \varepsilon _n\):

$$\begin{aligned} G_j(h)= H_j, \quad H_j = H(\omega _j), \quad j = 1, \dots , n. \end{aligned}$$
(15)

Theorem 3.1 implies [18].

Theorem 3.2

If Jacobian \(\frac{\partial (G_1, \dots , G_n)}{\partial (h_1, \dots , h_n)} \ne 0 \) at the point \(h^*\) then function \(G(h)\) is locally invertible in a vicinity of \(h^*\) and inverse problem P has unique solution for every \(h\) from that vicinity.

Below we present an example of numerical solutions to inverse problem P for a three-sectional diaphragm. The table shows the test results of numerical solution to the inverse problem of reconstructing permittivities of a three-section diaphragm at three frequencies. The test values of the transmission coefficient are taken from the solution to the forward problem.

\(F(\omega _{1,2,3} )\)

Calculated \(\varepsilon _{1,2,3} \)

True \(\varepsilon _{1,2,3} \)

\(\begin{array}{l} 0.012 + i \cdot 0.036 \\ 0.025 - i \cdot 0.012 \\ 0.029 + i \cdot 0.014 \\ \end{array}\)

\(\begin{array}{l} - 1.713 + i \cdot 0.078, \\ 1.523 - 0.085 \\ 4.01 + i \cdot 0.13 \\ \end{array}\)

\(\begin{array}{l} - 1.7 \\ 1.5 \\ 4 \\ \end{array}\)

\(\begin{array}{l} 0.073 - i \cdot 0.177 \\ - 0.269 - i \cdot 0.197 \\ - 0.052 - i \cdot 0.22 \\ \end{array}\)

\(\begin{array}{l} 1.702 - i \cdot 0.0004, \\ - 1.499 + i \cdot 0.006 \\ 3.996 + i \cdot 0.003 \\ \end{array}\)

\(\begin{array}{l} 1.7 \\ - 1.5 \\ 4 \\ \end{array}\)

\(\begin{array}{l} 0.106 + i \cdot 0.061 \\ 0.096 - i \cdot 0.023 \\ 0.102 + i \cdot 0.046 \\ \end{array}\)

\(\begin{array}{l} 1.716 - i \cdot 0.0004, \\ 1.48 - i \cdot 0.013 \\ - 3.928 + i \cdot 0.037 \\ \end{array}\)

\(\begin{array}{l} 1.7 \\ 1.5 \\ - 4 \\ \end{array}\)

\(\begin{array}{l} - 0.0004 - i \cdot 0.00376 \\ - 0.0045 + i \cdot 0.00368 \\ - 0.0057 - i \cdot 0.00134 \\ \end{array}\)

\(\begin{array}{l} - 1.708 - i \cdot 0.008, \\ 1.5 + i \cdot 0.0007 \\ - 3.982 + i \cdot 0.017 \\ \end{array}\)

\(\begin{array}{l} - 1.7 \\ 1.5 \\ - 4 \\ \end{array}\)

\(\begin{array}{l} - 0.00005 - i \cdot 0.0005 \\ - 0.002 + i \cdot 0.001 \\ - 0.002 - i \cdot 0.0004 \\ \end{array}\)

\(\begin{array}{l} - 1.708 + i \cdot 0.03, \\ - 1.499 - i \cdot 0.03 \\ - 3.982 - i \cdot 0.044 \\ \end{array}\)

\(\begin{array}{l} - 1.7 \\ - 1.5 \\ - 4 \\ \end{array}\)

Parameters of the three-section diaphragm are \(a = 2,\) \(b = 1,\) \(c = 2,\) \(A = 1,\) \(l_1 = 1,\) \(l_2 = 1.5\); the excitation frequencies \(\omega _1 =2.5,\) \(\omega _2 = 1.7,\) and \(\omega _3 = 2\). The first, second, and third columns of the table shows, respectively, the values of transmission coefficient \(F\), calculated values of permittivity of a section, and true values of (real) permittivity of a section.

We see that in all examples the error of computations does not exceed 3 % which proves high efficiency of the method.

4 One-Sectional Diaphragm: Explicit Solution to the Inverse Problem

From (7) for a one-sectional diaphragm we have

$$\begin{aligned} \frac{Ae^{i\gamma _0 l_1}}{F}&= g(z),\nonumber \\ g(z)&= \cos z + i\left( \frac{z}{2\gamma _0 l_1} + \frac{\gamma _0 l_1}{2z} \right) \sin z,\\ z&=\gamma _1 l_1 = l_1 \sqrt{k_1^2 - \frac{\pi ^2}{a^2}},\nonumber \end{aligned}$$
(16)

where \(z\) is generally a complex variable. From (16) we obtain a relation for the transmission coefficient

$$\begin{aligned} F=\frac{Ae^{i\gamma _0 l_1}}{g(z)} , \end{aligned}$$
(17)

which, together with formulas (3) and (4), gives an explicit solution to the forward problem under study.

When the inverse problem is solved, \(\varepsilon _1\) is considered as an unknown quantity that should be determined from Eq. (16) in terms of \(F\).

List the most important properties of \(g(z)\) which easily follows from its explicit representation:

  1. (i)

    \(g(z)\) is an entire function.

  2. (ii)

    \(g(z)\) has neither real zeros nor poles. This fact is in line with physical requirements that the transmission coefficient does not vanish and is a bounded quantity at real frequencies.

  3. (iii)

    \(g(z)\), also considered as a function of real \(\tau \), is not invertible locally at the origin because it is easy to check that \(g'(0)= 0\). Next, the inverse of \(g(z)\) is a multi-valued function. In fact, the inverse function does not exist globally according to the statement in Remark concerning violation of uniqueness.

  4. (iv)

    \(g(z)\) is not a fractional-linear function; therefore \(g(z)\) performs one-to-one conformal mappings only of certain regions of the complex plane onto regions of the complex plane.

  5. (v)

    It is easy to check up that \(g'(\tau )\ne 0\) for (real) \(\tau \ne 0\). Hence, \(g(z)\) is invertible locally at the real point \(\tau \ne 0\).

Assuming that \(\varepsilon _1\) is real it is reasonable to introduce a real variable

$$\begin{aligned} \tau = \gamma _1 l_1 = l_1 \sqrt{k_1^2 - \frac{\pi ^2}{a^2}} > 0 \end{aligned}$$
(18)

which may be used for parametrization. Extract the real and imaginary part of \(g(\tau )\), denoting them by \(x\) and \(y\),

$$\begin{aligned} \left\{ \begin{array}{l} x = \cos \tau , \\ y = h(\tau )\sin \tau , \\ \end{array} \right. \quad \text { where } h(\tau ) = \frac{\tau }{2C} + \frac{C}{2\tau }, \; C = \gamma _0 l_1. \end{aligned}$$
(19)

Equation (16) is equivalent to the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \cos \tau =p, &{} p=\mathop {\mathrm {Re}}\nolimits \left( \frac{Ae^{-i\gamma _{0}l_{1}}}{F}\right) ,\\ h(\tau )\sin (\tau )=q, &{} q=\mathop {\mathrm {Im}}\nolimits \left( \frac{Ae^{-i\gamma _{0}l_{1}}}{F}\right) ,\\ \end{array}\right. } \end{aligned}$$
(20)

where \(p\) and \(q\) are known values. Using the results of Appendix I we finally obtain from (20) an explicit formula for the sought (real) permittivity

$$\begin{aligned} \varepsilon _1 = \frac{1}{\omega ^2\mu _0 }\left( {\left( {\frac{\pi }{a}} \right) ^2 + \left( {\frac{\tau }{l_1 }} \right) ^2} \right) , \end{aligned}$$
(21)

here

$$\begin{aligned} \tau =\tau _{1} = C \left( \frac{|q|+\sqrt{p^{2}+q^{2}-1}}{\sqrt{1-p^{2}}}\right) \end{aligned}$$
(22)

when \(\varepsilon _1 > \varepsilon _0\) and

$$\begin{aligned} \tau =\tau _{2}=C \left( \frac{\sqrt{1-p^{2}}}{|q|+\sqrt{p^{2}+q^{2}-1}}\right) \end{aligned}$$
(23)

when \(\frac{\pi ^{2}}{a^{2}\omega ^{2}\mu _0} < \varepsilon _1 < \varepsilon _0\).

Formulas (21)–(23) constitute explicit solution of inverse problem P under study.

Using the reasoning and results of Appendix I we prove the following result stating the existence and uniqueness of solution to the inverse problem of finding permittivity of a one-sectional diaphragm in a waveguide of rectangular cross-section.

Theorem 4.1

Assume that \(|p| < 1\) and \(p^2 + q^2 \ge 1\). Then inverse problem P has only one solution expressed by (22) if \(\frac{\tau _1}{C} > 1\), \(\cos \tau _1 = p\), and \(sign(q) = sign(\sin (\tau _1))\). If \(\frac{\tau _2}{C} < 1\), \(\cos \tau _2 = p\), and \(sign(q) = sign(\sin (\tau _2))\), inverse problem P has only one solution expressed by (23). Otherwise, inverse problem P has no solution.

Remark 4.1

If \(p = 1\), then \(q\) must be equal zero and \(\tau = 2\pi n,\) \(n \in Z\). If \(p= - 1\), then \(q\) must be equal to zero and \(\tau = \pi + 2\pi n,\) \(n \in Z\). In these cases inverse problem P has has infinitely many solutions; therefore they are excluded from Theorem.

5 Conclusion

We have developed a numerical-analytical method of solution to the inverse problem of reconstructing permittivities of \(n\)-sectional diaphragms in a waveguide of rectangular cross-section. For a one-sectional diaphragm, a solution in the closed form is obtained and the uniqueness is proved. These results make it possible to use the case of a one-sectional diaphragm in a waveguide of rectangular cross-section as a benchmark test problem and perform a complete analysis of the inverse scattering problem for arbitrary \(n\)-sectional diaphragms.