Effective High-Precision Analysis of Thin Asymmetric Inductive Diaphragm in Rectangular Waveguide Using Integral Equation Method

Abstract

This paper proposes a solution of the electrodynamic problem of determining the generalized scattering matrix of infinitely thin asymmetric one-sided inductive diaphragm in rectangular waveguide using the integral equation method. The problem is reduced to solving the system of integral equations in terms of the number of incident modes falling on the inhomogeneity from the left partial region. The efficiency of the new solution of electrodynamic problem is achieved owing to the correct way of taking into account the singularity of tangential electric field in the diaphragm aperture using the Gegenbauer polynomials. The Galerkin method is used to reduce each integral equation to the system of linear algebraic equations in complex coefficients of the expansion of tangential electric field in the diaphragm window. Numerical investigation of the obtained solution was conducted for determining the equivalent parameters of diaphragm in the frequency band where only the principal mode can propagate along the waveguide without attenuation. The possibility of effective high-accuracy calculation of the generalized scattering matrix of infinitely thin asymmetric inductive diaphragm in rectangular waveguide with due regard for singularity of tangential electric field at the sharp ridge in the diaphragm window has been confirmed.

1. Introduction

Inductive inhomogeneities in rectangular and square waveguides are widely used [1]–[6] in creating cavity resonators, filters, sections of differential phase shift, devices for measuring coefficients of the scattering matrix in waveguide duct, matching units of waveguide-to-coax transitions and complex loadings, etc.

Usually, the designing of specified devices of microwave technology is based on assumption of their symmetry that essentially simplifies the process of electrodynamic analysis of individual elements. However, in practice, there are no ideally symmetrical waveguide structures in microwave technology. Despite the fact that modern technology base makes it possible to manufacture high precision microwave devices, the estimation of tolerances is an important designing problem with an appropriate efficiency indicator, since setting the strict structure size deviations along with the high accuracy of manufacture stipulates significant unjustified material expenses.

There are two basic approaches to building analysis algorithms of tolerances on manufacture of microwave devices. One of them is based on the analysis of parameter sensitivity of appropriate longitudinally nonuniform structure depending on the change of its geometrical dimensions as illustrated in paper [7] using an example of determination of tolerances on the manufacture of microstrip devices. The other approach to determining the tolerances anticipates the use of the Monte Carlo stochastic method [8], according to which results can be obtained with an accuracy sufficient for practical implementation of the majority of microwave devices on condition of a large number of numerical tests.

Irrespective of the choice of one of the specified approaches for designing each individual device with due regard for possible inaccuracies of fabrication, it is necessary to have effective calculation algorithms of asymmetric structures that appear in such device during the production process. As anticipated, these algorithms can be obtained by implementing the solutions of complex electrodynamic problems. That is why, it is important to have a numerical database that can be used for adjusting the specified algorithms.

Usually, the size deviations of the specified longitudinally nonuniform structures from idealized models are very small. Therefore, the change of the device characteristics caused by inaccuracies of the manufacture can be perceived only by using the algorithms with high accuracy of calculations. The comparative analysis of the algorithm for electrodynamic calculation of parameters of inductive diaphragm of finite thickness with asymmetric window in rectangular waveguide can be considered as an example of using such numerical database. With the reduction of diaphragm thickness and increase of its asymmetry, the calculation parameters must tend toward the appropriate values for asymmetric infinitely thin inductive diaphragm in rectangular waveguide.

The most complete bibliography for the issues of calculation and application of diaphragms in rectangular waveguide is presented in [9]. It reveals that the construction of a fair quantity of microwave devices is based on using the ideal model of thin inductive diaphragm. An assumption of infinitely thin diaphragm that is used in [4], [5] for designing bandpass filters allows us to significantly simplify the analysis of structure under analysis since its entire single mode scattering matrix is determined by one complex reflection coefficient.

As noted in [10], the possible use of the approximate model of diaphragm in the form of its single-wave scattering matrix is limited by its operating frequency band where only the principal mode H₁₀ can propagate without attenuation. The use of diaphragm in the composition of longitudinally inhomogeneous structure is provided by utilizing in calculations of its generalized scattering matrix that takes into account the interaction of adjacent inhomogeneities in terms of higher-order modes [10].

The solution of the electrodynamic problem for classical basic element in the form of thin asymmetric one-sided diaphragm was derived in [11]. The problem was reduced to solving the system of integral equations in terms of the number of incident waves falling on diaphragm. For each of them, a system of linear algebraic equations was obtained by the Galerkin method. This system was obtained in relation to the complex coefficients of the expansion of unknown tangent electric field in the diaphragm window by using the series of proper coordinate functions.

It has been shown that for achieving a high calculation accuracy of the generalized scattering matrix of diaphragm, a large number of coordinate functions must be taken into account. Consequently, the calculation results [11] that are in good agreement with exact solution for reactive conductance of diaphragm were obtained at considerable computing time expenditure. Therefore, the search for alternative approaches of creating effective algorithms of solving the electrodynamic problem for infinitely thin asymmetrical inductive diaphragm is still a topical problem. We refer here to the approaches that could combine the possibility of obtaining high-accuracy results of calculating the generalized scattering matrix with relatively small expenditure of computer resources.

One of the approaches for obtaining the high-accuracy calculation results is the method of partial regions taking into account the singularity of tangential electric field at the sharp edge in the diaphragm window. A high-accuracy calculation of diaphragm reactive conductance based on this method was achieved in paper [9]. In fact, it reflects the single-wave scattering matrix of inhomogeneity in rectangular waveguide with operating frequency band where only the principal mode H₁₀ can propagate along the waveguide without attenuation.

However, the information about the reactive conductance of diaphragm is insufficient if the diaphragm is combined with several basic elements creating a complex longitudinally irregular structure. For ensuring the possibility of using the diaphragm as a component of such longitudinally irregular structure, it is necessary to have capability for calculating its generalized scattering matrix with high accuracy. As noted in [9], [12], the high calculation accuracy is achieved by using algorithms taking into account the singularity of tangential electric field in the aperture of joined waveguides. In addition to the technique of electric field approximation by using the Gegenbauer polynomials that is employed in [9], there is a considerable quantity of other approaches for calculating the division of field at the interface of partial regions [12]. Each approach to approximation of tangential electric field defines its own specific peculiarities.

This study investigates the technique of electric field approximation by using the Gegenbauer polynomials with due regard for [9]; it indicates that the results obtained in [11] for calculating the diaphragm reactive conductance can be extended to the general case of finding the generalized scattering matrix of this inhomogeneity without any restrictions on the structure size and frequency band. The main distinction of the given approach from that in paper [11] is the due regard for singularity of tangential electric field in the diaphragm window [9]. In fact, this paper carries out a high-accuracy analysis of infinitely thin asymmetric inductive diaphragm in rectangular waveguide based on combining approaches [9], [11] for solving the specified electrodynamic problem.

2. Generalized Mathematical Model of Diaphragm

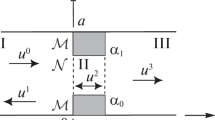
Electrodynamic structure under consideration is schematically shown in Fig. 1 displaying the longitudinal cross section of rectangular waveguide with infinitely thin diaphragm, the plane of which is parallel to the broad wall of waveguide. Here, a is the waveguide width, c is the width of diaphragm window. The scalar problem is under consideration, the solution of which does not depend on the waveguide height b.

Fig. 1.

Physical model of thin diaphragm.

Let us perform the electrodynamic analysis of physical model (Fig. 1) aimed at finding its generalized scattering matrix, the use of which guarantees a high-accuracy simulation of diaphragm as a component of arbitrary longitudinally inhomogeneous structure in rectangular waveguide having arbitrary small distances between adjacent irregularities. Let us use the common designation of generalized scattering matrix [12] $S_{mn}^{(\mu \nu )}$ implying that the n-th mode of the ν-th waveguide transforms into the m-th mode of the μ-th waveguide, where m = 1, 2, …, M and n = 1, 2, …, N.

Determination of $S_{mn}^{(\mu \nu )}$ of the given structure implies the solving of N problems of diffraction of electromagnetic waves on diaphragm. According to this designation, we shall number the eigenfunctions of rectangular waveguide with one index in the ascending order of critical wave numbers. The determination of parameters of generalized scattering matrix involves the need of using a variant of the integral equation method, the partial investigation of which was conducted in [9], [11]. As shown in [11], this approach makes it possible to combine all N solutions of electrodynamic problems of diffraction into one computational procedure.

The solving of key problem will be conducted by using the approximation of ideal conductance of diaphragms and metal walls of rectangular waveguide not filled with dielectric. For the sake of simplicity, we shall assume that the input and output waveguides are the same, while eigenfunctions of partial regions on both sides of diaphragm are identical. For this case, an integral equation of principal mode H₁₀ of rectangular waveguide was obtained in [9] with respect to unknown tangential electric field in the diaphragm window on condition of the incident wave falling on the electrodynamic structure under consideration. This equation enables us to compute the input complex conductance of diaphragm in the frequency band where only the principal mode of rectangular waveguide can propagate.

An approach selected for solving the electrodynamic problem in question involves combining the solutions of integral equations obtained in [9], [11] for the general case of incidence of the entire spectrum of primary electromagnetic modes $H_{n0}$ on the diaphragm from the left partial region. With due regard for homogeneity of the structure along axis y, the electric vector of each of these modes has only one nonzero component that is parallel to the narrow wall of waveguide. Analytical expressions for eigenfunctions of waveguide can be found in accordance with the well-known definition of the generalized scattering matrix $S_{mn}^{(\mu \nu )}$ .

Taking into account the asymmetry of structure under consideration and boundary conditions at metal walls of rectangular waveguide, we must leave the tangential components of eigenfunctions of waveguide in explicit form:

$$ {{\Psi }_{m}}={{A}_{m}}\sin ({{\alpha }_{m}}x), $$

(1)

where ${{\alpha }_{m}}=m\pi /a$ , $m=1,2,...,M$ ; and ${{A}_{m}}$ are the normalizing factors.

The solving of electrodynamic problem under consideration involves the need of using the generalized system of integral equations obtained in [11] in accordance with the technique of equating the tangential components of electric and magnetic fields at the interface of partial regions as was shown in [14]. For the sake of convenience of further analysis, we shall rewrite the specified system of integral equations in the form:

$$ \sum\limits_{m}{{{Y}_{m}}}{{{\Psi }}_{m}}\int\limits_{0}^{c}{E{{{\Psi }}_{m}}dx}={{Y}_{n}}{{{\Psi }}_{n}}, $$

(2)

where E is the unknown tangential electric field in the coupling aperture; $\Psi_m$ and $\Psi_n$ are the tangential components of scalar eigenfunctions of rectangular waveguide; $Y_m$ and $Y_n$ are their corresponding conductances; m = 1, 2, …, M; n = 1, 2, …, N; M is the number of modes that are taken into account in expanding the electric field in waveguide; N is the number of modes that one after another fall on irregularity forming a sequence of diffraction problems. An expression for $\Psi_n$ is determined by formula (1) while replacing m with index n.

It should be noted that system (2) is fundamentally different from model [9] by its complex right-hand side that combines solutions of N diffraction problems in terms of the number of waves that alternatively fall on the diaphragm on the left. For each n we solve the system of integral equations (2) using Galerkin’s method [14]. According to this method, similar to [9], the unknown values of E in the coupling aperture are approximated by series of coordinate functions $\Phi_i$ that take into account the singularity of tangential electric field at the sharp ridge of diaphragm:

$$ E(x)=\sum\limits_{i}{{{\Phi }_{i}}}, $$

(3)

$$ {{\Phi }_{i}}={{D}_{i}}{{[1-{{(x/c)}^{2}}]}^{1/2}}C_{2i-1}^{(1)}(x/c), $$

(4)

where $C_{2i-1}^{(1)}(x/c)$ are the unpaired Gegenbauer polynomials; i = 1, 2, …, I; I is the number of expansion terms. The oddness of Gegenbauer polynomials in expression (4) is the evidence of nonsymmetrical placement of diaphragm in the transverse plane of rectangular waveguide.

Substituting expressions (3) and (4) into (2), in accordance with the Galerkin method for each n we obtain a system of linear algebraic equations with respect to unknown complex coefficients $D_i$

$$ \sum\limits_{i}{{{D}_{i}}\sum\limits_{m}{{{Y}_{m}}{{\eta }_{gm}}{{\eta }_{im}}}}={{Y}_{n}}{{\eta }_{gn}}, $$

(5)

where g = 1, 2, …, G; G is the number of equations in the system that describe the diaphragm properties; $\eta_{im}$ ( $\eta_{gm}$ , $\eta_{gn}$ ) are the coupling coefficients of approximating functions $\Phi_i$ ( $\Phi_g$ ) of diaphragm window with eigenfunctions of waveguide $\Psi_m$ ( $\Psi_n$ ).

It should be noted that the left-hand side of relationship (5) forms the square matrix of coefficients at unknowns, where index i expands the system in rows, while index g expands it in columns. Each component of the matrix of right-hand side of expression (5) corresponds to the solution of individual diffraction problem caused by the specified eigenmode of rectangular waveguide falling on diaphragm. It can be seen that the square matrix of coefficients at unknowns does not depend on the form of right-hand side of system (5). It enables us to solve system (5) by using the software program for solving the system of linear algebraic equations with many right-hand sides. In this case, all components forming the matrix of coefficients must be determined in advance.

Let us determine the coupling coefficient of the i-th approximating function of diaphragm window $\Phi_i$ with the m-th eigenfunction of waveguide $\Psi_m$ in the following form:

$$ {{\eta }_{im}}=\int\limits_{0}^{c}{{{{\Phi }}_{i}}}{{{\Psi }}_{m}}dx. $$

(6)

Coupling coefficients $\eta_{gm}$ and $\eta_{gn}$ are computed by using formula (6) on condition of the appropriate change of indices.

The calculation of coupling coefficients (6) is conducted by using expressions for tangential components of eigenfunctions of waveguide $\Psi_m$ and $\Psi_n$ that are determined by formula (1).

For computing coupling coefficients in accordance with formula (6) we shall use relationship [9] that can be rewritten in the form:

$$ \begin{aligned} &\int\limits_{0}^{c}{{{({{c}^{2}}-{{x}^{2}})}^{\nu -1/2}}C_{2i+1}^{(\nu )}}(x/c)\sin {{\alpha }_{m}}xdx \\ &={{(-1)}^{i}}\pi {{c}^{\nu }}\Gamma (2i+2\nu +1)/[(2i+1)!\Gamma (\nu ) {{(2{{\alpha }_{m}})}^{\nu }}]{{J}_{\nu +2i+1}}({{\alpha }_{m}}c), \end{aligned} $$

(7)

where $C_{2i+1}^{(\nu )}(x/c)$ is the unpaired Gegenbauer polynomial; $\Gamma (2i+2\nu +1)$ and $\Gamma (\nu )$ are gamma functions; and ${{J}_{\nu +2i+1}}({{\alpha }_{m}}c)$ is the Bessel function of the first kind.

Substituting value ν = 1 into expression (7), we finally obtain:

$$ \begin{aligned} &\int\limits_{0}^{c}{{{({{c}^{2}}-{{x}^{2}})}^{1/2}}C_{2i+1}^{(1)}}(x/c)\sin {{\alpha }_{m}}xdx \\ & ={{(-1)}^{i}}\pi c\Gamma (2i+3)/[(2i+1)!\Gamma (1) (2{{\alpha }_{m}})]{{J}_{2i+2}}({{\alpha }_{m}}c). \end{aligned}. $$

(8)

In accordance with expressions (1), (4) and (6), coupling coefficients of the i-th approximating function of diaphragm window $\Phi_i$ with the m-th eigenfunction of waveguide $\Psi_m$ can be presented in the following form:

$$ {{\eta }_{im}}=\int\limits_{0}^{c}{{{[1-{{(x/c)}^{2}}]}^{1/2}}C_{2i-1}^{(1)}(x/c){{\Psi }_{m}}}dx. $$

(9)

The further analysis involves the need of matching formulas (8) and (9). To this end, component $c^2$ in expression (8) should be factored outside the integral sign, and notations i should be substituted with (i – 1). Hence, expression (8) assumes the form:

$$ \begin{aligned} &\int\limits_{0}^{c}{{{[1-{{(x/c)}^{2}}]}^{1/2}}C_{2i-1}^{(1)}}(x/c)\sin {{\alpha }_{m}}xdx \\ & ={{(-1)}^{i-1}}\pi \Gamma (2i+1)/[(2i-1)! (2{{\alpha }_{m}})]{{J}_{2i}}({{\alpha }_{m}}c). \end{aligned} $$

(10)

Substituting (1) and (10) into (9) and calculating the obtained integral in accordance with [15], we have

$$ {{\eta }_{im}}=\sqrt{2/a}{{(-1)}^{i-1}}\pi \Gamma (2i+1)/[(2i-1)! (2{{\alpha }_{m}})]{{J}_{2i}}({{\alpha }_{m}}c). $$

(11)

Coupling coefficients $\eta_{gm}$ and $\eta_{gn}$ are determined by formula (11) on condition of the appropriate change of indices.

3. Model Verification

The practical use of obtained formulas involves the need to estimate the correctness of calculating the coupling coefficients by using the Gegenbauer polynomials for approximating the tangential electric field in diaphragm window. To this end, we shall use an alternative approach to determining the coupling coefficients based on the numerical integration theory [16].

The Gaussian method is one of the best methods of numerical integration of the product of fast oscillating functions [16]. In order to solve the current problem, we shall use the Gaussian 96-point quadrature formula from [11] having the form:

$$ \begin{aligned} \int\limits_{p}^{q}f(x)dx &=(q-p)/2\sum\limits_{\mu }{f({{x}_{\mu }}){{u}_{\mu }}}, \\ {{x}_{\mu }}&=(p+q)/2+(q-p)/2{{v}_{\mu }}, \\ \mu &=1,2,...,96, \end{aligned} $$

(12)

where ${u}_{\mu }$ and ${v}_{\mu }$ are the table values of expansion coefficients of function $f(x)$ .

In accordance with the problem under consideration for coupling coefficients $\eta_{im}$ using formula (12), we shall obtain the following relationship:

$$ {{\eta }_{im}}=\sqrt{a/2}\sum\limits_{\mu }{{{u}_{\mu }}}{{[1-{{({{x}_{\mu }}/c)}^{2}}]}^{1/2}} C_{2i-1}^{(1)}({{x}_{\mu }}/c)\sin {{\alpha }_{k}}{{x}_{\mu }}, $$

(13)

where ${{x}_{\mu }}=c/2+c/2{{v}_{\mu }}$ , $\mu =1,2,...,96$ .

The values of Gegenbauer’s polynomials in (13) are calculated by using the recurrent formula [15]:

$$ C_{\nu }^{(\sigma )}(x)=[2x(\nu +\sigma -1)C_{\nu -1}^{(\sigma )}(x)-(\nu +2\sigma -2)C_{\nu -2}^{(\sigma )}(x)]/\nu, $$

(14)

where $C_{0}^{(\sigma )}(x)=1$ and $C_{1}^{(\sigma )}(x)=2\sigma x$ .

Substituting values σ = 1 into formula (14), we obtain a simple relationship for computing Gegenbauer’s polynomials:

$$ C_{\nu }^{(1)}(x)=[2x\nu C_{\nu -1}^{(1)}(x)-\nu C_{\nu -2}^{(1)}(x)]/\nu. $$

(15)

For checking the results obtained by formula (15), we shall use an alternative formula in accordance with the integral relationship presented in [15], the applicability domains of which lie within limits x > 1:

$$ \begin{aligned} C_{\nu }^{(\sigma )}(x)&=\Gamma (2\sigma +\nu )\Gamma [(2\sigma +1)/2]/\Lambda \int\limits_{0}^{\pi }(x +\sqrt{{{x}^{2}}-1}\cos \varphi {{)}^{\nu }}{{\sin }^{2\sigma -1}}\varphi d\varphi ,\\ \Lambda &=\sqrt{\pi }\nu !\Gamma (2\sigma )\Gamma (\sigma ). \end{aligned} $$

(16)

According to the solution of electrodynamic problem under consideration, formula (16) is substantially simplified and can be reduced to the following form:

$$ C_{\nu }^{(1)}(x)=\Gamma (2+\nu )/(2\nu !)\int\limits_{0}^{\pi }(x +\sqrt{{{x}^{2}}-1}\cos \varphi {{)}^{\nu }}\sin \varphi d\varphi, $$

(17)

where the integral is computed by using the Gaussian 96-point formula.

4. Results of Numerical Investigations

The estimation of the application area of the selected method of numerical integration implies the need to conduct calculations of coupling coefficients $\eta_{im}$ by formulas (11) and (13) using relationships (15) and (17) for control of calculation accuracy. The comparative analysis of these results indicates that for small values of m numerical values of $\eta_{im}$ determined by analytical formula (11) correspond with high accuracy to data obtained by using relationships (13), (15) and (17) for numerical calculation. The calculation data essentially differ when the values of index m approach the order of the Gaussian formula. As follows from the results of this analysis, for high-accuracy calculations, where index m can reach high values, we must use analytical formula (11).

Subsequent calculations with respect to finding the generalized scattering matrix of diaphragm will be performed similar to [11]. Using the obtained analytic relationships, the calculations of elements of the specified matrix will be conducted in the following sequence. Specifying the values of I and M, in accordance with the known sizes of the structure, we calculate the matrix of coupling coefficients. For the known value of frequency, we calculate the normalized conductances of modes that are taken into account in solving the diffraction problem. The obtained data are used for forming the matrix of coefficients at unknowns. This matrix will be used in the routine for solving the systems of linear algebraic equations with numerous right-hand sides. The solving of this system determines the division of tangential electric field in the diaphragm window. The generalized scattering matrix of diaphragm will be found based on this division by using formulas [17].

We will start the investigations of properties of obtained solutions from the analysis of input conductance of infinitely thin inductive diaphragm, having the window width equal to a half width of rectangular waveguide c = a/2. The study of asymmetrical diaphragm characteristics is a key problem of the current analysis because the exact solution exists for this case. Paper [9] presents the value of diaphragm reactive conductance calculated with high accuracy for ratio c = a/2 and the value of frequency parameter 2a/λ = 1.4, where λ is the wavelength in free space. For a rectangular waveguide having the broad wall size of 48 mm, this value of frequency parameter corresponds to the operating frequency of 4.375 GHz. The values of normalized input conductance of diaphragm at this frequency in accordance with [9] is as follows:

$$ {{Y}_{1}}=\frac{1-{{R}_{1}}}{1+{{R}_{1}}}=G+jB=1-4.835147j, $$

(18)

where R₁ is the coefficient of mode H₁₀ reflection from diaphragm; G is the active component that numerically is equal to the ratio of wave resistances of waveguides on both sides of diaphragm; B is the normalized reactive conductance of diaphragm.

For obtaining the result of (18), paper [11] makes use of the well-known approximation method implying that the ratios between the transverse dimensions of diaphragm and rectangular waveguide are directly proportional to the numbers of electromagnetic waves that are taken into account therein. Additional investigation of the specified rule was conducted in [11] based on the exact solution for reactive conductance of infinitely thin asymmetrical inductive diaphragm in rectangular waveguide. Using the notations employed in this paper, this rule can be written as follows:

$$ c/a=I/M. $$

(19)

If for this approximation technique the rule (19) of the correct selection of numbers of electromagnetic waves taken into account in diaphragm window and the rectangular waveguide is known, the calculation of the generalized scattering matrix with due regard for singularity of tangential electric field at the sharp ridge of diaphragm involves the need to carry out additional examination of the phenomenon of relative convergence.

The most correct way of conducting this investigation is to use an example of infinitely thin asymmetric one-sided inductive diaphragm located in the transverse plane of waveguide and connected with its narrow wall. For determining the ratio between the number of approximating functions in the diaphragm window and the number of eigenmodes employed in the expansion of tangential electric field in waveguide, we shall perform calculations of reactive conductance of diaphragm for a number of values of M depending on the order of the system of linear algebraic equations I.

The results of specified calculations indicate a very fast convergence of data for reactive conductance of diaphragm as a function of $B=f(M,I)$ with an increase of the order of equation system I. At M = const the calculation data of function $B=f(M,I)$ are stabilized for each value of order I ≥ 3. It should be noted that with an increase of I, the number of eigenmodes M required for getting a high-accuracy solution of relationship (18) substantially increase. We refer here to the eigenmodes that are taken into account in forming the matrix coefficients of system of linear algebraic equations (5).

For the correct selection of I value, initially we shall conduct an examination of reactive conductance with the smallest value of I = 2 that corresponds to the solution of system of linear algebraic equations (5) of the second order.

The possibility of comparing the results obtained in this study with well-known data [11] during the numerical examinations implies the need, along with the normalized input conductance of diaphragm, to use the modulus and phase of the transmission coefficient of principal mode of rectangular waveguide passing through diaphragm as an element of single-mode scattering matrix. Numerical values of modulus $\mu =|S_{11}^{(21)}|$ and phase $\varphi =\arg [S_{11}^{(21)}]$ of the transmission coefficient that are calculated in accordance with exact value (18) of the diaphragm input conductance correspond to μ = 0.3822293 and φ = 67.528159°, respectively. All the results of studies were obtained for the physical model of diaphragm (Fig. 1) in accordance with formulas (5) and (11).

For investigating the properties of obtained solution based on the integral equation method with due regard for singularity of tangential electric field at the sharp ridge of diaphragm, we calculated its reactive conductance depending on the order of system (5) and the number of modes M in the expansion of electric field in waveguide.

Figure 2 displays the calculation data for relatively small values of M, which include relative error

$$ \delta =(|{{B}_{\rm exact}}|-|{{B}_{\rm appr}}|)/|{{B}_{\rm exact}}|\times 100 $$

of calculating the reactive conductance of asymmetric diaphragm depending on the number of eigenmodes in determination of matrix coefficients of the system of linear algebraic equations (5) at I = 2.

Fig. 2.

Relative error of calculating diaphragm reactive conductance as function of number of eigenmodes M that are taken into account in the expansion of electric field in waveguide while determining the coefficients of system of linear algebraic equations (5).

As follows from the calculation results at a small number of eigenmodes M, we can observe a fast reduction of relative computation error of reactive conductance. After achieving the value of M = 2,000, the reactive conductance of asymmetrical diaphragm slows tends to exact value (18) as it is shown in Fig. 2 and in Table 1 reflecting the calculation results for large values of M. In this case, the relative error of computing the diaphragm reactive conductance becomes minimal if the number of eigenmodes taken into account while determining the matrix coefficients of equation system exceeds M = 8,000 (Table 1).

Table 1. Convergence of normalized reactive conductance, modulus and phase of transmission coefficient of rectangular waveguide for large values of the number of eigenmodes that are taken into account in determining the matrix coefficients of the system of linear algebraic equations (5)

At I = 2 and M = 8,000, relative error amounts to δ = 0.0049% that corresponds to the absolute value of normalized reactive conductance of diaphragm equal to –4.83491. As can be seen from the analysis of Table 1, further increase of computation accuracy continues to rise with an increase of M. Hence, at M = 12,000 the relative error is δ = 0.001303%, while at M = 14,000 we have δ = 0.0002689%. Finally, at M = 14,650 we get the exact value of normalized reactive conductance B = –4.835147 and relative error δ = 0.0%.

Along with determination of relative error δ, the calculation of diaphragm reactive conductance (Table 1) illustrates the convergence of calculation results of reactive conductance B, modulus of μ, and phase φ of the transmission coefficient of the rectangular waveguide principal mode passage through diaphragm for large vales of M.

The results in Table 1 show that initially values of δ reduce achieving the exact value δ = 0 at M = 14,650, and then gradually increase (with minus sign) with further rise of M. The values of modulus μ = 0.38222932 and phase φ = 67.528159° of the transmission coefficient of principal mode of rectangular waveguide passing through the thin asymmetrical diaphragm as well as the exact value of its reactive conductance that is equal to –4.835147 in accordance with formula (18) are achieved at M = 14,650.

Thus, the relationship $\delta =f(M,I=$ const) has the minimum at M_opt = 14,650 that should be taken into account in practical problems on the use of the obtained solution of electrodynamic problem in determining the generalized scattering matrix of infinitely thin asymmetrical inductive diaphragm in rectangular waveguide.

As follows from Table 1, the characteristic $\delta =f(M,I=$ const) is asymmetric with respect to optimal value M_opt that corresponds to the exact value of reactive conductance of diaphragm. It can be seen that in the region of values M > M_opt an increase of M affects the accuracy of determining the normalized reactive conductance of diaphragm much less than in the region M < M_opt.

Using Table 1 and Fig. 2, we can determine the number of eigenmodes M taken into account in expansion of the electric field in waveguide in the process of determining the matrix coefficients of the system of linear algebraic equations (5). In this case, it is necessary to solve the equation system for achieving the required calculation accuracy of reactive conductance B and related to it modulus μ and phase φ of the transmission coefficient of the principal mode of rectangular waveguide passing through diaphragm.

It should be noted that the fast convergence of calculation results in using the method of integral equations with correct regard for singularities of field at the ridge in coordinate approximating functions (Gegenbauer’s polynomials) was demonstrated also in solving the problems for eigenmodes of coaxial sector and 4-ridged waveguides [18], [19] and also the quadrature waveguides with longitudinal infinitely thin metal plate [20].

5. Example Use

For determining data that may indicate the continuation of theoretical investigations initiated in [11] and having vital importance for practical application of results obtained in this study, we shall consider an example of determining the coefficient of mode H₂₀ reflection from diaphragm as element $S_{22}^{(11)}$ . This example illustrates the possibility of calculating the generalized scattering matrix of infinitely thin asymmetrical inductive diaphragm in rectangular waveguide with due regard for singularity of tangential electric field at the interface of partial regions. It is based on high-accuracy results obtained in [11] by using the integral equation method on condition of approximating the tangential electric field in diaphragm window by its coordinate function expansion into series.

In accordance with [11] for the dimension ratio of diaphragm window and waveguide c/a = 0.5 and frequency parameter 2a/λ = 2.2 that corresponds to frequency 6.875 GHz for the waveguide with width of 48 mm, we have:

$$ \begin{aligned} S_{22}^{(11)}&=(-0.656089,\;0.092295j), \\ |S_{22}^{(11)}|&=0.662549, \\ \arg [S_{22}^{(11)}]&={{171.992473}^{\circ }}. \end{aligned} $$

(20)

The corresponding data obtained as a result of computing reflection coefficient $S_{22}^{(11)}$ , its modulus $|S_{22}^{(11)}|$ and phase $\arg [S_{22}^{(11)}]$ by solving the system of linear algebraic equations (5) using formula (11) for the coupling coefficients of coordinate functions of diaphragm window that take into account the singularity of tangential electric field at the interface of partial regions with egenfunctions of rectangular waveguide is presented in Table 2. It shows the convergence of obtained results of calculating reflection coefficient $S_{22}^{(11)}$ , its modulus $|S_{22}^{(11)}|$ and phase $\arg [S_{22}^{(11)}]$ with increasing order I of the system of linear algebraic equations (5) at M = const to the high-accuracy data from paper [11].

Table 2. Convergence of calculation results of coefficient of mode H₂₀ reflection from diaphragm for large values of the number of eigenmodes

Table 2 demonstrates rapid convergence of calculation results of reflection coefficient $S_{22}^{(11)}$ , its modulus $|S_{22}^{(11)}|$ and phase $\arg [S_{22}^{(11)}]$ depending on the order I of the system of linear algebraic equations (5). The calculation data is stabilized at I ≥ 4.

The analysis of results in Table 1 reveals that in conducting calculations of the diaphragm parameters in the frequency band when only principal mode of rectangular waveguide can propagate along waveguide without attenuation, it is sufficient to use the second order (I = 2) of the system of linear algebraic equations (5). When performing calculations of parameters of the generalized scattering matrix, it is necessary to solve the specified system in the fourth or fifth approximations as illustrated in Table 2.

The comparative analysis indicates that the results presented in Table 2 accurately agree with data in [11], where the properties of solving the electrodynamic problem by the method of integral equations are investigated on condition of approximating the tangential electric fields in waveguide and diaphragm window by using series ${{{\Psi }}_{m}}={{A}_{m}}\sin ({{\alpha }_{m}}x)$ ; ${{\Phi }_{k}}={{B}_{k}}\sin ({{\beta }_{k}}x)$ , where ${{\alpha }_{m}}=m\pi /a$ , ${{\beta }_{k}}=k\pi /c$ , ${{A}_{m}}=\sqrt{2/a}$ , and ${{B}_{k}}=\sqrt{2/c}$ .

6. Conclusions

This paper presents a solution for the electrodynamic problem of determining the generalized scattering matrix of infinitely thin asymmetrical one-sided inductive diaphragm in rectangular waveguide obtained by using the method of integral equations and taking into account singularities of tangential electric field at the sharp ridge in diaphragm window.

In such a case, we examined two approaches to finding the coupling coefficients of coordinate functions that approximate the tangential electric field in diaphragm window using eigenfunctions of rectangular waveguide. One of them ensures the derivation and use of analytical expressions using Gegenbauer’s polynomials. Another approach is based on numerical integration of the product of coordinate functions of diaphragm window and eigenfunctions of waveguide. A conclusion has been made on the basis of performed calculations. It implies that the high-precision determination of elements of the generalized scattering matrix involves the need to use only analytical relationships.

The effect of the number of electromagnetic waves taken into account during the expansion of electric field in waveguide and the coordinate functions in diaphragm window on the accuracy of calculation of the generalized scattering matrix was studied. It was shown that for the calculation of diaphragm parameters in the frequency band where only the principal mode of rectangular waveguide can propagate without attenuation, it is sufficient to use two coordinate functions with correct regard for the singularities at the ridge. The relative error of calculating the reactive conductance of diaphragm depending on the number of electromagnetic waves taken into account in waveguide while solving the system of linear algebraic equations of the second order was estimated.

The possibility of calculating the generalized scattering matrix of infinitely thin asymmetrical inductive diaphragm in rectangular waveguide with due regard for singularity of the tangential electric field at the interface of partial regions was demonstrated by using an example of finding the coefficient of wave H₂₀ reflection from diaphragm as element $S_{22}^{(11)}$ .

A fast rate of convergence of calculation results of reflection coefficient $S_{22}^{(11)}$ , its modulus $|S_{22}^{(11)}|$ and phase $\arg [S_{22}^{(11)}]$ depending on the order of system of linear algebraic equations was achieved. It has been shown that the values of the coefficient of wave H₂₀ reflection from diaphragm determined on the basis of solving the system of equations of the fourth and fifth orders practically coincide.

The results of diaphragm examination using the obtained solution have not only an independent significance, for example as matching elements of some microwave devices. They can be also used in developing the analysis algorithms for estimating tolerances on manufacture of microwave devices, for accuracy control of calculating the electrodynamic parameters of structures with very thin diaphragms by using the general methods for solving the electrodynamic problems aimed at analysis of waveguide structures with thin diaphragms. In addition, the results of this study can be applied in developing of algorithms for fast and high-accuracy calculation of frequency characteristics of multistage asymmetrical waveguide structures.