1 INTRODUCTION

Waveguides are widely used in the physics of microwave oscillations [1]. As it is known, plane-transverse inhomogeneities are often used in waveguide technique to form resonators and matching elements. The most popular among them are thin metal diaphragms, which are placed perpendicular to the longitudinal axis of the waveguide and partially overlap its cross section.

The problems of diffraction of electromagnetic waves by diaphragms and other inhomogeneities are considered in the lecture notes of Yu. Schwinger [2].

Waveguides with resonant structures and other inhomogeneities are used as mode converters or as filters. An analysis of the waveguide bandpass filter on complex resonant diaphragms with L-shaped ridges is given in [3, 4]. The possibility of using a waveguide filter with resonant diaphragms for the irradiator of mirror antennas is shown in [5].

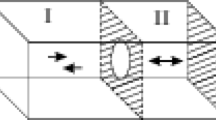
In this work, we study the two-dimensional diffraction problem of a TE–wave in an infinite diaphragmed waveguide with a built-in rectangular resonator (Fig. 1). The resonator in the waveguide corresponds to region II between two sequentially arranged parallel diaphragms. Some resonance properties of a rectangular resonator with a hole in the wall, by means of a computational experiment, were established in [6], where it was shown that the resonance frequencies of a straight-line resonator with a small hole in the wall are close to the natural frequencies of the same resonator but without a hole.

Fig. 1
figure 1

Infinite diaphragmed waveguide with resonance region.

Full size image

In this paper, we will use the method of integral-series identity [7] when reducing paired series functional equations on diaphragms to a regular infinite system of linear algebraic equations (ISLAE).

We will study the diffraction problem from the point of view of the resonant propagation of a wave through region II. Besides the monograph [8], in which many specific examples of problems with resonant scattering are given, we note [9], where the problem of the resonant transmission of the main wave of a rectangular waveguide through a diaphragm is studied. We also note the well-known effect of resonant reflection of the main wave from the abrupt expansion of the waveguide [10].

2 THE TWO-DIMENSIONAL DIFFRACTION PROBLEM IN AN INFINITE DIAPHRAGMED WAVEGUIDE

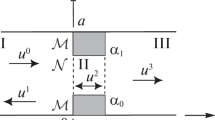
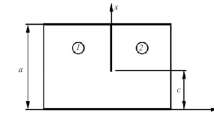
Let us consider the two-dimensional diffraction problem of a TE-polarized wave in an infinite plane waveguide with a built-in rectangular resonator with holes (Fig. 2). Let \(a\) be the cross-sectional size of the waveguide. The resonator corresponds to the region \(0<x<a\), \(0<z<c\) between two resonant diaphragms located in the planes \(z=0\), \(z=c\) the cross section of the waveguide. We denote by \(\mathcal{N}_{0}=(\alpha_{0},\beta_{0})\) the hole of the diaphragm located in the plane \(z=0\), and by \(\mathcal{M}\) its remaining part. Similar notation, but with the index \(c\), will be used for the second diaphragm located in the plane \(z=c\). Thus, all the parameters of the waveguide structure can be set by the sizes of the resonator \(a,c\) and its holes in the walls \(\mathcal{N}_{0}=(\alpha_{0},\beta_{0}),\mathcal{N}_{c}=(\alpha_{c},\beta_{c})\).

Fig. 2
figure 2

Infinite waveguide with rectangular resonator.

Full size image

Suppose that there are no free currents and charges, the medium is homogeneous and isotropic, the electromagnetic field is harmonically dependent on time, and this dependence has the form \(e^{-i\omega t}\) and does not depend on the coordinate \(y\). The potential functions of TE polarized eigenwaves have the form

$$\varphi_{n}(x)e^{\pm i\gamma_{n}z},\quad\varphi_{n}(x)=\sqrt{2/a}\sin\frac{\pi nx}{a},\quad\gamma_{n}=\sqrt{\kappa^{2}-\left(\pi n/a\right)^{2}},\quad n=1,2,\dots,$$

moreover \(Re\gamma_{n}>0\) or \(Im\gamma_{n}>0\). The sign \(+\) corresponds to waves of positive orientation (propagating to the right or decaying to the right) and the sign—corresponds to waves of negative orientation (propagating to the left or decaying to the left). The wave number \(\kappa\) is directly proportional to the frequency of electromagnetic waves.

Let eigne wave \(u^{0}(x,z)=\varphi_{l}(x)e^{i\gamma_{l}z}\) run on the diaphragm in the plane \(z=0\) out of the waveguide. We will look the reflected wave (\(z<0\)) in the form \(u^{1}(x,z)=\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)e^{-i\gamma_{n}z},\) standing wave (\(0<z<c\)) and refracted wave (\(z>c\)) in the form

$$u^{2}(x,z)=\sum_{n=1}^{+\infty}\left(b_{n}e^{i\gamma_{n}z}+c_{n}e^{-i\gamma_{n}z}\right)\varphi_{n}(x),\quad u^{3}(x,z)=\sum_{n=1}^{+\infty}d_{n}\varphi_{n}(x)e^{i\gamma_{n}z}$$

respectively. We write down the boundary conditions and the conjugation conditions for \(z=0\). On the metal \(\mathcal{M}_{0}=\{0<x<\alpha_{0}\}\cup\{\beta_{0}<x<a\}\) we have

$$\varphi_{l}(x)+\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)=0,$$
(1)
$$\sum_{n=1}^{+\infty}b_{n}\varphi_{n}(x)=-\sum_{n=1}^{+\infty}c_{n}\varphi_{n}(x),$$
(2)

and on the hole \(\mathcal{N}_{0}=\{\alpha_{0}<x<\beta_{0}\}\) we have

$$\varphi_{l}(x)+\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}\left(b_{n}+c_{n}\right)\varphi_{n}(x),$$
(3)
$$\gamma_{l}\varphi_{l}(x)-\sum_{n=1}^{+\infty}a_{n}\gamma_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}\left(b_{n}-c_{n}\right)\gamma_{n}\varphi_{n}(x).$$
(4)

Now we write down the boundary conditions and the conjugation conditions on the second diaphragm (\(z=c\)). On metal \(\mathcal{M}_{c}=\{0<x<\alpha_{c}\}\cup\{\beta_{c}<x<a\}\) we have

$$\sum_{n=1}^{+\infty}d_{n}\varphi_{n}(x)e^{i\gamma_{n}c}=0,$$
(5)
$$\sum_{n=1}^{+\infty}\left(b_{n}e^{i\gamma_{n}c}+c_{n}e^{-i\gamma_{n}c}\right)\varphi_{n}(x)=0,$$
(6)

and at the hole \(\mathcal{N}_{c}=\{\alpha_{c}<x<\beta_{c}\}\) we have

$$\sum_{n=1}^{+\infty}\left(b_{n}e^{i\gamma_{n}c}+c_{n}e^{-i\gamma_{n}c}\right)\varphi_{n}(x)=\sum_{n=1}^{+\infty}d_{n}\varphi_{n}(x)e^{i\gamma_{n}c},$$
(7)
$$\sum_{n=1}^{+\infty}\left(b_{n}e^{i\gamma_{n}c}-c_{n}e^{-i\gamma_{n}c}\right)\gamma_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}d_{n}\gamma_{n}\varphi_{n}(x)e^{i\gamma_{n}c}.$$
(8)

We denote

$$I^{0}_{nm}=\int\limits_{\mathcal{M}_{0}}\varphi_{n}(t)\varphi_{m}(t)dt,\quad J^{0}_{nm}=\int\limits_{\mathcal{N}_{0}}\varphi_{n}(t)\varphi_{m}(t)dt,$$
$$I^{c}_{nm}=\int\limits_{\mathcal{M}_{c}}\varphi_{n}(t)\varphi_{m}(t)dt,\quad J^{c}_{nm}=\int\limits_{\mathcal{N}_{c}}\varphi_{n}(t)\varphi_{m}(t)dt.$$

Theorem 1. The problem of the electromagnetic wave diffraction on diaphragm (hole in the wall of the resonator) is reduced to ISLAE

$$b_{k}-\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\sum_{m=1}^{+\infty}\frac{1}{\gamma_{m}}I^{0}_{nm}J^{0}_{mk}+\sum_{n=1}^{+\infty}c_{n}I^{0}_{nk}=\sum_{m=1}^{+\infty}\frac{\gamma_{l}}{\gamma_{m}}J^{0}_{lm}J^{0}_{mk},$$
(9)
$$\sum_{n=1}^{+\infty}b_{n}e^{i\gamma_{n}c}I^{c}_{nk}+c_{k}e^{-i\gamma_{k}c}-\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\gamma_{n}\sum_{m=1}^{+\infty}\frac{1}{\gamma_{m}}I^{c}_{nm}J^{c}_{mk}=0$$
(10)

relative to the coefficients \(b_{n}\), \(c_{n}\) of the standing wave \(u^{2}(x,z)\).

Note that the ISLAE (9), (10) should be solved together relative to the vector \(\left(b_{1},b_{2},\dots,c_{1},c_{2},\dots\right)\).

Proof. From (1), (2) and (3) follows that (3) is fulfilled on \(\mathcal{N}_{0}\) and on \(\mathcal{M}_{0}\). Then \(a_{l}=\left(b_{l}+c_{l}\right)-1,\) \(a_{n}=\left(b_{n}+c_{n}\right),\) \(n\not=l.\) We exclude the variables \(a_{n}\) from (4) and get on \(\mathcal{N}_{0}\)

$$\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\varphi_{n}(x)=\gamma_{l}\varphi_{l}(x).$$
(11)

To regularize paired series functional equations (2), (11), we use the integral-series identity (ISI)

$$\int\limits_{\mathcal{N}_{0}\cup\mathcal{M}_{0}}\left(\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\varphi_{n}(t)\right)K(x,t)dt=\sum_{n=1}^{+\infty}b_{n}\varphi_{n}(x),$$

where \(K(x,t)=\sum_{m=1}^{+\infty}\frac{1}{\gamma_{m}}\varphi_{m}(x)\varphi_{m}(t).\) We have from the ISI by (11) on \(\mathcal{N}_{c}\)

$$\sum_{n=1}^{+\infty}b_{n}\varphi_{n}(x)=\sum_{m=1}^{+\infty}\frac{\gamma_{l}}{\gamma_{m}}J^{0}_{lm}\varphi_{m}(x)+\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\sum_{m=1}^{+\infty}\frac{1}{\gamma_{m}}I^{0}_{nm}\varphi_{m}(x).$$
(12)

Project pair equation (2) and (12) on functions \(\varphi_{k}(x)\). The result will be (9).

Now we consider the boundary and conjugation conditions for \(z=c\) (on the second diaphragm). From (5), (6) and (7) it follows that (7) is fulfilled both on \(\mathcal{N}_{c}\) and on \(\mathcal{M}_{c}\), then \(d_{n}e^{i\gamma_{n}c}=(b_{n}e^{i\gamma_{n}c}+c_{n}e^{-i\gamma_{n}c}).\) We exclude \(d_{n}\) from (8) and get on \(\mathcal{N}_{c}\)

$$\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\gamma_{n}\varphi_{n}(x)=0.$$
(13)

ISI takes place

$$\int\limits_{\mathcal{N}_{c}\cup\mathcal{M}_{c}}\left(\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\gamma_{n}\varphi_{n}(t)\right)K(x,t)dt=\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\varphi_{n}(x).$$

We have from the ISI by (13) on \(\mathcal{N}_{c}\)

$$\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\varphi_{n}(x)=\sum_{n=1}^{+\infty}c_{n}e^{-i\gamma_{n}c}\gamma_{n}\sum_{m=1}^{+\infty}\frac{1}{\gamma_{m}}I^{c}_{nm}\varphi_{m}(x)$$
(14)

Project pair equation (6) and (14) on functions \(\varphi_{k}(x)\). The result will be (10). \(\Box\)

3 COMPUTATIONAL EXPERIMENT

An approximate solution of the ISLAE (9)–(10) will be sought by the truncation method. We write down truncated set of linear algebraic equations (SLAE)

$$b_{k}-\sum_{n=1}^{N}b_{n}\gamma_{n}\sum_{m=1}^{M}\frac{1}{\gamma_{m}}I^{0}_{nm}J^{0}_{mk}+\sum_{n=1}^{N}c_{n}I^{0}_{nk}=\sum_{m=1}^{M}\frac{\gamma_{l}}{\gamma_{m}}J^{0}_{lm}J^{0}_{mk},$$
(15)
$$\sum_{n=1}^{N}b_{n}e^{i\gamma_{n}c}I^{c}_{nk}+c_{k}e^{-i\gamma_{k}c}-\sum_{n=1}^{N}c_{n}e^{-i\gamma_{n}c}\gamma_{n}\sum_{m=1}^{M}\frac{1}{\gamma_{m}}I^{c}_{nm}J^{c}_{mk}=0.$$
(16)

Note that the SLAE (15)–(16) has a block structure of the form

$$\begin{pmatrix}\mathbf{B}_{0}&\mathbf{C}_{0}\\ \mathbf{B}_{0}&\mathbf{C}_{0}\end{pmatrix}\begin{pmatrix}\mathbf{b}\\ \mathbf{c}\end{pmatrix}=\begin{pmatrix}\mathbf{y}\\ \mathbf{0}\end{pmatrix},$$
(17)

where square blocks of size \(N\times N\) are denoted by capital letters and small are vectors of size \(N\). As numerical experiments show, for the internal convergence of the truncation method, it is sufficient to restrict ourselves to the case when \(N=M=20\). Note that the matrix of the system (17) has dimension \(2N\times 2N=40\times 40\).

We set the resonator sizes \(a=1.1\), \(c=2.2\) in dimensionless quantities. The calculation results have shown that the dependencies on the coefficients of the reflected (in region I) and transmitted (in region III) waves in the spectral parameters \(\kappa\) have resonances at frequencies close to the eigen frequencies \(\kappa_{m,n}\) of the resonator without holes. Moreover, the hole parameters \(\mathcal{N}_{0}=(\alpha_{0},\beta_{0})\), \(\mathcal{N}_{c}=(\alpha_{c},\beta_{c})\) affect the \(S\)-scattering matrix.

Fig. 3 shows the dependencies of the parameters \(S_{11}\) (solid line) and \(S_{21}\) (dashed line) of the \(S\)-scattering matrix of the spectral parameter \(\kappa\), which varies within the eigne frequency \(\kappa_{1,1}\approx 3.1931\). The holes are chosen as follows: \(\mathcal{N}_{0}=\mathcal{N}_{c}=(0.4,0.7)\).

Fig. 3
figure 3

Dependencies of the parameters of the scattering matrix \(S\) on the spectral parameter \(\kappa\).

Full size image

4 CONCLUSION

The diffraction problem of a TE-wave in a plane waveguide with an integrated resonator is reduced to an infinite set of linear algebraic equations for the field expansion coefficients in the resonator region.

Computational experiments have shown that the dependencies of the modules of the coefficients of the reflected and transmitted (in region III) waves are resonant in nature. Resonances are observed at incident wave frequencies close to the eigenfrequencies of the resonator without holes. Thus, it can be concluded that near the eigen frequencies of the resonator, partial or complete passage of the incident wave is possible, while the parameters of the holes in the resonator walls significantly affect the \(S\)-scattering matrix of this waveguide structure.