On the Size of the Representative Volume Element Used for the Strength Prediction: A Statistical Survey Applied to the Particulate Reinforce Metal Matrix Composites (PRMMCs)

Abstract

Particulate reinforced metal matrix composites (PRMMCs) are typical random heterogeneous materials whose global behavior depends on the microstructural characterisics. Recently a numerical approach was developed (Hachemi et al., Int J Plast 63:124–137, 2014 [1], Chen et al. Direct methods for limit and shakedown analysis of structures, 2015 [2]), by applying it to a typical PRMMC material WC/Co, we presented how the ultimate strength and endurance limit can be predicted from the material microstructures. Due to the randomness in the microstructures of PRMMCs, size of the representative volume element (RVE) has a nontrivial influence over the predicted effective behaviors. In order to understand how size of RVEs contribute to the result and based on that to eliminate its influence, a numerical investigation is performed in the present study. In this study, a large number of representative volume element (RVE) samples representing a representative PRMMC material, WC-20 Wt% Co, were built from artificial microstructures. The samples are obviously different in size, and by deploying the established numerical approach to these samples, ultimate strength and endurance limit were calculated. Afterwards, the derived material strengths were analyzed by multiple inferential statistical models. The statistical study reveals how strength and other effective material properties react to the change of the RVE size. On that basis, the study proposed a feasible and computationally inexpensive solution to minimize the size effect.

1 Introduction

Over the past three decades, particulate reinforced metal matrix composites (PRMMCs) have been transformed from a topic of scientific and intellectual interest to materials of broad technological and commercial significance [3]. In many industrial sectors, a clear trend can be seen that the application of PRMMCs prevail and gradually replace the conventional metallic materials in structural components. This trend in turn fosters the need to strengthen the understanding of the material behavior and based on that further reduce the development period of new PRMMC materials. Components made from PRMMCs often operate under variable loads with unknown time history. In order to evaluate the serviceability of these materials, their fatigue behaviors have to be well understood.

In many existing works, based on experimental observation, the dependence of the fatigue behavior of PRMMCs on the microstructural characteristics, such as size [4, 5] and distribution of the reinforcement phase [6, 7] have been investigated. In addition to these experimental works, numerical methods based on the micromechanical finite element (FE) analysis were also developed and applied to the PRMMC materials. By using these numerical methods, one can predict the macroscopic effective material behavior of interest from the material microstructure, and this significantly reduces the time for developing new PRMMC materials. For PRMMCs, one material behavior of particular interest is their load bearing capacity. However, according to [8], this is probably the most disputed part. Despite the difficulties arising from modeling the representative material morphology and defining the boundary conditions, Füssl and Lachner proposed in [8] to determine the strength from the limit analysis. The similar technique has been presented in many studies, c.f. [9, 10]. In these papers, the global material strength, both ultimate strength and endurance limit, were predicted by applying the direct method to the representative volume element (RVE) and converting the results to their corresponding macro quantities by means of the homogenization. Compared to the analytical approaches, the greatest advantage of such approach is that the influence of the material microstructure can be immediately identified.

In our latest studies, this numerical technique was extended to the random heterogeneous PRMMC materials. One major challenge pertained to these materials is, that the microstructure can not be embodied by one individual RVE model. Due to this reason, we proposed to predict the material strength from many RVE models called statistical equivalent representative volume element (SERVE). Although the method has been successfully implemented to an representative PRMMC material, WC-Co, with different binder contents and the results obtained from SERVEs were carefully interpreted by statistical models, one important issue, the size effect, is still not fully exposed. The size effect can be explained as follows: For nonperiodic materials, the absence of periodicity of material excludes to embody the infinite domain of the material by an individual RVE of finite size; therefore the predicted material behavior depends largely on the adopted RVE size.

In brief, the RVE size has to exceed a critical value to ensure that the simulation results are independent of both the RVE size and the spatial distribution of the reinforcements [11]. Regarding the determination of the RVE size, Hill [12] has provided an insight from an energetic point of view and developed a condition which requires the equality to hold for a sufficiently large RVEs. Because this condition, which is referred as the Hill’s condition, made no hypothesis on the link between stresses and strains, therefore it should be compatible with any constitutive law. Beside Hill’s condition, there are many pragmatic approaches for determining the RVE size, e.g. windowing method [13] which arbitrarily builds RVEs with fixed window size and compares between predicted results from different windows; boundary condition method [14] which examines the consistency between predictions obtained from statically uniform boundary conditions (SUBC), kinematically uniform boundary conditions (KUBC), and periodic boundary conditions (PBC); size convergence approach [15] which gradually enlarges the RVE size and accepts the size where the prediction is stabilized.

In addition to the pragmatic approaches, the problem of RVE size determination has been intensively studied from a theoretical perspective. For example, Drugan and Willis [16] studied a linear elastic composite and proposed a criterion for determining the minimum RVE size by comparing the ratio of the magnitude of nonlocal terms to the magnitude of local terms. According to this criterion, the minimum RVE size is required to be at maximum twice the reinforcement diameter for any reinforcement concentration level. This criterion has been subsequently approved in few subsequent studies [17, 18]. In multiple studies concerning different types of composite materials, a general observation has been reported that the size required for predicting the effective elastic behavior is relatively small and depends only on the volume fraction [19]. Beyond the scope of linear elasticity, many studies confirmed that the minimum size of an RVE needed to capture the nonlinear behavior are much larger than the ones for determining the linear behavior [20, 21]. In our previous study [22], we observed from few RVE samples built from the real scanning electron microscope (SEM) images of WC-Co, that the disparity between the models becomes more obvious when plastic deformation accumulates. Based on this observation, we concluded that all indicators for checking the fulfillment of the size requirement are necessary but insufficient criteria. Therefore a remedy to the difficulty of determining the RVE size is to use SERVE models.

According to the concept of SERVE, the material behavior of a random composite should be evaluated from a series of statistically equivalent RVE samples [23]. The evaluation should be based on statistical descriptors such as mean-value, variances, and probability density function [24]. When the size of SERVEs increases, each SERVE sample tends to become the RVE and differences among them become negligible [25]. Meanwhile, using typical statistical analysis techniques such as correlation analysis, the dominant factors influencing the material constitutive properties can be identified [26].

To achieve a satisfactory level of reliability, the number of SERVE samples should be guaranteed to exceed a threshold value. This threshold value can be determined from the margin of error, the confidence level and the standard deviation of the data. Among existing studies, the number of RVEs varies significantly. In most studies only a small number of samples, e.g. 15 [27] or 25 [28], are used to predict the material behavior. Only seldom would an extremely large number of samples be adopted for the analogous purpose [29].

Although by using SERVE models the difficulty for determining the RVE size and eliminating the size effect is greatly reduced, it is still an open question that, how large should each statistically equivalent RVE be—especially, if the aim of the homogenization study is not only to predict the mean value, but also other statistical characteristics of an effective behavior. As has been summarized, the minimal RVE size depends on the type of the behavior to be studied. Due to this reason, the objective of the present study is to expose how to determine the size of RVEs used for determining the material strength. In the present study, the material investigated in our previous works, tungsten carbide-cobalt hard metal with 20 Wt.% of the binder phase, WC-20 Wt.% Co, was again used as an representative PRMMC material. WC-Co is one of the most used materials in industrial applications where hardness and wear resistance are crucial. The initial phase of this composite, WC, is the toughest in comparison to other hard phases used in tool materials. However, due to the lack of sufficient toughness WC alone is not applicable for harsh applications since it cannot resist deformation and wear well. This drawback can be compensated by the counterpart Co phase. As the second phase, Co provides the necessary toughness and other advantageous binder properties. In addition to that, what is also unique of WC-Co is the almost perfect compatibility existed between its two constitutes and, as a consequence, WC-Co is widely used in the machining, mining, forming and similar industries [30].

To understand how size of the RVE models influences the effective ultimate strength and endurance limit predicted for this material, we built 3 sample groups. Each sample group consists of 500 RVE models built from artificial microstructures of the material. RVE models in 3 sample groups have the same configuration but the different RVE size. By deploying the established numerical approach to these samples, ultimate strength and endurance limit were calculated and the results were analyzed through statistical models with a particular focus on the size effect. On the basis of the statistical analyses, in the end of the work, a feasible and computationally inexpensive solution is proposed for minimizing the size effect.

2 Shakedown of RVE Models

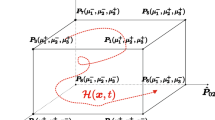
The strength of the WC-Co composite was predicted from RVE samples using the static direct method based on the Melan’s theorem [31]. Before presenting how this method was applied to heterogeneous materials, first we revisit some fundamental micromechanical principles. Based on these principles results of the numerical simulation of the RVE models were interpreted and converted to the corresponding macroscopic effective quantities. The micromechanical laws adopted in the present study were based on the mean field homogenization theory according to which the material can be reflected in two well-separated scales: the microscopic scale is small enough for the heterogeneities to be identified. In contrary to that, the macroscopic scale is large enough for the heterogeneities to be expelled. The two scales are well-separated and they are described by two coordinate systems: the global coordinate system $\varvec{x}$ and local coordinate system $\varvec{y}$. The following relationship holds

$$\begin{aligned} \varvec{y}=\dfrac{\varvec{x}}{\varepsilon } \; . \end{aligned}$$

(1)

${\varepsilon }$ is a small scale parameter which determines the size of the RVE.

For a heterogeneous material, when it is submitted to an external loading, its microscopic stress field $\varvec{\sigma }$ in $\varvec{y}$ and its macroscopic counterpart $\varvec{\Sigma }$ satisfy the relationship

$$\begin{aligned} \varvec{\Sigma } =\frac{1}{\Omega }\int _{\varOmega }{\varvec{\sigma }(\varvec{y})dV}=\left\langle \varvec{\sigma }(\varvec{y}) \right\rangle . \end{aligned}$$

(2)

Here $\left\langle \cdot \right\rangle$ stands for the averaging operator, and $\Omega$ indicates the RVE domain. Similarly, the relationship between strain measures satisfies

$$\begin{aligned} \varvec{E} =\frac{1}{\Omega }\int _{\varOmega }{\varvec{\varepsilon }(\varvec{y})dV}=\left\langle \varvec{\varepsilon }(\varvec{y}) \right\rangle . \end{aligned}$$

(3)

The local strain $\varvec{\varepsilon }$ can be decomposed into two parts: The average value $\varvec{E}$ and a fluctuating part $\varvec{\varepsilon }^*$

$$\begin{aligned} \varvec{\varepsilon }(\varvec{u})=\varvec{E}+ \varvec{\varepsilon }^*\;. \end{aligned}$$

(4)

When all constituents of a RVE are elastic, the overall behavior of the RVE is elastic as well. In this circumstance, $\varvec{\Sigma }$ and $\varvec{E}$ are correlated by an effective elastic tensor $\overline{\mathbb {C}}$

$$\begin{aligned} \varvec{\Sigma } =\overline{\mathbb {C}}:\varvec{E}. \end{aligned}$$

(5)

In case that the heterogeneous material to be considered behaves isotropically in the macro scale, same to the single phase material, $\overline{\mathbb {C}}$ can be uniquely determined from two elastic constants, such as effective Young’s modulus $\bar{E}$ and effective Poisson’s ratio $\bar{\nu }$.

When the composite material is composed of elasto-plastic constituents, its macroscopic ultimate strength $\varSigma _U$ and endurance limit $\varSigma _\infty$, which correspond to plastic and shakedown limit in the RVE scale, can be studied by incorporating homogenization techniques with direct methods. As formulated by Magoariec et al. [32], when the shakedown state is attained in the micro scale, stress field pertained to the reference elastic body $\mathscr {B}^E$, $\varvec{\sigma }^e$, and the time invariant residual stress field $\bar{\varvec{\rho }}$ are required to satisfy following conditions

$$\begin{aligned} \varvec{\sigma }^e: \left\{ \begin{array}{r@{\;\;}ll} &{} \varvec{\nabla }\cdot \varvec{\sigma }^e = 0 \quad &{} {\text {in}} \; \varOmega ,\\ &{}\varvec{\sigma }^e= \mathbb {C}:(\varvec{E}+\varvec{\varepsilon }^*) &{} \text {in} \; \varOmega ,\\ &{} \varvec{\sigma }^e \cdot \varvec{n} \qquad &{}\text {anti-periodic on} \; \partial \varOmega ,\\ &{} \varvec{u}^* &{}\text {periodic on} \; \partial \varOmega ,\\ &{}\left\langle \varvec{\varepsilon }\right\rangle =\varvec{E} . \end{array} \right. \end{aligned}$$

(6)

$$\begin{aligned} \bar{\varvec{\rho }}: \left\{ \begin{array}{r@{\;\;}ll} &{} \varvec{\nabla }\cdot \bar{\varvec{\rho }} = 0 \qquad &{} {\text {in}} \; \varOmega ,\\ &{}\bar{\varvec{\rho }} \cdot \varvec{n} \qquad &{} \text {anti-periodic on} \; \partial \varOmega . \end{array} \right. \end{aligned}$$

(7)

Here, $\varOmega$ indicates the RVE domain, $\partial \varOmega$ the surface, $\varvec{n}$ the outer normal, and $\varvec{u}^*$ the fluctuation part of the displacement corresponds to $\varvec{\varepsilon }^*$.

Although shakedown problem in the RVE scale can be studied by either strain or stress approach [32], in present study we consider exclusively the stress approach. For stress approach the load prescribed on RVE is the macroscopic stress $\varvec{\varSigma }$. Because the material to be studied is non-periodic, a small specification is made on conditions (6) and (7), where, instead of enforcing the node-wise anti-periodicity of the residual stresses and periodicity of the fluctuating displacement, we apply the statically uniform boundary conditions (SUBC) on the purely elastic reference RVE. As a consequence, the shakedown problem yields $\bar{\varvec{\rho }} \cdot \varvec{n}= \varvec{0}$ on $\partial \varOmega$ and one can prove that, in the absence of the body force $\left\langle \bar{\varvec{\rho }} \right\rangle =\varvec{0}$, so $\bar{\varvec{\rho }}$ does not contribute to the macroscopic stress.

By discretizing the physical fields in (6) and (7) by means of the FE formulations, the application of the static theorem to RVEs composed of elastic perfectly plastic materials leads to following optimization problem

$$\begin{aligned} \begin{aligned} \underset{\bar{\varvec{\rho }},\alpha }{\text {minimize}}&-\alpha \\ \text {subject to}&\sum _{i=1}^{NG} \varvec{C}_i \, \bar{\varvec{\rho }}_i = \varvec{0} \; ,\\&F(\alpha \varvec{\sigma }^e_{ik}+\bar{\varvec{\rho }}_i) - \sigma _{Y\,i}^2 \le 0 \\&\forall i \in [1,NG] \,; k \in [1, NV]\; . \end{aligned} \end{aligned}$$

(8)

Here, $\alpha$ is referred to as the load factor, $\varvec{C}$ the equilibrium matrix, $\bar{\varvec{\rho }}_i$ the stress tensor associated with the ith Gaussian point, $\varvec{\sigma }^e_{ik}$ the abbreviation of $\varvec{\sigma }^e_i(\varvec{P}_k)$ which means the $\varvec{\sigma }^e$ at Gaussian point i and load vertex k, $\sigma _Y$ the yield strength, F the yield function, NG the number of Gaussian points, and NV the number of vertices. Both phases were assumed to obey the von Mises yield condition. Meanwhile, it is worthy to note that, although in few studies, e.g. [33], it is suggested to replace the yield strength by fatigue limit of the material to meet with the safety requirement, the present study still sticks with the convention adopted in most existing works, such as [10, 34], in which initial yield strength of the material is used. This choice is made since there is no available data on the fatigue test of the binder cobalt alloy. Solving (8) yields the load capacity of the RVE, and depending on if $k=1$ or $k > 1$ the calculated strength corresponds to either plastic limit or endurance limit. In the present study, the load scenario considered is restricted to non-reversed uniaxial stress, in this case $NV=2$ and $\varvec{\sigma }^e_{ik}=0$ for all $k=2$.

For RVE models considered in the present study, (8) turns out to be a large scale optimization problem. In order to solve such a problem within a reasonable time, it requires the problem to be carefully formulated and submitted to powerful optimization algorithm. Several studies, e.g. [35, 36], acknowledged that by replacing the original inequality constraints by Euclidean ball constraints, the sparsity of the Karush-Kuhn-Tucker (KKT) system can be better exploited and thus the problem can be solved more efficiently. This conclusion is approved by our own observations. For this reason, the recommended reformulation is applied to all optimization problems evaluated in the present study. The specific workflow to reformulate (8) can refer to [35].

After reformulation, the static problem can be viewed as a typical SOCP problem with $n_i=5$, and therefore it can be handled by commercial optimization solvers such as Gurobi [37], CPLEX [38], MOSEK [39], among others. In our previous studies [1, 2], we proposed to solve (8) by the general purpose interior-point method solver IPOPT [40, 41]. Compared to listed commercial SOCP solvers, the advantage of IPOPT is that it can handle a large variety of nonlinear optimization problems. However, the price paid to achieve such a generality is that, when IPOPT is not carefully customized to the problem, its efficiency on solving particular typed problems, such as SOCP, is inferior to the listed commercial solvers. In order to find a solver that, besides rendering an accurate solution, also demonstrates an excellent numerical efficiency, in the present study we compared results from two selected solvers: the general purpose solver IPOPT and the SOCP solver Gurobi; after confirming that the discrepancy between results obtained from two solvers is negligible, the SOCP solver Gurobi is adopted for solving optimization problems originating from PRMMC samples due to its outstanding efficiency (Details see this chapter).

3 Statistical Models for the Interpretation of Numerical Results

Since we propose to predict the global material behavior from SERVE samples, the study of the size effect is also based on rigorous statistical methods. In the present study, we consider an RVE size to be sufficient if it results in effective behaviors that are statistically equivalent to their counterparts predicted from larger RVEs. Here, statistical equivalent is reflected from two aspects: the statistical characteristics of one effective behavior and the correlation between different effective behaviors. These two conditions were checked by statistical models presented in the present section.

In order to check if the statistical characteristics of one effective behavior is size independent, its mean value $\bar{x}$ and the standard deviation s were compared to quantities derived from RVEs of a greater size. Next to that, hypothesis tests were applied to examine if effective behaviors predicted from the current size and a larger size can be regarded as belonging to the same statistics. To this end, two hypothesis tests, namely the Kolmogorov-Smirnov test (K-S test) and Wilcoxon rank sum test (rank sum test), were employed. K-S test examines if two samples X and Y are from the same continuous distribution. Null and alternative hypotheses of this test are

$$\begin{aligned} H_0: \;&\text {Two samples are from the same continuous distribution} \\ H_a: \;&\text {Two samples are from the distinctive continuous distribution} \end{aligned}$$

The decision of a two samples K-S test is made based on the distance between the empirical distribution functions of two samples, where the empirical distribution function indicates the cumulative distribution function of a sample that jumps up by 1 / n at each of the n data points. The rank sum test, on the other hand, can be seen as a nonparametric equivalent to t-test which does not require the data to be subjected to the normal distribution. Null and alternative hypotheses of rank sum test are

$$\begin{aligned} H_0: \;&\text {Two samples are from continuous distributions with equal medians} \\ H_a: \;&\text {Two samples are not from continuous distributions with equal medians} \end{aligned}$$

In addition to the hypothesis test, we also study if the relationship between different effective behaviors, e.g. the relationship between the effective Young’s modulus $\bar{E}$ and the global endurance limit $\varSigma _\infty$, changes if the size of RVE increases. To this end, the Pearsons correlation coefficient r from two random variables X and Y defined as follows is evaluated

$$\begin{aligned} r_{XY}=\frac{\sum _{i=1}^{N}(X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{\sum _{i\,=\,1}^{N}(X_i-\bar{X})^2}\sqrt{\sum _{i\,=\,1}^{N}(Y_i-\bar{Y})^2}} \; . \end{aligned}$$

(9)

Here $\bar{X}$ and $\bar{Y}$ are mean values of the statistics X and Y, respectively. When more than two random variables are considered, matrix of correlation plots is a convenient way to present the data. In such matrix, the correlation between every two random variables $(X_i,Y_j)$ is plotted as a component of the matrix, and the histogram of an individual variable is plotted in the diagonal. Matrix correlation plot is employed as a main tool for data presentation in the present study.

4 Comparison Between Optimization Solvers

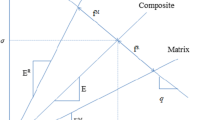
Before investigating the size effect on the strength prediction for PRMMC samples, a comparative study was performed on a benchmark model to check if results from the general purpose nonlinear optimization solver IPOPT and the SOCP solver Gurobi are consistent. The benchmark model chosen for the comparative study is the classic plate with a hole model that has been studied in abundant direct method literature, c.f. [42,43,44]. The geometry of the model is shown in Fig. 1 with the dimensions given in Table 1. We study the strength of the structure submitted to two distributed pressures $P_x$ and $P_y$. By considering $P_x$ and $P_y$ as basic loads $\hat{P}_1$ and $\hat{P}_2$, a vertex in the load space spanned by $\hat{P}_1$ and $\hat{P}_2$ can be uniquely defined as ($\cos \theta ,\sin \theta$) by introducing an angle $\theta$. This way, the load factor $\alpha$ under different combinations of two loads can be calculated by varying the magnitude of $\theta$. Due to the symmetry of the geometry and loads, the finite element model contains only 1 / 4 of the geometry. The model adopts eight node linear solid elements and material properties outlined in Table 2. In order to be consistent with existing literature, the material is considered in this numerical study as an elastic-perfect plastic material.

To evaluate the limit and shakedown load of the given model, first the geometry and the FE mesh were built in the commercial FE software ABAQUS [45] for calculating the elastic stress $\varvec{\sigma }^e$. In this calculation, the magnitude of both basic loads were fixed to 100 MPa. The model configuration and the von Mises stress of $\varvec{\sigma }^e$ can be seen in Fig. 2.

Fig. 1

Geometry of the plate with a hole model

Table 1 Dimensions of the benchmark model

Table 2 Material properties of the benchmark model

Fig. 2

Elastic stresses of the plate with a hole model

After $\varvec{\sigma }^e$ was calculated, the information of the finite element model and the elastic stresses were output to Matlab [46]. In Matlab the formulation of the shakedown problem (8) is realized through an in-house Matlab finite element code. Using the information passed by the commercial finite element software, the matrices involved in the objective function and constraints were first evaluated on the element level and then assembled into global matrices in sparse forms. The form of the shakedown problem eventually used for the computation was customized to the solver. When IPOPT is used as the solver, Jacobian and Hessian matrices used to assemble the reduced Karush-Kuhn-Tucker (KKT) system were calculated. Based on the Jacobian and Hessian matrices provided, IPOPT finds the optimal solution to a series of barrier problems following the steps outlined in [41]. When commercial solver Gurobi is used, the effort for evaluating Jacobian and Hessian matrices can be reduced, and the difficulties lie in finding an appropriate scaling factor and an optimal set of solver parameters which prevent the solver from slow convergence near the optimum. In the present study, the linear system corresponding to the equality constraints was scaled so that the entries in it are in the same order.

Before the shakedown problem pertained to the benchmark model was calculated by two solvers, we first compared results of IPOPT adopting original formulation (8) and the reformulated one. We noticed that, although original form demands more time to compute, results derived from both forms are identical (discrepancy between results is less than 0.001%). Next we fixed to the reformulated form and compared results of two solvers. Result of the comparative study can be seen in Table 3. In this table, abbreviation “GUR” indicates the solver Gurobi, and “IPO” the solver IPOPT. Superscript 1P means only one load vertex is considered, and this corresponds to the limit analysis. In contrast to that, the superscript 2P indicates that load $P_x$ and $P_y$ are enforced to vary proportionately. Table 3 shows that, although the discrepancy is slightly increased, the error is still tolerable and with the maximum value around 0.1%. This way, we confirmed that the problem can be handled by both IPOPT and Gurobi. In the present study, most configuration parameters in IPOPT use the default values, and in this circumstance the time it costs for IPOPT to solve this problem is about 10 times compared to the Gurobi. For this reason, Gurobi was used to solve the shakedown problems pertained to RVE models, while IPOPT was used only occasionally to cross-validate the results of IPOPT on selected models.

Table 3 Comparison of load factor $\alpha$ determined by two optimization solvers (Gurobi and IPOPT)

Fig. 3

Feasible load domains of the plate with a hole model

Next, we compared our own results to literature in Fig. 3. Because results from IPOPT and Gurobi are almost identical, the discrepancy between them is neglected; in the following the result is presented indiscriminately as $\alpha$. Results in Fig. 3 were obtained by shakedown analyses considering one vertex (limit load), two vertices (proportionally varied tow loads) and four vertices (independently varied two loads). Results from our own calculation are found to be in line with results in [42,43,44]. For this reason, we confirmed the validity of our numerical formulation.

Fig. 4

Inclusion process with fixed grain size

5 Numerical Study of PRMMC Samples

The numerical study of the representative PRMMC material, WC-Co 20 Wt.%, is based on 1,500 RVE models. The models fall into three sample groups, each group consists of 500 samples. The samples were modeled from artificial morphologies generated by a simple random sequential adsorption (RSA) algorithm as shown in Fig. 4. The algorithm is developed in Matlab on the matrix basis. According to this algorithm, the RVE domain is initialized as a zero matrix and the program continuously projects prism shaped geometry into this matrix. After each projection, zero elements in the matrix are set to one if they belong to the prism domain and remain zero otherwise. The value of elements will not be reset if they have already been picked in previous iterations. Parameters controlling the projection, such as prism size, rotation angle, and center of the projection, are all random numbers. In order to be consistent with real WC-Co microstructures, the algorithm adopts a configuration that the diameter of WC grains, $d_{WC}$, obeys a normal distribution with mean value 3 $\upmu$m and standard deviation 0.8 $\upmu$m. The position where each particle locates is independent from the others and therefore there is no predefined clustering. Due to the high carbide content of the material, before a new grain is to be projected, it is very likely that the corresponding RVE domain is already partially assigned to other grains. When this happens, the algorithm will neither reject the projection of the new grain nor record the overlapping information such as the grain boundaries. The new grain is simply projected and merged with the old ones to form a unity. Although there are many obvious advantages to introduce grain boundaries to the model, due to the numerical difficulty and tremendous computational cost it requires, the data may become too expensive and thus statistical analysis becomes impossible. For this reason, the simplest idealization is adopted and the overlapping problem between grains is not explicitly accounted for. The projection stops when binder contents reach a certain threshold. Based on the image analyses of 50 SEM images obtained from WC-20 Wt.% Co, we noticed that the volume percent of the binder phase, Co Vol.%, follows a normal distribution featured by the mean value 37.5 and the standard deviation 2.7. This distribution was adopted as the termination criterion for generating artificial RVE samples that represent the material. The finite element models were built in commercial FE solver ABAQUS and meshed by a uniform mesh configuration: the element type is fixed to linear wedge elements (C3D6); elements covering non-critical regions were assigned with a global size of 0.8 $\upmu$m; while elements near the phase boundaries are of a finer density with an edge size of 0.2 $\upmu$m. Under this configuration, the number of elements for an RVE sample having a size 40–40–1 $\upmu$m varies between 15,000 and 20,000. The reason of using a layer of 3D wedge elements instead of 2D elements to represent the composite structure is that the results of direct method predicted from the former element type demonstrate significantly less mesh dependency. More detailed discussion on this issue can be found in [2].

Table 4 Description of sample groups

Fig. 5

RVE samples of WC-20 Wt.% Co with $d_{WC} \sim N(3.0, 0.8\,\upmu \text {m})$ in different sizes

The sample groups used to study the size effect were numbered successively as Group 1, 2 and 3, the parameters used for generating the models in these groups are detailed in Table 4. The RVEs in three groups differ only in their size: Samples in Group 1 have a size of 30–30–1 $\upmu$m, while in Group 2 a greater size 40–40–1 $\upmu$m, and in Group 3 the greatest size 80–80–1 $\upmu$m. In order to provide an intuitive insight about the models, we randomly picked one sample from each group and compared the microstructures in Fig. 5. The binder content in three groups is slightly different—this can be interpreted as a consequence of converting microstructures to finite element mesh. The mesh pattern adopted for all three groups are identical and, in consequence, FE models in different groups have very different number of nodes and elements (Fig. 5). The load type used for calculating the strength were uniformly fixed to SUBC. According to this boundary condition configuration, nodes lying on the RVE surfaces were prescribed with nodal forces corresponding to the global stress, and their degrees of freedoms are not restrained so that they can deform freely. Materials of both phases are considered as elastic perfect plastic materials with parameters given in Table 5. In the present study, we investigate only the strength of the composite material subjected to the uniaxial tensile load: For each RVE, it’s ultimate strength $\varSigma _U$ derived by solving the optimization problem (8) with $NV=1$ and endurance limit $\varSigma _\infty$, which corresponds to the case $NV=2$, were calculated on both x and y directions, and the average was considered as the effective property of the sample. In order to emphasize the strengthening effect of the reinforcement phase, the strength of an RVE was presented after normalized with respect to the yield strength of the binder phase $\sigma _Y^{Co}$. The anisotropy ratio of a predicted effective behavior x defined as

$$\begin{aligned} \zeta _x =\max (x_1/x_2,x_2/x_1) \end{aligned}$$

(10)

which measures the dissimilarity of a predicted effective behavior in two normal directions was evaluated for selected macroscopic properties and considered as an important indicator for evaluating the sufficiency of the RVE size. One necessary condition for an RVE size to be sufficient is that $\zeta _x$ predicted from this size should be close to one.

Table 5 Material properties of both phases

Table 6 Material parameters predicted from RVE samples having different sizes

We evaluated several key effective material parameters and their associated statistical descriptors (Table 6). Unlike most numerical studies of this kind, in Table 6 we did not observe a manifest trend where scatter of data reduces when RVE size increases. This phenomenon implies that, for predicting certain material parameters, e.g. $\bar{E}$, a small RVE size may suffice and renders unbiased prediction. Moreover, in a statistical sense, RVE samples become more isotropic when its size becomes larger. The degree of anisotropy reflected by the magnitude of $\zeta$ depends on the effective behavior of interests. Roughly speaking, $\zeta$ indicates the level how interactive localized behavior within a RVE body average and set-off. In this vein, comparing three parameters illustrated in Table 6, i.e. $\zeta _{\bar{E}}$, $\zeta _{\varSigma _U}$, and $\zeta _{\varSigma _\infty }$, it is clear that localized behavior has greatest influence over $\varSigma _\infty$, and RVEs are required to be exceptionally large to smear out these effects.

Fig. 6

Cumulative distribution functions of $\varSigma _U$ for RVEs of different sizes

Fig. 7

Cumulative distribution functions of $\varSigma _\infty$ for RVEs of different sizes

Beside presenting results by means of statistical indicators, cumulative distribution function of $\varSigma _U$ and $\varSigma _\infty$ are compared in Figs. 6 and 7, respectively. Function diagrams in these figures demonstrate a greater difference among sample groups compared to Table 6. In order to understand quantitatively how similar these results are, we performed hypothesis tests on subsets randomly sampled from the existing data. In this case study, 50 RVEs were randomly picked from each sample group, and every two of them were submitted to K-S test and rank sum test with a significance level fixed to 0.05. This sampling process was repeated for 300 times and derived results were recorded in Table 7. In this table, $H_0 \%$ represents the percentage of tests in which null hypothesis $H_0$ was not rejected. $p^*$ is calculated from the p value as follows

$$\begin{aligned} p^* =\max (p, 1-p)\; . \end{aligned}$$

(11)

$p^*$ value presented in Table 7 is averaged over 300 tests. The purpose for introducing this variable is to avoid averaging p that arises from different sides, such as 0.01 and 0.99. The letter “all” in the table corresponds to samples picked indiscriminately from three sizes. One can see from the table that, compared to $\bar{E}$ and $\varSigma _U$, $\varSigma _\infty$ is more sensitive to size because $H_0$ is rejected for a greater amount of times. Meanwhile, for more than half of 300 tests applied to 40 $\upmu$m (Group 2) and 80 $\upmu$m (Group 3) RVEs, $H_0$ were favored which confirms the similarity of RVEs in these two sizes.

Table 7 Hypothesis tests on randomly sampled RVEs of different sizes

Fig. 8

Correlation matrix evaluated from Group 1 (30–30–1 $\upmu$m artificial RVEs of WC-20 Wt.% Co, $d_{WC} \sim N(3.0, 0.8)$), r = correlation coefficient

Fig. 9

Correlation matrix evaluated from Group 2 (40–40–1 $\upmu$m artificial RVEs of WC-20 Wt.% Co, $d_{WC} \sim N(3.0, 0.8)$), r = correlation coefficient

We evaluated the correlation matrix for all aforementioned sample groups. One can notice from Figs. 8, 9 and 10 that, despite different r values, the fashion in which the considered material parameters are correlated is independent from the size. More specifically, homogenized elastic module $\bar{E}$ is strongly correlated to WC Vol.%, but $\varSigma _U$ and $\varSigma _\infty$ are only subtly correlated to WC Vol.%. This suggests that morphology has a more crucial impact to $\varSigma _U$ and $\varSigma _\infty$ compared to $\bar{E}$. In addition to that, for all three groups, r between $\varSigma _U$ and $\varSigma _\infty$ are quite small, which reveals that the linear correlation between them is quite weak.

Fig. 10

Correlation matrix evaluated from Group 3 (80–80–1 $\upmu$m artificial RVEs of WC-20 Wt.% Co, $d_{WC} \sim N(3.0, 0.8)$), r = correlation coefficient

6 Conclusions

In this paper, using an representative material, WC-20 Wt.% Co, it is presented how size of RVE models influences the strength of PRMMC materials predicted from the direct method. On the basis of 500 realizations for each selected RVE size (30, 40 and 80 $\upmu$m), we performed the shakedown analyses and observed from the result that the global material behavior predicted from different sizes has more commons than dissimilarities in a statistical sense. Also, the correlation between different global material parameters, which is represented by the correlation coefficient r, is independent from the model size. For all concerned material parameters, their mean values are less sensitive to size compared to variances, thus smaller RVEs are sufficient if the task is to predict the mean value of a certain material parameter. The variance of a global material behavior is introduced by both composite structure and the RVE size, where the latter one is undesired and becomes less critical when RVE size exceeds a certain threshold.

On removing the variance caused by RVE size—the so called size effect, a viable solution is proposed in the present paper: One can check the sufficiency of the RVE size through applying hypothesis tests repeatedly on results predicted from one size and a much greater size. If the chance to reject the hypothesis that the data are from the same continuous distribution is small, e.g. less than 10%, then it is justified to conclude that the size effect is expelled and results from two sizes are statistically equivalent. According to this criterion, it can be concluded that the size 40–40–1 $\upmu$m is sufficient for the strength prediction of the current material, because it is statistically equivalent to a much greater size 80–80–1 $\upmu$m. It is worthy to note that the disadvantage of this method is that it requires a large amount of data as input. For this reason, the conventional approaches which are based on indicator such as the anisotropy ratio, still have significant practical values and thus should not be abandoned. In addition to that, it is also plausible to overcome the size effect by first taking the size as a random variable for generating RVEs, and then removing its influence by means of advanced statistical learning methods. Although from a theoretical point of view this approach appears to be uncomplicated, in practice it might be challenging to find a capable statistical model to interpret the results.

In our future study, the focus would be put on interpreting the relationship between different effective material behaviors, and the goal is to reveal from a mechanical perspective how do these behaviors are correlate.