Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In order to obtain a well-operating electromechanical system, it is important to perform the stability and oscillation analysis of its corresponding mathematical model. An oscillation in a dynamical system is either self-excited or hidden attractor [7, 8, 10, 11]. An attractor is called a hidden attractor if its basin of attraction does not intersect with small neighborhoods of equilibria, otherwise, it is called a self-excited attractor. The basin of attraction of self-excited attractor is associated with an unstable equilibrium. In other words, the self-excited attractors can be localized numerically by the following standard computational procedure: a trajectory, which starts from a point of an unstable manifold in a neighborhood of an unstable equilibrium, after a transient process is attracted to the state of oscillation and traces it. In contrast, hidden attractor’s basin of attraction is not associated with unstable equilibria. Recent examples of hidden attractors can be found in The European Physical Journal Special Topics: Multistability: Uncovering Hidden Attractors, 2015 (see [2, 4–6, 12–16, 18–20]).

Hidden oscillations appear naturally in systems without equilibria, describing various mechanical and electromechanical models with rotation. In 1902 Arnold Sommerfeld described one of the first examples of such models [17]. He studied vibrations caused by a motor actuating on unbalanced rotor and discovered the resonance capture phenomenon (Sommerfeld effect). Discussing the nature of this capture phenomenon, Sommerfeld wrote: “This experiment corresponds roughly to the case in which a factory owner has a machine set on a poor foundation running at 30 horsepower. He achieves an effective level of just 1/3, however, because only 10 horsepower are doing useful work, while 20 horsepower are transferred to the foundational masonry” [3].

Further we will consider mechanical model actuated by DC motor, where the Sommerfeld effect corresponds to the existence of hidden oscillation. We will also demonstrate when Sommerfeld effect is absent for the same model actuated by synchronous motor.

2 Unbalanced Rotor on a Rigid Platform

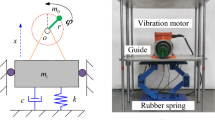
Following the work [1], we consider the first electromechanical system, which is unbalanced rotor placed on a rigid platform. The platform can move only horizontally and is connected to a wall by means of damping and elastic elements (see Fig. 1). The system of equations of motion is the following:

$$\displaystyle\begin{array}{rcl} J\ddot{\varphi }& =& \mathcal{G}(\dot{\varphi }) + m_{0}l\ddot{x}\sin \varphi, \\ (M + m_{0})\ddot{x} +\beta \dot{ x} + cx& =& m_{0}l\left (\dot{\varphi }^{2}\cos \varphi +\ddot{\varphi }\sin \varphi \right ). {}\end{array}$$
(1)

Here φ is the rotation angle of the rotor, x is the displacement of the platform, J is the moment of inertia of the rotor, m 0 is the eccentric mass of the rotor, M is the mass of the platform, c is stiffness, β is friction coefficient, l is the eccentricity of mass m 0, and \(\mathcal{G}(\dot{\varphi })\) is the motor torque.

Fig. 1
figure 1

Scheme of unbalanced rotor on a rigid platform

Full size image

Let us consider two different types of motor for this system and see whether the Sommerfeld effect can be found.

2.1 Sommerfeld Effect in the System

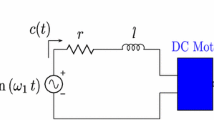
First, we consider a limited power DC motor

$$\displaystyle{ \mathcal{G}(\dot{\varphi }) =\varDelta -k\dot{\varphi }, }$$
(2)

where Δ and k are constant parameters of the motor.

For computer simulation we take the following parameters: J = 0. 014, M = 10. 5, m 0 = 1. 5, l = 0. 04, k = 0. 005, c = 5300, β = 5, and Δ = 0. 49. For initial data \(\dot{x}(0) = x(0) =\varphi (0) =\dot{\varphi } (0) = 0\) the Sommerfeld effect occurs. For other initial data \(\dot{x}(0) = x(0) =\varphi (0) = 0,\dot{\varphi }(0) = 40\) we observe normal operation—the achievement of desired rotational velocity of our mechanical system.Footnote 1 The transient processes for both the initial data and the corresponding attractors are shown in Fig. 2. Comparison of this situation with experiment of Sommerfeld gives the following result: when the Sommerfeld effect occurs, the effective level of only about 1/4 is achieved (comparing to the normal operation). Note that in this example we have the coexistence of attractors, which are hidden in the sense of mathematical definition. But from a physical point of view, the zero initial data correspond to typical start of the system, so the Sommerfeld effect can be easily localized, while the normal operation is hidden.

Fig. 2
figure 2

Sommerfeld effect and normal operation in unbalanced rotor on a rigid platform

Full size image

2.2 Absence of the Sommerfeld Effect

Consider now the following mathematical model of synchronous motor:

$$\displaystyle{ J\ddot{\theta } = -\alpha \dot{\theta }-\sin \theta, }$$
(3)

where θ is the phase difference between the rotating magnetic field and the rotor (θ = φ −ω t, where φ is the rotation angle of the rotor as before), α is the coefficient of damper windings, and ω is the current frequency in the stator windings.

Then the equations of “unbalanced rotor on a rigid platform” system take the form:

$$\displaystyle\begin{array}{rcl} J\ddot{\theta }& =& -\alpha \dot{\theta }-\sin \theta +m_{0}l\ddot{x}\sin (\omega t+\theta ), \\ (M + m_{0})\ddot{x} +\beta \dot{ x} + cx& =& m_{0}l\left ((\omega +\dot{\theta })^{2}\cos (\omega t+\theta ) +\ddot{\theta }\sin (\omega t+\theta )\right ).\qquad {}\end{array}$$
(4)

In [9] it was mathematically rigorously proved that there is no Sommerfeld effect in system (4) if it is actuated asynchronously (asynchronous actuation means that \(x(0) =\dot{ x}(0) =\dot{\theta } (0) = 0\)). It is shown that the following equation is valid for sufficiently small l and large t:

$$\displaystyle{ (M + m_{0})\ddot{x} +\beta \dot{ x} + cx = m_{0}l\omega ^{2}\cos \omega t + O(l^{2}). }$$
(5)

After the transient process the synchronous machine reaches normal operation mode with the rotation frequency of rotor equal to ω + O(l). The platform oscillations can be approximated by the harmonic oscillation with the frequency ω + O(l) and the amplitude

$$\displaystyle{ \frac{m_{0}l\omega ^{2}} {\sqrt{(c - (M + m_{0 } )\omega ^{2 } )^{2 } +\beta ^{2 } \omega ^{2}}} + O(l^{2}). }$$
(6)

Thus, if the eigenfrequency of the platform is less than ω, then in the case of asynchronous actuation system (4) always passes resonance and enters normal operation mode after transient process.

Fig. 3
figure 3

Normal operation in unbalanced rotor on a rigid platform

Full size image

Computer simulation of (4) with parameters J = 0. 014, M = 10. 5, m 0 = 1. 5, l = 0. 04, α = 0. 5, c = 5300, β = 5, ω = 90, and initial data \(\dot{x}(0) = x(0) =\varphi (0) =\theta (0) =\dot{\varphi } (0) =\dot{\theta } (0)+\omega = 0\) gives a normal operation, which is shown in Fig. 3. The normal operation is a hidden attractor in the sense of mathematical definition, but from a physical point of view, it is easily localized. Remark that the computation with other initial data does not reveal any other coexisting attractors, thus our experiments expand the work [9], where the limitation on initial data is assumed.

3 Conclusion

In this paper two types of vibrational units with unbalanced rotors are considered. It is demonstrated that under certain conditions system (1) and (2) experiences the Sommerfeld effect, namely the resonance capture phenomenon. Here the Sommerfeld effect can be regarded as the coexistence of hidden oscillations since the system has no equilibrium states. Also an example of similar model without Sommerfeld effect is shown.