1 Introduction

Indeed, the accurate establishment of mathematical models that reflect the motion behavior of a system is crucial for dynamic analysis [1, 2]. In the context of the vibration system driven by unbalanced rotors, extensive research has been conducted from various perspectives [3,4,5,6], resulting in significant contributions to the advancement of vibration theory. However, certain complex problems cannot be fully explained solely from the mechanical system's perspective. The interaction between the mechanical and electrical components becomes essential to understanding and addressing these issues. This consideration leads to the concept of non-ideal systems [7, 8], where the coupling between the mechanical and electric parts plays a significant role in the system's behavior.

Brazilian scientist Balthazar led a team that has made significant contributions to the study of non-ideal systems and established a series of researches [9, 10]. Summarizing their findings and results, the non-ideal system has two remarkable characteristics as follows: firstly, the energy source is limited, referred to as the non-ideal source; secondly, there is an energy exchange between the energy source and its support structure. For instance, an unbalanced motor or an exciter mounted on a flexible support structure can influence the response of the rotary system [11].

In many physical phenomena of the non-ideal system, Sommerfeld effect must be mentioned, which was first proposed by Sommerfeld [12] and comprehensively summarized by Kononenko [13]. In engineering, the rated velocities of some machines fall within the far resonance range, meaning they inevitably pass through the resonance point [14]. For non-ideal systems, the structural response provides a kind of energy trap or energy sink, causing the rotatory velocity to get stuck at resonance [15]. As the power supply continues to increase, a jump phenomenon in the velocity occurs [16]. In summary, the frequency capture and the velocity jump are two prominent features of Sommerfeld effect.

In some excellent books by Nayfeh [1], Blekhman [2] and Cveticanin [17], different analytical methods are presented to explain the mechanism of Sommerfeld effect. These classical methods involve adding the equation representing the motion of the motor to the mathematical model of the non-ideal system. This inclusion allows for the depiction of the coupled relationship between the vibration system and its driven energy source. Consequently, the non-ideal system possesses one more degree of freedom compared to the ideal system. It is important to highlight that the differential equations of motion for the non-ideal system exhibit nonlinearity due to this coupled relationship. The nonlinearity is a result of the interaction between the vibration system and the driven energy source, which introduces complexities into the dynamic behavior of the system.

With the development of the coupling dynamics of electromechanical systems, a significant number of engineering problems have been successfully addressed. As a result, there has been increasing attention from scholars toward investigating Sommerfeld effect in various classical vibration systems to avoid energy sink phenomena [18,19,20,21,22]. One proposed method to quickly pass through resonance is to increase the foundation damping. However, it is acknowledged that this approach is not the ideal solution due to the potential loss of vibration efficiency. To avoid frequency capture issues, another approach involves using two unbalanced rotors installed on the same plate [19]. This method is considered to act as a vibration absorber, effectively controlling the frequency capture phenomenon [20]. Furthermore, researchers have studied signal processing techniques to characterize and identify the Sommerfeld effect, which can potentially be extended to actively or passively control this phenomenon [21].

In recent years, Samantaray and his teammates have conducted extensive research on Sommerfeld effect in numerous rotating machinery applications, which has proven to be highly beneficial for mechanical design [23,24,25,26]. They specifically studied a rigid rotor system driven by a universal joint, using the method of the bond graph model to analyze the transient dynamics [27]. Furthermore, they explored Sommerfeld effect in systems where the universal joint was connected to a flexible shaft, and interestingly, they observed jump phenomena at two different velocity ranges [28]. Their research also extended to reciprocating systems like the crank and rocker mechanism, where they considered the safety and reliability of machines. In this context, they deduced the power requirement necessary for a smooth transition through resonance [26].

The current research on the Sommerfeld effect mechanism is comprehensive; however, most of the findings heavily rely on the equation of DC motor as the driven source. In practical industrial applications, AC motor is more commonly used as the driven source. Therefore, there is a pressing need to investigate the dynamic characteristics of non-ideal systems driven by AC motor. Unfortunately, there are relatively few studies on the dynamic behavior of such systems, and experimental investigations are scarce. To address this gap in experimental research, this paper introduces a study of a non-ideal system driven by an AC motor. The primary focus is on exploring the effects of the Sommerfeld effect while taking into account motor parameters such as electromagnetic torque and power. By conducting this investigation, the paper aims to enhance our understanding of non-ideal systems driven by AC motors and how the Sommerfeld effect manifests in such scenarios. This research could have significant implications for practical industrial applications, bridging the gap between theoretical knowledge and real-world AC motor-driven systems.

This paper is structured as follows: In Sect. 2, the dynamic model of the vibration system is presented, and the differential equations of motion for the model are established. In Sect. 3, the response solution of the system is derived, and its stability conditions are obtained. Section 4 is dedicated to the numerical analysis of the Sommerfeld effect, with experimental verification of the results. Finally, conclusions are given.

2 Dynamic model and motion differential equations

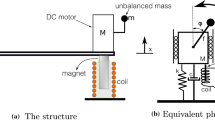
Figure 1a shows the dynamic model of a spring mass damping system excited by an unbalanced rotor. The corresponding experimental machine is shown in Fig. 1b. It is essential to note that the unbalanced rotor is driven by an AC motor, which also serves as the vibration motor. The vibration motor is mounted on an aluminum plate supported by rubber springs, making the system a non-ideal vibration system [9]. For the vibration motor, two unbalanced mass blocks are fixed at both ends of AC motor shaft (the unbalanced rotor), where m0 denotes the unbalanced mass and r denotes the unbalanced radius. The unbalanced rotor rotates counterclockwise around point o, where \(\varphi\) is the phase angle. The aluminum plate can only move in x direction due to the constraints of the guide rail. The stiffness and damping of the rubber spring are k and c, respectively. Finally, the mass of the vibration system is represented by m1 (excluding the unbalanced rotor).

Fig. 1
figure 1

The non-ideal vibration system. a Dynamic model. b Experimental machine

Full size image

Based on Fig. 1, generalized coordinates x and \(\varphi\) are selected to deduce the kinetic energy, the potential energy and the dissipation function of the vibration system. By applying Lagrange equation and introducing the steady-state electromagnetic torque of AC motor, the motion differential equations of the system can be derived as follows[6]:

$$m\ddot{x} + c\dot{x} + kx = m_{0} r(\dot{\varphi }^{2} \cos \varphi + \ddot{\varphi }\sin \varphi )$$
(1)
$$J\ddot{\varphi } + c_{1} \dot{\varphi } = T_{e} (\dot{\varphi }) + m_{0} r\ddot{x}\sin \varphi .$$
(2)

where \(\dot{ \bullet } = {\text{d}}( \bullet )/{\text{d}}t\), \(\ddot{ \bullet } = {\text{d}}^{{2}} ( \bullet )/{\text{d}}t^{{2}}\), \(m = m_{1} + m_{0}\),\(J\) is the moment of inertia of the unbalanced rotor, \(T_{e} = \frac{{3n_{p} R_{r} U^{2} }}{{(\omega_{s} - n_{p} \dot{\varphi })\left[ {(L_{r} + L_{s} )^{2} \omega_{s}^{2} + (R_{s} + \frac{{R_{r} \omega_{s} }}{{\omega_{s} - n_{p} \dot{\varphi }}})^{2} } \right]}}\) is the steady-state electromagnetic torque, \(\omega_{s} = 2{\uppi }f\) is the angular frequency of stator power, and the definition of the other parameters of AC motor and the values of all parameters are shown in Table 1.

Table 1 System parameters
Full size table

3 Theoretical analysis

3.1 Analytical solution

By comparing the motion equation of the motor, it is evident that the second term \(m_{0} r\ddot{x}\sin \varphi\) on the right-hand side of Eq. (2) represents the load torque, which is also referred to the electromechanical coupling term. Considering the characteristics of the non-ideal source, it becomes essential to study whether AC motor can supply sufficient power to overcome the energy sink when the response amplitude x of the system is at its maximum [17]. It is well known that x approaches its maximum only when the system operates at the resonant point. Therefore, the investigation will focus on the scenario when the system resonates.

Since Sommerfeld effect refers to the change in the angular velocity of the rotor near the resonance region, the damping term and the external excitation term in Eq. (1) can be regarded as small or weak terms compared to others [17]. So, the small parameter \(\varepsilon < < 1\) is introduced to indicate the smallness of certain terms in the equations. Considering that the angular velocity is close to a constant in the steady state, the term \(\ddot{\varphi }\sin \varphi\) can be neglected. Introducing symbols \(\omega_{n}^{2} = k/m\), \(\varepsilon\chi_{1} = m_{0} r/m\), \(\varepsilon\varsigma = c/m\) to obtain the standard equation, the expression form of Eq. (1) with the small parameter \(\varepsilon\) is arranged as follow:

$$\ddot{x} + \omega_{n}^{2} x = \varepsilon (\chi_{1} \dot{\varphi }^{2} \cos \varphi - \varsigma \dot{x})$$
(3)

If the system runs in steady-state motion, the amplitude A, the angular velocity \(\dot{\varphi } = \Omega\) and the phase angle \(\Theta\) of the system response should be constant. Based on the average method, the solution of Eq. (3) can be assumed in the following form [1]:

$$x = A\cos (\varphi + \Theta ) = A\cos \psi$$
(4)
$$\dot{x} = - A\omega_{n} \sin \psi$$
(5)
$$\ddot{x} = - \dot{A}\omega_{n} \sin \psi - (\Omega + \dot{\Theta })A\omega_{n} \cos \psi$$
(6)

When \(\varepsilon \ne 0\), the constraint condition of Eq. (5) needs to be added as follow:

$$\dot{A}\cos \psi - \dot{\Theta }A\sin \psi = (\Omega - \omega_{n} )A\sin \psi$$
(7)

Substituting Eqs. (4–6) into Eq. (3), we have:

$$- \dot{A}\omega_{n} \sin \psi - A\dot{\Theta }\omega_{n} \cos \psi - A\omega_{n} (\Omega - \omega_{n} )\cos \psi = \varepsilon (\chi_{1} \Omega^{2} \cos \varphi + \varsigma A\omega_{n} \sin \psi ),$$
(8)

By combining Eqs. (7) and (8), the analytical expression of \(\dot{A}\) and \(\dot{\Theta }\) can be derived as follows:

$$\frac{{{\text{d}}A}}{{{\text{d}}t}} = - \frac{\varepsilon }{{\omega_{n} }}(\chi_{1} \Omega^{2} \cos \varphi + A\omega_{n} \varsigma \sin \psi )\sin \psi$$
(9)
$$\frac{{{\text{d}}\Theta }}{{{\text{d}}t}} = \varepsilon \sigma_{1} - \frac{\varepsilon }{{A\omega_{n} }}\left( {\chi_{1} \Omega^{2} \cos \varphi + A\omega_{n} \varsigma \sin \psi } \right)\cos \psi$$
(10)

From the right-hand side of Eqs. (1) and (2), it can be observed that \(x\) and \(\varphi\) are coupled to each other. Substituting \({\text{d}}\varphi = \Omega {\text{d}}t\) and \(\ddot{\varphi } = \dot{\Omega }\) into Eqs. (9) and (10), the state equations of the electromechanical coupling system changing with \(\varphi\) can be obtained:

$$\frac{{{\text{d}}\Omega }}{{{\text{d}}\varphi }} = \frac{\varepsilon }{\Omega }(T_{m} (\Omega ) - A\chi_{2} \omega_{n} \Omega \cos \psi \sin \varphi )$$
(11)
$$\frac{{{\text{d}}A}}{{{\text{d}}\varphi }} = - \frac{\varepsilon }{{\Omega \omega_{n} }}(\chi_{1} \Omega^{2} \cos \varphi + A\omega_{n} \varsigma \sin \psi )\sin \psi$$
(12)
$$\frac{{{\text{d}}\Theta }}{{{\text{d}}\varphi }} = \frac{{\varepsilon \sigma_{1} }}{\Omega } - \frac{\varepsilon }{{A\omega_{n} \Omega }}(\chi_{1} \Omega^{2} \cos \varphi + A\omega_{n} \varsigma \sin \psi )\cos \psi$$
(13)

where \(\varepsilon T_{m} (\Omega ) = [T_{e} (\Omega ) - c_{1} \Omega )]/J\), \(\varepsilon \sigma_{1} = \omega_{n} - \Omega\),\(\varepsilon \chi_{2} = m_{0} r/J\).

If time \(t\) is considered as a variable,\(\Omega\), \(A\) and \(\Theta\) are also the functions of \(\varphi\). Therefore, they can be considered small fluctuations around their mean values \(\omega\), \(a\), \(\theta\). Based on the perturbation method, \(\Omega\), \(A\) and \(\Theta\) are expressed in the following forms:

$$\begin{gathered} \Omega = \omega + \varepsilon f_{\omega }^{{}} \hfill \\ A = a + \varepsilon f_{a}^{{}} \hfill \\ \Theta = \theta + \varepsilon f_{\theta }^{{}} \hfill \\ \end{gathered}$$
(14)

where \(f_{\omega }^{{}}\),\(f_{a}^{{}}\) and \(f_{\theta }^{{}}\) are small quantities to represent the small fluctuations around the mean values.

Taking the average of \(\Omega\), \(A\) and \(\Theta\) over a motion period of \(0\sim 2{\uppi }\) as their mean values, the integral average of Eqs. (11–13) are as follows:

$$\omega{^\prime} = \frac{\varepsilon }{\omega }\left[ {T_{m} (\omega ) + \frac{1}{2}\chi_{2} a\omega_{n} \omega \sin \theta } \right]$$
(15)
$$a{^\prime} = - \frac{\varepsilon }{2\omega }\left( {a\varsigma + \chi_{1} \frac{{\omega^{2} }}{{\omega_{n} }}\sin \theta } \right)$$
(16)
$$\theta{^\prime} = \frac{\varepsilon }{\omega }\left( {\sigma_{2} - \frac{{\chi_{1} \omega^{2} }}{{2a\omega_{n} }}\cos \theta } \right)$$
(17)

where \(\varepsilon \sigma_{2} = \omega_{n} - \omega\),\(\bullet^{\prime} = {\text{d}}( \bullet )/{\text{d}}\varphi\).

Although the higher-order approximate solutions of the system can be obtained by Eq. (14), the first-order approximation of each physical quantity is enough for qualitative analysis based on the solution form of the perturbation method. Therefore, when \(\omega{^\prime} = 0\), \(a{^\prime} = 0\) and \(\theta{^\prime} = 0\), we can obtain the first approximation solution (amplitude \(a\) and phase angle \(\theta\)) for the steady state motion of the system as follows:

$$a = \frac{{m_{0} \omega^{2} r}}{{m\omega_{n} \sqrt {4(\omega_{n} - \omega )^{2} + c^{2} /m^{2} } }}$$
(18)
$$\tan \theta = \frac{c}{{2m(\omega_{n} - \omega )}}$$
(19)

By substituting Eqs. (18) and (19) into Eq. (15) and considering \(\omega^{\prime} = 0\), the torque balance equation of the motor when the system runs in the steady state can be obtained as follow:

$$T_{e} (\omega ) - T_{L} (\omega ) = 0$$
(20)

where \(T_{L} (\omega ) = c_{1} \omega + c\omega_{n}^{2} a_{{}}^{2} /(2\omega )\) is the total load torque of the motor.

3.2 Stability analysis

Based on Lyapunov-Poincare method, the first approximation solutions are perturbed as follows[6]:

$$\omega = \omega_{c} + \varepsilon \omega_{1} ,\;\;a = a_{c} + \varepsilon a_{1} ,\;\;\theta = \theta_{c} + \varepsilon \theta_{1}$$
(21)

where \(\omega_{c}\), \(a_{c}\), \(\theta_{c}\) represent the steady-state value, and \(\varepsilon \omega_{1}\), \(\varepsilon a_{1}\), \(\varepsilon \theta_{1}\) represent the perturbed terms.

Substituting Eq. (21) into Eqs. (15–17), the state equation of the system can be obtained as follow:

$${\mathbf{y}}{^\prime} = {\mathbf{By}}$$
(22)

where \({\mathbf{y}}{^\prime} = [\omega_{1}{^\prime} ,a_{1}{^\prime} ,\theta_{1}{^\prime} ]^{{\text{T}}}\), \({\mathbf{y}} = [\omega_{1} ,a_{1} ,\theta_{1} ]^{{\text{T}}}\), \({\mathbf{B}} = [b_{ij} ]_{(i,j = 1,2,3)}\).

The characteristic roots of Eq. (22) are deduced as follow:

$$\lambda^{3} + B_{1} \lambda^{2} + B_{2} \lambda + B_{3} = 0$$
(23)

By applying Routh-Hurwitz criterion, the stability conditions of the system are derived. The first stability condition is as follow:

$$B_{1} = \frac{1}{J}\left( {\frac{{c\omega_{n}^{2} a^{2} }}{{2\omega^{2} }} - T_{n} } \right) + \frac{c}{{m_{0} }} > 0$$
(24)

where \(T_{n} = {\text{d[}}T_{e} (\omega ) - c_{1} \omega ]/{\text{d}}\omega < 0\).

The second stability condition is as follow:

$$B_{3} = \frac{{ca^{2} \omega_{n}^{2} }}{{J\omega^{2} }}\left[ {(2\omega_{n} - \omega )(\omega_{n} - \omega ) + \frac{{3c^{2} }}{{8m^{2} }}} \right] - \frac{{c^{2} T_{n} }}{{4Jm^{2} }} - \frac{1}{J}\left( {\frac{{ca^{2} \omega_{n}^{2} }}{{2\omega^{2} }} + T_{n} } \right)(\omega_{n} - \omega )^{2} > 0$$
(25)

The third stability condition is as follow:

$$\begin{aligned} B_{1} B_{2} - B_{3} & = \frac{1}{{4J^{2} m^{3} \omega^{4} }}\left\{ {c\left\{ {4T_{n}^{2} m^{2} \omega^{4} - 4JT_{n} mc\omega^{4} + J^{2} \omega^{4} c^{2} + 4J^{2} \omega^{4} m^{2} (\omega_{n} - \omega )^{2} } \right\} + 2a^{4} m^{2} c\omega_{n}^{4} m^{2} \left( {2\omega_{n}^{2} - 3\omega_{n} \omega + \omega^{2} } \right)} \right. \\ & \;\;\;\; + \left. {2a^{4} m^{2} c\omega_{n}^{4} c^{2} + a^{2} m\omega_{n}^{2} \omega^{2} \left\{ { - 6T_{n} mc^{2} + Jc[3c^{2} + 4m^{2} (\omega_{n} - \omega )^{2} ] - 4T_{n} m^{3} (2\omega_{n}^{2} - 3\omega_{n} \omega + \omega^{2} )} \right\}} \right\} > 0 \\ \end{aligned}$$
(26)

4 Numerical analysis and experiment

This section will adopt quantitative and qualitative investigations on Sommerfeld effect by using methods of numerical analysis and experiment. The relevant parameters are shown in Table 1.

4.1 Sweep frequency experiment

To prove the existence of the Sommerfeld effect in the experimental machine shown in Fig. 1b, acceleration and deceleration experiments of the motor are conducted as depicted in Fig. 2. The experimental scheme is as follows: firstly, the target velocity is initially set to 650rpm; secondly, the motor velocity is changed by 2rpm every second, and the motor is driven by a Siemens frequency converter G120; finally, during the experiment, the velocity and the vibration amplitude are recorded using a DH5922D data acquisition instrument.

Fig. 2
figure 2

Sweep frequency experiment. a Velocity of motor. b Vibration amplitude. c Electromagnetic torque of motor. d Power of motor

Full size image

From Fig. 2a, it is evident that the motor velocity exhibits two jumps during both acceleration (point a to b) and deceleration (point e to f). This observation confirms the existence of Sommerfeld effect in the vibration system driven by AC motor. Furthermore, it is noteworthy that the jump amplitude during acceleration is greater than that during deceleration.

In Fig. 2b, we can observe a similar difference in vibration amplitude jumps as in the motor velocity. A larger jump in velocity corresponds to a larger jump in vibration amplitude. When observing the amplitude curve changes, we notice that the amplitude increases slightly when the motor starts and stops. This occurs because the rotational velocity of the motor is relatively low, approaching the natural frequency of the fixed base in the experimental system. This proximity to the natural frequency leads to resonance, causing a slight increase in vibration amplitude during motor startup and shutdown.

In Fig. 2c, the changes in the electromagnetic torque of AC motor \(T_{e}\) are displayed. According to the mechanical characteristics of AC motor, once the motor is powered, the electromagnetic torque \(T_{e}\) rapidly reaches the maximum value, indicated by point g, corresponding to the goal velocity. At this point, the electromagnetic torque significantly exceeds the load torque, resulting in an additional electromagnetic torque being utilized to increase the motor's velocity. As the motor continues to operate, it seeks the torque balance point, leading to a reduction in the electromagnetic torque. This behavior is consistent with the mechanical characteristics of an AC motor. As the motor reaches its desired velocity, the electromagnetic torque approaches a level that matches the load torque, achieving a stable operating condition.

There are three jumps in Fig. 2c. The first and third jumps are caused by Sommerfeld effect, while the second jump is due to the deceleration command of the velocity. When Sommerfeld effect occurs, such as point a to b and point e to f, it also has a significant impact on the electromagnetic torque of AC motor. For example, the curve from g to c would be smooth if there were no Sommerfeld effect. The curve jumps from a to b because the motor's velocity escapes the frequency capture of the vibration system. As a result, the motor no longer requires as much electromagnetic torque. Similarly, the curve will suddenly increase when there is a frequency capture, such as at point e to f, which also causes the curve to become unsmooth.

In general, the electromagnetic torque decreases as the motor's velocity increases, according to the mechanical characteristics of AC motor. By observing Fig. 2c, it can be seen that the electromagnetic torque value from point g to c is greater than that of point d to h, even though the velocities are the same. This is because deceleration is different from acceleration, and the motor does not require a significant amount of electromagnetic torque during deceleration. Only when the electromagnetic torque is less than the load torque will there be a negative angular acceleration, reducing the velocity to zero.

Comparing Fig. 2a–c, the change in the electromagnetic torque is consistent with the change in the velocity. Between 150 and 200 s in Fig. 2a, the velocity barely increases, indicating that the vibration system captures the motor’s velocity. Similarly, the velocity barely decreases from 280 to 340 s. When observing points g to a in Fig. 2c, the electromagnetic torque curve decreases significantly at the beginning and then becomes slow when Sommerfeld effect occurs. Especially during the later stage of the velocity deceleration, the electromagnetic torque curve hardly changes when frequency capture happens.

Comparing the velocity, amplitude, and torque, the system enters the capture state after 150 s due to the almost horizontal velocity curve. However, the vibration amplitude increases dramatically during this stage. The electromagnetic torque decreases more slowly. When the phenomenon of the velocity jump occurs, the electromagnetic torque curve also exhibits a jump. These variations can be analyzed by considering the vibration amplitude. The significant decrease in vibration amplitude is a result of the velocity exceeding the resonance point, causing it to escape the frequency capture of the vibration system. As a consequence, the load torque reduces, and the motor no longer requires as much electromagnetic torque. Consequently, the motor quickly finds a new balance point, leading to the observed jump in the electromagnetic torque curve.

The change in motor power is essentially consistent with its electromagnetic torque change, as shown in Fig. 2d. The only difference is that the power increases after the frequency capture occurs. This observation also elucidates the mechanism of Sommerfeld effect, wherein the motor's energy is utilized to increase the vibration rather than the velocity.

Based on Fig. 2c and d, it is evident that Sommerfeld effect still exists in the vibration system driven by the unbalanced rotor, even if the electromagnetic torque and motor power are sufficient to achieve the goal velocity. The reason for this is that during the occurrence of Sommerfeld effect, the torque and power of the motor do not reach their maximum values but remain less than the load torque for a certain period. In other words, as long as the electromagnetic torque remains greater than the load torque, the frequency capture of the vibration system does not occur. Similarly, this is also because the motor's torque is large enough to avoid the frequency capture.

In summary, Sommerfeld effect does exist in the vibration system driven by AC motor with an unbalanced rotor. If the electromagnetic torque of AC motor is insufficient to overcome its load torque during the frequency capture region, the motor's velocity will not increase. On the other hand, if the electromagnetic torque is sufficient, there will be a jump in the motor's velocity. This phenomenon highlights the significance of the electromagnetic torque in determining the behavior of the motor and its interaction with the vibration system.

4.2 Numerical analysis

In the sweep frequency experiment, clear asymmetry jumps in the acceleration and deceleration of velocity are observed. It is well known that the AC motor velocity is related to the power frequency. To better understand the mechanism of Sommerfeld effect's jumps, especially the relationship between input (power) and output (velocity and amplitude), the data in Fig. 2 is represented differently, with the power frequency f from the converter as the abscissa axis in Fig. 3a and b. Since the motor velocity is changed by 2 rpm every second in the experimental process, the changed rate of the frequency is approximately equal to 1/30 every second. Numerical analysis based on Eqs. (18) and (20) is shown in Fig. 3c and d. By comparing the theoretical and experimental results, it is evident that the two trends are consistent. The comparison between theory and experiment in Fig. 3 allows for a deeper understanding of Sommerfeld effect’s behavior and the correlation between power frequency and jumps in the system's acceleration and deceleration velocities.

Fig. 3
figure 3

Comparison of experimental data and numerical results. a Experimental velocity. b Experimental vibration amplitude.c Numerical velocity. d Numerical vibration amplitude

Full size image

When f is greater than 8.5 Hz, the vibration system begins to capture the motor's velocity. As shown in Fig. 3a, the velocity curve becomes almost horizontal. Despite the increasing frequency, the motor gains more and more energy. However, the motor's velocity does not increase. This is because the extra energy is used by the vibration system to increase the vibration, as depicted in Fig. 3b. As the frequency increases, the amplitude experiences a significant rise. In conclusion, Sommerfeld effect adheres to the principle of energy conservation. The additional energy is directed toward increasing the vibration amplitude rather than accelerating the motor's velocity, resulting in the observed behavior in the system.

Both theoretical analysis and experimental results demonstrate that the vibration amplitude curve exhibits a hard nonlinearity, curving to the right. Without considering the effect of the non-ideal source, the amplitude would show linear vibration as depicted in Fig. 1. Therefore, it is essential to take into account the impact of the non-ideal source in dynamic analysis. In summary, the nonlinearity introduced by the non-ideal source significantly affects the vibration behavior, and its consideration is crucial for accurate dynamic analysis.

Due to its nonlinear characteristics, the jump point of the upward velocity does not coincide with that of the downward velocity, reflecting the feature of time delay. Specifically, as the power frequency f increases, the amplitude x changes from point a to b; on the other hand, as f decreases, x from point c to d. While Sommerfeld effect exhibits hard nonlinearity, it is fundamentally different from stiffness nonlinearity, as observed in Fig. 3b. The nonlinear behavior in the amplitude-frequency curve of the non-ideal system is primarily caused by the system's frequency capture phenomenon. This occurs when the angular velocity of the motor matches the excitation frequency of the external excitation force, leading to resonance near the natural frequency of the system and causing the frequency capture phenomenon.

As it is well known, once resonance occurs, the system's amplitude increases rapidly. In this scenario, the larger amplitude necessitates more energy input, considering energy conservation. However, the non-ideal source cannot provide infinite energy, leading to the situation where all the increased energy from the AC motor is utilized to maintain the resonant motion of the system. Consequently, there is no excess energy available to increase the angular velocity of the motor.

However, the frequency capture ability of the system does not persist indefinitely. Its existence is contingent on the condition that the amplitude increases with the rise of the power frequency. In reality, when the amplitude surpasses the resonant point, it starts to decrease, causing the system to vibrate without requiring as much energy. According to Eq. (2), assuming the same amount of input energy as before, the vibration now releases the excess energy, with some energy suddenly applied to the angular acceleration of the motor. Consequently, after the motor acquires significant angular acceleration, its angular velocity jumps from point a to b, as illustrated in Fig. 3c.

Next, let's analyze the velocity jump when the power frequency f decreases. As shown in Fig. 3d, although f passes through point b during the downward process, there is no jump phenomenon. This absence of a jump is because the system's amplitude does not change rapidly from point b to c. However, when f passes through point c, the amplitude jumps from point c to d. This sudden change in amplitude causes the load torque to increase rapidly. If the original input electromagnetic torque remains unchanged, the right-hand side of Eq. (2) will include a negative torque, leading to negative angular acceleration. Consequently, the velocity of the motor jumps again.

In summary, the Sommerfeld effect exhibits both the frequency capture ability and the amplitude-frequency characteristics of hard nonlinearity. Additionally, the existence of multiple equilibrium states in non-ideal vibration systems is demonstrated by theory and experiment in Fig. 3. These dynamic properties are analyzed from the viewpoint of torque balance in the following content.

The experiments confirm the existence of Sommerfeld effect in the non-ideal vibration system driven by AC motor. Therefore, it is essential to investigate the mechanism of Sommerfeld effect in this type of system. Figure 4 illustrates the relationship between the electromagnetic torque and the load torque near the resonance region under different power frequencies of the motor.

Fig. 4
figure 4

Torques with different power frequencies. a Velocity and torques.b Velocity and torque differences

Full size image

From Fig. 4a, it is evident that the electromagnetic torque curve of AC motor is a nonlinear function of velocity, which distinguishes it from the mechanical characteristics of DC motor [9]. The electromagnetic torque Te of AC motor initially increases with the velocity until it reaches its maximum value. Afterward, the electromagnetic torque decreases with the further increase in velocity until it intersects with the load torque TL. It is worth noting that the velocity corresponding to the intersection between the electromagnetic torque and the load torque satisfies the torque balance equation Eq. (20).

Based on Eq. (18), the first approximation amplitude is also a nonlinear function of velocity, which results in a peak in the TL curve near the resonance region. Due to the existence of three intersections between TL and certain portions of the Te curves, it reflects the multi-solution characteristic of the nonlinear equation. The frequency region with three intersection points corresponds to the region where Sommerfeld effect appears. As a result, Sommerfeld effect can occur only when the velocity is within this specific frequency region. In other words, the Sommerfeld effect can only occur near the resonance region.

To better illustrate the relationship of the three intersection points, TL is subtracted from Te, as shown in Fig. 4b. It can be observed that not all curves have three zero points, indicating that certain conditions need to be met for the occurrence of Sommerfeld effect. The mechanism of Sommerfeld effect lies in the presence of three points simultaneously, which leads to the velocity jump. For instance, at 9.4 Hz and 11.1 Hz, there is no jump because of two reasons. Firstly, the velocity at 9.4 Hz operates in sub-resonance. Secondly, the electromagnetic torque at 11.1 Hz always exceeds its load torque, which prevents frequency capture. As the power frequency enters the region between 9.9 Hz and 10.7 Hz, the motor's velocity becomes captured. Therefore, only when the power frequency is greater than 10.7 Hz can it escape from frequency capture.

In summary, Fig. 4 employs the torque balance method to explain the mechanism of Sommerfeld effect. It is demonstrated that the occurrence of Sommerfeld effect depends on the relationship between the electromagnetic torque and the load torque.

As is well known, the existence of multi-roots in nonlinear systems necessitates further stability criteria. Figure 5 presents the three stability conditions corresponding to Fig. 3. It can be observed that the first stability condition in Fig. 5a and the third stability condition in Fig. 5c are satisfied under different power frequencies, while only the second stability condition in Fig. 5b is not satisfied in certain frequency regions. Therefore, the stability criterion condition of the non-ideal vibration system driven by AC motor in this model can be simplified to use only the second stability condition.

Fig. 5
figure 5

Stability conditions. a First condition. b Second condition.c Third condition

Full size image

Based on the previous analysis, we understand that the velocity jump is caused by the abrupt change in the load torque of the AC motor due to system resonance. Observing Fig. 5b, if the stability coefficient corresponding to the amplitude is negative, it implies that the amplitude is unstable. In other words, the actual system will not operate at this amplitude.

If the Sommerfeld effect occurs, there will be three zero points on the curve Te − TL in Fig. 4b. According to the stability criterion in Fig. 5b, one of these points is unstable. Therefore, the final stable state of the system will be chosen between the other two points. When the electromagnetic torque curve is tangent to the load torque curve at a critical frequency, there are only two points of intersection between the two torque curves in Fig. 4a, and both points of intersection are stable. Assuming that the system is at the maximum value of the critical frequency, even a slight increase in the power frequency will cause a jump in the motor's velocity. Similarly, when the system is at the minimum critical state, a slight reduction in the power frequency also leads to a jump.

In summary, the selected motion characteristic of the nonlinear vibration system leads to the velocity jump. In other words, the torque balance equation of the motor has the property of multiple solutions, resulting in multiple steady-state motions. Based on Fig. 5b, it can be observed that the zero point of the torque difference curve in the ascending stage is unstable, while the zero point in the descending stage is stable.

4.3 Fixed frequency experiment

To verify the presence of multiple steady state motions, velocities corresponding to specific goal velocities are chosen based on Figs. 3 and 4. Velocities of 400rpm, 500rpm, and 650rpm are selected, which all lie outside the frequency capture region. Specifically, 400rpm and 500rpm represent power frequencies that belong to sub-resonance, while 650rpm represents a power frequency that belongs to super-resonance.

As illustrated in Fig. 6a, when the goal velocity is set at 600rpm, two different actual velocities are observed. It is evident that the motor velocity jumps between 600 and 650rpm during the acceleration stage and between 600 and 500rpm during the deceleration stage. This observation confirms that 600rpm is within the frequency capture region.

Fig. 6
figure 6

Fixed frequency experiment. a Velocity of motor. b Vibration amplitude.c Electromagnetic torque of motor. d Power of motor

Full size image

According to Fig. 6b, the system exhibits two stable actual velocities in the sub-resonance and super-resonance regions, respectively. This distinction can also be observed in the amplitude change, as the amplitude of 600rpm in sub-resonance is greater than that in super-resonance. These findings further support the existence of multiple steady state motions in the non-ideal vibration system driven by AC motor.

In Fig. 6c, it can be observed that the electromagnetic torques of the two steady-state motions at 600 rpm are different. The electromagnetic torque of 600 rpm in the sub-resonance region is greater than that in the super-resonance region due to the different amplitudes, leading to different load torques. The switching of the power frequency in the converter results in several curve spikes in the acceleration stage. However, such spikes do not exist in the deceleration stage because the electromagnetic torque must be less than the load torque during deceleration.

Comparing Fig. 6a and c, it should be noted that the electromagnetic torque is a function of the actual velocity. In the acceleration stage, when the actual velocities of 500 rpm and 600 rpm are close, their electromagnetic torques are also close. However, the power of the motor is dependent on the amplitude since the load torque is related to the amplitude. In other words, the power of the motor represents the input energy, while the amplitude represents the output energy. Therefore, the change in motor power must follow the law of energy conservation.

In conclusion, this set of fixed frequency experiments confirms that Sommerfeld effect will occur whenever the capture condition is satisfied. Additionally, the motion of the electromechanical coupling system must adhere to the law of energy conservation. The experimental observations and analyzes support the understanding of Sommerfeld effect and its impact on the dynamics of the non-ideal vibration system driven by AC motor.

5 Conclusion

Taking the mechanical characteristics of AC motor into consideration, this paper investigates Sommerfeld effect theoretically, numerically, and experimentally in a spring mass damping system excited by an unbalanced rotor. The results demonstrate the presence of Sommerfeld effect in the vibration system driven by an AC motor. Even when the torque and power of the motor are sufficient to reach the desired velocity, frequency capture can still occur if the electromagnetic torque of the motor is less than its load torque. The mechanism behind frequency capture lies in the fact that the non-ideal source cannot provide infinite energy instantaneously. As a result, the increased energy of AC motor is used to sustain the resonant motion of the system rather than increasing the angular velocity. Once the angular velocity of AC motor surpasses the resonance point, the vibration amplitude of the system rapidly decreases, releasing excess energy to boost the motor's angular velocity. This leads to a jump phenomenon in the system's velocity. Additionally, the electromagnetic torque and power of AC motor undergo significant changes during this process. Particularly, the substantial change in power reflects the occurrence of frequency capture, as confirmed by experimental verification. The torque balance equation can be utilized to determine whether the system exhibits Sommerfeld effect. If the condition for the existence of Sommerfeld effect is satisfied, there will be three intersection points between the electromagnetic torque and the load torque, resulting in the jump phenomenon in the motor's velocity. It is important to note that the jump phenomenon occurs both during the acceleration and deceleration of the motor's velocity, with a time lag between them. This is attributed to the hard nonlinear nature of the amplitude-frequency characteristic curve, which contributes to the selective motion characteristics of the system.