Nonlinear Dynamics of Self and Parametrically Excited Systems with Non-ideal Energy Source

Abstract

Vibrations of a non-ideal system with nonlinear damping and periodically varying stiffness are presented in the chapter. The system is excited by rotating unbalanced mass attached to the DC motor with limited power. Rotation of the motor is tuned to the period of varying stiffness in 1:2 ratio which corresponds to the principal parametric resonance. Nonlinear damping is represented by Rayleigh model which may generate self-excitation. The analytical solutions obtained by Krylov–Bogoliubov-Mitropolsky method for the two degree of freedom model show an existence of the internal loop on the resonance curve and transition zones from periodic to quasi-periodic oscillations. Chaotic or hyper-chaotic vibrations are detected by numerical simulations and an influence of the non-ideal energy source on the motion type is presented.

1 Introduction

Structural elements of mechanical, aerospace or civil engineering objects are subjected to various excitation sources. Self-excited vibrations belong to a special class of vibrations occurring in the nature or in the structures produced by men. Their characteristic feature is that they are generated by constant input, independent of time [10, 13]. An energy transfer is controlled by the system itself and oscillation arise due to its internal properties. Classical examples are flutter of airplane wings, chatter in machining or shimmy of vehicle whiles. The self-excitation can be soft, with a stable limit cycle, or hard (catastrophic) when a limit cycle is unstable and a solution may tend to zero or to infinity. The second, totally different class, are vibrating systems with periodically varied coefficients [4, 9, 10]. In machine dynamics the coefficients are related to periodically changing stiffness or mass moment of inertia. The main feature of parametric oscillations is that for selected parameters instability zones occur and the amplitude of oscillations gets large values. These zones, called parametric resonances, are dependent on amplitude and frequency of varied coefficients and damping of the system. Apart from self and parametric vibrations also the system can be excited by direct applied periodic force. Then the periodic component occurs on the right side of the equations and the model becomes inhomogeneous. In some cases all mentioned above vibrations may exist at the same time and then due to interactions interesting, and sometimes unexpected, phenomena may arise [1, 14, 15, 17]. If the model consists of self-excited terms and parametric with external excitations are tuned 1:2 they interact strongly in the vicinity of the principal parametric resonance [15]. Inside the resonance zone even five periodic solutions are possible but only two of them are stable. Moving away from the resonance the interaction with self-excitation becomes strong and then quasi-periodic oscillation takes place, followed by the second kind Hopf bifurcation.

Often in mathematical models excitations are defined by simple harmonic force and dynamics of the energy source (DC motor for example) and its interactions with the main system are neglected. This kind of model is called ideal [2]. In contrast, systems with limited power have to consider interactions with the main structure [5,6,7]. The effect of non-ideal energy source was first detected by Sommerfeld [11]. During the experimental tests Sommerfeld observed instabilities in a linear structure with one degree of freedom. The explanation was found when the characteristic of the motor was taken into account. The formulated complete model considered coupling with the energy source confirmed results obtained by experiment.

The non-ideal energy source introduces an additional degree of freedom and differential equations of motion are expressed by a coordinate describing motion of the energy source. In consequence the model is represented by autonomous equations without time given in a direct form [2]. The introduction of new coordinate ϕ transforms harmonic excitation $sin\omega t$ into $sin\phi$, which is a nonlinear function of the coordinate. A non-ideal model of a parametric and self-excited system with one degree of freedom was analyzed in paper [16] where the importance of the proper modelling of the energy source was presented, either for regular or chaotic oscillations. In the present chapter the model is extended for a chain of coupled oscillators. Detailed analysis is demonstrated for two coupled Rayleigh-Mathieu-Duffing oscillators with a non-ideal energy source.

2 Model of the Structure

A model of the studied structure is a chain of coupled oscillators excited by rotating unbalanced mass attached to the DC motor with limited power. Due to this fact the motor plays a role of a non-ideal energy source. The rotating mass excites the system with S-degrees of freedom but the oscillators influence the rotor motion as well. Thus, the coupled oscillators together with the rotor are represented by S + 1 generalized coordinates.

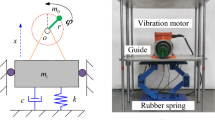
As presented in Fig. 1 motion of oscillators is described by x_i coordinates, i = 1,2…S, while ϕ and is angle of rotation of the DC motor. The oscillators are connected by springs, considered in further investigation as nonlinear of Mathieu-Duffing type which are nonlinear and may produce parametric vibrations. Dampers in Fig. 1 are represented by nonlinear Rayleigh functions which may generate self-excitation.

Fig. 1

Non-ideal system with parametric and self-excitation with many degrees of freedom

Kinetic energy of the system takes the form

$$T = \frac{1}{2}\left( {J_0 + m_0 r^2 } \right)\dot{\phi }^2 + \frac{1}{2}m_0 \dot{x}_1^2 + \dot{x}_1 \dot{\phi }rm_0 {\text{cos}}\phi + \mathop \sum \limits_{i = 1}^s \frac{1}{2}m_i \dot{x}_i^2$$

(1)

where r, m₀, J₀ are radius, unbalanced mass and mass moment of inertia of the rotor and m_i is mass of the selected oscillator.

Let us assume temporarily that the system is linear and conservative, then its potential energy is defined as

$$\begin{array}{c}V=\frac{1}{2}{k}_{1}{x}_{1}^{2}+{m}_{0}g({x}_{1}+rsin\phi )+\sum\limits_{i=1}^{s-1}\frac{1}{2}{k}_{i,i+1}{\left({x}_{i}-{x}_{i+1}\right)}^{2}+\frac{1}{2}{k}_{S}{x}_{S}^{2}\end{array}$$

(2)

where, g is gravity acceleration, ${x}_{i}$ displacement of m_i mass, k_1, k_S, k_i,i+1 linear stiffness of the first spring, the last spring, and springs connecting i and i + 1 oscillators. Applying kinetic and potential energies to Lagrange equations of the second kind, and considering notation presented in Fig. 1, we obtain a set of S + 1 ordinary differential equations of motion of coupled oscillators with the DC motor. The terms related to static displacements and gravity force components are equal therefore they are pared. The term ${m}_{0}gr\mathrm{cos}\phi$ is also assumed as small and can be neglected [7].

To include nonlinear damping and stiffens the additional nonlinear functions $\tilde{f }$ are added to the model. These functions depend on generalized coordinates and velocities. We assume that nonlinearities are of ε order, where ε is a formal small parameter. Thus, equations of motion of the complete nonlinear system take the final form

$$\begin{array}{c}\begin{array}{c}\ddot{\phi }=\varepsilon \left[\tilde{G }\left(\dot{\phi }\right)-{\tilde{q }}_{2}{\ddot{X}}_{1}\mathrm{cos}\phi \right]\\ {\ddot{X}}_{1}+{M}_{1}({a}_{11}{X}_{1}+{a}_{12}{X}_{2}+...+{a}_{1S}{X}_{S})=\varepsilon {M}_{1}{\tilde{f }}_{1}+{\tilde{q }}_{1}{\dot{\phi }}^{2}sin\phi -{\tilde{q }}_{1}\ddot{\phi }cos\phi \end{array}\\ {\ddot{X}}_{2}+{M}_{2}({a}_{21}{X}_{1}+{a}_{22}{X}_{2}+...+{a}_{2S}{X}_{S})=\varepsilon {M}_{2}{\tilde{f }}_{2}\\ \vdots \\ {\ddot{X}}_{S}+{M}_{S}({a}_{S1}{X}_{1}+{a}_{S2}{X}_{2}+...+{a}_{SS}{X}_{S})=\varepsilon {M}_{S}{\tilde{f }}_{S}\end{array}$$

(3)

Functions with tilde are expressed by small parameter, $\tilde{G }\left(\dot{\phi }\right)=\varepsilon G\left(\dot{\phi }\right)$ and ${\tilde{f }}_{i}=\varepsilon {f}_{i}$. Furthermore, Eq. (3) are expressed in dimensionless form by introducing dimensionless time $\tau ={\omega }_{1}t$ and coordinates ${X}_{j}=\frac{{x}_{j}}{{x}_{0}}$, where ${\omega }_{1}=\sqrt{\frac{{k}_{1}}{{m}_{1}}}$, ${x}_{0}=\frac{{m}_{1}g}{{k}_{1}}$. Parameters a_ij represent linear parts of stiffness coefficients, ${M}_{i}=\frac{{m}_{i}}{{m}_{1}}{, q}_{1}=\frac{{m}_{0}r}{M+{m}_{0}}$, ${q}_{2}=\frac{{m}_{0}r}{{J}_{0}+{m}_{0}{r}^{2}}$, ${\tilde{q }}_{1}=\varepsilon {q}_{1}$ and functions ${\tilde{f }}_{i}={\tilde{f }}_{i}({X}_{1},{X}_{2},...{X}_{S},{\dot{X}}_{1},{\dot{X}}_{2},...,{\dot{X}}_{S},\tau )$ are nonlinear functions of dimensionless time and coordinates.

The first equation of set (3) is a driving equation of the DC motor defined as

$$G\left(\dot{\phi }\right)=L\left(\dot{\phi }\right)-H\left(\dot{\phi }\right)$$

(4)

where $H\left(\dot{\phi }\right)$ is a resistant torque and $L\left(\dot{\phi }\right)$ is torque generated by the motor. According to [2, 7], $G\left(\dot{\phi }\right)$ can be accepted by the linear function

$$G\left(\dot{\phi }\right)={u}_{1}-{u}_{2}\dot{\phi }$$

(5)

approximating the resultant torque generated by the rotor. Coefficient ${u}_{1}$ represent voltage supplied to the DC motor while ${u}_{2}$ depends on the motor characteristic. Excitation of the system occurs in the second equation of Eq. (3). It is worth mentioning that the model is time independent which is characteristic feature of non-ideal systems.

3 Two Degrees of Freedom Model with Non-ideal Energy Source

Detailed analysis of the considered system is performed for two degrees of freedom model presented in Fig. 2.

Fig. 2

Non-ideal system with parametric and self-excitation with two degrees of freedom

Equation of motion of the presented model take the form

$$\begin{array}{c}\left({J}_{0}+{m}_{0}{r}^{2}\right){\phi }^{^{\prime\prime} }=G({\phi }^{^{\prime}})-{m}_{0}r{{x}^{^{\prime\prime} }}_{1}cos\phi \\ {m}_{1}{{x}^{^{\prime\prime} }}_{1}+{f}_{1}\left(x,{x}^{^{\prime}}\right)+{k}_{1}{x}_{1}+{\widehat{k}}_{1}{x}_{1}^{3}+\left({k}_{12}-{\widehat{k}}_{12}\mathrm{cos}2\nu t\right)\left({x}_{1}-{x}_{2}\right)\\ ={m}_{0}r{{\phi }^{^{\prime}}}^{2}\left(\mathrm{sin}\phi -{\phi }^{^{\prime\prime} }\mathrm{cos}\phi \right)\\ {m}_{2}{{x}^{^{\prime\prime} }}_{2}+{f}_{2}(x,{x}^{^{\prime}})+{k}_{2}{x}_{2}+{\widehat{k}}_{2}{x}_{2}^{3}-\left({k}_{12}-{\widehat{k}}_{12}\mathrm{cos}2\nu t\right)\left({x}_{1}-{x}_{2}\right)=0\end{array}$$

(6)

where prime denotes derivative with respect to time.

The system is composed of two self-excited oscillators with nonlinear damping of Rayleigh type defined as: $f_1 = - \alpha_1 X_1^{\prime} + \beta_1 X_1^{{\prime}3}, f_2 = - \alpha_2 X_2^{\prime} + \beta_2 X_2^{{\prime}3}$ and nonlinear Duffing springs:${k}_{1}{x}_{1}+{\widehat{k}}_{1}{x}_{1}^{3}$, ${k}_{2}{x}_{2}+{\widehat{k}}_{2}{x}_{2}^{3}$. The oscillators are coupled by a linear spring with periodically varied stiffness ${\widehat{k}}_{12}\mathrm{cos}2\nu t$. The system is excited by non-ideal energy source—DC motor with the rotating unbalanced mass.

Introducing dimensionless time$\tau ={\omega }_{1}t$, where ${\omega }_{1}^{2}=\frac{{k}_{1}}{{m}_{1}}, \quad {m}_{1}={m}_{10}+{m}_{0}$, and small formal parameter ε, Eq. (6) is transformed to the form

$$\begin{array}{c}\ddot{\phi }=\varepsilon \left[\tilde{G }\left(\dot{\phi }\right)-{\tilde{q }}_{2}{\ddot{X}}_{1}\mathrm{cos}\phi \right]\\ {\ddot{X}}_{1}+{\delta }_{1}{X}_{1}+{\delta }_{12}\left({X}_{1}-{X}_{2}\right)=\varepsilon \left[{\tilde{f }}_{1}\left({X}_{1},{X}_{2},{\dot{X}}_{1},{\dot{X}}_{2},\tau \right)+{\tilde{q }}_{1}\left({\dot{\phi }}^{2}\mathrm{sin}\phi -\ddot{\phi }\mathrm{cos}\phi \right)\right]\\ {\ddot{X}}_{2}+M{\delta }_{2}{X}_{2}-M{\delta }_{12}\left({X}_{1}-{X}_{2}\right)=\varepsilon \left[M \hspace{0.17em}{\tilde{f }}_{2}\left({X}_{1},{X}_{2},{\dot{X}}_{1},{\dot{X}}_{2},\tau \right)\right]\end{array}$$

(7)

where dot denotes derivative with respect to dimensionless time τ.

Equations (7) are transformed from generalized coordinates X_i to quasi-normal coordinates Y_i by a linear transformation

$$\begin{array}{c}{Y}_{1}={X}_{1}+{\lambda }_{21}{X}_{2}+...+{\lambda }_{S1}{X}_{S}\\ {Y}_{2}={X}_{1}+{\lambda }_{22}{X}_{2}+...+{\lambda }_{S2}{X}_{S}\\ \vdots \\ {Y}_{S}={X}_{1}+{\lambda }_{2S}{X}_{2}+...+{\lambda }_{SS}{X}_{S}\end{array}$$

(8)

where λ_ij are coefficients of linear modes normalized to the first coordinate, therefore, λ_i1 = 1.

After transformation to normal coordinates we get

$$\ddot{\phi }=\varepsilon \left[\stackrel{\sim }{\Gamma }\left(\omega \right)+{\tilde{q }}_{2}\left({\psi }_{1}{\ddot{Y}}_{2}-{\psi }_{2}{\ddot{Y}}_{1}\right)\mathrm{cos}\phi \right]$$

(9)

$$\begin{array}{c}{\ddot{Y}}_{1}+{p}_{1}^{2}{Y}_{1}=\varepsilon \left[-{\tilde{F }}_{d1}-{\stackrel{\sim }{\gamma }}_{1}{({Y}_{2}{\psi }_{1}-{Y}_{1}{\psi }_{2})}^{3}+\left({Y}_{2}{\eta }_{1}-{Y}_{1}{\eta }_{2}\right)\stackrel{\sim }{\mu }\mathrm{cos}2\phi \right]\\ +M{\lambda }_{12}\left[-{\tilde{F }}_{d2}-{\stackrel{\sim }{\gamma }}_{2}{\chi }^{3}{({Y}_{1}-{Y}_{2})}^{3}-\left({Y}_{2}{\eta }_{1}-{Y}_{1}{\eta }_{2}\right)\stackrel{\sim }{\mu }\mathrm{cos}2\phi \right]\end{array}$$

(10)

$$\begin{array}{c}{\ddot{Y}}_{2}+{p}_{2}^{2}{Y}_{2}=\varepsilon \left[-{\tilde{F }}_{d1}-{\stackrel{\sim }{\gamma }}_{1}{({Y}_{2}{\psi }_{1}-{Y}_{1}{\psi }_{2})}^{3}+\left({Y}_{2}{\eta }_{1}-{Y}_{1}{\eta }_{2}\right)\stackrel{\sim }{\mu }\mathrm{cos}2\phi \right]\\ +M{\lambda }_{22}\left[-{\tilde{F }}_{d2}-{\stackrel{\sim }{\gamma }}_{2}{\chi }^{3}{({Y}_{1}-{Y}_{2})}^{3}-\left({Y}_{2}{\eta }_{1}-{Y}_{1}{\eta }_{2}\right)\stackrel{\sim }{\mu }\mathrm{cos}2\phi \right]\end{array}$$

(11)

where

${\tilde{F }}_{d1}=\left[-{\stackrel{\sim }{\alpha }}_{1}+{\stackrel{\sim }{\beta }}_{1}{\left({\psi }_{1}{\dot{Y}}_{2}-{\psi }_{2}{\dot{Y}}_{1}\right)}^{2}\right]\left({\psi }_{1}{\dot{Y}}_{2}-{\psi }_{2}{\dot{Y}}_{1}\right)$,

${\tilde{F }}_{d2}=\left[-{\stackrel{\sim }{\alpha }}_{2}+{\stackrel{\sim }{\beta }}_{2}{\chi }^{2}{\left({\dot{Y}}_{1}-{\dot{Y}}_{2}\right)}^{2}\right]\chi \left({\dot{Y}}_{1}-{\dot{Y}}_{2}\right)$,

are Rayleigh damping functions expressed in normal coordinates, p₁ and p₂ are natural frequencies of the system. Parametric excitation is represented by term $\stackrel{\sim }{\mu }\mathrm{cos}2\phi$ with amplitude $\tilde{\mu }$ and frequency $2\dot{\phi }$

If ε is equal to zero then the system is fully uncoupled. However, if ε is a small positive number then all coordinates are fully coupled and depending on the angular velocity of the DC motor and frequency of the periodically varying stiffness various resonance states can occur. We focus on the resonance zone when the rotor speed is synchronized with the parametric excitation in the ration 1:2. This situation corresponds to the principal parametric resonance. Additionally the system includes self-excitations which interact with parametric and externally excited vibrations.

3.1 Analytical Solutions

Let us consider vibrations around the principal parametric resonance. The rotor rotates with angular velocity $\dot{\phi }={\omega }_{1}$ in the vicinity of the first natural frequency p₁, thus we can write

$${p}_{1}-{\omega }_{1}=\varepsilon {\Delta }_{1}$$

(12)

where Δ₁ is a frequency detuning parameter. Parametric excitation frequency is tuned with the rotor speed.

We also assume that system is weakly nonlinear and therefore the first quasi-normal coordinate Y₁ plays the main role in the response and the second Y₂ is close to zero in the first order approximation. Thus, Eqs. (9)–(11) are reduced to the form

$$\frac{{d}^{2}\phi }{dt}=\varepsilon \left[\Gamma \left({\omega }_{1}\right)+{\tilde{q }}_{2}{\psi }_{2}{\ddot{Y}}_{1}\mathrm{cos}\phi \right]$$

(13)

$$\begin{array}{c}{\ddot{Y}}_{1}+{p}_{1}^{2}{Y}_{1}=\varepsilon \left\{-{\stackrel{\sim }{\alpha }}_{1}{\psi }_{2}{\dot{Y}}_{1}+{\stackrel{\sim }{\beta }}_{1}{\psi }_{2}^{3}{\dot{Y}}_{1}^{3}+{\stackrel{\sim }{\gamma }}_{1}{\psi }_{2}^{3}{Y}_{1}^{3}-{Y}_{1}{\eta }_{2}\stackrel{\sim }{\mu }\mathrm{cos}2\phi \right.\\ \left.+{\tilde{q }}_{1}\left({\omega }^{2}\mathrm{sin}\phi -\ddot{\phi }\mathrm{cos}\phi \right)+M{\lambda }_{12}\left[{\stackrel{\sim }{\alpha }}_{2}\chi {\dot{Y}}_{1}-{\stackrel{\sim }{\beta }}_{2}{\chi }^{3}{\dot{Y}}_{1}^{3}-{\stackrel{\sim }{\gamma }}_{2}{\chi }^{3}{Y}_{1}^{3}+{Y}_{1}{\eta }_{2}\stackrel{\sim }{\mu }\mathrm{cos}\phi \right]\right\}\end{array}$$

(14)

For the weakly nonlinear system we assume that vibrations amplitude and the angular velocity ${\omega }_{1}$ are slowly varying in time. To determine analytical solutions it is convenient to introduce new coordinates

$${Y}_{1}=A\mathrm{cos}(\phi +\psi )$$

(15)

$${\dot{Y}}_{1}=-A{p}_{1}\mathrm{cos}(\phi +\psi )$$

(16)

Computing the first time derivative of Y₁ and comparing with Eq. (16) we get

$$\frac{dA}{dt}\mathrm{cos}\left(\phi +\psi \right)-\frac{d\psi }{dt}A\mathrm{sin}\left(\phi +\psi \right)=\left({\omega }_{1}-{p}_{1}\right)A\mathrm{sin}\left(\phi +\psi \right)$$

(17)

The second time derivative takes the form

$${\ddot{Y}}_{1}=-\frac{dA}{dt}{p}_{1}\mathrm{sin}\left(\phi +\psi \right)-\left({\omega }_{1}+\frac{d\psi }{dt}\right)A{p}_{1}\mathrm{cos}\left(\phi +\psi \right)$$

(18)

Substituting (15)–(18) into Eqs. (13)–(14) we get a set of the first order differential equations

$$\frac{d{\omega }_{1}}{dt}=\varepsilon \left\{\stackrel{\sim }{\Gamma }\left({\omega }_{1}\right)-{\tilde{q }}_{2}{\psi }_{2}{A}_{1}{p}_{1}\omega \mathrm{cos}\phi \mathrm{cos}(\phi +\psi )\right\}$$

(19)

$$\frac{dA}{dt}=\varepsilon \left\{{f}_{1A}\left(A,\phi ,\psi \right)+M{\lambda }_{12}{f}_{2A}\left(A,\phi ,\psi \right)\right\}\mathrm{sin}\left(\phi +\psi \right)+{\varepsilon }^{2}...$$

(20)

$$\frac{d\psi }{dt}=\varepsilon \left\{{\Delta }_{1}+\frac{1}{A}\left[{f}_{1A}\left(A,\phi ,\psi \right)+M{\lambda }_{12}{f}_{2A}\left(A,\phi ,\psi \right)\right]\right\}\mathrm{cos}\left(\phi +\psi \right)+{\varepsilon }^{2}...$$

(21)

where

$$\begin{array}{c}{f}_{1A}\left(A,\phi ,\psi \right)=-\frac{{\tilde{q }}_{1}{{\omega }_{1}}^{2}}{{p}_{1}}sin\phi -A{\stackrel{\sim }{\alpha }}_{1}{\psi }_{2}sin\left(\phi +\psi \right)+\frac{3}{4}{A}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{1}{\psi }_{2}^{3}sin\left(\phi +\psi \right)\\ -\frac{1}{4}{A}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{1}{\psi }_{2}^{3}sin3\left(\phi +\psi \right)+\frac{A\stackrel{\sim }{\mu }}{2{p}_{1}}{\eta }_{2}cos\left(\phi -\psi \right)+\frac{A\stackrel{\sim }{\mu }}{2{p}_{1}}{\eta }_{2}cos\left(3\phi +\psi \right)\\ -\frac{3}{4}\frac{{A}^{3}{\stackrel{\sim }{\gamma }}_{1}}{{p}_{1}}{\psi }_{2}^{3}cos\left(\phi +\psi \right)-\frac{1}{4}\frac{{A}^{3}{\stackrel{\sim }{\gamma }}_{1}}{{p}_{1}}{\psi }_{2}^{3}cos3\left(\phi +\psi \right)\end{array}$$

$$\begin{array}{c}{f}_{2A}\left(A,\phi ,\psi \right)=A{\stackrel{\sim }{\alpha }}_{2}\chi sin\left(\phi +\psi \right)-\frac{3}{4}{A}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{2}{\chi }^{3}sin\left(\phi +\psi \right)\\ +\frac{1}{4}{A}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{2}{\chi }^{3}sin3\left(\phi +\psi \right)-\frac{A\stackrel{\sim }{\mu }}{2{p}_{1}}{\eta }_{2}cos\left(\phi -\psi \right)-\frac{A\stackrel{\sim }{\mu }}{2{p}_{1}}{\eta }_{2}cos\left(3\phi +\psi \right)\\ +\frac{3}{4}\frac{{A}^{3}{\stackrel{\sim }{\gamma }}_{2}}{{p}_{1}}{\chi }^{3}cos\left(\phi +\psi \right)+\frac{1}{4}\frac{{A}^{3}{\stackrel{\sim }{\gamma }}_{2}}{{p}_{1}}{\chi }^{3}cos3\left(\phi +\psi \right)\end{array}$$

Functions $A\left(t\right), \phi \left(t\right), \psi \left(t\right)$ are slowly changing in time. To find the approximate solutions we apply Krylov–Bogoliubov-Mitropolsky method [3]. In the first approximation we write

$${\omega }_{1}={\Omega }_{1}+\varepsilon {U}_{1}\left({\phi }_{1},{\Omega }_{1},{a}_{1},{\xi }_{1}\right)$$

(22)

$$A={a}_{1}+\varepsilon {U}_{2}\left(\phi ,{\Omega }_{1},{a}_{1},{\xi }_{1}\right)$$

(23)

$$\psi ={\xi }_{1}+\varepsilon {U}_{3}\left({\phi }_{1},{\Omega }_{1},{a}_{1},{\xi }_{1}\right)$$

(24)

where ${U}_{1}\left(\phi ,\Omega ,a,\xi \right), {U}_{2}\left(\phi ,\Omega ,a,\xi \right), {U}_{3}(\phi ,\Omega ,a,\xi )$ are also slowly varying functions. To get solutions for Ω₁, a₁, ξ₁, we average the right sides of Eqs. (19)–(21) through the vibration period

$$\frac{d{\Omega }_{1}}{dt}=\frac{\varepsilon }{2\pi }\underset{0}{\overset{2\pi }{\int }}{f}_{\Omega 1}d\varphi, \frac{d{a}_{1}}{dt}=\frac{\varepsilon }{2\pi }\underset{0}{\overset{2\pi }{\int }}{f}_{a1}d\varphi, \frac{d{\xi }_{1}}{dt}=\frac{\varepsilon }{2\pi }\underset{0}{\overset{2\pi }{\int }}{f}_{\xi 1}d\varphi$$

(25)

and we obtain

$$\frac{d{\Omega }_{1}}{dt}=\varepsilon \left\{\Gamma \left({\Omega }_{1}\right)-\frac{1}{2}{a}_{1}{p}_{1}{\tilde{q }}_{2}{\Omega }_{1}{\psi }_{2}\mathrm{cos}{\xi }_{1}\right\}$$

(26)

$$\begin{array}{c}\frac{d{a}_{1}}{dt}=\varepsilon \left\{-\frac{1}{2}{\stackrel{\sim }{\alpha }}_{1}{\psi }_{1}{a}_{1}+\frac{3}{8}{{a}_{1}}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{1}{\psi }_{2}^{3}+\frac{1}{4}{a}_{1}\frac{\stackrel{\sim }{\mu }}{{p}_{1}}{\eta }_{2}\mathrm{sin}2{\xi }_{1}\right.\\ \left.+M{\lambda }_{12}\left[\frac{1}{2}{\stackrel{\sim }{\alpha }}_{2}\chi {a}_{1}-\frac{3}{8}{{a}_{1}}^{3}{{p}_{1}}^{2}{\stackrel{\sim }{\beta }}_{2}{\chi }^{3}-\frac{1}{4}{a}_{1}\frac{\stackrel{\sim }{\mu }}{{p}_{1}}{\eta }_{2}\mathrm{sin}2{\xi }_{1}\right]-\frac{1}{2}{\tilde{q }}_{1}\frac{{{\Omega }_{1}}^{2}}{{p}_{1}}\mathrm{cos}{\xi }_{1}\right\}\end{array}$$

(27)

$$\begin{array}{c}\frac{d{\xi }_{1}}{dt}=\varepsilon \left\{{\Delta }_{1}-\frac{3}{8}{{a}_{1}}^{2}\frac{{\stackrel{\sim }{\gamma }}_{1}}{{p}_{1}}{\psi }_{2}^{3}+\frac{1}{4}\frac{\stackrel{\sim }{\mu }}{{p}_{1}}{\eta }_{2}\mathrm{cos}2{\xi }_{1}\right.\\ \left.+M{\lambda }_{12}\left[\frac{3}{8}{{a}_{1}}^{2}\frac{{\stackrel{\sim }{\gamma }}_{2}}{{p}_{1}}{\chi }^{3}-\frac{1}{4}\frac{\stackrel{\sim }{\mu }}{{p}_{1}}{\eta }_{2}\mathrm{cos}2{\xi }_{1}\right]+\frac{1}{2}{\tilde{q }}_{1}\frac{{{\Omega }_{1}}^{2}}{{a}_{1}{p}_{1}}\mathrm{sin}{\xi }_{1}\right\}\end{array}$$

(28)

In a steady state $\frac{d{\Omega }_{1}}{dt}=0, \frac{d{a}_{1}}{dt}=0, \frac{d{\xi }_{1}}{dt}=0$, thus Eqs. (26)–(28) become nonlinear algebraic equations enabling determining amplitude and phase of vibrations and angular velocity of the motor in the vicinity of the first principal parametric resonance.

3.2 Stability Analysis

Stability analysis of the obtained solutions is based on Eqs. (26)–(28) which can be written in the consistent form

$$\begin{array}{c}\frac{d{\Omega }_{1}}{dt}={\Gamma }_{1}\left({a}_{1}, {\Omega }_{1}, {\xi }_{1}\right)\\ \frac{d{a}_{1}}{dt}={\Gamma }_{2}\left({a}_{1}, {\Omega }_{1}, {\xi }_{1}\right)\\ \frac{d{\xi }_{1}}{dt}={\Gamma }_{3}\left({a}_{1},{\Omega }_{1}, {\xi }_{1}\right)\end{array}$$

(29)

Perturbing above equations and subtracting unperturbed from perturbed we get a set of equations in perturbations

$$\begin{array}{c}\frac{d{\delta }_{\Omega 1}}{dt}={\left(\frac{\partial {\Gamma }_{1}}{\partial {\Omega }_{1}}\right)}_{0}{\delta }_{\Omega 1}+{\left(\frac{\partial {\Gamma }_{1}}{\partial {a}_{1}}\right)}_{0}{\delta }_{a1}+{\left(\frac{\partial {\Gamma }_{1}}{\partial {\xi }_{1}}\right)}_{0}{\delta }_{\xi 1}\\ \frac{d{\delta }_{a1}}{dt}={\left(\frac{\partial {\Gamma }_{2}}{\partial {\Omega }_{1}}\right)}_{0}{\delta }_{\Omega 1}+{\left(\frac{\partial {\Gamma }_{2}}{\partial {a}_{1}}\right)}_{0}{\delta }_{a1}+{\left(\frac{\partial {\Gamma }_{2}}{\partial {\xi }_{1}}\right)}_{0}{\delta }_{\xi 1}\\ \frac{d{\delta }_{\xi 1}}{dt}={\left(\frac{\partial {\Gamma }_{3}}{\partial {\Omega }_{1}}\right)}_{0}{\delta }_{\Omega 1}+{\left(\frac{\partial {\Gamma }_{3}}{\partial {a}_{1}}\right)}_{0}{\delta }_{a1}+{\left(\frac{\partial {\Gamma }_{3}}{\partial {\xi }_{1}}\right)}_{0}{\delta }_{\xi 1}\end{array}$$

(30)

where δ means variation of the selected function and the subscript “0” denotes derivatives in the steady state. Stability depends on the values of the roots of the characteristic determinant of (30). The solution is stable if all real parts of the roots are negative, otherwise the system is unstable.

The derivatives take definitions

$$\left( {\frac{\partial \Gamma_1 }{{\partial \Omega_1 }}} \right) = - \varepsilon \tilde{U}_2 - \frac{1}{2}\varepsilon ap_1 \tilde{q}_2 \psi_2 \cos \xi_1 ,\left( {\frac{\partial \Gamma_1 }{{\partial a}}} \right) = - \frac{1}{2}\varepsilon p_1 \tilde{q}_2 \psi_2 \Omega_1 \cos \xi_1 ,$$

$$\left( {\frac{\partial \Gamma_1 }{{\partial \xi_1 }}} \right) = \frac{1}{2}\varepsilon ap_1 \tilde{q}_2 \psi_2 \Omega_1 \sin \xi_1 ,\left( {\frac{\partial \Gamma_2 }{{\partial \Omega_1 }}} \right)_0 = - \varepsilon \frac{{\tilde{q}_1 \Omega_1 }}{p_1 }\cos \xi_1 ,$$

$${\left(\frac{\partial {\Gamma }_{2}}{\partial \mathrm{a}}\right)}_{0}=\frac{1}{2}\upvarepsilon \left[-{\stackrel{\sim }{\mathrm{\alpha }}}_{1}{\uppsi }_{2}+\frac{9}{4}{\mathrm{a}}^{2}{{\mathrm{p}}_{1}}^{2}{\stackrel{\sim }{\upbeta }}_{1}{\uppsi }_{2}^{3}+\frac{{\upeta }_{2}}{2{\mathrm{p}}_{1}}\stackrel{\sim }{\upmu }\mathrm{sin}2{\upxi }_{1}+\mathrm{M}{\uplambda }_{21}\left({\stackrel{\sim }{\mathrm{\alpha }}}_{2}\upchi -\frac{9}{4}{\mathrm{a}}^{2}{{\mathrm{p}}_{1}}^{2}{\stackrel{\sim }{\upbeta }}_{2}{\upchi }^{3}-\frac{{\upeta }_{2}}{2{\mathrm{p}}_{1}}\stackrel{\sim }{\upmu }\mathrm{sin}2{\upxi }_{1}\right)\right]$$

$$\left( {\frac{\partial \Gamma_2 }{{\partial \xi_1 }}} \right) = \frac{1}{2p_1 }\varepsilon \left( {a\tilde{\mu }\eta_2 \cos 2\xi_1 - M\lambda_{21} a\tilde{\mu }\eta_2 \cos 2\xi_1 + \tilde{q}_1 \Omega_1^2 \sin \xi_1 } \right),$$

$$\left( {\frac{\partial \Gamma_3 }{{\partial a}}} \right) = \frac{1}{2p_1 }\varepsilon \left( { - \frac{3}{2}a\tilde{\gamma }_1 \psi_2^3 + \frac{3}{2}M\lambda_{21} a\tilde{\gamma }_2 \chi^3 - \frac{1}{a^2 }\tilde{q}_1 \Omega^2 \sin \xi_1 } \right),$$

$$\left( {\frac{\partial \Gamma_3 }{{\partial \xi_1 }}} \right)_0 = \frac{1}{2p_1 }\varepsilon \left( {\frac{{\tilde{q}_1 }}{a}\Omega_1^2 \cos \xi_1 - \tilde{\mu }\eta_2 \sin 2\xi_1 - M\lambda_{21} \eta_2 \tilde{\mu }\sin 2\xi_1 } \right).$$

4 Numerical Analysis of Regular Oscillations

Nonlinear oscillations of the two degrees freedom model with non-ideal energy source and parametric and self-excitations are analyzed for the following data

$${\alpha }_{1}=0.1, {\beta }_{1}=0.05, {\gamma }_{1}=0.1, {\alpha }_{2}=0.1, {\beta }_{2}=0.05, {\gamma }_{2}=0.1,$$

$$\mu =0.2, M=0.5, {\delta }_{1}=1, {\delta }_{12}=0.3, {\delta }_{2}=1$$

(31)

Natural frequencies of the system, modal coefficients and coefficients related to coordinate transformation take values

$p_1 = 0.766,\;p_2 = 1.168$, $\lambda_{12} = 4.754,\;\lambda_{22} = - 0.421$

$$\chi = 0.192,\;\psi_1 = 0.919,\;\psi_2 - 0.0813,\;\eta_1 = 1.112,\;\eta_2 = 0.112$$

(32)

Let us assume that the characteristic of the DC motor is defined by function $\Gamma \left(\dot{\phi }\right)$ (Eq. (5)). Parameter u₁ (related to the supplied voltage) is varied in domain ${u}_{1}\in \left(0, 1.8\right)$, parameter u₂ is fixed, u₂ = 1.5.

Resonance curves for the principal parametric resonance are presented in Fig. 3. The curves in black are determined for the steady state on the basis of analytical solutions (26)–(28) while the stability checked by computing characteristic roots of Eq. (30). Unstable solutions are marked by dashed lines. The analytical solutions are stable close to the first natural frequency p₁. Moving away from this frequency solutions become unstable and the quasi periodic oscillations occur (Fig. 3a).

Fig. 3

Vibration amplitudes in the vicinity of the principal parametric resonance around frequency p₁, a amplitude against u₁ parameter and b amplitude against excitation frequency ${\Omega }_{1}$

The quasi-periodic solutions are obtained by a direct integration of equations of motion (7) and then solutions are transformed from generalized (physical) coordinates to quasi-normal coordinates using transformation (8). Because the motion has a beating nature with modulated amplitude it is denoted by dotes indicating maximal and minimal values of the amplitude. As we can observe quasi-periodic motion starts when the stability of periodic solution is lost. The modulation of the amplitude decreases moving away from the resonance zone. The periodic solution bifurcates to quasi-periodic via the second kind Hopf bifurcation, not indicated in the figure. Varying parameter u₁ we can observe also change in the angular speed of the DC motor. Therefore, the shape of the resonance curve against angular velocity ${\Omega }_{1}$ is different than against parameter u₁ as presented in Fig. 3b. The additional fully stable loop occurs on the left branch of the resonance curve. This solution is in agreement with results published in the paper [16] for one degree of freedom model. For the ideal system [15], excited by a motor with infinite power, the loop arises on the declining branch and it is only partially stable. In contrast the loop existing in the non-ideal model arises on the inclining branch and is fully stable.

The detailed changes in the amplitude and angular velocity can be observed on the basis of the averaged Eqs. (26)–(28) which have been modelled in the Matlab –Simulink package and then solved numerically. Figure 4 and Fig. 5 present solutions ${a}_{1}\left(t\right)$ and ${\Omega }_{1}\left(t\right)$ while supplied voltage is slowly increasing and decreasing, respectively.

Fig. 4

Amplitude and angular velocity of the motor against slowly increasing in time parameter ${u}_{1}\in (0.4-2.4)$

Fig. 5

Amplitude and angular velocity of the motor against slowly decreasing in time parameter ${u}_{1}\in (2.4-0.4)$

Two different scales are used in the figures, red color represents amplitude while blue angular velocity (frequency of excitation) of the computed solutions. Modulation of amplitude are clearly visible out of the resonance zone. This result is an effect of interactions between parametric and external vibrations and additional interaction with the non-ideal energy source. Therefore, quasi-periodic oscillations are observed on the angular velocity curves (blue line).

Modulation of the oscillations increases close to the resonance zone and inside the resonance zone transits to periodic with constant amplitude, both either for the main system or angular velocity of the motor. Inside the resonance zone two local maxima occur. The drop of angular velocity in the middle of the resonance zone (blue line in Fig. 4) is related with the limited power supply which is too small to maintain the response to be continuously increasing.

Time histories of amplitude a₁ and angular velocity Ω₁ outside and inside the resonance region for selected parameters u₁ are presented in Fig. 6. Amplitude modulations very close to the frequency locking for u₁ = 1.1 and u₁ = 1.53 are presented in Fig. 6a, c.

Fig. 6

Time histories of vibration amplitudes and angular velocity against parameter u₁ parameter; a u₁ = 1.1, b u₁ = 1.2, c u₁ = 1.53, d u₁ = 1.70

Inside the resonance for u₁ = 1.2 where the frequency locking takes place amplitude is constant (Fig. 6b). For u₁ = 1.7 (Fig. 6d), far away from the resonance, amplitude modulations are much smaller and oscillation frequency is increased.

5 Chaotic Oscillations of Nonlinear Two Degrees of Freedom System with Non-ideal Energy Source

Apart from regular oscillations which can be periodic or quasi-periodic also more complex chaotic oscillations may occur [12]. One of the main criterion for the motion classification is based on Lyapunov exponent. Parameters (31) are accepted to check regular periodic or quasi-periodic dynamics. For this purpose bifurcation diagrams based on Lyapunov exponents are computed for varied parameter u₁ in domain ${u}_{1}\in (0-6)$. The computations have been performed till steady state has been achieved, transient solutions have been rejected.

Lyapunov exponents diagram is presented in Fig. 7. As we can see values of the exponents do not exceed zero values which confirms regular oscillations in the analyzed domain of bifurcation parameter u₁. Examples of Poincaré maps for ${X}_{1}, {\dot{X}}_{1}$ coordinates are presented in Fig. 8.

Fig. 7

Lyapunov exponents against u₁ parameter for the non-ideal system with two degrees of freedom, parameters (31); μ = 0.2

Fig. 8

Phase portraits for selected parameters u₁,, μ = 0.2, a u₁ = 0.80, b u₁ = 1.30, c u₁ = 1.70, d u₁ = 2.2, e u₁ = 2.6, f u₁ = 3.2

As it has been mentioned the considered system is autonomous and time is not present in the direct form therefore the base of solution sampling and then plotting period $T={\pi}$ has been applied.

The map in Fig. 8b corresponds to a periodic solution and the attractor gets a shape of a single closed curve. In the rest maps the oscillations are quasi-periodic occurring due to nonlinear dynamics of the whole coupled system. The most complex structure of the attractor is presented in Fig. 8a, f, just before and after the resonance zone. Then, a very strong impact of self-excitation on the system dynamics takes place. In Fig. 8c–e the quasi-periodic motion is related to couplings of the whole structure and smaller influence of self-excitation.

A detailed motion classification based on Lyapunov exponents is proposed in Table 1.

Table 1 Type of attractors and Lyapunov exponents for selected parameter u₁; μ = 0.2

For periodic motion just one, out of six, Lyapunov exponent is equal to zero, rest get negative values. Quasi-periodic motion is characterized by two or three exponents equal to zero and they are called respectively as quasi-periodic oscillations of the first or the second kind (see Fig. 8f).

Dynamics of the non-ideal system is analyzed also for larger parametric excitation by increasing μ parameter up to $\mu =1.0$ and keeping the same values of the rest coefficients. Now, the maximal Lyapunov exponent gets positive values as presented in diagram in Fig. 9. These zones indicate chaotic oscillations of the system. The first chaotic region occurs out of the resonance for ${u}_{1}\in (\mathrm{0,1.2})$ with a minor windows of regular motion. On Poincaré map for ${u}_{1}=0.6$ we obtain periodic oscillations while for ${u}_{1}=0.7$ and ${u}_{1}=1.1$ oscillations become chaotic (Fig. 10a–c).

Fig. 9

Lyapunov exponents against u₁ parameter for non-ideal system with two degrees of freedom, parameters (31); μ = 1.0

Fig. 10

Phase portraits for selected parameters u₁, μ = 1.0, a u₁ = 0.60, b u₁ = 0.70, c u₁ = 1.10, d u₁ = 1.80, e u₁ = 2.22, f u₁ = 2.40, g u₁ = 2.55, h u₁ = 2.80

Other two chaotic regions occur next to ${u}_{1}\approx 2.2$ and ${u}_{1}\approx 2.5$ with quasi-periodic oscillations between them (Fig. 10f). For large values of ${u}_{1}$ parameter the only regular motion takes place (Fig. 10h).

The Lyapunov exponents corresponding to bifurcation diagram in Fig. 9 and Poincaré maps are collected in Table 2. For ${u}_{1}=0.70$, ${u}_{1}=$ 2.22, ${u}_{1}=$ 2.55, values of the maximal Lyapunov exponent are positive, which means that for these parameters oscillations are chaotic. This fact is also confirmed by strange chaotic attractors presented on Poincaré maps. For ${u}_{1}=1.1$, and attractor presented in Fig. 10c, two exponents are positive. This motion is called hyper-chaotic. In the rest cases one or two exponents are equal to zero what indicates periodic or quasi-periodic motion.

Table 2 Type of attractors and Lyapunov exponents for selected parameter u₁; μ = 1.0

The additional numerical simulations (not presented here) show that the model with non-ideal energy source has much higher tendency in transition to complex dynamics, including chaos or hyper-chaos, than its ideal counterpart. This is the effect of the additional degree of freedom related to nonlinear DC motor dynamics.

6 Conclusions

The interactions between external, parametric and self-excited vibrations are studied in the paper. The model assumed as non-ideal, includes the additional degree of freedom of the energy source (DC motor). The parametric and external excitations are tuned in 1:2 ratio which leads to very strong interactions in the principal parametric zone. The analytical solutions based on the Krylov–Bogoliubov-Mitropolsky method show that in the vicinity of this zone the phenomenon of frequency locking takes place. The system vibrates periodically. The influence of the non-ideal energy source is observed by local decrease of the amplitude and angular velocity inside the resonance zone against the supplied voltage. On the resonance characteristic—amplitude against excitation frequency—this effect creates a loop on the increasing branch of the resonance curve and the loop is fully stable. The phenomenon is in contrast to the ideal system where the loop arises on the declining branch and its upper part is stable [15]. Outside the principal parametric resonance, after the Hopf bifurcation of the second kind, the system transits to quasi-periodic oscillations. Based on the extended numerical simulation, apart from periodic or quasi-periodic, also chaotic or hyper-chaotic vibrations may arise while parametric excitation is increased. This fact is confirmed by computed Lyapunov exponents and strange chaotic attractors plotted on Poincaré maps. The dynamics of the non-ideal model differs from the ideal system in a case of regular vibrations as well as chaotic motion. The non-ideal model is more sensitive in the transition to chaotic oscillations when compared with its counterpart.