Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Prediction of the performance of civil infrastructure systems exposed to natural hazards is associated with significant uncertainties, pertaining to the description of the hazard characteristics as well as to the properties of the system under consideration (Ellingwood 2001; Vickery et al. 2006; Resio et al. 2012). This is especially true when life-cycle analysis is considered (Wen and Kang 2001; Taflanidis and Beck 2009) since the aforementioned description needs to address the anticipated exposure (Kumar et al. 2015) and system behavior over a large time period. A probabilistic approach provides a rational and consistent framework for addressing such uncertainties (Jaynes 2003) using probability models to describe the relative likelihood of different properties of the natural hazard and of the system itself. This then facilitates the description of the performance through the natural hazard risk, quantified by the probabilistic integral that corresponds to the expected value of some risk consequence measure over the established probability models for the system and its excitation (hazard).

Assessment of this risk entails ultimately evaluation of the probabilistic integral quantifying it. Analytical approximations and specialized approaches (Rackwitz 2001; Der Kiureghian 1996; Taflanidis 2010) can be adopted for this purpose but include an unknown, unavoidable error and can further impose restrictions on the complexity of the models adopted to characterize and analyze risk. On the other hand, approaches relying on stochastic (i.e., Monte Carlo) simulation offer a high-accuracy solution and more importantly impose no constraints on the complexity of the assumed numerical and probability models (Au and Beck 2003; Taflanidis and Beck 2009). They involve, however, higher computational cost, a feature which prohibited for some time their widespread adoption. Advances over the last decade in computer hardware and simulation algorithms, in particular the wide use of distributed/parallel computing (Fujimoto 2001), have contributed in reducing this computational burden traditionally associated with stochastic simulation approaches, and have facilitated the detailed modeling and solution of problems that were until recently considered as computationally intractable (Resio and Westerink 2008; Pellissetti 2008; Hardyniec and Charney 2015), increasing the popularity of simulation-based frameworks for quantifying/estimating natural hazard risk. Still in many instances, for example, for real-time risk estimation or in applications with complex nonlinear dynamical models, the computational burden associated with simulation-based approaches is still prohibitive.

The use of surrogate models (also frequently referenced as metamodels) is a popular approach for addressing this challenge and for further alleviating the computational cost associated with such simulation-based frameworks for natural hazard risk assessment (Gavin and Yau 2007; Tsompanakis et al. 2009; Gidaris et al. 2014). Surrogate models offer a computationally inexpensive input/output relationship based on a database of observations obtained through the initial (expensive) simulation model. The up-front cost for obtaining this database is of course high, but once the surrogate model is established, all future evaluations require small computational burden. This chapter discusses the adoption of kriging metamodels within this context. For illustration, two different applications are considered, involving two different hazards: seismic risk assessment utilizing stochastic ground motion modeling and real-time hurricane risk estimation. Various implementation issues are discussed, such as (a) the advantages of kriging metamodeling approach over other surrogate models, (b) the approaches for obtaining high efficiency when the output under consideration is high dimensional (over 10,000) through integration of principal component analysis, and (c) the explicit incorporation of the prediction error associated with the kriging metamodel into the risk formulation. The discussions demonstrate the great benefits that the combination of kriging and stochastic simulation provides for natural hazard risk assessment. This combination can foster a comprehensive and detailed characterization of risk, in terms of the models selected for the system and the natural hazard and for the uncertainty quantification, and at the same time an efficient estimation for it. Initially, the general framework for simulation-based risk quantification and assessment is presented, and then the discussion focuses on kriging implementation and the two specific applications examined.

2 Risk Quantification and Assessment

Risk Quantification

Evaluation of response/performance under natural hazards requires adoption of appropriate numerical models for (1) the natural hazard (excitation), (2) the system of interest, and (3) the system performance (Fig. 4.1). The combination of the first two models provides the system response vector, denoted \( \mathbf{z}\in {\mathbb{R}}^{n_{\mathrm{z}}} \) herein with individual response quantities denoted as z k. The performance evaluation model assesses, then, the favorability of this response, based on the chosen criteria.

Fig. 4.1
figure 1

Model for natural hazard risk description. Illustration example corresponds to seismic risk

Full size image

The characteristics of these models are not known with absolute certainty. Uncertainties may pertain to: (1) the variability of primary characteristics of excitation events, for example, intensity or occurrence rates, or of secondary properties typically given by predictive relationships based on these primary characteristics (Holland 1980; Rezaeian and Der Kiureghian 2010; Mavroeidis and Papageorgiou 2003), such as duration of excitation or pressure distribution along domains of interest; (2) the properties of the system itself, for example, related to parameters influencing restoring forces or to damping characteristics for structural systems (Liel et al. 2009); and (3) the parameters related to the performance of the system, for example, thresholds defining fragility (i.e., acceptable performance) of system components (Gardoni et al. 2002). Characterizing these uncertainties through a probabilistic description leads then to a versatile quantification of natural hazard risk (Taflanidis and Beck 2009; Taflanidis et al. 2013a).

To formalize these ideas, let \( \boldsymbol{\uptheta} \in \Theta \subset {\mathbb{R}}^{n_{\theta }} \) denote the augmented n θ-dimensional vector of model parameters where Θ represents the space of possible model parameter values. As illustrated in Fig. 4.1, vector θ is composed of all the model parameters for the individual system, θ s; excitation, θ m (primary) and θ g (secondary); and performance evaluation, θ p, models. For addressing the uncertainty in θ, a probability density function (PDF) p(θ) is assigned to it that quantifies our available knowledge in the context of probability logic (knowledge on hazard characteristics or properties of system under consideration). For given values for the model parameters θ the risk consequence measure, representing the utility of the response from a decision-theoretic point of view, is given by \( h\left(\boldsymbol{\uptheta} \right):{\mathbb{R}}^{n_{\uptheta}}\to {\mathbb{R}}^{+} \). This measure is related to the performance/consequences that can be calculated based on the estimated response z (performance given that an excitation event has occurred), whereas it can be additionally dependent, for example within life-cycle analysis studies, to assumptions made about the rate of occurrence of excitation events (incorporation of the probability of such events occurring). Natural hazard risk, R, is finally described by the probabilistic integral that corresponds to the expected value of h(θ) over the probability models:

$$ R={\displaystyle {\int}_{\Theta}h\left(\boldsymbol{\uptheta} \right)p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}. $$
(4.1)

Through different selections of the risk consequence measure, different risk quantifications can be addressed, ranging from life-cycle cost to reliability (Taflanidis and Beck 2009; Jia et al. 2014). A specific consequence measure utilized in a variety of different risk applications, for example, within system reliability analysis or life-cycle cost estimation (Ellingwood 2001; Goulet et al. 2007; Jia and Taflanidis 2013), is the probability that some response quantity z k (e.g., peak interstory drift for a structure) will exceed some threshold β k that determines acceptable performance. For certain applications, for example, within seismic risk assessment, where this concept can be used to represent the fragility of system components, it is common to incorporate a prediction error in this definition (Porter et al. 2006; Taflanidis et al. 2013b); this can be equivalently considered as the aforementioned threshold corresponding to an uncertain quantity with some chosen distribution (this distribution ultimately determines the cumulative distribution function for the component fragilities). A common choice for the latter (Porter et al. 2006) is lognormal distribution. The equivalent representation is then that the threshold that determines acceptable performance is given by (β k ∙ε βk) with ε βk having a lognormal distribution with median equal to one and logarithmic standard deviation σ βk. This then leads to the following risk consequence measure

$$ \begin{array}[b]{l}h\left(\boldsymbol{\uptheta} \right)=P\left[{z}_{\mathrm{k}}\left(\boldsymbol{\uptheta} \right)\ge {\beta}_{\mathrm{k}}{\varepsilon}_{\upbeta \mathrm{k}}\big|\boldsymbol{\uptheta} \right]=P\left[ \ln \left({\varepsilon}_{\upbeta \mathrm{k}}\right)\le \ln \left({z}_{\mathrm{k}}\left(\boldsymbol{\uptheta} \right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)\big|\boldsymbol{\uptheta} \right]\\[10pt] \qquad\ =\Phi \left(\displaystyle\frac{ \ln \left({z}_{\mathrm{k}}\left(\boldsymbol{\uptheta} \right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)}{\sigma_{\upbeta \mathrm{k}}}\right),\end{array} $$
(4.2)

where Φ(.) denotes the standard normal cumulative distribution (CDF). For σ βk = 0, representing the case that no uncertainty is considered in the description of β k , this measure simplifies to an indicator function, being one if z k>β k and zero if not.

Coupled with stochastic simulation (i.e., Monte Carlo) approaches for estimating the probabilistic integral in Eq. (4.1), as will be discussed next, the framework illustrated in Fig. 4.1 for risk quantification imposes no restriction on the complexity of the adopted numerical or probability modes and ultimately facilitates a generalized, versatile description of natural hazard risk and has been implemented successfully for studies considering a variety of hazards (wind, surge, waves, earthquakes) and structural systems (Taflanidis et al. 2011, 2013a, b; Gidaris and Taflanidis 2015).

Risk Assessment

The estimation of risk given by Eq. (4.1) requires calculation of a multidimensional probabilistic integral. To support adoption of probability and numerical models with higher complexity, this calculation can be established through a stochastic (i.e., Monte Carlo) simulation. Using a finite number, N, of samples of θ drawn from proposal density q(θ), an estimate for R and the coefficient of variation for that estimate (quantifying its accuracy), δ, are given by

$$ \widehat{R} = \frac{1}{N}{\displaystyle {\sum}_{j=1}^Nh\left({\boldsymbol{\uptheta}}^j\right)\frac{p\left({\boldsymbol{\uptheta}}^j\right)}{q\left({\boldsymbol{\uptheta}}^j\right)}}\ \ \mathrm{and}\ \ \delta \approx \frac{1}{\sqrt{N}}\sqrt{\frac{1/N{\displaystyle {\sum}_{j=1}^N{\left(h\left({\boldsymbol{\uptheta}}^j\right)p\left({\boldsymbol{\uptheta}}^j\right)/q\left({\boldsymbol{\uptheta}}^j\right)\right)}^2}}{{\widehat{R}}^2}-1,} $$
(4.3)

where θ j denotes the jth sample. The proposal densities may be used to improve the accuracy of this estimation, i.e., reduce the coefficient of variation, by focusing the computational effort on regions of the Θ space that contribute more to the integrand of the probabilistic integral of Eq. (4.1)—this corresponds to the concept of importance sampling (IS). For problems with a large number of model parameters, choosing efficient importance sampling densities for all components of θ is challenging (Taflanidis and Beck 2008) and can lead to convergence problems for the estimator in Eq. (4.3); thus, it is preferable to formulate IS densities only for the important components of θ, i.e., the ones that have the biggest influence on the seismic risk, and use q(θ) = p(θ) for the rest (Taflanidis and Beck 2008). For natural hazard risk applications, the primary parameters related to the hazard (θ m in Fig. 4.1) are generally expected to have the strongest impact on the calculated risk (Taflanidis and Beck 2009), so selection of IS densities may focus only on them.

Evaluating, now, the computational efficiency of this simulation-based estimation, the most demanding task in most practical applications is the calculation of the model response z. The computational burden for generating the required samples, for estimating performance/consequences given that response, or for calculating the sample average is typically very small. Thus, the formulation allows to seamlessly integrate recent advances in high-performance computing (parallel/distributed computing) to perform the required N evaluations of the system performance independently, in parallel mode. This significantly reduces the computational barriers that have been traditionally associated with approaches based on stochastic simulation. It also forms the foundation of an efficient assessment of risk for different seismic risk quantifications as well as the efficient estimation of risk under different design scenarios corresponding to different assumptions for p(θ) through some appropriate selection of the proposal densities q(θ) [more details may be found in (Gidaris and Taflanidis 2015)]. For applications, though, involving computationally intensive, high-fidelity numerical models, the burden for this analysis can be still prohibitive, especially for real-time applications. Surrogate modeling can be adopted in these cases to improve efficiency.

3 Kriging Metamodeling for Natural Hazard Risk Assessment

Surrogate models (metamodels) provide a simplified representation of the input/output relationship of complex processes, requiring large computational cost for their evaluation. Various such models have been proposed in the literature, such as neural networks (NNs) (Hajela and Berke 1992), response surface approximations (RSAs) (Gavin and Yau 2007), moving least squares RSA (MLS RSA) (Breitkopf et al. 2005), or kriging (Sacks et al. 1989), sharing the same principle; they generate the approximate, surrogate model based on information from a sufficient (typically small) number of intelligently selected evaluations of the exact model (typically referenced as support points or training set) or even a combination of model evaluations and experimental data (Gardoni et al. 2002, 2003). That surrogate model is then adopted as an approximation to the input/output relationship for the exact, complex model.

Preliminary Considerations for Surrogate Modeling Within Risk Assessment

Within natural hazard risk assessment, metamodels can be implemented to approximate high-fidelity numerical models utilized for providing the response vector z. The underlying assumption for this selection is that the performance evaluation model in Fig. 4.1 is for most applications numerically simple, so establishing the surrogate model for the response z, rather than directly for the risk consequence measure h(θ), is necessary and also more advantageous since it additionally removes one level of approximation which provides a higher accuracy in the surrogate modeling approach (Jin et al. 2001). This also means that the input vector \( \mathbf{x}\in {\mathbb{R}}^{n_{\mathrm{x}}} \) that needs to be considered for the surrogate model is composed of only θ m, θ g, and θ s in the context of Fig. 4.1 representation, that is, excluding any parameters related to the performance evaluation model θ p. Furthermore, the metamodel can be built to approximate a function of the response and not the response directly, for example, if risk consequence measure of Eq. (4.2) is utilized then the surrogate model should be built for approximating the logarithm of each response quantity ln(z k) rather than the response quantity itself z k.

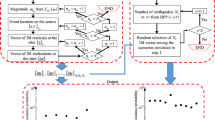
Within this context, let \( \mathbf{x}\in {\mathbb{R}}^{n_{\mathrm{x}}} \) and \( \mathbf{y}\in {\mathbb{R}}^{n_{\mathrm{y}}} \) denote, respectively, the input and output vectors considered for the surrogate model implementation. For forming the metamodel initially, a database with n m observations is obtained that provides information for the x-y pair. This process is also known as the design of experiments (DoE). For this purpose, n m samples for {x j j = 1,…,n m}, also known as support points, are created within some domain X. Preliminary selection of the samples can be based on some space-filling approach (Latin hypercube sampling), with adaptive refinements also an option (Dubourg et al. 2011). The domain X should cover the expected range of values possible for each x i (informed by the range of possible values within Θ) that will be needed in the evaluation of the risk integral. It should be stressed that this does not require a firm definition for p(θ), simply knowledge of the range for which the kriging metamodel will be used so that the support points extend over this range. Using this dataset the metamodel can be formulated and a kriging metamodel is considered here for this purpose.

Kriging Formulation

A quick overview of kriging implementation is presented next. More details on the fundamental principles and computational details behind this implementation may be found in Sacks et al. (1989) and Lophaven et al. (2002).

The kriging predictor for each component y i of y corresponds to a Gaussian variable N(ŷ i(x), σ 2i (x)) with mean ŷ i(x) and variance σ 2i (x) (Sacks et al. 1989). The response output can be approximated through this predictor, leading to

$$ {y}_{\mathrm{i}}\left(\mathbf{x}\right)={\widehat{y}}_{\mathrm{i}}\left(\mathbf{x}\right)+{\varepsilon}_{\mathrm{i}}^g{\sigma}_{\mathrm{i}}\left(\mathbf{x}\right), $$
(4.4)

where ε gi is a standard Gaussian variable. Here, we will present the case that a single surrogate model is developed for the entire output vector y. This approach significantly reduces computational complexity but could potentially reduce accuracy (if the optimal surrogate models corresponding to different components y i are expected to be drastically different).

The fundamental building blocks of kriging are the n p dimensional basis vector, f(x), and the correlation function, R(x l,x m), defined through hyper-parameter vector s. The former provides a “global” model in the X space [and is ultimately similar to the global prediction provided by RSA], while the latter creates a “localized” deviation/correction weighting the points in the training set based on their closeness to the target point x. The general concept is similar to the moving character of MLS RSA (Breitkopf et al. 2005). Typical selections for these functions are a full quadratic basis and a generalized exponential correlation, respectively, leading to

$$ \begin{array}[b]{l}\mathbf{f}\left(\mathbf{x}\right)={\left[1\kern0.5em {x}_1\ \cdots\ {x}_{n_{\mathrm{x}}}\ {x}_1^2\ {x}_1{x}_2\ \cdots\ {x}_{n_{\mathrm{x}}}^2\right]}^T\kern0.5em ;\ {n}_{\mathrm{p}}=\left({n}_{\mathrm{x}}+1\right)\left({n}_{\mathrm{x}}+2\right)/2\\[6pt] {}R\left({\mathbf{x}}^l,{\mathbf{x}}^m\right)={\displaystyle {\prod}_{i=1}^{n_{\mathrm{x}}} \exp \left[-{s}_i\left|{\mathbf{x}}_i^l-{\mathbf{x}}_i^m\right|{}^{s_{n_{\mathrm{x}}+1}}\right]};\ \boldsymbol{s}=\left[{s}_1\ \cdots\ {\mathrm{s}}_{n_{\mathrm{x}}+1}\right].\end{array} $$
(4.5)

Then, for the set of n m observations (training set) with input matrix \( \mathbf{X}={\left[{\mathbf{x}}^1\ \cdots\ {\mathbf{x}}^{n_{\mathrm{m}}}\right]}^T\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{x}}} \) and corresponding output matrix \( \mathbf{Y}={\left[\mathbf{y}\left({\mathbf{x}}^1\right)\ \cdots\ \mathbf{y}\left({\mathbf{x}}^{n_{\mathrm{m}}}\right)\right]}^T\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{y}}} \), we define the basis matrix \( \mathbf{F}={\left[f\left({\mathbf{x}}^1\right)\dots f\left({\mathbf{x}}^{n_{\mathrm{m}}}\right)\right]}^T\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{p}}} \) and the correlation matrix \( \mathbf{R}\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{m}}} \) with the lm element defined as R(x l,x m), l, m=1,…,n m. Also for every new input x, we define the correlation vector \( \mathbf{r}\left(\mathbf{x}\right)={\left[R\left(\mathbf{x},{\mathbf{x}}^l\right)\dots R\left(\mathbf{x},{\mathbf{x}}^{n_{\mathrm{m}}}\right)\right]}^T \) between the input and each of the elements of X. The mean kriging prediction (given as row vector) is then

$$ \widehat{\mathbf{y}}\left(\mathbf{x}\right)=\mathbf{f}{\left(\mathbf{x}\right)}^T{\boldsymbol{\upalpha}}^{*}+\mathbf{r}{\left(\mathbf{x}\right)}^T{\boldsymbol{\upbeta}}^{*}, $$
(4.6)

where matrices \( {\boldsymbol{\upalpha}}^{*}\in {\mathbb{R}}^{n_{\mathrm{p}}\times {n}_{\mathrm{y}}} \) and \( {\boldsymbol{\upbeta}}^{*}\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{y}}} \) are given by

$$ {\boldsymbol{\upalpha}}^{*}={\left({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{Y};\ {\boldsymbol{\upbeta}}^{*}={\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{F}{\boldsymbol{\upalpha}}^{*}\right). $$
(4.7)

Through the proper tuning of the hyper-parameters s of the correlation function, kriging can efficiently approximate very complex functions. The optimal selection of s is typically based on the maximum likelihood estimation (MLE) principle, where the likelihood is defined as the probability of the n m observations, and maximizing this likelihood with respect to s ultimately corresponds to optimization

$$ {\mathbf{s}}^{\ast }=\underset{\mathbf{s}}{ \arg \min}\left[{\left|\mathbf{R}\right|}^{{\scriptscriptstyle \frac{1}{n_m}}}{\displaystyle {\sum}_{i=1}^{n_y}{\tilde{\sigma}}_i^2/{\gamma}_i}\right], $$
(4.8)

where |.| stands for determinant of a matrix; γ i is a weight for each output quantity, typically chosen as the variance over the observations Y; and \( {\tilde{\sigma}}_i^2 \) corresponds to the process variance (mean square error of the metamodel), given by the diagonal elements of the matrix \( {\left(\mathbf{Y}-\mathbf{F}{\boldsymbol{\upalpha}}^{*}\right)}^T{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{F}{\boldsymbol{\upalpha}}^{*}\right)/{n}_{\mathrm{m}} \). Standard approaches for solving this optimization are given in (Lophaven et al. 2002).

An estimate for σ 2i (x), which can be equivalently considered as the variance for the prediction error between the real process y i and the kriging prediction ŷ i, is also provided through the kriging metamodel. This is a local estimate, meaning that it is a function of the input x and not constant over the entire domain X, and for output y i is given by

$$ {\sigma}_{\mathrm{i}}^2\left(\mathbf{x}\right)={\tilde{\sigma}}_{\mathrm{i}}^2\left[1+\mathbf{u}{\left(\mathbf{x}\right)}^T{\left({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\mathbf{u}\left(\mathbf{x}\right)-\mathbf{r}{\left(\mathbf{x}\right)}^T{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)\right], $$
(4.9)

where \( \mathbf{u}\left(\mathbf{x}\right)={\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)-\mathbf{f}\left(\mathbf{x}\right) \).

Derivative information can be also easily obtained by noting that vectors α * and β * are independent of x. Denoting by J f and J r the Jacobian matrices with respect to x of f and r, respectively, the gradients for the median predictions and the error variance are

$$ \begin{array}{l}\nabla \widehat{\mathbf{y}}\left(\mathbf{x}\right)={\mathbf{J}}_{\mathrm{f}}{\left(\mathbf{x}\right)}^T{\boldsymbol{\upalpha}}^{*}+{\mathbf{J}}_{\mathrm{r}}{\left(\mathbf{x}\right)}^T{\boldsymbol{\upbeta}}^{*}\\[6pt] {}\nabla {\sigma}_{\mathrm{i}}^2\left(\mathbf{x}\right)=2{\tilde{\sigma}}_{\mathrm{i}}^2\left[\mathbf{u}{\left(\mathbf{x}\right)}^T{\left({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\left({\mathbf{F}}^T{\mathbf{R}}^{-1}{\mathbf{J}}_{\mathrm{r}}\left(\mathbf{x}\right)-{\mathbf{J}}_{\mathrm{f}}\left(\mathbf{x}\right)\right)-\mathbf{r}{\left(\mathbf{x}\right)}^T{\mathbf{R}}^{-1}{\mathbf{J}}_{\mathrm{r}}\left(\mathbf{x}\right)\right].\end{array} $$
(4.10)

This information can be used, for example, for calculating the design points for the integrand of Eq. (4.1) for forming IS densities or when the application of interest corresponds to a design optimization problem and kriging is simultaneously developed for risk assessment as well as for performing the optimization with respect to the system design variables (Gidaris et al. 2014).

Validation of Metamodel

The performance of the metamodel can be validated directly by the process variance \( {\tilde{\sigma}}_{\mathrm{i}}^2 \) or by calculating different error statistics for each one of the components of the output vector y, such as the coefficient of determination RD 2i or the mean percent error ME i, using a leave-one-out cross-validation approach (Kohavi 1995). This approach is established by removing sequentially each of the observations from the database, using the remaining support points to predict the output for that one and then evaluating the error between the predicted and real responses. The validation statistics are subsequently obtained by averaging the errors established over all observations. For the considered implementation for risk assessment, where one is concerned about providing adequate accuracy over the ensemble of scenarios considered (rather than for each separate scenario), high values for the coefficient of determination are of particular importance since they indicate that the kriging model can describe very well the variability within the initial database. The performance of the metamodel can be improved primarily by increasing the number of support points n m or by their proper selection (Picheny et al. 2010). Other potential strategies for such performance improvement could be the change of the correlation function or the basis functions (Jia and Taflanidis 2013).

Advantages of Kriging

Compared to other surrogate modeling approaches, especially approaches that entail matrix manipulations only, such as RSA and MLS RSA, kriging offers some distinct advantages:

  • It corresponds to an interpolation metamodel, meaning that the predictions for any input x that belongs in the initial dataset X will match the exact corresponding output. The same is not necessarily true for many other metamodels (like RSA) that establish a local averaging (regression metamodels).

  • It provides a variance for the prediction error which is also a function of the location x. In other surrogate modeling approaches, this variance is typically treated as constant over the entire input domain (Taflanidis et al. 2013a).

  • It involves only matrix manipulations for its implementation with matrix inversions that need to be performed only once, in the definition of α * and β * in Eq. (4.7). This ultimately should be attributed to the fact that the correlation matrix R is dependent only on the training set X. In MLS RSA, that can provide similar accuracy as kriging (Simpson et al. 2001), the equivalent matrix of weights (establishing the local correction aspects of the methodology and having a similar role as R) is explicitly dependent on the input x, meaning that the inversions involved are different for each different input x. The implications of this property are significant. Kriging implementation requires keeping in memory only matrices α * and β * (rather than the high-dimensional matrices Y, F, and R). Also, evaluations over a large number of different inputs, as required within stochastic simulation setting, can be efficiently established through proper matrix manipulations, simply by augmenting vectors f(x) and r(x) over all these inputs. It should be noted, though, that for evaluation over a single point, the complexity of kriging is higher than the one for MLS RSA (Simpson et al. 2001).

  • The optimization in Eq. (4.8) for the parameters of the correlation function can be performed highly efficiently (at least for identifying local minima). The established approaches for optimization of the parameters related to the weight matrix in RSA are more computationally intensive (Loweth et al. 2010) requiring some cross-validation approach over the training set.

Risk Assessment Through Kriging Modeling

Once the metamodel has been established, it can be directly used to approximate the response z and subsequently the consequence measure within the stochastic simulation-based evaluation in Eq. (4.3). Additionally, the prediction error of the metamodel can be directly incorporated in this estimation, altering ultimately the consequence measure. For example, for the measure given by Eq. (4.2) and assuming that the kriging prediction is developed for ln(z k), giving \( \ln {z}_{\mathrm{k}}= \ln {\widehat{z}}_{\mathrm{k}}\left(\mathbf{x}\right)+{\varepsilon}_{\mathrm{k}}^g{\sigma}_{\mathrm{k}}\left(\mathbf{x}\right) \), we have

$$ \begin{array}{l}h\left(\boldsymbol{\uptheta} \right)=P\left[ \ln \left({\varepsilon}_{\upbeta \mathrm{k}}\right)\le \ln \left({z}_{\mathrm{k}}\left(\boldsymbol{\uptheta} \right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)\big|\boldsymbol{\uptheta} \right]\\[10pt] \qquad\ =P\left[ \ln \left({\varepsilon}_{\upbeta \mathrm{k}}\right)\le \ln \left({\widehat{z}}_{\mathrm{k}}\left(\mathbf{x}\right)\right)+{\varepsilon}_{\mathrm{k}}^g{\sigma}_{\mathrm{k}}\left(\mathbf{x}\right)- \ln \left({\beta}_{\mathrm{k}}\right)\big|\boldsymbol{\uptheta} \right]\\[10pt] \qquad\ =P\left[ \ln \left({\varepsilon}_{\upbeta \mathrm{k}}\right)-{\varepsilon}_{\mathrm{k}}^g{\sigma}_{\mathrm{k}}\left(\mathbf{x}\right)\le \ln \left({\widehat{z}}_{\mathrm{k}}\left(\mathbf{x}\right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)\big|\boldsymbol{\uptheta} \right]=\Phi \left(\frac{ \ln \left({\widehat{z}}_{\mathrm{k}}\left(\mathbf{x}\right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)}{\sqrt{\sigma_{\upbeta \mathrm{k}}^2+{\sigma}_{\mathrm{k}}^2\left(\mathbf{x}\right)}}\right),\end{array} $$
(4.11)

where the last equality is based on the fact that since ln(ε βk) and ε g k σ k (x) are zero mean Gaussian variables, their difference will also be a normal variable with zero mean and standard deviation the quantity in the denominator within the Gaussian CDF in Eq. (4.11).

The kriging implementation is demonstrated next in two examples, where additional characteristics for it are showcased.

4 Seismic Risk Assessment Through Stochastic Ground Motion Modeling

In the last decades, significant advances have been established in seismic risk decision management through the development of assessment methodologies based on detailed socioeconomic metrics quantifying life-cycle performance (Goulet et al. 2007). Powerful frameworks, widely acknowledged to provide the basis for these advances, have been the consequence-based engineering (CBE) (Abrams et al. 2002) of the Mid-America Earthquake (MAE) Center and the performance-based earthquake engineering (PBEE) (Moehle and Deierlein 2004; Bozorgnia and Bertero 2004) of the Pacific Earthquake Engineering Research (PEER) center, which represent two of the most important advances for probabilistic description of seismic risk. Within this setting, comprehensive risk quantification can be established by evaluating the structural performance through nonlinear dynamic response analysis (Goulet et al. 2007), rather than through simplified approaches such as pushover analysis. This has implications both for the system model and for the natural hazard model; for the latter, an excitation model needs to be considered that can provide a description for the entire ground acceleration time history. The framework in Fig. 4.1 is consistent with the aforementioned approaches though it is founded upon a system-theoretic formulation for the problem: consideration of exposure/vulnerability/consequence modules and quantification of the parametric modeling uncertainty within the description of each of these models. Note that in this case, each response quantity z k corresponds to a different engineering demand parameter (EDP) that is utilized to describe the performance of the structural system (Goulet et al. 2007).

The implementation of surrogate modeling in this setting can greatly enhance the efficiency of seismic risk assessment (Zhang and Foschi 2004; Buratti et al. 2010), especially for studies examining design optimization (Möller et al. 2009; Gidaris et al. 2014). This implementation is discussed here considering applications where stochastic ground motion models are utilized to describe the excitation. The discussion starts with a quick overview of this hazard modeling approach.

Seismic Risk Modeling Through Stochastic Ground Motion Models

Stochastic ground motion models (Boore 2003; Rezaeian and Der Kiureghian 2010; Vetter et al. 2016) have been gaining increased attention within the structural engineering community for description of seismic hazard (Jensen and Kusanovic 2014; Gidaris et al. 2014). They are based on modulation of a stochastic sequence (typically white noise), \( \mathbf{w}\in W \), through functions that address the frequency and time-domain characteristics of the excitation. The parameters of these functions (corresponding to the secondary parameters θ g in Fig. 4.1) represent characteristics such as the duration of excitation or average frequency content and can be related to seismological parameters (corresponding to primary parameters θ m in Fig. 4.1), such as the moment magnitude, M, or rupture distance, r rup, by appropriate predictive relationships. Description of the uncertainty in the seismological parameters and these predictive relationships facilitates then the comprehensive description of the seismic hazard. For the former, this is established through a probabilistic hazard analysis (Kramer 1996), whereas for the latter, this is established through the process of developing the predictive relationships for the ground motion model itself (Rezaeian and Der Kiureghian 2010).

One additional attractive feature of this ground motion modeling is the fact that potential near-fault effects can be easily incorporated within it. This is facilitated through the addition to the broadband component of the excitation, described through a stochastic ground motion model, of a directivity pulse (Mavroeidis and Papageorgiou 2003) addressing the longer-period component of the excitation. This pulse has its own parameters (included in θ g in Fig. 4.1) that are dependent upon θ m. Therefore, the probabilistic foundation for describing the pulse characteristics is the same as for the broadband component. The fact that not all near-fault excitations include directivity pulses can be addressed through adoption of a model describing the probability of occurrence of such pulses (Shahi and Baker 2011), also dependent upon θ m. When pulses are not included, the ground motion is described only through its broadband component. This approach ultimately supports a complete probabilistic description of the seismic hazard in close proximity to active faults (Gidaris and Taflanidis 2015).

Implications to Kriging Implementation

The use of stochastic ground motion models to describe the hazard leads ultimately to system response that is a function of not only θ but w as well. Due to the high dimensionality of w (stemming from partitioning of the entire duration of the excitation to appropriate time intervals), the development of a surrogate model for the entire input vector composed of both θ and w is impractical. To address this challenge, an alternative formulation can be considered (Zhang and Foschi 2004; Schotanus et al. 2004; Gidaris et al. 2015) by separating the input space into two vectors: the first corresponding to the stochastic sequence and the second to the remaining model parameters. The impact of the first one (stochastic sequence) is addressed by assuming that under its influence, each response quantity z k follows a lognormal distribution with median \( {\overline{z}}_{\mathrm{k}} \) and logarithmic standard deviation σ zk, which corresponds to a common assumption within earthquake engineering (Zhang and Foschi 2004; Jalayer and Cornell 2009; Aslani and Miranda 2005; Shome 1999). This means that

$$ \ln \left({z}_k\right)={\varepsilon}_k{\sigma}_{zk}+ \ln \left({\overline{z}}_k\right), $$
(4.12)

with ε k corresponding to a standard Gaussian variable. The metamodel needs to be developed with respect to only the low-dimensional θ vector, to provide predictions for these two statistical quantities, corresponding to the statistics for the EDPs of interest due to the influence of the white noise. Therefore, the output vector y is in this case composed of both \( \ln \left({\overline{z}}_{\mathrm{k}}\right) \) and σ zk for all the EDPs of interest. Once the metamodel has been established, it can be directly used to estimate the risk consequence measure, which then needs to be appropriately modified to take into account the approximation of Eq. (4.12). Assuming that the kriging prediction error for σ zk is small, this leads to the following modification for the consequence measure (Gidaris et al. 2015):

$$ h\left(\boldsymbol{\uptheta} \right)=\Phi \left(\frac{ \ln \left({\widehat{\overline{z}}}_{\mathrm{k}}\left(\mathbf{x}\right)\right)- \ln \left({\beta}_{\mathrm{k}}\right)}{\sqrt{\sigma_{\upbeta \mathrm{k}}^2+{\sigma}_{\mathrm{k}}^2\left(\mathbf{x}\right)+{\widehat{\sigma}}_{\mathrm{zk}}^2\left(\mathbf{x}\right)}}\right), $$
(4.13)

where \( {\widehat{\overline{z}}}_{\mathrm{k}}\left(\mathbf{x}\right) \) and \( {\widehat{\sigma}}_{\mathrm{zk}}^2\left(\mathbf{x}\right) \) correspond to the median kriging predictions for the \( \ln \left({\overline{z}}_{\mathrm{k}}\right) \) and σ zk, respectively, and σ 2k (x) is the kriging prediction error variance for \( \ln \left({\overline{z}}_{\mathrm{k}}\right) \).

Illustrative Implementation

This approach is demonstrated next considering the structure and hazard description in Gidaris et al. (2015). The structure, shown in Fig. 4.2, corresponds to design A in the benchmark study presented in Goulet et al. (2007). The total masses per floor are also shown in the figure. To demonstrate the versatility of the framework and its ability to assess risk for structures equipped with seismic protective devices, an additional case study is considered through incorporation of fluid viscous dampers. The structure without dampers is referenced as building A, whereas the structure with the dampers, building B.

Fig. 4.2
figure 2

Four-story reinforced benchmark building, (a) elevation and (b) plan views

Full size image

Structural Model

The lateral system consists of two exterior moment-resisting frames in each direction, with interior intermediate gravity frames. The resultant structural model corresponds to a two-dimensional four-bay frame modeled in OpenSees (McKenna 2011). The nonlinear hysteretic behavior of the structure is taken into account through lumped plasticity beam-column elements, modeled by using the modified Ibarra-Medina-Krawinkler nonlinear hinge model (Ibarra et al. 2005) with degrading strength and stiffness characteristics. To reduce the number of random variables, the approach proposed in Liel et al. (2009) is adopted here; perfect correlation is assumed for strength/stiffness and ductility characteristics for each one of the ten different potential plastic hinges. Under this assumption, 20 independent variables need to be considered, namely, column strength/stiffness (c s,nc) and column ductility (c d,nc) for six different columns and beam strength/stiffness (b s,nb) and beam ductility (b d,nb) for four different beams. Finally, the structural model is assumed to have Rayleigh damping with damping ratio ζ associated with the first and third modes. The structural model parameter vector is ultimately θ s = {c s,nc c d,nc b s,nb b d,nb ζ; nb = 1,…,4, nc = 1,…,6}. Building B is upgraded with fluid viscous dampers. A velocity exponent equal to 0.5 is considered for all dampers, representing a common value for seismic applications, whereas the dampers are placed in the exterior bays of the moment-resisting frame as indicated in Fig. 4.2. The damping coefficients are chosen as [9370, 4370, 2620, 2050] (kN(s/m)0.5) for the dampers within each story following the design process in Gidaris and Taflanidis (2015). These dampers are modeled in OpenSees utilizing the ViscousDamper material, corresponding to a Maxwell model implementation (Christopoulos and Filiatrault 2006), whereas the axial stiffness is taken as 250,000 kN/m for all dampers.

Seismic Hazard Model

For describing the seismic hazard, the same excitation model as in Jia et al. (2014) is adopted. The broadband component for the excitation is represented through a point source model (Boore 2003; Taflanidis and Beck 2009) based on a parametric description of the temporal envelope and radiation spectrum of the ground motion, both given as function of M and r rup. Near-fault characteristics are incorporated through the velocity pulse model proposed by Mavroeidis and Papageorgiou (2003) that has as input parameters the pulse period amplitude T p, a parameter that controls its amplitude A p, the oscillatory character (number of half cycles) γ p, and its phase v p. Ultimately, the excitation model parameter vector is θ g = [M, r, A p, T p, γ p, v p] when considering excitations with directivity pulses and θ g = [M, r] when considering excitations without such pulses. Metamodels need to be separately developed for each of the excitation models and will be abbreviated as P and NP, respectively.

Metamodel Formulation

Two different structural models (buildings A and B) and two different excitation models (P and NP) are considered for the surrogate model development leading to four different cases. The response quantities approximated are the peak interstory drifts δ k and absolute peak floor accelerations ä k for all floors k = 1,..,4. The model parameter vector x has 23 components for the NP excitation and 27 components for the P excitation, whereas the domains defining X are chosen (Gidaris et al. 2015) based on the anticipated value range for each parameter. For example, for the P excitation, the selection is based on the characteristics of ground motions exhibiting near-fault components and the observed properties of those components (Shahi and Baker 2011; Mavroeidis and Papageorgiou 2003).

An adaptive refinement strategy is established to select the number of support points. Table 4.1 reports the number of support points n m used for each metamodel, as well as validation metrics such as the average coefficient of determination and average mean error over δ k and ä k denoted as ARD 2 δ , ARD 2 ä , AME δ , and AME ä , respectively, calculated through a cross-validation approach. It is evident that challenges are encountered in developing the metamodel for building A and P excitation, leading to a larger value for the total number of support points. This stems from resonance conditions created by the directivity pulse which contribute to significantly higher variability in the response and ultimately to greater difficulty in the developed model to accurately capture this variability. The results indicate that the accuracy established is high, with average coefficients of determination higher than 96 % for \( \ln \left({\overline{z}}_{\mathrm{k}}\right) \) (79 % for σ zk) and average mean errors lower than 15 % (lower than 13.3 % for σ zk). As discussed previously, the high values for the coefficient of determination are especially important for the considered risk assessment implementation. The metamodel performance for the NP excitation is exceptionally good, showing that adequate accuracy would be possible with even lower values for the number of support points, but even for the P excitation the metamodel performance is more than adequate, especially for the acceleration responses. The lower overall accuracy for the drift responses should be attributed to the stronger impact from the nonlinear hysteretic structural behavior that results in larger variability for the drift responses. For the building equipped with dampers, the protection against such large inelastic responses offered by the dampers results in reduction of that variability and ultimately in higher accuracy of the established surrogate model.

Table 4.1 Validation metrics of the different surrogate models developed
Full size table

Risk Assessment

Next, the optimized kriging metamodel is utilized for estimating seismic risk. For the basic comparisons in this section, the risk is defined as the probability that the response will exceed acceptable threshold β k (i.e., a range will be considered for β k demonstrating the efficiency of the approach for different risk levels) with σ βk taken equal to 0.2. For the seismic hazard, two different cases are considered. In the first case, denoted as NP hazard, it is assumed that no excitations include near-fault effects (so only the NP excitation model is utilized). In the second case, denoted as PP hazard, the possibility of including a near-fault pulse is considered through the probability model developed by Shahi and Baker (2011) that quantifies the probability of an excitation to include a pulse dependent upon other seismicity characteristics (distance to fault rupture, moment magnitude). A detailed description of the seismic hazard characterization for this case is provided in Jia et al. (2014) and Gidaris and Taflanidis (2015). This leads to risk quantification as

$$ R={\displaystyle {\int}_{\Theta}{\displaystyle \sum_{\varepsilon_{\mathrm{p}}=\left\{ yes, no\right\}}h(\boldsymbol{\uptheta} |{\varepsilon}_{\mathrm{p}})}P({\varepsilon}_{\mathrm{p}}|M,r)p(\boldsymbol{\uptheta} )d\boldsymbol{\uptheta}} $$
(4.14)

where ε p is a binary (outcomes {yes, no}) random variable describing the probability of pulse existence, \( P({\varepsilon}_{\mathrm{p}}|M,r) \) is the probability model for it, and the risk consequence measure \( h(\boldsymbol{\uptheta} |{\varepsilon}_{\mathrm{p}}) \) is estimated based on the P excitation (or surrogate model) if ε p = yes and the NP excitation (or surrogate model) if ε p = no.

Details for the chosen probability models p(θ) are included in Gidaris et al. (2015). Stochastic simulation with N = 10,000 samples is utilized for the estimation of the seismic risk. Importance sampling is established for M with density chosen [based on prior experience (Taflanidis and Beck 2009)] as truncated Gaussian with mean 6.8 and standard deviation 1.0. For the PP hazard, importance sampling is also formulated for ε p based on observed sensitivity in Jia et al. (2014), with 80 % of the excitations taken to include a pulse. The estimates from the surrogate model, denoted as SE, are compared against the estimates calculated through the high-fidelity model, denoted as HF. Indicative results are presented in Fig. 4.3, in all cases as plots of the probability of failure (risk) against the threshold β k. The coefficient of variation (for the stochastic simulation) for the risk estimated through the surrogate model and all considered cases is not higher than 9.0 and 17.0 % for probabilities of failure as low as 10−2 and 10−3, respectively, demonstrating the relatively high accuracy that can be established even for rare-event simulations.

Fig. 4.3
figure 3

Probability P[z k ≥ β] of exceeding a specific threshold based on high-fidelity model (OpenSees) and kriging metamodel for peak interstory drift [parts (a), (c), (e)] and peak floor acceleration [parts (b), (d), (f)] of the third floor of buildings A and B. Top [parts (a), (b)] and middle [parts (c), (d)] rows correspond to PP and NP hazards, respectively, for building A and bottom row to building B for NP hazard

Full size image

The comparison between the risk estimated from the high-fidelity model and the kriging metamodel indicates that the accuracy achieved is very high. Even for building A and the PP hazard, utilizing primarily a surrogate model (excitation model P) that encountered greater challenges to provide satisfactory accuracy, the agreement achieved is high. As anticipated from the accuracy characteristics of the kriging metamodel, the agreement is closer for the NP hazard (compared to the PP hazard) and for building B (compared to building A). Comparison between buildings A and B shows that retrofitting with fluid viscous dampers greatly contributes to mitigating risk for drift responses.

The total CPU time (computational burden) for the seismic risk assessment utilizing the surrogate model for building A is only 530 s for the PP case and 108 s for the NP case. The larger value for the former stems from the larger number of support points utilized for the P excitation model. These numbers represent a significant reduction of computational burden when compared to the high-fidelity model which requires 210.9 h for the PP case and 187.4 h for the NP case. The corresponding CPU times for building B are 64 s for the PP case and 39 s for the NP case when surrogate model is used, whereas the high-fidelity model requires 180.5 h for the PP case and 165.7 h for the NP case (smaller values because the nonlinear dampers contribute to less severe inelastic structural response).

It is evident, therefore, that the surrogate modeling implementation facilitates a highly efficient and accurate seismic risk assessment for structures equipped or not with seismic protective devices; a large number of samples can be used with a negligible computational effort, whereas the provided risk estimates are close to the ones obtained from the high-fidelity approach. Of course, some initial computational effort is required for the development of the database to inform the surrogate model. Once this model is established, it can be used, though, for any risk quantification desired.

For demonstration, the risk quantified as the expected repair cost per seismic event for the ceiling or the partition walls is further calculated, utilizing the subassembly approach to estimate repair cost (Porter et al. 2001). The vulnerability information from FEMA-P-58 2012 is utilized; three different damage states are considered for both subassemblies, with the probability of exceeding each damage described by a fragility function as in Eq. (4.2) and approximated through the kriging surrogate model through Eq. (4.13). This fragility information is then coupled with the repair cost for each damage state to provide the total repair cost. The repair costs per seismic event are reported in Table 4.2 for both buildings for seismic hazard PP. The high accuracy achieved using the kriging approximation is again evident by comparing the results obtained from the HF and SE approaches.

Table 4.2 Expected repair cost per seismic event for partition walls and ceiling for buildings A and B for seismic hazard PP
Full size table

5 Real-Time Hurricane Risk Assessment

Hurricane risk assessment has received a lot of attention in the past decade, in response to the 2005 and 2008 devastating hurricane seasons. Of special interest in this case is the development of real-time tools that can provide efficient assessment during landfalling events to guide decisions of emergency response managers, whereas one of the greater advances in this field has been the development and adoption of high-fidelity numerical simulation models (corresponding to the system model for the description in Fig. 4.1) for reliable and accurate prediction of surge/wave responses for a specific hurricane event (Resio and Westerink 2008). These models permit a detailed representation of the hydrodynamic processes, albeit at the cost of greatly increased computational effort (more than a few thousand CPU hours for analyzing each hurricane event). They are based on a high-resolution grid description of the entire coastal region of interest (including more than a few million nodes), using detailed bathymetric data, and with the wind pressure time history of the hurricane (excitation model for Fig. 4.1 description) as input (Vickery et al. 2009) can simulate the surge and wave responses. The adoption of such models increases though, significantly, the computational cost for estimating hurricane risk. This is intensified by the fact that for appropriately assessing the hurricane impact, the simulation needs to extend a few (4–5) days prior to landfall. This is essential for both numerical convergence and for capturing all changes in the wave and surge environment that can be of significant importance (Dietrich et al. 2011).

To address this challenge, surrogate modeling concepts have been considered by various researchers in the past decade (Irish et al. 2009; Taflanidis et al. 2012; Das et al. 2010) with kriging (Jia and Taflanidis 2013) facilitating a computationally efficient implementation especially for real-time risk assessment. This is discussed in this section, starting with a review of hurricane modeling to fit within the description provided in Fig. 4.1.

Hurricane Modeling

Among the various methodologies for hurricane risk assessment, a probabilistic approach, frequently referenced as the joint probability method (JPM), has been gaining popularity within the engineering community (Toro et al. 2010; Resio et al. 2007). The approach relies on a simplified description of each hurricane/storm scenarios through a small number of model parameters, corresponding to the characteristics close to landfall. These primary parameters, representing vector θ m in Fig. 4.1, are the location of landfall x o, the angle of approach at landfall α, the central pressure c p, the forward speed during final approach to shore v f, and the radius of maximum winds R m leading to θ m = [x o α c p v f R m]T. The variability of the hurricane track and characteristics prior to landfall is also important, but directly incorporating this variability in the hurricane description would increase significantly the number of model parameters and so it is avoided. Instead, this variability is approximately addressed by appropriate selection of the hurricane track history prior to landfall, so that important anticipated variations, based on regional historical data, are described.

This modeling approach leads to characterization of hurricane risk through the probabilistic integral in Eq. (4.1) with main source of uncertainty θ = θ m. This quantification can be adopted for describing the long-term risk in a region (Resio et al. 2007, 2012) as well as for real-time applications (Smith et al. 2011). In the former case, p(θ) is chosen based on anticipated regional trends and climatological models, whereas in the latter case, it is provided by the national weather service prior to landfall in the form of a most probable hurricane track/intensity prediction along with statistical errors associated with this prediction. Part (b) of Fig. 4.4 demonstrates an example for the latter.

Fig. 4.4
figure 4

(a) Typical grid size for ADCIRC high-fidelity model and (b) details of landfalling to Oahu hurricane considered in the demonstration example (results shown in Fig. 4.5)

Full size image

An important challenge in this application is the fact that the number of output response quantities of interest, representing the impact of the hurricane over a large coastal region, is typically large. Examples of such responses include (1) the storm surge (ζ), i.e., still-water level, defined as the average sea level over a several-minute period; (2) the significant wave height (H s) (possibly along with the corresponding peak period T p); (3) the wave run-up level, defined as the sea level including run-up of wind waves on the shore; and (4) the time that normally dry locations are inundated. Temporal and spatial variation is very important. With respect to the first aspect, the response variables may refer to maximum responses over the entire hurricane history or to responses at specific time instances prior to landfall. With respect to the second aspect, the response will be typically estimated in a large number of locations, expressed in some grid format [either corresponding to the initial grid for the high-fidelity model or to some lower resolution interpolated version (Taflanidis et al. 2013a)], which is the main characteristic of the analysis contributing to the large dimension of the output vector. Each component of z corresponds ultimately to a specific response variable [e.g., any of the (1)–(4) described above] for a specific coastal location and specific time. The dimension of n z can easily exceed 106, depending on the type of application.

Dimension Reduction Through Principal Component Analysis

This large dimension of the response output imposes significant challenges in terms of both computational speed and, perhaps more importantly, memory requirements (Jia and Taflanidis 2013). The latter are particularly important for supporting the development of cyber-enabled platforms (Kijewski-Correa et al. 2014) that can be deployed in real time, allowing emergency response managers to simultaneously perform different types of analyses.

To address this challenge, the adoption of principal component analysis (PCA) as dimensional reduction technique was proposed in Jia and Taflanidis (2013) to reduce the dimensionality of the output vector by extracting a smaller number of latent outputs to represent the initial high-dimensional output. Considering the strong potential correlation between responses at different times or locations in the same coastal region (which are the main attributes contributing to the high dimension of the output vector), this approach can significantly improve computational efficiency without compromising accuracy.

PCA starts by converting each of the output components into zero mean and unit variance under the statistics of the observation set (composed of n m observations) through the linear transformation

$$ {\underline{z}}_{\mathrm{k}}=\frac{z_{\mathrm{k}}-{\mu}_{\mathrm{k}}^z}{\sigma_{\mathrm{k}}^z},\ \mathrm{with}\ {\mu}_{\mathrm{k}}^z=\frac{1}{n_{\mathrm{m}}}{\displaystyle \sum_{h=1}^{n_{\mathrm{m}}}{z}_{\mathrm{k}}^h},{\sigma}_{\mathrm{k}}^z=\sqrt{\frac{1}{n_{\mathrm{m}}}{{\displaystyle \sum_{h=1}^{n_{\mathrm{m}}}\left({z}_{\mathrm{k}}^h-{\mu}_{\mathrm{k}}^z\right)}}^2}. $$
(4.15)

The corresponding (normalized) vector for the output is denoted by \( \underline {\mathbf{z}}\in {\mathbb{R}}^{n_{\mathrm{z}}} \) and the observation matrix by \( \underline {\mathbf{Z}}\in {\mathbb{R}}^{n_{\mathrm{m}}\times {n}_{\mathrm{z}}} \). The idea of PCA is to project the normalized \( \underline {\mathbf{Z}} \) into a lower dimensional space by considering the eigenvalue problem for the associated covariance matrix \( {\underline {\mathbf{Z}}}^T\underline {\mathbf{Z}} \) and retaining only the m c largest eigenvalues. Then \( {\underline {\mathbf{Z}}}^T=\mathbf{P}{\mathbf{Y}}^T+\boldsymbol{\uptau} \) where P is the n z × m c dimension projection matrix containing the eigenvectors corresponding to the m c largest eigenvalues, Y is the corresponding n m × m c observation matrix for the principal components (latent outputs), and τ is the error introduced by not considering all the eigenvalues (Tipping and Bishop 1999). If λ i is the ith largest eigenvalue, m c can be selected so that the ratio

$$ {\displaystyle {\sum}_{j=1}^{m_{\mathrm{c}}}{\lambda}_j}/{\displaystyle {\sum}_{j=1}^{n_{\mathrm{z}}}{\lambda}_j} $$
(4.16)

is greater than some chosen threshold r 0 [typically chosen as 99 %]. This then means that the selected latent outputs can account for at least r 0 of the total variance of the data (Tipping and Bishop 1999). It is then m c <min(n m, n z) with m c being usually a small fraction of min(n m, n z). For n m <<n z, obviously, m c <<n z, leading to a significant reduction of the dimension of the output.

The latent outputs, denoted by y i , i = 1,…,m c are the outputs with observations that correspond to the ith column of Y and the outputs for which the kriging metamodel is ultimately developed (in other words, m c = n y in the terminology established in Sect. 4.3). The relationship between the initial output vector and the vector of the latent outputs is \( \underline {\mathbf{z}}=\mathbf{P}\mathbf{y} \). Kriging is then formulated for the output vector y. Of particular importance is the fact that in this case the elements of y have an associated relevance, represented by its variance, which is proportional to λ j , the portion of the variability within the initial database represented from this latent output. This means that, contrary to common approaches for normalizing vector y within the surrogate model optimization of Eq. (4.8) through the introduction of weights γ i , in this case, no normalization should be established, i.e., γ i  = 1. This equivalently corresponds to latent outputs with larger values of λ j being given higher priority in the surrogate model optimization. The alternative approach is to develop a separate surrogate model for each output separately (Jia and Taflanidis 2013). This does not increase memory requirements but has an impact though on the computational time for developing and implementing the surrogate mode.

The linear relationships between y and \( \underline {\mathbf{z}} \) finally allow for a direct transformation of the probability models for the predictions for these two quantities [a Gaussian variable under linear transformation still follows a Gaussian distribution]. Considering additionally the inverse of transformation in Eq. (4.15) to transform these predictions back to the original space, we have (Jia and Taflanidis 2013) that the kriging-based predictor for z follows a Gaussian distribution with mean

$$ \widehat{\mathbf{z}}\left(\mathbf{x}\right)={\boldsymbol{\Sigma}}^z\left(\mathbf{P}\widehat{\mathbf{y}}\left(\mathbf{x}\right)\right)+{\boldsymbol{\upmu}}^z $$
(4.17)

and variance \( {\underset{\sim \mathrm{zk}}{\sigma}}^2\left(\mathbf{x}\right) \) for z k(x) corresponding to the diagonal elements of the matrix

$$ {\boldsymbol{\Sigma}}^z\left[\mathbf{P}\boldsymbol{\Sigma } \left(\mathbf{x}\right){\mathbf{P}}^T+{\upsilon}^2\mathbf{I}\right]{\boldsymbol{\Sigma}}^z, $$
(4.18)

where Σ z is the diagonal matrix with elements σ zk , μ z is the vector with elements μ zk k = 1,…,n z, Σ(x) is the diagonal matrix with elements σ 2k (x), k = 1,…,m c, and υ 2 I stems from error τ. An estimate for the latter is given by

$$ {\upsilon}^2={\displaystyle {\sum}_{j={m}_{\mathrm{c}}+1}^{n_{\mathrm{z}}}{\lambda}_j/\left({n}_{\mathrm{z}}-{m}_{\mathrm{c}}\right)} $$
(4.19)

corresponding to the average variance of the discarded dimensions when formulating the latent output space. This Gaussian predictor for z can be then used in risk assessment with the error, characterized through variance \( {\underset{\sim \mathrm{zk}}{\sigma}}^2\left(\mathbf{x}\right) \) used to provide an appropriate modification of the risk consequence measure (Jia and Taflanidis 2013), similar to the approach discussed earlier in Eq. (4.11) [\( {\underset{\sim \mathrm{zk}}{\sigma}}^2\left(\mathbf{x}\right) \) needs to replace σ 2k (x) in this case].

Illustrative Implementation

This approach has been implemented to develop efficient tools for real-time hurricane risk assessment for the Hawaiian islands (Taflanidis et al. 2013a; Kijewski-Correa et al. 2014; Jia and Taflanidis 2013) and recently for New Orleans (Taflanidis et al. 2014). Results from the former are discussed briefly here. The database utilized in this case comes from a regional flood study (Kennedy et al. 2012) consisting of 603 storms with θ = θ m representing the only source of uncertainty in the risk characterization. The high-fidelity model chosen to accurately predict the surge and wave response is a combination of the ADCIRC and SWAN numerical models (Bunya et al. 2010; Kennedy et al. 2012) and consists of 1,590,637 nodes and 3,155,738 triangular elements. Each simulation utilizing this model requires over 1500 CPU hours to complete. Grid characteristics are also shown in part (a) of Fig. 4.4.

The response output considered here corresponds to the maximum (over the hurricane duration) significant wave heights H s in the region extending from 157.392°W to 158.584°W and 21.11°N to 21.90°N, close to Oahu island, and storm surge ζ for near-shore/inland locations around the coast of the island of Oahu with average distance of 300 m and up to the 4 m contour. The former has dimension n z = 12,800 and the latter n z = 77,175 leading to high-dimensional application. Based on the database, a single kriging metamodel with PCA is implemented with m c = 40, which account for 99 % of the total variability in the corresponding initial outputs. This selection reduces the sizes of the matrices that need to be stored in memory by over 90 %. For the optimized metamodel, the average coefficient of determination and average mean error over all nodal points in the initial response space are 0.948 and 4.51 % for significant wave height and 0.930 and 5.33 % for storm surge, respectively. The probability of misclassification for the surge (i.e., identifying a location as inundated when it is not and vice versa) is 2.6 %. These error statistics show that the kriging metamodel provides high-accuracy approximations to the hurricane response (small errors).

This computational efficiency of the established metamodel can then be utilized to support the development of stand-alone tools (Taflanidis et al. 2013a) or, perhaps more importantly, cyber-enabled portals supporting wide online dissemination and collaborative environments (Kijewski-Correa et al. 2014). As indicated previously, these tools can be used to estimate the regional long-term risk or provide real-time predictions during landfalling events. The latter is demonstrated in Figs. 4.4 and 4.5. Part (b) of Fig. 4.4 shows the hurricane scenario considered; in this case, the risk assessment is performed 42 h prior to landfall. Details on the quantification of the uncertainty on θ based on standard meteorological prediction errors are included in Taflanidis et al. (2013a). Figure 4.5 then shows results for the wave height contours with probability of being exceeded 5 % [part (a)] and the probability that surge will exceed threshold β [part (b)] for location with coordinates 21.3769°N, 157.9666°W, which is near the shoreline of East Loch inside Pearl Harbor. The predictions with and without considering the kriging prediction error (i.e., taking \( {\underset{\sim \mathrm{zk}}{\sigma}}^2\left(\mathbf{x}\right)=0 \)) are included in this plot. The comparison indicates that the prediction error can have a significant impact on the calculated risk, and it will lead to more conservative estimates for rare events (with small probabilities of occurrence). This demonstrates that it is important to explicitly incorporate it in the risk estimation framework.

Fig. 4.5
figure 5

Risk assessment results for scenario illustrated in Fig. 4.4b. (a) Wave height with 5 % probability of exceedance close to Oahu and (b) probability of surge exceeding thresholds β at location with coordinates 21.3769°N, 157.9666°W

Full size image

The total evaluation time required for this risk assessment (for N = 2000 samples) is only 25 s on Intel(R) Xeon(R) CPU E5-1620 3.6 GHz with 8 GB of memory. These results correspond to a huge reduction of computational time compared to the high-fidelity model, which required a few thousand CPU hours for analyzing a single hurricane scenario. Thus, the kriging metamodel with PCA makes it possible to efficiently assess hurricane risk in real time for a large region (high-dimensional correlated outputs) providing at the same time a high-accuracy estimate for the calculated risk. Similar efficiency has been reported for implementation to New Orleans region (Taflanidis et al. 2014). This efficiency has been exploited to develop cyber portals that offer enhanced visualization capabilities as well as a versatile online collaborative environment (Kijewski-Correa et al. 2014).

6 Conclusions

Simulation-based modeling or risk estimation approaches facilitate a comprehensive and detailed characterization of natural hazard risk, with advances in computer and computational science dramatically reducing the computational burden associated with these approaches. This chapter examined the integration of kriging surrogate modeling in this context for further reduction of this burden. Kriging establishes a computationally inexpensive input/output relationship based on a database of observations obtained through the initial (expensive) simulation model. It enjoys a straightforward optimization (to improve its accuracy) and relies only on matrix manipulations (with no matrix inversions needed for its implementation), which supports a highly efficient calculation of the output for multiple inputs, as required within a stochastic simulation setting. Additionally, it provides a prediction error that is also a function of the input (and not constant over the examined domain), whereas the incorporation of that error in the risk assessment can significantly impact the risk estimates and improve their accuracy, especially when analyzing rare events. For applications with high-dimensional output, kriging can be integrated with principal component analysis to improve computational efficiency and reduce the memory requirements for the metamodel deployment. These characteristics are particularly useful for the development of automated risk assessment tools and were demonstrated in this chapter considering implementation for real-time hurricane risk estimation. In the other example considered, the seismic risk assessment when stochastic ground motion modeling is considered for the hazard description, it was shown that despite the high dimensionality of the input, stemming from the stochastic sequence involved in the ground motion model, through proper assumptions, approximately addressing the impact of the stochastic sequence in this case, kriging can still facilitate an efficient and accurate risk assessment. Overall, the chapter demonstrated the potential that kriging offers within a simulation-based setting for describing natural hazard risk.