1 Introduction

Past design and planning efforts in coastal areas have focused on taking the best information possible and applying it to the task at hand, even though this information may have been only marginally sufficient for such efforts. Over the years, we have continued to learn about the physical processes and the statistical characteristics of these processes, sometimes without a disaster to prompt a paradigm shift in our response and other times following a disaster. On the one hand, it has never seemed prudent to do nothing and allow coastal areas to be inundated, lives lost and property destroyed without trying to mitigate hazards and risks faced by these communities. On the other hand, pressures of increased coastal land use and development continue to contribute to a situation in which coastal disasters appear to be increasing at an alarming rate in spite of efforts to mitigate these problems.

One key facet of the problem faced by coastal engineers and planners alike is the dearth of high-quality information. Historically, in studies of coastal hazards and risks, the roles of alleatory and epistemic uncertainty are either included via a qualitative conservative factor or neglected. Thus, in a typical study of extreme storm surges, the annual exceedance probability (AEP) for surges is defined as 1 − F(η), where F(η) is the cumulative distribution function (CDF) of surges, that is

$$ F(\eta ) = \int\limits_{0}^{\eta } {p(\eta_{*} )d\eta_{*} } , $$
(1)

where p denotes the probability density function, η is the surge height and η* is a dummy integration variable. The mean interval between events with a surge of η or higher (the mean Return Period for η), or T r (η), can be defined as

$$ T_{r} (\eta ) = \frac{1}{1 - F(\eta )}. $$
(2)

In this paper, all of the figures will be given in terms of mean return periods, T r , since many people find it easier to envision processes in intervals of time rather than in terms of small AEPs. It is easy to convert from one form to another via Eqs. 1 and 2. It should be recognized that although we have chosen to use the more intuitive form here, this is still only a measure of the mean interval between occurrences of a particular surge level and actual occurrences are randomly distributed around this mean.

As written in Eq. 2, the form for the mean return period should not be taken to imply that estimates obtained can neglect uncertainty and still provide an unbiased estimate of the hazard exposure and its associated risk. In this paper, we intend to show that the effect of uncertainty is to systematically shift the mean return period from its deterministic estimate toward lower values. For example, a particular surge height that is expected on the average once every 100 years, neglecting uncertainty, will be expected more frequently if the effects of uncertainty are included. If this particular surge value is relevant to a critical parameter used in project design or site planning, such a reduction in the expected mean interval between events (or conversely an increase in the AEP) might diminish the expected performance of the design or planning concept to an unacceptable level.

We will begin with an examination of the impact of uncertainties on surge values in the typical AEP range used for levee design in the New Orleans area. Like many historical designs in the United States, this value was selected as that associated with an AEP of approximately 10−2, or a return period of 100 years. Due to limitations in computational power in the late 1950s, early efforts to estimate such surge levels attempted to associate the surge level used for a specific design to a single design storm, termed the “Standard Project Hurricane (SPH)” (Graham and Nunn 1959). This effectively reduced the number of degrees of freedom in storm behavior to one parameter, which was typically selected as storm intensity. All other storm parameters (for example, storm size, forward storm speed, landfall location, etc.) were deterministically related to storm intensity. A major problem with this approach is that, if a second factor (such as storm size, angle of storm approach to the coast, storm duration or river stage) significantly affects design conditions and/or planning considerations, the design storm approach cannot accurately capture all pertinent aspects of surges for design and planning. Since many of these other parameters have been shown to affect surges significantly (Irish et al. 2008, 2009; Resio et al. 2009), it is very important to consider the inherent variation of these other terms and not to use a single value for each of these terms simply for expediency.

Another popular early method for estimating hurricane storm surges for an AEP of 10−2 was the reliance on only historical data. Two very significant problems stymied this approach, the small sample of storms at a site and the complexity of the hurricane surge response at the coast. The complexity of surge response at the coast makes it impossible to consider all of the surges as though they are drawn from a single homogeneous population. Figure 1 from Irish et al. (2009) shows the pattern of hurricane surges along the coast of Texas, with the along-coast distance scaled by radius to maximum wind speed (the most common hurricane size parameter used by researchers). If five storms affecting an area are all drawn from the region greater than or equal to a distance of twice the radius to maximum wind speed from the location of the maximum surge, they would not be statistically equivalent to five storms drawn from the region near the peak surge location. Thus, the fact that surges at the coast are not influenced by a single storm parameter complicates the interpretation of historical data. Irish et al. (2011) show that this complication leads to a substantial increase in the uncertainty in estimates of F(η) based solely on historical storms that have occurred in an area compared to those that rely on methods based on all storms that could occur in that same area.

Fig. 1
figure 1

Numerically simulated surge (using the ADCIRC model) plotted against dimensionless alongshore surge distribution, showing the similarity in surge scaling for hurricanes of different sizes and intensities (from: Irish et al. 2009). In this figure, x’ is the deviation between a site and the landfall location divided by the radius to maximum winds

Full size image

In this range of probabilities, it will be shown that the effect of uncertainty depends primarily on two factors, the sum of all uncertainties and the characteristic variation of F(η). Moreover, since the variation of F(η) is typically nonlinear over a wide range, this effect will vary as a function of the AEP and relative magnitudes of uncertainties in this range. Using data from the New Orleans area, the impact of the uncertainty will be shown to be moderate, however, certainly not negligible for design purposes.

A second part of this paper will examine the effect of neglecting a source of variability in the determination of a design surge level. As an example of this, we will compare initial estimates of surge heights along the Mississippi River levees obtained for the value of river discharge that existed at the time of Hurricane Katrina in 2005, to estimates of surge heights that include variations of river discharge in a probabilistic fashion. In this section, it will be shown that the magnitude of deviations between these two estimates for design values at a 10−2 AEP can exceed 1.0 m.

The final part of this paper will investigate the impact of uncertainties on much longer return periods, such as used for the design of large, critical infrastructure in coastal areas. In many instances, the intended annual probability of exceedance for these designs is in the 10−4–10−6 range. Similar to the development of the SPH, early attempts to deal with probabilities of hurricane surges in this extreme range led to the formulation of the concept of a “Probable Maximum Hurricane (PMH)” (Schwerdt et al. 1979), defined as the hurricane that would produce the surge “that may be expected from the most severe combination of critical meteorological conditions that are reasonably possible for the region.” By definition, such a storm would have an infinite recurrence period and could never be exceeded. However, attempts to define such a hurricane were of necessity very subjective due to a wide range of factors, including the dearth of reliable data on hurricanes, the lack of understanding of surge response at the coast, and the lack of record length in the sample.

In recent years, there has been an effort to shift from a single design event of the “Probable Maximum Hurricane” or “Probable Maximum Flood” type to a risk-based design. For some applications such as nuclear power plants sited in coastal areas, the AEP has been established at a value of 10−6. For other applications, such as some major coastal levees in parts of the world, the AEP has been established at a value of 10−4. As an example of the potential impact of uncertainty in this range of AEPs, we shall examine differences in the deterministically specified central pressures compared to estimates that include the effects of potential sampling variability. In our example included here, it will be shown that deviations in the expected central pressures in this range would exceed 30 mb in areas along the west coast of Florida. In turn, scaling arguments suggest that this could create differences in the estimated surge values of more than 20 %.

2 The impact of uncertainties in the 10−2 AEP range

As noted in the introduction, the complex character of hurricane surge responses makes it difficult to estimate surge probabilities from historical storms alone. This means that whereas detailed reconstructions of wind fields in historical storms are extremely valuable for validating storm surge models, such reconstructions contain far too many degrees of freedom to be estimated robustly from the existing sample. Instead, as noted in Resio et al. (2009), Irish et al. (2009), and IPET (2009), the hurricane wind field must be parameterized by a relatively small number of variables, typically storm intensity (characterized by central pressure), storm size (characterized by radius to maximum wind speed), the forward speed of the storm, the angle of the storm track with the coast, the location of landfall and a term that treats the peakedness of the wind speeds along the radial. A complete wind field can be reconstructed from these variables using a planetary boundary layer (PBL) model (Thompson and Cardone 1996; Vickery and Skerjl 2000) or a parametric wind model based on the Holland B formulation (Holland 1980).

Details of wind fields in each historical hurricane are expected to exhibit some degree of deviation from the theoretical PBL-model estimates. In turn, such deviations will create differences in surges generated by the PBL-model winds compared to more detailed wind fields. A good analysis of the impact of using wind fields based on a small set of parameters versus wind fields based on more precise wind field reconstruction methods can be found in Cardone and Cox (2009). Part of their conclusions notes that the use of carefully derived parameters based on post-storm analyses provides relatively faithful wind fields for application to surge prediction, whereas the use of forecast parameters does not. In this paper, we shall assume that post-storm analyses are utilized in describing the storm parameters and their probabilities, when critical design criteria are being developed.

Similar to the approach of Resio et al. (2009), an estimate of the CDF of surge heights can be made using a multidimensional integral over all retained wind-field variables in conjunction with a Heaviside Function. However, it is also important to include the impact of the effects of deviations in surges due to errors in the overall wind fields, that is

$$ F(\eta ) = \int { \ldots \int {p(x_{1} ,x_{2} , \ldots ,x_{n} ,\varepsilon_{w} )H[\eta - \Uppsi (x_{1} ,x_{2} , \ldots ,x_{n} ) + \varepsilon_{w} ]} } {\text{d}}x_{1} {\text{d}}x_{2} \ldots {\text{d}}x_{n} {\text{d}}\varepsilon $$
(3)

where \( x_{1} ,x_{2} \ldots ,x_{n} \) represent the storm parameters used to characterize a given storm, \( \Uppsi (x_{1} ,x_{2} \ldots ,x_{n} ) \)represents the numerical model used to convert the set of wind fields, combined with information on bathymetry, topography and roughness, into surge estimates, ε w can be taken as a first estimate to be the “error” term due to wind field deficiencies and H (·) is the Heaviside Function, equal to 1 if · ≥ 0 and equal to 0 if · < 0.

Additional deviations such as those due to model deficiencies, unresolved scales, and errors in the digital elevation model are also expected to contribute to the uncertainty of modeled surges. In the modeling performed to determine surge levels in the Gulf of Mexico, the final form for the CDF integral is

$$ F(\eta ) = \int { \ldots \int {p(c_{p} ,R_{\max } ,v_{f} ,\theta_{l} ,x,B)p(\varepsilon_{w + m} )H[\eta - \Uppsi (x_{1} ,x_{2} , \ldots ,x_{n} ) + \varepsilon_{w + m} ]} } {\text{d}}x_{1} {\text{d}}x_{2} \ldots {\text{d}}x_{n} {\text{d}}\varepsilon_{w + m} $$
(4)

where the new error term ε w+m is simply the sum of the storm parameterization errors and modeling errors, that is

$$ \varepsilon_{w + m} = \varepsilon_{w} + \varepsilon_{m} $$

and the terms c p , R max, ν f , θ l , x, and B refer to the central pressure, radius to maximum winds, forward storm speed, angle of the storm track at the coast, landfall location, and radial wind peakedness factor, respectively and the error term has been separated from the rest of the probability distribution for clarity. In this form, the “error” term allows us to include additional effects on water levels, such as tides (albeit in an uncoupled, linear fashion).

Data analyses have shown that the radial wind-speed peakedness parameter in mature storms within the Gulf of Mexico tended to fall within the range of 0.9–1.6. Furthermore, numerical sensitivity tests showed that the adoption of a constant value of 1.27 for storms centered more than 90 nm from the coast provided a reasonable first approximation to both the wind fields and the surges. Thus, if we add the effects of B-variations into the “error” term, we can reduce the CDF equation to

$$ F(\eta ) = \int { \ldots \int {p(c_{p} ,R_{\max } ,v_{f} ,\theta_{l} ,x)p(\varepsilon |\eta )H[\eta - \Uppsi (x_{1} ,x_{2} , \ldots ,x_{n} ) + \varepsilon ]} } {\text{d}}x_{1} {\text{d}}x_{2} \ldots {\text{d}}x_{n} {\text{d}}\varepsilon $$
(5)

In this form, ε is considered to include, at a minimum, the following terms:

  1. (1)

    tides,

  2. (2)

    random variations in B,

  3. (3)

    track variations not captured in storm set,

  4. (4)

    model errors (including errors in bathymetry, errors in model physics, etc.), and

  5. (5)

    errors in wind fields due to neglect of variations not included in the PBL winds.

IPET (2009) provides some discussion of the estimation of the values of these terms for the New Orleans area. As a very rough approximation to their value, the overall standard deviation of the sum of the deviations in this area is approximately equal to 0.6 m plus 15 % of the “deterministic” surge value. Figure 2 shows the estimated surge heights for the range of return periods between 50 and 500 years that are obtained in this manner along with the value one would obtain if this source of variation were neglected.

Fig. 2
figure 2

Comparison of expected surge heights as a function of return period for calculations with and without uncertainty in modeling considered for a typical location in the St Bernard Parish area near New Orleans

Full size image

If the distribution of surges were known exactly, the deviation between the two curves shown in Fig. 2 (modeling uncertainty) would be an appropriate measure of the total uncertainty in estimated surge heights over the return period range shown here. However, due to the finite (relatively small) sample size available for hurricanes in any local area, sampling errors are not negligible and need to be considered in the overall expectation of the AEP. Consequently, the encounter probability for exceeding a specific surge height cannot be taken directly from Eq. 5. Given the sampling uncertainty, the risk of encountering a surge height other than the deterministic estimate will be non-zero, and the effect of encountering other possible values should be considered when estimating for surge hazards/risks.

A more realistic treatment of the risk can be obtained by quantifying the effects related to their probabilistic variation around the deterministic value. The estimated standard deviation, typically used to construct control curves around the deterministic estimate, provides a good means of quantifying the spread of the probabilities around the deterministic estimate; and in this context, the probability of a given surge value can be written in terms of an integral in two dimensions with a delta function to reduce it back to a single dimension

$$ p(\eta ) = \int\limits_{0}^{\infty } {\int\limits_{ - \infty }^{\infty } {p[\hat{\eta }(T_{r} ) + \varepsilon_{s} } |\hat{x}]} p(\hat{\eta })p(\varepsilon_{s} )\delta (\hat{\eta } + \varepsilon_{s} - \eta )d\varepsilon_{s} d\hat{\eta }(T_{r} ) $$
(6)

where \( \hat{\eta }(T_{r} ) \) denotes the deterministic estimate of η for a given return period and ε s denotes the deviation from the deterministic surge estimate related to sampling error.

In Eq. 6, the estimate for p(ε s ) is taken as a Gaussian distribution with the mean value at \( \hat{\eta } \) and the standard deviation taken from the equation for estimating confidence bands, which will have the form

$$ p(\varepsilon_{s} |\hat{\eta }) = \frac{1}{{\sigma (\hat{\eta })\sqrt 2 \pi }}e^{{ - \frac{1}{2}\left( {\frac{\varepsilon }{{\sigma (\hat{\eta })}}} \right)_{2} }} $$
(7)

where \( \sigma (\hat{\eta }) \) is the standard deviation of the estimate at a given value of \( \hat{\eta } \).

Figure 3 shows the new estimate of surge values over the range of return periods from 50 to 500 years. As can be seen here, the differences among the three curves are in the range 0.5–1.0 m and are definitely of the magnitude which should be considered in designs. Although not particularly obvious in this specific example, the impact of the sampling variability is very much a function of return period, since the standard deviation in the uncertainty term increases with return period and decreases as a function of increasing sample length, as shown in Resio et al. (2009). Furthermore, the form of the integral is such that as the coefficient of variability of the extremal distribution flattens, the impact of the sampling uncertainty term (and in fact all of the uncertainty terms) will increase. This point will be emphasized more in the subsequent section on the impact of uncertainty on very low probability estimates.

Fig. 3
figure 3

Comparison of expected surge heights as a function of return period for calculations with and without uncertainty in modeling considered for a typical location in the St Bernard Parish area near New Orleans, along with the expected valued when sampling error is also considered

Full size image

3 The impact of river discharge on surges propagating in a river

In most computer simulations used to estimate flood frequencies in the United States, it has been assumed that river discharge can be treated as a constant. For example, in initial simulations used to estimate design surges in the New Orleans area, it was assumed that the Mississippi River discharge coincident with Hurricane Katrina would be suitable to use in all simulations, since it was somewhat typical of flows during that time of the year. Subsequently, it was recognized that this was not a suitable approximation, since the levels and pattern of surges within the river vary remarkably as a function of both river discharge and storm characteristics, as shown in Fig. 4 for examples of two different storms combined with four different river discharges. This figure clearly illustrates two important characteristics of the surge-discharge relationship. First, the surge levels become relatively insensitive to river discharge as the section of the river not leveed on both sides (i.e., the unconfined area) is approached. Second, as one moves upriver, the pattern of surges inside the confined river levees varied remarkably as a function of both storm characteristics and river discharge, indicating that it is quite important to consider both sources of variation when estimating design surge levels in sections of rivers confined within river levees.

Fig. 4
figure 4

Surge levels along the Mississippi River as a function of River Mile for two selected storms and four river discharges. The left-hand panel was Storm 15 in the run sequence, and the right-hand panel was Storm 35 in the run sequence. The “base discharge” for these runs was taken as the river discharge during the time of Hurricane Katrina (approximately 4,300 cubic meters per second)

Full size image

In Fig. 4, the distance upriver is given in terms of the distance upriver from a fixed reference point. Levees on the west side of the Mississippi River begin about 15 km upriver from the zero reference point near the river’s outlet into the Gulf of Mexico. Levees on the east side of the river begin about 50 km upriver from the zero reference point. Storm numbers in the titles of these plots refer to the sequence numbers used in defining a particular storm used in the Joint Probability Method—Optimal Sampling simulations (Resio et al. 2009), with storm 15 representing a storm that made landfall west of the New Orleans area and storm 35 representing a storm that made landfall within the general New Orleans area.

Since the effect of discharge on surge varies substantially as a function of position along the river, there is no simple constant discharge that can be considered as the “correct” discharge to be used as representative of a particular return period for all locations along the river. Thus, although the discharge may be considered as approximately constant over the length analyzed here, there is no single value that could be used to represent an appropriate discharge for simulations of the 100-year value (AEP of 10−2. Instead, it is necessary to allow river discharge to vary as a probabilistic function, in a fashion similar to the variation of the storm characteristics, in order to estimate the surge probabilities within the river.

Given that discharge within the Mississippi River varies strongly as a function of month as does the number and intensity of hurricanes, it is important to consider correlations between storm characteristics and river discharge within a comprehensive method of estimating surge probabilities. After some testing, it was found that although the time interval of mid-August through early September clearly contained the most intense storms, the sample size was too small to draw any statistically significant conclusions regarding monthly variations of hurricane intensity during the hurricane season; therefore, we were forced to limit our consideration of seasonal variations in storm characteristics to monthly storm frequencies. Since storm intensity and river discharge were negatively correlated in our sample, this omission might tend to introduce a small degree of conservatism into our final results.

Three complete sets of storms were simulated on river discharges of approximately 6,000, 24,000, and 42,000 cubic meters per second, chosen to cover most of the range of discharges within the Mississippi River during the hurricane season. The following equation, integrating over both discharge and local surge height for a specific discharge, was used to obtain the CDF for the overall surge distribution, which now includes the effects of variable discharge

$$ F(\eta ) = \int {\int {p(\eta_{*} |Q)p(Q)H(} \eta - \eta_{*} )dQd\eta_{*} } $$
(8)

where Q is the river discharge.

A comparison of results for the 10−2 AEP surge based on the use of a single value for the river discharge (approximately 4,300 cubic meters per second, the discharge coincident with Hurricane Katrina) in all simulations and results based on Eq. 8 is given in Table 1. The locations here are arranged from upriver to downriver and as can be observed in this table, the difference is greater than 1 m at the upstream locations (25 %) and goes to zero as the points get nearer to the coast. In this case, the results of the combined surge and variable discharge simulations produced the controlling surge levels within the Mississippi River and were incorporated into the levee designs for much of the southern portion of the river.

Table 1 Comparison of estimate 10−2 AEP surges based on a fixed discharge and based on variable discharge
Full size table

4 The impact of uncertainties in the 10−4–10−6 AEP range

In this section, we shall examine the potential role of uncertainty on two traditional approaches to estimating very low probability surges for designs in coastal areas: 1) the concept that a physical upper limit for surges exists and can be quantitatively defined and 2) the concept that adequate information exists for estimating a surge associated with a prescribed AEP in the 10−4–10−6 range. In the first situation, there must be substantial support for the existence of a physical upper limit in order for it to be used in critical applications. Resio et al. (2009), Irish et al. (2009) and Irish and Resio (2010) have shown that the response of surge heights at the coast can be addressed as a function of several variables. In this approach, the maximum surge level can be approximated as

$$ \eta_{\max } = \Upphi_{1} (\Updelta p)\Upphi_{2} (R_{\max } )\Upphi_{3} (x - x_{0} )\Upphi_{4} (v_{f} )\Upphi_{5} (\theta_{f} ) $$
(9)

where the multiplicative functions \( \Upphi_{i} \) should be understood to depend on the specific bathymetric/topographic setting of the specific point being investigated via the numerical model \( \Uppsi \). The primary set of dependencies include storm intensity (defined in terms of the pressure differential, ∆p, the peripheral pressure minus the central pressure), storm size, the relative position of the point of interest to the point of hurricane landfall (x − x 0), the forward storm speed, and the angle of intersection between the storm track and angle of the coastline. Irish and Resio (2010) have shown that four of the five functions in Eq. 9 have asymptotic limits in extensive tests along the Texas coast and elsewhere.

The one function that does not have a clear upper limit in the potential maximum surge formulation is the pressure differential term, ∆p. To examine the effect of the pressure differential on maximum surge, let us examine the simple case of a steady-state wind over a shelf of constant width and depth. In this case analogous to Resio and Westerink (2008), a simple linear approximation for the surge at the coast yields

$$ \begin{gathered} \hfill \\ \eta = \frac{{\rho_{a} }}{{\rho_{w} }}\frac{{c_{d} V^{2} L}}{gh} \hfill \\ \end{gathered} $$
(10)

where \( \rho_{a} ,\;\rho_{w} \, \) are the densities of air and water, respectively; c d is the coefficient of drag; V is the wind speed; L is the shelf width; g the acceleration due to gravity; and h is the water depth on the shelf.

This simple form can also be shown to be appropriate for more complex wind fields with a specified geometric similarity, such as found in hurricanes, and more complex offshore configurations.

In a wind system such as a hurricane with high winds moving circularly around a pressure minimum, the wind and pressure distribution will tend toward a cyclostrophic balance near the center of a hurricane. In this region, the outward centripetal acceleration is balanced by the pressure gradient, and the maximum wind speed tends to scale linearly with the square root of the pressure differential. If we assume a purely cyclostrophic flow exists, the force balance depends on only two terms, the centripetal force directed outward away from the center of the storm and the pressure gradient force directed inward toward the center of the storm; consequently, in the vicinity of the maximum wind speed, the governing equation for the force balance is of the form

$$ \frac{{V_{\max }^{2} }}{{R_{\max } }}\sim \frac{\Updelta p}{{R_{\max } }}; $$
(11)

where V max is the maximum wind speed, which is consistent with a linear relationship between velocity squared and the pressure differential, independent of storm size. For a constant (no wind-speed dependence) coefficient of drag such as might be expected in the high wind-speed cores of hurricanes (Powell et al. 2003), and noting that the pressure differential will be linearly proportional to V 2 in a cyclostrophic balance, it is expected that the maximum surge in hurricanes will depend approximately linearly on the pressure differential. This result was confirmed numerically in a wide range of simulation along the Mississippi coast using simulations computed by the SLOSH code (Niedoroda et al. 2010).

However, as the size of a hurricane becomes larger and larger, the geostrophic terms in the force-balance equation become the same order as the cyclostrophic terms and this equation changes its form to

$$ \frac{{V_{\max }^{2} }}{{R_{\max } }} + fV_{\max } \sim \frac{\Updelta p}{{R_{\max } }} ; $$
(12)

where fV max is the coriolis acceleration.

In this situation, an increase in the storm size parameter could cause a decrease in the maximum wind speed and can have a larger effect on the total storm surge than the increase in size. In areas with smaller shelf widths, this effect can lead to a situation in which smaller storms can produce larger surges than a larger storm with the same intensity.

For a number of years now, the theoretical concept a “Maximum Possible Intensity (MPI)” has been postulated, based on a combination of theoretical and empirical evidence from around the world, see for example Emanuel (1987) and Tonkin et al. (2000). Typical estimates for coastal waters around the United States are in the range 880–885 mb. If we adopted a single value, say of 880 mb, as a definitive MPI value for an application, one would now be able to estimate asymptotic limits for all of the functions involved in the surge calculations and might be tempted to treat the results from such a simulation as a deterministic upper limit. However, it is clear that there will be substantial uncertainty in all of the terms involved in such a calculation. In addition to this, these sources of uncertainty related to the quantification of the MPI, uncertainty due to potential modeling errors, must be considered if one is truly seeking an ultimate upper limit for surge heights. As noted previously, investigations into the magnitudes of these uncertainties suggest that the sum of their standard deviations will typically be in the range of 10–15 % of the deterministically estimated value, which for estimated maximum surges along the Gulf Coast of the United States yields potential uncertainties in the range of 1–2 ms in magnitude, plus any additional impact due to climatic variability on the MPI via its direct link to sea surface temperature. In this context, the use of a deterministic value alone may not be as conservative or as straightforward as once believed, since the actual upper limit might have to consider the choice of a reasonable upper limit on the uncertainty.

Given the complications introduced by uncertainties in the purely deterministic approach, it might seem prudent to consider the impact of uncertainties on statistically based estimates of very low probability surges. If we compare best-fit estimates of central pressure associated with AEPs in the range of 10−4–10−6 to the MPI value, this could give us an idea of whether or not we could justify the use of a higher central pressure, in other words a less intense storm, based on its AEP.

As an example of this, we will analyze data for the west coast of Florida. Most of these storms move east to west through this area. However, most storms moving in this direction usually have passed over Florida before emerging into the Gulf of Mexico and do not produce large storm surges along the west coast of the state. In order to focus our analysis on storms of the type that could produce significant surges along the west coast of Florida, we shall stratify our storm sample to include only storms with a general west to east motion in a latitude–longitude box with boundaries at 81 and 85°W longitude and 25 and 30°N latitude and will further limit the storms to those with central pressures that are less than 990 mb in this box. Using the most recent reanalysis data available from NCDC (National Climate Data Center www.ncdc.noaa.gov), we find that most storms before about 1940 did not report central pressures; consequently, we shall further limit our data set for analysis to the interval 1940–2009 (70 years).

Table 2 shows a list of the selected storms, their central pressures and the years in which they occurred. If one used a storm size assumed to represent the 1 % CDF value for storm size, one might argue that the 10−6 value for the overall likelihood of a surge event could be approximated by a 10−4 value for intensity and a 10−2 value of storm size if these two parameters were truly independent. Table 3 gives the results for a generalized extreme value (GEV) analysis in terms of the expected central pressure associated with selected return periods (taken here as just 1 over the annual frequency) and the standard deviation as a measure of the confidence band of this estimate up to the 10−4 AEP value. It should be noted here the surge response function usually limits the most severe impact of a hurricane to a region substantially less than the 5-degree latitude (555 km) length of coast analyzed here; consequently, we have to account for the difference in the length of coast considered to be a “direct hit” and the length of coast considered in the analysis upon which Table 3 is based in order to characterize the likelihood of a storm severely impacting a particular site. Just as an approximation here from the along-coast pattern of surges shown in Fig. 1, let us assume that a direct hit occurs when the storm makes landfall within a ±1 R max distance along the coast, centered on the location of the maximum surge at the site of interest. Since we used an approximate along-coast distance of about 555 km in our analysis of storm frequencies in Tables 2 and 3, the fact that our maximum surge response is associated with a storm with a radius to maximum wind speed of 65 km introduces another factor of about 4 into the estimated return periods shown in Table 3. To be a bit more precise, the factor is 555/(65 × 2) = 4.26; however, since we are only including this for the purposes of discussion, we will only use a factor of 4. Thus, a 10,000-year value would become approximately the 40,000-year value with this adjustment for the difference in the spatial window for the hurricane direct hits versus the spatial window length considered in those tables. Given this assumption, the 884-mb estimate for the 10,000-year central pressure in Table 3 might be considered to be representative of a 40,000-year event (in other words a factor of 4 times less likely) and the actual 10,000-year event for this smaller spatial window might be equivalent to a 2,500-year event in this table, estimated to be around 903 mb.

Table 2 Storms included in analysis of extremes for Florida West Coast
Full size table
Table 3 Estimated central pressures of hurricanes for selected AEPs and return periods in West Florida within a 555-km window
Full size table

In most applications, estimates in a table such as Table 3 would be used deterministically, and the size of the confidence bands would only be noted as an ancillary piece of information. In the context of such a deterministic interpretation, the probability that a storm would strike within ±65 km of a specific site, the estimate of the 1-in-10,000 central pressure is about 23 mb higher than our assumed value of 880 mb for the MPI and that this lower frequency-based estimate would be used in place of the deterministic upper limit. However, this implies that uncertainty has no impact on our risk estimates, which not only runs counter to intuition but will be shown here to lead to serious underestimation.

The form of the extremal distribution that generated the values in Table 3 was based on a best-fit GEV distribution. In the case of the west Florida hurricanes, the best-fit distribution was very close to a simple Gumbel distribution, so we will use the Gumbel distribution in this example. From our analysis, we obtain the following estimate of the cumulative distribution function (CDF) from Table 3, with ∆p in this case denoting the value of the pressure differential, related to the central pressure by the relationship ∆p = 1,013 − c p ,

$$ F^{\prime}(\Updelta p) = \exp \left\{ { - \exp \left[ { - \left( {\frac{{\Updelta p - a_{0} }}{{a_{1} }}} \right)} \right]} \right\} $$
(13a)

where a 0 = 31.7 and a 1 = 12.34 F′(∆p) is the best fit to the data not adjusted to an annual basis and the Poisson–Gumbel distribution for return period is:

$$ T_{r} = \frac{1}{{\lambda [1 - F^{\prime}(\Updelta p)]}} $$
(13b)

where λ is the annual frequency and T y is the return period in years, which yields for the annualized CDF, F(η):

$$ F(\Updelta p) = 1 - \frac{1}{{\lambda T_{r} }}. $$
(13c)

It should be noted that the annual frequency factor is simply the number of storms that occurred divided by four times the number of years where the additional factor of four in the denominator comes from the spatial adjustment mentioned previously.

If no uncertainty existed in our estimate of the CDF for pressure deviations, the encounter risk of a particular pressure deviation could be taken directly from Eq. 13c (which would essentially provide results equivalent to those in Table 3); however, the risk of encountering a particular magnitude of pressure differential, for a fixed expected value of annual frequency, should be understood to be non-zero for other values than the single deterministically estimated value; and the effect of possible values deviating from the deterministic estimate should be considered when forming a “risk-based” estimate of the exposure to a particular extreme value. A more realistic treatment of the risk associated with the return periods in Table 3 can be obtained by quantifying the effects related to their probabilistic variation around the deterministic value. The estimated standard deviation, typically used to construct control curves around the deterministic estimate, provides a good means of quantifying the spread of the probabilities around the deterministic estimate, and in this context, the probability of a pressure differential can be written in terms of an integral in two dimensions with a delta function to reduce it back to a single dimension (Eq. 6).

Since it is easier for most people to understand the context of return periods rather than AEPs, we shall first convert to a return period representation for our results before they are presented, using standard forms for this conversion,

$$ T_{r} (\Updelta p) = \frac{1}{1 - F(\Updelta p)} $$
(14)

with

$$ F(x) = \int\limits_{0}^{\infty } {\int\limits_{ - \infty }^{\infty } {p[\Updelta \hat{p}(T_{r} ) + \varepsilon } |\Updelta \hat{p}]} p(\Updelta \hat{p})p(\varepsilon )H(\Updelta \hat{p} + \varepsilon - \Updelta p)d\varepsilon d\hat{x}(T_{r} ). $$

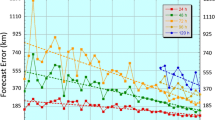
Figure 5 shows the results of this integration for three cases compared to the original deterministic estimate. Case 1 is the deterministic solution for the return period based on the best-fit Gumbel distribution. Case 2 is a test of the numerical algorithm generated by representing the probability of the deviations as a delta function (i.e., all of the probability exactly on the deterministic line), which was computed as a test case for the integration algorithm. As expected, this case exhibited no significant deviations from Case 1, so the Case 1 and Case 2 lines are identical. Case 3 shows the results using standard deviations equal to the estimated standard deviations divided by two, simply to provide an indication of how nonlinear the dependence is on the standard deviation in confidence band when compared to Case 4; and Case 4 shows the results for the standard deviations as fit to the data in Table 3. These results indicate that the very low probability tail of the distribution is markedly affected by standard deviations comparable to those obtained in the fit to the Florida west coast data on central pressures.

Fig. 5
figure 5

Comparison of “risk-based” return periods for central pressures without uncertainty considered (Cases 1 and 2) and with uncertainty considered (Cases 3 and 4) for the West Florida site using data from 1940–2009. Case 4 represents the actual estimate for the West Florida site

Full size image

A curious aspect of these results is the increasing deviation between the lines as the return period increases. Whereas the 10,000-year value for the distribution that includes the full uncertainty (Case 4) is slightly higher than the MPI value of 880 mb assumed here, the 40,000-year value has a much lower value (850 mb). This suggests that the role of uncertainty in very low probabilities is to act as a sort of filter for how long of a time period one can extrapolate before the uncertainty begins to become a dominant contributor to the distribution. Even at the 10,000-year value for the central pressure, the pressure differential has already been increased by about 20 % over its value with uncertainty neglected. Since values for maximum possible surges in many areas along the west Florida coast are around 10 ms, the impact of including this uncertainty would add about 2 ms to the design surge levels over the deterministically estimated values.

A second interesting aspect of the analyses of extreme surges in the New Orleans area is that most of these curves tend to fall into the Fisher-Tippett Type III category, which means that they tend toward an upper limit that can be estimated from the values of the GEV coefficients. On the one hand, this seems very natural, since we expect that most phenomena in nature are bounded by physically based upper limits. However, in the portion of such curves that begin to “flatten out” in terms of their rate of variation with respect to increasing return period, the role of uncertainty will play a very important role in assessing the actual hazards and associated risks. It should be noted that the ultimate limit of the Fisher-Tippett III GEV (or Weibull distribution) is very similar in this respect to the problem with selecting a single deterministic value for any upper limit, and if this limit is set without regard for the uncertainty inherent in such an estimate, which can produce substantial underestimates of the actual hazards and risks.

5 Conclusions

In this paper, it is shown that uncertainty manifests itself in different forms for different applications of design and planning for surge levels with different ranges of AEPs. However, in all cases, it seems that it is time to adopt methods that formally account for uncertainty, since the effects appear to be significant in the entire range of problems facing designers and planners in coastal areas today.

It is shown here that for typical design/planning applications with AEPs in the range of 1 × 10−2–5 × 10−2, typical design surge levels at sites in New Orleans would be underestimated by about 0.5–1.0 m if a deterministic estimate of surges were used, neglecting uncertainties inherent in modeling and sampling. Fortunately, recent re-design of the new hurricane risk reduction system in New Orleans, although not quantifying the effects of these uncertainties, recognized that such uncertainties were important and included substantial, subjective (larger than 1 m) estimates of their impact to compensate for them. However, new risk-based methods being used to investigate and quantify risks in these areas following the implementation of the new system currently neglect these uncertainties.

It is also shown here that oversimplification of an analysis, such as using a single river discharge level along the entire Mississippi River when performing surge simulations for design, cannot capture the actual variability within the river-surge system. Results obtained from such an analysis can vary both toward over-conservatism and under-conservatism, depending on the location of a point along the river and the storm producing the surges. An alternative analysis that incorporates river discharge, as was utilized in the re-design of the new hurricane risk reduction system in New Orleans along the mainline Mississippi River Levee (MRL) system, is introduced here and shown to yield significant differences, up to slightly over 1 m for the 1 × 10−2 AEP, in many locations along the river.

Finally, we performed an analysis of very low probability event in the AEP range 1 × 10−4–1 × 10−6, such as might be used to design/plan for either large flood protection systems or critical facilities in coastal areas. In this case, it is shown that the application of a single “design storm” related to a concept of Maximum Possible Intensity or other such upper-limit descriptor must consider the uncertainty associated with surge estimates for such a storm in order to adequately represent the actual risk for such a storm. Furthermore, the neglect of uncertainty in estimates of surges associated with very long return periods results in a substantial underestimate of the expected surges associated with such return periods. The potential magnitude of this effect along the west coast of Florida in the Gulf of Mexico is shown to be approximately 20 %, certainly a non-negligible effect.