A Fast Maximum Likelihood-Based Estimation of a Modal Model

Abstract

In this paper, the ML-MM estimator, a multivariable frequency-domain maximum likelihood estimator based on a modal model formulation, will be represented and improved in terms of the computational speed and the memory requirements. Basically, the design requirements to be met in the ML-MM estimator were to have accurate estimate for both of the modal parameters and their confidence limits and, meanwhile, having a clear stabilization chart which enables the user to easily select the physical modes within the selected frequency band. The ML-MM method estimates the modal parameters by directly identifying the modal model instead of identifying a rational fraction polynomial model. In the ML-MM estimator, the confidence bounds on the estimated modal parameters (i.e., frequency, damping ratios, mode shapes, etc.) are derived directly by inverting the so-called Fisher information matrix and without using many linearization formulas that are normally used when identifying rational fraction polynomial-based models. Another advantage of the ML-MM estimator lies in its potential to overcome the difficulties that the classical modal parameter estimation methods face when fitting an FRF matrix that consists of many (i.e., 4 or more) columns, i.e., in cases where many input excitation locations have to be used in the modal testing. For instance, the high damping level in acoustic modal analysis requires many excitation locations to get sufficient excitation of the modes. In this contribution, the improved ML-MM estimator will be validated and compared with some other classical modal parameter estimation methods using simulated datasets and real industrial applications.

15.1 Introduction

Over the last decades, a number of algorithms have been developed to estimate modal parameters from measured frequency or impulse response function data. A very popular implementation of the frequency-domain linear least squares estimator optimized for the modal parameter estimation is called Least Squares Complex Frequency-domain (LSCF) estimator [1]. The LSCF estimator uses a discrete-time common denominator transfer function parameterization. In [2], the LSCF estimator is extended to a poly-reference case (pLSCF). The pLSCF estimator uses a right matrix fraction description (RMFD) model. LSCF and pLSCF estimators were optimized both for the memory requirements and for the computation speed. The main advantages of those estimators are their speed and the very clear stabilization charts they yield even in the case of highly noise-contaminated frequency response functions (FRFs). Regardless of their very clear stabilization charts, these estimators have two main drawbacks. The first drawback is that the damping estimate is not always reliable where it decreases with increasing the noise level, and this situation becomes worse for the highly damped and weakly excited modes [3]. A second drawback is that the confidence bounds on the estimates are unavailable. Although these intervals can be constructed after the estimation as shown in [4, 5], these estimates are always higher than the maximum likelihood estimator (MLE). LSCF and pLSCF estimators are essentially deterministic curve fitting algorithms in which the estimation process is achieved without using information on the statistical distribution of the data. By taking knowledge about the noise on the measured data into account, the modal parameters can be derived using the so-called frequency-domain maximum likelihood estimator (MLE) with significant higher accuracy compared to the ones developed in the deterministic framework. MLE for linear time invariant systems was introduced in [6]. A multivariable frequency-domain maximum likelihood estimator was proposed in [1] to identify the modal parameters together with their confidence intervals where it was used to improve the estimates that are initially estimated by LSCF estimator. In [7], the poly-reference implementation for MLE was introduced to improve the starting values provided by pLSCF estimator. Both of the ML estimators introduced in [1] and [7] are based on a rational fraction polynomial model, in which the coefficients are identified. The modal parameters are then estimated from the identified coefficients in a second step. In these estimators, the uncertainties on the modal parameters are calculated from the uncertainties on the estimated polynomial coefficients by using some linearization formulas. These linearization formulas are straightforward when the relation between the modal parameter and the estimated coefficients is explicitly known but can be quite involved for the implicit case. Moreover, they may fail when the signal-to-noise ratio is not sufficiently large [8]. In [9, 10], a non-linear least squares (NLS) estimation method based on the modal model formulation is introduced. The Gauss-Newton method is used to solve the NLS problem and the Multivariate Mode Indicator Function (MMIF) is used to generate initial values for the modal parameters of the modal model.

Recently, a multivariable frequency-domain modal parameter estimator called ML-MM [11–13] has been introduced. The key challenges behind introducing the ML-MM estimator were to keep the benefit of the well-known Polymax estimator while giving other additional features. The benefit of the Polymax estimator that the ML-MM estimator keeps is the construction of a very clear stabilization diagram in a very fast way. The other additional features that ML-MM estimator adds are the highly accurate modal parameters it estimates together with their confidence bounds. This method belongs to the class of maximum likelihood-based estimation techniques. Taking into account the uncertainty on the measurements, the ML-MM estimator estimates the modal parameters together with their confidence bounds by directly identifying the modal model in a maximum likelihood sense. In the ML-MM method, the Gauss-Newton method together with Levenberg-Marquardt loop is used to solve a NLS problem. Using Levenberg-Marquardt loop during the iterations forces the ML-MM cost function to converge. Identifying directly the modal model instead of a rational fractional polynomial model gives the advantage of having the confidence bounds on the estimated modal parameters directly without using linearization formulas which have to be used to extend the uncertainty from the estimated polynomial coefficients to the estimated modal parameters in case of identifying a rational fractional polynomial model. Another advantage found of the ML-MM estimator lies in its potential to overcome the difficulties that the classical modal parameter estimation methods face when fitting an FRF matrix that consists of many (i.e., 4 or more) columns, i.e., in cases where many input excitation locations have to be used in the modal testing. For instance, the high damping level in acoustic modal analysis requires many excitation locations to get sufficient excitation of the modes [14]. In this contribution, the ML-MM method will be represented, including an algorithm variant that significantly speeds up the execution of the method. The fast implementation will be validated and compared to the basic implementation of the method using simulated examples and industrial applications cases.

15.2 Maximum Likelihood Estimation Based on the Modal Model (ML-MM)

15.2.1 The Basic Implementation of the ML-MM Estimator

In this section, the theoretical formulation of the ML-MM estimator will be introduced. Assuming the different frequency response functions (FRFs) to be uncorrelated the (negative) log-likelihood function reduces to [15, 16]

$$ {\mathrm{K}}_{ML-MM}\left(\theta \right)={\displaystyle \sum_{o=1}^{N_o}} \ {\displaystyle \sum_{k=1}^{N_f}}{E}_o\left(\theta, {\omega}_k\right){E}_o^H\left(\theta, {\omega}_k\right) $$

(15.1)

with N _f the number of the frequency lines, N _o the number of the measured responses (outputs), ()^H the complex conjugate transpose of a matrix, ω _k the circular frequency, θ the model parameters vector, and E _o (θ, ω _k ) the error equation corresponds to the o ^th output degree of freedom (DOF) as a row vector given as follows:

$$ {E}_o\left(\theta, {\omega}_k\right)=\left[\begin{array}{ccc} \frac{H_{o1}\left({\omega}_k\right) - {\hat{H}}_{o1}\left(\theta, {\omega}_k\right)}{\sqrt{var\left({H}_{o1}\left({\omega}_k\right)\right)}} & \cdots & \frac{H_{o{N}_i}\left({\omega}_k\right) - {\hat{H}}_{o{N}_i}\left(\theta, {\omega}_k\right)}{\sqrt{var\left({H}_{o{N}_i}\left({\omega}_k\right)\right)}} \end{array}\right]\ \in\ {\mathrm{\mathbb{C}}}^{1\times {N}_i} $$

(15.2)

with ${H}_o\left({\omega}_k\right)\ \in\ {\mathrm{\mathbb{C}}}^{1\times {\mathrm{N}}_{\mathrm{i}}}$ the measured FRFs, $v\mathrm{a}\mathrm{r}\left({H}_o\left({\omega}_k\right)\right)\in\ {\mathrm{\mathbb{R}}}^{1\times {\mathrm{N}}_{\mathrm{i}}}$ the variance of the measured FRFs, and ${\hat{H}}_o\left(\theta, {\omega}_k\right)\ \in\ {\mathrm{\mathbb{C}}}^{1\times {\mathrm{N}}_{\mathrm{i}}}$ the FRFs represented by the displacement-over-force modal model formulation written as follows:

$$ \hat{H}\left(\theta, {\omega}_k\right)={\displaystyle \sum_{r=1}^{N_m}}\left(\frac{\psi_r{L}_r}{s_k-{\lambda}_r}+\frac{\psi_r^{*}{L}_r^{*}}{s_k-{\lambda}_r^{*}}\right)+\frac{LR}{s_k^2}+UR $$

(15.3)

with $\hat{\mathrm{H}}\left(\theta, {\omega}_k\right)\in\ {\mathrm{\mathbb{C}}}^{N_o\times {N}_i}$ is the FRFs matrix with N _o outputs and N _i inputs, N _m is the number of the identified modes, ${\psi}_r\in\ {\mathrm{\mathbb{C}}}^{N_o\times 1}$ the r ^th mode shape, λ _r the r ^th pole, ${s}_k=j{\omega}_k$, ()* stands for the complex conjugate of a complex number, ${L}_r\in\ {\mathrm{\mathbb{C}}}^{1\times {N}_i}$ the r ^th participation factor, $LR\in\ {\mathrm{\mathbb{C}}}^{N_o\times {N}_i}$ and $UR\in\ {\mathrm{\mathbb{C}}}^{N_o\times {N}_i}$ the lower and upper residual terms. The model parameters vector $\theta ={\left[{\theta}_{\psi_o}\ {\theta}_{LU{R}_o\ }{\theta}_L\ {\theta}_{\lambda}\right]}^T$ is a column vector containing all the parameters of the modal model represented by Eq. 15.3. ${\theta}_{\psi_o}$ and ${\theta}_{LU{R}_o}$ are all the mode shapes elements, lower and upper residuals term elements correspond to output o. ${\theta}_{\psi_o}$, ${\theta}_{LU{R}_o}$, θ _L , and θ _λ are written as follows:

$$ \begin{aligned}[b]{\theta}_{\psi_o}&=\left[{\psi}_{o1}\ {\psi}_{o2}\dots ..{\psi}_{o{N}_m}\right],\kern0.5em {\theta}_{LU{R}_o}=\left[L{R}_{o1}\dots L{R}_{o{N}_i}\ U{R}_{o1}\dots .U{R}_{o{N}_i}\right],\\ {\theta}_L&=\left[{L}_1\ {L}_2\dots .{L}_{N_m}\right],\kern0.5em {\theta}_{\lambda }=\left[{\lambda}_1\ {\lambda}_2\dots .{\lambda}_{N_m}\right]\end{aligned} $$

(15.4)

The maximum likelihood estimates of θ are given by minimizing the ML-MM cost function presented by Eq. 15.1 using Gauss-Newton optimization algorithm together with Levenberg-Marquardt approach to ensure the convergence. The Gauss-Newton iterations are given by

• (a) solve $\left({J}_m^T{J}_m\right)\ \mathrm{v}\mathrm{e}\mathrm{c}\left({\delta}_m\right)=-{J}_m^T\ {E}_m \$ for vec(δ _m )

• (b) set ${\theta}_{m+1}={\theta}_m+{\delta}_m$

with

$$ {E}_m=\left[\begin{array}{c} vec\left({E}_1\right) \\ vec\left({E}_2\right) \\ \vdots \\ vec\left({E}_{N_o}\right) \end{array}\right]\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f{N}_o\times 1} $$

(15.5)

with vec(.) the column-stacking operator, ${J}_m=\frac{\partial E\left({\theta}_m\right)}{\partial {\theta}_m}\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f{N}_o\times 2{N}_m\left({N}_o+{N}_i\right)+4{N}_i{N}_o}$ is the Jacobian matrix at iteration m and $vec\left({\delta}_m\right)\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\left({N}_o+{N}_i\right)+4{N}_i{N}_o \times 1}$ are the perturbations on the parameters. To have a relatively fast and numerically stable implementation, the Jacobian matrix J _m is written in the following (well-structured sparse form):

$$ J=\left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {\Gamma}_1 & 0 & \dots & 0 & {\Phi}_1^L & {\Phi}_1^{\lambda} \\ 0 & {\Gamma}_2 & \dots & 0 & {\Phi}_2^L & {\Phi}_2^{\lambda} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & \dots & {\Gamma}_{N_o} & {\Phi}_{N_o}^L & {\Phi}_{N_o}^{\lambda} \end{array}\right] $$

(15.6)

with ${\Gamma}_o\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f\times 2\left({N}_m+2{N}_i\right)}$ the error derivatives with respect to the mode shapes and the residual terms for output o, ${\Phi}_o^L\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f\times 2{N}_m\left({N}_i-1\right)}$ is the error derivative with respect to the participation factors for output o and ${\Phi}_o^{\lambda }\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f\times 2{N}_m}$ is the error derivative with respect to the poles for output o. Taking into account the structure of that Jacobian matrix, the normal equation, $\left({J}_m^T{J}_m\right)\ \mathrm{v}\mathrm{e}\mathrm{c}\left({\delta}_m\right)=-{J}_m^T\ {E}_m$, can be written as follows:

$$ \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {R}_1 & 0 & \dots & 0 & {S}_1^L & {S}_1^{\lambda} \\ 0 & {R}_2 & \dots & \vdots & {S}_2^L & {S}_2^{\lambda} \\ \vdots & 0 & \ddots & 0 & \vdots & \vdots \\ 0 & \dots & 0 & {R}_{N_o} & {S}_{N_o}^L & {S}_{N_o}^{\lambda} \\ {S}_1^{L^H} & {S}_2^{L^H} & \dots & {S}_{N_o}^{L^H} & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^L & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{L\lambda} \\ {S}_1^{\lambda^H} & {S}_2^{\lambda^H} & \dots & {S}_{N_o}^{\lambda^H} & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{\lambda L} & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{\lambda} \end{array}\right]\;\left\lceil\begin{array}{c} \varDelta vec\left({\Psi}_1\right) \\ \varDelta vec\left({\Psi}_2\right) \\ \vdots \\ \varDelta vec\left({\Psi}_{N_o}\right) \\ \\ \varDelta vec(L) \\ \\ \\ \varDelta \lambda \\ \end{array}\right\rceil = -\left\lceil\begin{array}{c} {\Gamma}_1^Hvec\left({E}_1\right) \\ {\Gamma}_2^Hvec\left({E}_2\right) \\ \vdots \\ {\Gamma}_{N_o}^Hvec\left({E}_{N_o}\right) \\ - \\ {\displaystyle \sum_{o=1}^{N_o}}{\Phi}_{\mathrm{o}}^{{\mathrm{L}}^{\mathrm{H}}}vec\left({E}_{\mathrm{o}}\right) \\ {\displaystyle \sum_{\mathrm{o}=1}^{N_o}}{\Phi}_{\mathrm{o}}^{\uplambda^{\mathrm{H}}}vec\left({E}_{\mathrm{o}}\right) \end{array}\right\rceil $$

(15.7)

The sub-matrices in Eq. 15.7 are given as following:

$$ \begin{array}{l}{R}_o={\Gamma}_o^H{\Gamma}_o\kern0.5em \in\ {\mathrm{\mathbb{R}}}^{2\left({N}_m+2{N}_i\right)\times 2\left({N}_m+2{N}_i\right)}\kern1.5em {S}_o^L={\Gamma}_o^H{\Phi}_o^L\kern0.5em \in\ {\mathrm{\mathbb{R}}}^{2\left({N}_m+2{N}_i\right)\times 2{N}_m\left({N}_i-1\right)}\kern1em {S}_o^{\lambda }={\Gamma}_o^H{\Phi}_o^{\lambda }\ \in\ {\mathrm{\mathbb{R}}}^{2\left({N}_m+2{N}_i\right)\times 2{N}_m}\\ {T}_o^L={\Phi}_o^{L^H}{\Phi}_o^L\kern0.5em \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\left({N}_i-1\right)\times 2{N}_m\left({N}_i-1\right)}\kern1em {T}_o^{\lambda }={\Phi}_o^{\lambda^H}{\Phi}_o^{\lambda}\kern0.5em \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 2{N}_m}\kern5.5em {T}_o^{L\lambda }={\Phi}_o^{L^H}{\Phi}_o^{\lambda }\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\left({N}_i-1\right)\times 2{N}_m}\\ {T}_o^{\lambda L}={\Phi}_o^{\lambda^H}{\Phi}_o^L\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 2{N}_m\left({N}_i-1\right)}\end{array} $$

(15.8)

The major gain in the calculation time comes from the use of the structure of the normal equations. Using some elimination and substitution procedures yields to

$$ \Delta vec\left({\Psi}_o\right)=-{R}_o^{-1}\kern0.5em \left({\Gamma}_o^Hvec\left({E}_o\right)+{S}_o^L\ \Delta vec(L)+{S}_o^{\lambda }\ \Delta \lambda \right) $$

(15.9)

$$ \begin{array}{c} \left\lceil\Delta \mathrm{vec}(L)\right\rceil\\ \Delta \lambda \end{array}={M}^{-1}\ D $$

(15.10)

$$ M=\left[\begin{array}{cc} {M}_1 & {M}_2 \\ {M}_3 & {M}_4 \end{array}\right] = \left[\begin{array}{cc} {\displaystyle \sum_{o=1}^{N_o}}{T}_o^L-{S}_o^{L^H}{R}_o^{-1}{S}_o^L & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{L\lambda }-{S}_o^{L^H}{R}_o^{-1}{S}_o^{\lambda} \\ {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{\lambda L}-{S}_o^{\lambda^H}{R}_o^{-1}{S}_o^L & {\displaystyle \sum_{o=1}^{N_o}}{T}_o^{\lambda }-{S}_o^{\lambda^H}{R}_o^{-1}{S}_o^{\lambda} \end{array}\right]\ \in \kern0.5em {\mathrm{\mathbb{R}}}^{2{N}_m{N}_i\times 2{N}_m{N}_i} $$

(15.11)

$$ D=\left[\begin{array}{c} {\displaystyle \sum_{o=1}^{N_o}}\left({S}_o^{L^H}{R}_o^{-1}{\Gamma}_o^H-{\Phi}_o^{L^H}\right){E}_o \\ {\displaystyle \sum_{o=1}^{N_o}}\left({S}_o^{\lambda^H}{R}_o^{-1}{\Gamma}_o^H-{\Phi}_o^{\lambda^H}\right){E}_o \end{array}\right]\kern0.75em \in \kern0.75em {\mathrm{\mathbb{R}}}^{2{N}_m{N}_i\times 1} $$

(15.12)

Solving Eq. 15.10 leads to the update of the participation factors elements and the poles, while the update of the mode shapes and residual terms elements are obtained by substitution of Eq. 15.10 into Eq. 15.9. In this way, the direct inversion of the full matrix (J ^T _m J _m ) can be avoided leading to significant reduction in the calculation time. To derive the uncertainty (confidence) bounds of the estimated modal parameters, the approximation given by [6] can be used as follows:

$$ COV\left(\psi, LR,UR,L,\lambda \right)\approx {\left[{J}^TJ\right]}^{-1} $$

(15.13)

J is the Jacobian matrix evaluated in the last iteration step of the Gauss-Newton algorithm. Taking into account the structure of the Jacobian matrix and by using the matrix inversion lemma [17], the uncertainties on the poles and the participation factors, can be derived as follows:

$$ COV\left(L,\lambda \right)={M}^{-1} $$

(15.14)

where M is given by Eq. 15.11. The uncertainty bounds of the estimated mode shapes and lower and upper residual terms can be derived as follows:

$$ \begin{aligned}[b]\mathrm{C}\mathrm{O}\mathrm{V}\left({\psi}_o,L{R}_o,U{R}_o\right)&={R}_o^{-1}+{\beta}_o\\ {\beta}_o&={A}_o{S}_o^{L^H}{R}_o^{-1}+{G}_o{S}_o^{\lambda^H}{R}_o^{-1}\\ {A}_o&= {R}_o^{-1}\left({S}_o^L{\left[{M}_1-{M}_2{M}_4^{-1}{M}_3\right]}^{-1}+{S}_o^{\lambda}\left(-{\left[{M}_4-{M}_3{M}_1^{-1}{M}_2\right]}^{-1}{M}_3{M}_1^{-1}\right)\ \right)\\ {G}_o&={R}_o^{-1}\left({S}_o^L\left(-{M}_1^{-1}{M}_2{\left[{M}_4-{M}_3{M}_1^{-1}{M}_2\right]}^{-1}\right)+{S}_o^{\lambda }{\left[{M}_4-{M}_3{M}_1^{-1}{M}_2\right]}^{-1}\ \right)\end{aligned} $$

(15.15)

Since the presented ML-MM estimator is basically a non-linear optimization algorithm and thus iterative, it requires good starting values for all the entire modal parameters of the modal model (see Eq. 15.3). These starting values of all the modal parameters are obtained by applying the well-known Polymax estimator to the measured FRFs. The Polymax estimator is selected since it provides a very clear stabilization chart in a fast way. This will help the user to select the really physical vibration modes in the selected frequency band which in turns leads to obtain good staring values for all the modal parameters to start the iterative ML-MM estimator. Figure 15.1 shows a schematic description of the basic ML-MM estimator.

Fig. 15.1

Schematic representation of the basic ML-MM estimator

15.2.2 A Fast Implementation of the ML-MM Estimator

In this section, an alternative implementation of the ML-MM estimator will be discussed. The aim of this alternative implementation is to speed up the implementation of the algorithm. In Sect. 15.2.1, the basic implementation, in which all the modal parameters (i.e., mode shapes, participation factors, poles, upper and lower residual terms) of the modal model are simultaneously updated at each iteration of the Gauss-Newton optimization, is introduced. In Eq. 15.3, when the poles λ _r and the participation factors L _r are given, it is clear that the mode shapes ψ _r and the lower and upper residuals (LR, UR) can be calculated easily in a linear least squares sense. This can be done by writing Eq. 15.3 for all the values of the frequency axis of the FRF data, and basically the unknown parameters (i.e., ψ, LR, UR) are then found as the least-squares solution of these equations. This approach is basically what so-called the LSFD estimator [18, 19]. The size of the mode shapes vector and the lower and upper residual matrices is mainly dependent on the number of outputs N _o , and in modal testing the number of outputs (responses) N _o is normally much higher than the number of inputs (excitation points) N _i . So, one idea to significantly decrease the computational time of the ML-MM estimator is to exclude the mode shapes and the lower and upper residuals from the updated parameters vector $\theta ={\left[{\theta}_{\psi }\ {\theta}_{LUR\ }{\theta}_L\ {\theta}_{\lambda}\right]}^T$. This can be done as follows (see Fig. 15.2):

Fig. 15.2

Schematic representation of the fast ML-MM estimator

• At each iteration of the Gauss-Newton algorithm

  • 1. Only the participation factors θ _L and the poles θ _λ are updated

  • 2. The mode shapes and the lower and the upper residuals are calculated in linear least-squares sense using the LSFD estimator.

This will lead to huge reduction in the number of columns of the Jacobian matrix, hence the size of the normal equations matrix. Now, the Jacobian matrix ${J}_m=\partial E{\theta}_{{\left(L,\lambda \right)}_m}/\partial {\theta}_{{\left(L,\lambda \right)}_m}\in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f{N}_o\times 2{N}_m\left({N}_i+1\right)}$ is the derivative of the equation error with respect to the participation factors and the poles. It can be seen that the number of the columns of the Jacobian matrix has been reduced to $2{N}_m\left({N}_i+1\right)$ columns compared to the previous one which has $2{N}_m\left({N}_o-1\right)+4{N}_i{N}_o$ columns. The new Jacobian matrix is given as:

$$ J=\left[\begin{array}{ccccc} {\Gamma}_{L1} & 0 & \dots & 0 & {\Phi}_{L1}^{\lambda} \\ 0 & {\Gamma}_{L2} & \dots & 0 & {\Phi}_{L2}^{\lambda} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & {\Gamma}_{L{N}_i} & {\Phi}_{L{N}_i}^{\lambda} \end{array}\right]\kern0.5em \in\ {\mathrm{\mathbb{R}}}^{2{N}_i{N}_f{N}_o\times 2{N}_m\left({N}_i+1\right)} $$

(15.16)

with ${\Gamma}_{Li}\ \in \kern0.5em {\mathrm{\mathbb{R}}}^{2{N}_o{N}_f\times 2{N}_m}$ the equation error derivatives with respect to the participation factors of all the identified modes for the input location i where $i=1,2,..{N}_i$ and ${\Phi}_{Li}^{\lambda }\ \in \kern0.75em {\mathrm{\mathbb{R}}}^{2{N}_o{N}_f\times 2{N}_m}$ is the equation error derivative with respect to the poles of all the identified modes for input i. Taking into account the structure of that Jacobian matrix, the reduced normal equations, $\left({J}_m^T{J}_m\right)\ vec\left({\delta}_m\right)=-{J}_m^T\kern0.5em {E}_m$, can be written as follows:

$$ \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {R}_{L1} & 0 & \dots & 0 & {S}_1^{L\lambda} \\ 0 & {R}_{L2} & \dots & 0 & {S}_2^{L\lambda} \\ 0 & 0 & \ddots & \vdots & \vdots \\ \vdots & \vdots & \ddots & {R}_{L{N}_i} & {S}_{N_i}^{L\lambda} \\ {S_1^{L\lambda}}^H & {S_2^{L\lambda}}^H & \dots & {S_{N_i}^{L\lambda}}^H & {\displaystyle \sum_{i=1}^{N_i}}{T}_{Li}^{\lambda} \end{array}\right] \quad \left\lceil\begin{array}{c} \varDelta {L}_1 \\ \varDelta {L}_2 \\ \vdots \\ \varDelta {L}_{N_i} \\ \varDelta \lambda \end{array}\right\rceil =- \left\lceil\begin{array}{c} {\Gamma}_{L1}^Hvec\left({E}_1\right) \\ {\Gamma}_{L2}^Hvec\left({E}_2\right) \\ \vdots \\ {\Gamma}_{L{N}_i}^Hvec\left({E}_{N_i}\right) \\ --- \\ {\displaystyle \sum_{i=1}^{N_i}}{\Phi}_{Li}^{\lambda^H}vec\left({E}_{\mathrm{i}}\right) \\ \end{array}\right\rceil $$

(15.17)

with ${R}_{Li}={\Gamma_{Li}}^H{\Gamma}_{Li}\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 2{N}_m}$, ${S}_i^{L\lambda }={\Gamma_{Li}}^H{\Phi}_{Li}^{\lambda }\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 2{N}_m}$, ${T}_{Li}^{\lambda }={\Phi_{Li}^{\lambda}}^H{\Phi}_{Li}^{\lambda }\ \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 2{N}_m}$, $vec\left({E}_i\right)\in\ {\mathrm{\mathbb{R}}}^{2{N}_f{N}_o\times 1}$ the error vector corresponds to input i and all the outputs at all the frequency lines, $\Delta {L}_i\in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 1}$ a vector contains all the perturbations on the real and imaginary parts of the participation factors correspond to input i and all the identified modes, and $\Delta \lambda \in\ {\mathrm{\mathbb{R}}}^{2{N}_m\times 1}$ a vector contains the perturbations on the real and imaginary parts of the identified poles. Using some elimination and substitution procedures yields the perturbations on the poles and the participation factors respectively as follows:

$$ \Delta \lambda ={\left[{\displaystyle \sum_{i=1}^{N_i}}{T}_{Li}^{\lambda }-{S_i^{L\lambda}}^H{\left({R}_{Li}\right)}^{-1}{S}_i^{L\lambda}\right]}^{-1}\left[{\displaystyle \sum_{i=1}^{N_i}}{S_i^{L\lambda}}^H{\left({R}_{Li}\right)}^{-1}{\Gamma}_{Li}^Hvec\left({E}_i\right)-{\Phi}_{Li}^{\lambda^H}vec\left({E}_{\mathrm{i}}\right)\right] $$

(15.18)

$$ \Delta {L}_i=-{\left({R}_{Li}\right)}^{-1}\left[{\Gamma}_{Li}^Hvec\left({E}_i\right)+{S}_i^{L\lambda}\Delta \lambda \right] $$

(15.19)

Once these perturbations are calculated, the poles and the participation factors are updated to be used for a new iteration. Before moving to the new iteration, the updated poles and participation factors will be used to calculate the mode shapes and the lower and upper residuals in a linear least-squares sense using the LSFD estimator. Since in this fast implementation of the ML-MM estimator the mode shapes and the residual terms are assumed to be certain parameters (i.e., they are assumed to have no errors hence they are not updated during the Gauss-Newton iterations), the uncertainty bounds on those parameters cannot be retrieved. So, only the uncertainty bounds on the poles and the participation factors will be retrieved. These uncertainty bounds on the poles and the participation factors can be calculated using Eq. 15.13 substituting the Jacobian matrix with the one represented in Eq. 15.16. Taking into account the structure of the Jacobian matrix and by using the matrix inversion lemma, the uncertainties (variances) on the poles and participation factors can be derived respectively as follows:

$$ cov\left(\lambda \right)={\left[{\displaystyle \sum_{i=1}^{N_i}}{T}_{Li}^{\lambda }-{S_i^{L\lambda}}^H{\left({R}_{Li}\right)}^{-1}{S}_i^{L\lambda}\right]}^{-1} $$

(15.20)

$$ cov\left({L}_i\right)={\left({R}_{Li}\right)}^{-1}{S}_i^{L\lambda }cov\left(\lambda \right){S_i^{L\lambda}}^H{\left({R}_{Li}\right)}^{-1}+{\left({R}_{Li}\right)}^{-1} $$

(15.21)

15.3 Validations and Discussion

In this section, both implementations of the ML-MM estimator (i.e., basic and fast ones) will be validated and compared to some other estimators like the pLSCF (Polymax), polyreference Least-squares Complex Exponential (pLSCE) estimator, and the Maximum Likelihood common denominator polynomial model –based (ML-CDM) estimator. Polymax [2, 20] is a linear-least squares frequency domain estimator, which fits a right matrix fraction description (RMFD) polynomial model to the measured FRFs. Then, the poles and the participation factors are derived from the optimized denominator coefficients, while the mode shapes and the lower and upper residuals are estimated in a second step using the LSFD estimator [15.18]. The pLSCE estimator [21–23] is a linear least-squares time-domain estimator, which uses the impulse response function to retrieve the poles and the participation factors and then the mode shapes and the residual terms can be estimated in a second step by fitting the modal model equation (see Eq. 15.3) to the measured FRFs using the pre-estimated poles and the participation factors. The ML-CDM estimator [1] is a frequency-domain estimator fits a common-denominator polynomial model to the measured FRFs in a non-linear least squares sense using Gauss-Newton algorithm. The poles are retrieved as the roots of the denominator coefficients, and the mode shapes together with the participation factors are obtained by decomposing the residues matrices to rank-one matrices using singular value decomposition (SVD). These residues matrices are estimated by fitting the pole-residue model to the measured FRFs in a linear least-squares sense. Both ML-CDM and ML-MM estimator are maximum likelihood estimators. But the model which is being used to fit the measured FRFs is different. ML-MM, as it is mentioned before, fits directly the modal model to the measured FRFs, while ML-CDM fits a common-denominator polynomial model. Since both ML-MM and ML-CDM are maximum likelihood estimators, both of them can deliver the uncertainty bounds on the estimated modal parameters as long as the equation error is weighted by the variance of the measured FRFs. So, the comparison between the ML-MM and the ML-CDM will be extended to include also the predicted uncertainty while for the Polymax and the pLSCE estimators the comparison will be done in terms of the bias error and the root mean squares error (RMSE). So, in the following sections these estimators will be compared to each other using simulated FRFs and some real industrial applications.

15.3.1 Seven DOF System with Mixed Noise [White and Relative Noise]

In this section, simulated FRFs of a 7-DOF system will be used to validate and compare the proposed ML-MM estimator with the other estimators (i.e., Polymax, pLSCE, and ML-CDM). The first column of the FRF matrix will be used (i.e., ${N}_o=7,\ {N}_i=1$). The exact FRFs are contaminated with a combination of uncorrelated white and relative noise. At each frequency line, the noise variance is taken as a summation of constant variance, which corresponds to the white noise component, and a relative variance that corresponds to the relative noise component. Figure 15.3 shows the driving point FRF together with the noise standard deviation. To perform Monte-Carlo simulations, 500 disturbed data sets have been generated.

Fig. 15.3

The noisy FRFs (gray dots), the exact FRFs (thin-black line), and the FRFs standard deviation (thick-gray line) of the 7-DOF system

Figure 15.4 shows the absolute value of the bias error on the estimated frequency and damping estimates. The order of the different methods in the figure legend corresponds to the order of the bars in the plot. From Fig. 15.4, it can be seen that the ML-MM estimator improves the frequency and damping estimates that are initially estimated by the pLSCF (PolyMAX) estimator. It can be seen that the ML-MM gives the lowest bias error for, almost, all the identified modes compared with the other estimators, and this is for the frequency and the damping estimates.

Fig. 15.4

The absolute value of the bias error on the estimated resonance frequencies (top) and the estimated damping ratios (bottom) (The order of the different methods in the figure legend corresponds to the order of the bars in the plot.)

In terms of the RMSE of the frequency and damping estimates, Fig. 15.5 (The order of the different methods in the figure legend corresponds to the order of the bars in the plot.) shows that the performances of both ML-CDM and ML-MM estimators are very comparable. However, one can note that the ML-MM estimator gives a lower RMSE of the frequency and damping for the last two modes (i.e., 6th and 7th modes). These modes are not well excited compared to the other modes (examine Fig. 15.3, there are two peaks above 35 Hz correspond to the 6th and 7th modes). From Figs. 15.4 and 15.5, we can sum up that the ML-MM estimator gives estimates with lower bias error and lower variance in comparison with the other estimators under test.

Fig. 15.5

The RMSE on the estimated resonance frequencies (top) and the estimated damping ratios (bottom) (The order of the different methods in the figure legend corresponds to the order of the bars in the plot.)

Concerning the predicted uncertainty bounds of the estimated modal parameters, Fig. 15.6 compares the predicted standard deviation (std) (see Eq. 15.14 or 15.20 for the ML-MM estimator) to the sample standard deviation on the resonance frequency and the damping ratio of the 1st mode. In this figure, the predicted std is presented by the dots while the sample std is presented by the gray solid line. From this figure, one can see that the ML-CDM and the ML-MM estimators show a good agreement between the predicted and the sample (true) standard deviation on both the frequency and damping estimate. Although both ML-MM and ML-CDM show good agreement between the predicted and the sample std, the ML-MM estimator predicts the uncertainty bounds with a lower variability in comparison with the ML-CDM estimator (i.e., the black dots for the ML-MM are more clustered together in comparison with the ones for the ML-CDM).

Fig. 15.6

Monte-Carlo simulations results of the 7-DOF system: comparison between the predicted (black dots) and sample (gray solid line) standard deviation on the frequency (left) and damping ratio (right) of the first mode: ML-CDM (top), and ML-MM (bottom)

In fact, this higher variability on the uncertainty prediction which the ML-CDM shows comes from the fact that it uses some complex linearization formulas to propagate the uncertainty from the estimated polynomial coefficients to the modal parameters (i.e., from the denominator coefficients to the frequency and damping estimates), which is not the case for the ML-MM estimator. The ML-MM estimator estimates the uncertainty on the modal parameters directly without the need to use these linearization formulas since it fits directly the modal model (not polynomial model) to the measured data. This is an advantage of the ML-MM estimator where the uncertainty on all the model parameters can be estimated in a direct and simple way compared with the polynomials-based estimators like the ML-CDM estimator. For the ML-MM estimator, the results shown in Fig. 15.6-bottom confirm the correctness of Eq. 15.14 to predict the uncertainty bounds on the poles, hence the frequency and damping estimates. Equation 15.15 shows that the ML-MM estimator can deliver the uncertainty bounds on the estimated mode shapes as well. To check the validity of this prediction, the predicted std and the sample std over the 500 Monte-Carlo runs are compared to each other for the estimated 7^th mode shape elements, and these results are shown in Fig. 15.7. The relative predicted standard deviation presented with black dots is not in full agreement with the relative sample standard deviation presented by a gray solid line, but they are still quit close to each other. Although it can be seen that the relative predicted standard deviation is slightly underestimated, by examining the relative bias error on the mode shapes it was found that the relative bias error of the mode shape elements is within the predicted 68 % ($\pm \sigma$) confidence bound, which can be considered as an indicator for the correctness of this predicted confidence bounds. All the ML-MM’s results shown previously have been obtained using the basic (slow) implementation of the method. To validate the fast implementation introduced in section 2.2, the fast ML-MM will be compared to the basic (slow) implementation in terms of the computational speed, the bias error, and the predicted confidence bounds on the estimated resonance frequencies and damping ratios.

Fig. 15.7

Monte-Carlo simulations results of the 7-DOF system: comparison between the relative predicted (black dots) and relative sample (gray solid line) standard deviation of the seventh mode shape elements obtained by the ML-MM estimator

Figure 15.8 shows the cost function convergence and the computational time taken to reach convergence for both of the basic ML-MM and the fast ML-MM estimators. It can be seen that both implementations converge to the same value. Although both of them converge to almost the same value, the fast ML-MM is indeed faster since it takes only 0.98 s while the basic ML-MM takes 1.19 s. The small difference in the computational time is due to the fact that the system under test is very simple (${N}_o=7,\ {N}_i=1,{N}_m=7$). Concerning the accuracy of the estimated parameters, Table 15.1 shows that the fast implementation of the ML-MM estimator leads to almost the same estimates’ accuracy as the ones obtained by the basic implementation where it can be seen that the bias error on the resonance frequency and damping ratios of the basic ML-MM and the fast ML-MM are very comparable. Figure 15.9 shows that the fast implementation gives a good prediction for the uncertainty on the resonance frequencies and the damping ratios. From this figure, one can see that there is a good agreement between the predicted standard deviation (black dots) and the sample standard deviation (solid line) and this is for the frequency and the damping estimate. Table 15.2 shows the mean value (over 500 Monte-Carlo runs) of the predicted standard deviation on the frequency and the damping estimates for both implementations of the ML-MM estimators (i.e., the basic and the fast implementations). In general, one can see that the fast ML-MM delivers estimates with a bit lower uncertainty bounds compared to the basic ML-MM. This agrees with the fact that adding additional parameters to the model increases the attainable uncertainty on the estimated model parameters [24]. In the basic ML-MM implementation, adding the mode shapes and the lower and upper residuals as uncertain parameters increases the uncertainty bounds on all the modal model’s parameters. This explains why the basic ML-MM leads to estimates with higher uncertainty bounds compared to the fast ML-MM.

Table 15.1 Fast ML-MM versus basic ML-MM in terms of bias error

Fig. 15.8

Cost function convergence and the computational time: Basic ML-MM (left) and Fast ML-MM (right)

Fig. 15.9

Monte-Carlo simulations results of the 7-DOF system: comparison between the predicted (black dots) and sample (gray solid line) standard deviation on the frequency (left) and damping ratio (right) of the first mode obtained from the fast implementation of the ML-MM estimator

Table 15.2 Fast ML-MM versus basic ML-MM in terms of predicted uncertainty bounds

15.3.2 Flight Flutter Testing

In this section, the proposed ML-MM estimator will be validated and compared with some other estimators (i.e., the pLSCF (Polymax), the pLSCE and the ML-CDM estimators) using experimentally measured FRFs that were measured during a business jet in-flight testing. These types of FRFs are known to be highly contaminated by noise. During this test, both the wing tips of the aircraft are excited during the flight with a sine sweep excitation through the frequency range of interest by using rotating fans. The forces are measured by strain gauges. Next to these measurable forces, turbulences are also exciting the plane resulting in rather noisy FRFs. Figure 15.10 shows some typical coherence functions and the corresponding FRFs, which clearly show the noisy character of the data. During the flight, the accelerations were measured at nine locations while both the wing tips were excited (two inputs).

Fig. 15.10

Typical multiple coherence functions (right) and typical FRFs (left) for the tested business jet (the frequency axis is hidden for confidentiality)

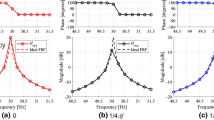
The different estimators (i.e., Polymax, pLSCE, ML-CDM, basic ML-MM and fast ML-MM) are applied to the data to extract the modal parameters of the modes lie within the selected band. Figure 15.11 shows the stabilization charts constructed by the Polymax and the time-domain pLSCE estimators. It can be seen that Polymax gives extremely clear stabilization chart in comparison to the pLSCE. The very clear stabilization char that Polymax yields was the main reason behind selecting Polymax as starting values generator for the ML-MM estimator (see Figs. 15.1 and 15.2). The cost function convergence and the computational time for both the basic ML-MM and the fast ML-MM estimators are shown in Fig. 15.12. One can see that both of them converge to almost the same value, while the computational time of the fast ML-MM is less than the one of the basic ML-MM. A comparison between the different estimators was made on basis of the estimated modal model. An easy but very popular way to check the quality of the estimated modal model is to look to the quality of the fit between the measured FRFs and the modal model synthesized FRFs. Figure 15.13 shows a comparison between all the estimators in terms of the quality of the fit between one of the measured FRFs and the corresponding synthesized one. It can be seen that the ML-CDM estimator resulted in perfect fit of the pole-residues model (i.e., ML-CDM (Residue matrices)). Nevertheless this common denominator based algorithm loses the fit quality by converting the pole-residue model to the modal model to obtain the mode shapes and the participation factors by reducing the residues to a rank-one matrix using singular value decomposition (SVD) (i.e., ML-CDM (SVD on residue matrices)). This degradation on the fit quality is clear in Fig. 15.13. It can be seen from Fig. 15.13 that both ML-MM estimators (i.e., basic and fast) outperform the linear least-squares estimators (pLSCF and pLSCE), and the ML-CDM (SVD on residue matrices) while keeping the residues as rank-one matrices (i.e., multiplication of the mode shape column vector and the participation factors row vector, see Eq. 15.3).

Fig. 15.11

The stabilization chart constructed for the business jet data set: Polymax (left) and pLSCE (right)

Fig. 15.12

The convergence of the ML-MM cost function during the iterations and the computational time taken for 30 iterations: basic ML-MM (left) and fast ML-MM (right)

Fig. 15.13

A comparison between the measured (thin-gray line) and the synthesized (thick-black line) FRF (the shown FRF measured from a sensor at the tail of the aircraft)

The MAC between the mode shapes of the basic and the fast ML-MM estimators is shown in Fig. 15.14. It shows that there is a good agreement between the mode shapes estimated by each technique. Some of the mode shapes estimated by the fast ML-MM estimater are shown in Fig. 15.15. Since the variances of the measured FRFs were available in this data set, this enabled us to get, from the ML-MM estimator, the uncertainty bounds on the estimated resonance frequencies and damping ratios. The uncertainty bounds on the resonance frequencies and the damping ratios together with their uncertainty bounds estimated by both the basic and the fast ML-MM are shown in Table 15.3. Figure 15.16 shows the sum of the measured FRFs together with the location of the selected modes, and the sum of the synthesized FRFs. The first remark we can draw from Table 15.3 is that the estimates of the fast ML-MM are estimated with lower uncertainty bounds compared with the ones estimated by the basic ML-MM. As it was noticed and discussed in the simulation part (Sect. 15.3.1), having lower uncertainty bounds using the fast ML-MM agrees with the fact that decreasing the number of the uncertain parameters in the model decreases the uncertainty bounds on those parameters [24]. Secondly, it can be seen that modes 1,3 and 9, which are very dominant and have large contribution to the FRFs sum compared to the other modes, are estimated with lower uncertainty bounds either by the basic ML-MM or the fast ML-MM, and this is in particular for the frequency estimates. However, the basic and the fast ML-MM give the damping estimate of the first mode with higher uncertainty bounds compared to some other modes. The reason behind that could be at the first peak there are two very close modes and normally the estimation of the very close modes is accompanied with high level of uncertainty. Moreover, this mode is estimated with a relatively high level of damping. Also, it can be noticed that modes 2, 7, and 10 are estimated with a relatively higher uncertainty bounds which agrees with the fact that those modes do not have a large contribution to the FRF sum indicating that they are weakly excited/observed.

Fig. 15.14

MAC between the basic ML-MM and the fast ML-MM

Fig. 15.15

Some mode shapes estimated by the Fast ML-MM estimator (from 1 to 8: increasing the natural frequency)

Table 15.3 Estimated resonance frequencies and damping ratios together with their predicted standard deviation

Fig. 15.16

Sum of the FRFs with the Fast ML-MM fit

15.3.3 Fully Trimmed Car

In automotive engineering, experimental modal analysis (EMA) is considered as a “commodity” tool and accurate models are needed for modelling and finite element updating. A typical example of a challenging modal analysis application is the structural analysis of a trimmed car body. In this example, data from a fully trimmed car was used. The accelerations of the fully equipped car were measured at 154 locations, while four shakers were simultaneously exciting the structure. This gives a total of 616 FRFs. More details about this test setup can be found in [25]. The different estimators under test are applied to the measured FRFs to identify the modes within the frequency band [3.30 Hz]. In Fig. 15.17, the stabilization charts constructed by the Polymax and the time-domain pLSCE estimators are shown. Indeed, as we saw before in the in-flight data set Polymax outperforms the time-domain pLSCE in terms of the clarity of the stabilization chart. In Table 15.4, Figs. 15.18 and 15.19 a comparison between the different estimators is presented in terms of the quality of the fit between the measured (dotted-gray line) and the synthesized (solid-black line) FRFs. The linear least-squares estimators (i.e., pLSCF and pLSCE) give a comparable mean fitting error and correlation. For the common denominator polynomial –based maximum likelihood estimator (ML-CDM), the quality of the fitting is dramatically degraded by reducing the residue matrices to a rank-one matrix to get the mode shapes and the participation factors. Comparing the degradation of the fitting quality of the ML-CDM in this case to the case of the previous example (i.e., inflight data set in Sect. 15.3.2), it seems that the degradation of the fitting quality by transferring common denominator model into modal model tends to be more problematic for the highly-damped case, e.g., fully trimmed car.

Fig. 15.17

Stabilization chart constructed by Polymax (top) and pLSCE (bottom) for measurements on a fully trimmed car

Fig. 15.18

Comparison between the modal models obtained by different estimators under test for one FRF of the fully trimmed car data set (Measured FRF: dotted gray line Synthesized FRF: solid black line)

Fig. 15.19

Comparison between the modal models obtained by different estimators under test for one FRF of the fully trimmed car data set (Measured FRF: dotted gray line Synthesized FRF: solid black line)

Table 15.4 Mean fitting error and correlation between the synthesized and measured FRFs for the fully trimmed car

The basic ML-MM and the fast ML-MM give very comparable results, and they outperform the other estimators in terms of the quality of the fit between the measured and the synthesized FRFs. Figure 15.20 shows the cost function convergence and the computational time for both the basic and the fast ML-MM estimators. With this relatively huge data set (${N}_i=4,\ {N}_o=154$), one can see clearly the difference in the time taken by each implementation. The time taken by the fast ML-MM is almost 1/4 the time taken by the basic ML-MM. Figure 15.21 shows that there is a good agreement between the mode shapes estimated by both the basic ML-MM and the fast ML-MM. The resonance frequencies and damping ratios of the estimated modes are shown in Table 15.5 while some typical mode shapes estimated by the fast ML-MM estimator are shown in Fig. 15.22.

Fig. 15.20

Cost function convergence and the computational time for the basic ML-MM (left) and the fast ML-MM (right)

Fig. 15.21

MAC between the mode shapes estimated by the basic ML-MM and the fast ML-MM

Table 15.5 The basic ML-MM and the fast ML-MM modal results for the fully trimmed car

Fig. 15.22

Some typical mode shapes estimated by the fast ML-MM estimator applied to the fully trimmed car data set

15.3.4 Acoustic Modal Analysis of a Car Cavity

This experimental case concerns the cabin characterization of fully trimmed sedan car (see Fig. 15.23) using acoustic modal analysis. The acoustic modal analysis of a car cavity (cabin) is, in general, accompanied by using many excitation sources (up to 12 sources in some cases) and the presence of highly-damped complex modes [10, 14]. Due to the high level of the modal damping in such application, the many excitation locations are required to get sufficient excitation of the modes across the entire cavity. It has been observed that the classical modal parameter estimation methods have some difficulties in fitting an FRF matrix that consists of many (i.e., 4 or more) columns, i.e., in cases where many input excitation locations have been used in the experiment [10, 14].

Fig. 15.23

Picture of Sedan car under test (left) and its CAE cavity model (right)

Multiple inputs multiple output (MIMO) test were carried out inside the cavity of the Sedan car where 34 microphones located both on a roving array with spacing equal to around 20 cm and near to boundary surfaces captured the responses simultaneously. A total of 18 runs were performed to measure the pressure distribution over the entire cavity (both cabin and trunk) resulting in 612 response locations (${N}_o=612$). For each run, up to 12 loudspeakers (${N}_i=12$) switched on sequentially were used for acoustic excitation. The excitation sources locations and some of the measurement points are show in Fig. 15.24. Continuous random white noise was chosen as excitation signal and the FRFs were measured up to 800 Hz using H ₁ estimator with 150 averages. More details about the measurements procedure can be found in [26]. Some typical measured FRFs are shown in Fig. 15.25.

Fig. 15.24

Excitation sources (loudspeakers) locations inside the car cavity (left), microphones roving array inside the cavity (middle), and measurement points on boundary surface (right)

Fig. 15.25

Typical FRF of one point measured in the cavity due to all the 12 excitation sources

For this case study, because of the time limitation the pLSCE and the ML-CDM estimators will be excluded from the comparison. Since we have anyway to use the pLSCF (Polymax) to generate starting values for the ML-MM estimator, the comparison will be done between the pLSCF (Polymax) and the ML-MM estimators. A frequency band between 30 and 200 Hz has been selected to perform the acoustic modal estimation. Due to a memory requirement issue, it was not possible to apply the basic ML-MM to the full data set. Therefore, for the comparison between the basic ML-MM and the fast ML-MM in terms of their cost functions convergence and their computational time only 10 columns of the FRF matrix, i.e., all the measured responses due to 10 excitation sources are used. The Polymax has been applied to the FRFs to generate starting values of all the modal parameters (i.e., poles, mode shapes, participation factors and lower and upper residuals) to start both the basic ML-MM and the fast ML-MM estimators. In Fig. 15.26 – top, the cost function convergence and the computational time for both estimators are shown. It can be seen that although both estimators converge to a comparable value of the cost function the fast ML-MM is very fast compared to the basic ML-MM where it takes only 14 min whereas the basic implementation takes 81 min. Figure 15.26–bottom shows that both the basic ML-MM and the fast ML-MM give the same fitting quality where it can be seen that the sum of the synthesized FRFs either from the basic implementation or from the fast implementation of the ML-MM perfectly fits the measured one. Figure 15.26 clearly shows that the proposed fast implementation of the ML-MM method yields the same improved modal model as the one obtained from the basic implementation while outperforming the basic implementation in terms of the computational time and the memory requirements.

Fig. 15.26

Top: decreasing of the cost function of the basic ML-MM (left) and the fast ML-MM (right) with the computational time taken. Bottom: the fit between the measured FRFs sum and the synthesized FRFs sum for the basic ML-MM (left) and the fast ML-MM (right)

Now, both the Polymax and the fast ML-MM will be applied to the full data set (i.e., taking into account all the excitation sources). The stabilization chart has been constructed by Polymax as it is shown in Fig. 15.27 to generate starting values for the modal parameters of the corresponding modes within the selected band. Then, the initial modal model estimated by Polymax is iteratively optimized by the fast ML-MM method.

Fig. 15.27

Polymax stabilization chart when applied to the full data set of the FRFs measured inside the Sedan car cavity

Figure 15.28 shows the decrease of the ML-MM cost function at each iteration. The analysis was stopped after 20 iterations. Figure 15.30 shows that the initially modal model estimated by Polymax is drastically improved during the iterations of the ML-MM estimator. It can be seen from that figure that the ML-MM synthesis results are superior to the Polymax synthesis results. Some typical mode shapes identified with Polymax and ML-MM estimators are shown and compared with the numerical ones in Fig. 15.30. One can see that the estimated mode shapes by Polymax and the ML-MM are comparable. However, the mode shapes estimated by the ML-MM method is more similar to the numerical mode shapes. It can be seen that there are some differences between Polymax and the ML-MM method in terms of the frequencies and damping estimates. Actually, these differences in the values of the frequency and the damping estimates are reflected as an improvement in the goodness of the fit between the measured and the synthesized FRFs (see Fig. 15.29). Moreover, it was found that the mode shapes estimated by the ML-MM method shows a good independency as compared to the ones of Polymax. This can be evidenced by looking to the AutoMAC matrix for both Polymax and ML-MM that are shown graphically in Fig. 15.31. It can be seen from this figure that the off diagonal elements of the ML-MM AutoMAC matrix have lower values as compared to the ones of Polymax.

Fig. 15.28

Decrease of the fast ML-MM cost function at each iteration cavity

Fig. 15.29

Improved FRF curve fit when using fast ML-MM as compared to Polymax

Fig. 15.30

Some typical acoustic mode shapes of the Sedan interior cabin identified by Polymax and ML-MM as compared to the ones predicted by the CAE model

Fig. 15.31

Auto MAC: Polymax (right) and ML-MM (left)

15.4 Conclusions

The basic implementation of the ML-MM (Maximum Likelihood estimator based on modal model) estimator is represented and improved in terms of the memory requirements and the computational time. The proposed fast implementation of the estimator, the fast ML-MM, has been validated and compared with the basic implementation (basic ML-MM) and with some other estimators (e.g., Polymax, pLSCE and ML-CDM) suing simulated example and three real industrial applications. From the presented results, it is found that the fast implementation of the ML-MM estimator gives very comparable performance as compared with the basic implementation in terms of the accuracy of the estimated modal parameters and the predicted confidence bounds while outperforming the basic ML-MM in terms of the computational time and the memory requirements. As compared with Polymax, pLSCE and ML-CDM, the fast ML-MM estimator results in better estimates for the modal parameters, and it is capable to properly deal with high modal densities, highly damped systems and FRF matrices with many references (excitation sources) and provides superior FRF synthesis results.