Optimal Modal Parameter Estimation for Highly Challenging Industrial Cases

Abstract

In this paper, the recently-developed MLMM method (Maximum Likelihood estimation of a Modal Model) will be introduced and applied to challenging industrial cases. Specific about the method is that the well-established statistical concept of maximum likelihood estimation is applied to estimate directly a modal model based on measured Frequency Response Functions (FRFs). Due to the nature of this model, the optimal modal parameters are estimated using an iterative Gauss-Newton minimization scheme. The method is able to tackle some of the remaining challenges in modal analysis. For instance, in highly-damped cases (e.g. acoustic cavity modal analysis, trimmed body modal analysis) where it is needed to use a large amount of excitation locations to sufficiently excite the modes and to obtain a reliable modal model, the more classical modal parameter estimation methods sometimes fail to achieve a high-quality curve-fit of the measured FRF data. Due to the iterative minimization of the cost function, MLMM is able to estimate a model that very closely represents the measurements. Another benefit of the method is that additional constraints can be imposed to the model. For instance, it is possible to impose that real modes and participation factors are estimated and/or to impose that the estimated modal model is reciprocal (as prescribed by the modal theory). More classical modal parameter estimation methods have rarely the possibly to fully integrate these constraints and the obtained modal parameters are typically altered in a subsequent step to satisfy the desired realness and reciprocity constraints. It is obvious that this may lead to sub-optimal results, as for instance evidenced by a degradation of the quality of the fit between the identified modal model and the measurements. The applicability of MLMM to estimate a constrained modal model will be demonstrated using challenging industrial applications.

19.1 Introduction

The modal parameters are basically defined as the eigenvalues and eigenvectors of the linear dynamic model for a vibratory structure. For a certain vibratory structure, a linear model can be written in terms of the frequency response functions (FRFs) as:

$$ \left\{X\left({\omega}_k\right)\right\}=\left[H\left({\omega}_k\right)\right]\ \left\{F\left({\omega}_k\right)\right\} $$

(19.1)

where $\left\{X\left({\omega}_k\right)\right\}\in {\mathbb{C}}^{N_o\times 1}$ the discrete Fourier transformed (DFT) displacement response with N _o the number of measured outputs, $\left\{F\left({\omega}_k\right)\right\}\in {\mathbb{C}}^{N_i\times 1}$ the Fourier transformed force inputs with N _i the number of measured inputs, $\left[H\left({\omega}_k\right)\right]{\mathbb{\in}\,\mathbb{C}}^{N_o\times {N}_i}$ the FRFs matrix, and ω _k is the frequency variable at frequency line k. Different frequency-domain parametric models can be used to represent the frequency response functions (FRFs) matrix of a linear time-invariant system describing the relation between the DFT spectra of the input and output signals [1]. The model that is used mostly is the rational form model: a rational of two polynomials either in s-domain or in z-domain. Another model that is also well known is the state-space representation. In this paper, the so-called “modal model” is used, where the FRFs matrix is directly written in terms of the modal parameters:

$$ \widehat{H}\left(\theta, {\omega}_k\right)=\left(\sum_{r=1}^{N_m}\frac{\varPsi_r{L}_r}{j{\omega}_k-{\lambda}_r}+\frac{\varPsi_r^{\ast }{L}_r^{\ast }}{j{\omega}_k-{\lambda}_r^{\ast }}\right)+\frac{\left[ LR\right]}{{\left(j{\omega}_k\right)}^2}+\left[ UR\right] $$

(19.2)

with $\widehat{H}\left(\theta, {\omega}_k\right)\in {\mathbb{C}}^{N_o\times {N}_i}$ the frequency response functions (FRFs) matrix with N _o outputs and N _i inputs, N _m the number of the identified modes, ω _k  = 2πf _k the circular frequency at frequency f _k [Hz], ${\Psi}_r\in {\mathbb{C}}^{N_o\times 1}$ the r ^th mode shape where r = 1 , 2 ,  .  .  , N _m , λ _r  =  − σ _r  + jω _d , r the r ^th pole with σ _r the damping factor of mode r and ω _d , r the damped natural frequency [rad/s], (.)^∗ stands for the complex conjugate of a complex number, ${L}_r\in {\mathbb{C}}^{1{\times N}_i}$ is the r ^th participation factors vector, $\left[ LR\right]\in {\mathbb{R}}^{N_o\times {N}_i}$ and $\left[ UR\right]\in {\mathbb{R}}^{N_o\times {N}_i}$ are the lower and upper residual terms used to compensate for the out-of-band modes (assuming a displacement over force FRF in this case), and θ is the parameter vector (i.e. θ = [Ψ _r , L _r , λ _r , LR, UR]). The multiplication Ψ _r L _r is called the residue matrix R _r of the r ^th mode.

Curve fitting aims to match the analytical expression (19.2) (or an equivalent model) to experimental FRF data over a chosen frequency range. During the process, some or all of the modal parameters in the model are determined. Most of the existing modal parameter estimation methods are achieving the full estimation process in two steps. In the first step, the poles (λ _r ) and the participation factors (L _r ) are estimated using rational-polynomial-based models. Then, the mode shapes Ψ _r and the residuals terms ([LR], [UR]) are estimated in a second step by solving a linear least-squares problem using (19.2). In [2], the modal parameters are estimated using a frequency-domain output-error optimization technique that uses the pole-residue model as a parameterization form.

The experimentally-driven modal model (19.2) can be used for several modal analysis applications (e.g. structural modifications, noise prediction, FEM updating, sensitivity analysis, etc. [3,4,5]). For these applications and according to the modal theory, the estimated modal models have to fulfill some important properties. For instance, in the FEM calibration process, the experimentally driven modal models have to incorporate real mode shapes rather than complex ones. This is because the mode shapes obtained from the finite element models are typically real in nature, whereas the mode shapes obtained from experimental measurements are complex. Also in acoustic modal analysis, it can be desired to obtain real mode shapes instead of complex ones to avoid phase lag between different mode shape components so that easier to interpret mode shapes are obtained. In structural modifications prediction and structure coupling/decoupling applications, obtaining a high quality reciprocal modal model is an important requirement. The existing modal parameter estimation methods rarely consider those two important constraints (i.e. real modes and FRFs reciprocity), and the obtained modal models are typically altered in a subsequent step to satisfy the desired constraints. This may lead to sub-optimal results, as for instance evidenced by a degradation of the quality of the fit between the final identified modal model and the measurements. A comprehensive review on the constrained modal parameter estimation is given in [7]. Apart from those two physically motivated constraints, it was also observed that the existing modal parameters estimation techniques are facing some difficulties when fitting an FRFs matrix with so many columns, i.e. in case where many input excitation locations have to be used in the modal test. For instance, obtaining clean and symmetric mode shapes when performing structural modal analysis of a full car requires many excitation locations to get sufficient excitation of the modes. Another important example where the use of many excitation sources is required is the acoustic modal analysis of a car cavity. The high level of damping in the car cavity requires many excitation locations to get sufficient excitation of the acoustic modes [6, 8,9,10].

These are true remaining challenge and of great interest to the automotive OEMs. In this paper, a recently developed modal parameter estimation method called MLMM (Maximum Likelihood estimation of a Modal Model) will be introduced and applied to some challenging industrial cases.

19.2 Maximum Likelihood Estimation of a Modal Model: MLMM

19.2.1 MLMM Theory

The iterative MLMM modal parameter estimation method is a multivariable (i.e. MIMO) frequency-domain modal estimation method that uses the modal model to represent the measured frequency response functions (FRFs) over a chosen frequency band. The MLMM method is originally introduced in [11] and further improved in terms of the computational time in [12]. In [7], the MLMM method is adapted to take into account some desired and physically motivated constraints in the optimization process. The MLMM method belongs to the category of the maximum likelihood estimators that is known to be asymptotically consistent and efficient [1, 13, 14]. The “MLMM” abbreviation stands for Maximum Likelihood (estimation of a) Modal Model. The MLMM method optimizes the modal model (19.2) directly instead of optimizing a rational fraction polynomial model. The optimization process tunes the parameters of the modal model to minimize the following quadratic-like cost function so that a best match between the modal model and the measurements is obtained:

$$ {{\ell}}_{MLMM}\left(\theta \right)=\sum_{i=1}^{N_i}\sum_{o=1}^{N_o}\sum_{k=1}^{N_f}{\left|{E}_{io}\left(\theta, {\omega}_k\right)\right|}^2 $$

(19.3)

with ${E}_{io}\left(\theta, {\omega}_k\right)\mathbb{\in}\,\mathbb{C}$ the weighted residual (i.e. the error between the measured FRF H _io (ω _k ) and ${\widehat{H}}_{io}\left(\theta, {\omega}_k\right)$ represented by the modal model (19.2)). This residual is a nonlinear function of the modal model parameters θ, and it is defined as:

$$ {E}_{io}\left(\theta, {\omega}_k\right)=\frac{H_{io}\left({\omega}_k\right)-{\widehat{H}}_{io}\left(\theta, {\omega}_k\right)}{\sigma_{H_{io}}^2\left({\omega}_k\right)} $$

(19.4)

where ${\sigma}_{H_{io}}^2\left({\omega}_k\right)$ is the variance of the measured FRF and θ is a column vector contains all the parameters of the modal model (19.2) (i.e. poles, participation factors, mode shapes and residual terms). In the cost function (19.3), the measurements with small uncertainty (i.e. ${\sigma}_{H_{io}}^2\left({\omega}_k\right)$ is small) are more important than those with a large uncertainty (i.e. ${\sigma}_{H_{io}}^2\left({\omega}_k\right)$ is large). The true ML estimator uses the complete covariance matrix as weighting functions in the equation error, however obtaining this matrix correctly (i.e. full rank matrix) is not feasible from the practical point of view, which is particularly true for the modal testing cases where so many outputs and inputs are measured. Therefore, only the diagonal elements of this matrix are used as it is shown in equation (19.4). The variance can be easily calculated using the coherence functions and the FRFs themselves. The consequences of using only the diagonal elements of the covariance matrix is that the estimator will be less efficient (i.e. the uncertainty bounds on the estimates will be higher), but the consistency property will be kept [1, 13]. If the equation error is taken as unweighted one, which could be the case if the FRFs variance is not available, the MLMM will become a non-linear least-squares (NLS) estimator, which is asymptotically consistent but not efficient (i.e. the delivered uncertainty bounds are meaningless). The minimization of the cost function (19.3) is achieved by implementing the Levenberg-Marquardt algorithm (a combination of Gradient and Newton-Gauss methods). The p ^th iteration step of the algorithm is given by:

$$ \mathfrak{R}\left({J}_{p-1}^H{J}_{p-1}+{\alpha}_{LM_{p-1}} diag\left({J}_{p-1}^H{J}_{p-1}\right)\right)\ {\delta \theta}_{p-1}=-\mathfrak{R}\left({J}_{p-1}^H{\kern0.5em E}_{p-1}\right) $$

(19.5)

with J = ∂E/∂θ the complex-valued Jacobian of the vector ${E}{\left(\theta,{\omega}_k\right)}$, δθ _p  = θ _p  − θ _p − 1, and α _LM the Levenberg-Marquardt parameter. Increasing the parameter α _LM will enlarge the convergence region of the cost function. Once the cost function reaches a convergence, the optimum parameters of the modal model over a chosen frequency range are obtained. The convergence of the cost function is defined either by a relative error between two consecutive calculated cost functions or by reaching a given maximum number of iterations. If the variance of the FRFs is used as a weighting function in the error equation, the confidence bounds on the estimated modal parameters can be obtained by inverting the so-called Fisher information matrix [1] as follows:

$$ cov\left(\theta \right)={\left[2\ \mathfrak{R}\left({J}^HJ\right)\right]}^{-1} $$

(19.6)

where J is the Jacobian of the last iteration in the optimization process. The diagonal elements of cov(θ) are the variances of the estimated modal parameters. References [7, 11, 12] give a detailed description of the implementation equations of the MLMM method. Since MLMM is an iterative method that performs a nonlinear optimization process, initial values for the all the modal parameters of expression (19.2) are needed to start the optimization process. The polyreference least-squares complex frequency-domain (pLSCF) estimator [15, 16], known as Polymax, will be used to generate initial values for the poles and the participation factors. Then, the initial values for the mode shapes, lower and upper residuals can be determined easily by solving linear least-squares problem using (19.2).

19.2.2 Constrained MLMM: Reciprocal Modal Model & Real Mode Shapes

19.2.2.1 Reciprocity Constraint

A reciprocal frequency response functions (FRFs) matrix requires symmetric residues (R _r  = Ψ _r L _r ) and symmetric residual matrices ([LR],[UR]). If MIMO measurements are available, this condition can be checked on the FRFs matrix: H _oi (ω _k ) = H _io (ω _k ) for the o ^th row and the i ^th column. On the level of the modal model, evaluating (19.2) for DOF o and i shows that the reciprocity principle for a specific mode r and the upper and lower residual terms yields:

$$ {\Psi}_{i_r}{L}_{o_r}={\Psi}_{o_r}{L}_{i_r}\ \& \ {LR}_{oi}={LR}_{io}\ \& \ {UR}_{oi}={UR}_{io} $$

(19.7)

Hence, to identify a reciprocal modal model with the MLMM method the residual matrices have to be symmetric and the participation factors have to be identical (up to scaling factor) to the mode shape coefficients at the input stations. Therefore, to identify a reciprocal modal model using the iterative MLMM method the same optimization procedure described in Sect. 19.2.1 will be achieved taking into account the reciprocity constraint in the optimized modal model (19.2). Imposing reciprocity in the identified modal model means that (19.2) will be reformulated as follows:

$$ \widehat{H}\left(\theta, {\omega}_k\right)=\left(\sum_{r=1}^{N_m}\frac{Q_r{\phi}_r{L}_r}{j{\omega}_k-{\lambda}_r}+\frac{Q_r^{\ast }{\phi}_r^{\ast }{L}_r^{\ast }}{j{\omega}_k-{\lambda}_r^{\ast }}\right)+\frac{{\left[ LR\right]}_{rec}}{{\left(j{\omega}_k\right)}^2}+{\left[ UR\right]}_{rec} $$

(19.8)

with ${Q}_{r\ }\mathbb{\in}\,\mathbb{C}$ the scaling factor (the ratio between the mode shape element at the driving point DOF and the corresponding participation factor), ${\phi}_r\in {\mathbb{C}}^{N_o\times 1}$ the mode shape vector in which the mode shape element that corresponds to a driving point DOF are imposed to be identical to the participation factors element that corresponds to that driving point DOF, ${L}_r\in {\mathbb{C}}^{1\times {N}_i}$ the participation factors row vector, ${\left[ UR\right]}_{rec\ }\in {\mathbb{R}}^{N_o\times {N}_i}$ and ${\left[ LR\right]}_{rec}\in {\mathbb{R}}^{N_o\times {N}_i}$ the upper and lower residual matrices in which the symmetry property is imposed. The iterative MLMM method will optimize the reciprocal modal model (19.8) in such a way that the best match between the measurements and the modal model is obtained.

19.2.2.2 Real Mode Shapes

Estimation of real (normal) mode shapes requires that the structure under test has a proportional damping which is a quite hypothetical form of damping. The main reason for the introduction of the proportionally damped systems assumption is that the numerical complexity of the calculations with this assumption is lower than for the general viscous damping. Systems with proportional damping form a compromise between the undamped system models from finite element model analysis and the generally viscously damped system models from experimental modal analysis. The hypothesis of proportional damping of a given mode corresponds to a purely imaginary residue matrix [2, 3]. This corresponds to $\mathfrak{R}\left({\Psi}_r{L}_r\right)=0$ in equation (19.2). To identify a modal model that incorporates real mode shapes, the constraint $\mathfrak{R}\left({\Psi}_r{L}_r\right)=0$ will be imposed in the optimization process of the MLMM method described in Sect. 19.2.1 giving at the end a modal model with purely imaginary residues.

In case reciprocity and the real mode shapes constraints are applied simultaneously, which is often needed for advanced engineering based on the experimental modal model, the MLMM method, using the optimization procedure described in Sect. 19.2.1, will identify the modal model (19.8) with imposing that $\mathfrak{R}\left({Q}_r{\phi}_r{L}_r\right)=0$ where Q _r , ϕ _r , and L _r are the same as they are defined in Sect. 19.2.2.1. In the optimization process of the MLMM method it is also taken into account for each mode that the pole remains stable during the iterations (i.e. its real part is negative). Moreover, when applying the reciprocity and real mode shapes constraint simultaneously the frequency mass sensitivity is negative, and the residue at the input point is negative imaginary [7].

19.3 Applications

In this section, the applicability of the iterative constrained MLMM in the frame of structural modal testing and the vibro-acoustic modal analysis will be presented by means of three different data sets. The first part of this section will deal with the application of the constrained MLMM method in the field of structural modal testing using two different data sets measured from two different fully equipped cars. The second part of this section will show the applicability of the constrained MLMM method in the field of the acoustic modal analysis using acoustic data set measured for a fully trimmed car cavity. These cases are challenging because of the high level of damping, high modal density, and the (very) large amount of columns of the FRFs matrix to be fitted. Since the main objective of the users applying the reciprocity and real mode shapes constraints is to obtain models that accurately represent the structure under test, the main criterion that is going to be used as a validation tool is the quality of the fit between the obtained modal model and the measured data. The quality of the obtained modal model from the iterative MLMM method will be compared to the one obtained from the well-known Polymax estimator [15, 16]. Polymax relies on a (non-iterative) linear least-squares optimization to estimate the modal parameters. The poles and the participation factors are calculated first by fitting a right matrix fraction description polynomial model to the measured FRFs. Then, the mode shapes together with the residual terms are calculated in a second LSFD step by fitting the modal model to the measured FRFs. Although the real mode shapes and reciprocity constraints can be applied in the existing LSFD estimator the obtained constrained modal model from the LSFD solution is not always of high quality since the LSFD belongs to the linear least-squares estimators, which are known to be biased estimators. Another disadvantage of the existing LSFD estimator is that the reciprocity condition is not applied to the lower and upper residual terms. The iterative MLMM method is specifically developed to overcome both drawbacks.

19.3.1 Structural Modal Analysis Applications

In this subsection, the applicability of the iterative constrained MLMM method in the frame of structural modal testing, more specifically in automotive modal analysis, will be presented by means of two different data sets measured on two different fully equipped cars. The main difference between the two data sets is the number of references (i.e. excitation sources) used to measure the FRFs matrix. The second data set has 26 inputs, while the first one has four inputs. Having more references (inputs) leads to have a higher modal density since many close modes will be excited and estimated. Therefore, this difference in the number of inputs between the two data sets will increase the data size in terms of the total number of the FRFs to be fitted and the number of modes to be optimized.

19.3.1.1 First Fully Equipped Car Example: With a Reasonable Amount of Input Locations

In this example, the accelerations of the fully equipped car were measured at 154 locations, while 4 shakers were simultaneously exciting the structure. This gives a total of 616 FRFs. At the shaker locations, accelerometers were also installed to measure the accelerations. Therefore, the data set has four driving points; hence, a 4 × 4 block of the full FRFs matrix is expected to be symmetric due to the fact that the FRFs of the collocated DOFs should be reciprocal. More details about this test setup can be found in [17]. Figures 19.1 and 19.2 show the car geometry and some measured FRFs respectively. The iterative MLMM will be applied to the 616 measured FRFs with the aim to obtain an accurate experimentally-driven modal model that verifies the reciprocity and real mode shapes conditions. To start the iterative MLMM method, initial values for the modal model parameters (19.2) will be generated by applying Polymax to the measured FRFs.

Fig. 19.1

First fully equipped car geometry

Fig. 19.2

Typical FRFs for the first car example

Figure 19.3 shows the Polymax stabilization chart from which about 18 physical modes become visible in the analysis band. Starting from these initial values for the modal model parameters, the iterative MLMM estimator was then used to optimize the modal model (19.8) with imposing that the mode shapes are real (Purely imaginary residues: $\mathfrak{R}\left({Q}_r{\phi}_r{L}_r\right)=0$).

Fig. 19.3

The 1st fully equipped car example: Polymax stabilization chart

In Fig. 19.4, the decrease of the MLMM cost function (19.3) and the evolution of the frequencies and damping ratios at each iteration are shown. In the same figure, the calculation time taken by the MLMM method is given. It is clear that while iterating, MLMM is successfully decreasing the error between the model and the measured FRFs. The frequency values seem to be very consistent during the iteration, while for some modes the damping ratio estimates are increasing considerably. This is consistent with the fact that natural frequencies are typically estimated with much smaller uncertainty than damping ratios [18, 19].

Fig. 19.4

The decrease of the MLMM cost function and the evolution of the frequencies and damping ratios at each iteration

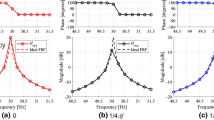
In Figs. 19.5 and 19.6, the synthesized FRFs are compared with the measured ones for some selected reciprocal and non-reciprocal FRFs respectively. From Fig. 19.5, one can see that the FRFs are well measured where the reciprocity principle is verified between the FRFs that are expected to be reciprocal (the red and blue measurement curves do not differ too much). Therefore, the traditional approach of imposing the reciprocity constraint after the Polymax modal parameter estimation, is expected to also yield acceptable results. Nevertheless, the optimal MLMM solution is still significantly better. This can be seen by comparing both approaches in the frequency range between 20 and 30 Hz in Fig. 19.5. In Fig. 19.6, in which the fit quality is shown for some non-reciprocal FRFs, one can see that the MLMM synthesis results in general are superior to the results from the traditional approach. These results show that with the iterative MLMM an accurate modal model that verifies some physical motivated constraint like FRFs reciprocity and real mode shapes can be obtained.

Fig. 19.5

Improved FRF curve fit for reciprocal FRFs (FRF Karo1+Z/Karo 25+Z & FRF Karo25+Z/Karo 1+Z) when using MLMM as compared to the Polymax estimator: (Left) Polymax estimator; (Right) iterative MLMM estimator. Red & blue: measured reciprocal FRFs; Black: synthesized FRF by Polymax; Green: Synthesized FRF by iterative MLMM

Fig. 19.6

Improved FRF curve fit for non-reciprocal FRFs (measurement in red) when using MLMM (green) as compared to Polymax (black)

In Fig. 19.7, the modal assurance criterion (MAC) between real and complex mode shapes estimated by MLMM starting from the same initial mode set is represented. It can be seen from that figure that the real and complex mode shapes are in general in a good agreement except for modes 9, 11, 12, 15, 16 and 18. By checking the level of the complexity of those modes, one can see from Fig. 19.7 that those modes have the lowest Modal Phase Collinearity (MPC) and highest Mean Phase Deviation (MPD) respectively in comparison with the other modes (see [22] for definition of MPC and MPD). Moreover, it can be seen from the stabilization chart that most of those modes (except mode 18) are either very close modes or not well stabilized in the stabilization chart. Therefore, those modes are seemingly coupled with high level of uncertainties.

Fig. 19.7

(Top) Cross MAC between complex and real mode shapes estimated by MLMM; (Bottom-Left) Complex mode shapes Modal Phase Collinearity (MPC); (Bottom-Right) Complex mode shapes Mean Phase Deviation (MPD)

19.3.1.2 Second Fully Equipped Car Example: With a Very Large Number of Input Locations

The second example that will be used is a data set measured on a midsize car. The car was excited at 26 locations, while the acceleration responses were measured at 149 locations. Therefore, the FRFs matrix contains 3874 FRFs. The challenges with this data set are the huge amount of references used to obtain the FRFs matrix and the high modal density, which make the fitting process with the existing methods to be troublesome.

In Fig. 19.8, some measured FRFs are shown. The aim of this modal test was to obtain an experimental modal model that will be used for stiffness identification and structural modification purposes. Obtaining an accurate reciprocal modal model that incorporates real mode shapes was an important requirement. For confidentiality reasons, no absolute frequency values will be shown. An initial modal model is created by applying Polymax to the measured FRFs as explained in Sect. 19.3.1.1. Figure 19.9 shows the Polymax stabilization chart. Although the FRFs matrix has so many references and the model size used is relatively high, Polymax is still able to give a relatively clear stabilization chart in a numerically stable way. This was the main motivation behind selecting Polymax as starting values generator for the MLMM method. The MLMM method is then applied with the aim to further improve the initial Polymax modal model. In the MLMM optimization process the reciprocity and real mode shapes constraints are imposed. In Fig. 19.10, the performance of the MLMM method during the different iterations is represented in terms of the decreasing of the cost function and the evolution of the resonance frequencies and damping ratio. The accuracy of both the final MLMM model and the initial model is evaluated in Fig. 19.11 where the synthesized FRFs from both models are compared to the measured ones.

Fig. 19.8

Typical FRFs for the second car example (the frequency axis is made invisible for confidentiality reasons)

Fig. 19.9

The 2nd fully equipped car example: Polymax stabilization chart

Fig. 19.10

The decrease of the MLMM cost function and the evolution of the frequencies and damping ratios at each iteration

Fig. 19.11

The quality of the identified modal model in terms of the goodness of the fit for some selected FRFs: measured FRFs (Red), synthesized FRFs using linear least squares solution (Blue), and synthesized FRFs using MLMM method (Green) (the frequency axis is made invisible for confidentiality reason)

It can be seen from Fig. 19.10 that the error between the measurements and the optimized modal model is successfully decreased through the different iterations of the MLMM method, which at the end gives a modal model that outperforms the initial one. This is also very clear from the results shown in Fig. 19.11 where it can be seen that the MLMM modal model is far better than the initial modal model. In comparison with the previous example (Sect. 19.3.1.1, FRF matrix with only 4 inputs), this example (with 26 inputs) shows clearly that the traditional methods are having difficulties in fitting an FRF matrix with a very large amount of columns. As a global measure of the accuracy of the estimated modal models, Table 19.1 presents the global mean fitting error and correlation between the measured and the synthesized FRFs. One can see from this table that the global fit error is significantly decreased and likewise the correlation between the measured and the synthesized FRFs increases. The complexity of the mode shapes with and without imposing real mode shapes during the MLMM iterations can be assessed in Fig. 19.12 for some modes. The mode shapes in both cases were also compared using the modal assurance criterion (MAC). From the complexity plots, it can be concluded that the MLMM with the real mode shape constraint activated normalizes the mode shapes and the obtained normal mode shapes agree well with the complex counterparts in terms of MAC value and the resonance frequency values for the selected set of modes. It should be mentioned that for those complex mode shapes that have low MPC value, they do not agree well with the estimated real modes in terms of MAC value.

Table 19.1 2nd fully equipped car example: mean fitting error & correlation between the measured and synthesized FRFs

Fig. 19.12

Mode shape complexity plots for some selected modes (for the plot at the right side, the MAC is calculated with respect to the complex mode shapes)

19.3.2 Acoustic Modal Analysis Application

This experimental case concerns the cabin characterization of fully trimmed sedan car using acoustic modal analysis. The acoustic modal analysis of a car cavity (cabin), in general, implies the use of many excitation sources (up to 12 sources in some cases) and the presence of highly-damped modes [9, 20]. Due to the high level of the modal damping in such application, the many excitation locations are required to get sufficient excitation of the modes across the entire cavity and to avoid mode shape distortions that typically occur when a low number of acoustic sources are used. It has been observed that the classical modal parameter estimation methods have some difficulties in fitting an FRF matrix that consists of many (i.e. 4 or more) columns, i.e. in cases where many input excitation locations have been used in the experiment [9, 20].

Multiple inputs multiple output (MIMO) test were carried out inside the cavity of the Sedan car where 34 microphones located both on a roving array with spacing equal to around 20 cm and near to boundary surfaces captured the responses simultaneously. A total of 18 runs were performed to measure the pressure distribution over the entire cavity (both cabin and trunk) resulting in 612 response locations (in this paper a subset of N _o  = 527 have been used). For each run, up to 12 loudspeakers switched on sequentially were used for acoustic excitation. The excitation sources locations used in this paper ( N _i  = 10 out of the available 12) are shown in Fig. 19.13 (Right). Continuous random white noise was chosen as excitation signal and the FRFs were measured up to 800 Hz using H ₁ estimator with 150 averages. Some typical measured FRFs are shown in Fig. 19.14. More details about the measurements procedure can be found in [21].

Fig. 19.13

Sedan car under test: (Left) Microphones roving array inside the cavity; (Middle) one of the acoustical sources; (Right) source locations

Fig. 19.14

Typical FRF of one microphone measured in the cavity due to 10 excitation sources: full measured frequency band is shown with the selected band for modal analysis highlighted

A frequency band from 44 till 220 Hz was selected for modal parameter estimation. Polymax was applied to the large database (527 microphones, 10 acoustic sources, 450 spectral lines). In order to have a sufficient number of lines in the stabilization diagram, a model order of 150 was used. Based on the stabilization diagram, 13 modes were retained. The acoustic cavity and the flexible walls of the cavity constitute a coupled vibro-acoustic system and hence the modes of the system generally will consist of an acoustic part (pressure waves in cavity air) and a structural part (flexural waves in cavity walls). Therefore and despite the fact that both excitation and response measurement quantities are from the acoustic domain, also more structurally related modes may be retrieved from the analysis. Nevertheless, it appears that the selected modes are to a large extent “acoustically dominant” modes. Using the same Polymax poles, both real and complex mode shapes have been estimated. The curve-fitting quality is represented in Table 19.2 (Polymax columns). Afterwards, 10 MLMM iterations are applied to the Polymax initial estimates, both using the general complex mode formulation of the modal model and the constrained real modal model. Also the MLMM results are represented in Table 19.2. Whereas Table 19.2 provides averaged results over all FRFs, Fig. 19.15 shows the curve-fitting results of a typical FRF. From Table 19.2 it can be concluded that, obviously, the fitting quality degrades when using real instead of complex mode shapes in Polymax. When comparing MLMM with Polymax, it is clear that substantial improvements are obtained in terms of curve-fitting quality, both for general complex modes and real modes. Interesting to observe is that the real MLMM results are superior to the complex Polymax results, indicating that although the real modal model has less parameters that can be tuned, still superior results are obtained, thanks to the optimization process in MLMM.

Table 19.2 Mean fitting error & correlation between the measured and synthesized FRFs: 1-step Polymax versus 10 iterations in MLMM (In both cases a real and a complex model is fitted)

Fig. 19.15

Typical acoustic FRF curve-fitting results. MLMM with real modes performs better than the traditional (real and complex) approach Polymax cases

A comparison between real and complex mode shapes is made in Fig. 19.16. Several mode shape pairs have lower MAC values. These are precisely the modes that show quite some complex behaviour when using the general (complex) modal model (wave propagation when animating the mode shape, higher complexity indicators such as MPC and MPD [22]). An example of such mode shape pair is provided in Fig. 19.17. The (complex) mode shape (Right) had quite high complexity indicators: MPC = 84%, MPD = 26°). The MAC between the real and complex mode shape is 81%. Real mode shapes are typically easier to interpret and may be more suited for correlation with FE models [23]. Some other real MLMM mode shapes are represented in Fig. 19.18.

Fig. 19.16

MAC values between complex and real mode shapes (MLMM with 10 iterations)

Fig. 19.17

(Left) Easily interpretable Real mode shape; (Right) complex mode shape with phase differences

Fig. 19.18

Real mode shapes obtained by applying MLMM

19.4 Conclusions

An advanced iterative frequency-domain modal parameter estimation technique called MLMM is presented and successfully validated using some real challenging industrial applications. The MLMM method estimates directly the modal model by minimizing iteratively the errors between the measured FRFs and the modal model using a non-linear optimization technique. The main design requirement of the MLMM method was to deliver high quality modal models that could accurately fit an entire FRF matrix with a (very) large amount of columns; while at the same time to incorporate some physically motivated constraints like FRF reciprocity and real (normal) mode shapes. The application of the MLMM method to the structural and acoustic modal testing domains showed that the MLMM method compared to the traditional modal estimators is capable to achieve its target of delivering more accurate modal models; even when the constraints are taken into account.