Keywords

10.1 Introduction

Modal parameter estimation (MPE) refers to system identification of vibrating structures by fitting a known parametric model to measured frequency (FRF) or impulse (IRF) response functions. The parameters computed, i.e. complex natural frequencies, mode-shapes and participation vectors, and modal scaling factors [1], describe the dynamics of the structure under test in a linear regime. As such, MPE finds applications in analyses of vibrating structures like finite-element model verification and validation, reduced-order modeling, sub-structuring etc. With a long history [2] of successfully proposed approaches associated with it, the maturity of this branch of research may be gauged by the current research focus being on statistical approaches [3], operational modal parameter estimation [4] and minimizing user interaction during the MPE process [5, 6]. Applicability to industrial (and noisy) data is the driving force behind investigations and much effort has been put into handling and tracking of measured functions and validation of results from realistically damped systems.

The current standard commercial algorithms (e.g. PolyMax [7]) employ a two-step process for the computation of the said parameters. The Unified Matrix Polynomial Approach (UMPA) [8] provides a general framework for various algorithms and is also used in this work. UMPA utilizes measured FRFs (or IRFs) to compute a rational fraction model (Equation 10.3) by minimizing residuals in a least-squares sense. The complex natural frequencies and participation vectors are obtained in the first step by carrying out an eigen-value decomposition on a companion matrix derived from the denominator matrix-coefficients. The numerator coefficients on the other hand are eliminated [7] or left unused [8]. After the selection of valid poles (typically done by the analyst using a stabilization/consistency chart [9]), the calculation of the residue and the residuals from the pole-residue representation of FRFs (Equation 10.11) is accomplished in a second step. The modal model is often validated by using metrics like modal assurance criterion (MAC) [10], mean phase correlation (MPC), mean phase deviation (MPD) and synthesis correlation coefficient [9, 11].

The present research aims at answering a more basic question – can the numerator coefficients be manipulated to make the complete residue information available during the pole selection phase, to be included in the stabilization chart?

10.2 Theoretical Background

A left matrix-factor description (MFD) is used to ascribe a rational fraction model to measured FRF data (Equation 10.1). The complete process is transferable to a right MFD form, but for the sake of simplicity, only one development is discussed.

$$\displaystyle \begin{aligned} \Big[H(s)\Big]_{N_o\times N_i}=\bigg[\sum_{i=0}^m \Big[[\alpha_i] s^i \Big]\bigg]^{-1}_{N_o\times N_o} \bigg[\sum_{i=0}^{m-1} \Big[[ \beta_i ] s^i \Big]\bigg]_{N_o\times N_i } + \bigg[\sum_{i= -n_l}^{n_u} \Big[[R_i ] s^i \Big]\bigg]_{N_o\times N_i} {} \end{aligned} $$
(10.1)

Here, [H(s)] represents the transfer function (s = j(2πf), for measured frequency response functions, f being the sampled frequency in Hz). Its size is defined by the number of outputs (N o) and the number of inputs (N i) for each frequency line observed (N f). The denominator polynomial model order is indicated by m, while n l and n u indicate the order of the polynomials used to represent the lower and upper residuals respectively.

The description in Equation 10.1 is in terms of complex frequency. The equation holds for N f number of frequencies on the positive imaginary frequency axis and N f on the negative imaginary frequency axis. The reader is referred to the concept of characteristic space in [2]. Naturally, since the negative frequencies are not measured, they are simply assigned as complex conjugates of the positive imaginary axis in the complex plane. The FRFs are also assigned as complex conjugates of the corresponding positive frequency FRFs.

The terms in Equation 10.1 can be rearranged to result in the system shown in Equation 10.2, which is effectively the rational fraction model with additional numerator coefficients for inclusion of residual terms. This is discussed in detail by Fladung [12] and hereafter, the values n l = 2, n u = 0 are used for physical inertia and stiffness residuals.

$$\displaystyle \begin{aligned} \bigg[\sum_{i=0}^m \Big[[ \alpha_i] s^i \Big] \Big[H(s)\Big]\bigg] = \bigg[\sum_{i=-n_l}^{m+n_u}\Big[[ \hat{\beta }_i ] s^i \Big]\bigg] {} \end{aligned} $$
(10.2)

To avoid calculation of the trivial solution, without any loss in generality, the highest alpha coefficient is assumed to be the identity matrix. Equation 10.3 for each frequency (N ω = 2N f frequency lines) is then be used to set up an over-determined system of linear equations, which is solved in a least squares sense to recover the matrix coefficients. The complete setup of the over-determined least-squares problem is shown in Appendix B of [8] for a right MFD formulation, which is simply the transposed version of the left MFD equation.

$$\displaystyle \begin{aligned} \bigg[\sum_{i=0}^{m-1} \Big[[ \alpha_i ] s^i\Big] \Big[H(s)\Big]\bigg] - \bigg[\sum_{i=-n_l}^{m+n_u} \Big[[ \hat{\beta}_i ] s^i\Big]\Big[I\Big]\bigg]=\bigg[-\Big[I\Big]\Big[H(s)\Big]s^m\bigg] {} \end{aligned} $$
(10.3)

The inversion of the Vandermonde-type matrix obtained by arranging the measurements in Equation 10.3 is an ill-conditioned problem and often a Z-transform approach is used to improve the conditioning. By substituting s = exp(2jπf Δt), the complex two-sided FRF is wrapped around a unit circle such that any increase in the frequency values is essentially a rotation in the complex plane. Here, f is the frequency under transformation and Δt is the discrete time interval obtained from the Nyquist criterion. Employing orthogonal polynomials [8] for frequency tranformation results is another approach to improve conditioning, but is computationally more expensive.

Once the least squares solution for the rational fraction matrix-coefficients (both [α i] and \([\hat {\beta }_i]\)) is computed, the residue and the numerator matrix-coefficients may be separated using a simple, fully determined de-convolution solution as shown in [12]. Hence for each model order iteration, the complete set of [α], [β], \([\hat \beta ]\) and [R] coefficients is available i.e. Equation 10.4 is fully defined.

$$\displaystyle \begin{aligned}{}[H(s)]= [\alpha(s)]^{-1} [\beta(s)] + [R(s)]= [\alpha(s)]^{-1} [\hat{\beta}(s)] {} \end{aligned} $$
(10.4)

Where,

$$\displaystyle \begin{aligned}{}[\alpha(s)] = \bigg[\sum_{i=0}^m \Big[[\alpha_i] s^i \Big]\bigg]_{N_o\times N_o}\end{aligned}$$
$$\displaystyle \begin{aligned}{}[\beta(s)] = \bigg[\sum_{i=0}^{m-1} \Big[[ \beta_i ] s^i \Big]\bigg]_{N_o\times N_i }\end{aligned}$$
$$\displaystyle \begin{aligned}{}[R(s)] = \bigg[\sum_{i= -n_l}^{n_u} \Big[[R_i ] s^i \Big]\bigg]_{N_o\times N_i}\end{aligned}$$
$$\displaystyle \begin{aligned}{}[\hat{\beta}(s)] = \bigg[\sum_{i=0}^{m-1} \Big[[I][ \beta_i ] s^i \Big]\bigg]_{N_o\times N_i } + \bigg[\sum_{i=0}^m \Big[[\alpha_i] s^i \Big]\bigg]_{N_o\times N_o} \bigg[\sum_{i= -n_l}^{n_u} \Big[[R_i ] s^i \Big]\bigg]_{N_o\times N_i}\end{aligned}$$

Normally, the numerator matrix-coefficients remain unused and are discarded [8] or they are expressed in the form of denominator matrix-coefficients [7] to improve the speed of the least-squares solution. The denominator coefficients are used to construct a companion matrix, and its eigen-values and eigen-vectors (state-vectors of the order of the polynomial) are calculated. These poles and vectors are then used to build the stabilization chart.

However, instead of utilizing anything but the denominator matrix-coefficients, all the available information is used to compute the residues. The algorithm from Vu [13, 14] allows the inverse of a square matrix-coefficient polynomial to be described as a ratio of its adjoint (matrix-coefficient) polynomial and the characteristic (monic) equation (Equation 10.5).

$$\displaystyle \begin{aligned}{}[\alpha]^{-1}_{N_o\times N_o} = \frac{\bigg[\sum_{i=0}^{(N_o-1)m} \Big[[ \alpha_i^+]_{N_o\times N_o} s^i\Big]\bigg]}{\sum_{i=0}^{N_om} d_i s^i} = \frac{[\alpha^+]}{d} {} \end{aligned} $$
(10.5)

The algorithm requires recursive computation of a new set of matrices as defined in Equation 10.6 and coefficients as defined in Equation 10.7 for the nth model order.

$$\displaystyle \begin{aligned}{}[B_{d,c}] = \sum^{c}_{v=1}\sum^{d}_{w=1}\Big([B_{d-w,c-v}][\alpha_w][\alpha_0]^{v-1}\Big) {} \end{aligned} $$
(10.6)

Where, c = 1, 2, …, N o; d = 0, 1, …, N o ∗ n; and, [B 0,c] = [α 0]c

$$\displaystyle \begin{aligned} b_{j, i} = \frac{1}{j}\sum^{j}_{c=1}\sum^{i}_{d=0}\Big((-1)^{c-1}b_{j-c, i-d}*trace([B_{d, c}])\Big) {} \end{aligned} $$
(10.7)

Where,i = 0, 1, 2, …, N o ∗ n

The coefficients required in Equation 10.5 are then computed using the Equations 10.8 and 10.9.

$$\displaystyle \begin{aligned} d_i = a_{N_o,i} {} \end{aligned} $$
(10.8)
$$\displaystyle \begin{aligned}{}[\alpha^+_i] = \sum^{N_o-1}_{c=0}\sum^{i}_{d=0}\Big((-1)^{c}b_{N_o-1-c, i-d}*trace([B_{d, c}])\Big) {} \end{aligned} $$
(10.9)

The eigen-solution using the companion matrix leads to the same poles as the roots of the characteristic equation [15]. In other words, the characteristic equations of a square polynomial matrix and the companion matrix constructed using its matrix-coefficients is identical. The monic denominator-polynomial can hence be used to to obtain the eigen-frequencies present in the frequency range of interest.

The FRF matrix (or generally the transfer function matrix) is expressed using Equations 10.4 and 10.5 as:

$$\displaystyle \begin{aligned}{}[H(s)]_{N_o\times N_i}= \frac{[\alpha^+(s)]_{N_o\times N_o}[\beta(s)]_{N_o\times N_i}}{d(s)_{1\times 1}} + [R(s)]_{N_o\times N_i} {} \end{aligned} $$
(10.10)

The residues for each of the poles are computed by substituting the partial-fraction model (Equation 10.11) of the FRF in Equation 10.10.

$$\displaystyle \begin{aligned} \Big[H(s)\Big]_{N_o\,\times\,N_i}= \sum_{r=0}^{N_r}\bigg(\frac{[A_r]_{N_o\,\times\,N_i}}{s-\lambda_r} + \frac{[A_r]^*_{N_o\,\times\,N_i}}{s-\lambda_r^*}\bigg) + \bigg[\sum_{i=-n_l}^{n_u}[R_i]s^i\bigg]_{N_o\,\times\,N_i} {} \end{aligned} $$
(10.11)

In conjunction with Equation 10.17, UMPA uses this equation system for the second least-squares step for estimating the scaling factors and modal vectors [8]. Equation 10.12 is over-determined using the frequencies available according to the frequency range selected.

(10.12)

By multiplying the resulting equation throughout by the factor (s − λ r), the equation for the residue [A r] of the rth pole emerges (Equation 10.13).

$$\displaystyle \begin{aligned} \Big[A_r\Big]_{N_o\,\times\,N_i} = \lim_{s\to\lambda_r} \bigg(\Big[H(s)\Big]*(s-\lambda_r)\bigg) = \lim_{s\to\lambda_r}\bigg(\Bigg[\frac{[\alpha^+(s)][\beta(s)]}{d(s)} + [R(s)]\Bigg]*(s-\lambda_r) \bigg) {} \end{aligned} $$
(10.13)

Since λ r is a root of the polynomial represented by d(s), the limit takes an indeterminate form (the numerator and denominator both vanish at λ r). However, since the denominator is now a monic polynomial, L’Hôpitals rule may easily applied to compute the limit for the residue.

$$\displaystyle \begin{aligned} \Big[A_r\Big]_{N_o\,\times\,N_i}= \bigg(\frac{[\alpha^+(s)][\beta(s)]}{d'(s)}\bigg) \bigg|{}_{s=\lambda_r} {} \end{aligned} $$
(10.14)

Hence, the residue is calculated for each pole at each model order using Equation 10.15. This added information is beneficial in applying an additional filter to the stabilization chart during the pole selection stage to test for consistency of residues between successive model order iterations.

(10.15)

The residue in Equation 10.15 is evaluated in the Z-domain and it must be scaled back to the complex-domain of the original FRFs so that it may be used to reconstruct FRFs. The scaling factor is derived in Equation 10.16 and is dependent on the Z-domain pole.

$$\displaystyle \begin{aligned} \Big[A_r\Big]_{(j\omega)}=\frac{\Big[A_r\Big]_{(s)}}{s_r*\Delta t} {} \end{aligned} $$
(10.16)

It is also noteworthy that the residue is of unity rank. The rows of the residue matrix are the modal vectors scaled by appropriate entries from the participation vectors. Therefore, the row-wise (or column-wise) MAC is expected to be unity, indicating complete linear dependency of the residue matrix on each row/column. The structure of the residue matrix is shown in Equation 10.17.

$$\displaystyle \begin{aligned} \Big[A_r\Big]_{N_o\,\times\,N_i}= Q_r [L_r]_{N_o\,\times\,2N_r} [\psi_r]^H_{2N_r\,\times\,N_i} {} \end{aligned} $$
(10.17)

Here, Q r is the modal scaling factor, [L r] is the matrix of modal participation vectors and [ψ r] is the matrix of mode shape vectors. H denotes the Hermitian (complex-conjugate transpose) operation on a matrix.

The comparison of the residue matrices obtained from the proposed methodology and the “traditional” process can hence be accomplished using MAC at each pole. Additionally, MPC and MPD metrics [16] that are applied to modal vectors can also be applied to the residue matrix after reshaping it into a vector.

A summary of the current modal parameter estimation process, alongside the proposed method, is shown in Fig. 10.1.

Fig. 10.1
figure 1

The basic modal parameter estimation algorithm along with proposed modifications to bypass the second stage

Full size image

10.3 Analysis

The proposed method was evaluated on a theoretical system which is shown in Fig. 10.2. The lumped parameter model’s FRF matrix was constructed using complete information about the masses, stiffness coefficients and proportional-damping coefficients. The square FRF (9 × 9) matrix was then truncated to a rectangular size ((N o =) 4 outputs and (N i =) 9 inputs) to mimic experimental matrix sizes.

Fig. 10.2
figure 2

The 9-DoF lumped mass system used for evaluating the proposal. The lumped masses are represented by the solid blocks, while the dashed lines each represent a spring and dash-pot connecting the masses. The blue highlights represent the input locations (the long dimension of the FRF matrix), while the green highlight implies the output locations that are “observed” i.e. DoFs which the FRF matrix is truncated to (the short dimension of the FRF matrix)

Full size image

Figure 10.3 shows the Complex Mode Indicator Function (CMIF) used to select a suitable frequency range of interest for the MPE process. The model order (m) is a user-input and for this case ranged from 2 to 10. The proposed method was applied post the least squares estimate of the matrix-coefficients. Using the traditional process, the stabilization chart (Fig. 10.4), was constructed to select valid poles and was limited to a participation vector consistency check (blue diamonds). Due to the proposed approach, the calculation of residues for all computed poles allowed for an additional consistency check (for residues). This was applied to the pole results to obtain the stabilization chart shown in Fig. 10.5. Table 10.1 shows the tolerances used to construct these stabilization charts.

Fig. 10.3
figure 3

Complex Mode Indicator Function for the system under test. The bands limit the number of frequencies used for the least squares solution from 13.75 to 40 Hz

Full size image
Fig. 10.4
figure 4

Stabilization with participation vector comparison. Solid symbols indicate the selected poles

Full size image
Fig. 10.5
figure 5

Stabilization chart with residue comparison between iterations. The solid symbols indicate the selected poles and are numerically the same as the ones shown selected in Fig. 10.4

Full size image
Table 10.1 Tolerances utilized for the construction of the stabilization chart. The legends in Figs. 10.4 and 10.5 may be referred for the symbols used [8]
Full size table

From a comparison of the Figs. 10.4 and 10.5, it is observed that the poles showing consistency in participation vector estimates also show consistency in their residue estimates. Although this is expected for the current case due to absence of noise, it must be noted that this extra consistency parameter may be useful towards plotting very clear stabilization charts in practical situations and for autonomous parameter estimation. It has been shown that inclusion of the residue information (from the second-step least squares computation) in the pole selection phase is seen to improve the clarity of the stabilization chart [16].

To compare the models obtained from the two approaches, the residues were also computed using the second least-squares step for the selected poles in Fig. 10.4. The two sets were compared using a modal assurance criterion approach. This is possible due to the structure of the residue matrix, shown in Equation 10.17. The column-wise MAC was expected to show complete linear dependence of the columns and this was indeed the case. Figure 10.6 shows a MAC plot of residue for each of the 6 poles (3 positive frequencies and 3 negative frequencies). The columns of the residues correspond to the long dimension (4 elements in 9 vectors) and show a unity MAC value throughout. The MAC plots also indicate that the residues from the proposed method are of unity rank since the residues from the traditional two-step process are forced to be of unity rank.

Fig. 10.6
figure 6

MAC matrix for dependence of columns of the residue matrix obtained from traditional and the proposed process for the three poles

Full size image

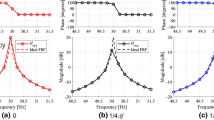
The FRFs were then reconstructed using the residue from the traditional as well as the proposed approach, and plotted against the original FRFs (Fig. 10.7, for example). It may be seen from the reconstructed FRF curves that the proposed process identifies the same modal model as traditional process. Of course, a deviation between the two modal models is to be expected in presence of noise in the measurements.

Fig. 10.7
figure 7

Comparison of reconstructed FRFs using the traditional two-step approach and the proposed one-step approach against the original FRF for input 1 and output 1

Full size image

The residues, after being reshaped as vectors were also plotted in the complex plane (Fig. 10.8) and the mean phase correlations indicated that both the methods resulted in real modes. The low deviations from the mean phase for all the poles and the imaginary nature of the residues both indicate a correct estimation of the modal model.

Fig. 10.8
figure 8

Plot of the complex residues to evaluate the Mean Phase Correlation (MPC) and Mean Phase Deviation (MPD). No scaling of the residues resulting from the proposed methodology has been performed

Full size image

It is worthwhile to mention that there is no restriction on the complexity or scaling of the modal residue under the proposed scheme. There are various scaling strategies for the participation vectors that have been applied to clear up the stabilization diagram and ease the process of pole selection for the user through a clean stabilization chart [16]. From Fig. 10.8 it can also be seen that the residue matrix obtained in the two cases is practically identical.

10.4 Conclusions

In the presented work, a “single-step” modal parameter estimation algorithm (Direct Estimation of Residues from Rational-fraction Polynomials, or DERRP) is proposed. The procedure is based on the computation of the adjoint matrix-coefficient polynomial and the characteristic equation from a rational fraction matrix-description of the measured FRF matrix. It is shown that the proposed algorithm makes the residues available for comparison during the plotting of the stabilization chart. Modal parameters are estimated using the proposed and the traditional two-step approach for a multi-degree-of freedom lumped mass system and compared using existing model-validation techniques. The results indicate that the estimated parameters are accurate and completely define the modal model of the system under investigation.

The merit of the proposal lies in the fact that complete residue information is available to be used at the pole selection phase. Hence, the poles that are extracted from the stabilization chart convey a greater statistical confidence. Additionally, the pole selection phase is essentially transformed to allow model validation. With the (scaled) residue information for selected poles already available, the need for the second least-squares solution step is eliminated. The algorithm is expected to be helpful in effectively automating the pole selection process and hence the complete MPE process.